Abstract
Ferro liquids derive their magneto–viscous behavior from the suspended magnetic nanomaterial that enables tunable changes in temperature, as well as nano-structured fluid characteristics. A theoretical model that depicts the bioconvection flow of cross nanofluid with a magnetic dipole subjected to a cylindrical surface was developed and numerically solved. The model encountered nonlinear thermal radiation, activation energy, and second order slip. The flow equations were reduced and are presented in dimensionless forms, and they were solved numerically using the shooting technique, which is a built-in feature of MatLab. The model encountered symmetrical constraints for predicting velocity, temperature, concentration, and gyrotactic microorganism distribution and profiles. Moreover, the numerical values were computed for local Nusselt number, local Sherwood number, and motile density number against each physical parameter.
1. Introduction
Nanofluids have increasingly attracted the interest of researchers due to the beneficial aspects of their use in several industrial processes and fields such as geothermal technology, mechanical-chemistry, nuclear reactor cooling, microelectronics, product degradation, refrigerants for nuclear reactors, solar cells, oil emulsions, and bio-medical applications. Recently, for scientific purposes nanoparticles have helped to develop a better understanding of the relationship between heat and mass analysis phenomenon in the presence of chemical reactions. Nanofluids are a mixture of a base fluid (ethylene glycol, oil, and water) and nanoparticles (1–100 nm) that are uniquely dissolved as a suspension. The presence of nanoparticles in a base liquid boosts its thermal features, which leads to a significant enhancement in various thermal extrusion systems. Due to stable and improved thermal conductivity, the nanoparticles play valuable roles in the cooling processes, solar energy systems, radioactive waves, chemo-therapy, and alternate sources of energy. The initial idea that; ed towards such enriched thermo–physical nanoparticles was reported by Choi [1] in 1995. Later on, Buongiorno [2] established several slip mechanisms of nanofluids that deal with the roles of Brownian motion and thermophoresis aspects in such homogenous mixtures. Comprehensive studies in literature that examine heat and mass transportation based on Buongiorno’s nanofluid model [2] are available. Uddin et al. [3] investigated the thermal potential of nanofluid utilization over a convectively heated vertical surface featuring Newtonian heating. Sui et al. [4] investigated a Maxwell nanofluid with slip effects that was characterized by generalized flux expressions. A thermally radiative nanofluid flow with uniform thermal conductivity under the influence of magnetic field was numerically inspected by Afzal and Aziz [5]. Fetecau and co-workers [6] reported an interesting extension associated with the natural convective flow of fractional nanofluids configured by an isothermal plate. Based on reported graphical computations, it has been claimed that the change in wall shear stress is more progressive for a fractional order nanofluid than an ordinary nanofluid. The rheological consequences of a Williamson nanofluid with thermal radiation, as caused by a stretching and shrinking geometry, was addressed by Bhatti and Rashidi [7]. Turkyilmazoglu [8] examined the heat transfer characteristics in the single phase flow of nanoparticles over a wall jet. Nadeem et al. [9] dealt with the flow of a micropolar nanofluid induced by an oscillatory porous surface subjected to slip consequences. A practically reported investigation concerned with cooling of solid particles with nano-materials over a moving bed was reported by Turkyilmazoglu [10]. Waqas et al. [11] discussed multiple momentum and thermal slip features over a moving disk, where a dimensionless model was proposed and numerically tackled via a shooting procedure. The analytical evaluation of third grade nanofluid over an accelerated surface was done by Khan and Shehzad [12]. A stability analysis for single phase nanofluid flow influenced by magnetic field was recently performed by Turkyilmazoglu [13]. Some critical reviews have pointed out that a strong understanding for nano fluid behavior has not been established yet, and a lot of further research is needed in the field of nanofluids’ property characterization [14,15].
The fascinating application of bioconvection in biological systems, bio-technology, and medical sciences has drawn extensive scientific interest and investigations, especially in the 21th century. The phenomenon of bioconvection is associated with the floating of microorganisms at the macroscopic level due to density gradients. In fact, microorganisms convey a diverse palette of materials in industrial and commercial products like ethanol and fertilizers. Molecular heat transfer or convection is considered a physical phenomenon that is associated with the transpiration of heat within matter. Naturally, it has been observed that cold and hot winds bring changes in environmental temperature. Microorganisms are considered a source of convection in liquids, and they mimic the movement of nanoparticles in nanofluids. The phenomenon of bioconvection is assumed to be an impulsive unicellular microbe movement within fluids that results in their unequal distribution due to their relative densities with respect to fluid molecules. Usually, the movements of unicellular microbes are classified as taxis, and, depending upon the stimulus and direction of movement, the taxis can further be subcategorized asphototaxis, gyrotaxis, gravitaxis, etc. The bioconvection patterns of fluids with unicellular microbes are highly sensitive to illumination with electromagnetic waves. Therefore, phototaxis is regarded as the key factor responsible for changes in bioconvection patterns because most microbes are positively phototactic. Bioconvection has applications in bio-technology for biofuels. Bioconvection is usually classified according to various types of microorganisms like chemotaxis, gyrotactic, and geotactic microorganisms. An interesting feature about microorganisms is their movement of such self-oriented objects in specified direction in a given environment. Gyrotactic microorganisms are encountered in the practical applications like hydrogen and biodiesel production, which is considered one of the most useful energy resources in water treatment plants. In order to further explore the significance of such microorganisms, it is necessary to explore the behavior of such swimming microorganisms, along with mass transfer consequences. The phenomenon of bioconvection is related to the microscopic level swimming of such microorganisms in random liquids. Some useful applications based on the bioconvection phenomenon involve bio-fuels, enzymes, biosensors, bio-reactors, agriculture biotechnology, and nano-drug formulations. It has been emphasized that microorganisms are self-repelled, while nanoparticle transpiration is based on Brownian motion and thermophoresis features. However, the utilization of microorganisms in nanoparticles has been found to improve the stability of nanoparticles and to enhance their thermo–physical features. The leading approach to bioconvection, specified for nanofluids, was initiated by Kuznetsov [16,17], and this approach was further worked on by numerous researchers in the presence of different flow features. The suspension of magnetized nanoparticles containing gyrotactic microorganisms was numerically examined by Akbar and Khan [18]. Raju et al. [19] focused on the wedge flow of Casson nanofluid subjected to the gyrotactic microorganisms and thermal radiation features. Khan et al. [20] reported the gyrotactic microorganism phenomenon in a moving cone with a suspension of nanoparticles. Numerical continuations were successfully performed by employing a finite difference technique. The study of a mixed convection nanofluid flow with the involvement of bioconvection in a vertical cylinder was handled by Sudhagar et al. [21]. Khan et al. [22] focused on the impact of nonlinear thermal radiation in flow of the Burgers nanofluid, which contains gyrotactic microorganisms. Sohail et al. [23] focused on the rheological prospective of the bioconvection flow of a non-Newtonian nanofluid with temperature-dependent thermal characteristics. 3D simulations for the slip flow of a Casson nanofluid with gyrotactic microorganisms were presented by Nayak et al. [24]. Khaled et al. [25] utilized bioconvection in a tangent hyperbolic nanoliquid in the presence of nonlinear thermal radiation features. Tlili et al. [26] explored the activation energy and thermal radiation aspects of the flow of an Oldroyd-B nanofluid configured by a stretched cylinder. The flow pattern was further truncated with the amplification of second order slip and convective boundary constraints near the surface.
Ferroliquids comprise an inimitable type of magnetized nanoparticles suspended in a solo domain and a transporting material. The basic concept of such ferromagnetic materials was conceptualized by Stephen [27]. Ferromagnetic material and energy transportation flow can be regulated by external magnetism, a subject that has attracted numerous scientists because its massive applicability in microelectro–mechanical systems (MEMS), lithographic patterning, chemical engineering, and biomedicine [28,29,30].
Due to their interdisciplinary dynamics and complex rheological features, the non-Newtonian materials are still objects of great appreciation in chemical, mechanical, and processing engineering fields. Substantially significant nonlinear materials include polymer solutions, slurries, human blood, polymer melts, paints, printing ink, gum solution, and honey. However, it is commonly stated that a single constitutive relation for explaining the all physical consequences of such non-Newtonian materials cannot be predicted. To this end, some diverse viscoelastic fluid models have been proposed in the literature; cross nanofluid is one of these models that has been characterized as a subclass of non-Newtonian fluid that has industrial importance due to the presence of its time constant. This fluid model is also used to synthesize the polymeric solutions. Some reported continuations of this non-Newtonian fluid model with different features and geometries can be seen in [31,32,33,34,35,36].
After carefully examining the literature, the main motivation of this investigation was to develop a mathematical model for the bioconvection of cross nanofluid with a magnetic dipole induced by a stretched cylinder in a symmetrical way. The reported novel flow problem was tackled via the following processes:
- The cross nanofluid was inspected with related equations over a stretching cylinder with magnetic dipole aspects.
- Nanofluid features, like Brownian movement and thermophoresis, were inspected via the famous Buongiorno nanofluid model.
- A famous ferroliquid was inspected to gather whether its thermal physical features were like those of non-Newtonian nanofluids.
- Heat transfer mechanisms were characterized by thermal radiation, variation thermal conductivity, and heat absorption generation features.
- Second order slip effects were implemented near the surface to control the boundary layer of moving nanoparticles.
- The well posed modeled equations for current flow problem were numerically tackled by imposing a shooting technique.
2. Flow Model
Figure 1 shows the flow problem of the time-dependent ferromagnetic flow of a cross nanofluid that was induced with a magnetic dipole. Additionally, nonlinear thermal radiation, activation energy, and gyrotactic motile microorganisms were affected by a dipole that was modeled over a stretching cylinder. The hydromagnetic properties contributed to the magnetization of the nanoliquid. The magnetic dipole, assumed to be along the y-axis, occupied the center from the surface. The magnetic dipole in the positive direction, which divided the cylinder in two symmetric parts, resulted in the same magnetic force that is associated with saturated ferroliquids. Second order slip relations were employed on the stretched surface. The variable thermal conductivity and thermal radiation were implemented in the energy equations, while the activation energy features were implemented in the concentration equation by taking symmetric parameters in account. The Joule heating and viscous effects were ignored by assuming that the internal heat transfer within the fluid particles was quite small. Convective Nield boundary constraints were carried out to perform the heat and mass transfer analyses. Considering the Buongiorno model, the thermophoresis and Brownian movement impact were introduced into the model. In view of such assumptions, the constructed flow model resulted in the following set of equations [35,36].
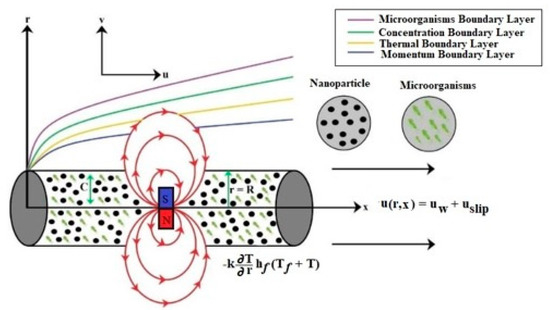
Figure 1.
Geometrical illustration of the flow problem.
The governing relations for thermal radiation and heat absorption and generation are expressed in the following forms:
In view of the above-defined relations, Equation (4) is modified into following form:
where and are velocity components, are cylindrical coordinates, is magnetic permeability, is the nanofluid density, is the volume suspension coefficient, is gravity, is nanoparticle concentration, is temperature, is the Stefan Boltzmann constant, is the nanoparticle density, are the temperature-dependent heat absorption/generation coefficients, is thermal conductivity, is the mean absorption coefficient, is the Brownian diffusion coefficient, is the liquid heat capacity to nanoparticles heat capacity ratio, is the heat source sink, is the chemical reaction, is the activation energy, is the power law index, is the thermophoretic diffusion coefficient, is the maximum amount of swimming cells, is chemotaxis, and , and represent the temperature, concentration, and microorganism density far away from the surface, respectively.
The above flow equations retain following boundary conditions:
The slip velocity defined in Equation (8) is assumed to be second order in following form [37,38,39]:
where is the Knudsen number, and are continual, is the molecular mean free path, and represents the momentum coefficient.
2.1. Interaction of Ferromagnetic Dipole
Aferroliquidis affected by magnetic force, which is subjected to amagnetic dipole with thescalar potential of:
where is the strength of the magnetic dipole The expression for magnetic force is given by:
The absolute magnetic field is directly tied to the seductive body force. The magnitude seductive intensity is given below:
In view of Equations (11) and (12), Equation (13) yields:
The expression of magnetization with temperature can be utilized in the following form:
where , and are magnetization, the paramagnetic constant and, the Curie temperature, respectively. It is known that a ferrohydrodynamic interaction must satisfy
2.2. Dimensionless Variables
In order to reduce the flow equations in dimensionless forms, the following dimensionless variables are reported [31,32]:
The proper utilization of the above-reported transformations in the governing flow equations yields:
where , , and are the non-dimensional velocity profile, temperature distribution, volumetric concentration of the nonmaterial, and the density of the motile microorganisms, respectively. Furthermore, is the curvature parameter, is the Weissenberg number, is the ferromagnetic parameter, is the mixed convection parameter, is the buoyancy ratio parameter, is the bioconvection Rayleigh number, is the Lewis number, is the radiation parameter, is the thermophoresis number, is the Brownian motion, is the Prandtl number, is the temperature ratio parameter, is the activation energy, is the chemical reaction parameter, is the heat source parameter, is the bioconvection constant, is the bioconvection Lewis number, is the Peclet number, is the time-dependent parameter, is the first order velocity slip, and is the second order velocity slip; these are defined below:
2.3. Physical Quantities
The physical quantities involved in the reported study are the wall shear stress , the local Nusselt number , the local Sherwood number , and the density of motile microorganisms , which are defined as:
The non-dimensional form of the above expression is:
where is the Reynolds number.
3. Numerical Approach
In this section, ashooting scheme is adopted to develop the numerical solution of non-dimensional differential Equations (18)–(20) with the boundary condition represented in Equations (21) and (22). Following the basic methodology of this technique, this dimensionless boundary value flow system was converted into first order system via the following substations:
with boundary conditions:
4. Physical Interpretation of Results
After successfully performing the numerical computations of formulated problem, this section discussesthe physical consequences of various flow parameters like the ferrohydrodynamic interaction parameter, including the Weissenberg number , the first order velocity slip , the second order velocity slip , the mixed convection parameter , the bouncy ratio parameter , the time-dependent parameter , the Prandtl number , the thermophoresis parameter , the Biot number , the temperature ratio parameter , the Brownian motion , the bioconvection Raleigh number , the Lewis number , the bioconvection Lewis number , the Peclet number on the variation of velocity the temperature distribution the concentration distribution , and the density of motile microorganism profile Since this flow model wasbased on theoretical assumptions instead of experimental data, the physical parameterswere assigned fixed arbitrary values like , and . It is worth mentioning that all the graphical analyses were reported for two cases—flat plate and stretching cylinder Such a comparative analysis wasmore useful to appreciate the significance of each parameter on both configurations simultaneously.
Figure 2 interprets the physical behavior of ferro-hydrodynamic interaction parameter against the velocity profile The flow velocity was reduced with higher values of the ferro-hydrodynamic interaction parameter . It was further noticed that the decreasing trend wasmore dominant in case of the stretching cylinder. Figure 3 reveals the impact of the Weissenberg number on the velocity distribution The declining trend wasdue to variations of associated with relaxation times, where the velocity field effectivelydecelerated. Physically, an incremental increase in resulted in a larger relaxation time, which offered resistance to the flow and subsequently the velocity profile decreased. The results communicated in Figure 4 show a declining velocity distribution forseveral values of the first order velocity slip . The utilization of slip consequences altered the velocity distribution and control the associated boundary layer. The decreasing trend was more permanent for . The slip flow phenomenon has valuable applications in the petroleum industry and geo-physics. Figure 5 portrays the impact of the second order velocity slip on . Again, similar to first order slip parameter, a decreasing variation in was been captured for the second order slip . The change in velocity distribution for the mixed convection parameter is shown in Figure 6. Physically, the mixed convection parameter reflected the ratio of the buoyancy force to the viscous force. The higher values of reflected the higher buoyancy ratio force; consequently, an increasing variation in fluid particles was observed. The behaviors of the bouncy ratio parameter and the bioconvection Raleigh number are illustrated in Figure 7 and Figure 8, respectively. It was found that the velocity profile decayed with growing the values of both the bouncy ratio parameter and the bioconvection Raleigh number . When was assigned its maximum value, the buoyancy force due caused bybioconvection reduced the fluid velocity. It was found that the effects of various temperature, concentration, and gyrotactic microorganism parameters on velocity were quite small, though thisis not discussed here.
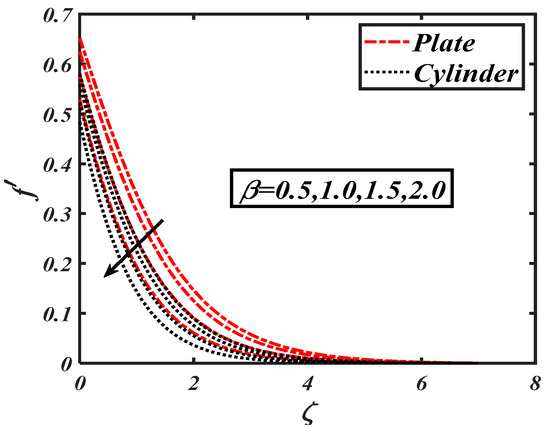
Figure 2.
Impact of the ferromagnetic parameter () on the variation of velocity ().
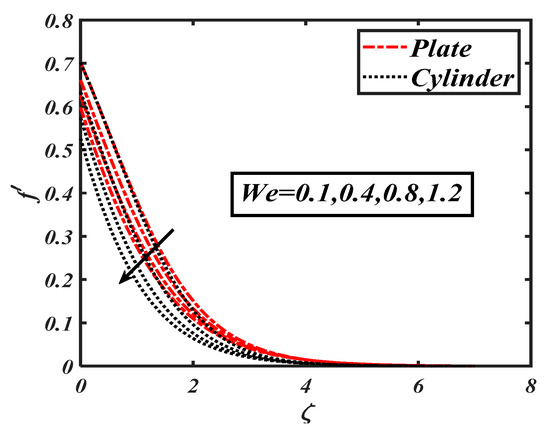
Figure 3.
Impact of the Weissenberg number () on .
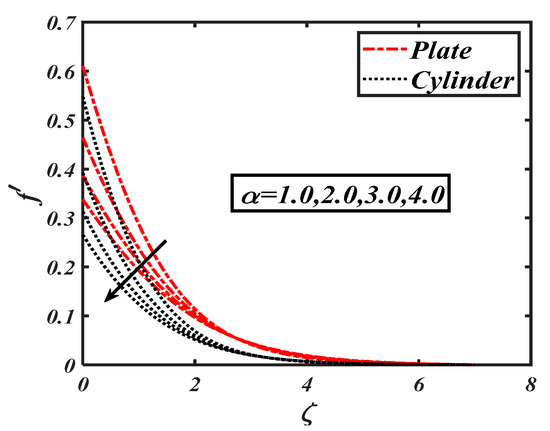
Figure 4.
Impact of the first order velocity slip () on .
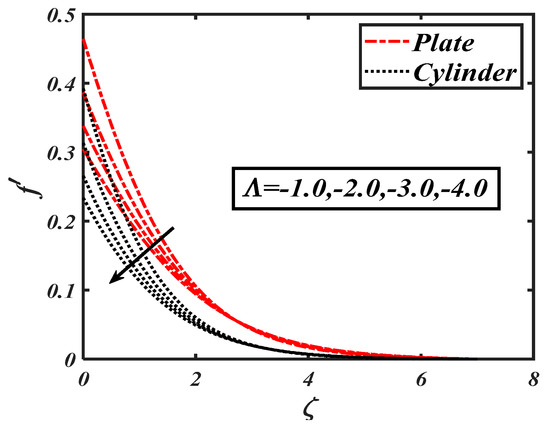
Figure 5.
Impact of the second order velocity slip () on .
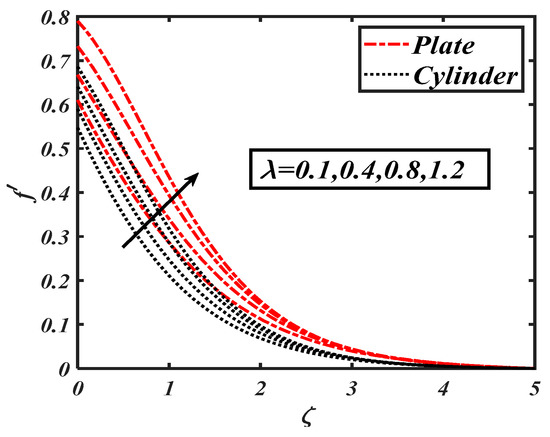
Figure 6.
Impact of the mixed convection parameter () on .
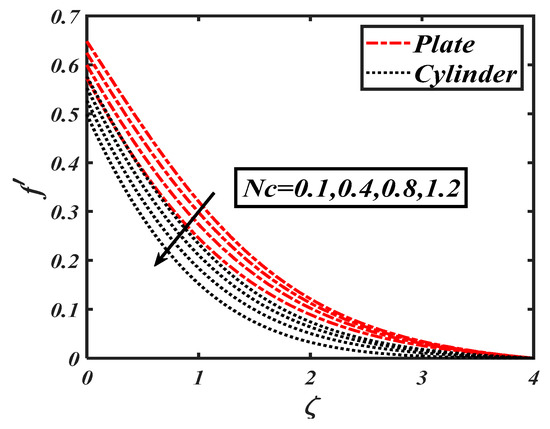
Figure 7.
Impact of the bouncy ratio parameter () on .
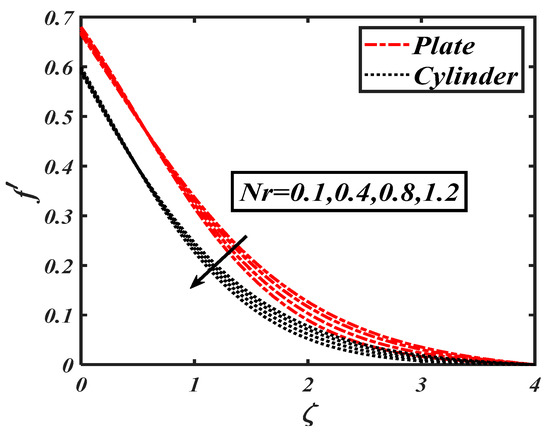
Figure 8.
Impact of the Raleigh number () on .
The change in the temperature distribution for various parameters is explored in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Again, the graphical results are reported for flat surface by taking and stretching cylinder with . Figure 9 addressed the significance of ferro-hydrodynamic interaction parameter on the temperature field . The presence of ferrohydrodynamic interaction parameters is more useful forimproving the temperature field , which is more convenient for flat surface geometry.
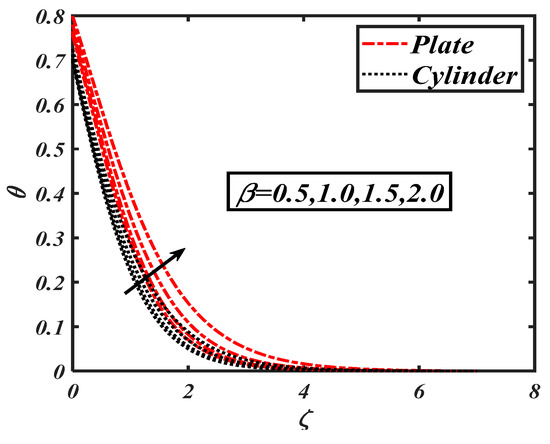
Figure 9.
Impact of on the temperature field ().
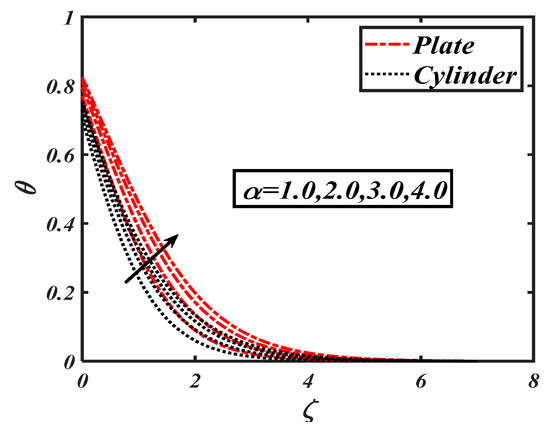
Figure 10.
Impact of on .
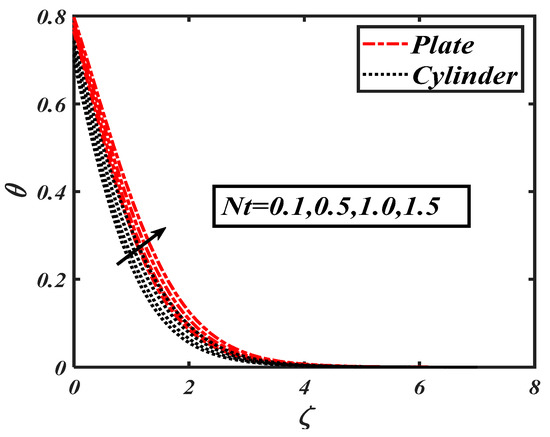
Figure 11.
Impact of the thermophoresis parameter () on .
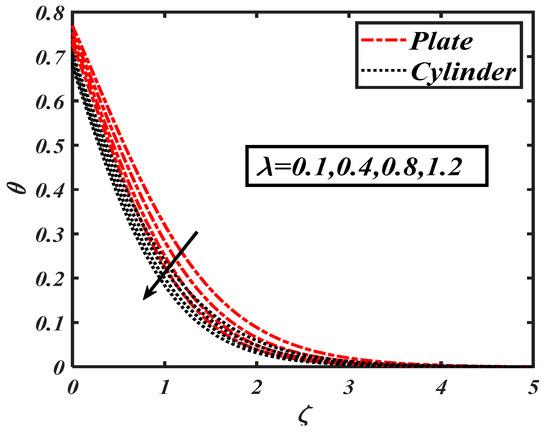
Figure 12.
Impact of on .
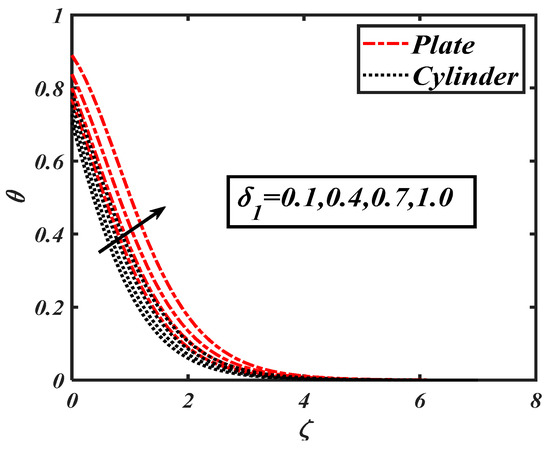
Figure 13.
Impact of the heat source parameter () on .
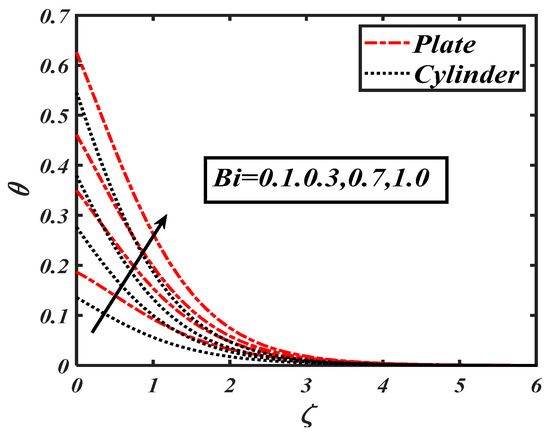
Figure 14.
Impact of the Biot number () on .
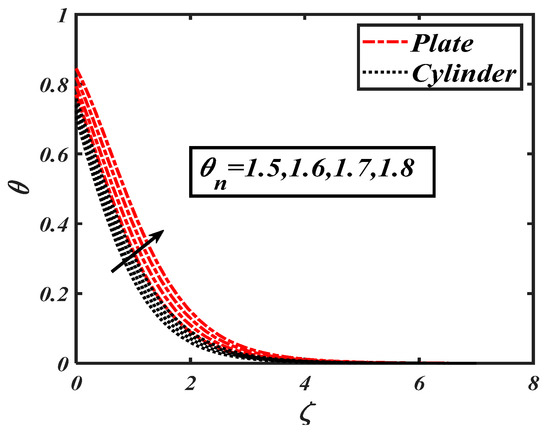
Figure 15.
Impact of the temperature ratio parameter() on .
Figure 10 shows the influence of the first order slip parameter on It is seen that increased with the increasing of . Figure 11 shows the role of the thermophoresis parameter on temperature field It was noticed that higher values of caused an efficient enhancement of temperature behavior. The thermophoresis phenomenon wasassociated with fluid particle motion from hot to cold regions due to an increasing temperature gradient. The effectof the mixed convection parameter on the temperature distribution is shown in Figure 12. It is evident that temperature distribution decreased with the growing of .
Figure 13 shows the observations based on the variation of the heat source parameter Physically, heat source is considered an external source of energy thatefficiently enhances nanoparticle temperature. The graphical explanation for the Biot number versus temperature distribution is shown in Figure 14. From the figure, it can be estimated that increased with the rising values of . The Biot number had a relationship with the heat transfer coefficient in which temperature fewup to themaximum level. Whensimulating the overall physical consequences of all these parameters, it was found that the changes in temperature due to heat source parameter, Biot number, and the thermophoresis parameter were progressive.
Figure 15 shows the variation of the temperature ratio parameter on the nanoparticle temperature . The temperature distribution was upturned as was assigned maximum values.
The concentration of nanoparticles was examined for various parameters, as shown in Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20. The impact of the thermophoresis variable on the concentration profile is shown in Figure 16. In increased concentration distribution was impacted by variations of due to temperature and concentration gradients. Figure 17 shows the effects of the Brownian motion on the concentration distribution . By comparing the change in concentration due to these flow parameters, it was found that the activation energy and thermophoresis parameters were more effective atenhancing the concentration profile.
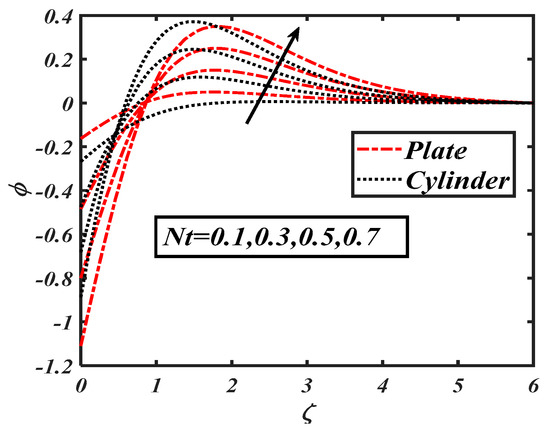
Figure 16.
Impact of on the concentration profile ().
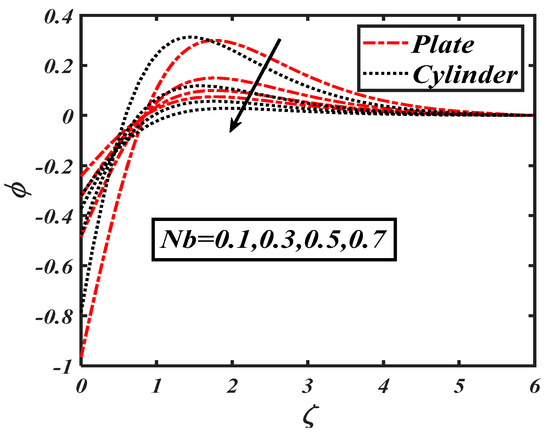
Figure 17.
Impact of the Brownian motion () on .
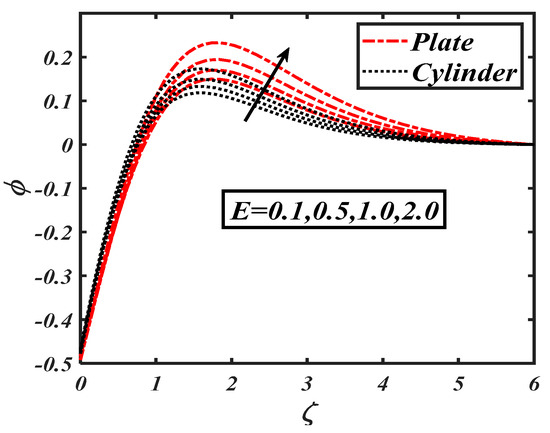
Figure 18.
Impact of the activation energy constant () on .
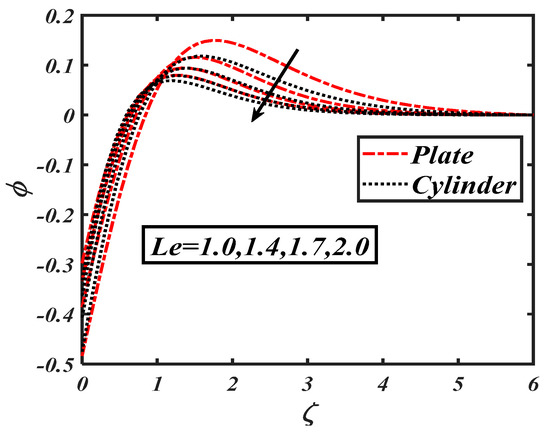
Figure 19.
Impact of the Lewis number () on .
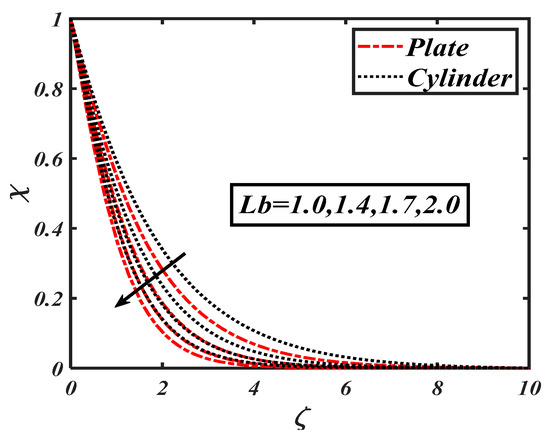
Figure 20.
Impact of the bioconvection Lewis number () on microorganism concentration ().
The Brownian motion, which is the random movement of fluid particles, was found to more effectively reduce the concentration distribution. Figure 18 shows the impacts of the activation energy constant on . The physical activation energy is the minimum energy amount which is necessaryfor each step of the reaction process. Figure 19 characterizes the impact of the Lewis number on A decrease in the concentration distribution is reported due to the fact that the Lewis number wasinversely proportional to the mass diffusion. The significance of the bioconvection Lewis number on the density of motile microorganisms is shown in Figure 21. It is seen that microorganism concentration declined with increases in the bioconvection Lewis number. Figure 22 demonstrates the deviation of the Peclet number versus the microorganism profile The relationship of the density of microorganism decay with the rising of Peclet number can be clearly observed. The higher values of corresponded to a minimum motile diffusivity, due to which a declining microorganism was configured. Figure 23 shows the effect of , which is the bioconvection Rayleigh number, on , which increased with an increasing The output of on is shown in Figure 23. It wasobserved that an increment in led to an increment in In was further found that changes in the microorganism profile werequite dominant for the bioconvection Lewis number and Peclet number.
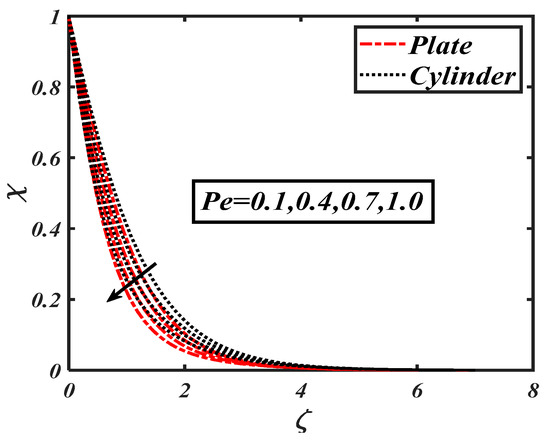
Figure 21.
Impact of the Peclet number () on .
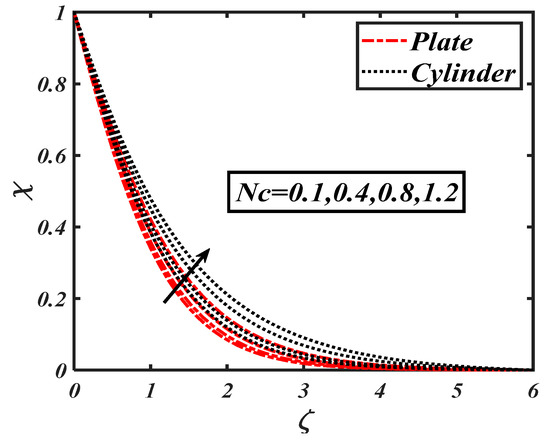
Figure 22.
Impact of the bioconvection Rayleigh number () on .
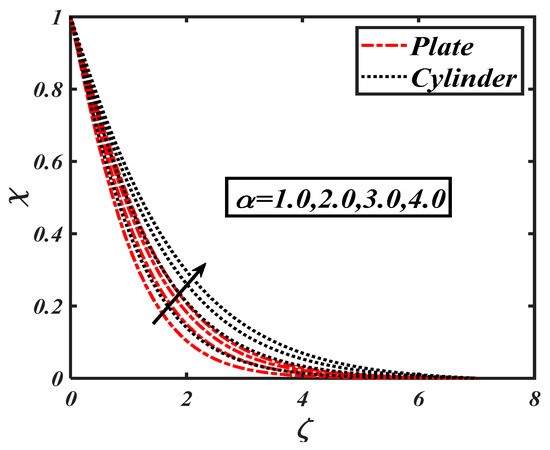
Figure 23.
Impact of on
The variation in for various values of , and is shown in Table 1. Here, the numerical results were update for the moving plate and the stretching cylinder It was found that increased with enlarged values of and , while the reverse trend wasrevealed for all remaining parameters. Moreover, it is important to remark that theincreasing trend for the moving plate case wasrelatively minimal. Table 2 shows the numerical computations for against various values of , and An increasing change in was observed for , and Table 3 shows that increased by varying , and ; however, the opposite numerical iterations were noted for , and The numerical treatment for in view of involved flow parameters like , and for two different values of is shown in Table 4. It was noticed that got higher values for , and However, with the increment of and for both cases, decreased. Finally, Table 5 summarizes the range of various involved parameters, as well as the response of velocity, temperature, concentration, and microorganism profiles against these flow parameters.

Table 1.
Variation of for different values of , and

Table 2.
Numerical variation in the local Nusselt number for , and Pr: Prandtl number.

Table 3.
Numerical variation in the local Sherwood number for , and

Table 4.
Numerical variation in local motile density for , and

Table 5.
The range of parameters and theirresponse tovelocity, temperature, concentration, and microorganism profiles.
5. Conclusions
The current research was concernedwith thebioconvection flow of a cross nanofluid over a stretched surface that wasexposed to a magnetic dipole. The analysis wassupported by novel multidisciplinary features like thermal radiation, heat absorption generation, activation energy, and the second order slip. The governing equations for the present flow model were constructed and numerically solved using the shooting procedure. The graphical results for both flat configuration and stretched cylinder were reported for each flow parameter. The main observations are summarized as:
- For the viscous case, i.e., the fluid velocity was larger than that of .
- When , the flow problem was reduced to a flat plate, while represents the flow induced by the stretching cylinder.
- The effects of these parameters were more effective for the plate than the cylinder.
- The variation of slip factors, the buoyancy ratio constant, the Rayleigh number, and the ferrohydrodynamic interaction parameter decayed the velocity profile for the flat plate and the stretching cylinder.
- More improved temperature distribution was claimed with the interaction of slip factors, the Biot number, the ferrohydrodynamic interaction constant, and the curvature parameter. The change in temperature wasmore dominant for flow in the flat plate case than the stretching cylinder case.
- The increase of the temperature ratio parameter, the thermophoresis parameter, and the Brownian motion constant led to anenhanced temperature profile.
- The presence of activation energy and the thermophoresis parameter increased the concentration profile, while a decreasing trend was noticed with the Lewis number.
- The microorganism distribution decreased with thePeclet number and thebioconvection Lewis number.
- It was further found that the buoyancy ratio constant and the first order slip parameter canlead to increments in the microorganism distribution.
- The observations based on the reported results can be used to improve thermal extrusion processes, bio-technology, biofuels, enzymes, etc.
Author Contributions
Conceptualization, Z.A., K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T.; methodology, H.W., A.A., S.U.K. and S.A.M.; software, H.W., A.A., S.U.K., S.A.M.; validation, Z.A., K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T.; writing—original draft preparation, Z.A., K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T.; writing—review and editing, Z.A., K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T.; supervision, I.T.; project administration, K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T.; funding acquisition, K.A.-K., H.W., A.A., S.U.K., S.A.M. and I.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Authors are grateful to reviewers for useful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| are the velocity components |
| is the Brownian diffusion coefficient |
| is the magnetic permeability |
| is the nanofluid density |
| is volume suspension coefficient |
| is gravity |
| is the nanoparticle concentration |
| is temperature |
| determines the Stefan Boltzmann constant |
| is the nanoparticle density |
| is the strength of the magnetic dipole |
| is the thermal conductivity |
| is the mean absorption coefficient, |
| is the thermophoretic diffusion coefficient |
| is the liquid heat capacity to nanoparticles heat capacity ratio |
| is the heat source sink |
| is the chemical reaction, |
| is the activation energy |
| is the Power law index |
| is chemotaxis |
| is the maximum amount of swimmingcells |
| is the free stream temperature |
| is the free stream concentration |
| is the free stream microorganism density |
| is the Knudsen number |
| represents the momentum coefficients |
| is the molecular mean free path |
| is the magnetic force |
| is magnetization |
| is the paramagnetic constant |
| is the Curie temperature |
| is the dimensionless velocity profile |
| is the dimensionless temperature profile |
| is the dimensionless concentration profile |
| is the dimensionless microorganism profile |
| is the Weissenberg number |
| is the ferromagnetic parameter |
| is the mixed convection parameter |
| is the buoyancy ratio parameter |
| is the bioconvection Rayleigh number |
| is the Lewis number |
| is the radiation parameter |
| is the thermophoresis number |
| is Brownian motion |
| is the Prandtl number |
| is the temperature ratio parameter |
| is activation energy |
| is the chemical reaction parameter |
| is the heat source parameter |
| is the bioconvection constant |
| is the bioconvection Lewis number |
| is the Peclet number |
| is the time-dependent parameter |
| is the first order velocity slip |
| is the second order velocity slip |
| is the wall shear stress |
| is the local Nusselt number |
| is the local Sherwood number |
| is the density of motilemicroorganisms |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fuids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transf. 2005, 128, 240–250. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.A.; Ismail, A.I. MHD Free Convective Boundary Layer Flow of a Nanofluid past a Flat Vertical Plate with Newtonian Heating Boundary Condition. PLoS ONE 2012, 7, e49499. [Google Scholar] [CrossRef]
- Sui, J.; Zheng, L.; Zhang, X. Boundary layer heat and mass transfer with Cattaneo–Christov double-diffusion in upper-convected Maxwell nanofluid past a stretching sheet with slip velocity. Int. J. Therm. Sci. 2016, 104, 461–468. [Google Scholar] [CrossRef]
- Afzal, K.; Aziz, A. Transport and heat transfer of time dependent MHD slip flow of nanofluids in solar collectors with variable thermal conductivity and thermal radiation. Results Phys. 2016, 6, 746–753. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D.; Azhar, W.A. Natural Convection Flow of Fractional Nanofluids Over an Isothermal Vertical Plate with Thermal Radiation. Appl. Sci. 2017, 7, 247. [Google Scholar] [CrossRef]
- Bhatti, M.; Rashidi, M.M. Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. J. Mol. Liq. 2016, 221, 567–573. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Flow of nanofluid plane wall jet and heat transfer. Eur. J. Mech. B Fluids 2016, 59, 18–24. [Google Scholar] [CrossRef]
- Nadeem, S.; Ullah, N.; Khan, A.U. Impact of an oblique stagnation point on MHD micropolar nanomaterial in porous medium over an oscillatory surface with partial slip. Phys. Scr. 2019, 94, 065209. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Cooling of Particulate Solids and Fluid in a Moving Bed Heat Exchanger. J. Heat Transf. 2019, 141, 114501. [Google Scholar] [CrossRef]
- Waqas, H.; Shehzad, S.A.; Khan, S.U.; Imran, M. Novel Numerical Computations on Flow of Nanoparticles in Porous Rotating Disk with Multiple Slip Effects and Microorganisms. J. Nanofluids 2019, 8, 1423–1432. [Google Scholar] [CrossRef]
- Khan, S.U.; Shehzad, S.A. Brownian movement and thermophoretic aspects in third grade nanofluid over oscillatory moving sheet. Phys. Scr. 2019, 94, 095202. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Single phase nanofluids in fluid mechanics and their hydrodynamic linear stability analysis. Comput. Methods Programs Biomed. 2020, 187, 105171. [Google Scholar] [CrossRef] [PubMed]
- Minea, A.A.; Buonomo, B.; Burggraf, J.; Ercole, D.; Karpaiya, K.R.; di Pasqua, A.; Sekrani, G.; Steffens, J.; Tibaut, J.; Wichmann, N.; et al. NanoRound: A benchmark study on the numerical approach in nanofluid’s simulation. Int. Commun. Heat Mass Transf. 2019, 108, 104292. [Google Scholar] [CrossRef]
- Minea, A.A. A Review on Electrical Conductivity of Nanoparticle-Enhanced Fluids. Nanomaterials 2019, 9, 1592. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.V. The onset of nanofluidbioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 10–1421. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluidbioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 100. [Google Scholar] [CrossRef]
- Akbar, N.S.; Khan, Z.H. Magnetic field analysis in a suspension of gyrotactic microorganisms and nanoparticles over a stretching surface. J. Magn. Magn. Mater. 2016, 410, 72–80. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Hoque, M.M.; Sivasankar, T. Radiative flow of Casson fluid over a moving wedge filled with gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 575–583. [Google Scholar] [CrossRef]
- Khan, W.A.; Rashad, A.; Abdou, M.; Tlili, I. Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. Eur. J. Mech. B Fluids 2019, 75, 133–142. [Google Scholar] [CrossRef]
- Sudhagar, P.; Kameswaran, P.K.; Kumar, B.R.; Kameswaran, K.; Kumar, B. Gyrotactic Microorganism Effects on Mixed Convective Nanofluid Flow Past a Vertical Cylinder. J. Therm. Sci. Eng. Appl. 2019, 11, 041018. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A. Impact of nonlinear thermal radiation and gyrotactic microorganisms on the Magneto-Burgers nanofluid. Int. J. Mech. Sci. 2017, 130, 375–382. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Shah, Z.; Kumam, P.; Thounthong, P. Exploration of temperature dependent thermophysical characteristics of yield exhibiting non-Newtonian fluid flow under gyrotactic microorganisms. AIP Adv. 2019, 9, 125016. [Google Scholar] [CrossRef]
- Nayak, M.K.; Prakash, J.; Tripathi, D.; Pandey, V.S.; Shaw, S.; Makinde, O.D. 3D Bioconvective multiple slip flow of chemically reactive Cassonnanofluid with gyrotactic micro-organisms. Heat Transfer Asian Res. 2019, 49, 135–153. [Google Scholar] [CrossRef]
- Al-Khaled, K.; Khan, S.U.; Khan, I. Chemically reactive bioconvection flow of tangent hyperbolic nanoliquid with gyrotactic microorganisms and nonlinear thermal radiation. Heliyon 2020, 6, e03117. [Google Scholar] [CrossRef] [PubMed]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.; Imran, M. Activation Energy and Second Order Slip in Bioconvection of Oldroyd-B Nanofluid over a Stretching Cylinder: A Proposed Mathematical Model. Processes 2019, 7, 914. [Google Scholar] [CrossRef]
- Stephen, P.S. Low Viscosity Magnetic Fluid Obtained by the Colloidal Suspension of Magnetic Particles. U.S. Patent 3,215,572, 2 November 1965. [Google Scholar]
- Rosensweig, R. Heating magnetic fluid with alternating magnetic field. J. Magn. Magn. Mater. 2002, 252, 370–374. [Google Scholar] [CrossRef]
- Aminfar, H.; Mohammadpourfard, M.; Mohseni, F. Two-phase mixture model simulationof the hydro-thermal behavior of an electrically conductive ferrofluids in thepresence of magnetic fields. J. Magn. Magn. Mater. 2012, 324, 830–842. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Fetecau, C.; Muhammad, S. Effects on heat transfer ofmultiphase magnetic fluid due to circular magnetic field over a stretching surfacewith heat source/sink and thermal radiation. Results Phys. 2017, 7, 3353–3360. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Coll. Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.; Tlili, I.; Awais, M.; Shadloo, M.S. Significance of Bioconvective and Thermally Dissipation Flow of Viscoelastic Nanoparticles with Activation Energy Features: Novel Biofuels Significance. Symmetry 2020, 12, 214. [Google Scholar] [CrossRef]
- Khan, N.; Nabwey, H.A.; Hashmi, M.S.; Khan, S.; Tlili, I. Khan A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink. Symmetry 2019, 12, 62. [Google Scholar] [CrossRef]
- Azam, M.; Shakoor, A.; Rasool, H.; Khan, M. Numerical simulation for solar energy aspects on unsteady convective flow of MHD Cross nanofluid: A revised approach. Int. J. Heat Mass Transf. 2019, 131, 495–505. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Khan, S.; Waqas, H.; Nabwey, H.A.; Tlili, I. Utilization of Second Order Slip, Activation Energy and Viscous Dissipation Consequences in Thermally Developed Flow of Third Grade Nanofluid with Gyrotactic Microorganisms. Symmetry 2020, 12, 309. [Google Scholar] [CrossRef]
- Waqas, M.; Jabeen, S.; Hayat, T.; Khan, M.I.; Alsaedi, A. Modeling and analysis for magnetic dipole impact in nonlinear thermally radiating Carreaunanofluid flow subject to heat generation. J.Magn. Magn. Mater. 2019, 485, 197–204. [Google Scholar] [CrossRef]
- Li, Y.; Waqas, H.; Imran, M.; Farooq, U.; Mallawi, F.; Tlili, I. A Numerical Exploration of Modified Second-Grade Nanofluid with Motile Microorganisms, Thermal Radiation, and Wu’s Slip. Symmetry 2020, 12, 393. [Google Scholar] [CrossRef]
- Alwatban, A.; Khan, S.; Waqas, H.; Tlili, I. Interaction of Wu’s Slip Features in Bioconvection of Eyring Powell Nanoparticles with Activation Energy. Processes 2019, 7, 859. [Google Scholar] [CrossRef]
- Khan, S.U.; Waqas, H.; Shehzad, S.A.; Imran, M. Theoretical analysis for tangent hyperbolic nanoparticles with combined electrical MHD, activation energy and Wu’s slip features: A mathematical model. Phys. Scr. 2019, 94, 125211. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).