Generalized Dual-Root Lattice Transforms of Affine Weyl Groups

Abstract

Discrete transforms of Weyl orbit functions on finite fragments of shifted dual root lattices are established. The congruence classes of the dual weight lattices intersected with the fundamental domains of the affine Weyl groups constitute the point sets of the transforms. The shifted weight lattices intersected with the fundamental domains of the extended dual affine Weyl groups form the sets of labels of Weyl orbit functions. The coinciding cardinality of the point and label sets and corresponding discrete orthogonality relations of Weyl orbit functions are demonstrated. The explicit counting formulas for the numbers of elements contained in the point and label sets are calculated. The forward and backward discrete Fourier-Weyl transforms, together with the associated interpolation and Plancherel formulas, are presented. The unitary transform matrices of the discrete transforms are exemplified for the case $A_2$.

1. Introduction

The purpose of this article is to develop discrete Fourier-Weyl transforms [1,2,3,4,5,6] on finite fragments of shifted dual root lattices that correspond to affine Weyl groups. The kernels of the discrete transforms are formed by four types of complex-valued Weyl orbit functions [7,8] that are labeled by shifted weight lattices [9]. Each developed discrete transform manifests a unique boundary behavior that depends on the type of orbit function, together with underlying lattice shifts of its point and label sets.

Induced by four sign homomorphisms of Weyl groups [10], § 4.1, the four types of complex-valued Weyl orbit functions form multivariate generalizations of the classical trigonometric functions. Two sign homomorphisms exist for the Weyl groups of any crystallographic root systems, and an additional two are generated by root systems with two root lengths. The fundamental domain of an affine Weyl group constitutes a generalization of the one-dimensional interval, in which the orbit functions are studied. The basic boundary behavior of each Weyl orbit function on the borders of the fundamental domains is determined by the underlying sign homomorphism [2], § 4. As generalizations of the discrete trigonometric transforms, the discrete Fourier-Weyl transforms have been recently developed on refined dual weight [2,3], weight [4] and dual root lattices [1]. The extended affine Weyl group and its fundamental domain determine the labels of orbit functions that correspond to the dual-root lattice Fourier-Weyl transforms [1]. The Weyl orbit functions of the systems $B_n$ and $C_n$ are directly linked to multivariate (anti)symmetric cosine and sine functions [11,12]. The sixteen types of multivariate symmetric and antisymmetric cosine (SMDCT I–VIII and AMDCT I–VIII) [13] and sixteen types of sine transforms (SMDST I–VIII and AMDST I–VIII) [14] generalize via (anti)symmetrization with respect to the permutation group $S_n$ the classical one-dimensional eight types of cosine (DCT I–VIII) and eight types of sine transforms (DST I–VIII) [15]. Each (anti)symmetric discrete trigonometric transform possesses a unique boundary behavior due to the precise shifting of its nodes or labels of the functions and due to the positioning of the nodes and labels relative to their respective fundamental domains.

The shifting of the dual weight and weight lattices as the sets of transform nodes and labels of Weyl orbit functions, respectively, leads to generalizations of the discrete transforms of types I-IV [9]. The crucial property of admissibility of the lattice shifts stems from the preservation of Weyl group invariance of each shifted lattice. Admissible shifts of the dual root lattices need to be classified since the goal of the current article is to develop the discrete transforms with points from the shifted dual root lattices and labels from the shifted weight lattice. The admissible shifts of the weight lattices are already classified in [9], § II.C and it appears that the classification of the admissible shifts of the dual root lattices coincides precisely with the congruence decompositions of the dual weight lattices [16]. Thus, the resulting discrete transforms are also interpreted as transforms on finite fragments of rescaled dual weight lattice congruence classes. Each admissible shift of the weight lattice induces the corresponding dual shift $\theta$-homomorphism of the affine Weyl group [9], § II.F. The products of the shift and sign homomorphisms create the $\gamma$-homomorphism that controls the argument symmetries of dual weight lattice transforms [9], § II.G. Establishing the similar shift $\widehat{\theta }$- and $\widehat{\gamma }$-homomorphisms of the extended affine Weyl group permits a description of the label sets of the current shifted dual-root lattice Fourier-Weyl transforms. Linking together the numbers of shifted weights inside the fundamental domains of the extended affine Weyl groups and the number of representants of congruence classes of the dual weight lattices contained in the fundamental domains of the affine Weyl groups requires a study of specifically adapted invariant polynomials [1], § 4.3. The common cardinality of the point and label sets provides, in turn, existence of the novel shifted dual root lattice Fourier-Weyl transforms.

The entire group-theoretical formalism of shifted discrete transforms potentially generalizes the 16 classical types of discrete cosine and sine transforms together with 32 multivariate (anti)symmetric trigonometric transformations that are related to systems $A_1$ and $C_n$, respectively, to the entire collection of crystallographic root systems. The variety of novel types of the discrete Fourier-Weyl transforms is especially striking for the sequence of root systems $A_n$, $n\ge 2$ when considering that there exist $2n+2$ types of discrete transformations for each root system. Each constructed discrete transform induces its corresponding Fourier methods [5,17] together with the multivariate Chebyshev polynomial methods [10,18,19,20,21]. The detailed formulation of the shifted dual-root lattice transforms conceivably enables exact matrix implementation of the central splitting [22], § 7 of the dual weight Fourier-Weyl transforms [2,3] and, thus, provides the first step towards their fast recursive computation [15], Ch. 4. Using the concept of extended Weyl orbit functions [23], § V.A and composing together transformations on congruence classes of the dual weight lattice or subtracting these classes from the entire dual weight lattice produces vast numbers of novel extended discrete transforms. Among the available subtractive and additive transforms for the root system $A_2$ appear unique new variants of the cosine and sine transforms on the honeycomb triangular dots with armchair boundaries [23]. Moreover, the shifted dual-root lattice discretized Weyl orbit functions potentially serve as a foundation for solving novel modifications of quantum particle propagation models in graphene quantum dots [24,25,26], compactified trigonometric models [27], mechanical graphene vibration models [28,29], and quantum field lattice models [24].

This paper is organized as follows. In Section 2, the pertinent facts regarding the congruence decompositions of weight lattices, classification of admissible shifts of dual root lattices, and definitions of shift $\theta$- and $\widehat{\theta }$-homomorphisms are contained. Section 3 is devoted to the description of $\gamma$- and $\widehat{\gamma }$-homomorphisms and related symmetries of Weyl orbit functions on shifted dual root lattices. In Section 4, the identical cardinalities of the point and label sets are verified and explicit counting formulas for the common numbers of elements in these sets are listed. Section 5 details the discrete orthogonality of Weyl orbit functions on shifted dual-root lattices and the corresponding discrete Fourier-Weyl transforms. Examples of the unitary transform matrices for the root system $A_2$ are also included. Comments and follow-up questions are included in the last section.

2. Shift Homomorphisms of Extended Weyl Groups

The goal of Section 2 is to establish notation and recall advanced facts that are related to root lattices, congruence decompositions of weight lattices, and extended affine Weyl groups. The classification of admissible shifts of the dual root lattices is identified with the congruence decompositions and shift $\theta$- and $\widehat{\theta }$-homomorphisms are introduced.

2.1. Congruence Decomposition of Weight Lattices

The notation of this article is established in papers [1,2,3]. Recall that each simple Lie algebra $\mathfrak{g}$ from the classical four series $A_n (n\ge 1)$, $B_n (n\ge 3)$, $C_n (n\ge 2)$, $D_n (n\ge 4)$, together with the five exceptional cases $E_6,E_7,E_8,F_4,G_2$, induces its set $\Delta =\{{\alpha }_1,\dots ,{\alpha }_n\}$ of the simple roots [30,31]. Indexing the simple roots in $\Delta$, the set I and its extension $\widehat{I}$ are formed by n and $n+1$ naturally ordered indices, respectively,

$$I=\{1,\dots ,n\},\widehat{I}=\{0,\dots ,n\}.$$

For the cases of simple Lie algebras with two different root lengths, the sets of simple roots $\Delta$ are disjointly decomposed into the sets ${\Delta }_s$ of the short simple roots and the sets ${\Delta }_l$ of the long simple roots,

$$\Delta ={\Delta }_s\cup {\Delta }_l.$$

The sets of simple roots $\Delta$ form non-orthogonal bases of the Euclidean spaces ${\mathbb{R}}^n$ with the standard scalar products $⟨·,·⟩$. Each simple root ${\alpha }_i\in \Delta$, $i\in I$ is related to the dual simple root ${\alpha }_i^{\vee }$ by

$${\alpha }_i^{\vee }=\frac{2{\alpha }_i}{⟨{\alpha }_i,{\alpha }_i⟩}.$$

To every simple root ${\alpha }_i\in \Delta$, $i\in I$ corresponds a reflection $r_i$ that is given by the standard formula

$$r_{i}a=a-⟨a,{\alpha }_i^{\vee }⟩{\alpha }_i,a\in {\mathbb{R}}^n.$$

Reflections $r_i$ generate an irreducible Weyl group $W=⟨r_1,\dots ,r_n⟩$ and each irreducible Weyl group W generates the entire root system $\Pi =W\Delta$ of the given simple Lie algebra $\mathfrak{g}$. The highest root $\xi \in \Pi$ is of the form

$$\xi =m_1{\alpha }_1+\dots +m_n{\alpha }_n.$$

The set of dual simple roots ${\Delta }^{\vee }=\{{\alpha }_1^{\vee },\dots ,{\alpha }_n^{\vee }\}$ generates the entire dual root system ${\Pi }^{\vee }=W{\Delta }^{\vee }$ and the highest dual root $\eta \in {\Pi }^{\vee }$ is of the form

$$\eta =m_1^{\vee }{\alpha }_1^{\vee }+\dots +m_n^{\vee }{\alpha }_n^{\vee }.$$

Table 1 lists the expansion coefficients of the highest root $m_1,\dots ,m_n$ and of the highest dual root $m_1^{\vee },\dots ,m_n^{\vee }$ in [3]. The zeroth expansion coefficients are set additionally as $m_0=m_0^{\vee }=1$.

Table 1. Non-trivial non-equivalent admissible shifts of dual root and weight lattices.

	${\mathit{A}}_1$	${\mathit{A}}_{\mathit{n}}$, $\mathit{n}\ge 2$	${\mathit{B}}_{\mathit{n}}$, $\mathit{n}\ge 3$	${\mathit{C}}_{\mathit{n}}$, $\mathit{n}\ge 2$	${\mathit{D}}_{\mathit{n}}$, $\mathit{n}\ge 4$	${\mathit{E}}_6$	${\mathit{E}}_7$
${\nu }^{\vee }$	${\omega }_1^{\vee }$	${\omega }_1^{\vee },\dots ,{\omega }_n^{\vee }$	${\omega }_1^{\vee }$	${\omega }_n^{\vee }$	${\omega }_1^{\vee },{\omega }_{n-1}^{\vee },{\omega }_n^{\vee }$	${\omega }_1^{\vee },{\omega }_5^{\vee }$	${\omega }_6^{\vee }$
$\varrho$	$\frac{1}{2}{\omega }_1$	∅	∅	$\frac{1}{2}{\omega }_n$	∅	∅	∅

The root lattice Q is the $\mathbb{Z}$-span of the set of simple roots $\Delta$,

$$Q=\mathbb{Z}{\alpha }_1+\dots +\mathbb{Z}{\alpha }_n.$$

The dual weight lattice is $\mathbb{Z}$-dual to the root lattice Q,

$$P^{\vee }=\{{\omega }^{\vee }\in {\mathbb{R}}^n|⟨{\omega }^{\vee },{\alpha }_i⟩\in \mathbb{Z},\forall {\alpha }_i\in \Delta \}=\mathbb{Z}{\omega }_1^{\vee }+\dots +\mathbb{Z}{\omega }_n^{\vee },$$

with the dual fundamental weights ${\omega }_i^{\vee }$ given by

$$⟨{\omega }_i^{\vee },{\alpha }_j⟩={\delta }_{ij}.$$

The dual root lattice is the $\mathbb{Z}$-span of the set of dual simple roots ${\Delta }^{\vee },$

$$Q^{\vee }=\mathbb{Z}{\alpha }_1^{\vee }+\dots +\mathbb{Z}{\alpha }_n^{\vee }.$$

The weight lattice is $\mathbb{Z}$-dual to the dual root lattice $Q^{\vee }$,

$$P=\{\omega \in {\mathbb{R}}^n|⟨\omega ,{\alpha }_i^{\vee }⟩\in \mathbb{Z},\forall {\alpha }_i^{\vee }\in {\Delta }^{\vee }\}=\mathbb{Z}{\omega }_1+\dots +\mathbb{Z}{\omega }_n,$$

(1)

with the fundamental weights ${\omega }_i$ given by

$$⟨{\omega }_i,{\alpha }_j^{\vee }⟩={\delta }_{ij}.$$

The ${\alpha }^{\vee }$-basis is related to the ${\omega }^{\vee }$-basis by the transpose of Cartan matrix $C^T$ with entries given by $C_{ij}=⟨{\alpha }_i,{\alpha }_j^{\vee }⟩$, $i,j\in I$ as

$${\alpha }_j^{\vee }=\sum _{i\in I}{(C^T)}_{ji}{\omega }_i^{\vee }.$$

(2)

Two subsets of indices $J,J^{\vee }\subset I$ are introduced as

$$J=\{j\in I\mid m_j^{\vee }=1\},J^{\vee }=\{j\in I\mid m_j=1\}.$$

(3)

The weight lattice P decomposes into $\left|J\right|+1$ congruence classes of the root lattice Q and the dual weight lattice $P^{\vee }$ decomposes into $|J^{\vee }|+1$ congruence classes of the dual root lattice $Q^{\vee }$,

$$P=Q\cup \bigcup _{j\in J}\{{\omega }_j+Q\},P^{\vee }=Q^{\vee }\cup \bigcup _{j\in J^{\vee }}\{{\omega }_j^{\vee }+Q^{\vee }\}.$$

(4)

Note that the sets of indices $J,J^{\vee }$ are empty for the simple Lie algebras $G_2$, $F_4$, and $E_8$.

For each element w of any Weyl group W, there exists a minimal number of reflections $r_i$, that are necessary to generate w, called the length of w. The unique element of W with the longest length, named the opposite involution, is denoted by $w_0$. Removing a generator $r_i$ from the set of generators of W, a parabolic subgroup $W_i=⟨r_1,\dots ,r_{i-1},r_{i+1},\dots ,r_n⟩$ is generated. The parabolic subgroup $W_i$ also forms a Weyl group that is not necessarily irreducible. The opposite involution in $W_i$ is denoted by $w_i$.

2.2. Admissible Shifts of Dual Root and Weight Lattices

A shift ${\nu }^{\vee }\in {\mathbb{R}}^n$ of the dual root lattice $Q^{\vee }$ is called admissible if the shifted dual root lattice ${\nu }^{\vee }+Q^{\vee }$ is invariant under the action of the Weyl group,

$$W({\nu }^{\vee }+Q^{\vee })={\nu }^{\vee }+Q^{\vee }.$$

(5)

Two admissible shifts ${\nu }^{\vee }$ and ${\tilde{\nu }}^{\vee }$, such that ${\tilde{\nu }}^{\vee }={\nu }^{\vee }+q^{\vee }$ with $q^{\vee }\in Q^{\vee }$ lead to the same shifted dual root lattice ${\nu }^{\vee }+Q^{\vee }={\tilde{\nu }}^{\vee }+Q^{\vee }$ and are defined to be equivalent. Proving that the admissible shifts of the dual root lattice are precisely elements of the dual weight lattice, the following proposition provides classification of the admissible shifts of the dual root lattice up to this equivalence.

Proposition 1.

The following statements are equivalent for any ${\nu }^{\vee }\in {\mathbb{R}}^n$.

1.

${\nu }^{\vee }$ is an admissible shift of $Q^{\vee }$,

2.

${\nu }^{\vee }-W{\nu }^{\vee }\subset Q^{\vee }$,

3.

for all $i\in I$ it holds that

$${\nu }^{\vee }-r_i{\nu }^{\vee }\in Q^{\vee },$$

(6)

4.

${\nu }^{\vee }\in P^{\vee }$.

Proof. 

$(1)\Rightarrow (2)$: if ${\nu }^{\vee }$ is admissible, then for every $w\in W$ and every $q_1^{\vee }\in Q^{\vee }$, there exists $q_2^{\vee }\in Q^{\vee }$, such that $w({\nu }^{\vee }+q_1^{\vee })={\nu }^{\vee }+q_2^{\vee }$. Since the dual root lattice $Q^{\vee }$ is W-invariant, it follows that

$${\nu }^{\vee }-w{\nu }^{\vee }=w{q}_1^{\vee }-q_2^{\vee }\in Q^{\vee }.$$

$(2)\Rightarrow (3)$: if for every $w\in W$ it holds that ${\nu }^{\vee }-w{\nu }^{\vee }\in Q^{\vee }$, then this equality is also valid for all $r_i\in W$.

$(3)\Rightarrow (4)$: for any ${\nu }^{\vee }=y_1{\alpha }_1^{\vee }+\dots +y_n{\alpha }_n^{\vee }$ expressed in ${\alpha }^{\vee }$-basis, condition (6) is, for each $i\in I$, rewritten as

$${\nu }^{\vee }-r_i{\nu }^{\vee }=\sum _{j=1}^n{y}_j⟨{\alpha }_j^{\vee },{\alpha }_i⟩{\alpha }_i^{\vee }=\sum _{j=1}^n{y}_j{C}_{ij}{\alpha }_i^{\vee }\in Q^{\vee },$$

which is equivalent to

$$\sum _{j=1}^n{y}_j{(C^T)}_{ji}\in \mathbb{Z}.$$

(7)

Transformation (2) yields that

$${\nu }^{\vee }=\sum _{j=1}^n{y}_j(\sum _{i=1}^n{(C^T)}_{ji}{\omega }_i^{\vee })=\sum _{i=1}^n(\sum _{j=1}^n{y}_j{(C^T)}_{ji}){\omega }_i^{\vee }.$$

Therefore, if condition (7) is valid for each $i\in I$, then ${\nu }^{\vee }\in P^{\vee }$.

$(4)\Rightarrow (1)$: Any $w\in W$ can be expressed as a product of generating reflections, thus there exist indices $i_1,i_2,\dots ,i_s\in I$, such that $w=r_{i_1}{r}_{i_2}\dots r_{i_s}$. Any ${\nu }^{\vee }=y_1{\omega }_1^{\vee }+\dots +y_n{\omega }_n^{\vee }\in P^{\vee }$, with $y_j\in \mathbb{Z}$, $j\in I$, satisfies for any $i\in I$ that

$${\nu }^{\vee }-r_i{\nu }^{\vee }=y_i{\alpha }_i^{\vee }\in Q^{\vee }.$$

(8)

From condition (8), it follows that there exist vectors $q_{i_1}^{\vee },\dots ,q_{i_s}^{\vee }\in Q^{\vee }$, such that ${\nu }^{\vee }-r_{i_1}{\nu }^{\vee }=q_{i_1}^{\vee }$, ${\nu }^{\vee }-r_{i_2}{\nu }^{\vee }=q_{i_2}^{\vee }$, …, ${\nu }^{\vee }-r_{i_s}{\nu }^{\vee }=q_{i_s}^{\vee }$. Subsequently, it holds that

$$\begin{array}{ll}{\nu }^{\vee }-w{\nu }^{\vee }& ={\nu }^{\vee }-r_{i_1}{r}_{i_2}\dots r_{i_s}{\nu }^{\vee }={\nu }^{\vee }-r_{i_1}{r}_{i_2}\dots r_{i_{s-1}}({\nu }^{\vee }-q_{i_s}^{\vee })\\ & ={\nu }^{\vee }-r_{i_1}{r}_{i_2}\dots r_{i_{s-2}}({\nu }^{\vee }-q_{i_{s-1}}^{\vee })+r_{i_1}{r}_{i_2}\dots r_{i_{s-1}}{q}_{i_s}^{\vee }\\ & =q_{i_1}^{\vee }+r_{i_1}{q}_{i_2}^{\vee }+r_{i_1}{r}_{i_2}{q}_{i_3}^{\vee }+\dots +r_{i_1}{r}_{i_2}\dots r_{i_{s-1}}{q}_{i_s}^{\vee }.\end{array}$$

Since $Q^{\vee }$ is W-invariant, the vector ${\tilde{q}}^{\vee }=q_{i_1}^{\vee }+r_{i_1}{q}_{i_2}^{\vee }+r_{i_1}{r}_{i_2}{q}_{i_3}^{\vee }+\dots +r_{i_1}{r}_{i_2}\dots r_{i_{s-1}}{q}_{i_s}^{\vee }$ is from the dual root lattice, ${\tilde{q}}^{\vee }\in Q^{\vee }$.

Thus, for all $w\in W$ there exists ${\tilde{q}}^{\vee }\in Q^{\vee }$, such that ${\nu }^{\vee }-w{\nu }^{\vee }={\tilde{q}}^{\vee }$ and for all $q^{\vee }\in Q^{\vee }$, it holds that

$$w({\nu }^{\vee }+q^{\vee })=-{\tilde{q}}^{\vee }+{\nu }^{\vee }+w{q}^{\vee }.$$

Therefore, there exists ${\tilde{q}}^{{}^{\prime }\vee }=w{q}^{\vee }-{\tilde{q}}^{\vee }\in Q^{\vee }$, such that $w({\nu }^{\vee }+q^{\vee })={\nu }^{\vee }+{\tilde{q}}^{{}^{\prime }\vee }$ and ${\nu }^{\vee }$ is admissible. ☐

Together with the congruence classes decomposition of the dual weight lattice (4), Proposition 1 provides classification of the admissible shifts of the dual root lattice. The equivalence classes of admissible shifts of $Q^{\vee }$ are represented by the trivial shift 0 and the non-trivial shifts ${\omega }_j^{\vee }$, $j\in J^{\vee }$, as listed in Table 1. Setting ${\omega }_0^{\vee }=0$, the non-equivalent admissible shifts ${\nu }^{\vee }$ of $Q^{\vee }$ are given as ${\omega }_j^{\vee }$ with indices $j\in J^{\vee }\cup \left\{0\right\}$.

A shift $\varrho \in {\mathbb{R}}^n$ of the weight lattice P is admissible if the shifted weight lattice $\varrho +P$ is invariant under the Weyl group,

$$W(\varrho +P)=\varrho +P.$$

(9)

The admissible shifts $\varrho$ and $\tilde{\varrho }$, such that $\tilde{\varrho }=\varrho +p$ with $p\in P$ lead to the same shifted weight lattice $\varrho +P=\tilde{\varrho }+P$ and are defined to be equivalent. A shift by any weight $\varrho \in P$ results in the lattice $\varrho +P=P$ and such shifts are equivalent to the trivial shift by 0 vector. The representatives of non-equivalent non-trivial admissible shifts of the weight lattice are classified in [9] and listed in Table 1. Similarly to Proposition 1, the admissibility of the shift $\varrho$ is according to Proposition 2.3 in [9] equivalent to the following property,

$$\varrho -W\varrho \subset P.$$

(10)

2.3. Dual Affine Weyl Groups and Dual Shift Homomorphism ${\theta }_{\varrho }$

An infinite extension of the Weyl group by shifts from the dual root lattice $Q^{\vee }$ forms the affine Weyl group $W^{\mathrm{aff}}$,

$$W^{\mathrm{aff}}=Q^{\vee }⋊W.$$

(11)

Any element $T(q^{\vee })w\in W^{\mathrm{aff}}$ acts naturally on ${\mathbb{R}}^n$ by

$$T(q^{\vee })w·a=wa+q^{\vee },a\in {\mathbb{R}}^n.$$

The fundamental domain F of $W^{\mathrm{aff}}$ that corresponds to this action is a simplex explicitly given by

$$F=\{a_1{\omega }_1^{\vee }+\dots +a_n{\omega }_n^{\vee }|a_0+a_1{m}_1+\dots +a_n{m}_n=1,a_i\ge 0,i\in \widehat{I}\}.$$

(12)

The affine Weyl group is generated by the reflections $r_i$ and affine reflection $r_0$ given by the formula

$$r_{0}a=r_{\xi }a+\frac{2\xi }{⟨\xi ,\xi ⟩},r_{\xi }a=a-\frac{2⟨a,\xi ⟩}{⟨\xi ,\xi ⟩}\xi ,a\in {\mathbb{R}}^n.$$

(13)

The set of generating reflections $r_0,r_1,\dots ,r_n$ is denoted by R,

$$R=\{r_0,r_1,\dots ,r_n\}.$$

(14)

For any $w^{\mathrm{aff}}=T(q^{\vee })w\in W^{\mathrm{aff}}$, a standard retraction homomorphism $\psi :W^{\mathrm{aff}}\to W$ and a mapping $\tau :W^{\mathrm{aff}}\to Q^{\vee }$ are defined by

$$\psi (w^{\mathrm{aff}})=w,\tau (w^{\mathrm{aff}})=q^{\vee }.$$

(15)

The dual shift homomorphism ${\theta }_{\varrho }:W^{\mathrm{aff}}\to U_2$ from the affine Weyl group to the multiplicative group $U_2=\{\pm 1\}$, which corresponds to an admissible shift $\varrho$ of the weight lattice P, is defined in [9] for any $w^{\mathrm{aff}}\in W^{\mathrm{aff}}$ by

$${\theta }_{\varrho }(w^{\mathrm{aff}})=e^{2\pi \mathrm{i}⟨\tau (w^{\mathrm{aff}}),\varrho ⟩}.$$

(16)

The values of ${\theta }_{\varrho }$ on the generators R of $W^{\mathrm{aff}}$ are for trivial admissible shifts equal to 1 and for non-trivial admissible shifts given by

$${\theta }_{\varrho }(r_i)=\{\begin{array}{ll}1,& i\in I,\\ -1,& i=0.\end{array}$$

(17)

The stabilizer ${\mathrm{Stab}}_{W^{\mathrm{aff}}}(a)$ forms a subgroup of $W^{\mathrm{aff}}$ of elements stabilizing $a\in {\mathbb{R}}^n$ and the discrete $ϵ$-fuction ϵ: ${\mathbb{R}}^n\to \mathbb{N}$ is defined by

$$\epsilon (a)=\frac{\left|W\right|}{|{\mathrm{Stab}}_{W^{\mathrm{aff}}}(a)|}.$$

(18)

Since the stabilizers ${\mathrm{Stab}}_{W^{\mathrm{aff}}}(a)$ and ${\mathrm{Stab}}_{W^{\mathrm{aff}}}(w^{\mathrm{aff}}a)$ are conjugated, the discrete counting function $\epsilon$ is $W^{\mathrm{aff}}$-invariant,

$$\epsilon (a)=\epsilon (w^{\mathrm{aff}}a),w^{\mathrm{aff}}\in W^{\mathrm{aff}}.$$

(19)

The standard action of W on the torus ${\mathbb{R}}^n/Q^{\vee }$ generates for $x\in {\mathbb{R}}^n/Q^{\vee }$ its isotropy groups $\mathrm{Stab}(x)$ and orbits $Wx$ of orders $\tilde{\epsilon }(x)$,

$$\begin{array}{c}\hfill \tilde{\epsilon }(x)=\left|Wx\right|,x\in {\mathbb{R}}^n/Q^{\vee }.\end{array}$$

The following three properties from Proposition 2.2 in [3] of the action of W on the torus ${\mathbb{R}}^n/Q^{\vee }$ are crucial for the discrete orthogonality of Weyl orbit functions. First, for any $x\in {\mathbb{R}}^n/Q^{\vee }$, there exist $x^{\prime }\in F\cap {\mathbb{R}}^n/Q^{\vee }$ and $w\in W$, such that

$$x=w{x}^{\prime }.$$

(20)

Second, for any two points $x,x^{\prime }\in F\cap {\mathbb{R}}^n/Q^{\vee }$ that satisfy $x^{\prime }=wx.$,$w\in W$, it holds that

$$x^{\prime }=x=wx.$$

(21)

Third, for any point $x\in F\cap {\mathbb{R}}^n/Q^{\vee }$, which is of the form $x=a+Q^{\vee }$, $a\in F$, the retraction homomorphism $\psi$ of the stabilizers provides relations $\psi ({\mathrm{Stab}}_{W^{\mathrm{aff}}}(a))=\mathrm{Stab}(x)$ and

$$\mathrm{Stab}(x)\cong {\mathrm{Stab}}_{W^{\mathrm{aff}}}(a).$$

(22)

Moreover, isomorphism (22) grants that, for $x=a+Q^{\vee }$, $a\in F$, it holds that

$$\epsilon (a)=\tilde{\epsilon }(x).$$

(23)

Note that, instead of $\tilde{\epsilon }(x).$, the symbol $\epsilon (x)$ is used for $\left|Wx\right|,x\in F\cap {\mathbb{R}}^n/Q^{\vee }$ in [2,3]. The algorithm for the calculation of the coefficients $\epsilon (x)$ is described in [3], § 3.7.

An infinite extension of the Weyl group by shifts from the root lattice Q forms the dual affine Weyl group $W_Q^{\mathrm{aff}}$,

$$W_Q^{\mathrm{aff}}=Q⋊W.$$

(24)

Any element $T(q)w\in W_Q^{\mathrm{aff}}$ acts naturally on ${\mathbb{R}}^n$ by

$$T(q)w·b=wb+q,b\in {\mathbb{R}}^n.$$

The fundamental domain $F_Q$ of $W_Q^{\mathrm{aff}}$ corresponding to this action is a simplex given by

$$F_Q=\{b_1{\omega }_1+\dots +b_n{\omega }_n|b_0+b_1{m}_1^{\vee }+\dots +b_n{m}_n^{\vee }=1,b_i\ge 0,i\in \widehat{I}\}.$$

(25)

By assigning to each $b,b^{\prime }\in F_Q$ its Kac coordinates $[b_0,b_1,\dots ,b_n]$ and $[b_0^{\prime },b_1^{\prime },\dots ,b_n^{\prime }]$ from (25), respectively, the point b is lexicographically higher than $b^{\prime }$, $b{>}_{\mathrm{lex}}{b}^{\prime }$, if for the first $i\in \widehat{I}$ for which $b_i$ differs from $b_i^{\prime }$ holds that $b_i>b_i^{\prime }$.

The dual affine Weyl group $W_Q^{\mathrm{aff}}$ is generated by the reflections $r_i$ and the dual affine reflection $r_0^{\vee }$ given by the formula

$$r_0^{\vee }b=r_{\eta }b+\frac{2\eta }{⟨\eta ,\eta ⟩},r_{\eta }b=b-\frac{2⟨b,\eta ⟩}{⟨\eta ,\eta ⟩}\eta ,b\in {\mathbb{R}}^n.$$

(26)

The set of generating reflections $r_0^{\vee },r_1,\dots ,r_n$ is denoted by $R^{\vee }$,

$$R^{\vee }=\{r_0^{\vee },r_1,\dots ,r_n\}.$$

(27)

2.4. Extended Dual Affine Weyl Group and Shift Homomorphism ${\widehat{\theta }}_{{\nu }^{\vee }}$

An infinite extension of the Weyl group by shifts in the weight lattice P forms the extended dual affine Weyl group $W_P^{\mathrm{aff}}$,

$$W_P^{\mathrm{aff}}=P⋊W.$$

(28)

Any element $T(p)w\in W_P^{\mathrm{aff}}$ acts naturally on ${\mathbb{R}}^n$ by

$$T(p)w·b=wb+p,b\in {\mathbb{R}}^n.$$

The crucial abelian subgroup $\Gamma \subset W_P^{\mathrm{aff}}$ comprises such elements, which leave the fundamental domain $F_Q$ invariant [30],

$$\Gamma =\{\mathfrak{1},{\upsilon }_i\in W_P^{\mathrm{aff}}\mid i\in J\},{\upsilon }_i=T({\omega }_i)w_i{w}_0.$$

(29)

Note that the order of the group $\Gamma$ is related to the index of connection c of the root system $\Pi$ and the determinant of the Cartan matrix C via formula

$$|\Gamma |=c=detC.$$

(30)

The extended dual affine Weyl group $W_P^{\mathrm{aff}}$ is expressed as a semidirect product of $W_Q^{\mathrm{aff}}$ and $\Gamma$,

$$W_P^{\mathrm{aff}}=W_Q^{\mathrm{aff}}⋊\Gamma .$$

(31)

Recall from [1] that the fundamental domain $F_P\subset F_Q$ of $W_P^{\mathrm{aff}}$ consists of the lexicographically highest point from each $\Gamma$-orbit of $F_Q$,

$$F_P=\{b\in F_Q\mid b={\max }_{>\mathrm{lex}}\Gamma b\}.$$

(32)

The action of any $\upsilon \in \Gamma$ on the point $b=[b_0,b_1,\dots ,b_n]\in F_Q$ is explicitly described by

$$\upsilon ·b=[b_{{\pi }_{\upsilon }(0)},\dots ,b_{{\pi }_{\upsilon }(n)}],$$

(33)

where ${\pi }_{\upsilon }$ denotes a permutation of the index set $\widehat{I}$. The permutations are specified in Table 1 of [1] from which the set of generators $R^{\Gamma }$ of $\Gamma$ is deduced and listed in Table 2. The extended dual affine Weyl group is generated by the generators $R^{\vee }$ of $W_Q^{\mathrm{aff}}$ and by the generators $R^{\Gamma }$ of $\Gamma$.

Table 2. Generators and orders of the groups $\Gamma$.

	${\mathit{A}}_{\mathit{n}}$	${\mathit{B}}_{\mathit{n}}$	${\mathit{C}}_{\mathit{n}}$	${\mathit{D}}_{2\mathit{k}}$	${\mathit{D}}_{2\mathit{k}+1}$	${\mathit{E}}_6$	${\mathit{E}}_7$
$R^{\Gamma }$	${\upsilon }_1$	${\upsilon }_n$	${\upsilon }_1$	${\upsilon }_1,{\upsilon }_{2k}$	${\upsilon }_{2k+1}$	${\upsilon }_1$	${\upsilon }_6$
$|\Gamma |$	$n+1$	2	2	4	4	3	2

For an arbitrary $M\in \mathbb{N}$, a subgroup ${\Gamma }_M$ of $W_P^{\mathrm{aff}}$ isomorphic to $\Gamma$ is given by

$${\Gamma }_M=\{\mathfrak{1},{\upsilon }_{M,i}\in W_P^{\mathrm{aff}}|i\in J\},{\upsilon }_{M,i}=T(M{\omega }_i)w_i{w}_0.$$

(34)

Assigning to each ${\upsilon }_i\in \Gamma$ the element ${\upsilon }_{M,i}\in {\Gamma }_M$ yields the isomorphism of $\Gamma$ and ${\Gamma }_M$,

$${\Gamma }_M\ni {\upsilon }_M\mapsto \upsilon \in \Gamma .$$

(35)

The action of ${\upsilon }_M\in {\Gamma }_M$ on $b\in {\mathbb{R}}^n$ is related to the action of the corresponding $\upsilon \in \Gamma$ by

$${\upsilon }_M·b=M\{\upsilon ·\frac{b}{M}\}.$$

(36)

Thus, ${\Gamma }_M$ acts naturally on the magnified domain $M{F}_Q$ with the fundamental domain that is equal to $M{F}_P$. Introducing the magnified Kac coordinates of $b=b_1{\omega }_1+\dots +b_n{\omega }_n\in M{F}_Q$ by $b=[b_0,b_1,\dots ,b_n]$ with $b_0=M-(m_1^{\vee }{b}_1+\dots +m_n^{\vee }{b}_n)$, the action is described by

$${\upsilon }_M·b={\upsilon }_M·[b_0,\dots ,b_n]=[b_{{\pi }_{\upsilon }(0)},\dots ,b_{{\pi }_{\upsilon }(n)}]$$

(37)

where ${\pi }_{\upsilon }$ is the permutation of $\widehat{I}$ assigned to $\upsilon$ which corresponds to ${\upsilon }_M$ by (35).

Taking any $w^{\mathrm{aff}}=T(p)w\in W_P^{\mathrm{aff}}$, an extended dual retraction homomorphism $\widehat{\psi }$ and a mapping $\widehat{\tau }$ are defined by

$$\widehat{\psi }(w^{\mathrm{aff}})=w,\widehat{\tau }(w^{\mathrm{aff}})=p.$$

(38)

To each admissible shift ${\nu }^{\vee }$ of the dual root lattice $Q^{\vee }$ is assigned a shift homomorphism ${\widehat{\theta }}_{{\nu }^{\vee }}$ from $W_P^{\mathrm{aff}}$ to the multiplicative group of c-th roots of unity $U_c$ by the formula that is given for any $w^{\mathrm{aff}}\in W_P^{\mathrm{aff}}$ as

$${\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}})=e^{2\pi \mathrm{i}⟨\widehat{\tau }(w^{\mathrm{aff}}),{\nu }^{\vee }⟩}.$$

(39)

The $\mathbb{Z}$-duality of the lattices P and $Q^{\vee }$ implies that, for trivial admissible shifts of the dual root lattice ${\nu }^{\vee }\in Q^{\vee }$, the values of the map (39) are identically equal to 1. Additionally, the $\mathbb{Z}$-duality enforces the unity values on the dual affine Weyl group, i.e., for any admissible shift ${\nu }^{\vee }\in P^{\vee }$, it holds that

$${\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}})=1,w^{\mathrm{aff}}\in W_Q^{\mathrm{aff}}.$$

(40)

The verification of the homomorphism property and values of ${\widehat{\theta }}_{{\nu }^{\vee }}$ on the generators $R^{\Gamma }$ of $\Gamma$ are contained in the following proposition.

Proposition 2.

The map ${\widehat{\theta }}_{{\nu }^{\vee }}:W_P^{\mathrm{aff}}\to U_c$, given by (39), is for any admissible shift ${\nu }^{\vee }$ of the dual root lattice $Q^{\vee }$ a homomorphism from the extended affine Weyl group $W_P^{\mathrm{aff}}$ to the multiplicative group of the c-th roots of unity $U_c$. The values of the map ${\widehat{\theta }}_{{\nu }^{\vee }}$ on the generators $R^{\Gamma }$ are given for each case as

$$\begin{array}{ll}{A}_n:& {\widehat{\theta }}_{{\omega }_j^{\vee }}({\upsilon }_1)=e^{2\pi \mathrm{i}\frac{n+1-j}{n+1}},j=1,\dots ,n,\end{array}$$

(41)

$$\begin{array}{ll}{B}_n:& {\widehat{\theta }}_{{\omega }_1^{\vee }}({\upsilon }_n)=-1,\end{array}$$

(42)

$$\begin{array}{ll}{C}_n:& {\widehat{\theta }}_{{\omega }_n^{\vee }}({\upsilon }_1)=-1,\end{array}$$

(43)

$$\begin{array}{ll}{D}_{2k}:& {\widehat{\theta }}_{{\omega }_1^{\vee }}({\upsilon }_i)=\{\begin{array}{ll}1& i=1,\\ -1& i=2k,\end{array},{\widehat{\theta }}_{{\omega }_{2k-1}^{\vee }}({\upsilon }_i)=\{\begin{array}{ll}-1& i=1\\ {(-1)}^{k+1}& i=2k,\end{array},{\widehat{\theta }}_{{\omega }_{2k}^{\vee }}({\upsilon }_i)=\{\begin{array}{ll}-1& i=1,\\ {(-1)}^k& i=2k,\end{array}\end{array}$$

(44)

$$\begin{array}{lll}{D}_{2k+1}:& & {\widehat{\theta }}_{{\omega }_1^{\vee }}({\upsilon }_{2k+1})=-1,{\widehat{\theta }}_{{\omega }_{2k}^{\vee }}({\upsilon }_{2k+1})={(-1)}^{k+1}\mathrm{i},{\widehat{\theta }}_{{\omega }_{2k+1}^{\vee }}({\upsilon }_{2k+1})={(-1)}^k\mathrm{i},\end{array}$$

(45)

$$\begin{array}{ll}{E}_6:& {\widehat{\theta }}_{{\omega }_1^{\vee }}({\upsilon }_1)=e^{\frac{2\pi \mathrm{i}}{3}},{\widehat{\theta }}_{{\omega }_5^{\vee }}({\upsilon }_1)=e^{\frac{4\pi \mathrm{i}}{3}},\end{array}$$

(46)

$$\begin{array}{ll}{E}_7:& {\widehat{\theta }}_{{\omega }_6^{\vee }}({\upsilon }_6)=-1.\end{array}$$

(47)

Proof. 

Directly from definition (5) of admissible shifts of the dual root lattice follows that, for any $w\in W$, it holds that ${\nu }^{\vee }-w^{-1}{\nu }^{\vee }\in Q^{\vee }$. Thus, the $\mathbb{Z}$-duality of the lattices P and $Q^{\vee }$ guarantees for any $p\in P$ that $⟨p,{\nu }^{\vee }-w^{-1}{\nu }^{\vee }⟩\in \mathbb{Z}$ and, hence,

$$e^{2\pi \mathrm{i}⟨wp,{\nu }^{\vee }⟩}=e^{2\pi \mathrm{i}⟨p,{\nu }^{\vee }⟩}.$$

(48)

Since the mapping (38) on the product of any two elements $w_1^{\mathrm{aff}},w_2^{\mathrm{aff}}\in W_P^{\mathrm{aff}}$ of the forms $w_1^{\mathrm{aff}}=T(p_1)w_1$ and $w_2^{\mathrm{aff}}=T(p_2)w_2$ yields that $\widehat{\tau }(w_1^{\mathrm{aff}}{w}_2^{\mathrm{aff}})=p_1+w_1{p}_2$, it follows that

$${\widehat{\theta }}_{{\nu }^{\vee }}(w_1^{\mathrm{aff}}{w}_2^{\mathrm{aff}})=e^{2\pi \mathrm{i}⟨\widehat{\tau }(w_1^{\mathrm{aff}}{w}_2^{\mathrm{aff}}),{\nu }^{\vee }⟩}=e^{2\pi \mathrm{i}⟨p_1+w_1{p}_2,{\nu }^{\vee }⟩}=e^{2\pi \mathrm{i}⟨p_1,{\nu }^{\vee }⟩}{e}^{2\pi \mathrm{i}⟨p_2,{\nu }^{\vee }⟩}={\widehat{\theta }}_{{\nu }^{\vee }}(w_1^{\mathrm{aff}}){\widehat{\theta }}_{{\nu }^{\vee }}(w_2^{\mathrm{aff}}).$$

For the generators ${\upsilon }_i\in R^{\Gamma }$, $i\in J$ and non-equivalent admissible shifts ${\nu }^{\vee }={\omega }_j^{\vee }$, $j\in J^{\vee }$, the explicit values of scalar products that are calculated via their relation to the inverse of the Cartan matrix,

$$⟨\widehat{\tau }({\upsilon }_i),{\nu }^{\vee }⟩=⟨{\omega }_i,{\omega }_j^{\vee }⟩={(C^{-1})}_{ij},$$

yield formulas (41)–(47). ☐

The non-trivial values of the homomorphism ${\widehat{\theta }}_{{\nu }^{\vee }}$ on the generators of $\Gamma$ in Proposition 2 allow for calculating ${\widehat{\theta }}_{{\nu }^{\vee }}$ on any element of the extended dual affine Weyl group $W_P^{\mathrm{aff}}$ via relations (31) and (40). The modification of the homomorphism ${\widehat{\theta }}_{{\nu }^{\vee }}$ to the group ${\Gamma }_M$ is a homomorphism ${\widehat{\theta }}_{M,{\nu }^{\vee }}:{\Gamma }_M\to U_c$, introduced for any admissible shift ${\nu }^{\vee }\in P^{\vee }$ and ${\upsilon }_M\in {\Gamma }_M$ by the following defining relation,

$${\widehat{\theta }}_{M,{\nu }^{\vee }}=e^{\frac{2\pi \mathrm{i}}{M}⟨\widehat{\tau }({\upsilon }_M),{\nu }^{\vee }⟩}.$$

(49)

The isomorphism correspondence (35) between ${\upsilon }_M\in {\Gamma }_M$ and $\upsilon \in \Gamma$ immediately induces relations

$$\widehat{\psi }({\upsilon }_M)=\widehat{\psi }(\upsilon ),$$

(50)

$$\widehat{\tau }({\upsilon }_M)=M\widehat{\tau }(\upsilon ),$$

(51)

which guarantee the equality

$${\widehat{\theta }}_{M,{\nu }^{\vee }}({\upsilon }_M)={\widehat{\theta }}_{{\nu }^{\vee }}(\upsilon ).$$

(52)

A subgroup ${\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b)$ of $W_P^{\mathrm{aff}}$ stabilizing a point $b\in F_Q$ admits the following semidirect product decomposition from [1],

$${\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b)={\mathrm{Stab}}_{W_Q^{\mathrm{aff}}}(b)⋊{\mathrm{Stab}}_{\Gamma }(b),b\in F_Q.$$

(53)

A discrete valued stabilizer counting function $h_{P,M}:{\mathbb{R}}^n\to \mathbb{N}$ is for any magnifying factor $M\in \mathbb{N}$ defined by

$$h_{P,M}(b)=\left|{\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})\right|,b\in {\mathbb{R}}^n.$$

(54)

Based on the decomposition (53), the calculation procedure for the counting function $h_{P,M}$ is detailed in [1], § 4.1.

3. Weyl Orbit Functions on Shifted Dual Root Lattices

The goal of Section 3 is to introduce the $\gamma$- and $\widehat{\gamma }$-homomorphisms of the affine and extended affine Weyl groups and demonstrate that they govern argument and label symmetries of Weyl orbit functions on the shifted dual root lattices. The point and label sets of the shifted dual-root lattice discretization are introduced.

3.1. Sign and $\gamma$-Homomorphisms

For each root system $\Pi$, there exist two sign homomorphisms $\sigma :W\to U_2$ on its Weyl group, the identity homomorphism $\mathfrak{1}$ and the determinant homomorphism ${\sigma }^e=det$, being defined on the generators $r_i$, $i\in I$ of W by

$$\mathfrak{1}(r_i)=1,{\sigma }^e(r_i)=-1,i\in I.$$

(55)

In the case of root systems with two different lengths of roots, there are two additional homomorphisms ${\sigma }^s$ and ${\sigma }^l$ that distinguish between the short and long roots and they are given on the generators of W by

$${\sigma }^s(r_i)=\{\begin{array}{ll}-1& {\alpha }_i\in {\Delta }_s,\\ 1& {\alpha }_i\in {\Delta }_l,\end{array}{\sigma }^l(r_i)=\{\begin{array}{ll}1& {\alpha }_i\in {\Delta }_s,\\ -1& {\alpha }_i\in {\Delta }_l.\end{array}$$

(56)

Recall also from [2] the values for the reflections with respect to the highest root $\xi$ and the dual $\eta$,

$$\begin{array}{lll}{\sigma }^s(r_{\xi })=1,& & {\sigma }^l(r_{\xi })=-1,\end{array}$$

(57)

$$\begin{array}{lll}{\sigma }^s(r_{\eta })=-1,& & {\sigma }^l(r_{\eta })=1.\end{array}$$

(58)

To any sign homomorphism $\sigma$ and any admissible shift $\varrho$ of the weight lattice is assigned the homomorphism ${\gamma }_{\varrho }^{\sigma }:W^{\mathrm{aff}}\to U_2$ given for $w^{\mathrm{aff}}\in W^{\mathrm{aff}}$ by relation

$${\gamma }_{\varrho }^{\sigma }(w^{\mathrm{aff}})={\theta }_{\varrho }(w^{\mathrm{aff}})·[\sigma \circ \psi (w^{\mathrm{aff}})].$$

(59)

Table II summarizes the values of ${\gamma }_{\varrho }^{\sigma }$ on the set of generators R of $W^{\mathrm{aff}}$ in [9].

The multiplicative group $U_c^{*}$ is introduced as

$$U_c^{*}=\{\begin{array}{ll}{U}_c& c\mathrm{even},\\ U_{2c}& c\mathrm{odd}.\end{array}$$

(60)

To any sign homomorphism $\sigma$ and any admissible shift ${\nu }^{\vee }$ of the dual root lattice is assigned the homomorphism ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }:W_P^{\mathrm{aff}}\to U_c^{*}$ defined for $w^{\mathrm{aff}}\in W_P^{\mathrm{aff}}$ by relation

$${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}})={\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}})·[\sigma \circ \widehat{\psi }(w^{\mathrm{aff}})].$$

(61)

The values of $\sigma \circ \widehat{\psi }$ on the set of generators $R^{\vee }$ of $W_Q^{\mathrm{aff}}$ are determined as

$$\sigma \circ \widehat{\psi }(r_i)=\{\begin{array}{ll}\sigma (r_i)& i\in I,\\ \sigma (r_{\eta })& i=0,\end{array}$$

(62)

and the values of $\sigma \circ \widehat{\psi }$ on the generators ${\upsilon }_i$ of $\Gamma$ are given in Table 1 in [1]. These values, together with values of ${\widehat{\theta }}_{{\nu }^{\vee }}$, given by formulas (40) and (41)–(47), determine fully generator values of the homomorphism ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }$.

Furthermore, the modified homomorphism ${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }:{\Gamma }_M\to U_c^{*}$ is defined for ${\upsilon }_M\in {\Gamma }_M$ by

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }_M)={\widehat{\theta }}_{M,{\nu }^{\vee }}({\upsilon }_M)·[\sigma \circ \widehat{\psi }({\upsilon }_M)].$$

(63)

The modified homomorphism ${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }$ is calculated from relations (50) and (52) as

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }_M)={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon ).$$

(64)

3.2. Generalized Coxeter Numbers and Signed Fundamental Domains

Important subsets $F^{\sigma }(\varrho )$ of the fundamental domain F of the affine Weyl group are introduced in [9] for any sign homomorphism $\sigma$ and any admissible shift of the weight lattice $\varrho$ by

$$F^{\sigma }(\varrho )=\{a\in F|{\gamma }_{\varrho }^{\sigma }({\mathrm{Stab}}_{W^{\mathrm{aff}}}(a))=\left\{1\right\}\}.$$

(65)

Defining the subsets $R^{\sigma }(\varrho )$ of $W^{\mathrm{aff}}$ by

$$R^{\sigma }(\varrho )=\{r\in R|{\gamma }_{\varrho }^{\sigma }(r)=-1\},$$

(66)

it is shown in [9] that the signed fundamental domain $F^{\sigma }(\varrho )$ comprises all of the points of F without the boundary points $H^{\sigma }(\varrho )$,

$$H^{\sigma }(\varrho )=\{a\in F|(\exists r\in R^{\sigma }(\varrho ))(ra=a)\}.$$

(67)

Generalized Coxeter numbers $m_{\varrho }^{\sigma }$ are introduced via the set $R^{\sigma }(\varrho )$ and marks $m_0,m_1,\dots ,m_n$ by

$$m_{\varrho }^{\sigma }=\sum _{r_i\in R^{\sigma }(\varrho )}{m}_i.$$

(68)

Note that for the trivial admissible shifts of the weight lattice $\varrho =0$, it holds that $m_0^{\mathfrak{1}}$ vanishes and $m_0^{{\sigma }^e}$ becomes the standard Coxeter number. The short and long Coxeter numbers $m_0^{{\sigma }^s}$, $m_0^{{\sigma }^l}$ are denoted by $m^s$, $m^l$ in [2], respectively. The values of $m_0^{{\sigma }^s}$, $m_0^{{\sigma }^l}$ for all cases of algebras with two root lengths are tabulated in Table 1 of [2].

Similarly to definition (65), essential subsets $F_P^{\sigma }({\nu }^{\vee })$ of the fundamental domain $F_P$ of the extended dual affine Weyl group are defined for any homomorphism $\sigma$ and admissible shift ${\nu }^{\vee }$ by

$$F_P^{\sigma }({\nu }^{\vee })=\{b\in F_P|{\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b))=\left\{1\right\}\}.$$

(69)

Since the interior points of $F_P$ have trivial stabilizer, the interior $\mathrm{int}(F_P)$ of $F_P$ is included in all $F_P^{\sigma }({\nu }^{\vee })$. The subsets $R^{\sigma ,\vee }$ and ${\Gamma }^{\sigma }({\nu }^{\vee })$ of the generators $R^{\vee }$ and group $\Gamma$ defined by

$$R^{\sigma ,\vee }=\{r\in R^{\vee }\mid \sigma \circ \widehat{\psi }(r)=-1\},$$

(70)

$${\Gamma }^{\sigma }({\nu }^{\vee })=\{r\in \Gamma \mid {\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r)\ne 1\},$$

(71)

induce the following subsets of boundaries of $F_P^{\sigma }({\nu }^{\vee })$,

$$H^{\sigma ,\vee }=\{b\in F_P|(\exists r\in R^{\sigma ,\vee })(rb=b)\},$$

(72)

$$H^{\sigma ,\Gamma }({\nu }^{\vee })=\{b\in F_P|(\exists r\in {\Gamma }^{\sigma }({\nu }^{\vee }))(rb=b)\}.$$

(73)

The subsets of boundaries $H^{\sigma ,\vee }$ and $H^{\sigma ,\Gamma }({\nu }^{\vee })$ provide analytic form of the sets $F_P^{\sigma }({\nu }^{\vee })$ in the following proposition.

Proposition 3.

For the sets $F_P^{\sigma }({\nu }^{\vee })$, it holds that

$$F_P^{\sigma }({\nu }^{\vee })=F_P\setminus (H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee })).$$

(74)

Proof. 

Let $b\in F_P$. If $b\notin F_P\setminus (H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee }))$, then $b\in H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee }))$ and from definitions (70), (71) and property (40), there exists $r\in R^{\sigma ,\vee }\cup {\Gamma }^{\sigma }({\nu }^{\vee })$, such that $r\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b)$ with ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r)\ne 1$. Therefore, ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}})\ne \left\{1\right\}$ and, consequently, $b\notin F_P^{\sigma }({\nu }^{\vee })$. Conversely, if $b\in F_P\setminus (H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee }))$, then taking into account semidirect product decomposition (53) yields that ${\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b)$ is either trivial or generated by elements from $(R^{\vee }\setminus R^{\sigma ,\vee })\cup (\Gamma \setminus {\Gamma }^{\sigma }({\nu }^{\vee }))$. Because it holds for $r\in (R^{\vee }\setminus R^{\sigma ,\vee })\cup (\Gamma \setminus {\Gamma }^{\sigma }({\nu }^{\vee }))$ that ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r)=1$, it follows ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b))=\left\{1\right\}$, which implies $b\in F_P^{\sigma }({\nu }^{\vee })$. ☐

The signed dual fundamental domains $F_Q^{\sigma }$ are introduced as subsets of the dual fundamental domain $F_Q$ of the dual affine Weyl group $W_Q^{\mathrm{aff}}$ by expression

$$F_Q^{\sigma }=\{b\in F_Q|\sigma \circ \widehat{\psi }({\mathrm{Stab}}_{W_Q^{\mathrm{aff}}}(b))=\left\{1\right\}\}.$$

(75)

The explicit description of the signed dual fundamental domains $F_Q^{\sigma }$ is determined by the following relations [2,3],

$$F_Q^{\sigma }=\{b_1^{\sigma }{\omega }_1+\dots +b_n^{\sigma }{\omega }_n|b_0^{\sigma }+m_1^{\vee }{b}_1^{\sigma }+\dots +m_n^{\vee }{b}_n^{\sigma }=1\},$$

(76)

with the symbols $b_0^{\sigma },\dots ,b_n^{\sigma }$ satisfying

$$\begin{array}{lll}{b}_0^{\mathfrak{1}},b_i^{\mathfrak{1}}\ge 0& & \mathrm{if}{\alpha }_i\in \Delta ,\\ b_0^{{\sigma }^e},b_i^{{\sigma }^e}>0& & \mathrm{if}{\alpha }_i\in \Delta ,\\ b_i^{{\sigma }^s}\ge 0& & \mathrm{if}{\alpha }_i\in {\Delta }_l,& & b_0^{{\sigma }^s},b_i^{{\sigma }^s}>0& & \mathrm{if}{\alpha }_i\in {\Delta }_s,\\ b_i^{{\sigma }^l}>0& & \mathrm{if}{\alpha }_i\in {\Delta }_l,& & b_0^{{\sigma }^l},b_i^{{\sigma }^l}\ge 0& & \mathrm{if}{\alpha }_i\in {\Delta }_s.\end{array}$$

(77)

Using the signed dual fundamental domain $F_Q^{\sigma }$, the description of the domains $F_P^{\sigma }({\nu }^{\vee })$ is simplified in the following proposition.

Proposition 4.

For the sets $F_P^{\sigma }({\nu }^{\vee })$, it holds that

$$F_P^{\sigma }({\nu }^{\vee })=\{b\in F_P\cap F_Q^{\sigma }|{\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{\Gamma }(b))=\left\{1\right\}\}.$$

(78)

Proof. 

Because both ${\mathrm{Stab}}_{W_Q^{\mathrm{aff}}}(b)$ and ${\mathrm{Stab}}_{\Gamma }(b)$ are subgroups of ${\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b)$, taking into account relation (40) yields for any $b\in F_P^{\sigma }({\nu }^{\vee })$ that

$${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{W_Q^{\mathrm{aff}}}(b))=\sigma \circ \widehat{\psi }({\mathrm{Stab}}_{W_Q^{\mathrm{aff}}}(b))=\left\{1\right\},$$

(79)

$${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{\Gamma }(b))=\left\{1\right\}$$

(80)

and, therefore, $b\in F_Q^{\sigma }$. Conversely, relations (79) and (80), together with the semidirect product decomposition (53), imply for any $b\in F_P$ that ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b))=\left\{1\right\}$ and, thus, $b\in F_P^{\sigma }({\nu }^{\vee })$. ☐

Because $\upsilon \in {\mathrm{Stab}}_{\Gamma }(b/M)$ if and only if ${\upsilon }_M\in {\mathrm{Stab}}_{{\Gamma }_M}(b)$, Proposition 4 and relation (64) provide description of the magnified domain $M{F}_P^{\sigma }({\nu }^{\vee })$,

$$M{F}_P^{\sigma }({\nu }^{\vee })=\{b\in M(F_P\cap F_Q^{\sigma })|{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_M}(b))=\left\{1\right\}\}.$$

(81)

3.3. Symmetry Properties

Each sign homomorphism $\sigma$ induces a family of complex-valued Weyl orbit functions ${\phi }_b^{\sigma }:{\mathbb{R}}^n\to \mathbb{C}$, labeled by parameter $b\in {\mathbb{R}}^n$, given for any $a\in {\mathbb{R}}^n$ as

$${\phi }_b^{\sigma }(a)=\sum _{w\in W}\sigma (w)e^{2\pi \mathrm{i}⟨wb,a⟩}.$$

(82)

The argument symmetry of orbit functions from Proposition 3.1 in [9] guarantees that, for an admissible shift $\varrho$ of the weight lattice, a shifted weight $b\in \varrho +P$, $w^{\mathrm{aff}}\in W^{\mathrm{aff}}$ and $a\in {\mathbb{R}}^n$, it holds that

$${\phi }_b^{\sigma }(w^{\mathrm{aff}}a)={\gamma }_{\varrho }^{\sigma }(w^{\mathrm{aff}}){\phi }_b^{\sigma }(a).$$

(83)

Moreover, the functions ${\phi }_b^{\sigma }$ vanish on the boundary $H^{\sigma }(\varrho )$,

$${\phi }_b^{\sigma }(a^{\prime })=0,a^{\prime }\in H^{\sigma }(\varrho ).$$

(84)

Thus, Weyl orbit functions ${\phi }_b^{\sigma }$, $b\in \varrho +P$ are (anti)invariant with respect to the affine Weyl group and it is sufficient to restrict them to the fundamental domain F. Furthermore, from vanishing property (84), it follows that the functions ${\phi }_b^{\sigma }$, $b\in \varrho +P$ are fully determined by their values in $F^{\sigma }(\varrho )$. As detailed in the following proposition, the restriction of the argument of Weyl orbit functions to the shifted refined dual root lattice implies their specific multiplicative transformation with respect to the action of extended affine Weyl group $W_P^{\mathrm{aff}}$ on the labels $b\in {\mathbb{R}}^n$.

Proposition 5.

Let ${\nu }^{\vee }$ be an admissible shift of $Q^{\vee }$ and $a\in \frac{1}{M}({\nu }^{\vee }+Q^{\vee })$, $M\in \mathbb{N}$. Subsequently, it holds for any $w^{\mathrm{aff}}\in W_P^{\mathrm{aff}}$ and $b\in {\mathbb{R}}^n$ that

$${\phi }_{M{w}^{\mathrm{aff}}(\frac{b}{M})}^{\sigma }(a)={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}}){\phi }_b^{\sigma }(a).$$

(85)

Moreover, the Weyl orbit function ${\phi }_{b^{\prime }}^{\sigma }$ vanishes for any $b^{\prime }\in M(H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee }))$,

$${\phi }_{b^{\prime }}^{\sigma }(a)=0,b^{\prime }\in M(H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee })).$$

(86)

Proof. 

For any $w^{\mathrm{aff}}=T(p)w^{\prime }\in W_P^{\mathrm{aff}}$ with $p\in P$, $w^{\prime }\in W$ and $a=({\nu }^{\vee }+s)/M$ with $s\in Q^{\vee }$, it holds that

$${\phi }_{M{w}^{\mathrm{aff}}(\frac{b}{M})}^{\sigma }(a)=\sum _{w\in W}\sigma (w)e^{2\pi \mathrm{i}⟨w{w}^{\prime }b,a⟩}{e}^{2\pi \mathrm{i}⟨Mwp,a⟩}.$$

(87)

Because ${\nu }^{\vee }$ is an admissible shift of $Q^{\vee }$ and the W-invariant weight lattice P is $\mathbb{Z}$-dual to $Q^{\vee }$, relation (48) and definition (39) yield

$$e^{2\pi \mathrm{i}⟨Mwp,a⟩}=e^{2\pi \mathrm{i}⟨wp,{\nu }^{\vee }+s⟩}=e^{2\pi \mathrm{i}⟨wp,{\nu }^{\vee }⟩}=e^{2\pi \mathrm{i}⟨p,{\nu }^{\vee }⟩}={\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}}).$$

Therefore, relation (87) and definition (61) imply that

$${\phi }_{M{w}^{\mathrm{aff}}(\frac{b}{M})}^{\sigma }(a)={\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}})\sum _{w\in W}\sigma (w)e^{2\pi \mathrm{i}⟨w{w}^{\prime }b,a⟩}={\widehat{\theta }}_{{\nu }^{\vee }}(w^{\mathrm{aff}})\sigma (w^{\prime }){\phi }_b^{\sigma }(a)={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}}){\phi }_b^{\sigma }(a).$$

From definitions (72) and (73), it follows that, for any $b^{\prime }\in M(H^{\sigma ,\vee }\cup H^{\sigma ,\Gamma }({\nu }^{\vee }))$, there exists an element $r\in R^{\sigma ,\vee }\cup {\Gamma }^{\sigma }({\nu }^{\vee })$, such that $r(b^{\prime }/M)=b^{\prime }/M$. Substituting such element r into label transformation relation (85) and taking into account definitions (70) and (71) yields

$${\phi }_{b^{\prime }}^{\sigma }(a)={\phi }_{Mr(\frac{b^{\prime }}{M})}^{\sigma }(a)={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r){\phi }_{b^{\prime }}^{\sigma }(a),$$

with $|{\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r)|=1$ and ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(r)\ne 1$. ☐

Thus, Weyl orbit functions evaluated at points $a\in ({\nu }^{\vee }+Q^{\vee })/M$ are under the action of the magnified extended dual affine Weyl group $MP⋊W$ on their labels $b\in {\mathbb{R}}^n$ multiplied by specific complex factors. Therefore, it is sufficient to restrict the labels of ${\phi }_b^{\sigma }(a)$ to the magnified fundamental domain $M{F}_P$ of $MP⋊W$. Furthermore, from analytic expression (74) and vanishing property (86), it follows that the family of functions ${\phi }_b^{\sigma }(a)$ with $a\in ({\nu }^{\vee }+Q^{\vee })/M$ is fully determined by their labels $b\in M{F}_P^{\sigma }({\nu }^{\vee })$.

3.4. Shifted Dual-Root Lattice Discretization

The shifted dual-root lattice discretization of Weyl orbit functions is produced for admissible shifts of the weight lattice $\varrho$ and dual root lattice ${\nu }^{\vee }$ by restricting the labels of orbit functions to the shifted weight lattice $\varrho +P$ and the arguments to the refined shifted dual root lattice $({\nu }^{\vee }+Q^{\vee })/M$. From argument and label symmetries in relations (83), (84), and Proposition 5, the discretized functions ${\phi }_b^{\sigma }(a)$ are labeled by the sets of labels

$${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })=(\varrho +P)\cap M{F}_P^{\sigma }({\nu }^{\vee })$$

(88)

and their arguments are restricted to the sets of points

$$F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })=\frac{1}{M}({\nu }^{\vee }+Q^{\vee })\cap F^{\sigma }(\varrho ).$$

(89)

In order to describe the finite set of points $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ explicitly, the symbols $s_i^{\sigma ,\varrho }$, $i\in \widehat{I}$ are introduced by

$$s_i^{\sigma ,\varrho }\in \{\begin{array}{ll}\mathbb{N}& r_i\in R^{\sigma }(\varrho ),\\ {\mathbb{Z}}^{\ge 0}& r_i\in R\setminus R^{\sigma }(\varrho ).\end{array}$$

(90)

The requirements for the points in ${\omega }^{\vee }$-basis to belong to the shifted dual root lattice

$$s_1^{\sigma ,\varrho }{\omega }_1^{\vee }+\dots +s_n^{\sigma ,\varrho }{\omega }_n^{\vee }\in {\nu }^{\vee }+Q^{\vee },$$

are reformulated for each simple Lie algebra $\mathfrak{g}$ and an admissible shift ${\nu }^{\vee }={\omega }_j^{\vee }$, $j\in J^{\vee }\cup \left\{0\right\}$ as the following conditions ${\mathrm{cond}}_{\mathfrak{g}}({\nu }^{\vee })$,

$$\begin{array}{lll}{A}_n:& & s_1^{\sigma ,\varrho }+2s_2^{\sigma ,\varrho }+3s_3^{\sigma ,\varrho }+\dots +n{s}_n^{\sigma ,\varrho }\equiv jmodn+1,j=0,\dots ,n,\end{array}$$

(91)

$$\begin{array}{lll}{B}_{2k+1}:& & s_1^{\sigma ,\varrho }+s_3^{\sigma ,\varrho }+s_5^{\sigma ,\varrho }+\dots +s_{2k+1}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j=0,\\ 1mod2& j=1,\end{array}\end{array}$$

(92)

$$\begin{array}{lll}{B}_{2k}:& & s_1^{\sigma ,\varrho }+s_3^{\sigma ,\varrho }+s_5^{\sigma ,\varrho }+\dots +s_{2k-1}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j=0,\\ 1mod2& j=1,\end{array}\end{array}$$

(93)

$$\begin{array}{lll}{C}_n:& & s_n^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j=0,\\ 1mod2& j=n,\end{array}\end{array}$$

(94)

$$\begin{array}{lll}{D}_{4k}:& & s_1^{\sigma ,\varrho }+s_3^{\sigma ,\varrho }+\dots +s_{4k-3}^{\sigma ,\varrho }+s_{4k-1}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j\in \{0,4k\},\\ 1mod2& j\in \{1,4k-1\},\end{array}\end{array}$$

(95)

$$\begin{array}{lll}& & s_{4k-1}^{\sigma ,\varrho }+s_{4k}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j\in \{0,1\},\\ 1mod2& j\in \{4k-1,4k\},\end{array}\end{array}$$

(96)

$$\begin{array}{lll}{D}_{4k+1}:& & 2s_1^{\sigma ,\varrho }+2s_3^{\sigma ,\varrho }+\dots +2s_{4k-1}^{\sigma ,\varrho }+3s_{4k}^{\sigma ,\varrho }+s_{4k+1}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod4& j=0,\\ 2mod4& j=1,\\ 3mod4& j=4k,\\ 1mod4& j=4k+1,\end{array}\end{array}$$

(97)

$$\begin{array}{lll}{D}_{4k+2}:& & s_1^{\sigma ,\varrho }+s_3^{\sigma ,\varrho }+\dots +s_{4k-1}^{\sigma ,\varrho }+s_{4k+2}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j\in \{0,4k+1\},\\ 1mod2& j\in \{1,4k+2\},\end{array}\end{array}$$

(98)

$$\begin{array}{lll}& & s_{4k+1}^{\sigma ,\varrho }+s_{4k+2}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j\in \{0,1\},\\ 1mod2& j\in \{4k+1,4k+2\},\end{array}\end{array}$$

(99)

$$\begin{array}{lll}{D}_{4k+3}:& & 2s_1^{\sigma ,\varrho }+2s_3^{\sigma ,\varrho }+\dots +2s_{4k+1}^{\sigma ,\varrho }+s_{4k+2}^{\sigma ,\varrho }+3s_{4k+3}^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod4& j=0,\\ 2mod4& j=1,\\ 1mod4& j=4k+2,\\ 3mod4& j=4k+3,\end{array}\end{array}$$

(100)

$$\begin{array}{lll}{E}_6:& & s_1^{\sigma ,\varrho }+2s_2^{\sigma ,\varrho }+s_4^{\sigma ,\varrho }+2s_5^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod3& j=0,\\ 1mod3& j=1,\\ 2mod3& j=5,\end{array}\end{array}$$

(101)

$$\begin{array}{lll}{E}_7:& & s_4^{\sigma ,\varrho }+s_6^{\sigma ,\varrho }+s_7^{\sigma ,\varrho }\equiv \{\begin{array}{ll}0mod2& j=0,\\ 1mod2& j=6,\end{array}\end{array}$$

(102)

$$\begin{array}{ll}{G}_2,E_8,F_4:& Ø.\end{array}$$

(103)

Thus, the point set $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ is of the following explicit form

$$F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })=\{\frac{s_1^{\sigma ,\varrho }}{M}{\omega }_1^{\vee }+\dots +\frac{s_n^{\sigma ,\varrho }}{M}{\omega }_n^{\vee }|s_0^{\sigma ,\varrho }+m_1{s}_1^{\sigma ,\varrho }+\dots +m_n{s}_n^{\sigma ,\varrho }=M,{\mathrm{cond}}_{\mathfrak{g}}({\nu }^{\vee })\}.$$

(104)

4. Cardinality of ${\Lambda }_{\mathit{P},\mathit{M}}^{\mathbf{\sigma }}(\mathbf{\varrho },{\mathbf{\nu }}^{\vee })$ and ${\mathit{F}}_{{\mathit{Q}}^{\vee },\mathit{M}}^{\mathbf{\sigma }}(\mathbf{\varrho },{\mathbf{\nu }}^{\vee })$

The purpose of Section 4 is to demonstrate that the point sets $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ and the label sets ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ have for $M>m_{\varrho }^{\sigma }$ the same numbers of elements. To this goal, associated $(\mathcal{R},\sigma ,{\nu }^{\vee })$-invariant polynomial spaces and their connection to the finite point and label sets need to be studied. The developed crucial Theorem 2 warrants the existence of the discrete Fourier-Weyl transforms on the shifted dual root lattice. The counting formulas for the common cardinalities of the point and label sets are also presented.

4.1. $(\mathcal{R},\sigma ,{\nu }^{\vee })$-Invariant Polynomials

The construction of the polynomial spaces starts with the notion of the extended m-degree from [1]. Recall that the polynomial vector space $\left[x\right]$ contains polynomials of $n+1$ variables $x\equiv {[x_0,\dots ,x_n]}^T$ over the complex numbers and the extended m-degree ${\mathrm{edg}}_m{x}^{\lambda }$ of any monomial $x^{\lambda }\equiv x_0^{{\lambda }_0}{x}_1^{{\lambda }_1}\dots x_n^{{\lambda }_n}$, $\lambda \equiv [{\lambda }_0,\dots ,{\lambda }_n]$ is given as

$${\mathrm{edg}}_m{x}^{\lambda }={\lambda }_0+m_1^{\vee }{\lambda }_1+\dots +m_n^{\vee }{\lambda }_n.$$

The extended m-degree of any polynomial $f\in \left[x\right]$ is then the maximum extended m-degree of homogeneous parts of f. Also recall from [3] that the finite weight set ${\Lambda }_M\subset P$ consists for any $M\in \mathbb{N}$ of the weights contained in the set $M{F}_Q$,

$${\Lambda }_M=P\cap M{F}_Q,$$

(105)

and it is explicitly described as

$${\Lambda }_M=\{{\lambda }_1{\omega }_1+\dots +{\lambda }_n{\omega }_n|{\lambda }_0+m_1^{\vee }{\lambda }_1+\dots +m_n^{\vee }{\lambda }_n=M,{\lambda }_i\in {\mathbb{Z}}^{\ge 0},i\in \widehat{I}\}.$$

(106)

Identifying each element $\lambda \in {\Lambda }_M$ with its Kac coordinates $[{\lambda }_0,\dots ,{\lambda }_n]$ from (106) yields that ${\mathrm{edg}}_m{x}^{\lambda }=M$ if and only if $\lambda \in {\Lambda }_M$. All of the linear combinations of monomials of extended m-degree equal to M form a vector subspace ${\Pi }_M\subset \left[x\right]$,

$${\Pi }_M=\left\{\sum _{\lambda \in {\Lambda }_M}{c}_{\lambda }{x}^{\lambda }\right|c_{\lambda }\in ,\lambda \in {\Lambda }_M\}.$$

The standard action [32,33] of any operator $\mathbb{G}\in {\mathrm{GL}}_{n+1}(\mathbb{C})$ on $\mathbb{C}\left[x\right]$ is determined by

$$\mathbb{G}·f(x)=f({\mathbb{G}}^{-1}x),f\in \mathbb{C}\left[x\right].$$

(107)

For any representation $\mathcal{R}:\Gamma \to {\mathrm{GL}}_{n+1}(\mathbb{C})$ of the abelian group (29) and a sign homomorphism $\sigma$ and an admissible shift of the dual root lattice ${\nu }^{\vee }$, a polynomial $f\in \mathbb{C}\left[x\right]$ is called $(\mathcal{R},\sigma ,{\nu }^{\vee })$-invariant if it, for all $\upsilon \in \Gamma$, satisfies

$$\mathcal{R}(\upsilon )·f={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon )f.$$

(108)

A vector subspace ${\Pi }_M^{\mathcal{R},\sigma ,{\nu }^{\vee }}\subset {\Pi }_M$ contains all $(\mathcal{R},\sigma ,{\nu }^{\vee })$-invariant polynomials from ${\Pi }_M$,

$${\Pi }_M^{\mathcal{R},\sigma ,{\nu }^{\vee }}=\{f\in {\Pi }_M\mid \mathcal{R}(\upsilon )·f={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon )f,\upsilon \in \Gamma \}.$$

Proposition 6.

Let ${\mathcal{R}}_1,{\mathcal{R}}_2$ be representations of Γ to ${\mathrm{GL}}_{n+1}(\mathbb{C})$ for which there exists $\mathbb{P}\in {\mathrm{GL}}_{n+1}(\mathbb{C})$, such that

(i) 

${\mathcal{R}}_2(\upsilon )={\mathbb{P}}^{-1}{\mathcal{R}}_1(\upsilon )\mathbb{P}$ for all $\upsilon \in \Gamma$, i.e., ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ are equivalent,

(ii) 

$\mathbb{P}·f\in {\Pi }_M$⇔$f\in {\Pi }_M$.

Subsequently, the spaces ${\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}$ and ${\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}$ are for any sign homomorphism σ and any admissible shift ${\nu }^{\vee }$ of the dual root lattice isomorphic,

$${\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}\simeq {\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}.$$

Proof. 

Assumption (ii) guarantees for any $f\in {\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}$ that $\mathbb{P}·f\in {\Pi }_M$. Definitions (107) and (108) and assumption (i) result to $({\mathcal{R}}_1,\sigma ,{\nu }^{\vee })$-invariance of $\mathbb{P}·f,$

$${\mathcal{R}}_1(\upsilon )·\mathbb{P}·f(x)=f({\mathbb{P}}^{-1}{\mathcal{R}}_1{(\upsilon )}^{-1}x)=f({\mathcal{R}}_2{(\upsilon )}^{-1}{\mathbb{P}}^{-1}x)=\mathbb{P}·{\mathcal{R}}_2(\upsilon )·f(x)={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon )\mathbb{P}·f(x)$$

and, therefore, $\mathbb{P}·f\in {\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}$. Conversely, it holds that, if $f\in {\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}$, then ${\mathbb{P}}^{-1}·f\in {\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}$. The map ${\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}\ni f\mapsto \mathbb{P}·f\in {\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}$ is linear and its inverse is the map ${\Pi }_M^{{\mathcal{R}}_1,\sigma ,{\nu }^{\vee }}\ni f\mapsto {\mathbb{P}}^{-1}·f\in {\Pi }_M^{{\mathcal{R}}_2,\sigma ,{\nu }^{\vee }}.$ ☐

The action (33) of $\Gamma$ on $F_Q$ given as permutations of the Kac coordinates $[b_0,\dots ,b_n]$ induces a faithful representation $\mathcal{A}:\Gamma \to {\mathrm{GL}}_{n+1}(\mathbb{C})$ by assigning to each element $\upsilon \in \Gamma$ its permutation matrix $\mathcal{A}(\upsilon )\in {\mathrm{GL}}_{n+1}(\mathbb{C})$,

$$\mathcal{A}(\upsilon ){[b_0,\dots ,b_n]}^T={[b_{{\pi }_{\upsilon }(0)},\dots ,b_{{\pi }_{\upsilon }(n)}]}^T.$$

(109)

Moreover, the action of the magnified group ${\Gamma }_M$ on $M{F}_Q$, determined by (36), firstly assigns each element ${\upsilon }_M\in {\Gamma }_M$ by isomorphism (35) the corresponding element $\upsilon \in \Gamma$ and, afterwards, its representation matrix $\mathcal{A}(\upsilon )$, i.e.,

$$\mathcal{A}({\upsilon }_M)=\mathcal{A}(\upsilon ).$$

(110)

The commuting diagonalizable matrices $\mathcal{A}(\upsilon )$ are simultaneously diagonalized via a unitary matrix $\mathbb{P}\in {\mathrm{GL}}_{n+1}(\mathbb{C})$. The diagonal representation $\mathcal{D}:\Gamma \to {\mathrm{GL}}_{n+1}(\mathbb{C})$ is given for any $\upsilon \in \Gamma$ by

$$\mathcal{D}(\upsilon )={\mathbb{P}}^{†}\mathcal{A}(\upsilon )\mathbb{P}.$$

(111)

The diagonal matrices $\mathcal{D}(\upsilon )$ are calculated for the generators of the non-trivial groups $\Gamma$ in relation (55) of [1] and the unitary conjugation matrices $\mathbb{P}$ are listed in Table 3 of [1]. Explicit forms of the unitary conjugation matrices $\mathbb{P}$ imply that each $\mathbb{P}$ satisfies the assumption of Proposition 4.5 of [1] and, therefore, it holds that

$$\mathbb{P}·f\in {\Pi }_M\iff f\in {\Pi }_M.$$

Thus, assumption (ii) in Proposition 6 is valid for the representations $\mathcal{A}$ and $\mathcal{D}$ and the following theorem follows.

Theorem 1.

Let $\mathcal{A}$ be the permutation representation (109) of Γ and $\mathcal{D}$ the corresponding diagonal representation (111). Subsequently, the spaces ${\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}$ and ${\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}$ are for any sign homomorphism σ and any admissible shift ${\nu }^{\vee }$ of the dual root lattice isomorphic,

$${\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}\simeq {\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}.$$

4.2. Cardinality of ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$

An auxiliary finite set of weights ${\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })$ is introduced by the relation

$${\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })=\{\lambda \in {\Lambda }_M\mid {\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_M}(\lambda ))=\left\{1\right\}\},$$

(112)

together with its complementary set ${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })$,

$${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })=\{\lambda \in {\Lambda }_M|{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_M}(\lambda ))\ne \left\{1\right\}\}.$$

(113)

The corresponding sets ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ and ${\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })$ of representative weights in ${\Gamma }_M$-orbits are determined as

$${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })=M{F}_P\cap {\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee }),$$

(114)

$${\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })=M{F}_P\cap {\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee }).$$

(115)

Since $M{F}_P$ is a fundamental domain of the action of ${\Gamma }_M$ on $M{F}_Q$, it holds that

$${\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })={\Gamma }_M{\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee }),$$

(116)

$${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })={\Gamma }_M{\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })$$

(117)

and the following disjoint decompositions of the weight sets ${\Lambda }_M$ and $M{F}_P\cap {\Lambda }_M$ are obtained,

$$\begin{array}{cc}\hfill {\Lambda }_M& ={\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })\cup {\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee }),\hfill \end{array}$$

(118)

$$\begin{array}{cc}\hfill M{F}_P\cap {\Lambda }_M& ={\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })\cup {\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee }).\hfill \end{array}$$

(119)

Depending on the admissible shift $\varrho$ of the weight lattice P and the sign homomorphism $\sigma$, auxiliary signed shift vectors ${\kappa }^{\sigma ,\varrho },$

$${\kappa }^{\sigma ,\varrho }={\kappa }_1^{\sigma ,\varrho }{\omega }_1+\dots +{\kappa }_n^{\sigma ,\varrho }{\omega }_n=[{\kappa }_0^{\sigma ,\varrho },{\kappa }_1^{\sigma ,\varrho },\dots ,{\kappa }_n^{\sigma ,\varrho }],$$

of the weight lattice are defined. For the trivial admissible shift $\varrho =0$ of the weight lattice, the signed shift vector coordinates ${\kappa }_i^{\sigma ,0}$ are given by

$$\begin{array}{lll}{\kappa }_i^{\mathfrak{1},0}=0,& & i\in I,\\ {\kappa }_i^{{\sigma }^e,0}=1,& & i\in I,\\ {\kappa }_i^{{\sigma }^s,0}=1,& & {\alpha }_i\in {\Delta }_s,& & {\kappa }_i^{{\sigma }^s,0}=0,& & {\alpha }_i\in {\Delta }_l,\\ {\kappa }_i^{{\sigma }^l,0}=0,& & {\alpha }_i\in {\Delta }_s,& & {\kappa }_i^{{\sigma }^l,0}=1,& & {\alpha }_i\in {\Delta }_l\end{array}$$

(120)

and the zero coordinates ${\kappa }_0^{\sigma ,0}$ are introduced by

$${\kappa }_0^{\mathfrak{1},0}=0,{\kappa }_0^{{\sigma }^e,0}=1,{\kappa }_0^{{\sigma }^s,0}=1,{\kappa }_0^{{\sigma }^l,0}=0.$$

(121)

In the case of the non-trivial admissible shift of the weight lattice $\varrho \ne 0$, the vectors ${\kappa }^{\sigma ,\varrho }$ are defined by setting their coordinates as

$$\begin{array}{lll}{A}_1:& & {\kappa }^{\mathfrak{1},\varrho }={\kappa }^{{\sigma }^e,\varrho }=[\frac{1}{2},\frac{1}{2}],\\ C_n:& & {\kappa }^{\mathfrak{1},\varrho }={\kappa }^{{\sigma }^l,\varrho }=[0,0,\dots ,0,\frac{1}{2}],\\ & & {\kappa }^{{\sigma }^e,\varrho }={\kappa }^{{\sigma }^s,\varrho }=[1,1,\dots ,1,\frac{1}{2}].\end{array}$$

(122)

The set ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ is related by ${\kappa }^{\sigma ,\varrho }$ shifts to the set ${\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ in the following proposition.

Proposition 7.

The set of weights ${\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ coincides for any $M\in \mathbb{N}$ with the ${\kappa }^{\sigma ,\varrho }$-shifted set ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee }),$

$${\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })={\kappa }^{\sigma ,\varrho }+{\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee }).$$

Proof. 

Firstly, for any coordinates $[{\lambda }_0,\dots ,{\lambda }_n]$ of any weight $\lambda ={\lambda }_1{\omega }_1+\dots +{\lambda }_n{\omega }_n\in P$ are the corresponding coordinates $[{\lambda }_0^{\sigma ,\varrho },\dots ,{\lambda }_n^{\sigma ,\varrho }]$ of ${\lambda }^{\sigma ,\varrho }={\lambda }_1^{\sigma ,\varrho }{\omega }_1+\dots +{\lambda }_n^{\sigma ,\varrho }{\omega }_n\in \varrho +P$ defined by

$${\lambda }_i^{\sigma ,\varrho }={\lambda }_i+{\kappa }_i^{\sigma ,\varrho },i\in \widehat{I}.$$

According to (81) and (88), any weight ${\lambda }^{\sigma ,\varrho }\in {\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ satisfies the conditions

$${\lambda }^{\sigma ,\varrho }\in (\varrho +P)\cap (M+m_{\varrho }^{\sigma })F_P,$$

(123)

$${\lambda }^{\sigma ,\varrho }\in (\varrho +P)\cap (M+m_{\varrho }^{\sigma })F_Q^{\sigma },$$

(124)

together with

$${\widehat{\gamma }}_{M+m_{\varrho }^{\sigma },{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_{M+m_{\varrho }^{\sigma }}}({\lambda }^{\sigma ,\varrho }))=\left\{1\right\}.$$

(125)

Defining relations (120)–(122), (68) and (76), (77) imply that ${\kappa }^{\sigma ,\varrho }\in (\varrho +P)\cap m_{\varrho }^{\sigma }{F}_Q^{\sigma }$ and, consequently, (124) grants that

$$\lambda \in P\cap M{F}_Q.$$

(126)

From Table 1 of [1], direct evaluation produces the invariance of the coordinates of the vectors ${\kappa }^{\sigma ,\varrho }$ under any permutation ${\pi }_{\upsilon }$, $\upsilon \in \Gamma$,

$${\kappa }_{{\pi }_{\upsilon }(i)}^{\sigma ,\varrho }={\kappa }_i^{\sigma ,\varrho },i\in \widehat{I}.$$

(127)

Taking into account (127) and comparing the action of ${\upsilon }_{M+m_{\varrho }^{\sigma }}\in {\Gamma }_{M+m_{\varrho }^{\sigma }}$ on ${\lambda }^{\sigma ,\varrho }\in (\varrho +P)\cap (M+m_{\varrho }^{\sigma })F_Q^{\sigma }$,

$${\upsilon }_{M+m_{\varrho }^{\sigma }}·{\lambda }^{\sigma ,\varrho }=[{\lambda }_{{\pi }_{\upsilon }(0)}^{\sigma ,\varrho },\dots ,{\lambda }_{{\pi }_{\upsilon }(n)}^{\sigma ,\varrho }]=[{\lambda }_{{\pi }_{\upsilon }(0)}+{\kappa }_0^{\sigma ,\varrho },\dots ,{\lambda }_{{\pi }_{\upsilon }(n)}+{\kappa }_n^{\sigma ,\varrho }],$$

(128)

to the action of ${\upsilon }_M\in {\Gamma }_M$ on $\lambda \in P\cap M{F}_Q$,

$${\upsilon }_M·\lambda =[{\lambda }_{{\pi }_{\upsilon }(0)},\dots ,{\lambda }_{{\pi }_{\upsilon }(n)}],$$

(129)

guarantees that the point ${\lambda }^{\sigma ,\varrho }$ is the lexicographically highest in its ${\Gamma }_{M+m_{\varrho }^{\sigma }}$-orbit whenever $\lambda$ is the lexicographically highest in its ${\Gamma }_M$-orbit. Thus, from properties (123), (126), and (32), it follows that

$$\lambda \in P\cap M{F}_P.$$

(130)

Comparing action (128) for the stabilizing ${\upsilon }_{M+m_{\varrho }^{\sigma }}\in {\mathrm{Stab}}_{{\Gamma }_{M+m_{\varrho }^{\sigma }}}({\lambda }^{\sigma ,\varrho })$ and action (129) of ${\upsilon }_M\in {\Gamma }_M$ on $\lambda \in P\cap M{F}_P$ requires ${\upsilon }_M$ to stabilize $\lambda$, i.e., ${\upsilon }_M\in {\mathrm{Stab}}_{{\Gamma }_M}(\lambda ).$ Therefore, equality of $\gamma$-homomorphisms (64) enforces

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_M}(\lambda ))={\widehat{\gamma }}_{M+m_{\varrho }^{\sigma },{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_{M+m_{\varrho }^{\sigma }}}({\lambda }^{\sigma ,\varrho })).$$

(131)

Unitary values of the ${\widehat{\gamma }}_{M+m_{\varrho }^{\sigma },{\nu }^{\vee }}^{\sigma }$-homomorphism (125) and relation (131) imply that

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\mathrm{Stab}}_{{\Gamma }_M}(\lambda ))=\left\{1\right\},$$

(132)

and, therefore, $\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee }).$

Conversely, $\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ implies the validity of (132) and (130). Defining relations (120)–(122), (68) and (76), (77) then guarantee that $\lambda \in P\cap M{F}_Q$ enforces (124). By comparing actions (128) and (129), property (130) forces relation (123), properties (132) and (131) guarantee (125), and it follows that ${\lambda }^{\sigma ,\varrho }\in {\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$. ☐

Proposition 8.

The dimension of ${\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}$ is for any $M\in \mathbb{N}$ equal to the cardinality of ${\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$,

$$dim{\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}=\left|{\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })\right|.$$

Proof. 

The polynomial $f_{\lambda }^{\sigma ,{\nu }^{\vee }}\in {\Pi }_M$ with $\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ is for any sign homomorphism $\sigma$ and any admissible shift of $Q^{\vee }$ introduced via the group action (36) as

$$f_{\lambda }^{\sigma ,{\nu }^{\vee }}(x)=\sum _{\upsilon \in {\Gamma }_M}{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }.$$

(133)

Any $\upsilon \in {\Gamma }_M$ is represented by (110) as a permutation matrix $\mathcal{A}(\upsilon )$ and, thus, the polynomial action (107) on the monomials is of the form

$$\mathcal{A}(\upsilon )·x^{\lambda }=x^{\upsilon ·\lambda }.$$

(134)

Substituting the permutation action (134) into defining relation (133) and taking into account magnifying relations (64) and (110), the polynomials $f_{\lambda }^{\sigma ,{\nu }^{\vee }}$, $\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ are verified to be $(\mathcal{A},\sigma ,{\nu }^{\vee })$-invariant, $f_{\lambda }^{\sigma ,{\nu }^{\vee }}\in {\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}.$

Because any $\upsilon \in {\mathrm{Stab}}_{{\Gamma }_M}\left(\lambda \right)$ satisfies from defining relation (114) that ${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})=1$, any general linear combination of $f_{\lambda }^{\sigma ,{\nu }^{\vee }}$ polynomials (133) is of the form

$$\begin{array}{ll}\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}{c}_{\lambda }{f}_{\lambda }^{\sigma ,{\nu }^{\vee }}(x)& =\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}\sum _{\upsilon \in {\Gamma }_M}{c}_{\lambda }{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }\\ & =\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}(\sum _{\upsilon \in {\mathrm{Stab}}_{{\Gamma }_M}(\lambda )}{c}_{\lambda }{x}^{\lambda }+\sum _{\upsilon \in {\Gamma }_M\setminus {\mathrm{Stab}}_{{\Gamma }_M}(\lambda )}{c}_{\lambda }{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda })\end{array}$$

$$\begin{array}{ll}& =\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}|{\mathrm{Stab}}_{{\Gamma }_M}(\lambda )|c_{\lambda }{x}^{\lambda }+\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}\sum _{\upsilon \in {\Gamma }_M\setminus {\mathrm{Stab}}_{{\Gamma }_M}(\lambda )}{c}_{\lambda }{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }.\end{array}$$

(135)

Because $M{F}_P$ is a fundamental domain of ${\Gamma }_M$ acting on $M{F}_Q$, the second term of (135) is a linear combination of monomials $x^{\lambda }$ with $\lambda \notin {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$. Because the monomials $x^{\lambda },\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ in the first term of (135) are linearly independent, setting (135) as equal to zero forces all $c_{\lambda }\in$ with $\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ to be also zero. Therefore, the polynomials $f_{\lambda }^{\sigma ,{\nu }^{\vee }}$ are linearly independent.

For any $(\mathcal{A},\sigma ,{\nu }^{\vee })$-invariant polynomial $f\in {\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}$ of the generic form

$$f(x)=\sum _{\lambda \in {\Lambda }_M}{c}_{\lambda }{x}^{\lambda }$$

and for any $\upsilon \in {\Gamma }_M$ imply invariance and magnifying properties (108), (64), (110), together with the monomial action (134) that

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }(\upsilon )\sum _{\lambda \in {\Lambda }_M}{c}_{\lambda }{x}^{\lambda }=\sum _{\lambda \in {\Lambda }_M}{c}_{\lambda }{x}^{\upsilon ·\lambda }.$$

(136)

The set of weights ${\Lambda }_M$ is invariant under ${\Gamma }_M$ and, therefore, comparing the coefficients in (136) results in ${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }(\upsilon )c_{\lambda }=c_{{\upsilon }^{-1}·\lambda }$ that is equivalent to

$${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})c_{\lambda }=c_{\upsilon ·\lambda }.$$

(137)

The disjoint decomposition (118) of the weight set ${\Lambda }_M$, together with orbit relations (116), (117), and coefficient transformation (137), ensures that

$$\begin{array}{ll}f(x)& =\sum _{\upsilon \in {\Gamma }_M}\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}|{\mathrm{Stab}}_{{\Gamma }_M}(\lambda ){|}^{-1}{c}_{\upsilon ·\lambda }{x}^{\upsilon ·\lambda }+\sum _{\upsilon \in {\Gamma }_M}\sum _{\lambda \in {\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })}{|{\mathrm{Stab}}_{{\Gamma }_M}(\lambda )|}^{-1}{c}_{\upsilon ·\lambda }{x}^{\upsilon ·\lambda }\end{array}$$

$$\begin{array}{ll}& =\sum _{\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })}|{\mathrm{Stab}}_{{\Gamma }_M}(\lambda ){|}^{-1}{c}_{\lambda }{f}_{\lambda }^{\sigma ,{\nu }^{\vee }}(x)+\sum _{\lambda \in {\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })}{|{\mathrm{Stab}}_{{\Gamma }_M}(\lambda )|}^{-1}{c}_{\lambda }\sum _{\upsilon \in {\Gamma }_M}{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }.\end{array}$$

(138)

Defining relation (115) ensures that, for any $\lambda \in {\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })$, there exists $\tilde{\upsilon }\in {\mathrm{Stab}}_{{\Gamma }_M}\left(\lambda \right)$, such that ${\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }(\tilde{\upsilon })\ne 1$ and, thus, the second term in (138) vanishes,

$$\sum _{\upsilon \in {\Gamma }_M}{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }=\sum _{\upsilon \in {\Gamma }_M}{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·(\tilde{\upsilon }·\lambda )}={\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }(\tilde{\upsilon })\sum _{\upsilon \in {\Gamma }_M}{\widehat{\gamma }}_{M,{\nu }^{\vee }}^{\sigma }({\upsilon }^{-1})x^{\upsilon ·\lambda }=0,$$

and the polynomials $f_{\lambda }^{\sigma ,{\nu }^{\vee }}$ generate the space ${\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}$. The constructed basis $f_{\lambda }^{\sigma ,{\nu }^{\vee }},\lambda \in {\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ provides, together with the shifting Proposition 7, the resulting relation for dimension of ${\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}$,

$$dim{\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}=|{\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })|=|{\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })|.$$

☐

4.3. Cardinality of $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$

The number of elements in the point sets $F_{Q^{\vee },M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ is linked to the dimensionality of the polynomial spaces of the diagonal representation ${\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}$ in the following proposition.

Proposition 9.

The dimension of ${\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}$ is for any $M\in \mathbb{N}$ equal to the cardinality of $F_{Q^{\vee },M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$,

$$dim{\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}=\left|F_{Q^{\vee },M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })\right|.$$

Proof. 

Invariance property (108) of the diagonal representation (111) guarantees that any polynomial from ${\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}$ is a linear combination of $(\mathcal{D},\sigma ,{\nu }^{\vee })$-invariant monomials. Thus, the set of $(\mathcal{D},\sigma ,{\nu }^{\vee })$- invariant monomials $x^{\lambda }$, $\lambda \in {\Lambda }_M$ satisfying for all $\upsilon \in \Gamma$

$$\mathcal{D}(\upsilon )·x^{\lambda }={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon )x^{\lambda }$$

(139)

forms a basis of ${\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}$. Because, for any ${\upsilon }_1,{\upsilon }_2\in \Gamma$, it holds that

$$\mathcal{D}({\upsilon }_1{\upsilon }_2)·x^{\lambda }=\mathcal{D}({\upsilon }_1)·(\mathcal{D}({\upsilon }_2)·x^{\lambda })={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\upsilon }_2)\mathcal{D}({\upsilon }_1)·x^{\lambda }={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }({\upsilon }_1{\upsilon }_2)x^{\lambda },$$

verifying the diagonal representation property (139) only for the generators of $\Gamma$ yields its validity for all $\upsilon \in \Gamma$. For any $\lambda =[{\lambda }_0,\dots ,{\lambda }_n]\in {\Lambda }_M$, with its Kac coordinates ${\lambda }_i\in {\mathbb{Z}}^{\ge 0}$, $i\in \widehat{I}$ satisfying the defining relation in (106)

$${\lambda }_0+m_1^{\vee }{\lambda }_1+\dots +m_n^{\vee }{\lambda }_n=M,$$

(140)

and for any diagonal generator $\mathcal{D}(\upsilon )=\mathrm{diag}(d_0,\dots ,d_n)$ of $\Gamma$ is condition (139) equivalent to the relation

$$d_0^{-{\lambda }_0}\dots d_n^{-{\lambda }_n}={\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(\upsilon ).$$

(141)

The explicit forms of the diagonal matrices in relation (55) of [1] provide the following reformulations of (141) for the non-trivial cases,

$$\begin{array}{lll}{A}_n:& & {\lambda }_1+2{\lambda }_2+3{\lambda }_3+\dots +n{\lambda }_n\equiv h_{{\nu }^{\vee }}^{\sigma }modn+1,\\ B_{2k+1}:& & {\lambda }_1+{\lambda }_3+\dots +{\lambda }_{2k+1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ B_{2k}:& & {\lambda }_3+{\lambda }_5+\dots +{\lambda }_{2k-1}+{\lambda }_{2k}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ C_n:& & {\lambda }_1\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ D_{2k+1}:& & 2{\lambda }_1+2{\lambda }_3+\dots +2{\lambda }_{2k-1}+3{\lambda }_{2k}+{\lambda }_{2k+1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod4,\\ D_{2k}:& & {\lambda }_{2k-1}+{\lambda }_{2k}\equiv \{\begin{array}{cc}0mod2& {\nu }^{\vee }\in \{{\omega }_0^{\vee },{\omega }_1^{\vee }\},\\ 1mod2& {\nu }^{\vee }\in \{{\omega }_{2k-1}^{\vee },{\omega }_{2k}^{\vee }\},\end{array}\\ & & {\lambda }_1+{\lambda }_3+\dots +{\lambda }_{2k-1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ E_6:& & {\lambda }_1+2{\lambda }_2+{\lambda }_4+2{\lambda }_5\equiv h_{{\nu }^{\vee }}^{\sigma }mod3,\\ E_7:& & {\lambda }_4+{\lambda }_6+{\lambda }_7\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\end{array}$$

(142)

where the values of $h_{{\nu }^{\vee }}^{\sigma }$ are listed in Table 3 and Table 4.

Table 3. The values of symbols $h_{{\nu }^{\vee }}^{\sigma }$, with admissible shifts of the dual root lattice ${\nu }^{\vee }={\omega }_j^{\vee }$, $j\in J^{\vee }\cup \left\{0\right\}$ for simple Lie algebras $\mathfrak{g}$ with one root length.

$\mathfrak{g}$	${\mathit{A}}_{2\mathit{k}+1}$			${\mathit{A}}_{2\mathit{k}}$	${\mathit{D}}_{4\mathit{k}}$				${\mathit{D}}_{4\mathit{k}+1}$
j	j			j	0	1	$4k-1$	$4k$	0	1	$4k$	$4k+1$
$h^{\mathfrak{1}}({\nu }^{\vee })$	j			j	0	1	1	0	0	2	3	1
$h^{{\sigma }^e}({\nu }^{\vee })$	$j+k+1$			j	0	1	1	0	0	2	3	1
$\mathfrak{g}$	${\mathit{D}}_{\mathbf{4}\mathit{k}+\mathbf{2}}$				${\mathit{D}}_{\mathbf{4}\mathit{k}+\mathbf{3}}$				${\mathit{E}}_{\mathbf{6}}$			${\mathit{E}}_{\mathbf{7}}$
j	0	1	$4k+1$	$4k+2$	0	1	$4k+2$	$4k+3$	0	1	5	0	6
$h^{\mathfrak{1}}({\nu }^{\vee })$	0	1	0	1	0	2	1	3	0	1	2	0	1
$h^{{\sigma }^e}({\nu }^{\vee })$	1	0	1	0	2	0	3	1	0	1	2	1	0

Table 4. The values of symbols $h_{{\nu }^{\vee }}^{\sigma }$, with admissible shifts of the dual root lattice ${\nu }^{\vee }={\omega }_j^{\vee }$, $j\in J^{\vee }\cup \left\{0\right\}$ for simple Lie algebras $\mathfrak{g}$ with two root lengths.

$\mathfrak{g}$	${\mathit{B}}_{4\mathit{k}}$	${\mathit{B}}_{4\mathit{k}+1}$	${\mathit{B}}_{4\mathit{k}+2}$	${\mathit{B}}_{4\mathit{k}+3}$	${\mathit{C}}_{\mathit{n}}$
j	j	j	j	j	0	n
$h^{\mathfrak{1}}({\nu }^{\vee })$	j	j	j	j	0	1
$h^{{\sigma }^e}({\nu }^{\vee })$	j	$j+1$	$j+1$	j	1	0
$h^{{\sigma }^s}({\nu }^{\vee })$	j	$j+1$	j	$j+1$	0	1
$h^{{\sigma }^l}({\nu }^{\vee })$	j	j	$j+1$	$j+1$	1	0

Introducing the auxiliary symbols $s_i\in {\mathbb{Z}}^{\ge 0}$ by relations

$$\begin{array}{lll}{s}_i^{\sigma ,\varrho }=1+s_i,& & r_i\in R^{\sigma }(\varrho ),\\ s_i^{\sigma ,\varrho }=s_i,& & r_i\in R\setminus R^{\sigma }(\varrho ),\end{array}$$

substituting them into expressions (91)–(102) and (104) and taking into account generalized Coxeter numbers formula (68) results to conclude that the number of points in $F_{Q^{\vee },M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ is equal to the number of solutions of the equations

$$s_0+m_1{s}_1+\dots +m_n{s}_n=M$$

(143)

and

$$\begin{array}{lll}{A}_n:& & s_1+2s_2+3s_3+\dots +n{s}_n\equiv h_{{\nu }^{\vee }}^{\sigma }modn+1,\\ B_{2k+1}:& & s_1+s_3+s_5+\dots +s_{2k+1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ B_{2k}:& & s_1+s_3+s_5+\dots +s_{2k-1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ C_n:& & s_n\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ D_{4k:}& & s_1+s_3+\dots +s_{4k-3}+s_{4k-1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ & & s_{4k-1}+s_{4k}\equiv \{\begin{array}{cc}0mod2& {\nu }^{\vee }\in \{{\omega }_0^{\vee },{\omega }_1^{\vee }\},\\ 1mod2& {\nu }^{\vee }\in \{{\omega }_{4k-1}^{\vee },{\omega }_{4k}^{\vee }\},\end{array}\\ D_{4k+1}:& & 2s_1+2s_3+\dots +2s_{4k-1}+3s_{4k}+s_{4k+1}\equiv h_{{\nu }^{\vee }}^{\sigma }mod4,\\ D_{4k+2}:& & s_1+s_3+\dots +s_{4k-1}+s_{4k+2}\equiv h_{{\nu }^{\vee }}^{\sigma }mod2,\\ & & s_{4k+1}+s_{4k+2}\equiv \{\begin{array}{cc}0mod2& {\nu }^{\vee }\in \{{\omega }_0^{\vee },{\omega }_1^{\vee }\},\\ 1mod2& {\nu }^{\vee }\in \{{\omega }_{4k+1}^{\vee },{\omega }_{4k+2}^{\vee }\},\end{array}\\ D_{4k+3}:& & 2s_1+2s_3+\dots +2s_{4k+1}+s_{4k+2}+3s_{4k+3}\equiv h_{{\nu }^{\vee }}^{\sigma }mod4,\\ E_6:& & s_1+2s_2+s_4+2s_5\equiv h_{{\nu }^{\vee }}^{\sigma }mod3,\\ E_7:& & s_4+s_6+s_7\equiv h_{{\nu }^{\vee }}^{\sigma }mod2.\end{array}$$

(144)

The solutions $s_i\in {\mathbb{Z}}^{\ge 0}$ of defining conditions (143) and (144) and solutions ${\lambda }_i\in {\mathbb{Z}}^{\ge 0}$ of defining equations (140) and (142) coincide for each case up to a permutation and, thus, their numbers are identical. ☐

Theorem 2.

For any $M\in \mathbb{N},M>m_{\varrho }^{\sigma }$, it holds that

$$|F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })|=|{\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })|.$$

Proof. 

Combining Propositions 8 and 9 together with Theorem 1 gives, for any $M\in \mathbb{N}$, the following equalities,

$$|F_{Q^{\vee },M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })|=dim{\Pi }_M^{\mathcal{D},\sigma ,{\nu }^{\vee }}=dim{\Pi }_M^{\mathcal{A},\sigma ,{\nu }^{\vee }}=\left|{\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })\right|.$$

☐

4.4. Counting Formulas

The counting formulas for the numbers of elements of the label sets ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$, with admissible shifts both trivial, are presented in [1]. Since, according to Proposition 7, the set ${\Lambda }_{P,M+m_{\varrho }^{\sigma }}^{\sigma }(\varrho ,{\nu }^{\vee })$ is the ${\kappa }^{\sigma ,\varrho }$-shifted set ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$, defined via relation (114), it follows that

$$|{\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })|=|{\tilde{\Lambda }}_{P,M-m_{\varrho }^{\sigma }}^{\sigma }({\nu }^{\vee })|.$$

(145)

The calculation of the cardinalities of the label sets ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$, $M>m_{\varrho }^{\sigma }$ is thus reverted to counting the weights in $\varrho$-independent sets ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$, $M\in \mathbb{N}$. The abelian group ${\Gamma }_M$ partitions the sets of weights ${\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })$ and ${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })$, defined by relations (112) and (113), into ${\Gamma }_M$-orbits and the sets ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ and ${\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })$ consist of exactly one point from each ${\Gamma }_M$-orbit. Thus, the number of points in ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$ and ${\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })$ is equal to the number of ${\Gamma }_M$-orbits in ${\tilde{\Lambda }}_{Q,M}^{\sigma }({\nu }^{\vee })$ and ${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })$, respectively.

The calculation process is based on disjoint decomposition (119), which yields the relation

$$|{\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })|=|M{F}_P\cap {\Lambda }_M|-|{\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })|.$$

(146)

Introducing the set of weights in ${\Lambda }_M$ fixed by a given $\gamma \in {\Gamma }_M$,

$${\mathrm{Fix}}_M(\gamma )=\{\lambda \in {\Lambda }_M\mid \gamma ·\lambda =\lambda \},$$

(147)

the Burnside’s lemma applied to the weight set ${\Lambda }_M$ provides the relation

$$|M{F}_P\cap {\Lambda }_M|=\frac{1}{c}\sum _{\gamma \in {\Gamma }_M}\left|{\mathrm{Fix}}_M(\gamma )\right|.$$

(148)

Moreover, employing the Burnside’s lemma to the set ${\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })$ produces the identity

$$|{\tilde{H}}_{P,M}^{\sigma }({\nu }^{\vee })|=\frac{1}{c}\sum _{\gamma \in {\Gamma }_M}\left|{\mathrm{Fix}}_M(\gamma )\cap {\tilde{H}}_{Q,M}^{\sigma }({\nu }^{\vee })\right|.$$

(149)

Following the notation from [34], the Ramanujan sums $c_n(j)$ with $n\in \mathbb{N}$, $j\in {\mathbb{Z}}^{\ge 0}$ that contain the Möbius function $\mu$ are introduced via relation

$$c_n(j)=\sum _{d|gcd(n,j)}\mu (\frac{n}{d})d,$$

(150)

and the counting function $a_j(n,m)$, $m\in \mathbb{N}$ is given by

$$a_j(n,m)=\frac{1}{n+m}\sum _{d|gcd(n,m)}{c}_d(j)(\begin{array}{c}\frac{n+m}{d}\\ \frac{n}{d}\end{array}).$$

(151)

The explicit counting formulas for the numbers of points in the label sets ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ are, for all cases, listed in the following theorem.

Theorem 3.

The numbers of elements in ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ are for any $M\in \mathbb{N},M>m_{\varrho }^{\sigma }$ and any admissible shifts of the weight lattice ϱ and the root lattice ${\nu }^{\vee }$, which are not both trivial, as determined by the following formulas.

1.

$A_1$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|=|{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_1,0)|=|{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_1,{\omega }_1^{\vee })|=\{\begin{array}{ll}k,& M=2k,\\ k+1,& M=2k+1,\end{array}\\ & |{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_1,{\omega }_1^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_1^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_1,0)|=\{\begin{array}{ll}k,& M=2k,\\ k,& M=2k+1.\end{array}\end{array}$$

2.

$A_n,n\ge 2$, $j\in I$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_j^{\vee })|=a_j(n+1,M),\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_j^{\vee })|=\{\begin{array}{ll}{a}_j(2m+1,M-2m-1),& n=2m,\\ a_{j+m+1}(2m+2,M-2m-2),& n=2m+1.\end{array}\end{array}$$

3.

$B_n,n\ge 3$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|=\{\begin{array}{ll}(\genfrac{}{}{0pt}{}{n+k}{n}),& M=2k+1,\\ \frac{1}{2}[(\genfrac{}{}{0pt}{}{2m+2k+l}{2m})+(\genfrac{}{}{0pt}{}{2m+2k+l-1}{2m})-(\genfrac{}{}{0pt}{}{m+k}{m})-(\genfrac{}{}{0pt}{}{m+k+l-1}{m})],& n=2m,M=4k+2l,\\ \frac{1}{2}[(\genfrac{}{}{0pt}{}{2m+2k+l+1}{2m+1})+(\genfrac{}{}{0pt}{}{2m+2k+l}{2m+1})-(\genfrac{}{}{0pt}{}{m+k}{m})],& n=2m+1,M=4k+2l,\end{array}\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_1^{\vee })|=\{\begin{array}{ll}\frac{1}{2}[(\genfrac{}{}{0pt}{}{2k+l}{4m+1})+(\genfrac{}{}{0pt}{}{2k+l-1}{4m+1})+(\genfrac{}{}{0pt}{}{k-1+l}{2m})],& n=4m+1,M=4k+2l,\\ \frac{1}{2}[(\genfrac{}{}{0pt}{}{2k+l}{4m+2})+(\genfrac{}{}{0pt}{}{2k+l-1}{4m+2})+(\genfrac{}{}{0pt}{}{k}{2m+1})+(\genfrac{}{}{0pt}{}{k+l-1}{2m+1})],& n=4m+2,M=4k+2l,\\ |{\Lambda }_{P,M-2n}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|,& \mathit{otherwise},\end{array}\\ & |{\Lambda }_{P,M}^{{\sigma }^s}(0,{\omega }_1^{\vee })|=\{\begin{array}{ll}\frac{1}{2}[(\genfrac{}{}{0pt}{}{2m+2k+l}{2m+1})+(\genfrac{}{}{0pt}{}{2m+2k+l-1}{2m+1})+(\genfrac{}{}{0pt}{}{m+k+l-1}{m})],& n=2m+1,M=4k+2l,\\ |{\Lambda }_{P,M-2}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|,& \mathit{otherwise},\end{array}\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(0,{\omega }_1^{\vee })|=\{\begin{array}{ll}|{\Lambda }_{P,2k+2}^{{\sigma }^e}(0,{\omega }_1^{\vee })|,& n=4m+2,M=2k,\\ |{\Lambda }_{P,2k-2n+4}^{{\sigma }^s}(0,{\omega }_1^{\vee })|,& n=4m+3,M=2k,\\ |{\Lambda }_{P,M-2n+2}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|,& \mathit{otherwise},\end{array}\end{array}$$

where $l\in \{0,1\}$.

4.

$C_n,n\ge 2$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|=|{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_n,0)|=(\genfrac{}{}{0pt}{}{n+k-1}{n}),k=\lceil \frac{M}{2}\rceil ,\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_n^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_n,0)|=(\genfrac{}{}{0pt}{}{k}{n}),k=\lfloor \frac{M}{2}\rfloor ,\end{array}$$

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{{\sigma }^s}(0,{\omega }_n^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^s}(\frac{1}{2}{\omega }_n,0)|=|{\Lambda }_{P,M-2n+2}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(0,{\omega }_n^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^l}(\frac{1}{2}{\omega }_n,0)|=|{\Lambda }_{P,M+2n-2}^{{\sigma }^e}(0,{\omega }_n^{\vee })|,\end{array}$$

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\Lambda }_{P,M-1}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\Lambda }_{P,M+1}^{{\sigma }^e}(0,{\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^s}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\Lambda }_{P,M-2n+1}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\Lambda }_{P,M+2n-1}^{{\sigma }^e}(0,{\omega }_n^{\vee })|.\end{array}$$

5.

$D_n,n\ge 4$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|=\{\begin{array}{ll}(\genfrac{}{}{0pt}{}{n+k}{n})+(\genfrac{}{}{0pt}{}{n+k-1}{n}),& M=2k+1,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2m+2k+1}{2m+1})+6(\genfrac{}{}{0pt}{}{2m+2k}{2m+1})+(\genfrac{}{}{0pt}{}{2m-1+2k}{2m+1})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2m-1+2k}{2m-1})-2(\genfrac{}{}{0pt}{}{m+k-1}{m-1})],& n=2m+1,M=4k,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2m+2k+2}{2m+1})+6(\genfrac{}{}{0pt}{}{2m+2k+1}{2m+1})+(\genfrac{}{}{0pt}{}{2m+2k}{2m+1})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2m+2k}{2m-1})],& n=2m+1,M=4k+2,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2m+2k}{2m})+6(\genfrac{}{}{0pt}{}{2m+2k-1}{2m})+(\genfrac{}{}{0pt}{}{2m+2k-2}{2m})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2m+2k-2}{2m-2})-2(\genfrac{}{}{0pt}{}{m+k}{m})-6(\genfrac{}{}{0pt}{}{m+k-1}{m})],& n=2m,M=4k,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2m+2k+1}{2m})+6(\genfrac{}{}{0pt}{}{2m+2k}{2m})+(\genfrac{}{}{0pt}{}{2m+2k-1}{2m})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2m+2k-1}{2m-2})-6(\genfrac{}{}{0pt}{}{m+k}{m})-2(\genfrac{}{}{0pt}{}{m+k-1}{m})],& n=2m,M=4k+2,\end{array}\end{array}$$

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_1^{\vee })|=\{\begin{array}{l}\frac{1}{4}[(\genfrac{}{}{0pt}{}{2k+1}{4m+3})+6(\genfrac{}{}{0pt}{}{2k}{4m+3})+(\genfrac{}{}{0pt}{}{2k-1}{4m+3})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2k-1}{4m+1})+2(\genfrac{}{}{0pt}{}{k-1}{2m})],& n=4m+3,M=4k,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2k+2}{4m+2})+6(\genfrac{}{}{0pt}{}{2k+1}{4m+2})+(\genfrac{}{}{0pt}{}{2k}{4m+2})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2k}{4m})+2(\genfrac{}{}{0pt}{}{k+1}{2m+1})+6(\genfrac{}{}{0pt}{}{k}{2m+1})],& n=4m+2,M=4k+2,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{2k+1}{4m+2})+6(\genfrac{}{}{0pt}{}{2k}{4m+2})+(\genfrac{}{}{0pt}{}{2k-1}{4m+2})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{2k-1}{4m})+6(\genfrac{}{}{0pt}{}{k}{2m+1})+2(\genfrac{}{}{0pt}{}{k-1}{2m+1})],& n=4m+2,M=4k,\\ |{\Lambda }_{P,M-2n+2}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|,& \mathit{otherwise},\end{array}\end{array}$$

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_{n-1}^{\vee })|=|{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|=\{\begin{array}{ll}|{\Lambda }_{P,2k+1}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|,& M=2k+1,\\ \frac{1}{4}[(\genfrac{}{}{0pt}{}{n+k}{n})+6(\genfrac{}{}{0pt}{}{n+k-1}{n})\\ \phantom{\frac{1}{4}}+(\genfrac{}{}{0pt}{}{n+k-2}{n})-(\genfrac{}{}{0pt}{}{n+k-2}{n-2})],& M=2k,\end{array}\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_{n-1}^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_n^{\vee })|=|{\Lambda }_{P,M-2n+2}^{\mathfrak{1}}(0,{\omega }_{n-1}^{\vee })|.\end{array}$$

6.

$E_6$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|=|{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_5^{\vee })|=\{\begin{array}{ll}\frac{1}{3}[|{\Lambda }_{6k}(E_6)|-(\genfrac{}{}{0pt}{}{k+2}{2})-(\genfrac{}{}{0pt}{}{k+1}{2})],& M=6k,\\ \frac{1}{3}[|{\Lambda }_{6k+3}(E_6)|-2(\genfrac{}{}{0pt}{}{k+2}{2})],& M=6k+3,\\ \frac{1}{3}|{\Lambda }_M(E_6)|,& \mathit{otherwise},\end{array}\\ \\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_1^{\vee })|=|{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_5^{\vee })|=|{\Lambda }_{P,M-12}^{\mathfrak{1}}(0,{\omega }_1^{\vee })|.\end{array}$$

7.

$E_7$:

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_6^{\vee })|=\{\begin{array}{ll}\frac{1}{2}|{\Lambda }_{2k+1}(E_7)|,& M=2k+1,\\ \frac{1}{2}[|{\Lambda }_{12k+2l}(E_7)|-\sum _{i=0}^3{d}_{li}(\genfrac{}{}{0pt}{}{4-i+k}{4})],& M=12k+2l,l\in \{0,\dots ,5\},\end{array}\\ \\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_6^{\vee })|=\{\begin{array}{ll}\frac{1}{2}[|{\Lambda }_{12k+2l-18}(E_7)|+\sum _{i=0}^3{d}_{l+3,i}(\genfrac{}{}{0pt}{}{2-i+k}{4})],& M=12k+2l,l\in \{0,1,2\},\\ \frac{1}{2}[|{\Lambda }_{12k+2l-18}(E_7)|+\sum _{i=0}^3{d}_{l-3,i}(\genfrac{}{}{0pt}{}{3-i+k}{4})],& M=12k+2l,l\in \{3,4,5\},\\ |{\Lambda }_{P,M-18}^{\mathfrak{1}}(0,{\omega }_6^{\vee })|,& \mathit{otherwise},\end{array}\end{array}$$

where

$$(d_{li})=(\begin{array}{cccc}1& 34& 64& 9\\ 2& 46& 55& 5\\ 5& 55& 46& 2\\ 9& 64& 34& 1\\ 16& 67& 25& 0\\ 25& 67& 16& 0\end{array}).$$

Proof. 

The counting formulas for the cardinality of ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ that correspond to the infinite series of groups ${\Gamma }_M$ of $A_n$, $n\ge 2$ are derived while applying Theorem 2. Because the weight lattices of $A_n$, $n\ge 2$ admit only trivial admissible shifts $\varrho =0$ and $J^{\vee }=I$, Theorem 2 specializes for $j\in I$ to

$$|F_{Q^{\vee },M}^{\sigma }(0,{\omega }_j^{\vee })|=|{\Lambda }_{P,M}^{\sigma }(0,{\omega }_j^{\vee })|.$$

Because of equations (143) and (144), $m_0^{\mathfrak{1}}=0$, and the relation $h_{{\nu }^{\vee }}^{\mathfrak{1}}=j$, as deduced from Table 3, the cardinality of $F_{Q^{\vee },M}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$, $j\in I$ is determined by the number of non-negative integer solutions of the system of equations

$$s_1+2s_2+3s_3+\dots +n{s}_n\equiv jmodn+1,s_0+s_1+\dots +s_n=M.$$

(152)

The number of non-negative integer solutions of the system (152) is according to Theorem 1 in [34] equal to $a_j(n+1,M)$. The counting formulas for the cardinality of $F_{Q^{\vee },M+n+1}^{{\sigma }^e}(0,{\omega }_j^{\vee })$, $j\in I$ are, for $n=2m$, similarly determined from relations (143), (144), $m_0^{{\sigma }^e}=n+1$, and Table 3. For $n=2m+1$, the counting formulas of $F_{Q^{\vee },M+n+1}^{{\sigma }^e}(0,{\omega }_j^{\vee })$, $j\in I$ coincide with the number of non-negative integer solutions of the system of equations

$$s_1+2s_2+3s_3+\dots +n{s}_n\equiv j+m+1modn+1,s_0+s_1+\dots +s_n=M.$$

(153)

The number of non-negative integer solutions of the system (153) is, according to Theorem 1 in [34], equal to $a_{j+m+1}(n+1,M)$.

The remaining cases of the counting formulas for the cardinality of ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ are calculated via relations (145), (146), (148), and (149). The calculating procedure is demonstrated on the cases $C_n,n\ge 2$ for which $J=\left\{1\right\}$, $J^{\vee }=\left\{n\right\}$, and ${\Gamma }_M=\{\mathfrak{1},{\upsilon }_{M,1}\}$. The values of the short and long Coxeter numbers are, according to Table 1 in [2], equal to $m_0^{{\sigma }^s}=2n-2$, $m_0^{{\sigma }^l}=2$, and, therefore, relation (145) yields the following equalities

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M}^{\mathfrak{1}}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(0,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-2n}^{{\sigma }^e}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^s}(0,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-2n+2}^{{\sigma }^s}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(0,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-2}^{{\sigma }^l}({\omega }_n^{\vee })|.\end{array}$$

For the non-trivial shift of the weight lattice $\varrho ={\omega }_n/2$, the values of $\gamma$-homomorphisms in Table II of [9] induce the four values of the shifted Coxeter numbers, as $m_{\varrho }^{\mathfrak{1}}=1$, $m_{\varrho }^{{\sigma }^e}=2n-1$, $m_{\varrho }^{{\sigma }^s}=2n-1$, $m_{\varrho }^{{\sigma }^l}=1$, and, thus, relation (145) yields the equalities

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_n,0)|=|{\tilde{\Lambda }}_{P,M-1}^{\mathfrak{1}}(0)|,\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_n,0)|=|{\tilde{\Lambda }}_{P,M-2n+1}^{{\sigma }^e}(0)|,\\ & |{\Lambda }_{P,M}^{{\sigma }^s}(\frac{1}{2}{\omega }_n,0)|=|{\tilde{\Lambda }}_{P,M-2n+1}^{{\sigma }^s}(0)|,\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(\frac{1}{2}{\omega }_n,0)|=|{\tilde{\Lambda }}_{P,M-1}^{{\sigma }^l}(0)|\end{array}$$

and

$$\begin{array}{ll}& |{\Lambda }_{P,M}^{\mathfrak{1}}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-1}^{\mathfrak{1}}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^e}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-2n+1}^{{\sigma }^e}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^s}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-2n+1}^{{\sigma }^s}({\omega }_n^{\vee })|,\\ & |{\Lambda }_{P,M}^{{\sigma }^l}(\frac{1}{2}{\omega }_n,{\omega }_n^{\vee })|=|{\tilde{\Lambda }}_{P,M-1}^{{\sigma }^l}({\omega }_n^{\vee })|.\end{array}$$

The number of elements in the weight sets ${\Lambda }_M$ is given for their Kac coordinates ${\lambda }_i\in {\mathbb{Z}}^{\ge 0}$, $i\in \widehat{I}$ by the defining equation in (106),

$${\lambda }_0+{\lambda }_1+2{\lambda }_2+\dots +2{\lambda }_n=M.$$

(154)

The counting formula in Theorem 3.3 from [3] and definition (147) of the fixed weights yield the expression

$$|{\Lambda }_M|=|{\mathrm{Fix}}_M(\mathfrak{1})|=\{\begin{array}{ll}(\genfrac{}{}{0pt}{}{n+k}{n})+(\genfrac{}{}{0pt}{}{n+k-1}{n}),& M=2k,\\ 2(\genfrac{}{}{0pt}{}{n+k}{n}),& M=2k+1.\end{array}$$

(155)

Taking into account definition (105) and evaluating relation (37) on the magnified domain $M{F}_Q$ together with the corresponding permutation from Table 1 in [1] implies that the elements from ${\mathrm{Fix}}_M({\upsilon }_{M,1})$ are determined by additional property ${\lambda }_0={\lambda }_1$ in (154) and, therefore, satisfy the condition,

$$2{\lambda }_1+2{\lambda }_2+\dots +2{\lambda }_n=M.$$

(156)

Equation (156) admits, according to Proposition 3.1 in [3], the following number of solutions

$$|{\mathrm{Fix}}_M({\upsilon }_{M,1})|=\{\begin{array}{ll}(\genfrac{}{}{0pt}{}{n+k-1}{n-1}),& M=2k,\\ 0,& M=2k+1.\end{array}$$

(157)

Thus, Burnside’s evaluating relation (148) provides the following counting formula for the number of ${\Gamma }_M$-orbits in ${\Lambda }_M$,

$$|M{F}_P\cap {\Lambda }_M|=\frac{1}{2}(|{\mathrm{Fix}}_M(\mathfrak{1})|+|{\mathrm{Fix}}_M({\upsilon }_{M,1})|)=(\genfrac{}{}{0pt}{}{n+\lfloor \frac{M}{2}\rfloor }{n}).$$

(158)

Starting with defining relation (63) and using Proposition 2, magnifying property (64) and values of the homomorphisms $\sigma \circ \widehat{\psi }({\upsilon }_1)$ in Table 1 from [1] yield the following $\widehat{\gamma }$-homomorphisms values,

$$\begin{array}{cc}{\widehat{\gamma }}_{M,{\omega }_n^{\vee }}^{\mathfrak{1}}({\upsilon }_{M,1})& ={\widehat{\gamma }}_{M,0}^{{\sigma }^e}({\upsilon }_{M,1})={\widehat{\gamma }}_{M,{\omega }_n^{\vee }}^{{\sigma }^s}({\upsilon }_{M,1})={\widehat{\gamma }}_{M,0}^{{\sigma }^l}({\upsilon }_{M,1})=-1,\\ {\widehat{\gamma }}_{M,0}^{\mathfrak{1}}({\upsilon }_{M,1})& ={\widehat{\gamma }}_{M,{\omega }_n^{\vee }}^{{\sigma }^e}({\upsilon }_{M,1})={\widehat{\gamma }}_{M,0}^{{\sigma }^s}({\upsilon }_{M,1})={\widehat{\gamma }}_{M,{\omega }_n^{\vee }}^{{\sigma }^l}({\upsilon }_{M,1})=1,\end{array}$$

that, in turn, provide the description of the auxiliary boundary sets,

$$\begin{array}{cc}{\tilde{H}}_{Q,M}^{\mathfrak{1}}({\omega }_n^{\vee })& ={\tilde{H}}_{Q,M}^{{\sigma }^e}(0)={\tilde{H}}_{Q,M}^{{\sigma }^s}({\omega }_n^{\vee })={\tilde{H}}_{Q,M}^{{\sigma }^l}(0)={\mathrm{Fix}}_M({\upsilon }_{M,1}),\\ {\tilde{H}}_{Q,M}^{\mathfrak{1}}(0)& ={\tilde{H}}_{Q,M}^{{\sigma }^e}({\omega }_n^{\vee })={\tilde{H}}_{Q,M}^{{\sigma }^s}(0)={\tilde{H}}_{Q,M}^{{\sigma }^l}({\omega }_n^{\vee })=Ø.\end{array}$$

The application of Burnside’s evaluation relation (149) on the auxiliary boundary sets generates their orbit counting relations,

$$\begin{array}{cc}|{\tilde{H}}_{P,M}^{\mathfrak{1}}({\omega }_n^{\vee })|& =|{\tilde{H}}_{P,M}^{{\sigma }^e}(0)|=|{\tilde{H}}_{P,M}^{{\sigma }^s}({\omega }_n^{\vee })|=|{\tilde{H}}_{P,M}^{{\sigma }^l}(0)|=|{\mathrm{Fix}}_M({\upsilon }_{M,1})|,\end{array}$$

(159)

$$\begin{array}{cc}|{\tilde{H}}_{P,M}^{\mathfrak{1}}(0)|& =|{\tilde{H}}_{P,M}^{{\sigma }^e}({\omega }_n^{\vee })|=|{\tilde{H}}_{P,M}^{{\sigma }^s}(0)|=|{\tilde{H}}_{P,M}^{{\sigma }^l}({\omega }_n^{\vee })|=0.\end{array}$$

(160)

Substituting orbit counting relations (158)–(160) into decomposition relation (146) produces the final counting formulas. ☐

5. Generalized Dual-Root Lattice Fourier-Weyl Transforms

The goal of Section 5 is to derive the discrete orthogonality relations of Weyl orbit functions, labeled by ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$, on the finite fragments of the shifted dual root lattices $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$. The corresponding discrete forward and backward Fourier-Weyl transforms, together with the Plancherel formulas, are presented. The unitary matrices of the discrete transforms are exemplified for the root system $A_2$.

5.1. Discrete Orthogonality on Shifted Dual Root Lattice

For any $M\in \mathbb{N}$, $M>m_{\varrho }^{\sigma }$, a scalar product of discrete complex valued functions $f,g:F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })\to$ is given by

$${⟨f,g⟩}_{F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}=\sum _{a\in F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}ϵ(a)f(a)\overline{g(a)}.$$

(161)

The Hilbert space of all complex valued functions $f:F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })\to$ with the scalar product (161) is denoted by ${\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$. In order to demonstrate that the orbit functions labeled by ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ are pairwise orthogonal within each family, the following basic discrete orthogonality formula is recalled from Proposition 6.3 in [1]. For any $\mu \in P$, it holds that

$$\sum _{y\in \frac{1}{M}{Q}^{\vee }/Q^{\vee }}{e}^{2\pi \mathrm{i}⟨\mu ,y⟩}=\{\begin{array}{ll}{M}^n& \mu \in MP,\\ 0& \mathrm{otherwise}.\end{array}$$

(162)

Theorem 4.

For any admissible shift ϱ of the weight lattice, any admissible shift ${\nu }^{\vee }$ of the dual root lattice, any $b,b^{\prime }\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ and any $M\in \mathbb{N},M>m_{\varrho }^{\sigma }$, it holds that

$${⟨{\phi }_b^{\sigma },{\phi }_{b^{\prime }}^{\sigma }⟩}_{F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}=|W|M^n{h}_{P,M}(b){\delta }_{b,b^{\prime }}.$$

(163)

Proof. 

Uniting the point set $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ with the boundary points produces the following set equality,

$$F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })\cup [\frac{1}{M}({\nu }^{\vee }+Q^{\vee })\cap H^{\sigma }(\varrho )]=F\cap \left[\frac{1}{M}({\nu }^{\vee }+Q^{\vee })\right].$$

Thus, taking into account that all functions ${\phi }_b^{\sigma }$ vanish according to (84) on the boundary $H^{\sigma }(\varrho )$, it holds that

$${⟨{\phi }_b^{\sigma },{\phi }_{b^{\prime }}^{\sigma }⟩}_{F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}=\sum _{a\in F\cap \left[\frac{1}{M}({\nu }^{\vee }+Q^{\vee })\right]}ϵ(a){\phi }_b^{\sigma }(a)\overline{{\phi }_{b^{\prime }}^{\sigma }(a)}.$$

The argument symmetry of the Weyl orbit functions (83) and $W^{\mathrm{aff}}$-invariance of the ϵ-function (19) imply for any $W^{\mathrm{aff}}\in W^{\mathrm{aff}}$ that

$$\begin{array}{c}ϵ(a){\phi }_b^{\sigma }(a)\overline{{\phi }_{b^{\prime }}^{\sigma }(a)}=ϵ(w^{\mathrm{aff}}a){\phi }_b^{\sigma }(w^{\mathrm{aff}}a)\overline{{\phi }_{b^{\prime }}^{\sigma }(w^{\mathrm{aff}}a)}.\end{array}$$

(164)

Firstly, using the invariance with respect to shifts from $Q^{\vee }$ in (164) produces the equality

$$\sum _{a\in F\cap \left[\frac{1}{M}({\nu }^{\vee }+Q^{\vee })\right]}ϵ(a){\phi }_b^{\sigma }(a)\overline{{\phi }_{b^{\prime }}^{\sigma }(a)}=\sum _{x\in F\cap [\frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }]}\widetilde{ϵ}(x){\phi }_b^{\sigma }(x)\overline{{\phi }_{b^{\prime }}^{\sigma }(x)}.$$

Secondly, from the W-invariance of $\widetilde{ϵ}(x){\phi }_b^{\sigma }(x)\overline{{\phi }_{b^{\prime }}^{\sigma }(x)}$ granted by (164) and from torus relations (20) and (21), it follows that

$$\sum _{x\in F\cap [\frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }]}\widetilde{ϵ}(x){\phi }_b^{\sigma }(x)\overline{{\phi }_{b^{\prime }}^{\sigma }(x)}=\sum _{y\in \frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }}{\phi }_b^{\sigma }(y)\overline{{\phi }_{b^{\prime }}^{\sigma }(y)}.$$

(165)

Because of the W-invariance of $\frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }$, which is a consequence of defining relation of the admissible shift ${\nu }^{\vee }$ of the dual root lattice (5), the following simplifications of (165) are obtained,

$$\begin{array}{ll}\sum _{y\in \frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }}{\phi }_b^{\sigma }(y)\overline{{\phi }_{b^{\prime }}^{\sigma }(y)}& =\sum _{w,w^{\prime }\in W}\sum _{y\in \frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }}\sigma (w{w}^{\prime })e^{2\pi \mathrm{i}wb-w^{\prime }{b}^{\prime },y⟩}\\ & =|W|\sum _{w^{\prime }\in W}\sum _{y\in \frac{1}{M}({\nu }^{\vee }+Q^{\vee })/Q^{\vee }}\sigma (w^{\prime })e^{2\pi \mathrm{i}⟨b-w^{\prime }{b}^{\prime },y⟩}\\ & =|W|\sum _{w^{\prime }\in W}\sigma (w^{\prime })e^{2\pi \mathrm{i}⟨b-w^{\prime }{b}^{\prime },\frac{{\nu }^{\vee }}{M}⟩}\sum _{y\in \frac{1}{M}{Q}^{\vee }/Q^{\vee }}{e}^{2\pi \mathrm{i}⟨b-w^{\prime }{b}^{\prime },y⟩}.\end{array}$$

(166)

Since the labels $b,b^{\prime }\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ are of the form $b=\varrho +\lambda$ and $b^{\prime }=\varrho +{\lambda }^{\prime }$, with the weights $\lambda ,{\lambda }^{\prime }\in P$, the admissibility of the shift $\varrho$ in (10), together with W-invariance of the weight lattice P, imply that

$$b-w^{\prime }{b}^{\prime }=\varrho -w^{\prime }\varrho +\lambda -w^{\prime }{\lambda }^{\prime }\in P.$$

In order to further simplify the second term in (166), two cases from the basic orthogonality relations (162) are distinguished. If $b-w^{\prime }{b}^{\prime }\in MP$, then it holds that $b/M=w^{\prime }{b}^{\prime }/M+p$ for some $p\in P$, $w^{\prime }\in W$ and, thus, $b/M$ and $b^{\prime }/M$ belong to the same $W_P^{\mathrm{aff}}$-orbit. Defining relation (88) of the label set ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ guarantees that both $b/M$ and $b^{\prime }/M$ are in the domain $F_P^{\sigma }({\nu }^{\vee })\subset F_P$ and, therefore, $b=b^{\prime }$. Thus, contrapositive implication provides that, if $b\ne b^{\prime }$, then for all $w^{\prime }\in W$ it holds that $b-w^{\prime }{b}^{\prime }\notin MP$ and basic orthogonality relations (162) grant that ${⟨{\phi }_b^{\sigma },{\phi }_{b^{\prime }}^{\sigma }⟩}_{F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}=0.$ If $b=b^{\prime }$, then basic orthogonality relations (162) guarantee that summands in (166) do not vanish only if $b-w^{\prime }b\in MP$, or equivalently $w^{\prime }\in \widehat{\psi }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b/M))$ and, thus,

$${\sum }_{w^{\prime }\in W}\sigma (w^{\prime })e^{2\pi \mathrm{i}⟨b-w^{\prime }{b}^{\prime },\frac{{\nu }^{\vee }}{M}⟩}{\sum }_{y\in \frac{1}{M}{Q}^{\vee }/Q^{\vee }}{e}^{2\pi \mathrm{i}⟨b-w^{\prime }{b}^{\prime },y⟩}={\delta }_{b,b^{\prime }}{M}^n{\sum }_{w^{\prime }\in \widehat{\psi }[{\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})]}\sigma (w^{\prime })e^{2\pi \mathrm{i}⟨b-w^{\prime }b,\frac{{\nu }^{\vee }}{M}⟩}.$$

(167)

Because, for $w_P\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b/M)$, the homomorphism kernel characterization $\widehat{\psi }(w_P)=1$ forces $w_P=1$, the subgroups ${\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b/M)$ and $\widehat{\psi }({\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(b/M))$ are isomorphic and taking into account defining relations (61) and (39) of the shift and $\widehat{\gamma }$-homomorphisms it follows that

$$\begin{array}{ll}\sum _{w^{\prime }\in \widehat{\psi }[{\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})]}\sigma (w^{\prime })e^{2\pi \mathrm{i}⟨b-w^{\prime }b,\frac{{\nu }^{\vee }}{M}⟩}& =\sum _{w^{\mathrm{aff}}\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})}\sigma \circ \widehat{\psi }(w^{\mathrm{aff}})e^{2\pi \mathrm{i}⟨\widehat{\tau }(w^{\mathrm{aff}}),{\nu }^{\vee }⟩}\\ & =\sum _{w^{\mathrm{aff}}\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})}{\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}}).\end{array}$$

(168)

Defining relation (88) of the label set ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ grants that $b/M\in F_P^{\sigma }({\nu }^{\vee })$ and defining relation (69) of the domain $F_P^{\sigma }({\nu }^{\vee })$ provides, in turn, that ${\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}})=1$ for all $w^{\mathrm{aff}}\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}\left(\frac{b}{M}\right)$ and thus, the sum in (168) results to

$$\sum _{w^{\mathrm{aff}}\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})}{\widehat{\gamma }}_{{\nu }^{\vee }}^{\sigma }(w^{\mathrm{aff}})=\sum _{w^{\mathrm{aff}}\in {\mathrm{Stab}}_{W_P^{\mathrm{aff}}}(\frac{b}{M})}1=h_{P,M}(b).$$

(169)

☐

5.2. Shifted Dual-Root Lattice Discrete Transforms

The orthogonal bases of the Hilbert spaces ${\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ that are constructed in the following theorem serve as fundamental tools for the formulation of the Fourier-Weyl transforms.

Theorem 5.

For any admissible shift ϱ of the weight lattice, any admissible shift ${\nu }^{\vee }$ of the dual root lattice and any $M\in \mathbb{N},M>m_{\varrho }^{\sigma }$, it holds that the functions ${\phi }_b^{\sigma }$, $b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ form an orthogonal basis of the Hilbert space ${\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$.

Proof. 

From Theorem 4 follows that the set of orthogonal functions ${\phi }_b^{\sigma }$, $b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ is linearly independent. The dimension of the Hilbert space of all complex-valued functions on $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ coincides with the cardinality of the set $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ and Theorem 2 provides that

$$|{\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })|=|F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })|=dim{\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }).$$

☐

The interpolating function $I{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }):{\mathbb{R}}^n\to$ of any function $f\in {\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ is taken as a linear combination of the basis functions ${\phi }_b^{\sigma }$, $b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ with complex coefficients $c_b{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })\in$,

$$I{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })=\sum _{b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })}{c}_b{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }){\phi }_b^{\sigma }(a),$$

(170)

that coincides with the interpolated function f on the point set $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$,

$$I{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })(a)=f(a),a\in F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }).$$

The frequency spectrum coefficients $c_b{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$ in (170) are uniquely determined by Theorems 4 and 5 and are calculated as standard Fourier coefficients,

$$c_b{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })=(|W|M^n{h}_{P,M}(b){)}^{-1}\sum _{a\in F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}ϵ(a)f(a)\overline{{\phi }_b^{\sigma }(a)},$$

(171)

and the corresponding Plancherel formulas also hold

$$\sum _{a\in F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}ϵ(a)f(a)\overline{g(a)}=|W|M^n\sum _{b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })}{h}_{P,M}(b)c_b{\left[f\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })\overline{c_b{\left[g\right]}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })}.$$

(172)

Equations (171) and (170) establish the forward and backward generalized discrete dual-root lattice Fourier-Weyl transforms, respectively, of the function $f\in {\mathcal{H}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$.

For any fixed ordering of the labels and points in the sets ${\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee })$ and $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$, the unitary transform matrices ${\mathbb{I}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee })$, which correspond to the generalized discrete dual-root lattice Fourier-Weyl transforms (171) are given by their entries as

$${({\mathbb{I}}_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }))}_{ba}=\sqrt{ϵ(a)(|W|M^n{h}_{P,M}{(b))}^{-1}}\overline{{\phi }_b^{\sigma }(a)},b\in {\Lambda }_{P,M}^{\sigma }(\varrho ,{\nu }^{\vee }),a\in F_{Q^{\vee },M}^{\sigma }(\varrho ,{\nu }^{\vee }).$$

(173)

Several explicit forms of the unitary transform matrices are demonstrated in the following section.

5.3. Unitary Transform Matrices of $A_2$

Firstly, the shifted point and label sets are explicitly constructed for the Lie algebra $A_2$. The marks and dual marks of $A_2$ are listed in [3] as

$$m_1=m_2=m_1^{\vee }=m_2^{\vee }=1.$$

Because the algebra $A_2$ only admits trivial shift $\varrho =0$ of the weight lattice and $R^{\mathfrak{1}}(0)=Ø$, $R^{{\sigma }^e}(0)=\{r_0,r_1,r_2\}$, defining relation (90) yields that $s_0^{\mathfrak{1},0},s_1^{\mathfrak{1},0},s_2^{\mathfrak{1},0}\in {\mathbb{Z}}^{\ge 0}$ and $s_0^{{\sigma }^e,0},s_1^{{\sigma }^e,0},s_2^{{\sigma }^e,0}\in \mathbb{N}$. Therefore, formulas for the point sets $F_{Q^{\vee },M}^{\sigma }(0,{\omega }_j^{\vee })$, $j\in \{1,2\}$ are determined by explicit formulas (91) and (104) as $\begin{array}{ll}{F}_{Q^{\vee },M}^{\mathfrak{1}}(0,{\omega }_j^{\vee })& =\{\frac{s_1^{\mathfrak{1},0}}{M}{\omega }_1^{\vee }+\frac{s_2^{\mathfrak{1},0}}{M}{\omega }_2^{\vee }|s_0^{\mathfrak{1},0}+s_1^{\mathfrak{1},0}+s_2^{\mathfrak{1},0}=M,s_1^{\mathfrak{1},0}+2s_2^{\mathfrak{1},0}\equiv j\mathrm{mod}3\},\\ F_{Q^{\vee },M}^{{\sigma }^e}(0,{\omega }_j^{\vee })& =\{\frac{s_1^{{\sigma }^e,0}}{M}{\omega }_1^{\vee }+\frac{s_2^{{\sigma }^e,0}}{M}{\omega }_2^{\vee }|s_0^{{\sigma }^e,0}+s_1^{{\sigma }^e,0}+s_2^{{\sigma }^e,0}=M,s_1^{{\sigma }^e,0}+2s_2^{{\sigma }^e,0}\equiv j\mathrm{mod}3\}.\end{array}$

Fixing the scaling factor $M=6$, the points of the sets $F_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })$ and $F_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })$ are given by their coordinates $\left(s_1^{\mathfrak{1},0}/M,s_2^{\mathfrak{1},0}/M\right)$ in ${\omega }^{\vee }$-basis as

$$\begin{array}{ll}{F}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })& =\{(\frac{1}{6},0),(0,\frac{1}{3}),(\frac{1}{3},\frac{1}{6}),(\frac{2}{3},0),(\frac{1}{6},\frac{1}{2}),(\frac{1}{2},\frac{1}{3}),(0,\frac{5}{6}),(\frac{5}{6},\frac{1}{6}),(\frac{1}{3},\frac{2}{3})\},\end{array}$$

(174)

$$\begin{array}{ll}{F}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })& =\{(0,\frac{1}{6}),(\frac{1}{3},0),(\frac{1}{6},\frac{1}{3}),(\frac{1}{2},\frac{1}{6}),(0,\frac{2}{3}),(\frac{5}{6},0),(\frac{1}{3},\frac{1}{2}),(\frac{2}{3},\frac{1}{3}),(\frac{1}{6},\frac{5}{6})\}\end{array}$$

(175)

and the points of the sets $F_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })$ and $F_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })$ are given by their coordinates $($ in ${\omega }^{\vee }$-basis as

$$\begin{array}{cc}{F}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })& =\{(\frac{1}{3},\frac{1}{6}),(\frac{1}{6},\frac{1}{2}),(\frac{1}{2},\frac{1}{3})\},\end{array}$$

(176)

$$\begin{array}{cc}{F}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })& =\{(\frac{1}{6},\frac{1}{3}),(\frac{1}{2},\frac{1}{6}),(\frac{1}{3},\frac{1}{2})\}.\end{array}$$

(177)

The description of the label sets ${\Lambda }_{P,M}^{\sigma }(0,{\omega }_j^{\vee })$, $j\in \{1,2\}$ starts by the construction of the weight sets (106) in the Kac coordinates $[{\lambda }_0,{\lambda }_1,{\lambda }_2]$ with ${\lambda }_0,{\lambda }_1,{\lambda }_2\in {\mathbb{Z}}^{\ge 0}$,

$${\Lambda }_M=\{{\lambda }_1{\omega }_1+{\lambda }_2{\omega }_2|{\lambda }_0+{\lambda }_1+{\lambda }_2=M\}.$$

The weight sets ${\Lambda }_6$ and ${\Lambda }_3$ expressed as unions of their ${\Gamma }_6$- and ${\Gamma }_3$-orbits, respectively, are evaluated, as follows,

$$\begin{array}{ll}{\Lambda }_6=& \left\{\right[6,0,0],[0,6,0],[0,0,6\left]\right\}\cup \left\{\right[5,1,0],[1,0,5],[0,5,1\left]\right\}\cup \left\{\right[5,0,1],[1,5,0],[0,1,5\left]\right\}\\ & \cup \left\{\right[4,2,0],[2,0,4],[0,4,2\left]\right\}\cup \left\{\right[4,1,1],[1,4,1],[1,1,4\left]\right\}\cup \left\{\right[4,0,2],[2,4,0],[0,2,4\left]\right\}\\ & \cup \left\{\right[3,3,0],[3,0,3],[0,3,3\left]\right\}\cup \left\{\right[3,2,1],[2,1,3],[1,3,2\left]\right\}\cup \left\{\right[3,1,2],[2,3,1],[1,2,3\left]\right\}\\ & \cup \left\{\right[2,2,2\left]\right\},\\ {\Lambda }_3=& \left\{\right[3,0,0],[0,3,0],[0,0,3\left]\right\}\cup \left\{\right[2,1,0],[1,0,2],[0,2,1\left]\right\}\cup \left\{\right[2,0,1],[1,2,0],[0,1,2\left]\right\}\\ & \cup \left\{\right[1,1,1\left]\right\}.\end{array}$$

The weights $[2,2,2]$ and $[1,1,1]$ in the centers of the magnified domains $F_Q$ are the only weights from ${\Lambda }_6$ and ${\Lambda }_3$ with non-trivial ${\Gamma }_6$- and ${\Gamma }_3$-stabilizers, respectively. Because, according to Proposition 2 and Table 1 from [1], it holds for $j\in \{1,2\}$ that

$${\widehat{\gamma }}_{6,{\omega }_j^{\vee }}^{\mathfrak{1}}({\mathrm{Stab}}_{{\Gamma }_6}([2,2,2]))={\widehat{\gamma }}_{3,{\omega }_j^{\vee }}^{{\sigma }^e}({\mathrm{Stab}}_{{\Gamma }_3}([1,1,1]))=\{1,e^{\frac{2\pi \mathrm{i}}{3}},e^{\frac{4\pi \mathrm{i}}{3}}\},$$

(178)

the weight sets ${\tilde{\Lambda }}_{P,6}^{\mathfrak{1}}({\omega }_j^{\vee })$ and ${\tilde{\Lambda }}_{P,3}^{{\sigma }^e}({\omega }_j^{\vee })$ of orbit representatives (114) are of the form

$$\begin{array}{ll}{\tilde{\Lambda }}_{P,6}^{\mathfrak{1}}({\omega }_j^{\vee })=& \left\{\right[6,0,0],[5,1,0],[5,0,1],[4,2,0],[4,1,1],[4,0,2],[3,3,0],[3,2,1],[3,1,2\left]\right\},\end{array}$$

(179)

$$\begin{array}{ll}{\tilde{\Lambda }}_{P,3}^{{\sigma }^e}({\omega }_j^{\vee })=& \left\{\right[3,0,0],[2,1,0],[2,0,1\left]\right\}.\end{array}$$

(180)

Shifting the orbit representative sets ${\tilde{\Lambda }}_{P,6}^{\mathfrak{1}}({\omega }_j^{\vee })$ and ${\tilde{\Lambda }}_{P,3}^{{\sigma }^e}({\omega }_j^{\vee })$ via Proposition 7 yields the final form of the label sets,

$$\begin{array}{ll}{\Lambda }_{P,6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })=& \left\{\right[6,0,0],[5,1,0],[5,0,1],[4,2,0],[4,1,1],[4,0,2],[3,3,0],[3,2,1],[3,1,2\left]\right\},\end{array}$$

(181)

$$\begin{array}{ll}{\Lambda }_{P,6}^{{\sigma }^e}(0,{\omega }_j^{\vee })=& \left\{\right[4,1,1],[3,2,1],[3,1,2\left]\right\}.\end{array}$$

(182)

The point sets $F_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$ and $F_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_j^{\vee })$, together with the label sets ${\Lambda }_{P,6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$ and ${\Lambda }_{P,6}^{{\sigma }^e}(0,{\omega }_j^{\vee })$, are depicted in Figure 1.

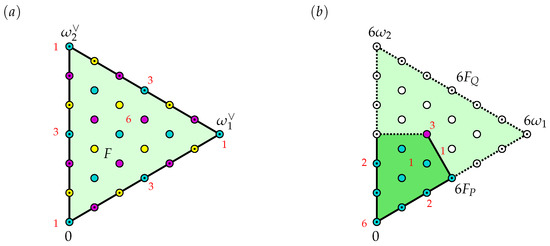
Figure 1. (a) The fundamental domain F of $A_2$, depicted as the equilateral triangle, contains 10 cyan nodes of the point set $F_{Q^{\vee },6}^{\mathfrak{1}}(0,0)$, nine magenta nodes of $F_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })$, and nine yellow nodes of $F_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })$. The nodes without the dotted ones on the boundary of F depict the four cyan points of $F_{Q^{\vee },6}^{{\sigma }^e}(0,0)$, three magenta points of $F_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })$, and three yellow points of $F_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })$. The red numbers represent the values of the discrete ϵ-function (18). (b) The domain 6F_Q of $A_2$, depicted as the equilateral triangle, contains nine cyan nodes in the kite-shaped domain 6F_P that form the sets of labels ${\Lambda }_{P,6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })$ and ${\Lambda }_{P,6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })$ The cyan nodes without the dotted ones on the boundary of 6F_Q depict the three labels of the sets ${\Lambda }_{P,6}^{{\sigma }^e}(0,{\omega }_1^{\vee })$ and ${\Lambda }_{P,6}^{{\sigma }^e}(0,{\omega }_2^{\vee })$. The red numbers represent the values of the discrete stabilizer counting function (54).

The functional formulas for the Weyl orbit functions of $A_2$, together with the discrete functions ϵ and $h_{P,M}$, are calculated in Example 6.1 from [1]. Fixing the scaling factor M = 6, the unitary matrices ${\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$ and ${\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$, which correspond to the ordering of point and label sets (174), (175), and (181)$\begin{array}{c}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })=\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee })+\mathrm{i}\mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_j^{\vee }),j\in \{1,2\},\end{array}\mathrm{with} \mathrm{their} \mathrm{entries} \mathrm{rounded}, \mathrm{are} \mathrm{determined} \mathrm{by} \begin{array}{ll}\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })=& (\begin{array}{ccccccccc}0.289& 0.289& 0.408& 0.289& 0.408& 0.408& 0.289& 0.289& 0.289\\ 0.441& 0.284& 0.221& -0.099& -0.041& -0.181& -0.214& -0.226& -0.186\\ 0.441& 0.284& 0.221& -0.099& -0.041& -0.181& -0.214& -0.226& -0.186\\ 0.284& -0.099& -0.262& -0.186& -0.140& 0.402& -0.186& -0.099& 0.284\\ 0.471& 0& -0.333& 0& -0.333& -0.333& 0.471& 0.471& 0\\ 0.284& -0.099& -0.262& -0.186& -0.140& 0.402& -0.186& -0.099& 0.284\\ 0.083& -0.250& 0.118& -0.250& 0.118& 0.118& 0.083& 0.083& -0.250\\ 0.221& -0.262& -0.255& 0.402& 0.313& -0.058& -0.041& -0.181& -0.140\\ 0.221& -0.262& -0.255& 0.402& 0.313& -0.058& -0.041& -0.181& -0.140\end{array}),\\ \mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_1^{\vee })=& (\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0.007& -0.50& 0.081& 0.271& -0.232& 0.152& -0.385& 0.378& -0.221\\ -0.007& 0.050& -0.081& -0.271& 0.232& -0.152& 0.385& -0.378& 0.221\\ 0.050& -0.271& 0.313& 0.221& -0.384& 0.071& 0.221& -0.271& 0.050\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -0.050& 0.271& -0.313& -0.221& 0.384& -0.071& -0.221& 0.271& -0.050\\ 0.144& -0.433& 0.204& -0.433& 0.204& 0.204& 0.144& 0.144& -0.433\\ 0.081& -0.313& 0.214& -0.071& 0.114& -0.328& -0.232& 0.152& 0.384\\ -0.081& 0.313& -0.214& 0.071& -0.114& 0.328& 0.232& -0.152& -0.384\end{array})\end{array}\mathrm{and}\begin{array}{ll}\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })=& (\begin{array}{ccccccccc}0.289& 0.289& 0.408& 0.408& 0.289& 0.289& 0.408& 0.289& 0.289\\ 0.441& 0.284& 0.221& -0.041& -0.099& -0.214& -0.181& -0.186& -0.226\\ 0.441& 0.284& 0.221& -0.041& -0.099& -0.214& -0.181& -0.186& -0.226\\ 0.284& -0.099& -0.262& -0.140& -0.186& -0.186& 0.402& 0.284& -0.099\\ 0.471& 0& -0.333& -0.333& 0& 0.471& -0.333& 0& 0.471\\ 0.284& -0.099& -0.262& -0.140& -0.186& -0.186& 0.402& 0.284& -0.099\\ 0.083& -0.250& 0.118& 0.118& -0.250& 0.083& 0.118& -0.250& 0.083\\ 0.221& -0.262& -0.255& 0.313& 0.402& -0.041& -0.058& -0.140& -0.181\\ 0.221& -0.262& -0.255& 0.313& 0.402& -0.041& -0.058& -0.140& -0.181\end{array}),\\ \mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{\mathfrak{1}}(0,{\omega }_2^{\vee })=& (\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ -0.007& 0.050& -0.081& 0.232& -0.271& 0.385& -0.152& 0.221& -0.378\\ 0.007& -0.050& 0.081& -0.232& 0.271& -0.385& 0.152& -0.221& 0.378\\ -0.050& 0.271& -0.313& 0.384& -0.221& -0.221& -0.071& -0.050& 0.271\\ 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0.050& -0.271& 0.313& -0.384& 0.221& 0.221& 0.071& 0.050& -0.271\\ -0.144& 0.433& -0.204& -0.204& 0.433& -0.144& -0.204& 0.433& -0.144\\ -0.081& 0.313& -0.214& -0.114& 0.071& 0.232& 0.328& -0.384& -0.152\\ 0.081& -0.313& 0.214& 0.114& -0.071& -0.232& -0.328& 0.384& 0.152\end{array}).\end{array}$ The unitary matrices ${\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })$ and ${\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })$, which correspond to the ordering of point and label sets (176), (177), and (182), are similarly explicitly computed from defining relation (173). The generalized dual-root Fourier-Weyl determinant homomorphism unitary matrices

$${\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_j^{\vee })=\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_j^{\vee })+\mathrm{i}\mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_j^{\vee }),j\in \{1,2\},$$

with their entries rounded, are determined by

$$\begin{array}{ll}\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })& =\left(\begin{array}{ccc}0& 0& 0\\ -0.197& 0.569& -0.371\\ 0.197& -0.569& 0.371\end{array}\right),\\ \mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_1^{\vee })& =\left(\begin{array}{ccc}0.577& 0.577& 0.577\\ 0.543& -0.100& -0.442\\ 0.543& -0.100& -0.442\end{array}\right)\end{array}$$

and

$$\begin{array}{ll}\mathrm{Re}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })& =\left(\begin{array}{ccc}0& 0& 0\\ 0.197& -0.569& 0.371\\ -0.197& 0.569& -0.371\end{array}\right),\\ \mathrm{Im}{\mathbb{I}}_{Q^{\vee },6}^{{\sigma }^e}(0,{\omega }_2^{\vee })& =\left(\begin{array}{ccc}0.577& 0.577& 0.577\\ 0.543& -0.100& -0.442\\ 0.543& -0.100& -0.442\end{array}\right).\end{array}$$

6. Concluding Remarks

• The algorithmic construction of the point and label sets of the shifted dual-root lattice transforms is attainable by various methods, as demonstrated in Section 5.3 for the $A_2$ case. For instance, the steps for formation of the point sets (104) start with direct determination of the ranges of the positive integer symbols $s_i^{\sigma ,\varrho }$, $i\in \widehat{I}$ in (90). Each solution of the equation

  $$s_0^{\sigma ,\varrho }+m_1{s}_1^{\sigma ,\varrho }+\dots +m_n{s}_n^{\sigma ,\varrho }=M$$

  is subsequently assigned its congruence class point set $F_{Q^{\vee },M}^{\sigma }(\varrho ,{\omega }_j^{\vee })$ by determining its inherent value $j\in J^{\vee }\cup \left\{0\right\}$ via substitution to the left hand-sides of Equations (91)–(102). Based on formula (81), the shifting Proposition 7 provides a straightforward construction method of label sets from the auxiliary weight sets ${\Lambda }_M$ and ${\tilde{\Lambda }}_{P,M}^{\sigma }({\nu }^{\vee })$. Direct sorting of the weight sets ${\Lambda }_M$ into ${\Gamma }_M$-orbits that produces relations (179) and (180) circumvents the implementation of the intricate explicit forms of the fundamental domains $F_P$ of the extended dual affine Weyl groups [1].
• The counting formulas in Theorem 3 and Theorem 5.5 of [1] for the identity sign homomorphism sets of points $F_{Q^{\vee },M}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$ and sets of labels ${\Lambda }_{P,M}^{\mathfrak{1}}(0,{\omega }_j^{\vee })$, $j\in \widehat{I}$ of $A_n$ provide a novel interpretation of the functions $a_j(m,n)$ in [34]. Combinatorial proof of the generalized Hermite reciprocity $a_j(m,n)=a_j(n,m)$ in [34] employs analogs of both point and label sets as well as stabilizer counting functions of $A_n$. Stemming from the presented discrete Fourier-Weyl transforms, potential further generalizations of the Hermite reciprocity, together with its combinatorial and algebraic implications to all crystallographic root systems, represents an open problem. Moreover, mathematical and physical consequences of the generalized Hermite reciprocity for the conceivably interconnected discrete transforms of $A_{n-1}$ and $A_M$ deserve further study.
• The collection of the developed shifted dual-root lattice discrete Fourier-Weyl transforms provides advantageous novel options for applications in digital data processing and Fourier and Chebyshev methods. Because the dual-weight lattice transforms [17] and related (anti)symmetric trigonometric transforms [13,14] exhibit very good interpolation properties, a similar feasibility of the currently developed discrete transforms is indicated. The interpolation properties of novel variants of discrete transforms on the honeycomb triangular dot with armchair boundaries [23] merit further testing. Numerical integration and approximation methods that are associated with the induced generalized Chebyshev polynomials [6,10,20,35] deserve further study. The modification of the discrete orthogonality relations of Macdonald polynomials [36] that would specialize to the current induced discrete polynomial orthogonality relations poses an open problem.
• The even complex-valued Fourier-Weyl transforms, as well as the even real-valued Hartley-Weyl transforms [37] of the six types of E-functions for root systems with two root lengths, are developed in [38]. The kernels of the sign homomorphism form the (anti)symmetrizing normal subgroups of Weyl groups inherent in E-functions. The generalization of the present shifted dual-root lattice discrete transforms to all types of E-functions deserves further study. Real-valued Hartley-Weyl transforms on the dual root lattice are developed in [1]. However, shifting the dual root lattice produces complex factors in label symmetries of Weyl orbit functions (85) that prevent apparent extension of the dual-root Hartley-Weyl transform to their shifted versions. A suitable modification of the point and label sets, including a possible adjustment of the multivariate Hartley kernel function [1,38], which would lead to viable real-valued shifted dual-root lattice transforms, represents an unsolved problem.