Abstract
Because most tasks on real-time systems are conducted periodically, its execution pattern is highly predictable. While such a property of real-time systems allows developing the strong schedulability analysis tools providing high analytical capability, it also leads that security attackers could analyze the predictable execution patterns of real-time systems and use them as attack surfaces. Among the few approaches to foil such a timing-inference security attack, TaskShuffler as a schedule randomization protocol received considerable attention owing to its simplicity and applicability. However, the existing TaskShuffler is only applicable to uniprocessor platforms, where the task execution pattern is quite simple to analyze when compared to multiprocessor platforms. In this study, we propose a new schedule randomization protocol for real-time systems on symmetry multiprocessor platforms where all processors are composed of the same architecture, which extends the existing TaskShuffler initially designed for uniprocessor platforms.
1. Introduction
The primary concerns in designing safe critical real-time systems are to develop a methodology to effectively allocate limited computing resources (e.g., memory and CPU (central processing unit)) to multiple real-time tasks (e.g., motor control and sensing), and to derive a mathematical analysis mechanism. This mechanism would ensure every operation conducted by real-time tasks are completed within predefined time units (called deadlines) to satisfy real-time requirements [1]. The former and latter, which are respectively referred to as real-time scheduling algorithms and schedulability analysis, have been extensively studied over the past several decades in the field of real-time systems [2,3,4].
Unlike conventional research, which mostly focuses on the timing guarantees under various computing environments with different operational constraints, recent studies have focused on the security aspect because the modern real-time systems are exposed to unknown security attacks. For instance, modern real-time systems are increasingly being connected to unsecured networks such as the Internet, which allows the sophisticated adversaries to launch security attacks on UAVs (unmanned aerial vehicles) [5], industrial control systems [6], and automobiles [7,8].
Predictability, which is a key property of real-time systems, facilitates the development of several effective schedulability analysis mechanisms, but causes an increase in the success ratio of security attacks because of easy timing inferences [9,10,11]. Because most of the real-time tasks are conducted periodically, the execution patterns can be highly predictable, and most of the strong schedulability analysis mechanisms such as deadline analysis (DA) [12] and response-time analysis (RTA) [13] exploit such a property to judge whether each real-time operation can be completed within the deadline on the target environment. Such a seemingly advantageous property plays a double-edged sword because the security attackers can analyze the predictable execution patterns of real-time systems and use them as attack surfaces. For example, recent studies have shown that an adversary can launch cache-based side-channel attacks by collecting information about important tasks or set up new covert channels [9,14]. The success ratio of such attacks is quite high because the periodic execution of real-time tasks results in repeated (based on the hyper-period of all real-time tasks on the system) scheduling patterns. After observing the real-time task schedules on the target systems, the adversary can predict future schedules of the system.
The main challenge in preventing such timing inference-based security attacks on real-time systems is making the initially predictable schedule unpredictable, while simultaneously satisfying the real-time constraint. Among the few proposed mechanisms that have been used to address the problem of the uniprocessor system, TaskShuffler (a schedule randomization protocol) has received considerable attention owing to its simplicity and applicability [15]. TaskShuffler exploits the notion of priority inversion budget, defined as the time interval between the finishing time of worst-case operation and deadline, of each task. Priority inversion budget value of each task implies that the task can complete its execution even if the other tasks execute for the amount of worst-case inversion budget instead of the task. Utilizing the calculated priority inversion budget value of each task, the TaskShuffler effectively selects random tasks at each schedule point and dynamically manages the value to induce uncertainty and satisfy the real-time constraint simultaneously.
As multiprocessor platforms have been increasingly adopted modern real-time systems to conduct highly resource-consuming tasks, the state-of-the-art techniques need to be tailored for multiprocessor platforms. For example, the latest embedded platforms developed for autonomous driving car consist of multiple CPUs to execute heavy-load tasks such as multiple sensing and image processing (e.g., NVIDIA Drive AGX Pegasus with 8-core “Carmel" CPUs based on ARM architecture) [16]. However, the existing TaskShuffler is only applicable to uniprocessor platforms, where the task execution pattern is quite simple to analyze when compared to multiprocessor platforms.
In this study, we propose a new schedule randomization protocol for real-time systems on symmetry multiprocessor platforms where all processors are composed of the same architecture, which extends the existing TaskShuffler initially designed for uniprocessor platforms. To develop a schedule randomization protocol for multiprocessor platforms, we need to address the following issues:
- (i)
- How to define the problem of improving the security (i.e., uncertainty of schedules) of real-time systems and satisfying the schedulability simultaneously on multiprocessor platforms, differentiating it from the uniprocessor case (Section 2),
- (ii)
- How to calculate the priority inversion budget value for each task on multiprocessors (Section 4.1),
- (iii)
- How to utilize the calculated priority inversion budget values in randomized schedules effectively, to improve uncertainty (Section 4.2), and
- (iv)
- How to satisfy the real-time requirement after applying the proposed schedule randomization protocol (Section 4.2).
To address point (i), we first recapitulate the underlying idea and purpose of the existing TaskShuffler designed for the uniprocessor case. Then, we define the problem for the multiprocessor case, which is addressed in this study. To address point (ii), we investigate each task’s surplus computing power allowed for lower-priority tasks without missing its corresponding deadline. To address point (iii), such lower-bound computing power is effectively utilized by the new schedule randomization protocol proposed in this study. In addition, we demonstrate that if the task set is schedulable with the fixed-priority (FP) preemptive scheduling, then it is schedulable with the proposed schedule randomization protocol; this addresses point (iv). Using experimental simulations, we then discuss various factors affecting the uncertainty of new schedules.
2. Problem Definition
TaskShuffler assumes that the attacker knows task sets’ parameters as well as scheduling policy of the target system [15]. The attacker aims at gleaning sensitive data such as the victim task’s private key in shared resources such as DRAM (dynamic random access memory). Figure 1 briefly presents a scenario where the attacker launches a cache side-channel attack exploiting the scheduling pattern of real-time systems. The attacker first hijacks a task consecutively executing with a victim task ; it assumes that is relatively easy to hijack compared to because is not related to the security operation. Then, the attacker fills all cache sets with ’s data before executes. Thereafter, operates a cryptographic operation with a private key. Here, all cache sets were already filled with ’ data, and thus some cache sets are replaced by ’ data. Later, reads cache sets and measures the latencies. Some cache sets used by result in slow latencies because of cache misses for . The attacker collects such timing information and reasons the location of the private key in the shared memory.
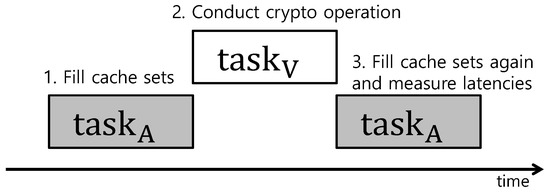
Figure 1.
Cache side-channel attack scenario.
To make such an attack scenario feasible, the attacker should monitor the execution pattern of the target system for a long time to catch the proper timing to launch the attack. Because the same execution pattern of real-time systems is (mostly) repeated, the success ratio of the attack would increase. Figure 2 presents the scheduling pattern of scheduled by a fixed-priority scheduling ( and have the highest and lowest priorities, respectively) without (Figure 2a) and with (Figure 2b) TaskShuffler on a uniprocessor platform. It shows which task executes in 200 time slots, and the number in each rectangle presents the task index executed at the time slot. As shown in Figure 2a, the scheduling pattern is repeated every 40 time units because the least common multiple of periods of tasks in is 40. On the other hand, the scheduling pattern is obfuscated by TaskShuffler (most importantly) without schedulability loss (Figure 2b). That is, every task both in Figure 2a,b completes its execution without any deadline miss. It implies that TaskShuffler could improve potential durability against timing-inference attacks by obfuscating the scheduling pattern of real-time systems without schedulability loss.

Figure 2.
Scheduling pattern of scheduled by fixed-priority scheduling without and with TaskShuffler on a uniprocessor platform.
In this study, we aim to develop a new schedule randomization protocol for multiprocessor platforms by extending the existing TaskShuffler initially designed for uniprocessor platforms. To achieve this, we first recapitulate the underlying idea and purpose of the existing TaskShuffler designed for the uniprocessor case. Then, we define the problem for the multiprocessor case, which is addressed in this study.
The key property of real-time systems is that most of the tasks operate repetitively at periodic intervals. This indicates that the same scheduling pattern for a certain period of time (e.g., one hyper-period of all tasks) can be exhibited in the next period. Although such property aids in developing better-performing analysis techniques that can easily judge the schedulability of real-time systems, an adversary can launch timing-inference attacks by collecting information about important tasks or set up new covert channels.
The TaskShuffler compensates for such shortcoming of real-time systems by reducing the predictability of schedules for real-time tasks. Therefore, even if an observer can record the exact schedule for a certain time period, the same will not be exhibited in the next period under the TaskShuffler. The underlying idea of the existing TaskShuffler is to pick up a random task from the ready queue, unlike most of the real-time systems where the highest priority task is selected for scheduling. Such counterintuitive mechanisms lead to the priority inversion problem and deadline misses, placing system safety at risk. To solve this problem, the TaskShuffler only allows limited priority inversion for each task. That is, it restricts the use of priority inversion so that every task meets the original real-time constraint (i.e., meeting deadlines). To this end, it calculates the lower-bound amount of priority inversion that each task can tolerate, using the TaskShuffler protocol. When the priority inversion limit is reached during execution, the lower-priority task stops running, and the highest priority task is selected to be scheduled.
Then, the TaskShuffler achieves the following goal G.
- G.
- Suppose that a task set is scheduled by a given FP scheduling algorithm S, and its schedulability is guaranteed by a given schedulability analysis A. Then, ’s schedulability is still guaranteed by a given schedulability analysis when it is scheduled by the FP algorithm incorporating the TaskShuffler protocol of uniprocessors.
Let be the set of schedulable task sets scheduled by FP scheduling, and be the set of task sets each of whose schedulability is guaranteed by a given schedulability analysis supporting FP scheduling. In addition, denotes the set of schedulable task sets scheduled by FP scheduling incorporating TaskShuffler, and is the set of task sets each of whose schedulability is guaranteed by a given schedulability analysis supporting FP scheduling incorporating TaskShuffler. Figure 3a shows the regions of task sets covered by , , , and for uniprocessor platforms. in Figure 3a indicates a well-known fact that every schedulable task set ’s schedulability is guaranteed by the given exact schedulability analysis (e.g., RTA supporting FP scheduling) [13]. Then, the TaskShuffler targets task sets belonging to () and applies the TaskShuffler protocol; note that task sets out of has nothing to do with the goal G. It utilizes a specialized schedulability analysis to support the FP scheduling incorporating the TaskShuffler protocol. When is conducted for each task , the lower-bound amount of priority inversion for each task is calculated, and the TaskShuffler exploits it without compromising the schedulability of task sets . Therefore, it achieves as shown in Figure 3a.
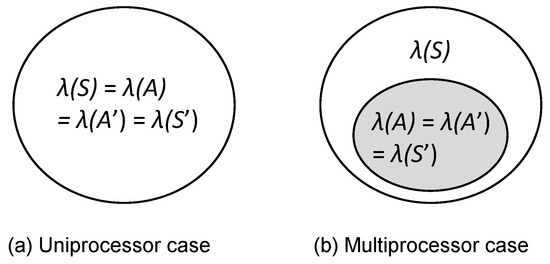
Figure 3.
The regions covered by each technique.
For multiprocessor platforms, there is no exact schedulability analysis for our system model [17], which provides as shown in Figure 3b. Therefore, we target in which tasks’ schedulabiliy are guaranteed by the DA schedulability analysis and aim at achieving the goal G on multiprocessors.
3. System Model
We consider a task set the Liu and Layland task (and system) model (considered as the de-fecto standard in the field of real-time scheduling theory) in which every task is scheduled by global, preemptive and work-conserving FP real-time scheduling algorithm on m identical multiprocessors [1]. A scheduling algorithm is called global, preemptive and work-conserving if a task migrates from one processor to another, a lower-priority task is preempted by a higher-priority one, and the processor is never idle when there are jobs to be executed, respectively. In FP scheduling, the priority is assigned to each task such that all jobs invoked by the same task have the same priority. The Liu and Layland model assumes that tasks are independent, no synchronization is needed, and resources (except processors or cores) are always available. According to the task model, we assume that all processors share the common cache and main memory. A task periodically invokes a job in every time units, and each job is supposed to execute for at most time units (also known as the worst-case execution time (WCET) ) to declare its completion. Every job invoked by should complete its execution in time units as a real-time constraint. j-th job invoked by a task is denoted by , and it is invoked at the release time and should finish its execution within the absolute deadline . We use the notation when it indicates an arbitrary job of a task . A job is said to be schedulable when it finishes its execution before its absolute deadline . Further, a task is said to be schedulable when all jobs invoked by are schedulable, and a task set is said to be schedulable when all tasks are schedulable. and represent the set of tasks whose priorities are lower than that of and that whose priorities are higher than that of , respectively. We consider online scheduling algorithms and offline schedulability analysis (in online scheduling algorithms and offline schedulability analysis, the priorities of pending or executing jobs (i.e., scheduled by the given scheduling algorithm) are determined after the system starts, while the schedulability of the given task set is judged before the system starts.)
4. Schedule Randomization Protocol for Multiprocessors
The key idea of our schedule randomization protocol is to select random jobs from the ready queue rather than the originally prioritized ones that are supposed to be selected by a given algorithm. This operation inevitably causes priority inversions for some tasks, which can induce an additional execution delay when compared to the existing schedule. This can result in a deadline miss in the worst case, even if the task is deemed schedulable by a given schedulability analysis. To avoid such situations, we should employ bounded priority inversions (calculated by the schedule randomization protocol) so that every task completes its execution before its corresponding deadline.
In this section, we first calculate the upper bound of allowed priority inversions for each task (in the first subsection), and then present how to effectively utilize such calculated priority inversions budget values in a schedule randomization protocol for multiprocessors.
4.1. Priority Inversion Budget Calculation
As an offline step of our schedule randomization protocol for multiprocessors, the maximum number of time units that are allowed for jobs of tasks in to execute when a job of the task waits for another job to complete should be calculated (we use a subscript ‘k’ if the notation is related to a task whose schedulability will be judged. We use a subscript ‘i’ if the notation is related to higher priority tasks of .). We refer such time units as the priority inversion budget, , which will be utilized in the online step of randomization protocol. We define the worst-case inversion budget as follows.
Definition 1.
(Priority inversion budget ) The priority inversion budget of a task is defined as the maximum amount of time units in [, ) that is allowed for jobs of tasks in to execute while a job of a task waits on multiprocessors, which ensures schedulability of .
Thus, can be lower-bound by calculating the allowable limit for delay in execution of caused by lower-priority jobs in without missing deadlines. To achieve this, we exploit the underlying mechanism of a well-known schedulability analysis called DA, which uses two notions of interference defined as follows.
Definition 2.
(Worst-case interference on ) The worst-case interference on a task in an interval on multiprocessors is defined as the maximum cumulative length of all the intervals in which is ready to execute but cannot be scheduled because of higher-priority jobs.
Definition 3.
(Worst-case interference of on ) The worst-case interference of a task on a task in an interval on multiprocessors is defined as the maximum cumulative length of all the intervals in which is ready to execute but cannot be executed on any processor when the job of the task is executing.
Using the definition of , is calculated as follows.
For a job to interfere at a time unit in [, ), there are m jobs at the time unit. By the definition of , is calculated as follows.
To upper bound , we use the concept of workload of a task in an interval of length ℓ, which is defined as the maximum amount of time units required for all jobs released from in the interval of length ℓ. As shown in Figure 4, the left-most job (called the carry-in job) of starts its execution at t (i.e., the beginning of the interval) and finishes it at . That is, it executes for without any delay. Thereafter, the following jobs are released and executed without any delay. By calculating the number of jobs executing for and the other jobs executing for a part of , the workload of in an interval of length ℓ (i.e., ) is calculated by [18].
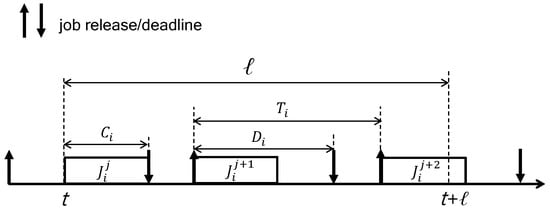
Figure 4.
The worst-case scenario in which the workload of is maximized in an interval of length ℓ.
Figure 5 illustrates the underlying idea of DA with an example in which the target task ’s schedulability is judged considering its four higher priority tasks on . In the interval , there is only one job of , and there is no deadline miss if ’s execution is not hindered by more than . As seen in Figure 5, can be larger than , and some portion of that inevitably executes in parallel with since we assume that each job cannot execution in parallel on more than one processor. Thus, DA limits the amount of to , which refines Equation (2) as follows.
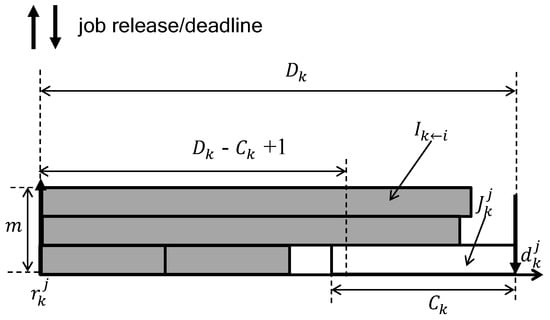
Figure 5.
An example of deadline analysis (DA) for four higher-priority tasks and a target task .
Theorem 1.
Suppose that scheduled by a given fixed-priority scheduling algorithm is deemed schedulable by DA, and tasks in do not delay more than . Then, is still schedulable with the randomization protocol.
Proof.
By the definition is schedulable if every job released by at can finish its execution within . From Equation (1), we have
The worst-case execution for is upper bounded by , and the time in which is hindered by higher-priority jobs is upper bounded by according to Equation (4). Therefore, if the tasks in do not delay for more than , then every job of can finish its execution within . □
4.2. Schedule Randomization Protocol
Based on the mechanism to calculate the priority inversion budget of each task explained in the previous section, we illustrate how the new schedule randomization protocol for multiprocessors operates in this section. Let be the ready queue in which active jobs are sorted in decreasing order of priority. It implies that and are the highest- and lowest-priority jobs in , respectively. We assume that TaskSuffler operates only when is greater than m because all active jobs will be selected for schedule, otherwise.
The TaskSuffler for multiprocessor conducts Algorithm 1 for at every scheduling decision. It first adds to the candidate list, (Line 1). If its remaining inversion budget is equal to zero, then it returns and highest-priority jobs in (Lines 2–4). Otherwise, with letting be the job in the current iteration, it iterates the following for through (Lines 5–11). If the remaining inversion budget of is larger than zero, it adds to the candidate list and considers the next job (Lines 6–7). Otherwise, it adds to the candidate list and stops the iteration (Lines 8–9). Then, if is smaller than or equal to m, it returns all jobs in and highest-priority jobs in . Otherwise, it returns randomly selected m jobs in . After Algorithm 1 is conducted, the selected m jobs execute until the next scheduling decision.
| Algorithm 1 TaskSuffler for multiprocessors. |
|
Let denote the task of the lowest-priority job among selected jobs, and denote the set of tasks that were not selected. The next schedule decision is made at
unless a new job arrives or any of the selected jobs finishes its execution before . Thus, the remaining inversion budget of every released job belonging to a task is deducted by one at each time unit until the next schedule decision will be made, a new job arrives, or any of the selected jobs finishes its execution before . The remaining priority inversion budget of each job is set to when is released.
Theorem 2.
Suppose that scheduled by a given fixed-priority scheduling algorithm is deemed schedulable by DA schedulability analysis, then it is still schedulable under the schedule randomization protocol.
Proof.
By Theorem 1, is schedulable if its execution is not hindered for more than by lower-priority tasks. ’s execution is interfered by lower-priority tasks only when ’s priority is lower than that of , and the amount of interference from lower-priority tasks cannot be larger than since the next scheduling decision is made before becomes zero owing to Equation (6). □
To implement TaskShuffler to the existing scheduler, the system should be capable for tracking tasks’ remaining execution times and priority inversion budgets. Such monitoring ability is already commonly available on many real-time systems, whose aim is to guarantee that they do not exceed their execution allowances [19,20]. Utilizing such the ability, TaskShuffler may impose additional scheduling decisions according to the policy of TaskShuffler, compared to the vanilla scheduling algorithms (e.g., rate monotonic). It naturally increases scheduling costs such as preemption (or context switching) and migration costs. The system designers should consider how much such scheduling costs will happen for their target systems when TaskShuffler is considered to improve the schedule entropy without schedulability loss.
4.3. Schedule Entropy for Multiprocessors
Because our goal is to improve the uncertainty in scheduling to foil the fixed schedule pattern of real-time scheduling, we need to evaluate the improvement in the uncertainty of our proposed schedule randomization protocol. To overcome this issue, we use the concept of schedule entropy initially designed for a uniprocessor [21,22,23]. The underlying idea of schedule entropy is to measure randomness (or unpredictability) of schedule at each time unit, called slot entropy, and derive the summation of all slot entropies over a hyper-period L (defined as the least common multiple of of all tasks ). The slot entropy at a time slot t for a task set is calculated as follows.
where is the probability mass function of a task appearing at time t. is obtained empirically by observing multiple hyper-periods [15]. Then, the schedule entropy is calculated by the summation of all slot entropies over a hyper-period L as follows.
According to the considered task model, we assume that all processors share the common cache and main memory. Then, it also implies that which processor is assigned to a task does not affect the level of scheduling entropy. That is, the level of scheduling entropy is influenced by whether is scheduled or not in a time slot. Such the assumption is the limitation of our study, and thus it should be considered as potential future work.
5. Evaluation
In this section, we evaluate the performance of our schedule randomization protocol with randomly generated synthetic task sets to understand the effect of our approach on various factors more fully.
We randomly generated even task sets from nine system utilization groups, for , that is, 100 instances per group. The system utilization of a task set is defined as the sum of the utilizations of all tasks () in the task sets. We considered three different numbers of processors and 8. Each system utilization group has five sub-groups, each of which has a fixed number of tasks; for and 8, the number of tasks for five sub-groups are {}, {} and {}. Each task period was randomly selected from {20, 40, 80, 160, 320, 640, 1280, 2560}, and each WCET was selected from . A total of 100 task sets were generated for each sub-group, and thus task sets were generated in total. As our goal is to improve the uncertainty of the schedule without compromising schedulability, we only selected the task sets whose schedulability is guaranteed by DA schedulability. We used rate-monotonic (RM) scheduling as our base scheduling algorithm in which our proposed schedule randomization was applied. To obtain the converged schedule entropy of each task set, we conducted a simulation for 10,000 hyper-periods of the task set as it ensures less than 0.01% (recommended to obtain the converged schedule entropy [15]) of difference in schedule entropy between those from 9999 and 10,000 hyper-periods.
Figure 6 shows the plot of average schedule entropy of each sub-group’s task sets (i.e., 100 task sets for each sub-group) over varying system utilization groups for and 8 (Due to limited space on x-axis, for is represented as [0.0, 0.1], [0.1, 0.2], ⋯, [0.7, 0.8], [0.8, 0.9].). As shown in Figure 6a, the schedule entropy of a task set is high on average when it consists of a large number of tasks (System utilization group [0.8, 0.9] exhibits an exceptional result because of heavy utilization of its task set, which result that most of the task sets exhibit zero schedule entropy). This is because a higher number of tasks with our schedule randomization protocol possibly provides larger options for tasks to be randomly selected in every time slot. For example, the schedule entropy at a time slot t of a task set having two tasks each of whose is 1/2 is 1, while is 2 if has four tasks each of whose is 1/4. This implies that a larger number of tasks for each task set can improve schedule entropy. In addition, Figure 6a demonstrates that task sets included in the groups whose system utilization is low or high (e.g., [0.0, 0.1], [0.1, 0.2], [0.7, 0.8] or [0.8, 0.9]) result in relatively low average schedule entropy while the others (e.g., [0.2, 0.3]–[0.6, 0.7]) results in high average schedule entropy. Because the task sets with low system utilization have less WCET, no process operates (i.e., processors are idling) in most of the time slots. When it comes to high utilization, most of the tasks have low values; therefore, the chances of tasks to be randomly selected are quite low. Therefore, a low schedule entropy results in both cases.
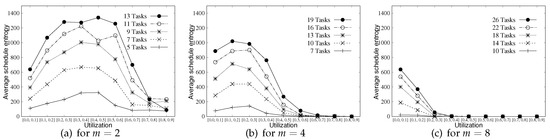
Figure 6.
Average schedule entropy for and 8.
From Figure 6a–c, we can observe that the average schedule entropy of task sets decreases as the number of processors m increases. This is mainly due to the underlying pessimism of the DA schedulability analysis in calculating in Equation (4). As Figure 5 implies, the DA schedulability analysis assumes that the execution corresponding to is performed as much as possible in the interval [, ) to upper bound . However, this does not happen in most cases since two jobs released consecutively from the same task may execute at intervals from each other, which implies that the amount of execution contributing to is overestimated under the DA schedulability analysis. Such pessimism of the DA schedulability analysis increases for a larger value of m. As our schedule randomization protocol is based on the DA schedulability analysis to derive , task sets with a lower value of (from a larger value of m) results in a lower average schedule entropy.
While Figure 6 presents the average schedule entropy over varying system utilization groups, Table 1, Table 2 and Table 3 show the maximum schedule entropy obtained from each setting. As the minimum schedule entropy of every setting is zero, Table 1, Table 2 and Table 3 also represent the range of schedule entropy that can be obtained from each setting. “-” in the tables represents a value lower than 0.1, and we exclude rows of the tables if all values corresponding to the row are “-”. The trends shown in Figure 6a–c also appear in Table 1, Table 2 and Table 3, but the maximum schedule entropy of task sets in the high system utilization group are relatively high compared to the average schedule entropy of those task sets. This indicates that a very low number of task sets in the high system utilization group shows exceptionally high schedule entropy from a certain task parameter setting following the considered task set generation method, and the other task sets are with zero schedule entropies.

Table 1.
m = 2.

Table 2.
m = 4.

Table 3.
m = 8.
One may wonder whether much additional scheduling overhead is required to apply our schedule randomization protocol into the existing scheduling algorithm. Note that the schedule decision on preemptive scheduling algorithm (basically considered in our paper) without the schedule randomization protocol is made only when a job finishes its execution or a new job is released. In addition, an additional schedule decision stemming from the schedule randomization protocol is made when (i.e., the remaining priority inversion budget value of ) of a job becomes zero. Figure 7 shows the ratio between the number of schedule decisions made by naive RM and that made by RM with the schedule randomization protocol. As shown in Figure 7, for task sets with high system utilization or for larger m shows less schedule decision ratio. With high system utilization or larger m, each task has a lower priority inversion budget as aforementioned, and the schedule randomization protocol works rarely with such settings. Overall, a high schedule decision ratio implies a larger scheduling overhead, and thus the system designers should carefully consider the trade-off between scheduling overhead and the degree of security they want to achieve for their target system.
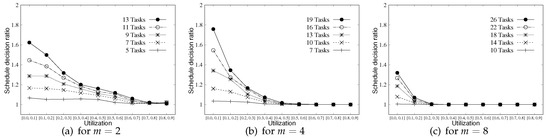
Figure 7.
Schedule decision ratio for and 8.
6. Related Work
The problem of information leakage for real-time systems has been addressed in several studies. Mohan et al. considered real-time tasks with different security levels and focused on information leakage on shared computing resources (e.g., RAM and cache). They proposed a mechanism for FP scheduling to flush the status of shared resources conditionally, which reduces the chances of an attacker from obtaining sensitive information of the resources [24]. Because they incorporated a security mechanism into the existing FP scheduling, an additional timing overhead was inevitably required. Therefore, they proposed a new sufficient schedulability analysis to accommodate that fact. In [25], an exact schedulability was proposed to improve the analytical capability. In addition, this work was extended to mixed-criticality systems in [26]
The aforementioned studies addressed the issues only for non-preemptive scheduling; therefore, Pellizzoni et al. extended this work to preemptive scheduling [27]. They extended it to a more general task model, and proposed an optimal priority assignment method that determines the task preemptibility.
Another approach to improve the security of real-time systems is to randomize the schedules without compromising schedulability. TaskShuffler addressed in this study was proposed by Yoon et al. for a preemptive FP scheduling algorithm [15]. The goal of TaskShuffler is to improve uncertainty in schedule and reduce the success ratio of timing inference attacks simultaneously. Kr¨uger et al. proposed an online schedule randomization protocol for time-triggered systems [28]. While the aforementioned two approaches are applicable to uniprocessor platforms, we focus on multiprocessor platforms.
7. Conclusions
In this study, we aimed to develop a new scheduling randomization protocol for symmetry multiprocessors to improve the security and conserve schedulability of real-time systems simultaneously, by extending the existing TaskShuffler initially designed for uniprocessors. To this end, we first define the problem of improving the security of real-time systems and satisfying the schedulability simultaneously on multiprocessor platforms, differentiating it from the uniprocessor case. Then, we employed DA schedulability to derive priority inversion budget values for each task, and proposed an algorithm to effectively utilize the calculated priority inversion budget values in randomized schedules to improve uncertainty. Based on the simulation results, we investigated the effect of our approach on various factors. Non-preemptive [29] or partitioned [2] scheduling will be considered in our future work.
As our study adopts a fundamental task model (of the Liu and Lyland) assuming no consideration of task dependency, resource consideration and scheduling costs (e.g., migration or preemption cost), it cannot be directly applied to actual real-time systems without relieving the assumptions. We also leave it as our promising future work.
Author Contributions
Conceptualization, H.B.; software, H.B.; data curation, H.B.; writing—original draft preparation, H.B. and C.M.K.; writing—review and editing, C.M.K.; supervision, C.M.K.; project administration, H.B.; funding acquisition, H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Incheon National University (International Cooperative) Research Grant in 2019.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, C.; Layland, J. Scheduling Algorithms for Multi-programming in A Hard-Real-Time Environment. J. ACM 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Brandenburg, B.B.; Gul, M. Global scheduling not required: Simple, near-optimal multiprocessor real-time scheduling with semi-partitioned reservations. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Porto, Portugal, 29 November–2 December 2016; pp. 1–15. [Google Scholar]
- Melani, A.; Bertogna, M.; Bonifaci, V.; Marchetti-Spaccamela, A.; Buttazzo, G. Schedulability Analysis of Conditional Parallel Task Graphs in Multicore Systems. IEEE Trans. Comput. 2016, 66, 339–353. [Google Scholar] [CrossRef]
- Biondi, A.; Buttazzo, G.C.; Bertogna, M. Schedulability Analysis of Hierarchical Real-Time Systems under Shared Resources. IEEE Trans. Comput. 2016, 65, 1593–1605. [Google Scholar] [CrossRef]
- Shepard, D.; Bhatti, J.; Humphreys, T. Drone Hack: Spoofing Attack Demonstration on a Civilian Unmanned Aerial Vehicle. GPS World 2012, 23, 30–33. [Google Scholar]
- Russotto, B.F. W32.stuxnet Dossier. Available online: http://www.symantec.com/content/en/us/enterprise/media/security_response/whitepapers/w32_stuxnet_dossier.pdf. (accessed on 6 March 2020).
- Koscher, K.; Czeskis, A.; Roesner, F.; Patel, S.; Kohno, T.; Checkoway, S.; McCoy, D.; Kantor, B.; Anderson, D.; Shacham, H.; et al. Experimental Security Analysis of a Modern Automobile. In Proceedings of the IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 16–19 May 2010; pp. 447–462. [Google Scholar]
- Checkoway, S.; Mccoy, D.; Kantor, B.; Anderson, D.; Shacham, H.; Savage, S.; Koscher, K.; Czeskis, A.; Roesner, F.; Kohno, T. Comprehensive Experimental Analyses of Automotive Attack Surfaces. In Proceedings of the Usenix Security Symposium, San Francisco, CA, USA, 8–12 August 2011; pp. 1–16. [Google Scholar]
- Son, J.; Alves-Foss, J. Covert Timing Channel Analysis of Rate Monotonic Real-Time Scheduling Algorithm in MLS Systems. In Proceedings of the IEEE Information Assurance Workshop, West Point, NY, USA, 21–23 June 2006; pp. 361–368. [Google Scholar]
- Yoon, M.K.; Mohan, S.; Choi, J.; Sha, L. Memory Heat Map:Anomaly detection in real-time embedded systems using memory behavior. In Proceedings of the 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- Zadeh, M.M.Z.; Salem, M.; Kumar, N.; Cutulenco, G.; Fischmeister, S. SiPTA: Signal processing for trace-based anomaly detection. In Proceedings of the ACM & IEEE International Conference on Embedded Software, Jaypee Greens, India, 12–17 October 2014; pp. 1–10. [Google Scholar]
- Bertogna, M.; Cirinei, M.; Lipari, G. Schedulability Analysis of Global Scheduling Algorithms on Multiprocessor Platforms. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 553–566. [Google Scholar] [CrossRef]
- Joseph, M.; Pandya, P. Finding response times in a real-time system. Comput. J. 1986, 29, 390–395. [Google Scholar] [CrossRef]
- Volp, M.; Hamann, C.J.; Hartig, H. Avoiding timing channels in fixed-priority schedulers. In Proceedings of the ACM Symposium on Information, Computer and Communication Security, Tokyo, Japan, 18–20 March 2008; pp. 1–10. [Google Scholar]
- Yoon, M.; Mohan, S.; Chen, C.; Sha, L. TaskShuffler: A Schedule Randomization Protocol for Obfuscation against Timing Inference Attacks in Real-Time Systems. In Proceedings of the IEEE Real-Time Technology and Applications Symposium (RTAS), Vienna, Austria, 11–14 April 2016; pp. 1–12. [Google Scholar]
- NVIDIA. Drive AGX Pegasus. Available online: https://developer.nvidia.com/drive/drive-agx (accessed on 8 April 2020).
- Fisher, N.; Goossens, J.; Baruah, S. Optimal Online Multiprocessor Scheduling of Sporadic Real-Time Tasks is Impossible. Real-Time Syst. 2010, 45, 26–71. [Google Scholar] [CrossRef]
- Bertogna, M.; Cirinei, M. Response-Time Analysis for globally scheduled Symmetric Multiprocessor Platforms. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Tucson, AZ, USA, 3–6 December 2007. [Google Scholar]
- Bernat, G.; Burns, A. New results on fixed priority aperiodic servers. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Phoenix, AZ, USA, 1–3 December 1999; pp. 68–78. [Google Scholar]
- Zabos, A.; Davis, R.; Burns, A.; Harbour, M.G. Spare capacity distribution using exact response-time analysis. In Proceedings of the Conference on Real-Time and Network Systems, Paris, France, 26–27 October 2009; pp. 97–106. [Google Scholar]
- Cachin, C. Entropy Measures and Unconditional Security in Cryptography. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1997; pp. 1–143. [Google Scholar]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Dodis, Y.; Smith, A. Entropic security and the encryption of high entropy messages. In Proceedings of the International Conference on Theory of Cryptography, Cambridge, MA, USA, 10–12 February 2005; pp. 1–22. [Google Scholar]
- Mohan, S.; Yoon, M.K.; Pellizzoni, R.; Bobba, R. Real-Time Systems Security through Scheduler Constraints. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Madrid, Spain, 8–11 July 2014; pp. 129–140. [Google Scholar]
- Baek, H.; Lee, J.; Lee, Y.; Yoon, H. Preemptive Real-Time Scheduling Incorporating Security Constraint for Cyber Physical Systems. IEICE Trans. Inf. Syst. 2016, E99-D, 2121–2130. [Google Scholar] [CrossRef]
- Baek, H.; Lee, J. Incorporating Security Constraints into Mixed-Criticality Real-Time Scheduling. IEICE Trans. Inf. Syst. 2017, E100.D, 2068–2080. [Google Scholar] [CrossRef]
- Pellizzoni, R.; Paryab, N.; Yoon, M.; Bak, S.; Mohan, S.; Bobba, R. A generalized model for preventing information leakage in hard real-time systems. In Proceedings of the IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Seattle, WA, USA, 13–16 April 2015; pp. 271–282. [Google Scholar]
- Krüger, K.; Völp, M.; Fohler, G. Vulnerability Analysis and Mitigation of Directed Timing Inference Based Attacks on Time-Triggered Systems. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Barcelona, Spain, 3–6 July 2018; pp. 1–17. [Google Scholar]
- Baek, H.; Jung, N.; Chwa, H.S.; Shin, I.; Lee, J. Non-Preemptive Scheduling for Mixed-Criticality Real-Time Multiprocessor Systems. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1766–1779. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).