Abstract
An analytical form-finding method for regular tensegrity structures based on the concept of force density is presented. The self-equilibrated state can be deduced linearly in terms of force densities, and then we apply eigenvalue decomposition to the force density matrix to calculate its eigenvalues. The eigenvalues are enforced to satisfy the non-degeneracy condition to fulfill the self-equilibrium condition. So the relationship between force densities can also be obtained, which is followed by the super-stability examination. The method has been developed to deal with planar tensegrity structure, prismatic tensegrity structure (triangular prism, quadrangular prism, and pentagonal prism) and star-shaped tensegrity structure by group elements to get closed-form solutions in terms of force densities, which satisfies the super stable conditions.
1. Introduction
Tensegrity structures refer to the stable structures that are based on the balance between their members in compressive or tensile states. This kind of structure is composed of struts carrying compressive forces and cables carrying tensile forces. The members are prestressed so that the structure gets its shape as well as rigidity in a self-equilibrated state in the absence of external loads [1]. Kennet Snelson designed and constructed the initial tensegrity model in 1947, the concept of which was then introduced by Fuller to define the very type of structure. In the last few decades, tensegrity structures have been widely studied and applied to various fields, such as civil engineering [2,3,4,5], aerospace [6,7], biology [8,9,10], mathematics [11], and robotics [12].
The process of determining the self-equilibrated configuration is known as form-finding [13], which is a necessity for tensegrity structures. The difficulties in solving the form-finding problems of tensegrity structures always lie in finding a self-equilibrated configuration, which satisfies the required specific properties of the structure [14]. A variety of studies about form-finding have been conducted. The existing form-finding methods can be divided into force design and shape design. Theories about force design have been developed a lot, such as searching feasible regions and optimizing internal forces with constraint conditions or given shape [7,15]. Shape design is usually based on force density method, dynamic relaxation method, or nonlinear structural analysis. Schek firstly developed the force density method for the form-finding of cable-nets in 1974 [16]. Following the track, many researchers have extended the concept of force density method [17,18,19,20,21,22]. The dynamic relaxation method has also been applied to tensile structures [23] and tensegrity structures [24]. Nonlinear structural analysis with fictitious material properties has been introduced [25,26]. Existing form-finding methods have been reviewed [27,28,29].
Form-finding methods can also be divided into two broad classes, analytical methods, and numerical methods [30]. Analytical methods are usually used for regular structures with a high level of symmetry, e.g., prismatic tensegrity structures [31,32], or truncated polyhedral tensegrity structures [33,34]. Zhang et al. studied the stability and configuration of symmetric prismatic tensegrity structures [35,36]. Zhang and Ohsaki used group theory and symmetry property of tetrahedral tensegrity structures [37], and Zhang et al. aimed at exploring the self-equilibrium and stability properties of all Z-based and rhombic TRP tensegrities respectively [38,39,40].
Numerical methods may have more extensive applications comparing with analytical methods. Numerical methods with force density concepts have been developed [41,42]. It may also turn into a nonlinear problem that intends to minimize the total length of cables or maximize that of struts [43]. Both dynamic relaxation method and nonlinear structural method, as mentioned, are also placed as numerical methods. Inspired by the dynamic relaxation method, Li et al. developed the Monte Carlo form-finding method for large scale regular and irregular tensegrity structures [13]. An energy method [44] and a marching process [45] for form-finding have been proposed. The genetic algorithm is a representative technique of Darwinian Theory and has been proposed for form-finding [46,47,48,49].
To make tensegrity structures into real applications, it is essential to ensure the stability condition. Maxwell’s rule for structures made of trusses was developed in 1864 [50], and then it was revised by Calladine [51]. Connelly defined the stability condition for tensegrity structures [44]. Deng and Kwan developed an energy-based approach to categorizing of the stability conditions of tensegrity structures [52]. Guest investigated a more natural way to calculate the tangent stiffness matrix [53]. According to Zhang and Ohsaki, the stable status of tensegrity structures can be divided into super-stability and prestress-stability [54]. A tensegrity structure is defined as a super-stable one if it is always stable regardless of the level of prestress and the selection of materials [28], while prestress stability relates to the stiffness matrix and its eigenvalues, as will be discussed later in this paper.
Though numerical methods can deal with more irregular and complicated structures, analytical methods appear to be the most effective way without iteration or the introduction of concepts from other disciplines. Moreover, it provides an opportunity of looking inside the relation between different force densities. Therefore, analytical methods remain optimal, especially when they are applied to regular tensegrities. In most of the previous studies, analytical solutions were deduced by the investigation of self-equilibrium and super-stability conditions. For example, Zhang et al. gave a unified solution for truncated regular tensegrities using the self-equilibrium and stability properties [38,39,40]. Group theory has been developed on structures with a large number of elements [34,35,36]. The method appears to be quite effective for structures with symmetric or periodic property, which are prevalent structural forms in practical engineering [55,56]. This paper follows the idea of group theory and divides the elements into groups to improve computational efficiency. Therefore, the analytical method proposed in this paper has broader applications in regular tensegrity structures comparing to the existing analytical methods.
In this paper, an analytical form-finding method based on the force density method is investigated to get a closed-form solution in terms of force densities. Only the topology and property of structural members are needed in advance. The proposed method can be divided into two main parts, equilibrium analysis and super-stability examination. The paper is organized as follows: Section 2 illuminates the basic concept of force density method and its usage in the process of form-finding, which is followed by the non-degeneracy condition. Section 3 presents the super-stability condition of tensegrity structures. The proposed method is depicted and discussed in Section 4. Examples of a planar tensegrity structure, three kinds of prismatic tensegrity structure (triangular prism, quadrangular prism, and pentagonal prism) and a star-shaped tensegrity structure are given in Section 5 to verify its efficiency and versatility.
2. Force Density Method and Self-Equilibrium Condition
2.1. Assumptions
The analytical method for form-finding bases on the equilibrium condition at the nodes. In this study, the fundamental assumptions for tensegrity structures are adopted as follows [18]:
- (a)
- Members are connected using pin joints;
- (b)
- No external loads are included, and the gravity is ignored;
- (c)
- Member failure is not considered: i.e., struts do not yield and cables do not bear compressive forces;
- (d)
- The structure is self-equilibrated and free-standing without any support;
- (e)
- The topology (connectivity between the nodes and members) of the tensegrity structure is known, and the geometrical configuration of the structure can be described in terms of nodal coordinates only.
2.2. Force Density Method
The force density of a structural member k is defined as
where fk and lk are the force and length of member k, respectively.
We define E as the force density matrix, which can be written directly from the force densities qk [31,50] as
where φ denotes the set of members connected to node i. It should be noted that sum of the entries in each row or column of the force density matrix in Equation (2) is zero, which is always true for free-standing structures. The equilibrium condition of tensegrity structures in terms of force density matrix E can be written as
where x, y, and z are the coordinates of the structural system. In other words, the equilibrium condition of tensegrity structures can be expressed in terms of force densities.
2.3. Non-Degeneracy Condition
According to Schek [16], matrix E is always square and symmetric, and positive-definite if all members are in tension. So, for cable-nets, which only possess positive values of force densities, E is invertible, and nodal coordinates can be uniquely determined by solving the linear Equation (3) [18]. However, there are struts in tensegrity structures, which means negative elements of E. So, matrix E is invariably singular with rank deficiency. Define the rank deficiency h of E as
where n is the number of free nodes.
From the equilibrium equations Equation (3), the solution space is spanned by h independent vectors. If h = 1, all nodes degenerate into one node; and if h = 2, it turns into a line passing through the base node; h = 3 and h = 4 forms a two-dimensional and three-dimensional space, respectively [18]. Therefore, to obtain a non-degenerate d-dimensional (d = 2 or 3) tensegrity structure, the rank deficiency h of E should satisfy the following condition
It should be noticed that Equation (5) is a necessary but not sufficient condition for non-degeneracy of condition tensegrity structures [27,29,44]. The sufficient conditions for tensegrities or self-equilibrated pin-jointed structures were investigated by Zhang and Ohsaki [57], and a rough explanation will be presented in the next section.
3. Stable Conditions
Self-equilibrium analysis and stability properties are the two critical points in the design of tensegrity structures, both of which can be dealt with by investigating the eigenvalues of the force density matrix [37].
A structure is regarded as stable if it satisfies [57]
where d is any nodal displacement vector, and K is the tangent stiffness matrix. It should be notable that the rigid-body motions are not included in d. The tangent stiffness matrix K of a tensegrity structure can be divided into two parts
where KE is the linear stiffness matrix, and KG is the geometrical stiffness matrix. Substitute Equation (7) into Equation (6)
An adaptive way to determine whether the stability condition is achieved was proposed [57]. A tensegrity structure is said to be super-stable if it keeps stable with any level of force densities satisfying self-equilibrium without inducing material failure [11,28]. Thus increased force densities only stiffen and stabilize the structure [38]. According to Zhang and Ohsaki, the sufficient super-stability conditions of a tensegrity structure are [54]:
- (i)
- the geometry matrix is full rank;
- (ii)
- the matrix E has (d+1) nonzero eigenvalues;
- (iii)
- the matrix E is positive semi-definite;
where d is the number of the dimension of the tensegrity structure.
For condition (iii), if the matrix E is not positive semi-definite, geometrical stiffness matrix KG will have negative eigenvalues and become dominant over the linear stiffness matrix KE at sufficiently large force densities in the elements. So the tangent stiffness matrix K fails to be positive definite, and the structure becomes unstable. Condition (ii) guarantees the self-equilibrium condition. Conditions (ii) and (iii) can be examined by the total number of zero-eigenvalues and the sign of the minimum eigenvalue respectively after eigenvalue decomposition of the force density matrix. According to Zhang [38], condition (i) will be satisfied in most cases if the structure is divisible.
Since the stable conditions of the prestress-stable structure relate to the level of force densities, we consider the super-stability condition for tensegrity structures in this paper.
4. Form-Finding Method
In this section, we are going to describe the form-finding method in detail and take a few examples to make it brighter. The process of the analytical form-finding method can be divided into assumptions (Section 4.1), equilibrium analysis (Section 4.2) and super-stability examination (Section 4.3) in terms of force densities. It should be noticed that the method is only suitable for regular and symmetric tensegrity structures. A brief flowchart of this method is presented in Figure 1. Assume that the topology and the type of each member are given.
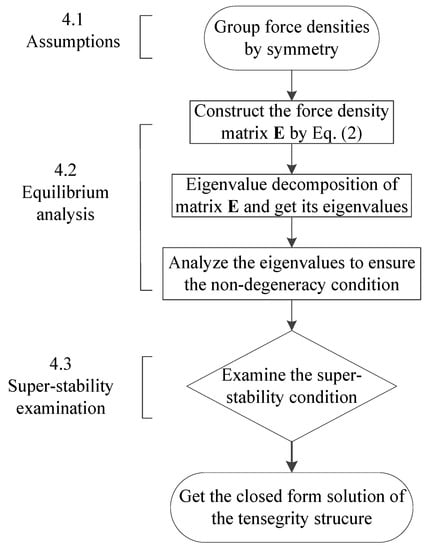
Figure 1.
Proposed analytical form-finding process and sections arrangement.
4.1. Assumptions
Set up force density variables for all members. If the member is a cable, we use numbers as the subscripts, i.e., q1, q2, q3, ...; otherwise, we use letters, i.e., qs, qb, ... Moreover, the number of variables of force densities can be reduced by making use of symmetry properties.
4.2. Equilibrium Analysis
As shown in Figure 1, the equilibrium analysis includes three main steps, the construction, decomposition, and ensuring the non-degenerate condition analysis of the force density matrix E. With the force densities assumed, the force density matrix E can be obtained according to Equation (2). Then the eigenvalues λ1, λ2, λ3, ... λn of matrix E can be determined by solving the equation [38]
where I is the unit matrix. The expanded form of Equation (9) is shown as
where A0(·), A1(·), ..., An-1(·) denote the polynomial functions in terms of the force densities and Equation (10) can be obtained by eigenvalue decomposition.
According to Section 2.3, the non-degeneracy condition has to be achieved to ensure self-equilibrium. Therefore, Equation (5) should be fulfilled. To achieve that, there should exist enough zero eigenvalues. For example, if there is a three-dimensional tensegrity structure, at least four of the eigenvalues should be zero. With the obtained expressions of eigenvalues, we should notice the number of zero eigenvalues before deciding expressions that are definitely greater than zero. Then, for the rest of eigenvalues, the value of which we cannot determine directly by the expressions set one or a few of them equal to zero so that a relationship between force densities can be obtained. The judging process is summarized as follows:
- Step 1: Calculate the rank deficiency h of the force density matrix E (Equation (4)).
- Step 2: Notice the number of expressions that are equal to zero and record it as t1. Usually, there is only one expression of eigenvalue equal to zero after the decomposition. We assume this eigenvalue as λ1.
- Step 3: Find all the expressions of eigenvalues that are definitely greater than zero and denote the number of eigenvalues as t2.
- Step 4: Select a few of the rest expressions of eigenvalues equal to zero. Record the number of expressions that are assumed to zero as t3, and t3 + t1 ≥ h should be satisfied.
- Step 5: Get the relationship between force densities from the equations in Step 4.
4.3. Super-Stability Examination
According to Section 3, the super-stability condition is usually satisfied if conditions (ii) and (iii) are fulfilled. It should be noticed that the non-degeneracy condition is identical to the condition (ii). So only condition (iii) remains to be examined.
The number of all eigenvalues is m, which includes (t3 + t1) zero eigenvalues, t2 positive eigenvalues and (m-t1-t2-t3) uncertain eigenvalues. If all of the uncertain eigenvalues are not less than zero, the structure is super stable. N1, N2, N3, ... represent nodes while M1, M2, ... denote members. A planar tensegrity structure, three types of prismatic tensegrity structures (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure will be analyzed in the next section.
5. Examples
In this section, examples are presented based on the proposed method. A planar tensegrity structure, three types of prismatic tensegrity structure (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure are selected as examples. The detailed descriptions of prismatic and star-shaped tensegrity structures can be found in chapters 7 and 8 of reference [57].
5.1. Planar Tensegrity
For a simple planar tensegrity structure with six cables and three struts, an explicit study is carried out to demonstrate the capability of the investigated method.
Suppose that the tensegrity structure, which is shown in Figure 2, has three kinds of force densities: q1, q2, and qs. q1 represents the force density of cable elements M1, M3, and M5; q2 denotes the force density of cable elements M2, M4, and M6; qs indicates the force density of struts. Then the force density matrix E can be given as
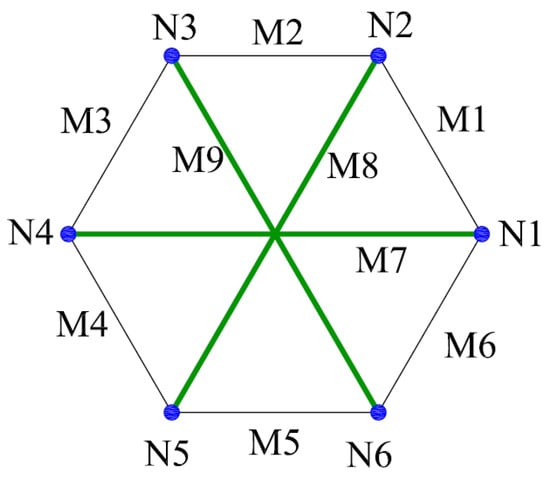
Figure 2.
Two-dimensional rotary symmetry planar tensegrity structure with six cables (black lines) and three struts (green lines).
Eigenvalues of the matrix E in Equation (11) are
From Equation (12), it should be noticed that qs is a negative value. Assume that λ2 is greater than zero. Therefore, λ3 and λ5 are always greater than zero. Then assume λ4 and λ6 equal to zero, so relationship among q1, q2, and qs is obtained as
To ensure that q1 is positive, q2 must be greater than -qs. q1 is known by Equation (13), and therefore λ2 is greater than 0. In conclusion, λ2, λ3, and λ5 in Equation (12) are greater than zero while the other three are equal to zero, which satisfies the super-stability condition of tensegrity structures.
5.2. Three-dimensional prismatic tensegrity structures
5.2.1. Triangular Prism
Suppose that the triangular prism tensegrity structure, shown in Figure 3, has four kinds of force densities: q1, q2, qb, and qs. q1 represents the force density of cable element M1, M2, M3; qb denotes the force density of M4, M5, M6; q2 denotes the force density of M7, M8, M9, and qs denotes the force density of struts. Then the force density matrix E can be given as
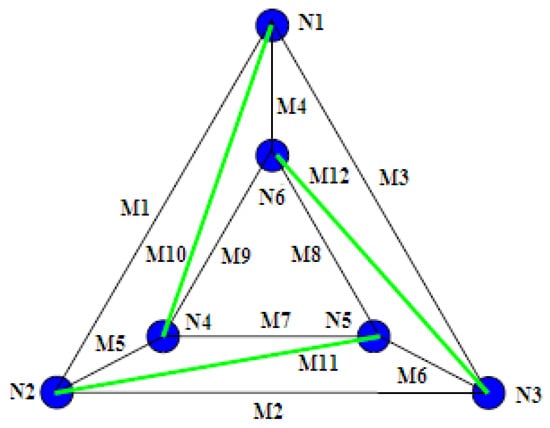
Figure 3.
Triangular prism rotary symmetry tensegrity structure with nine cables (black lines) and three struts (green lines).
Eigenvalues of the matrix E in Equation (14) are shown as
where q1, q2, qb are all positive values, and qs is negative because of the compression in struts. Set λ2 equal to zero to satisfy the non-degeneracy condition. Then, we have
Thus, it should be noticed that λ3 and λ5 are always greater than zero. Set λ4 and λ6 also equal to zero. Thus, the relationship among q1, q2, qb, and qs is obtained as
By substituting Equation (16) into Equation (17), we obtain
If both Equation (16) and Equation (17) are satisfied, the structure fulfills the non-degeneracy condition because four eigenvalues are zero. λ3 and λ5 in Equation (15) are greater than zero; the other eigenvalues in Equation (15) are all equal to zero so that the structure also satisfies the super-stability condition for tensegrity structures. The results are found the same with analytical solutions derived by Pellegrino and Tibert [27]. The relationship between variables q1, q2, and qs are plotted in the three-dimensional vector graph, shown in Figure 4.
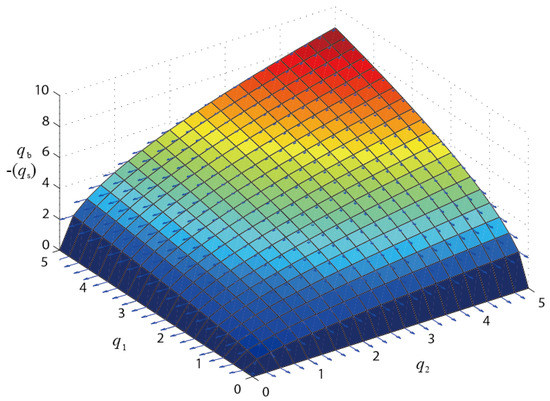
Figure 4.
Vector graph of the solutions for the relationship between variables q1, q2, and qs of the triangular prism rotary symmetry tensegrity structure.
5.2.2. Quadrangular Prism Tensegrity Structure
Suppose that the quadrangular prism tensegrity structure, which is shown in Figure 5, has four kinds of force densities: q1, q2, qb, and qs. q1 represents the force density of elements M1, M2, M3, M4; q2 represents the force density of M5, M6, M7, M8; qb represents the force density of M9, M10, M11, M12; and qs represents that of struts. Then the force density matrix E can be given as
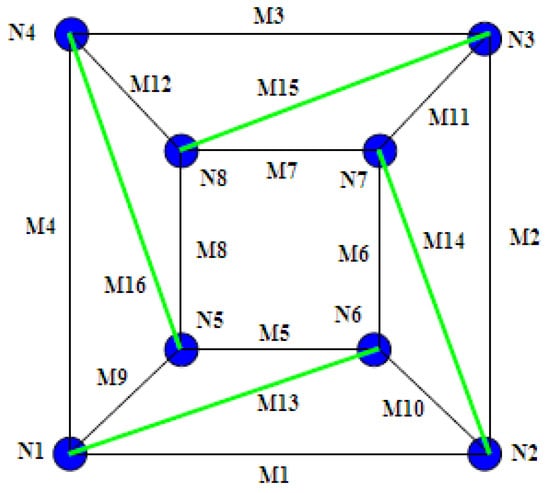
Figure 5.
Quadrangular prism rotary symmetry tensegrity structure with 12 cables (black lines) and 4 struts (green lines).
Eigenvalues of the matrix E in Equation (19) are
q1, q2 and qb, the force densities of cable members, are all positive values, and qs, the force density of struts, is negative. Presume that λ2 equals to zero. Then
It should be noticed that λ3, λ5 and λ7 are always greater than zero. Thus, the sign of λ1, λ2, λ3, λ5, and λ7 are determined. Set λ6 and λ8 or λ4 equal to zero.
Case 1: If we assume that λ6 and λ8 equal to zero, the relationship among q1, q2, qb, and qs is obtained as
By substituting Equation (21) into Equation (22), we obtain
Bringing Equation (22) and Equation (23) into Equation (20), we obtain λ4
If both Equation (21) and Equation (23) are satisfied, the structure achieves the non-degenerate condition because four eigenvalues, λ1, λ2, λ6, and λ8, are zero while the other eigenvalues are greater than zero. So the super-stability condition for tensegrity structures is satisfied.
Case 2: If we set λ4 equal to zero, the relationship between variables by substituting Equation (21) is shown as
Bring Equation (21) and Equation (25) into Equation (20), we obtain λ6 and λ8
Therefore, there are only three eigenvalues equal to zero while others are greater than zero. The non-degeneracy condition for tensegrity structures is not fulfilled. The relationship between variables q1, q2, and qs are plotted in the three-dimensional vector graph, shown in Figure 6.
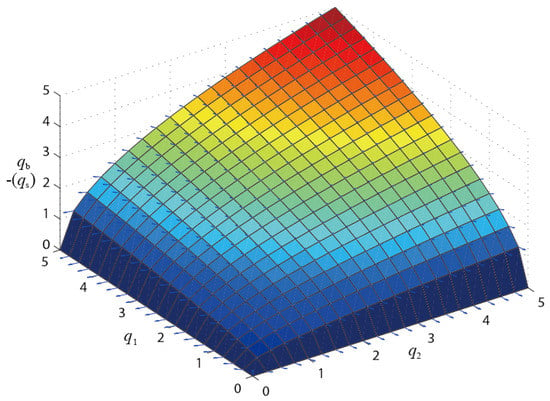
Figure 6.
Vector graph of the solutions for the relationship between variables q1, q2, and qb of the quadrangular prism rotary symmetry tensegrity structure.
5.2.3. Quadrangular Prism Tensegrity Structure
Suppose that the pentagonal prism tensegrity structure, as shown in Figure 7, has four kinds of force densities, q1, q2, qb, and qs; q1 represents the force density of elements M1, M2, M3, M4, M5; q2 represents the force density of M11, M12, M13, M14, M15; qb represents the force density of M6, M7, M8, M9, M10; and qs represents the force density of struts. Then the force density matrix E can be given as
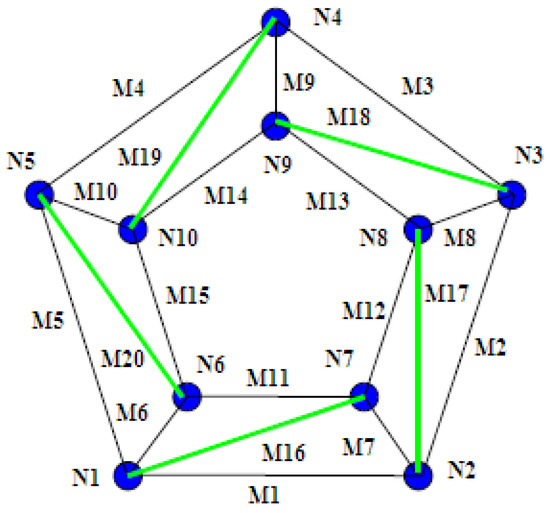
Figure 7.
Pentagonal prism rotary symmetry tensegrity structure with 15 cables (black lines) and 5 struts (green lines).
The first two eigenvalues of the matrix E in Equation (25) are shown as
Set λ2 equal to zero. We obtain
Substitute Equation (29) into the other eigenvalues
From Equation (30), since q1, q2, qb are all positive values, λ3, λ5, λ7, and λ9 are always greater than zero. However, the sign of λ4, λ6, λ8 and λ10 cannot be determined yet.
Case 1: Set both λ4 and λ8 equal to zero, the relationship among q1, q2, qs is obtained as
Substitute Equation (31) into Equation (30)
so the structure does not meet the requirement of the super-stability condition.
Case 2: Set λ6 and λ10 equal to zero, the relationship among q1, q2, qs is obtained as
Substitute Equation (33) into Equation (30), λ4 and λ8 are shown as
If Equation (32) are satisfied, the structure achieves the non-degeneracy condition because four eigenvalues, λ1, λ2, λ6, and λ10, are zero while the other eigenvalues are greater than zero. So the super-stability condition for tensegrity structures is satisfied. The relationship between variables q1, q2 and qs are plotted in the three-dimensional vector graph, shown in Figure 8.
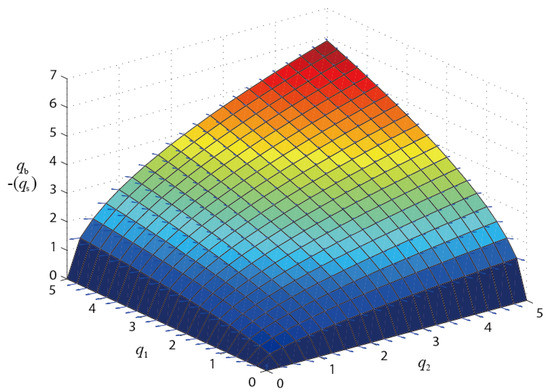
Figure 8.
Vector graph of the solutions for the relationship between variables q1, q2, and qb of the pentagonal prism rotary symmetry tensegrity structure.
5.3. Star-Shaped Tensegrity Structure
Suppose that the star-shaped tensegrity structure, as shown in Figure 9, has four kinds of force densities: q1, q2, qb, and qs. q1 represents the force density of elements M1, M2, M3; q2 represents the force density of elements M4, M5, M6; qb represents the force density of elements M7, M8, M9, M10; and qs represents that of struts. Then the force density matrix E can be given as
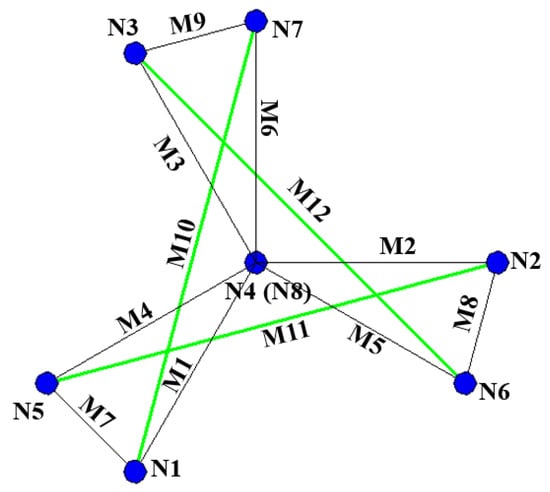
Figure 9.
Star-shaped rotary symmetry tensegrity structure with nine cables (black lines) and three struts (green lines).
The first two eigenvalues of the matrix E in Equation (33) are shown as
Set eigenvalue λ2 equal to zero. We obtain
Substitute Equation (37) into the other eigenvalues
From Equation (36), since q1, q2, qb are all positive value, λ3, λ4, λ5, and λ7 are always greater than zero. Set both λ6 and λ8 equal to zero, the relationship among q1, q2, qs is obtained as
If both Equations (35) and (37) are satisfied, the structure achieves the non-degeneracy condition because four eigenvalues are zero while the others are greater than zero in Equation (36) so that the super-stability condition for tensegrity structures is satisfied. The results of structures in Section 5.2 are found to be in good agreement with analytical solutions conjectured by Estrada, which used a unitary value [58]. The relationship between variables q1, q2, and qs are plotted in the three-dimensional vector graph, shown in Figure 10.
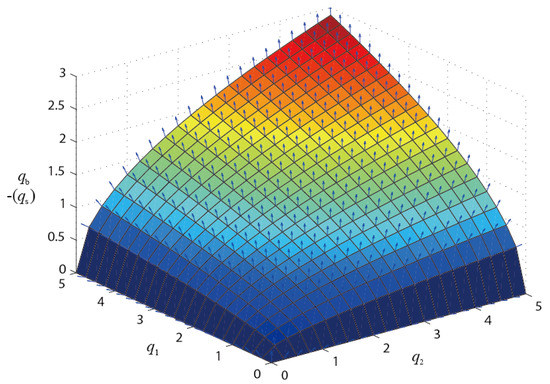
Figure 10.
Vector graph of the solutions for the relationship between variables q1, q2, and qb of the star-shaped rotary symmetry tensegrity structure.
6. Conclusions
An analytical method based on the force density method was proposed in this paper to get closed-form solutions for regular tensegrity structures with symmetry. The necessary condition for non-degeneracy of a tensegrity structure is that three or four eigenvalues of the matrix E are zero (two-dimensional tensegrities and three-dimensional tensegrities, respectively). A closed-form solution of the force densities is induced by setting the necessary number of eigenvalues to zero. Then, the super-stability conditions for tensegrity structures are examined.
Several examples were investigated comprehensively in this paper to verify the capability of the proposed technique. A planar tensegrity structure, three types of prismatic tensegrity structure (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure are included as examples, all of which have regular shapes. After the eigenvalue decomposition of the matrix force density E, a closed-form solution can be conjectured according to the non-degeneracy condition. The closed-form solution can help in understanding the design of regular tensegrity structures in many fields, both in robotics and architecture, as well as deployable structures. Though the proposed method is efficient enough to solve the examples mentioned above, more advanced methods should be developed for form-finding of more complex tensegrities, which will be studied in the future.
Author Contributions
Conceptualization, J.C. and J.F.; Methodology, J.Z.; Software, X.W.; Formal analysis, Q.Z. and J.C.; Writing—original draft preparation, Q.Z., X.W., and J.Z.; Writing—review and editing, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this article was supported by the National Natural Science Foundation of China (grant nos. 51822805, 51878147, and U1937202), the Natural Science Foundation of Jiangsu Province (grant nos. BK20170083) and Postgraduate Research and Practice Innovation Program of Jiangsu Province (grant nos. KYCX19_0091) The fourth author would also like to thank financial support from Japan Society for the Promotion of Science under KAKENHI 15KT0109 and open funding from Key Laboratory of C & PC Structures of Ministry of Education, Southeast University.
Acknowledgments
The authors thank the anonymous reviewers for their valuable comments and thoughtful suggestions which improved the quality of the presented work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Veenendaal, D.; Block, P. An overview and comparison of structural form finding methods for general networks. Int. J. Solids Struct. 2012, 49, 3741–3753. [Google Scholar] [CrossRef]
- Ali, N.B.H.; Rhode-Barbarigos, L.; Albi, A.A.P. Design optimization and dynamic analysis of a tensegrity-based footbridge. Eng. Struct. 2010, 32, 3650–3659. [Google Scholar]
- Fu, F. Non-linear static analysis and design of Tensegrity domes. Steel Compos. Struct. 2006, 6, 417–433. [Google Scholar] [CrossRef]
- Li, P.C.; Wu, M.E. Stabilities of cable-stiffened cylindrical single-layer latticed shells. Steel Compos. Struct. 2017, 24, 591–602. [Google Scholar]
- Cai, J.G.; Zhang, Q.; Feng, J.; Lee, S.H. Structural evaluation of a foldable cable-strut structure for kinematic roofs. Steel Compos. Struct. 2018, 29, 669–680. [Google Scholar]
- Tibert, A.G.; Pellegrino, S. Deployable tensegrity reflectors for small satellites. J. Spacecr. Rocket. 2002, 39, 701–709. [Google Scholar] [CrossRef]
- Li, T.; Jiang, J.; Deng, H. Form-finding methods for deployable mesh reflector antennas. Chin. J. Aeronaut. 2013, 26, 1276–1282. [Google Scholar] [CrossRef]
- Ingber, D.E. Tensegrity I: Cell structure and hierarchical systems biology. J. Cell Sci. 2003, 116, 1157–1173. [Google Scholar] [CrossRef] [PubMed]
- Stamenović, D. Effects of cytoskeletal prestress on cell rheological behavior. Acta Biomater. 2005, 1, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.G.; Yang, R.G.; Wang, X.Y.; Feng, J. Effect of initial imperfections of struts on the mechanical behavior of tensegrity structures. Compos. Struct. 2019, 207, 871–876. [Google Scholar] [CrossRef]
- Connelly, R.; Back, A. Mathematics and Tensegrity: Group and representation theory make it possible to form a complete catalogue of “strut-cable” constructions with prescribed symmetries. Am. Sci. 1998, 86, 142–151. [Google Scholar] [CrossRef]
- Bliss, T.; Werly, J.; Iwasaki, T. Experimental validation of robust resonance entrainment for cpg-controlled tensegrity structures. IEEE Trans. Control Syst. Technol. 2013, 21, 666–678. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.Q.; Cao, Y.P. A Monte Carlo form-finding method for large scale regular and irregular tensegrity structures. Int. J. Solids Struct. 2010, 47, 1888–1898. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J. Form-finding of tensegrity structures using an optimization method. Eng. Struct. 2015, 104, 126–132. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Luo, Y. Finding member connectivities and nodal positions of tensegrity structures based on force density method and mixed integer nonlinear programming. Eng. Struct. 2018, 166, 240–250. [Google Scholar] [CrossRef]
- Schek, H.J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Aboul-Nasr, G.; Mourad, S.A. An extended force density method for form finding of constrained cable nets. Case Stud. Struct. Eng. 2015, 3, 19–32. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Adaptive force density method for form-finding problem of tensegrity structures. Int. J. Solids Struct. 2006, 43, 5658–5673. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M.; Kanno, Y. A direct approach to design of geometry and forces of tensegrity systems. Int. J. Solids Struct. 2006, 43, 2260–2278. [Google Scholar] [CrossRef]
- Sánchez, J.; Serna, M.Á.; Morer, P.A. Multi-step force–density method and surface-fitting approach for the preliminary shape design of tensile structures. Eng. Struct. 2007, 29, 1966–1976. [Google Scholar] [CrossRef]
- Tran, H.C.; Lee, J. Advanced form-finding of tensegrity structures. Comput. Struct. 2010, 88, 237–246. [Google Scholar] [CrossRef]
- Feng, X.; Guo, S. A novel method of determining the sole configuration of tensegrity structures. Mech. Res. Commun. 2015, 69, 66–78. [Google Scholar] [CrossRef]
- Motro, R.; Najari, S.; Jouanna, P. Shell and Spatial Structures: Computational Aspects; Lecture Notes in Engineering 26; Springer: Berlin, Germany, 1987. [Google Scholar]
- Zhang, L.; Maurin, B.; Motro, R. Form-Finding of Nonregular Tensegrity Systems. J. Struct. Eng. 2006, 132, 1435–1440. [Google Scholar] [CrossRef]
- Pagitz, M.; Tur, J.M.M. Finite element based form-finding algorithm for tensegrity structures. Int. J. Solids Struct. 2009, 46, 3235–3240. [Google Scholar] [CrossRef]
- Ohsaki, M.; Zhang, J.Y. Nonlinear programming approach to form-finding and folding analysis of tensegrity structures using fictitious material properties. Int. J. Solids Struct. 2015, 69–70, 1–10. [Google Scholar] [CrossRef]
- Pellegrino, S.; Tibert, A.G. Review of Form-Finding Methods for Tensegrity Structures. Int. J. Space Struct. 2003, 18, 209–223. [Google Scholar]
- Juan, S.H.; Tur, J.M.M. Tensegrity frameworks: Static analysis review. Mech. Mach. Theory 2008, 43, 859–881. [Google Scholar] [CrossRef]
- Motro, R. Tensegrity: Structural Systems for the Future; Elsevier: San Diego, CA, USA, 2003. [Google Scholar]
- Koohestani, K.; Guest, S.D. A new approach to the analytical and numerical form-finding of tensegrity structures. Int. J. Solids Struct. 2013, 50, 2995–3007. [Google Scholar] [CrossRef]
- Connelly, R.; Terrell, M. Globally rigid Symmetric Tensegrities. Struct. Topol. 1995, 21, 59–78. [Google Scholar]
- Crane, C.D.; Duffy, J.; Correa, J.C. Static Analysis of Tensegrity Structures. J. Mech. Des. 2005, 127, 257–268. [Google Scholar] [CrossRef][Green Version]
- Murakami, H.; Nishimura, Y. Static and dynamic characterization of regular truncated icosahedral and dodecahedral tensegrity modules. Int. J. Solids Struct. 2001, 38, 9359–9381. [Google Scholar] [CrossRef]
- Raj, R.P.; Guest, S.D. Using Symmetry for Tensegrity Form-Finding. J. Int. Assoc. Shell Spat. Struct. 2006, 47, 245–252. [Google Scholar]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric prismatic tensegrity structures: Part I. Configuration and stability. Int. J. Solids Struct. 2009, 46, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric prismatic tensegrity structures. Part II: Symmetry-adapted formulations. Int. J. Solids Struct. 2009, 46, 15–30. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Self-equilibrium and stability of regular truncated tetrahedral tensegrity structures. J. Mech. Phys. Solids 2012, 60, 1757–1770. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Li, Y.; Cao, Y.P. Self-equilibrium and super-stability of truncated regular polyhedral tensegrity structures: A unified analytical solution. Proc. R. Soc. A 2012, 468, 3323–3347. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Li, Y.; Cao, Y.P. A unified solution for self-equilibrium and super-stability of rhombic truncated regular polyhedral tensegrities. Int. J. Solids Struct. 2013, 50, 234–245. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhu, S.X.; Li, S.X.; Xu, G.K. Analytical form-finding of tensegrities using determinant of force-density matrix. Compos. Struct. 2018, 189, 87–98. [Google Scholar] [CrossRef]
- Estrada, G.G.; Bungartz, H.J.; Mohrdieck, C. Numerical form-finding of 2D tensegrity structures. Int. J. Solids Struct. 2006, 43, 6855–6868. [Google Scholar] [CrossRef]
- Masic, M.; Skelton, R.E.; Gill, P.E. Algebraic tensegrity form-finding. Int. J. Solids Struct. 2005, 42, 4833–4858. [Google Scholar] [CrossRef]
- Burkhardt, R.; Solutions, T. The Application of Nonlinear Programming to the Design and Validation of Tensegrity Structures with Special Attention to Skew Prisms. J. -Int. Assoc. Shell Spat. Struct. 2006, 150, 3. [Google Scholar]
- Connelly, R. Rigidity and energy. Invent. Math. 1982, 66, 11–33. [Google Scholar] [CrossRef]
- Micheletti, A.; Williams, W.O. A marching procedure for form-finding for tensegrity structures. J. Mech. Mater. Struct. 2007, 2, 857–882. [Google Scholar] [CrossRef]
- Xu, X.; Luo, Y. Form-finding of nonregular tensegrities using a genetic algorithm. Mech. Res. Commun. 2010, 37, 85–91. [Google Scholar] [CrossRef]
- Yamamoto, M.; Gan, B.S.; Fujita, K.A. Genetic Algorithm Based Form-Finding for Tensegrity Structure. Procedia Eng. 2011, 14, 2949–2956. [Google Scholar] [CrossRef]
- Koohestani, K. Form-finding of tensegrity structures via genetic algorithm. Int. J. Solids Struct. 2012, 49, 739–747. [Google Scholar] [CrossRef]
- Seunghye, L.; Buntara, S.G.; Jaehong, L. A fully automatic group selection for form-finding process of truncated tetrahedral tensegrity structures via a double-loop genetic algorithm. Compos. Part B Eng. 2016, 106, 308–315. [Google Scholar]
- Maxwell, J.C. On the calculation of the equilibrium and stiffness of frames. Philos. Mag. 1864, 27, 294–299. [Google Scholar] [CrossRef]
- Calladine, C.R. Buckminster Fullews “tensegrity” structures and Clerk Maxwell’s rules for the construction of stiff frames. Int. J. Solids Struct. 1978, 14, 161–172. [Google Scholar] [CrossRef]
- Deng, H.; Kwan, A. Unified classification of stability of pin-jointed bar assemblies. Int. J. Solids Struct. 2005, 42, 4393–4413. [Google Scholar] [CrossRef]
- Guest, S. The stiffness of prestressed frameworks: A unifying approach. Int. J. Solids Struct. 2006, 43, 842–854. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Stability conditions for tensegrity structures. Int. J. Solids Struct. 2007, 44, 3875–3886. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Sun, Q.Z. Lower-order symmetric mechanism modes and bifurcation behavior of deployable bar structures with cyclic symmetry. Int. J. Solids Struct. 2018, 139–140, 1–14. [Google Scholar] [CrossRef]
- Chen, Y.; Sareh, P.; Feng, J.; Sun, Q.Z. A computational method for automated detection of engineering structures with cyclic symmetries. Comput. Struct. 2017, 191, 153–164. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Tensegrity Structures: Form, Stability, and Symmetry; Mathematics for Industry 6; Springer: Berlin, Germany, 2016. [Google Scholar]
- Estrada, G.G. Analytical and Numerical Investigations of Form-finding Methods for Tensegrity Structures. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).