Abstract
Transport properties of dense QCD matter are discussed. Using the Kubo formula for conductivity, we discuss some topological aspects of quark matter during the chiral transition. The close relation to Weyl semimetal is pointed out and anomalous Hall effect is demonstrated to be possible. In particular, it is shown that the spectral asymmetry of the quasi-particles plays an important role for the Hall conductivity in the magnetic field.
1. Introduction
Recently, much effort has been made theoretically or experimentally to explore the QCD phase diagram in the temperature–density plane [1], where various phase transitions have been proposed. Among them, deconfinement transition and chiral transition are fundamental subjects for QCD. Phenomenologically these transitions may affect the evolution of the universe or physics of compact stars. We, hereafter, consider the chiral transition mainly at low-temperature.
Many studies have shown that the chiral transition from the spontaneously symmetry-broken (SSB) phase to the quark-gluon plasma (QGP) phase should be present at some density and temperature, using the effective models of QCD, while at the moment it has not yet been directly proven from the first principle computations with lattice gauge theory due to the sign problem [2]. Recently, the possible appearance of the inhomogeneous chiral phase (iCP) has been suggested near the chiral transition, and extensively studied in various situations, including in the presence of magnetic field [3,4,5,6,7,8].
Here, we reveal a new aspect of the iCP in relation to Weyl semimetal (WSM) in condensed-matter physics [9]. We focus on the transport properties in the iCP to reveal some topological features inherent in the iCP. First, we shall see that the energy spectrum of quasi-particles in the iCP phase is the same as WSM, and the anomalous Hall effect (AHE) [10,11] also works in iCP. In this case, the AHE is brought about by the magnetic monopole in the momentum space. Next, we consider the Hall conductivity in the presence of magnetic field. This subject is important to understand the transport properties inside compact stars, such as thermal evolution of magnetars [12]. In condensed-matter physics, this subject has been also discussed to elucidate the transport properties of topological materials [13]. We shall see that anomalous Hall conductivity also appears as the magnetic-field-independent term due to the spectral asymmetry. Thus, the competition between AHE and the usual Hall effect is interesting as the strength of magnetic field increases.
2. Inhomogeneous Chiral Phase in Dense QCD and Weyl Semimetal
2.1. Dual Chiral Density Wave
iCP is characterized by the generalized order parameter,
for the symmetry breaking of . The order parameters are now spatially dependent, and various types of can be chosen, depending on the situation [6].
The dual chiral density wave (DCDW) is a kind of density wave and the DCDW phase is specified by the scalar and pseudoscalar condensates with spatial modulation [3],
The order parameters are the amplitude and the wavevector q. We, hereafter, focus on this type, because the phase degree of freedom is indispensable for manifestation of topological effects in iCP. Moreover, it may be the most favorable configuration in the presence of the magnetic field [6,7,8].
We take the Nambu–Jona-Lasinio (NJL) model as an effective model of QCD at a low-energy scale:
We, hereafter, consider the flavor symmetric u and d quark matter in the chiral limit . Then, the effective Lagrangian can read under the mean-field approximation as follows:
One may rewrite it in a simple form,
where and the spacelike vector by the use of the Weinberg transformation, . Thus, we can see that the amplitude of the DCDW provides the dynamical mass for the newly defined quarks (quasi-particles) described by , while the wavevector plays the role of the mean-field for them. The effective Hamiltonian operator in the momentum space then renders:
The single-particle energy can be easily extracted,
with for each flavor, where and denote the particle-antiparticle and spin degrees of freedom, respectively. Accordingly, this form suggests anisotropy of the Fermi sea in the momentum space: it deforms in an axial-symmetric way around the direction of q.
Thermodynamic potential can be easily evaluated for given temperature T and baryon number chemical potential , using the single-particle energy (7). Then, the values of the order parameters can be easily extracted: we can see that the DCDW phase appears around several times the normal nuclear density at (see Figure 1a), where the usual chiral transition has been expected [3]. It should be interesting to see that the value of the wavevector becomes rather high, (Figure 1b), which is reminiscent of the nesting effect of the Fermi surface. Actually, it has been
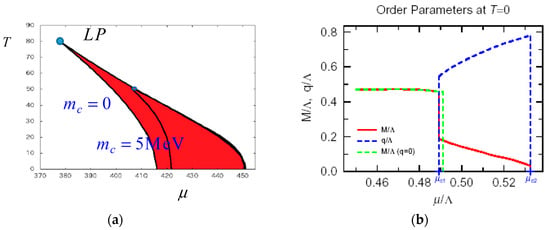
Figure 1.
(a) QCD phase diagram including the dual chiral density wave (DCDW) phase in the density–temperature plane from Karasawa and Tatsumi [14]. The triple point LP is called the Lifshitz point, where the spontaneously symmetry-broken (SSB) phase, the QGP phase, and iCP coexist. (b) Density dependence of the order parameters in the unit of the cut-off parameter , from Nakano and Tatsumi [3]. The dynamical mass in the usual chiral transition is also depicted by . Here we take .
Shown that the DCDW phase is always favored by the nesting effect at one plus one dimensions [15,16]. We also anticipate that the appearance of the phase with spatially modulating order should be a rather universal phenomenon during the phase transitions both described by the uniform order parameter such as FFLO state in the context of superconductivity [17,18].
2.2. Similarity with Weyl Semimetal
The energy spectrum for has a gap between positive and negative energies in momentum space. On the other hand, the energy spectrum for exhibits an interesting behavior, depending on the values of and ; for there is an energy gap, while there is no energy gap at the points, , with for the opposite case, . These points are called Weyl points in condensed-matter physics and the quasi-particle excitations can be expressed by the use of the Weyl Hamiltonian around these points. The latter case is actually realized in the DCDW phase. In Figure 2, we sketch the energy surface for and .
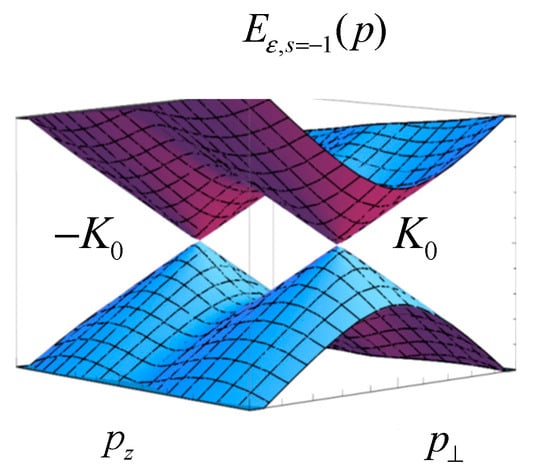
Figure 2.
Schematic view of the energy surface of the quasi-particles with in the momentum space. The Weyl points are located at on the axis, around which the excitations of the quasi-particles are described by the Weyl Hamiltonian.
Here we point out a similarity to Weyl semimetal. WSM is one of the topological materials and can be modeled by the Dirac type Hamiltonian [9],
where denotes the Bloch momentum, and is the spin–orbit coupling strength. The parameter in the CPT-violating term controls the spin-splitting due to magnetic impurities doped in the materials. Thus, one may immediately notice that Hamiltonian Equation (8) has the same structure as Equation (6) for the DCDW case; corresponds to . Some remarks are in order here: first, the parameter m can take without any inconsistency, in highly contrast to the DCDW phase, where implies no phase transition. Secondly, only the negative energy states (valence band) are occupied in WSM, while some Fermi sea (conduction band) is formed in the DCDW phase. Thirdly, there is a boundary in the WSM.
This is a new encounter of nuclear physics and condensed-matter physics in the context of compact stars. One may extract some hints or suggestions to transport properties in dense quark matter by way of studies of topological materials such as WSM.
3. Anomalous Hall Effect in iCP
3.1. Hall Conductivity
Once we notice similarities with WSM, what can we learn about the DCDW phase? We, hereafter, examine the possible anomalous Hall effect in the DCDW phase. When magnetic field is applied, off-diagonal resistivity is generally expressed as with magnetization . The first term is a usual one representing the Hall effect, while the second term implies that the Hall effect occurs without any magnetic field. Such an effect is called the anomalous Hall effect [9,10]. AHE provides firm experimental evidence of WSM [9]. It may affect the transport properties through modification of the Maxwell equations [19,20]. Its phenomenological implications should also be interesting for compact stars. In the following, we would like to demonstrate AHE in the DCDW phase, as in WSM. We shall see that the intrinsic contribution to AHE can be regarded as an “unquantized” version of the quantum Hall effect.
We can derive the Hall coefficient by way of the Kubo formula, considering a linear response to a tiny electric field [21]. For translational invariant systems, the Hall conductivity renders
where is the Berry curvature in the momentum space, defined by the Berry connection , . Note that the factor comes from the cancellation due to the different directions of the wave vector for u and d quarks. Once the eigenfunctions are known for any Hamiltonian , the Berry connection renders
When Equation (9) is further rewritten as
where is the Fermi-Dirac distribution function, we find that the formula in the parenthesis is the TKNN formula of 2D quantum Hall systems [22], where the Hall conductivity can be written as a momentum integral over the Brillouin zone,
where n denotes the band number and the integer is the first Chern number.
3.2. AHE in the DCDW Phase
Since the eigenenergy and eigenfunction are already obtained, it is straightforward to evaluate the Berry curvature in the DCDW phase. Then its z-component renders
where [20]. For , there appear two Weyl points at , and we can easily see that resembles the magnetic field produced by the Dirac monopole and antimonopole sitting at the Weyl points; indeed we can see that Equation (14) takes the approximate form, with around each Weyl point, .
Then, the contribution to the Hall conductivity from the Dirac sea can be evaluated as
The integral apparently diverges and depends on the cut-off scheme [23,24]. It is a subtle point; we must impose a physical condition to fix the finite term, which may be regarded as a kind of renormalization condition. The relevant condition for the DCDW phase is as , because AHE should vanish at the normal quark matter. This is achieved by using the gauge invariant regularizations such as the proper-time method or the heat-kernel method. Here, we apply the proper-time regularization (Figure 3 illustrates how the integral along axis works),
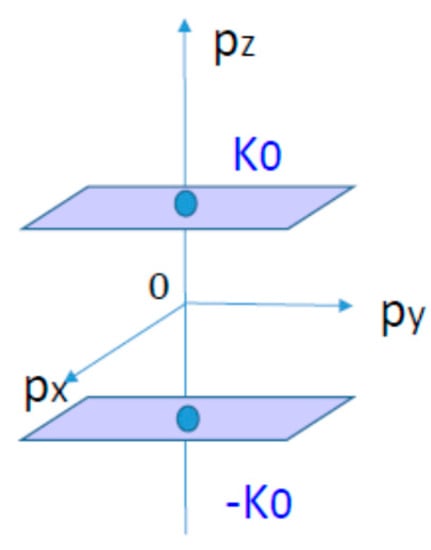
Figure 3.
Integral along the axis. The function changes its sign at the Weyl points for , while it is constant for .
The second term is evaluated to give , while the first term gives,
One may find this is related to the topological quantity by rewriting it as
where the quantity is nothing else but the Hall conductivity for 2D quantum Hall systems with the Chern number . Thus, we can regard the DCDW phase as a stack of 2D quantum Hall systems to the 3rd direction [21]. Eventually, we find
where we can easily check as , as it should be. Accordingly, the anomalous Hall current can be represented in the form . It is to be noted that this expression is somewhat different for the one for Weyl semimetal, where the contribution from the valence band reads . This is because AHE is possible there even if .
4. Transport Properties in the Presence of the Magnetic Field
4.1. Hall Conductivity
The effective Hamiltonian for quasi-particles in the DCDW phase is given as
where (), in the presence of the magnetic field. Since it has been shown that is the most favorable configuration [25], we set magnetic field along z-axis without loss of generality. Then, the Kubo formula gives the formula of the Hall conductivity [26],
where the Green functions are defined by , and the current operator is given by . Note that the TKNN formula is no longer useful in this case. Furthermore, we must carefully take into account the effect of an axial anomaly in the presence of the magnetic field. We then use the different approach from the previous section [27].
Streda has further rewritten Equation (21) into the following form [28],
where the first term corresponds to the classical Drude-Zener result,
at , and the second term can be expressed by the use of the number of state for each flavor to represent the quantum effect,
The number of states below the energy is defined by
where means no summation in the flavor space. It consists of the contribution of the Dirac sea and that of the Fermi sea . In the usual case, the first term gives no contribution and only the second term gives rise to the Hall conductivity. On the other hand, anomalous Hall conductivity just comes from the first term, when it is non-vanishing. We would like to demonstrate it.
4.2. Spectral Asymmetry and AHE
The effective Hamiltonian can be easily diagonalized [24] to give for each flavor ,
where denotes the particle–antiparticle states, and specifies the spin degree of freedom (See Figure 4). Note that there is no spin degree of freedom for the lowest Landau level (LLL); there occurs dimensional reduction for LLL and the eigenspinor is represented by two components.
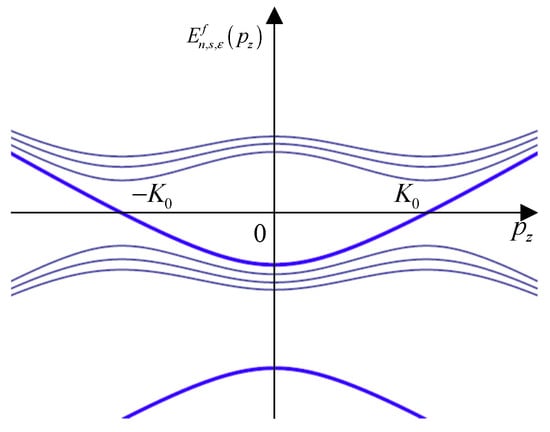
Figure 4.
Energy spectra as functions of . Thick lines denote the lowest Landau level (LLL).
One may immediately notice that the energy spectrum exhibits a peculiar feature: the spectrum for higher Landau levels with is symmetric with respect to the level line, while that of the LLL is asymmetric. Such spectral asymmetry of the LLL gives rise to an interesting consequence. It has been shown [29] that such spectral asymmetry has a topological origin and is related to axial anomaly. Consequently, it gives anomalous baryon number in the DCDW phase and spreads the DCDW phase in the wide region in the QCD phase diagram in the presence of the magnetic field [25]. More interestingly, axial anomaly induces spontaneous magnetization in the DCDW phase [30], which in turn induces anomalous Hall current.
Writing the baryon number operator in the normal ordering form, ( or ), we find by counting the number of the eigenstates below energy . The first term is the usual one and can be written as at . The quasi-particle density of states for the DCDW phase can be written as
Thereby reads
Thus, the contribution to the conductivity from the Fermi sea can be written as
The second term can be written as
We can see that it comes from the spectral asymmetry; it can also be represented in terms of the invariant introduced by Atiyah–Patodi–Singer [31], . The expression, Equation (30), is not well-defined as it is, and must be properly regularized to extract the physical result. Using Equation (26) and the following gauge-invariant regularization, we can evaluate the invariant [29] for each flavor.
Accordingly, the anomalous Hall conductivity can be given as
where . This is the same result as the previous one, Equation (19), as it should be, but it is interesting to see the different manifestation of the topological effect in two calculations; one is given by the Berry curvature and Dirac monopole at the Weyl points, and the other by spectral asymmetry. It is to be noted again that our result is different from the one for WSM; some authors have obtained the different result [32]:
where by using the momentum cut-off regularization for WSM. However, as is already mentioned, the invariant is given by the energy eigenstates, and gauge invariant regularizations must be used to obtain the relevant result.
It may be worth noting that for the quantized Hall effect in 2D Hall systems, with n being the number of bands [28]. On the other hand, in 3D Dirac materials with , and the whole contribution comes from with being the electron number [13], provided that the effect of impurities can be neglected.
5. Summary and Concluding Remarks
We have discussed some topological aspects of the transport properties in the DCDW phase, in relation to WSM. Anomalous Hall conductivity is derived in two ways, using the Kubo formula. We have seen two different manifestations of the topological effect; one comes from the magnetic monopoles sitting at the Weyl points in the momentum space, and the other from the spectral asymmetry.
We have seen that the result of the anomalous Hall conductivity is different between our case and Weyl semimetal. The reason is unclear, but the boundary effect should probably be taken into account to understand this difference.
Many subjects are left for further consideration. First of all, we must clarify the boundary effect for the anomalous Hall effect. At the same time, we must clarify the role of axial anomaly in the presence of the magnetic field, since it should be closely related to the spectral asymmetry.
The interplay of the usual Hall effect and AHE in the magnetic field is an interesting and important subject, not only theoretically but also phenomenologically for compact stars, especially for magnetars.
It is interesting to extend the current framework to involve the CPT odd term, . Then, we can incorporate the chiral magnetic effect [33], where plays a role of chiral chemical potential . It should also be interesting to study quantum phase transition between two cases, and , from the literature [34].
The effect of the tiny but finite current mass must be elucidated beyond the chiral limit. It may be a rather hard task, since there have been no analytical solutions yet. It may become important near the phase boundary, especially around the Lifshitz point at finite temperature (see Figure 1). On the other hand, one can expect that the effect is small in the well-developed phase at low-temperature. This subject will be left for future exploration.
Since the electrical current and the thermal current are related to each other, one may discuss thermal conductivity using the Wiedemann–Franz law at low-temperature. It well holds for electrons in metals, but the deviations from the Wiedemann–Franz law are sometimes observed, e.g., in QCD matter [35], where fluctuations play the important roles. Therefore, we must carefully discuss thermal conductivity. We expect that the Wiedemann–Franz law well holds for anomalous Hall conductivity in the DCDW phase, at least in the well-developed phase, where mean-field approximation should work well. This subject will be discussed elsewhere.
Author Contributions
T.T. designed the program of whole study, and wrote initial draft of manuscript. H.A. contributed in giving an interpretation to the Hall conductivity, and assisted in the presentation of manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
JSPS KAKENHI Grant Number JP19K03868.
Acknowledgments
One of the authors (T.T.) thanks the organizers for their hospitality during the conference “The Modern Physics of Compact Stars and Relativistic Gravity 2019”. The work of H.A. was supported by JSPS KAKENHI Grant Number JP19K03868.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Friman, B.; Hoehne, C.; Knoll, J.; Leupold, S.; Randrup, J.; Rapp, R. The CBM Physics book. Lect. Notes Phys. 2011, 814, 1. [Google Scholar]
- De Forcrand, P. Simulating QCD at finite density. PoS LAT 2009, 2009, 010. [Google Scholar]
- Nakano, E.; Tatsumi, T. Chiral symmetry and density waves in quark matter. Phys. Rev. 2005, D71, 114006. [Google Scholar] [CrossRef]
- Nickel, D. How manty phases meet at the chiral critical point? Phys. Rev. Lett. 2009, 103, 072301. [Google Scholar] [CrossRef]
- Nickel, D. Inhomogeneous phases in the Nambu-Jona-Lasinio and quark-meson model. Phys. Rev. 2009, D80, 074025. [Google Scholar] [CrossRef]
- Buballa, M.; Carignano, S. Inhomogeneous chiral condensates. Prog. Part. Nucl. Phys. 2015, 81, 39. [Google Scholar] [CrossRef]
- Tatsumi, T. Inhomogeneous Chiral Phase in Quark Matter. JPS Conf. Proc. 2018, 20, 011008. [Google Scholar]
- Abuki, H. Chiral crystallization in an external magnetic background: Chiral spiral versus real kink crystal. Phys. Rev. 2018, D98, 054006. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Pons, J.A.; Page, D. Neutron Stars-Cooling and Transport. Space Sci. Rev. 2015, 191, 239. [Google Scholar] [CrossRef]
- Konye, V.; Ogata, M. Magnetoresistance of a three-dimensional Dirac gas. Phys. Rev. 2018, B98, 195420. [Google Scholar] [CrossRef]
- Karasawa, S.; Tatsumi, T. Variational approach to the inhomogeneous chiral phase in quark matter. Phys. Rev. 2015, D92, 116004. [Google Scholar] [CrossRef]
- Baser, G.; Dunne, G.V. Twisted kink crystal in the chiral Gross-Neveu model. Phys. Rev. 2008, D78, 065002. [Google Scholar]
- Basar, G.; Dunne, G.V.; Thies, M. Inhomogeneous condensates in the thermodynamics of the chiral NJL2 model. Phys. Rev. 2009, D79, 105012. [Google Scholar]
- Fulde, P.; Ferrel, R.A. Superconductivity in a strong spin-exchange field. Phys. Rev. 1964, 135, A550. [Google Scholar] [CrossRef]
- Larkin, A.L.; Ovchinnikov, Y.N. Inhomogeneous state of supercomductors. Sov. Phys. JETP 1965, 20, 762. [Google Scholar]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799. [Google Scholar] [CrossRef]
- Ferrer, E.J.; de la Incera, V. Dissipationless Hall current in dense quark matter in a magnetic field. Phys. Lett. 2017, B769, 208. [Google Scholar] [CrossRef]
- Tatsumi, T.; Yoshiike, R.; Kashiwa, K. Anomalous Hall effect in dense QCD matter. Phys. Lett. 2018, B785, 46. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantised Hall Conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
- Grushin, A.G. Consequences of a condensed matter realization of Lorentz-violating QED in Weyl semi-metals. Phys. Rev. 2012, D86, 045001. [Google Scholar] [CrossRef]
- Goswani, P.; Tewari, S. Axionic field theory of (3+1)-dimensional Weyl semimetals. Phys. Rev. 2013, B88, 245107. [Google Scholar] [CrossRef]
- Frolov, I.E.; Zhukivsky, V.C.; Klimenko, G.K. Chiral density waves in quark matter within the Nambu-Jona-Lasinio model in an external magnetic field. Phys. Rev. 2010, D82, 076002. [Google Scholar] [CrossRef]
- Bastin, A.; Lewiner, C.; Betbeder-Matibet, O.; Nozieres, P. Quantum oscillations of the Hall effect of a Fermion gas with random impurity scattering. J. Phys. Chem, Solids 1971, 32, 1811. [Google Scholar] [CrossRef]
- Tatsumi, T.; Abuki, H. Hall effect in the inhomogeneous chiral phase. 2020. (in preparation). [Google Scholar]
- Streda, P. Theory of quantized Hall conductivity in two dimensions. J. Phys. 1982, C15, L717. [Google Scholar]
- Tatsumi, T.; Nishiyama, K.; Karasawa, S. Novel Lifshitz point for chiral transition in the magnetic field. Phys. Lett. 2015, B743, 66. [Google Scholar] [CrossRef]
- Yoshiike, R.; Nishiyama, K.; Tatsumi, T. Spontaneous magnetization of quark matter in the inhomogeneous chiral phase. Phys. Lett. 2015, B751, 123. [Google Scholar] [CrossRef][Green Version]
- Niemi, A.J.; Semenoff, G.W. Fermion number fractionization in quantum field theory. Phys. Rept. 1986, 135, 99. [Google Scholar] [CrossRef]
- Zyuzin, A.A.; Burkov, A.A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. 2012, B86, 115133. [Google Scholar] [CrossRef]
- Fukushima, K.; Khazrzeev, D.E.; Warringa, H.J. Chiral magnetic effect. Phys. Rev. 2008, D78, 074033. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Volovik, G.E. Emergent CPT violation from the splitting of Fermi points. Int. J. Mod. Phys. 2005, A20, 2795. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Rischke, D.H.; Sedrakian, A. Transport coefficients of two-flavor quark matter from the Kubo formalism. Phys. Rev. 2017, D95, 114021. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).