On Graph-Orthogonal Arrays by Mutually Orthogonal Graph Squares

Abstract

During the last two centuries, after the question asked by Euler concerning mutually orthogonal Latin squares (MOLS), essential advances have been made. MOLS are considered as a construction tool for orthogonal arrays. Although Latin squares have numerous helpful properties, for some factual applications these structures are excessively prohibitive. The more general concepts of graph squares and mutually orthogonal graph squares (MOGS) offer more flexibility. MOGS generalize MOLS in an interesting way. As such, the topic is attractive. Orthogonal arrays are essential in statistics and are related to finite fields, geometry, combinatorics and error-correcting codes. Furthermore, they are used in cryptography and computer science. In this paper, our current efforts have concentrated on the definition of the graph-orthogonal arrays and on proving that if there are $k$ MOGS of order $n$, then there is a graph-orthogonal array, and we denote this array by $G$-$OA\left(n^2,k,n,2\right).$In addition, several new results for the orthogonal arrays obtained from the MOGS are given. Furthermore, we introduce a recursive construction method for constructing the graph-orthogonal arrays.

1. Introduction

A graph is a couple $G=\left(U,E\right)$, where $U$ is a set of vertices and $E$ is a set of edges, and $E\subseteq U\times U$. The two ends of an edge are called two adjacent vertices. The set of pairwise non-adjacent vertices is called an independent set. A graph $G$ is called simple if it has no loops and multiple edges. Several research papers of graph theory concerning the study of simple graphs have been produced [1].

Definition 1.

Let$m$and$n$be positive integers. A complete bipartite graph on$\left(m,n\right)$vertices, denoted by$K_{m,n},$is a simple graph with distinct vertices$v_1,v_2,..,v_m$and$w_1,w_2,..,w_n$that satisfies the following properties: For all$i,k=1,2,..,m$, and for all$j,l=1,2,..,n,$

1. 

There exists an edge from each vertex$v_i$to each vertex$w_j$.

2. 

There is no edge from any vertex$v_i$to any other vertex$v_k$.

3. 

There is no edge from any vertex$w_j$to any other vertex$w_l$.

Definition 2.

The complete bipartite graphs$K_{3,2}$and$K_{3,3}$are illustrated in Figure 1.

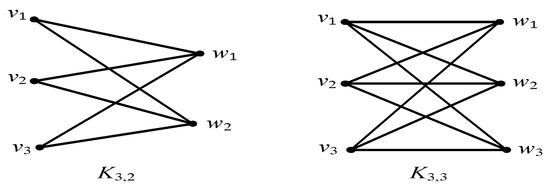
Figure 1. The complete bipartite graphs $K_{3,2}$ and $K_{3,3}.$

Bipartite graphs assume conspicuous functions in graph theory [2]. For instance, bipartite graphs are very helpful for studying problems of matching, such as job matching problem. Furthermore, bipartite graphs have very essential roles in theoretical consideration. For example, bipartite graphs can be used to describe the multipartite graphs [3].

A Latin square with order $n$ is an $n\times n$ matrix whose entries are taken from a set $A$ with $\left|A\right|=n$, where all elements of $A$ appear precisely one time in each row and each column. A pair of Latin squares with order $n$ are called orthogonal to each other if when one is overlaid on the other the ordered pairs ($i,j$) of corresponding entries contain all possible $n^2$ pairs, $A\times A$. A family of $k$ Latin squares of order $n$ (any two of them being orthogonal) is said to be a set of mutually orthogonal Latin squares (MOLS). The applications of MOLS are common, famous, and can be studied in many textbooks (see Laywine et al., [4] as an example). The reader can see [5], for a brief review of MOLS constructions.

Assume that $G$is a subgraph of $K_{n,n}$ with size $n$ (number of its edges). A square matrix $L$of order $n$is called a $G$-square if each element in ${\mathbb{Z}}_n$appears precisely $n$times, and all graphs $G_i$where $E\left(G_i\right)=\left\{\left(x,y\right):L\left(x,y\right)=i,i\in {\mathbb{Z}}_n\right\}$ are isomorphic to $G.$The index set for the rows and columns of $L$ is the group ${\mathbb{Z}}_n$. The two graph squares have the property that, when superimposed, every ordered pair occurs exactly once. Thus the squares are orthogonal. A set of graph squares $L_1,L_2,\dots ,L_k$ is pairwise orthogonal, or a collection of MOGS, if $L_i$ and $L_j$ are orthogonal for each $1\le i<j\le k$. For a survey of MOGS, see [6,7,8,9,10,11].

Hereafter, we will need the Kronecker product of the graph squares. As such, assume that $A$ is a graph square of order $m$ and that $B$ is a graph square of order $n$. Let us indicate the entry at row $i$ and column $j$ of $A$ by $a_{ij}.$ In the same way, we indicate the $\left(i,j\right)$ entry of $B$ by $b_{ij}.$ Hence the Kronecker type product of $A$ and $B$ is the $mn\times mn$ square $A\otimes B,$ presented by

$$A\otimes B=\left[\begin{array}{llll}\left(a_{11},B\right)\hfill & \left(a_{12},B\right)\hfill & \dots \hfill & \left(a_{1m},B\right)\hfill \\ \left(a_{21},B\right)\hfill & \left(a_{22},B\right)\hfill & \dots \hfill & \left(a_{2m},B\right)\hfill \\ ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill \\ \left(a_{m1},B\right)\hfill & \left(a_{m2},B\right)\hfill & \dots \hfill & \left(a_{mm},B\right)\hfill \end{array}\right]$$

Such that each entry $a$ of $A,\left(a,B\right)$ is the $n\times n$ matrix

$$\left(a,B\right)=\left[\begin{array}{llll}\left(a,b_{11}\right)\hfill & \left(a,b_{12}\right)\hfill & \dots \hfill & \left(a,b_{1n}\right)\hfill \\ \left(a,b_{21}\right)\hfill & \left(a,b_{22}\right)\hfill & \dots \hfill & \left(a,b_{2n}\right)\hfill \\ ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill \\ \left(a,b_{n1}\right)\hfill & \left(a,b_{n2}\right)\hfill & \dots \hfill & \left(a,b_{nn}\right)\hfill \end{array}\right]$$

For clearing this Kronecker type product structure, for $m=2,n=3,$ assume

$$A=\left[\begin{array}{ll}0\hfill & 0\hfill \\ 1\hfill & 1\hfill \end{array}\right],B=\left[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 1\hfill & 1\hfill \\ 2\hfill & 2\hfill & 2\hfill \end{array}\right]$$

Then, the Kronecker product’s construction gives the ensuing 6 × 6 matrix, whose entries are ordered pairs

$$A\otimes B=\left[\begin{array}{llllll}00\hfill & 00\hfill & 00\hfill & 00\hfill & 00\hfill & 00\hfill \\ 01\hfill & 01\hfill & 01\hfill & 01\hfill & 01\hfill & 01\hfill \\ 02\hfill & 02\hfill & 02\hfill & 02\hfill & 02\hfill & 02\hfill \\ 10\hfill & 10\hfill & 10\hfill & 10\hfill & 10\hfill & 10\hfill \\ 11\hfill & 11\hfill & 11\hfill & 11\hfill & 11\hfill & 11\hfill \\ 12\hfill & 12\hfill & 12\hfill & 12\hfill & 12\hfill & 12\hfill \end{array}\right]$$

Orthogonal arrays are essential in statistics where they are basically utilized in experimental design, hence they are immensely important in medicine, manufacturing and agriculture. The applications of orthogonal arrays in the statistical design of experiments are common, well-known, and can be studied from many textbooks (for instance, see Hedayat et al., [12]). Furthermore, they are used in cryptography and computer science. Officially, an orthogonal array can be characterized as follows.

Definition 3.

$($[12]$).$An$N\times k$matrix$A$whose entries are taken from$S$is called an orthogonal array with$s$levels, strength$t$and index$\lambda$$($for some$t$in the range$0\le t$$\le k)$if all$N\times t$subarrays of$A$containing each$t$-tuple rely on$S$precisely$\lambda$times in a row. The integers$N, k,s,t$and$\lambda$are considered the parameters of the orthogonal array which will be symbolized by$OA\left(N,k,s,t\right).$The orthogonal arrays with index unity$\left(\lambda =1\right)$are concerned here.

Example 1.

The following array is an orthogonal array relying on two levels ($s$= 2, i.e., all the elements in the array take only two values, 0 or 1), with a strength of three, of index unity, with eight runs and with four factors (variables). In an orthogonal array with a strength of three (with two levels), by taking any three column we will find each of the eight possibilities 000, 010, 001, 011, 101, 100, 110 and 111 equally as often.

$$OA\left(8,4,2,3\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 1& 1\\ 0& 1& 0& 1\\ 0& 1& 1& 0\\ 1& 0& 0& 1\\ 1& 0& 1& 0\\ 1& 1& 0& 0\\ 1& 1& 1& 1\end{array}\right]$$

A few creators like to speak of an orthogonal array as a $k\times N$ array rather than an $N\times k$ array. This saves the number of lines. The transposed array will be shown in our illustrations to save lines. Certain orthogonal arrays can be utilized to build MOLS, and conversely MOLS give a tool for building orthogonal arrays. Although Latin squares have numerous valuable properties, for some measurable applications these structures are excessively restrictive. The broader ideas of graph squares and MOGS offer greater adaptability. As such, MOGS likewise give an apparatus for building orthogonal arrays. This latter aspect is what concerns us in this paper.

The remaining part of the work is arranged as follows: Graph-orthogonal arrays by mutually orthogonal graph squares are given in Section 2. Recursive constructions of the graph-orthogonal arrays are presented in Section 3. For illustration, the applications of the graph-orthogonal arrays in the design of experiments are shown in Section 4. Finally, the conclusion is given in Section 5.

2. Graph-Orthogonal Arrays by Mutually Orthogonal Graph Squares

Many results of Latin squares can be stated in terms of transversal designs, defined as follows: A transversal design with $u$ groups of size $v$ and index $w,$ denoted by $T\left[u,w;v\right]$, is a triple $\left(Y,H,A\right)$, where

• $Y$ is a set of $uv$ elements;
• $H=\left\{H_1,\dots ,H_u\right\}$ is a family of $u,$ $v$-sets or groups which form a partition of $Y$;
• $A$ is a family of $u$-sets or blocks of elements so that each $u$-set in $A$ intersects each group $H_i$ in exactly one element, and any pair of elements from different groups occurs together in exactly $w$ blocks in $A.$

The partition of a set $Y$ is a collection of disjointed subsets of $Y$ whose union is $Y$. The disjoint means that for any two distinct subsets $Y_i$ and $Y_j,$ we find that $Y_i{{\displaystyle \cap }}^{}{Y}_j=\phi .$

Example 2.

Table 1shows the groups and blocks of a$T\left[4,1;3\right]$transversal design.

Table 1. The groups and blocks of a $T\left[4,1;3\right]$ transversal design.

	$A_1:y_{11}{y}_{21}{y}_{31}{y}_{41}$
	$A_2:y_{11}{y}_{22}{y}_{32}{y}_{42}$
$H_1:y_{11}{y}_{12}{y}_{13}$	$A_3:y_{11}{y}_{23}{y}_{33}{y}_{43}$
$H_2:y_{21}{y}_{22}{y}_{23}$	$A_4:y_{12}{y}_{21}{y}_{32}{y}_{43}$
$H_3:y_{31}{y}_{32}{y}_{33}$	$A_5:y_{12}{y}_{22}{y}_{33}{y}_{41}$
$H_4:y_{41}{y}_{42}{y}_{43}$	$A_6:y_{12}{y}_{23}{y}_{31}{y}_{42}$
	$A_7:y_{13}{y}_{21}{y}_{33}{y}_{42}$
	$A_8:y_{13}{y}_{22}{y}_{31}{y}_{43}$
	$A_9:y_{13}{y}_{23}{y}_{32}{y}_{41}$

Theorem 1.

([4]). The existence of a $T\left[u,1;v\right]$ transversal design is equivalent to the existence of a set of $u-2$ MOLS of order $v.$

Example 3.

The transversal design$T\left[4,1;3\right]$ given in Example 2 can be used to give a better illustration of Theorem 1 by constructing a pair of MOLS, $L_1$and$L_2$, of order three. For more illustration, the symbols in cell (1, 1) of the Latin squares will be determined. Consider the elements $y_{31},y_{41}$of the design. They are together in block$A_1,$with the elements$y_{11},y_{21}.$As such, the element in cell (1,1) of$L_1$is 1, while that of$L_2$is 1.Table 2 illustrates the construction and the Latin squares$L_1$and$L_2.$

Table 2. The construction and the Latin squares $L_1$ and $L_2$ for Example 3.

Position	Coordinate Elements	Elements Determining Entries	Arrays
1, 1	$y_{31},y_{41}\in A_1$	with $y_{11},y_{21}$	$L_1=\left[\begin{array}{ccc}1& 2& 3\\ 3& 1& 2\\ 2& 3& 1\end{array}\right],L_2=\left[\begin{array}{ccc}1& 3& 2\\ 3& 2& 1\\ 2& 1& 3\end{array}\right]$
1, 2	$y_{31},y_{42}\in A_6$	with $y_{12},y_{23}$
1, 3	$y_{31},y_{43}\in A_8$	with $y_{13},y_{22}$
2, 1	$y_{32},y_{41}\in A_9$	with $y_{13},y_{23}$
2, 2	$y_{32},y_{42}\in A_2$	with $y_{11},y_{22}$
2, 3	$y_{32},y_{43}\in A_4$	with $y_{12},y_{21}$
3, 1	$y_{33},y_{41}\in A_5$	with $y_{12},y_{22}$
3, 2	$y_{33},y_{42}\in A_7$	with $y_{13},y_{21}$
3, 3	$y_{33},y_{43}\in A_3$	with $y_{11},y_{23}$

Note that $L_1$and $L_2$ can be written as follows after calculating the entries modulo 3.

$$L_1=\left[\begin{array}{ccc}1& 2& 0\\ 0& 1& 2\\ 2& 0& 1\end{array}\right],L_2=\left[\begin{array}{ccc}1& 0& 2\\ 0& 2& 1\\ 2& 1& 0\end{array}\right].$$

It is easy to check that an $OA\left[v^2,u,v,2\right]$ orthogonal array has a $T\left[u,1;v\right]$ transversal design, and vice versa. The preceding is summarized by the following.

Theorem 2.

([4]). The following are equivalent:

1. 

$u-2$MOLS of order$v$;

2. 

a$T\left[u,1;v\right]$ transversal design;

3. 

an$OA\left[v^2,u,v,2\right]$ orthogonal array.

Example 4.

The following array (from Theorem 2 and the two MOLS of order three given in Example 3) gives an example of an orthogonal array$OA\left[9,4,3,2\right].$ The transpose of this array is as follows, where the first two rows represent the position after calculating its elements modulo 3.

$$\left[\begin{array}{ccccccccc}0& 0& 0& 1& 1& 1& 2& 2& 2\\ 0& 1& 2& 0& 1& 2& 0& 1& 2\\ 1& 2& 0& 0& 1& 2& 2& 0& 1\\ 1& 0& 2& 0& 2& 1& 2& 1& 0\end{array}\right]$$

Note that after obtaining the orthogonal array from the MOLS, we can add additional two rows (the first and the second rows). These two rows represent the position of the cells in the MOLS.

As such, it is easy to check that an $OA\left[v^2,u,v,2\right]$ orthogonal array is a $T\left[u,1;v\right]$ transversal design, and vice versa.

Definition 4.

If we have$k$mutually orthogonal$n\times n$$G$-squares, then by converting these squares to an$n^2\times 1$array by juxtaposing the$n$rows of the square and transposing, we get the graph-orthogonal array$G$-$OA\left(n^2,k,n,2\right)$by combining these arrays to form an$n^2\times k$array.

In this section, we prove that if there are $k$ mutually orthogonal $G$-squares of order $n$, then there is a $G$-$OA\left(n^2,k,n,2\right)$ $($Proposition 1$).\mathrm{Furthermore}$, there are some new results for the orthogonal arrays as directly applied to Proposition 1.

Proposition 1.

The existence of$k$mutually orthogonal$n\times n$$G$-squares based on$n$symbols implies the existence of an$G$-orthogonal array$G$-$OA\left(n^2,k,n,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $k$ mutually orthogonal $n\times n$ $G$-squares to an $n^2\times 1$ array by juxtaposing the $n$ rows of the $G$-square and transposing. Then, these arrays are combined to construct an $n^2\times k$ array. Since there are $k$ mutually orthogonal $G$-squares based on $n$ symbols, the number of the levels equals $n.\mathrm{Furthermore}$, since the $k$ $G$-squares are mutually orthogonal, then the superimposition of any two columns of the $n^2\times k$ array gives ${\mathbb{Z}}_n\times {\mathbb{Z}}_n,$ $i.e.$, the $n^2\times k$ array has strength two. □

Example 5.

We have the three mutually orthogonal$4K_2$-squares$M_0, M_1,$and$M_2$; see [12]$.$Then$,$we obtain the array$4K_2$-$OA\left(16,3,4,2\right),$this array can be represented by the$ℳ$, where${ℳ}^T$is the transpose of$ℳ.$

$$M_0=\left[\begin{array}{llll}0\hfill & 3\hfill & 1\hfill & 2\hfill \\ 1\hfill & 2\hfill & 0\hfill & 3\hfill \\ 2\hfill & 1\hfill & 3\hfill & 0\hfill \\ 3\hfill & 0\hfill & 2\hfill & 1\hfill \end{array}\right]M_1=\left[\begin{array}{llll}0\hfill & 2\hfill & 3\hfill & 1\hfill \\ 1\hfill & 3\hfill & 2\hfill & 0\hfill \\ 2\hfill & 0\hfill & 1\hfill & 3\hfill \\ 3\hfill & 1\hfill & 0\hfill & 2\hfill \end{array}\right]M_2=\left[\begin{array}{llll}0\hfill & 1\hfill & 2\hfill & 3\hfill \\ 1\hfill & 0\hfill & 3\hfill & 2\hfill \\ 2\hfill & 3\hfill & 0\hfill & 1\hfill \\ 3\hfill & 2\hfill & 1\hfill & 0\hfill \end{array}\right]$$

$${ℳ}^T=\left[\begin{array}{cccccccccccccccc}0& 3& 1& 2& 1& 2& 0& 3& 2& 1& 3& 0& 3& 0& 2& 1\\ 0& 2& 3& 1& 1& 3& 2& 0& 2& 0& 1& 3& 3& 1& 0& 2\\ 0& 1& 2& 3& 1& 0& 3& 2& 2& 3& 0& 1& 3& 2& 1& 0\end{array}\right]$$

All the following results are based on$\left(i\right)$Proposition 1 and$\left(ii\right)$the existence of MOGS for some classes of graphs that can be used as ingredients for obtaining new graph-orthogonal arrays.

Consider the addition is calculated modulo$n for the squares$of order$n.$See[11] for the ingredients from$I$to$IV.$These ingredients are as follows.

(I) 

The$n$mutually orthogonal$\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-squares are$M^s=\left(a_{ij}^s\right), a_{ij}^s=\alpha ,i=\beta ,j=\alpha +s\beta +{\beta }^2, n$is a prime$>2$and$s,\alpha ,\beta \in {\mathbb{Z}}_n$.

(II) 

The$\left(n-1\right)$mutually orthogonal$\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-squares are$M^s=\left(a_{ij}^s\right),$$a_{ij}^s=\left(s+1\right)i+j-c_i,s\in {\mathbb{Z}}_{n-1}, n is a prime>2,$and$c_i =\{\begin{array}{lll}1\hfill & if\hfill & i=1,\hfill \\ 0\hfill & \hfill & otherwise.\hfill \end{array}$

(III) 

If$n=9$, then$the three$mutually$orthogonal K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}$-$squares are$$M^s=\left(a_{ij}^s\right),s\in {\mathbb{Z}}_3,a_{ij}^s=\beta ,i=\alpha ,j={\alpha }^2+s\alpha +\beta ,$and$\alpha ,\beta \in {\mathbb{Z}}_9$.

(IV) 

I$f$$n=7$, then$the four$mutually$orthogonal 3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}$-$squares are M^s=\left(a_{ij}^s\right),s\in {\mathbb{Z}}_4, and i,j\in {\mathbb{Z}}_7,$let$\beta \in {\mathbb{Z}}_7$,then$a_{ij}^s=j,i=0,j\in {\mathbb{Z}}_7, a_{ij}^s=\beta ,i=1,$$j=2+\beta +s, a_{ij}^s=\beta ,i=2,j=4+\beta +2s, a_{ij}^s=\beta ,i=3,j=6+\beta +3s, a_{ij}^s=\beta ,i=4, j=1+\beta +4s, a_{ij}^s=\beta ,i=5,j=4+\beta +5s, a_{ij}^s=\beta ,i=6,j=6+\beta +6s.$

(V) 

The$n$mutually orthogonal$P_{n+1}$-squares are$M^s=\left(a_{ij}^s\right), a_{ij}^s=\alpha ,i=\alpha +s\beta -{\beta }^2,j=\alpha +\left(s+1\right)\beta -{\beta }^2,\alpha ,\beta ,s\in {\mathbb{Z}}_n$where$n$is a prime greater than$2$; see [9].

Theorem 3.

The existence of$n$mutually orthogonal$\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-squares based on$n$symbols implies the existence of a$\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-orthogonal array$\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-$OA\left(n^2,n,n,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $n$ mutually orthogonal $n\times n$ $\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-squares (Ingredient $I$) to an $n^2\times 1$ array by juxtaposing the $n$ rows of the $\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-square and transposing. Then, these arrays are combined to construct an $n^2\times n$ array. Since there are $n$ mutually orthogonal $\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-squares based on $n$ symbols, the number of the levels equals $n.\mathrm{Furthermore}$, since the $n$ $\left(K_{1,1}{{\displaystyle \cup }}^{}\frac{n-1}{2}{K}_{1,2}\right)$-squares are mutually orthogonal, the superimposition of any two columns of the $n^2\times n$ array gives ${\mathbb{Z}}_n\times {\mathbb{Z}}_n,$ $i.e.$, the $n^2\times n$ array has strength two. □

Theorem 4.

The existence of$\left(n-1\right)$mutually orthogonal$\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-squares based on$n$symbols implies the existence of an$\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-orthogonal array$\left(\left(n-2\right)K_{1,1}{K}_{1,2}\right)$-$OA\left(n^2, n-1,n,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $\left(n-1\right)$ mutually orthogonal $n\times n$ $\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-squares (Ingredient $II$) to an $n^2\times 1$ array by juxtaposing the $n$ rows of the $\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-square and transposing. Then, these arrays are combined to construct an $n^2\times \left(n-1\right)$ array. Since there are $\left(n-1\right)$ mutually orthogonal $\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-squares based on $n$ symbols, the number of the levels equals $n.\mathrm{Furthermore}$, since the $\left(n-1\right)$ $\left(\left(n-2\right)K_{1,1}{{\displaystyle \cup }}^{}{K}_{1,2}\right)$-squares are mutually orthogonal, the superimposition of any two columns of the $n^2\times \left(n-1\right)$ array gives ${\mathbb{Z}}_n\times {\mathbb{Z}}_n,$ $i.e.$, the $n^2\times \left(n-1\right)$ array has strength two. □

Lemma 1.

The existence of$three$mutually orthogonal$K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}$-squares based on$nine$symbols implies the existence of an$K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}$-orthogonal array$K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}$-$OA\left(81,3,9,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $\mathrm{three}$ mutually orthogonal $9\times 9$ $\left(K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}\right)$-squares (Ingredient $III$) into an $81\times 1$ array by juxtaposing the $\mathrm{nine}$ rows of the $\left(K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}\right)$-square and transposing. Then, these arrays are combined to construct an $81\times 3$ array. Since the $\mathrm{three}$ mutually orthogonal $K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2}$-squares are based on $\mathrm{nine}$ symbols, the number of the levels equals $\mathrm{nine}.\mathrm{Furthermore}$, since the $\mathrm{three}$ ($K_{1,3}{{\displaystyle \cup }}^{}3K_{1,2})$-squares are mutually orthogonal, then the superimposition of any two columns of $81\times 3$array gives ${\mathbb{Z}}_9\times {\mathbb{Z}}_9,$ $i.e.$, the $81\times 3$ array has strength two. □

Lemma 2.

The existence offour mutually orthogonal$3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}$-squares based on$seven$symbols implies the existence of an$3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}$-orthogonal array$3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}$-$OA\left(49,4,7,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $\mathrm{four}$ mutually orthogonal $7\times 7$ $\left(3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}\right)$-squares (Ingredient $IV$) to a $49\times 1$ array by juxtaposing the seven rows of the $\left(3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}\right)$-square and transposing. Then, these arrays are combined to construct an $49\times 3$ array. Since the $\mathrm{four}$ mutually orthogonal $3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2}$-squares are based on $\mathrm{seven}$ symbols, the number of the levels equals $\mathrm{seven}.\mathrm{Furthermore}$, since the $\mathrm{four}$ ($3K_{1,1}{{\displaystyle \cup }}^{}2K_{1,2})$-squares are mutually orthogonal, the superimposition of any two columns of the $49\times 4$array gives ${\mathbb{Z}}_7\times {\mathbb{Z}}_7,$ $i.e.,$ the $49\times 4$ array has strength two. □

Theorem 5.

The existence of$n$mutually orthogonal$P_{n+1}$-squares based on$n$symbols implies the existence of a$P_{n+1}$-orthogonal array$P_{n+1}$-$OA\left(n^2,n,n,2\right).$

Proof. 

The technique of the construction can be shown as follows. Convert each of the $n$ mutually orthogonal $n\times n$ $\left(P_{n+1}\right)$-squares (Ingredient $V$) into an $n^2\times 1$ array by juxtaposing the $n$ rows of the $\left(P_{n+1}\right)$-square and transposing. Then, these arrays are combined to construct an $n^2\times n$ array. Since the $n$ mutually orthogonal $P_{n+1}$-squares are based on $n$ symbols, the number of the levels equals $n.\mathrm{Furthermore}$, since the $n$ $\left(P_{n+1}\right)$-squares are mutually orthogonal, then the superimposition of any two columns of the $n^2\times n$ array gives ${\mathbb{Z}}_n\times {\mathbb{Z}}_n,$ $i.e.$, the $n^2\times n$ array has strength two. □

Lemma 3.

The existence ofthree mutually orthogonal$2K_{1,2}$-squares based on$four$symbols implies the existence of an$2K_{1,2}$-orthogonal array$2K_{1,2}$-$OA\left(16,3,4,2\right).$

Proof. 

We have $\mathrm{three}$ mutually orthogonal $2K_{1,2}$-squares; see [6]. The three mutually orthogonal $2K_{1,2}$-squares of order $4$ are defined as follows, where $\alpha ,\beta ,\gamma ,$and $\delta \in {\mathbb{Z}}_4,\alpha \ne \beta \ne \gamma \ne \delta .$

$$N_0=\left[\begin{array}{llll}\alpha \hfill & \delta \hfill & \gamma \hfill & \beta \hfill \\ \gamma \hfill & \beta \hfill & \alpha \hfill & \delta \hfill \\ \alpha \hfill & \delta \hfill & \gamma \hfill & \beta \hfill \\ \gamma \hfill & \beta \hfill & \alpha \hfill & \delta \hfill \end{array}\right]N_1=\left[\begin{array}{llll}\gamma \hfill & \delta \hfill & \alpha \hfill & \beta \hfill \\ \delta \hfill & \gamma \hfill & \beta \hfill & \alpha \hfill \\ \delta \hfill & \gamma \hfill & \beta \hfill & \alpha \hfill \\ \gamma \hfill & \delta \hfill & \alpha \hfill & \beta \hfill \end{array}\right]N_2=\left[\begin{array}{llll}\delta \hfill & \alpha \hfill & \beta \hfill & \gamma \hfill \\ \delta \hfill & \alpha \hfill & \beta \hfill & \gamma \hfill \\ \gamma \hfill & \beta \hfill & \alpha \hfill & \delta \hfill \\ \gamma \hfill & \beta \hfill & \alpha \hfill & \delta \hfill \end{array}\right]$$

Convert each of the $\mathrm{three}$ mutually orthogonal $4\times 4$ $2K_{1,2}$-squares into an $16\times 1$ array by juxtaposing the $\mathrm{four}$ rows of the $2K_{1,2}$-square and transposing. Then, these arrays are combined to construct a $16\times 3$ array, $\mathcal{N},$

$${\mathcal{N}}^T=\left[\begin{array}{cccccccccccccccc}\alpha & \delta & \gamma & \beta & \gamma & \beta & \alpha & \delta & \alpha & \delta & \gamma & \beta & \gamma & \beta & \alpha & \delta \\ \gamma & \delta & \alpha & \beta & \delta & \gamma & \beta & \alpha & \delta & \gamma & \beta & \alpha & \gamma & \delta & \alpha & \beta \\ \delta & \alpha & \beta & \gamma & \delta & \alpha & \beta & \gamma & \gamma & \beta & \alpha & \delta & \gamma & \beta & \alpha & \delta \end{array}\right]$$

Since the $\mathrm{three}$ mutually orthogonal $2K_{1,2}$-squares are based on $\mathrm{four}$ symbols, the number of levels equals $\mathrm{four}.\mathrm{Furthermore}$, since the three $2K_{1,2}$-squares are mutually orthogonal, the superimposition of any two columns of the $16\times 3$ array gives 16 different ordered pairs$,$ i.e., the $16\times 3$ array has strength two. □

Lemma 4.

The existence of$three$mutually orthogonal$C_4$-squares based on$four$symbols implies the existence of a$C_4$-orthogonal array$C_4$-$OA\left(16,3,4,2\right).$

Proof. 

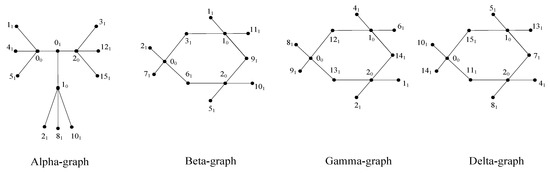
We have $\mathrm{three}$ mutually orthogonal $C_4$-squares; see [7]. The three mutually orthogonal $C_4$-squares of order $4$ are defined as follows, where $\alpha ,\beta ,\gamma ,$and $\delta \in {\mathbb{Z}}_4,\alpha \ne \beta \ne \gamma \ne \delta .$

$$P_0=\left[\begin{array}{llll}\alpha \hfill & \alpha \hfill & \beta \hfill & \beta \hfill \\ \alpha \hfill & \alpha \hfill & \beta \hfill & \beta \hfill \\ \gamma \hfill & \gamma \hfill & \delta \hfill & \delta \hfill \\ \gamma \hfill & \gamma \hfill & \delta \hfill & \delta \hfill \end{array}\right]P_1=\left[\begin{array}{llll}\alpha \hfill & \beta \hfill & \alpha \hfill & \beta \hfill \\ \gamma \hfill & \delta \hfill & \gamma \hfill & \delta \hfill \\ \alpha \hfill & \beta \hfill & \alpha \hfill & \beta \hfill \\ \gamma \hfill & \delta \hfill & \gamma \hfill & \delta \hfill \end{array}\right]P_2=\left[\begin{array}{llll}\alpha \hfill & \gamma \hfill & \gamma \hfill & \alpha \hfill \\ \delta \hfill & \beta \hfill & \beta \hfill & \delta \hfill \\ \delta \hfill & \beta \hfill & \beta \hfill & \delta \hfill \\ \alpha \hfill & \gamma \hfill & \gamma \hfill & \alpha \hfill \end{array}\right]$$

Convert each of the three mutually orthogonal 4 × 4 $C_4$-squares into a 16 × 1 array by juxtaposing the four rows of the $C_4$-square and transposing. Then, these arrays are combined to construct a 16 × 3 array, $𝒫$,

$${\mathcal{P}}^T=\left[\begin{array}{llllllllllllllll}\alpha \hfill & \alpha \hfill & \beta \hfill & \beta \hfill & \alpha \hfill & \alpha \hfill & \beta \hfill & \beta \hfill & \gamma \hfill & \gamma \hfill & \delta \hfill & \delta \hfill & \gamma \hfill & \gamma \hfill & \delta \hfill & \delta \hfill \\ \alpha \hfill & \beta \hfill & \alpha \hfill & \beta \hfill & \gamma \hfill & \delta \hfill & \gamma \hfill & \delta \hfill & \alpha \hfill & \beta \hfill & \alpha \hfill & \beta \hfill & \gamma \hfill & \delta \hfill & \gamma \hfill & \delta \hfill \\ \alpha \hfill & \gamma \hfill & \gamma \hfill & \alpha \hfill & \delta \hfill & \beta \hfill & \beta \hfill & \delta \hfill & \delta \hfill & \beta \hfill & \beta \hfill & \delta \hfill & \alpha \hfill & \gamma \hfill & \gamma \hfill & \alpha \hfill \end{array}\right]$$

Since the $\mathrm{three}$ mutually orthogonal $C_4$-squares are based on $\mathrm{four}$ symbols, the number of levels equals four$.\mathrm{Furthermore}$, since the three $C_4$-squares are mutually orthogonal, then the superimposition of any two columns of the $16\times 3$ array gives 16 different ordered pairs, i.e., the $16\times 3$ array has strength two. The $C_4$-$OA\left(16,3,4,2\right)$, $𝒫$^T, can be represented by the edge decomposition (as the graph squares), as shown in Figure 2. □

Figure 2. Edge decomposition of $K_{3,16}$ corresponding to $𝒫$^T.

In the following example, we convert the $G$-$OA\left(n^2,k,n,2\right)$ to $k$ mutually orthogonal $n\times n$ $G$-squares by reversing the technique in the proof of Proposition 1.

Example 6.

We have the array$ℒ=OA\left(25,3,5,2\right),$ where

$${ℒ}^T=\left[\begin{array}{ccccccccccccccccccccccccc}0& 0& 2& 4& 1& 2& 1& 1& 3& 0& 1& 3& 2& 2& 4& 0& 2& 4& 3& 3& 4& 1& 3& 0& 4\\ 0& 2& 1& 0& 4& 0& 1& 3& 2& 1& 2& 1& 2& 4& 3& 4& 3& 2& 3& 0& 1& 0& 4& 3& 4\\ 0& 1& 4& 2& 0& 1& 1& 2& 0& 3& 4& 2& 2& 3& 1& 2& 0& 3& 3& 4& 0& 3& 1& 4& 4\end{array}\right]$$

Now, we convert this array into three mutually orthogonal squares, $L_0, L_1,$ and $L_2.$

$$L_0=\left[\begin{array}{lllll}0\hfill & 0\hfill & 2\hfill & 4\hfill & 1\hfill \\ 2\hfill & 1\hfill & 1\hfill & 3\hfill & 0\hfill \\ 1\hfill & 3\hfill & 2\hfill & 2\hfill & 4\hfill \\ 0\hfill & 2\hfill & 4\hfill & 3\hfill & 3\hfill \\ 4\hfill & 1\hfill & 3\hfill & 0\hfill & 4\hfill \end{array}\right],L_1=\left[\begin{array}{lllll}0\hfill & 2\hfill & 1\hfill & 0\hfill & 4\hfill \\ 0\hfill & 1\hfill & 3\hfill & 2\hfill & 1\hfill \\ 2\hfill & 1\hfill & 2\hfill & 4\hfill & 3\hfill \\ 4\hfill & 3\hfill & 2\hfill & 3\hfill & 0\hfill \\ 1\hfill & 0\hfill & 4\hfill & 3\hfill & 4\hfill \end{array}\right],L_2=\left[\begin{array}{lllll}0\hfill & 1\hfill & 4\hfill & 2\hfill & 0\hfill \\ 1\hfill & 1\hfill & 2\hfill & 0\hfill & 3\hfill \\ 4\hfill & 2\hfill & 2\hfill & 3\hfill & 1\hfill \\ 2\hfill & 0\hfill & 3\hfill & 3\hfill & 4\hfill \\ 0\hfill & 3\hfill & 1\hfill & 4\hfill & 4\hfill \end{array}\right]$$

It is clear that the squares are three mutually orthogonal $\left(P_4{{\displaystyle \cup }}^{}2P_2\right)$-squares. See Figure 3, Figure 4 and Figure 5.

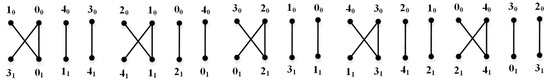
Figure 3. First edge decomposition of $K_{5,5}$ by $P_4{{\displaystyle \cup }}^{}2P_2$ corresponding to $L_0$.

Figure 4. Second edge decomposition of $K_{5,5}$ by $P_4{{\displaystyle \cup }}^{}2P_2$ corresponding to $L_1.$

Figure 5. Third edge decomposition of $K_{5,5}$ by $P_4{{\displaystyle \cup }}^{}2P_2$ corresponding to $L_2.$

3. Recursive Constructions of the Graph-Orthogonal Arrays

The production of graph-orthogonal arrays, defined below, is one strategy involving a systematic gluing together of graph-orthogonal arrays of small orders to obtain sets of graph-orthogonal arrays of larger orders.

Hereafter, we will directly represent the graph-orthogonal array as a $k\times N$ array rather than an $N\times k$ array.

Definition 5.

Assume that$X$is a graph-orthogonal array of order$m\times n^2$and that$Y$is a graph-orthogonal array of order$m\times l^2$. Let every row of the array$X$be divided into$n$sets where every set contains$n$elements, and the array$Y$is divided into$l$sets and every set contains$l$ elements.

$$X=\left[\begin{array}{lll}{X}_{11}\hfill & \dots \hfill & X_{1n}\hfill \\ X_{21}\hfill & \dots \hfill & X_{2n}\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ X_{m1}\hfill & \dots \hfill & X_{mn}\hfill \end{array}\right]Y=\left[\begin{array}{lll}{Y}_{11}\hfill & \dots \hfill & Y_{1l}\hfill \\ Y_{21}\hfill & \dots \hfill & Y_{2l}\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ Y_{m1}\hfill & \dots \hfill & Y_{ml}\hfill \end{array}\right]$$

where$\left|X_{ij}\right|=n,i\in \left\{1,2,\dots ,m\right\},j\in \left\{1,2,\dots ,n\right\}$and$\left|Y_{ij}\right|=l,i\in \left\{1,2,\dots ,m\right\},j\in \left\{1,2,\dots ,l\right\}.$Then

$$X\times Y=\left[\begin{array}{lllllllll}{X}_{11}\otimes Y_{11}\hfill & X_{11}\otimes Y_{12}\hfill & \dots \hfill & X_{11}\otimes Y_{1l}\hfill & \dots \hfill & X_{1n}\otimes Y_{11}\hfill & X_{1n}\otimes Y_{12}\hfill & \dots \hfill & X_{1n}\otimes Y_{1l}\hfill \\ X_{21}\otimes Y_{21}\hfill & X_{21}\otimes Y_{22}\hfill & \dots \hfill & X_{21}\otimes Y_{2l}\hfill & \dots \hfill & X_{2n}\otimes Y_{21}\hfill & X_{2n}\otimes Y_{22}\hfill & \dots \hfill & X_{2n}\otimes Y_{2l}\hfill \\ ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill & \hfill & ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill \\ X_{m1}\otimes Y_{m1}\hfill & X_{m1}\otimes Y_{m2}\hfill & \dots \hfill & X_{m1}\otimes Y_{ml}\hfill & \dots \hfill & X_{mn}\otimes Y_{m1}\hfill & X_{mn}\otimes Y_{m2}\hfill & \dots \hfill & X_{mn}\otimes Y_{ml}\hfill \end{array}\right].$$

As an illustration of this product construction, let

$$X=\left[\begin{array}{llll}0\hfill & 0\hfill & 1\hfill & 1\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill \end{array}\right]=\left[\begin{array}{ll}\left\{0,0\right\}\hfill & \left\{1,1\right\}\hfill \\ \left\{0,1\right\}\hfill & \left\{0,1\right\}\hfill \end{array}\right]=\left[\begin{array}{ll}{X}_{11}\hfill & X_{12}\hfill \\ X_{21}\hfill & X_{22}\hfill \end{array}\right]$$

$$Y=\left[\begin{array}{lllllllll}0\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 2\hfill \\ 0\hfill & 1\hfill & 2\hfill & 0\hfill & 1\hfill & 2\hfill & 0\hfill & 1\hfill & 2\hfill \end{array}\right]=\left[\begin{array}{lll}\left\{0,0,0\right\}\hfill & \left\{1,1,1\right\}\hfill & \left\{2,2,2\right\}\hfill \\ \left\{0,1,2\right\}\hfill & \left\{0,1,2\right\}\hfill & \left\{0,1,2\right\}\hfill \end{array}\right]=\left[\begin{array}{lll}{Y}_{11}\hfill & Y_{12}\hfill & Y_{13}\hfill \\ Y_{21}\hfill & Y_{22}\hfill & Y_{23}\hfill \end{array}\right]$$

Then the product construction yields the following array, whose elements are ordered pairs

$$X\times Y=\left[\begin{array}{llllll}{X}_{11}\otimes Y_{11}\hfill & X_{11}\otimes Y_{12}\hfill & X_{11}\otimes Y_{13}\hfill & X_{12}\otimes Y_{11}\hfill & X_{12}\otimes Y_{12}\hfill & X_{12}\otimes Y_{13}\hfill \\ X_{21}\otimes Y_{21}\hfill & X_{21}\otimes Y_{22}\hfill & X_{21}\otimes Y_{23}\hfill & X_{22}\otimes Y_{21}\hfill & X_{22}\otimes Y_{22}\hfill & X_{22}\otimes Y_{23}\hfill \end{array}\right]$$

In [6], El-Shanawany et al. proved that if $N\left(s, G\right)=p_1$, $N\left(t, H\right)=p_2$ and $min\left\{p_1,p_2\right\}=p,$ then $N\left(st, \mathbb{G}\right)=p$ $by$Proposition 3.2, where $\mathbb{G}\cong G\otimes H$.

Proposition 2.

([6]) If there are $p_1$-MOGS of order $s$ of the graph $G$ and $p_2$-MOGS of order $t$ of the graph $H$, then there are $p$-MOGS of order $st$ of the graph $\mathbb{G}\cong G\otimes H.$

Proposition 3.

Assume that$X$is a$G$-orthogonal array of order$m\times n^2$and that$Y$is an$H$-orthogonal array of order$m\times l^2$, then$X\times Y$is a$\left(G\otimes H\right)$-orthogonal array of order$m\times {(nl)}^2$.

Proof. 

Let $A_i,i\in \left\{1,2,\dots ,m\right\}$ be the $m$ mutually orthogonal graph squares of order $n$ for the graph $G$, and $B_i,i\in \left\{1,2,\dots ,m\right\}$ be the $m$ mutually orthogonal graph squares of order $l$ for graph $H.$

$$\begin{gathered} A_1=\left[\begin{array}{l}{X}_{11}\hfill \\ ⋮\hfill \\ X_{1n}\hfill \end{array}\right]A_2=\left[\begin{array}{l}{X}_{21}\hfill \\ ⋮\hfill \\ X_{2n}\hfill \end{array}\right]A_m=\left[\begin{array}{l}{X}_{m1}\hfill \\ ⋮\hfill \\ X_{mn}\hfill \end{array}\right] \\ {B}_1=\left[\begin{array}{l}{Y}_{11}\hfill \\ ⋮\hfill \\ Y_{1l}\hfill \end{array}\right]B_2=\left[\begin{array}{l}{Y}_{21}\hfill \\ ⋮\hfill \\ Y_{2l}\hfill \end{array}\right]B_m=\left[\begin{array}{l}{Y}_{m1}\hfill \\ ⋮\hfill \\ Y_{ml}\hfill \end{array}\right] \end{gathered}$$

Then, by Proposition 2, the Kronecker product of $A_i$ and $B_i,$ $i\in \left\{1,2,\dots ,m\right\}$, gives the $m$ mutually orthogonal $\left(G\otimes H\right)$-square $C_i$ of order $nl;$

$$C_1=A_1\otimes B_1=\left[\begin{array}{c}{X}_{11}\otimes Y_{11}\\ X_{11}\otimes Y_{12}\\ ⋮\hfill \\ X_{11}\otimes Y_{1l}\\ ⋮\hfill \\ X_{1n}\otimes Y_{11}\\ X_{1n}\otimes Y_{12}\\ ⋮\hfill \\ X_{1n}\otimes Y_{1l}\end{array}\right]C_2=A_2\otimes B_2=\left[\begin{array}{c}{X}_{21}\otimes Y_{21}\\ X_{21}\otimes Y_{22}\\ ⋮\hfill \\ X_{21}\otimes Y_{2l}\\ ⋮\hfill \\ X_{2n}\otimes Y_{21}\\ X_{2n}\otimes Y_{22}\\ ⋮\hfill \\ X_{2n}\otimes Y_{2l}\end{array}\right]C_m=A_m\otimes B_m=\left[\begin{array}{c}{X}_{m1}\otimes Y_{m1}\\ X_{m1}\otimes Y_{m2}\\ ⋮\hfill \\ X_{m1}\otimes Y_{ml}\\ ⋮\hfill \\ X_{mn}\otimes Y_{m1}\\ X_{mn}\otimes Y_{m2}\\ ⋮\hfill \\ X_{mn}\otimes Y_{ml}\end{array}\right]$$

Let

$$C_i^{\star }=\left[\begin{array}{lllllllll}{X}_{i1}\otimes Y_{11}\hfill & X_{i1}\otimes Y_{12}\hfill & \dots \hfill & X_{i1}\otimes Y_{1l}\hfill & \dots \hfill & X_{in}\otimes Y_{11}\hfill & X_{in}\otimes Y_{12}\hfill & \dots \hfill & X_{in}\otimes Y_{1l}\hfill \end{array}\right],i\in \left\{1,2,\dots ,m\right\}.$$

As such, by Proposition 1, we can construct the $\left(G\otimes H\right)$-orthogonal array $X\times Y$ of order $m\times {(nl)}^2$ as follows,

$$\begin{gathered} X\times Y=\left[\begin{array}{l}{C}_1^{\star }\hfill \\ C_2^{\star }\hfill \\ ⋮\hfill \\ C_m^{\star }\hfill \end{array}\right] \\ =\left[\begin{array}{ccccccccc}{X}_{11}\otimes Y_{11}& X_{11}\otimes Y_{12}& \dots & X_{11}\otimes Y_{1l}& \dots & X_{1n}\otimes Y_{11}& X_{1n}\otimes Y_{12}& \dots & X_{1n}\otimes Y_{1l}\\ X_{21}\otimes Y_{21}& X_{21}\otimes Y_{22}& \dots & X_{21}\otimes Y_{2l}& \dots & X_{2n}\otimes Y_{21}& X_{2n}\otimes Y_{22}& \dots & X_{2n}\otimes Y_{2l}\\ ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill & \hfill & ⋮\hfill & ⋮\hfill & \hfill & ⋮\hfill \\ X_{m1}\otimes Y_{m1}& X_{m1}\otimes Y_{m2}& \dots & X_{m1}\otimes Y_{ml}& \dots & X_{mn}\otimes Y_{m1}& X_{mn}\otimes Y_{m2}& \dots & X_{mn}\otimes Y_{ml}\end{array}\right], \end{gathered}$$

which represents the product of the orthogonal arrays,

$$X={\left[\begin{array}{lll}{X}_{11}\hfill & \dots \hfill & X_{1n}\hfill \\ X_{21}\hfill & \dots \hfill & X_{2n}\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ X_{m1}\hfill & \dots \hfill & X_{mn}\hfill \end{array}\right]}_{m\times n^2}Y={\left[\begin{array}{lll}{Y}_{11}\hfill & \dots \hfill & Y_{1l}\hfill \\ Y_{21}\hfill & \dots \hfill & Y_{2l}\hfill \\ ⋮\hfill & \hfill & ⋮\hfill \\ Y_{m1}\hfill & \dots \hfill & Y_{ml}\hfill \end{array}\right]}_{m\times l^2}$$

defined by Definition 5. □

Example 7.

To illustrate Proposition 3, let

$$A_1=\left[\begin{array}{ll}0\hfill & 0\hfill \\ 1\hfill & 1\hfill \end{array}\right]A_2=\left[\begin{array}{ll}0\hfill & 1\hfill \\ 0\hfill & 1\hfill \end{array}\right]$$

$$B_1=\left[\begin{array}{lll}0\hfill & 0\hfill & 0\hfill \\ 1\hfill & 1\hfill & 1\hfill \\ 2\hfill & 2\hfill & 2\hfill \end{array}\right]B_2=\left[\begin{array}{lll}0\hfill & 1\hfill & 2\hfill \\ 0\hfill & 1\hfill & 2\hfill \\ 0\hfill & 1\hfill & 2\hfill \end{array}\right]$$

$$C_1=A_1\otimes B_1=\left[\begin{array}{l}{X}_{11}\otimes Y_{11}\hfill \\ X_{11}\otimes Y_{12}\hfill \\ X_{11}\otimes Y_{13}\hfill \\ X_{12}\otimes Y_{11}\hfill \\ X_{12}\otimes Y_{12}\hfill \\ X_{12}\otimes Y_{13}\hfill \end{array}\right]C_2=A_2\otimes B_2=\left[\begin{array}{l}{X}_{21}\otimes Y_{11}\hfill \\ X_{21}\otimes Y_{12}\hfill \\ X_{21}\otimes Y_{13}\hfill \\ X_{22}\otimes Y_{11}\hfill \\ X_{22}\otimes Y_{12}\hfill \\ X_{22}\otimes Y_{13}\hfill \end{array}\right]$$

$$C_1=\left[\begin{array}{llllll}00\hfill & 00\hfill & 00\hfill & 00\hfill & 00\hfill & 00\hfill \\ 01\hfill & 01\hfill & 01\hfill & 01\hfill & 01\hfill & 01\hfill \\ 02\hfill & 02\hfill & 02\hfill & 02\hfill & 02\hfill & 02\hfill \\ 10\hfill & 10\hfill & 10\hfill & 10\hfill & 10\hfill & 10\hfill \\ 11\hfill & 11\hfill & 11\hfill & 11\hfill & 11\hfill & 11\hfill \\ 12\hfill & 12\hfill & 12\hfill & 12\hfill & 12\hfill & 12\hfill \end{array}\right]C_2=\left[\begin{array}{llllll}00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \\ 00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \\ 00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \\ 00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \\ 00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \\ 00\hfill & 01\hfill & 02\hfill & 10\hfill & 11\hfill & 12\hfill \end{array}\right]$$

$$X\times Y=\left[\begin{array}{l}{C}_1^{\star }\hfill \\ C_2^{\star }\hfill \end{array}\right]=\left[\begin{array}{llllll}{X}_{11}\otimes Y_{11}\hfill & X_{11}\otimes Y_{12}\hfill & X_{11}\otimes Y_{13}\hfill & X_{12}\otimes Y_{11}\hfill & X_{12}\otimes Y_{12}\hfill & X_{12}\otimes Y_{13}\hfill \\ X_{21}\otimes Y_{21}\hfill & X_{21}\otimes Y_{22}\hfill & X_{21}\otimes Y_{23}\hfill & X_{22}\otimes Y_{21}\hfill & X_{22}\otimes Y_{22}\hfill & X_{22}\otimes Y_{23}\hfill \end{array}\right]$$

$$X=\left[\begin{array}{ll}{X}_{11}\hfill & X_{12}\hfill \\ X_{21}\hfill & X_{22}\hfill \end{array}\right]=\left[\begin{array}{llll}0\hfill & 0\hfill & 1\hfill & 1\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill \end{array}\right]Y=\left[\begin{array}{lll}{Y}_{11}\hfill & Y_{12}\hfill & Y_{13}\hfill \\ Y_{21}\hfill & Y_{22}\hfill & Y_{23}\hfill \end{array}\right]=\left[\begin{array}{lllllllll}0\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 2\hfill \\ 0\hfill & 1\hfill & 2\hfill & 0\hfill & 1\hfill & 2\hfill & 0\hfill & 1\hfill & 2\hfill \end{array}\right]$$

Note:The product$Y\times X$gives a new graph-orthogonal array different from the graph-orthogonal array constructed by the product $X\times Y.$Furthermore, we can generalize Proposition 3 by the following Proposition 4, which can be proven by the same technique followed in the proof of Proposition 3.

Proposition 4.

Assume that$X_i$is a$G_i$-orthogonal array of order$m\times n_i^2$,$i\in \left\{1,2,\dots ,h\right\}.$Then${\prod }_{i=1}^h$X_iis a$\left(G_1\otimes G_2\otimes \dots \otimes G_h\right)$-orthogonal array of order $m\times {\left({\prod }_{i=1}^h{n}_i\right)}^2$.

Proof. 

It follows from Proposition 3. □

4. Applications of the Graph-Orthogonal Arrays in the Design of Experiments

The design of experiments is the main application of orthogonal arrays. The rows of the orthogonal arrays represent the tests (runs) or experiments to be implemented. For example, test plots of crops to be grown, integrated circuits to be etched, and so on. The columns of orthogonal arrays represent the different variables (factors) which are analyzed in order to know their effects. The entries in the orthogonal array determine the levels of the variables. If 11100 is a row in an orthogonal array, this may mean that in this experiment the first, second and third variables are at their “high” levels, and the fourth and fifth variables at their “low” levels. If the experiment is based on an orthogonal array with strength $t$, then we find that all the possible combinations of $t$ for the factors will occur together equally as often. Therefore, the purpose is to investigate the effects of the factors and how the factors interact. Finally, the orthogonal arrays are used to determine which level combinations are to be implemented. Now, we introduce an application of the $C_4$-orthogonal array $C_4$-$OA\left(16,3,4,2\right)$ in the design of experiments; this array is derived from Lemma 4 by using $\alpha =0,\beta =1,\gamma =2\mathrm{and} \delta =3$. This array is represented by the matrix $𝒫$ where

$${\mathcal{P}}^T=\left[\begin{array}{llllllllllllllll}0\hfill & 0\hfill & 1\hfill & 1\hfill & 0\hfill & 0\hfill & 1\hfill & 1\hfill & 2\hfill & 2\hfill & 3\hfill & 3\hfill & 2\hfill & 2\hfill & 3\hfill & 3\hfill \\ 0\hfill & 1\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 2\hfill & 3\hfill & 0\hfill & 1\hfill & 0\hfill & 1\hfill & 2\hfill & 3\hfill & 2\hfill & 3\hfill \\ 0\hfill & 2\hfill & 2\hfill & 0\hfill & 3\hfill & 1\hfill & 1\hfill & 3\hfill & 3\hfill & 1\hfill & 1\hfill & 3\hfill & 0\hfill & 2\hfill & 2\hfill & 0\hfill \end{array}\right]$$

Table 3 presents 16 experimental runs. It is clear that these experimental runs represent the rows of the orthogonal array $C_4$-$OA\left(16,3,4,2\right)$. Similarly, all the other results in the paper can be used for the design of several experiments.

Table 3. 16 experimental runs.

Experimental Runs	Factor (Levels)
	A	B	C
1	0	0	0
2	0	1	2
3	1	0	2
4	1	1	0
5	0	2	3
6	0	3	1
7	1	2	1
8	1	3	3
9	2	0	3
10	2	1	1
11	3	0	1
12	3	1	3
13	2	2	0
14	2	3	2
15	3	2	2
16	3	3	0

5. Conclusions

Mutually orthogonal Latin squares (MOLS) are used for constructing several orthogonal arrays, but the Latin squares are excessively restrictive. The more general concepts of mutually orthogonal graph squares (MOGS) offer more flexibility. MOGS are considered a generalization of the MOLS. Orthogonal arrays are essential in statistics and are related to finite fields, combinatorics, geometry, and error-correcting codes. The constructions of graph-orthogonal arrays have been investigated in the presented paper. This paper is the first that provides the mutually orthogonal graph squares as a tool for constructing the graph-orthogonal arrays. Furthermore, we introduced recursive constructions of the graph-orthogonal arrays.