An External Parameter Independent Novel Cost Function for Evolving Bijective Substitution-Boxes
Abstract
1. Introduction
1.1. Related Work
2. Preliminaries
3. Motivation and Contribution
Our Contribution
4. Experimental Setup
4.1. Common Parameters
4.2. Local Search Algorithm
4.3. Genetic and Tree
4.4. Hill Climbing Algorithm
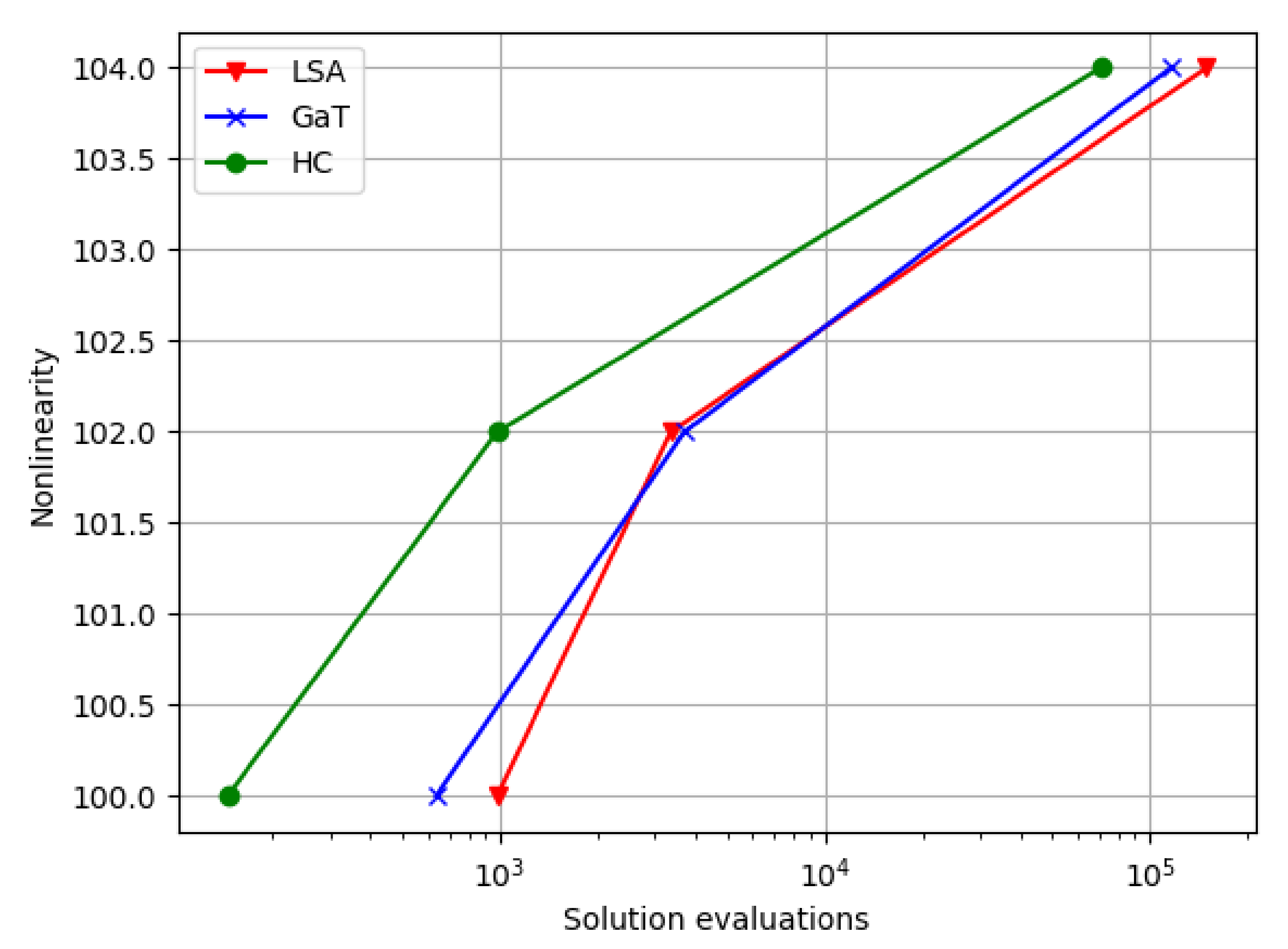
5. Results and Discussion
5.1. Definition of a New Cost Function
- if n is odd
- if n is even
5.2. Relation to Nonlinearity
- Set up a fixed number M of cost function upgrades.
- Execute hill climbing algorithm upgrading the value of the cost function regardless nonlinearity.
- Save the value of the cost function and the corresponding nonlinearity each time the cost function is upgraded.
- Repeat Step 3 until there is no available upgrade on the cost function (i.e., the function was updated M times).
5.3. Results with Our New Cost Function
- and if rule 1 is not satisfied
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Some Substitution Boxes with the Best Nonlinearity Achieved
- {7, 12, 21, 29, 17, 23, 10, 26, 31, 16, 27, 30, 28, 3, 5, 15, 8, 18, 1, 19, 9, 2, 11, 25, 4, 0, 6, 20, 22, 24, 13, 14}
- {28, 17, 1, 13, 38, 41, 46, 6, 0, 29, 53, 20, 59, 5, 24, 21, 35, 26, 61, 16, 48, 37, 58, 22, 55, 44, 39, 56, 34, 43, 15, 27, 51, 12, 62, 52, 14, 33, 10, 2, 31, 49, 57, 42, 11, 3, 30, 40, 36, 19, 63, 60, 4, 45, 32, 50, 47, 23, 54, 7, 9, 25, 8, 18}
- {14, 73, 38, 4, 71, 99, 108, 19, 61, 39, 82, 55, 60, 95, 125, 106, 23, 117, 119, 76, 120, 46, 7, 34, 96, 86, 28, 31, 81, 41, 42, 57, 87, 0, 79, 116, 13, 52, 74, 3, 33, 43, 25, 47, 68, 53, 16, 121, 85, 15, 17, 32, 63, 37, 26, 93, 29, 107, 6, 126, 22, 66, 124, 77, 89, 102, 30, 59, 75, 24, 40, 127, 88, 70, 98, 54, 109, 1, 48, 35, 112, 11, 90, 111, 92, 8, 114, 2, 94, 122, 80, 56, 100, 78, 27, 72, 103, 84, 45, 115, 101, 113, 20, 9, 44, 36, 123, 62, 64, 69, 83, 51, 104, 58, 105, 49, 12, 67, 21, 110, 10, 65, 5, 91, 97, 18, 50, 118}
- {236, 60, 6, 66, 185, 96, 206, 221, 167, 103, 159, 174, 156, 152, 239, 200, 45, 28, 38, 136, 107, 243, 34, 8, 71, 115, 201, 114, 157, 91, 47, 233, 16, 124, 70, 122, 46, 183, 203, 104, 158, 58, 179, 63, 166, 247, 123, 74, 230, 188, 72, 39, 145, 139, 210, 106, 125, 246, 205, 253, 204, 13, 20, 142, 56, 10, 128, 191, 198, 55, 197, 216, 116, 105, 195, 224, 144, 141, 22, 169, 138, 199, 154, 49, 234, 244, 121, 119, 252, 249, 153, 0, 112, 127, 75, 42, 160, 130, 209, 9, 193, 213, 172, 35, 102, 220, 109, 51, 53, 242, 180, 151, 120, 170, 111, 14, 44, 110, 215, 79, 255, 97, 11, 29, 99, 228, 81, 189, 147, 4, 192, 176, 184, 76, 163, 23, 26, 254, 5, 61, 133, 143, 214, 32, 37, 222, 88, 84, 171, 1, 146, 85, 30, 15, 212, 162, 187, 40, 41, 92, 94, 113, 186, 95, 232, 245, 12, 227, 235, 50, 150, 126, 148, 219, 100, 62, 131, 65, 68, 82, 226, 2, 57, 59, 223, 135, 80, 251, 31, 7, 36, 25, 155, 108, 98, 218, 118, 86, 101, 134, 54, 48, 78, 149, 21, 90, 207, 225, 217, 231, 18, 73, 69, 202, 129, 67, 24, 178, 237, 27, 240, 87, 137, 196, 161, 19, 168, 140, 173, 182, 190, 33, 229, 181, 3, 241, 83, 89, 17, 64, 132, 238, 208, 177, 93, 77, 211, 175, 165, 52, 250, 248, 194, 164, 117, 43}
Appendix B. Pseudo-Code of the Local Search Algorithm
Appendix C. Pseudo-Code of the Hill Climbing Algorithm
Appendix D. Procedure of the Genetic and Tree Algorithm
- Step 1: Randomly generate s-boxes which is taken as the initial population P. Save the current best nonlinearity in P to the value CN. If return the s-box with nonlinearity CN. If , then proceed to Step 4. Otherwise, sort P according to the value of the function CF (our cost function) and select the best M candidates to be the new farm, reduce NoE in and proceed to Step 2.
- Step 2: For each S, randomly select C successors from the neighborhood N(S) resulting of swap the outputs corresponding to a pair of different inputs of S, where S can also be chosen, and repetition is permitted. Then, for all S from the new population, determine the cost function CF and the nonlinearity. Update CN), reduce NoE in and proceed to Step 3.
- Step 3: If any s-box in P present nonlinearity greater or equals NEL return such s-box. In the case of , then proceed to Step 4. Otherwise, sort P according to the value of the function CF (and select the best M to become the new farm and proceed to Step 2.
- Step 4: Let be the s-box with nonlinearity higher or equal to NT and with cost CF(). Put . Search overall N(), until:
- (a)
- find s-box S’ with nonlinearity equal to NEL, then return S’
- (b)
- find s-box with nonlinearity greater than CN, then proceed to Step 5
- (c)
- find s-box with nonlinearity equal to CN and a improved cost than CF(), then proceed to Step 5.
- (d)
- no s-box from N() has values to go to option a, b or c, or the number of solution evaluations is depleted, then FAIL (unless the number of solution evaluations is depleted, one can ignore this failure condition to have the algorithm perform more exploration of the space, always returning to Step 3).
- Step 5: Let be an s-box from option Step 4 (b) or (c). Set CN = . Save with ordinal number of over N() into a LIFO (Last In First Out) stack and set j = 2 (ordinal number of the diagnostic s-box). Then proceed to Step 6.
- Step 6: Search the overall N() until:
- (a)
- find s-box S’ with nonlinearity equal to NEL, then return S’
- (b)
- find s-box with nonlinearity greater than CN, then proceed to Step 7
- (c)
- find s-box with nonlinearity equal to CN and a better cost than CF(), then proceed to Step 7.
- (d)
- the number of solution evaluations is depleted, then FAIL
- (e)
- no s-box from N() has values to go to option a, b or c, then proceed to Step 8
- Step 7: Set j = j + 1. Let be the s-box from the option Step 6 b or c. Set CN =. Save with ordinal number of over N() into the LIFO stack. Then proceed to Step 6.
- Step 8: Set j = j − 1. If j=0, then FAIL (this failure condition can be omitted like option d in Step 4), else resume from LIFO stack and proceed to Step 6.
References
- Coppersmith, D. The Data Encryption Standard (DES) and its strength against attacks. IBM J. Res. Dev. 1994, 38, 243–250. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. The Design of Rijndael; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2. [Google Scholar]
- Barreto, P.; Rijmen, V. The Khazad legacy-level block cipher. Primit. Submitt. NESSIE 2000, 97, 106. [Google Scholar]
- Piret, G.; Roche, T.; Carlet, C. PICARO–A block cipher allowing efficient higher-order side-channel resistance. In Proceedings of the International Conference on Applied Cryptography and Network Security, Singapore, 26–29 June 2012. [Google Scholar]
- Vaudenay, S.; Junod, P. Device and Method for Encrypting and Decrypting a Block of Data. U.S. Patent 7,499,542, 3 March 2009. [Google Scholar]
- Farah, M.B.; Kachouri, A.; Samet, M. Improvement of cryptosystem based on iterating chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2543–2553. [Google Scholar] [CrossRef]
- Ahmad, M.; Khaja, I.A.; Baz, A.; Alhakami, H.; Alhakami, W. Particle Swarm Optimization Based Highly Nonlinear Substitution-Boxes Generation for Security Applications. IEEE Access 2020, 8, 116132–116147. [Google Scholar] [CrossRef]
- Abd EL-Latif, A.A.; Abd-El-Atty, B.; Venegas-Andraca, S.E. Venegas-Andraca, A novel image steganography technique based on quantum substitution boxes. Opt. Laser Technol. 2019, 116, 92102. [Google Scholar] [CrossRef]
- Zahid, A.H.; Al-Solami, E.; Ahmad, M. A Novel Modular Approach Based Substitution-Box Design for Image Encryption. IEEE Access 2020. [Google Scholar] [CrossRef]
- Matsui, M. Linear cryptanalysis method for DES cipher. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Lofthus, Norway, 23–27 May 1993. [Google Scholar]
- Biham, E.; Shamir, A. Differential Cryptanalysis of the Data Encryption Standard; Springer Science & Business Media: New York, NY, USA, 1993. [Google Scholar]
- Budaghyan, L.; Carlet, C.; Pott, A. New classes of almost bent and almost perfect nonlinear polynomials. IEEE Trans. Inf. Theory 2006, 52, 1141–1152. [Google Scholar] [CrossRef]
- Nyberg, K. On the construction of highly nonlinear permutations. In Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques, Balatonfured, Hungary, 24–28 May 1992. [Google Scholar]
- Ahmad, M.; Haleem, H.; Khan, P.M. A new chaotic substitution box design for block ciphers. In Proceedings of the 2014 International Conference on Signal Processing and Integrated Networks (SPIN), Delhi, India, 20–21 February 2014; pp. 255–258. [Google Scholar]
- Farah, M.B.; Guesmi, R.; Kachouri, A.; Samet, M. A new design of cryptosystem based on S-box and chaotic permutation. Multimed. Tools Appl. 2020, 79, 19129–19150. [Google Scholar] [CrossRef]
- Clark, J.A.; Jacob, J.L.; Stepney, S. The design of S-boxes by simulated annealing. New Gener. Comput. 2005, 23, 219–231. [Google Scholar] [CrossRef]
- Tesař, P. A new method for generating high non-linearity s-boxes. Radioengineering 2010, 19, 23–26. [Google Scholar]
- Ahmad, M.; Ahmad, Z. Random search based efficient chaotic substitution box design for image encryption. IJRSDA 2018, 5, 131–147. [Google Scholar] [CrossRef]
- Carlet, C. Vectorial Boolean Functions for Cryptography, Encyclopedia of Mathematics and its Applications; Cambridge University Press: Cambridge, UK, 2010; pp. 398–470. [Google Scholar]
- Kazymyrov, O.; Kazymyrova, V.; Oliynykov, R. A Method for Generation of High-Nonlinear S-Boxes Based On Gradient Descent. IACR Cryptol. ePrint Arch. 2013, 2013, 578. [Google Scholar]
- Ivanov, G.; Nikolov, N.; Nikova, S. Cryptographically strong S-boxes generated by modified immune algorithm. In Proceedings of the International Conference on Cryptography and Information Security in the Balkans, Koper, Slovenia, 3–4 September 2015. [Google Scholar]
- Ivanov, G.; Nikolov, N.; Nikova, S. Reversed genetic algorithms for generation of bijective s-boxes with good cryptographic properties. Cryptogr. Commun. 2016, 8, 247–276. [Google Scholar] [CrossRef]
- Picek, S.; Papagiannopoulos, K.; Ege, B.; Batina, L.; Jakobovic, D. Confused by confusion: Systematic evaluation of DPA resistance of various s-boxes. In Proceedings of the International Conference in Cryptology in India, Dehli, India, 14–17 December 2014. [Google Scholar]
- Picek, S.; Cupic, M.; Rotim, L. A new cost function for evolution of s-boxes. Evol. Comput. 2016, 24, 695–718. [Google Scholar] [CrossRef]
- Picek, S.; Mariot, L.; Leporati, A.; Jakobovic, D. Evolving S-boxes based on cellular automata with genetic programming. In Proceedings of the Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017. [Google Scholar]
- Picek, S.; Mariot, L.; Yang, B.; Jakobovic, D.; Mentens, N. Design of S-boxes defined with cellular automata rules. In Proceedings of the Computing Frontiers Conference, Siena, Italy, 15–17 May 2017. [Google Scholar]
- Isa, H.; Jamil, N.; Z’aba, M. Hybrid heuristic methods in constructing cryptographically strong S-boxes. Int. J. Cryptol. Res. 2016, 6, 1–15. [Google Scholar]
- Menyachikhin, A. Spectral-linear and spectral-differential methods for construction of S-boxes with cryptographic parameters close to optimal values. Mat. Vopr. Kriptografii 2017, 8, 97–116. [Google Scholar]
- Lerman, L.; Veshchikov, N.; Picek, S.; Markowitch, O. On the construction of side-channel attack resilient s-boxes. In Proceedings of the International Workshop on Constructive Side-Channel Analysis and Secure Design, Paris, France, 13–14 April 2017. [Google Scholar]
- Martínez-Díaz, I. Búsqueda Local De S-Cajas Con Alta Varianza Del Coeficiente De Confusión. Master’s Thesis, Faculty of Math and Computer Sciences, University of Havana, Havana, Cuba, May 2019. [Google Scholar]
- Freyre-Echevarría, A. Evolución Híbrida De S-Cajas No Lineales Resistentes A Ataques De Potencia. Bachelor’s Thesis, Faculty of Math and Computer Sciences, University of Havana, Havana, Cuba, July 2020. [Google Scholar]
- Bolufé-Röhler, A.; Tamayo-Vera, D. Machine learning based metaheuristic hybrids for S-box optimization. J. Ambient Intell. Humaniz. Comput. 2020, 11, 5139–5152. [Google Scholar] [CrossRef]
- Ahmad, M.; Al-Solami, E. Evolving dynamic S-boxes using fractional-order hopfield neural network based scheme. Entropy 2020, 22, 717. [Google Scholar] [CrossRef]
- Ahmad, M.; Al-Solami, E.; Alghamdi, A.M.; Yousaf, M.A. Bijective S-Boxes Method Using Improved Chaotic Map-Based Heuristic Search and Algebraic Group Structures. IEEE Access 2020, 8, 110397–110411. [Google Scholar] [CrossRef]
- Ahmad, M.; Doja, M.N.; Beg, M.M.S. ABC optimization based construction of strong substitution-box. Wirel. Pers. Commun. 2018, 101, 1715–1729. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A.; Rhouma, R.; Belghith, S. Selective image encryption scheme based on DWT, AES S-box and chaotic permutation. In Proceedings of the 2015 International Wireless Communications and Mobile Computing Conference (IWCMC), Dubrovnik, Croatia, 24–28 August 2015; pp. 606–610. [Google Scholar]
- Razaq, A.; Alolaiyan, H.; Ahmad, M.; Yousaf, M.A.; Shuaib, U.; Aslam, W.; Alawida, M. A Novel Method for Generation of Strong Substitution-Boxes Based on Coset Graphs and Symmetric Groups. IEEE Access 2020, 8, 75473–75490. [Google Scholar] [CrossRef]
- Amin, M.; Abd El-Latif, A.A. Efficient modified RC5 based on chaos adapted to image encryption. J. Electron. Imaging 2010, 19, 013012. [Google Scholar] [CrossRef]
- Peng, J.; Abd El-Latif, A.A.; Belazi, A.; Kotulski, Z. Efficient chaotic nonlinear component for secure cryptosystems. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 989–993. [Google Scholar]
- Zahid, A.H.; Arshad, M.J.; Ahmad, M. A novel construction of efficient substitution-boxes using cubic fractional transformation. Entropy 2019, 21, 245. [Google Scholar] [CrossRef]
- Canteaut, A. Lecture notes on Cryptographic Boolean Functions. Inria Paris France. 2016. Available online: https://www.rocq.inria.fr/secret/Anne.Canteaut/poly.pdf (accessed on 1 October 2020).
- Rothaus, O.S. On “bent” functions. J. Comb. Theory Ser. A 1976, 20, 300–305. [Google Scholar] [CrossRef]
- Chabaud, F.; Vaudenay, S. Links between differential and linear cryptanalysis. In Proceedings of the Workshop on the Theory and Application of of Cryptographic Techniques, Perugia, Italy, 9–12 May 1994. [Google Scholar]
- Zhang, X.-M.; Zheng, Y. GAC—The criterion for global avalanche characteristics of cryptographic functions. J. Univers. Comput. Sci. 1996, 1, 320–337. [Google Scholar]
- Browning, K.; Dillon, J.; McQuistan, M.; Wolfe, A. An APN permutation in dimension six. Finite Fields Theory Appl. 2010, 518, 33–42. [Google Scholar]
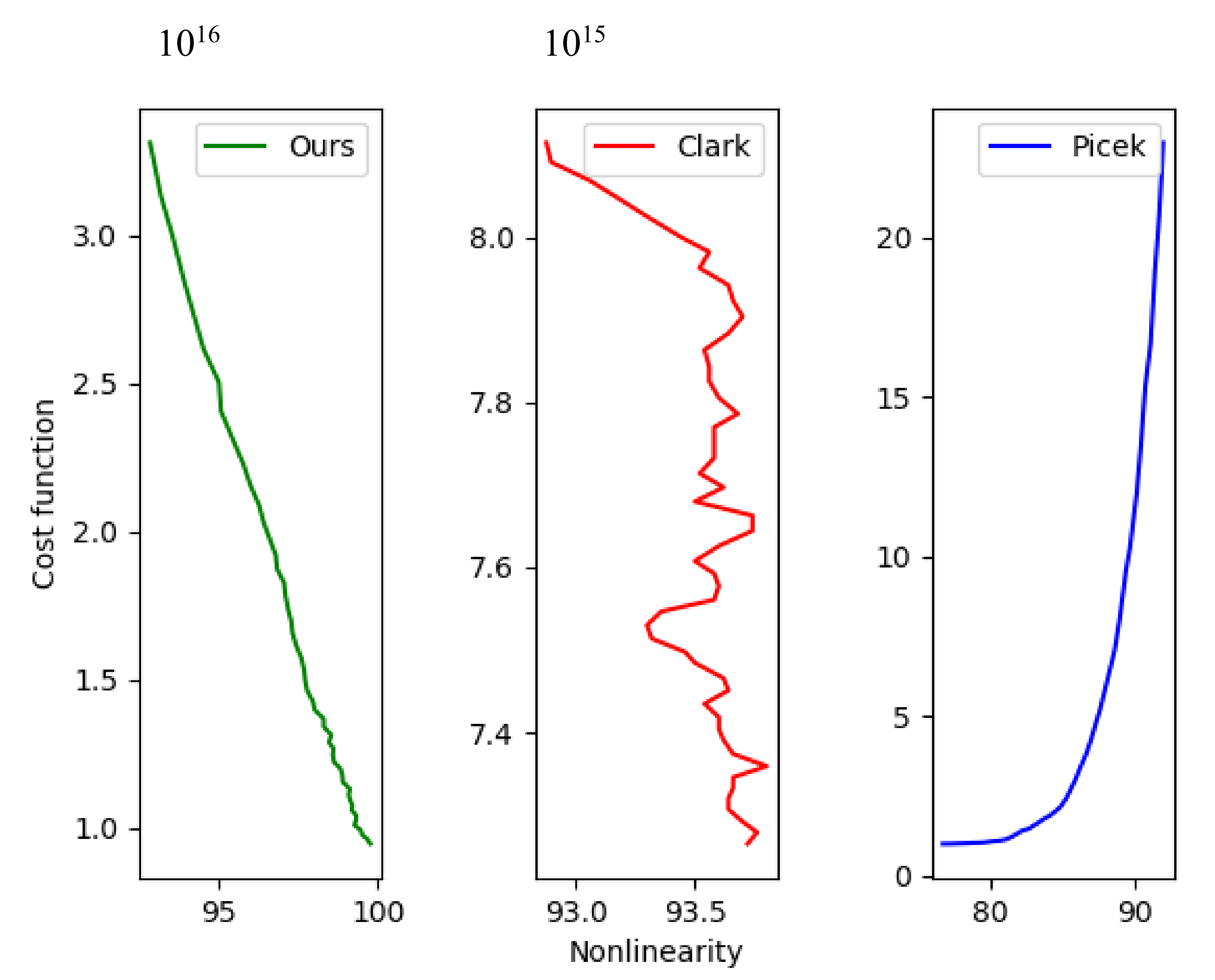
| S-Box Size | Experiments | Number of Evaluations | Maximum Nonlinearity |
|---|---|---|---|
| 100 | 125,000 | 12 | |
| 100 | 250,000 | 24 | |
| 30 | 500,000 | 56 | |
| 30 | 1,000,000 | 112 |
| S-Box Size | ||||
|---|---|---|---|---|
| NT | 8 | 20 | 46 | 102 |
| NEL | 10 | 22 | 48 | 104 |
| Cost Function | Clark’s | Picek’s | Ours |
|---|---|---|---|
| Correlation | −0.553 | 0.824 | −0.998 |
| p-value | 3.13 × | 2.04 × | 3.84 × |
| S-Box Size | ||||
|---|---|---|---|---|
| Correlation | −0.968 | −0.998 | −0.992 | −0.998 |
| p-value | 3.49 × | 2.03 × | 5.01 × | 3.84 × |
| Algorithm | Property | ||||
|---|---|---|---|---|---|
| LSA | 10/9.9 | 22/22 | 48/48 | 104/104 | |
| 4/5.8 | 6/7.08 | 6/8.07 | 8/9.6 | ||
| 16/22.88 | 32/38.24 | 56/59.2 | 88/94.4 | ||
| GaT | 10/10 | 22/22 | 48/48 | 104/104 | |
| 4/5.48 | 6/7.04 | 8/8.2 | 8/9.8 | ||
| 16/23.76 | 32/38.08 | 56/58.93 | 80/92.53 | ||
| HC | 10/9.8 | 22/22 | 48/48 | 104/104 | |
| 4/5.1 | 6/7.2 | 6/8 | 8/9.53 | ||
| 16/22.3 | 32/37.8 | 56/59.3 | 88/94.93 |
| Algorithm | ||||
|---|---|---|---|---|
| LSA | 10480 | 2358 | 7751 | 149,539 |
| GaT | 1260 | 1563 | 7007 | 116,266 |
| HC | 9831 | 1437 | 5162 | 70,596 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freyre-Echevarría, A.; Alanezi, A.; Martínez-Díaz, I.; Ahmad, M.; Abd El-Latif, A.A.; Kolivand, H.; Razaq, A. An External Parameter Independent Novel Cost Function for Evolving Bijective Substitution-Boxes. Symmetry 2020, 12, 1896. https://doi.org/10.3390/sym12111896
Freyre-Echevarría A, Alanezi A, Martínez-Díaz I, Ahmad M, Abd El-Latif AA, Kolivand H, Razaq A. An External Parameter Independent Novel Cost Function for Evolving Bijective Substitution-Boxes. Symmetry. 2020; 12(11):1896. https://doi.org/10.3390/sym12111896
Chicago/Turabian StyleFreyre-Echevarría, Alejandro, Ahmad Alanezi, Ismel Martínez-Díaz, Musheer Ahmad, Ahmed A. Abd El-Latif, Hoshang Kolivand, and Abdul Razaq. 2020. "An External Parameter Independent Novel Cost Function for Evolving Bijective Substitution-Boxes" Symmetry 12, no. 11: 1896. https://doi.org/10.3390/sym12111896
APA StyleFreyre-Echevarría, A., Alanezi, A., Martínez-Díaz, I., Ahmad, M., Abd El-Latif, A. A., Kolivand, H., & Razaq, A. (2020). An External Parameter Independent Novel Cost Function for Evolving Bijective Substitution-Boxes. Symmetry, 12(11), 1896. https://doi.org/10.3390/sym12111896







