Circular Intensely Orthogonal Double Cover Design of Balanced Complete Multipartite Graphs

Abstract

In this paper, we generalize the orthogonal double covers (ODC) of $K_{n,n}$ as follows. The circular intensely orthogonal double cover design (CIODCD) of $X=K_{\underset{m}{\underbrace{n,n,\dots ,n}}}$ is defined as a collection $T=\{G_{0_0},G_{1_0},\dots ,G_{{(n-1)}_0}\}\cup \{G_{0_1},G_{1_1},\dots ,G_{{(n-1)}_1}\}$ of isomorphic spanning subgraphs of $X$ such that every edge of $X$ appears twice in the collection $T,$ $\left|E(G_{i_0})\cap E(G_{j_0})\right|=\left|E(G_{i_1})\cap E(G_{j_1})\right|=0,i\ne j\mathrm{and} \left|E(G_{i_0})\cap E(G_{j_1})\right|=\lambda =\left(\begin{array}{l}m\\ 2\end{array}\right),i,j\in {\mathbb{Z}}_n.$ We define the half starters and the symmetric starters matrices as constructing methods for the CIODCD of $X$. Then, we introduce some results as a direct application to the construction of CIODCD of $X$ by the symmetric starters matrices.

1. Introduction

In this paper, we are concerned with the finite, undirected, and simple graphs. Let $V(G)$ and $E(G)$ denote the sets of vertices and edges of $G$, respectively. Many situations in various practically motivated problems and in mathematics and theoretical computer science can be captured by a graph. This simple structure has very widespread applications. It has several useful applications in operational research, such as, minimum cost path, and scheduling problems. It is also used in sociology. For example, to explore rumor spreading using social network analysis software.

An orthogonal double covers (ODC) of $K_{n,n}$ is a collection $H=\{G_0,G_1,\dots ,G_{n-1},F_0,F_1,\dots ,F_{n-1}\}$ of $2n$ spanning isomorphic subgraphs (called pages) of $K_{n,n}$ such that:

(i)

double cover property: Every edge of $K_{n,n}$ is in exactly one page of $\{G_0,G_1,\dots ,G_{n-1}\}$ and in exactly one page of $\{F_0,F_1,\dots ,F_{n-1}\};$

(ii)

orthogonality property: For $i,j\in \{0,1,\dots ,n-1\}$ and $i\ne j,$ $\left|E(G_i)\cap E(G_j)\right|=\left|E(F_i)\cap E(F_j)\right|=0;$ and $\left|E(G_i)\cap E(F_j)\right|=1$ for all $i,j\in \{0,1,\dots ,n-1\}.$

Some problems in statistical design theory [1] and the theory of Armstrong databases [2] are the motivation of studying the ODCs. ODCs have been investigated for more than 40 years. There is an extensive literature on the ODCs. The authors in [2,3] introduced the motivation and an overview of results and problems concerned with the ODCs. In [4,5], the authors have generalized the notion of an ODC to orthogonal decompositions of complete digraphs. Also, the ODC has been generalized to the suborthogonal double covers [5,6], and symmetric graph designs [7,8,9,10].

A technique to construct ODCs for Cayley graphs has been introduced by Scapellato et al. [11]. It has been shown that for all $(T,H)$ where $T$ is a $3$-regular Cayley graph on an abelian group there is an ODC, a few well known exceptions apart. Sampathkumar et al. [12] have constructed the cyclic ODCs of $4$-regular circulant graphs. El-Shanawany and El-Mesady [13] have introduced a technique to construct the CODCs of circulant graphs by several graph classes such as tripartite graphs, complete bipartite graphs, and disjoint union of $K_{1,2n-10}$ and butterfly. In [14], a technique for orthogonal labeling is produced for the corona product of two finite or infinite graph classes such as path, cycle, and star graphs. In addition, the nonexistence of the orthogonal $L$-labeling is proved for the corona product of $K_2$ and an infinite cycle.

For many years, the researchers have interested in the decompositions of graphs into Hamilton paths, or into Hamilton cycles. Bryant et al., [15] proved that a complete multipartite graph $K$ with $n>1$ vertices and $m$ edges can be decomposed into edge-disjoint Hamilton paths if and only if $m/(n-1)$ is an integer and the maximum degree of $K$ is at most $2m/(n-1)$. In [16], surveys results on cycle decompositions of complete multipartite graphs were introduced. The authors in [17] reduced the problem of finding an edge-decomposition of a balanced $r$-partite graph of large minimum degree into $r$-cliques to the problem of finding a fractional $r$-clique decomposition or an approximate one. All the previous results motivate us to the results of this paper. In this paper, we generalize the ODC of $K_{n,n}$ to the circular intensely orthogonal double cover design (CIODCD) of $X=K_{\underset{m}{\underbrace{n,n,\dots ,n}}}$. Since, the ODCs are very important in solving many problems in the statistical design and Armstrong databases, then the generalization of the ODCs to the CIODCD has a very important role in the statistical design theory and the relational databases. Now, the ODC can be considered as a special case of our generalization. Then the CIODCD can be utilized to model more general relational databases.

The paper is organized as follows. Section 2 introduces the basic definitions and terminologies that will be used throughout. Section 3 and Section 4 deal with the half and symmetric symmetric starters matrices, respectively.

2. Basic Definitions and Terminologies

Definition 1.

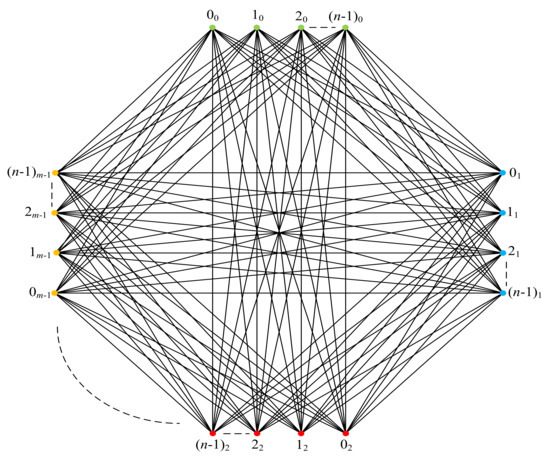
The complete multipartite graph$K_{a_1,\dots ,a_m}$is the simple graph on$n={\sum }_{i=1}^m{a}_i$vertices. The set of vertices is partitioned into$m$parts of cardinalities$a_1,a_2,\dots ,a_m;$an edge joins two vertices if and only if they belong to different parts. Thus$K_{1,1,\dots ,1}$is the complete graph$K_n$. The labeling of the vertices of

$$X\cong K_{\underset{m}{\underbrace{n,n,\dots ,n}}}$$

is shown in Figure 1. Let us decompose$X$into

$$\lambda K_{n,n},\lambda =\left(\begin{array}{c}m\\ 2\end{array}\right),$$

where the vertices of theith$K_{n,n}$are labeled by${\mathbb{Z}}_n\times \left\{s\right\}$and

$${\mathbb{Z}}_n\times \left\{t\right\},i=\left\{\begin{array}{ccc}t& if& s=0,\\ sm+t mod(s+1)& if& s>0.\end{array}\right.$$

Figure 1. Complete m-partite graph $X=K_{\underset{m}{\underbrace{n,n,\dots ,n}}}.$

Now, we will generalize the ODC of $K_{n,n}$ as follows. The circular intensely orthogonal double cover design (CIODCD) of $X$ is defined as a collection

$$T=\{G_{0_0},G_{1_0},\dots ,G_{{(n-1)}_0}\}\cup \{G_{0_1},G_{1_1},\dots ,G_{{(n-1)}_1}\}$$

of isomorphic spanning subgraphs of $X$ that satisfy the following:

(1)

double cover property: every edge of $X$ appears twice in the collection $T.$

(2)

intensely orthogonality property:

$$\left|E(G_{i_0})\cap E(G_{j_0})\right|=\left|E(G_{i_1})\cap E(G_{j_1})\right|=0,i\ne j\mathrm{and} \left|E(G_{i_0})\cap E(G_{j_1})\right|=\lambda =\left(\begin{array}{l}m\\ 2\end{array}\right),i,j\in {\mathbb{Z}}_n.$$

where

$$E(G_{i_0})\cap E(G_{j_1})=\{\underset{s,t}{{\displaystyle \cup }}(i_s,j_t)\}=\{(i_0,j_1),\dots ,(i_0,j_{m-1}),(i_1,j_2),(i_1,j_3)\dots ,(i_1,j_{m-1}),\dots ,(i_{m-2},j_{m-1})\}.$$

Note that

$$G_{x_k}\cong G_{x_k}^{0,1}\cup G_{x_k}^{0,2}\cup G_{x_k}^{0,3}\cup \dots \cup G_{x_k}^{0,m-1}\cup G_{x_k}^{1,2}\cup G_{x_k}^{1,3}\cup \dots \cup G_{x_k}^{1,m-1}\cup \dots \cup G_{x_k}^{m-2,m-1},x\in {\mathbb{Z}}_n,k\in {\mathbb{Z}}_2,$$

where the graphs:

$$G_{x_k}^{0,1},G_{x_k}^{0,2},G_{x_k}^{0,3},\dots ,G_{x_k}^{0,m-1},G_{x_k}^{1,2},G_{x_k}^{1,3},\dots ,G_{x_k}^{1,m-1},\dots ,G_{x_k}^{m-2,m-1}$$

share some vertices mutually. In Figure 2, a CIODCD of $K_{3,3,3}$ by $G\cong K_{1,3}^{0,1}\cup P_4^{0,2}\cup K_{1,3}^{1,2}$ is exhibited.

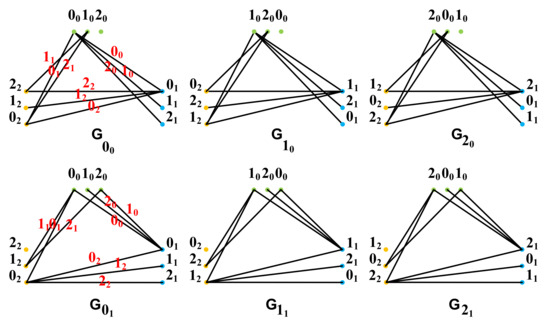
Figure 2. CIODCD of $K_{3,3,3}$ by $G\cong K_{{}_{1,3}}^{0,1}\cup P_4^{{}^{0,2}}\cup K_{{}_{1,3}}^{1,2}.$

3. CIODCDs by Half Starters Matrices

In this section, we will use two half starters matrices to construct CIODCDs of $X$ by two given graphs $G,F\in T.$ These two graphs allow us to introduce later two matrices represent them. That is, we often consider these two matrices instead of $G$ and $F$ respectively.

Definition 2.

Let$G$be a spanning subgraph of$X$and$a\in {\mathbb{Z}}_n.$Then the graph$G+a$ with

$$E(G+a)=\{(u_s+a,v_t+a):(u_s,v_t)\in E(G)\}$$

is called the $a$-translate of $G.$ Note that sums and differences are calculated in ${\mathbb{Z}}_n$ (i.e., sums and differences are calculated modulo $n$).

Definition 3.

Let$G$be a spanning subgraph of$X.$The length of an edge$e=(u_s,v_t)\in E(G)$is defined by$d(e)={(v-u)}_{i-1}$for all$u,v\in {\mathbb{Z}}_n.$Note that$X$has$\lambda$classes of edge lengths; one different class for each part of$X$.

Definition 4.

A spanning subgraph$G$of$X$is called a half starter graph with respect to${\mathbb{Z}}_n$if

(i)

$\left|E(G)\right|=\lambda n,$

(ii)

The lengths of all edges in$G$are mutually different,$i.e.,\{d(e):e\in E(G)\}={\mathbb{Z}}_n\times {\mathbb{Z}}_{\lambda }.$

As an immediate consequence of the Definition 2 and the Definition 3, the following result can be introduced.

Lemma 1.

If$G$is a half starter, then the union of all translates of$G$forms an edge decomposition of

$$X,i.e.{\cup }_{a\in {\mathbb{Z}}_n}E(G+a)=E(X).$$

Proof. 

We want to prove that

$$E(G+a)\cap E(G+b)=\phi , \mathrm{for} \mathrm{all} a,b\in {\mathbb{Z}}_n.$$

Using contradiction method, let

$$E(G+a)\cap E(G+b)\ge 1 \mathrm{for} \mathrm{all} a\ne b\in {\mathbb{Z}}_n.$$

Assume $(x_s,y_t)$ is an edge with length $l_{i-1}$ belongs to the intersection graph

$$E(G+a)\cap E(G+b).$$

Then

$$(x_s-a,y_t-a) \mathrm{and} (x_s-b,y_t-b)$$

are two distinct edges in $G$, both of them have length $l_{i-1}$. This leads to contradiction because $G$ is half starter. □

In what follows, we will represent a half starter $G$ by $\lambda \times n$ matrix $H\left(G\right)$ whose rows are arranged as follows,

$$R_{0,1},R_{0,2},\dots ,R_{0,m-1},R_{1,2},R_{1,3},\dots ,R_{1,m-1},R_{2,3},R_{2,4},\dots ,R_{2,m-1},\dots ,R_{m-2,m-1}.$$

The half starter $G$ can be decomposed into $\lambda$ bipartite graphs, each one can be generated by a row in the matrix $H,$ where the bipartite graph between the two sets ${\mathbb{Z}}_n\times \left\{s\right\}$ and ${\mathbb{Z}}_n\times \left\{t\right\}$ is generated by the row $R_{s,t},$ the edge set of the bipartite graph between the two sets ${\mathbb{Z}}_n\times \left\{s\right\}$ and ${\mathbb{Z}}_n\times \left\{t\right\}$ is

$$\{({(H(i,j+1))}_s,{(H(i,j+1)+j)}_t);j\in {\mathrm{Z}}_n\},i=\left\{\begin{array}{ccc}t& if& s=0,\\ sm+t mod(s+1)& if& s>0.\end{array}\right.$$

Note that the lengths of the edges of the bipartite graph between the two sets ${\mathbb{Z}}_n\times \left\{s\right\}$ and ${\mathbb{Z}}_n\times \left\{t\right\}$ are indexed by $i-1.$

The CIODCD of $K_{3,3,3}$ in Figure 2 can be represented by the following matrices.

$$H(G_{0_0})=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 1\\ 0& 0& 0\end{array}\right],H(G_{1_0})=\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& 2\\ 1& 1& 1\end{array}\right],H(G_{2_0})=\left[\begin{array}{ccc}2& 2& 2\\ 2& 0& 0\\ 2& 2& 2\end{array}\right],$$

$$H(G_{0_1})=\left[\begin{array}{ccc}0& 2& 1\\ 0& 0& 2\\ 0& 2& 1\end{array}\right],H(G_{1_1})=\left[\begin{array}{ccc}1& 0& 2\\ 1& 1& 0\\ 1& 0& 2\end{array}\right],H(G_{2_1})=\left[\begin{array}{ccc}2& 1& 0\\ 2& 2& 1\\ 2& 1& 0\end{array}\right].$$

Definition 5.

Two half starter matrices$H\left(G_0\right)$and$H\left(G_1\right)$are said to be intensely orthogonal if the elements of any row in the difference matrix$H\left(G_0\right)-H\left(G_1\right)$are all distinct and equal to${\mathbb{Z}}_n$.

Theorem 1.

If the two half starter matrices$H\left(G_0\right)$and$H\left(G_1\right)$are intensely orthogonal, then$T=\{G_{a_i}:a\in {\mathbb{Z}}_n,i\in {\mathbb{Z}}_2\}$with$G_{a_i}=(G_i+a)$is a CIODCDs of$X.$

Proof. 

Take into account the relation between the ith row of the half starter matrix $H\left(G\right)$ and the order $(s,t)$ that denotes the bipartite subgraph of $X$ between part $s$ and part $t.$ Firstly, from Lemma 1, all edges $(a_s,b_t)\in E(X)$ appear exactly in two subgraphs $G_{x_0}$ and $G_{y_1}$ thus the double cover property is done for all edges of $X.$ Now, let $x,y\in {\mathbb{Z}}_n$, and $k,l\in {\mathbb{Z}}_2.$ Since the ith row in $H\left(G\right)$ represents the bipartite subgraph of $X$ between part $s$ and part $t.$ Then the intensely orthogonality property will be satisfied if we prove that $\left|E(G_{x_k})\cap E(G_{y_{{}_l}})\right|=0$ if $k=l$ and $x\ne y$, and $\left|E(G_{x_k})\cap E(G_{y_{{}_l}})\right|=\lambda$ if $k\ne l.$

First case is satisfied directly from the definition of the construction. But if $k\ne l,$ let

$$G_{x_k}=G_{x_k}^{0,1}\cup G_{x_k}^{0,2}\cup G_{x_k}^{0,3}\cup \dots \cup G_{x_k}^{0,m-1}\cup G_{x_k}^{1,2}\cup G_{x_k}^{1,3}\cup \dots \cup G_{x_k}^{1,m-1}\cup \dots \cup G_{x_k}^{m-2,m-1}$$

and

$$G_{y_{{}_l}}=G_{y_l}^{0,1}\cup G_{y_l}^{0,2}\cup G_{y_l}^{0,3}\cup \dots \cup G_{y_l}^{0,m-1}\cup G_{y_l}^{1,2}\cup G_{y_l}^{1,3}\cup \dots \cup G_{y_l}^{1,m-1}\cup \dots \cup G_{y_l}^{m-2,m-1},$$

then for the first row of $A=H(G_0)$ and $B=H(G_1)$ we can find exactly one element $j$ where $A(1,j)-B(1,j)=y-x.$

Thus

$$A(1,j)+x=B(1,j)+y,$$

but this means that there is exactly one edge $e$ where

$$e=({(A(1,j)+x)}_0,{(A(1,j)+x+j)}_1)=({(B(1,j)+y)}_0,{(B(1,j)+y+j)}_1).$$

Then

$$e\in E(G_{0_k}^{0,1}+x)=E(G_{x_k}^{0,1}).$$

Also

$$e\in E(G_{0_l}^{0,1}+y)=E(G_{y_l}^{0,1}),$$

this is verified for the other rows of $H(G_0)$ and $H(G_1)$, then the intensely orthogonality property is satisfied and $\left|E(G_{x_k})\cap E(G_{y_{{}_l}})\right|=\lambda$ for more illustration, see (1), (2). □

$$G_{0_0}\equiv \left[\begin{array}{c}{G}_{0_0}^{0,1}\\ G_{0_0}^{0,2}\\ ⋮\\ G_{0_0}^{(m-2),(m-1)}\end{array}\right], G_{1_0}\equiv \left[\begin{array}{c}{G}_{1_0}^{0,1}\\ G_{1_0}^{0,2}\\ ⋮\\ G_{1_0}^{(m-2),(m-1)}\end{array}\right], \dots , G_{{(n-1)}_0}\equiv \left[\begin{array}{c}{G}_{{(n-1)}_0}^{0,1}\\ G_{{(n-1)}_0}^{0,2}\\ ⋮\\ G_{{(n-1)}_0}^{(m-2),(m-1)}\end{array}\right]$$

(1)

$$G_{0_1}\equiv \left[\begin{array}{c}{G}_{0_1}^{0,1}\\ G_{0_1}^{0,2}\\ ⋮\\ G_{0_1}^{(m-2),(m-1)}\end{array}\right], G_{1_1}\equiv \left[\begin{array}{c}{G}_{1_1}^{0,1}\\ G_{1_1}^{0,2}\\ ⋮\\ G_{1_1}^{(m-2),(m-1)}\end{array}\right], \dots , G_{{(n-1)}_1}\equiv \left[\begin{array}{c}{G}_{{(n-1)}_1}^{0,1}\\ G_{{(n-1)}_1}^{0,2}\\ ⋮\\ G_{{(n-1)}_1}^{(m-2),(m-1)}\end{array}\right]$$

(2)

4. CIODCDs by Symmetric Starters Matrices

In this section, we will study symmetric starter matrix of CIODCDs of $X$ by a given graph $G$. That is, we shall reduce two half starters matrices to one half starter matrix under certain conditions to construct a symmetric starter matrix.

Definition 6.

Let$G$be a spanning subgraph of$X,$the subgraph$G_u$of$X$with

$$E(G_u)=\{((b,a):(a,b)\in E(G)\}$$

is called symmetric graph of$G.$

Remark 1.

If$G$is a half starter, then$G_u$ is also a half starter.

Definition 7.

A half starter$G$is called a symmetric starter with respect to${\mathbb{Z}}_n$if$H(G)$and$H(G_u)$are intensely orthogonal.

Theorem 2.

Let$n$be a positive integer and let$G$be a half starter of$X$represented by the matrix$H(G).$Then$G$is a symmetric starter if and only if, for each row$R_{s,t}$of$H(G),$

$$\{R_{s,t}(j_{i-1})-R_{s,t}(-j_{i-1})+j_{i-1}:j_{i-1}\in {\mathbb{Z}}_n\}={\mathbb{Z}}_n.$$

Proof. 

We know that $G_u$ is a half starter and represented by $H(G_u).$ Since $(R_{s,t}^u(j_{i-1}),R_{s,t}^u(j_{i-1})+j_{i-1})$ is an edge in $E(G_u)$ we have $(R_{s,t}^u(j_{i-1})+j_{i-1},R_{s,t}^u(j_{i-1}))$ is an edge in $E(G)$ of length $-j_{i-1}.$ Therefore, $R_{s,t}(-j_{i-1})=R_{s,t}^u(j_{i-1})+j_{i-1}$ and thus $R_{s,t}^u(j_{i-1})=R_{s,t}(-j_{i-1})-j_{i-1}.$ Consequently, $H(G)$ and $H(G_u)$ are intensely orthogonal if and only if $\{R_{s,t}(j_{i-1})-R_{s,t}^u(j_{i-1})=R_{s,t}(j_{i-1})-(R_{s,t}(-j_{i-1})-j_{i-1})=R_{s,t}(j_{i-1})-R_{s,t}(-j_{i-1})+j_{i-1}:j_{i-1}\in {\mathbb{Z}}_n\}={\mathbb{Z}}_n.$ Hence, the double cover and the intensely orthogonality properties are verified, and the CIODCD of $X$ is constructed. □

For all the following results, the value of

$$\lambda =\left(\begin{array}{c}m\\ 2\end{array}\right).$$

Theorem 3.

Let$m,n\ge 2$be integers. Then the matrix$M(i+1,j+1)=i,i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n$is a symmetric starter matrix of a CIODCD of$X$by

$$F_1\cong \underset{\lambda }{\underbrace{K_{1,n}^{0,1}\cup K_{1,n}^{0,2}\cup \dots \cup K_{1,n}^{m-2,m-1}}}.$$

Proof. 

Since

$$M(i+1,j+1)=i,i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n,$$

then for each row of $M$ we have

$$\{R_{s,t}(j)-R_{s,t}(-j)+j:j\in {\mathbb{Z}}_n\}=\{(i)-(i)+j:j\in {\mathbb{Z}}_n\}={\mathbb{Z}}_n,$$

and hence, $M$ is a symmetric starter matrix. The edge set of $F_1$ is

$$E(F_1)=\{({(M(i+1,j+1))}_s,{(M(i+1,j+1)+j)}_t),i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n\}=\{({(i)}_s,{(i+j)}_t),$$

where $i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n\}.$□

Theorem 4.

Let$m\ge 2$be an integer and$n\equiv 1mod6$or$n\equiv 5mod6.$Then the matrix$M(i+1,j+1)=j,i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n$is a symmetric starter matrix of a CIODCD of$X$by$F_2\cong \underset{\lambda }{\underbrace{n{K}_2^{0,1}\cup n{K}_2^{0,2}\cup \dots \cup n{K}_2^{m-2,m-1}}}.$

Proof. 

Since

$$M(i+1,j+1)=j,i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n,$$

then for each row of $M$, we have

$$\{R_{s,t}(j)-R_{s,t}(-j)+j:j\in {\mathbb{Z}}_n\}=\{(j)-(n-j)+j:j\in {\mathbb{Z}}_n\}=\{3j:j\in {\mathbb{Z}}_n\}={\mathbb{Z}}_n,$$

where $\gcd (n,3)=1,$ and hence, $M$ is a symmetric starter matrix. The edge set of $F_2$ is

$$E(F_2)=\{({(M(i+1,j+1))}_s,{(M(i+1,j+1)+j)}_t),i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n\}=\{({(j)}_s,{(2j)}_t),$$

where $i\in {\mathbb{Z}}_{\lambda },j\in {\mathbb{Z}}_n\}.$□

Theorem 5.

Let$m\ge 2$be an integer and$n$be a positive integer. Then there is a CIODCD of$X$by

$$F_3\cong \underset{\lambda }{\underbrace{n{C}_4^{0,1}\cup n{C}_4^{0,2}\cup \dots \cup n{C}_4^{m-2,m-1}}}.$$

Proof. 

Let the matrix

$$M(F_3)={\left[\begin{array}{cccccccc}0& 1& \dots & 2n-1& 0& 1& \dots & 2n-1\\ 0& 1& \dots & 2n-1& 0& 1& \dots & 2n-1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 1& \dots & 2n-1& 0& 1& \dots & 2n-1\end{array}\right]}_{\lambda \times 4n},$$

then for each row of $M(F_3)$ we have

$$R_{s,t}(j)-R_{s,t}(-j)+j=\left\{\begin{array}{ccc}3j-2n& if& j<2n,\\ 3j+2n& if& j\ge 2n.\end{array}\right.$$

Hence, for $j\in {\mathbb{Z}}_{4n},$ we have

$$R_{s,t}(j)-R_{s,t}(-j)+j=3j+2n,$$

but these elements are mutually different and equal to ${\mathbb{Z}}_{4n}.$ This leads to that $M$ is a symmetric starter matrix. The edge set of $F_3$ is

$$\begin{gathered} E(F_3)=\{({(j)}_s,{(2j)}_t),({(j+n)}_s,{(2(j+n))}_t), \\ ({(j+n)}_s,{(2j)}_t),({(j)}_s,{(2(j+n))}_t),j\in {\mathbb{Z}}_n\}. \end{gathered}$$

□

For more illustration, let $m=3$ and $n=1,$ then there is a CIODCD of $K_{4,4,4}$ by $C_4^{0,1}\cup C_4^{0,2}\cup C_4^{1,2}.$ See Figure 3, where

$$M(C_4^{0,1}\cup C_4^{0,2}\cup C_4^{1,2})={\left[\begin{array}{cccc}0& 1& 0& 1\\ 0& 1& 0& 1\\ 0& 1& 0& 1\end{array}\right]}_{3\times 4}.$$

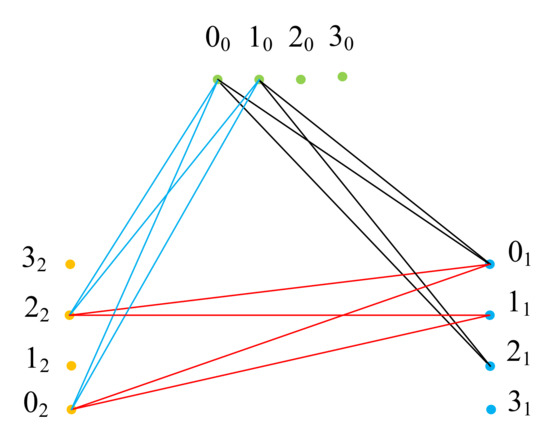
Figure 3. Symmetric starter of a CIODCD of $K_{4,4,4}$ by $C_4^{0,1}\cup C_4^{0,2}\cup C_4^{1,2}$.

Theorem 6.

Let$q$be a prime number. Then there is a CIODCD of$X$by

$$F_4\cong \underset{\lambda }{\underbrace{P_{q+1}^{0,1}\cup P_{q+1}^{0,2}\cup \dots \cup P_{q+1}^{m-2,m-1}}}.$$

Proof. 

Let the matrix

$$M(F_4)={\left[\begin{array}{cccccc}0& q-1^2& q-2^2& q-3^2& \dots & q-{(q-1)}^2\\ 0& q-1^2& q-2^2& q-3^2& \dots & q-{(q-1)}^2\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& q-1^2& q-2^2& q-3^2& \dots & q-{(q-1)}^2\end{array}\right]}_{\lambda \times q},$$

then for each row of $M(F_4)$ we have

$$\{R_{s,t}(j)-R_{s,t}(-j)+j:j\in {\mathbb{Z}}_q\}=\{(q-j^2)-(q-{(q-j)}^2)+j:j\in {\mathbb{Z}}_q\}=\{j:j\in {\mathbb{Z}}_q\}={\mathbb{Z}}_q,$$

and hence, $M(F_4)$ is a symmetric starter matrix. The edge set of $F_4$ is

$$E(F_4)=\{({(q-j^2)}_s,{(q-j^2+j)}_t),j\in {\mathbb{Z}}_q\}.$$

□

For more illustration, let $m=3$ and $q=5$, then there is a CIODCD of $K_{5,5,5}$ by $P_6^{0,1}\cup P_6^{0,2}\cup P_6^{1,2}.$ See Figure 4, where

$$M(P_6^{0,1}\cup P_6^{0,2}\cup P_6^{1,2})={\left[\begin{array}{ccccc}0& 4& 1& 1& 4\\ 0& 4& 1& 1& 4\\ 0& 4& 1& 1& 4\end{array}\right]}_{3\times 5}.$$

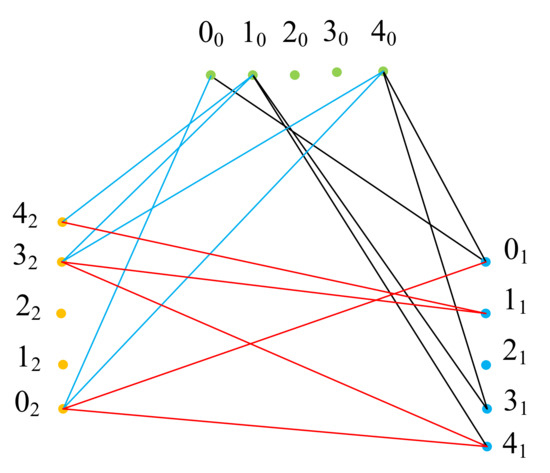
Figure 4. Symmetric starter of a CIODCD of $K_{5,5,5}$ by $P_6^{0,1}\cup P_6^{0,2}\cup P_6^{1,2}.$

5. Conclusions

In conclusion, we have generalized the orthogonal double covers (ODCs) of the complete bipartite graphs to the circular intensely orthogonal double cover design (CIODCD) of balanced complete multipartite graphs. We have defined the half starters and the symmetric starters matrices as constructing tools for the CIODCD of balanced complete multipartite graphs. Since, the ODCs are very important in solving many problems in the statistical design and Armstrong databases, then the generalization of the ODCs to the CIODCD has a very important role in the statistical design theory and the relational databases. Now, the ODC can be considered as a special case of our generalization. Then the CIODCD can be utilized to model more general relational databases. Finally, some results have been introduced as a direct application to this generalization.