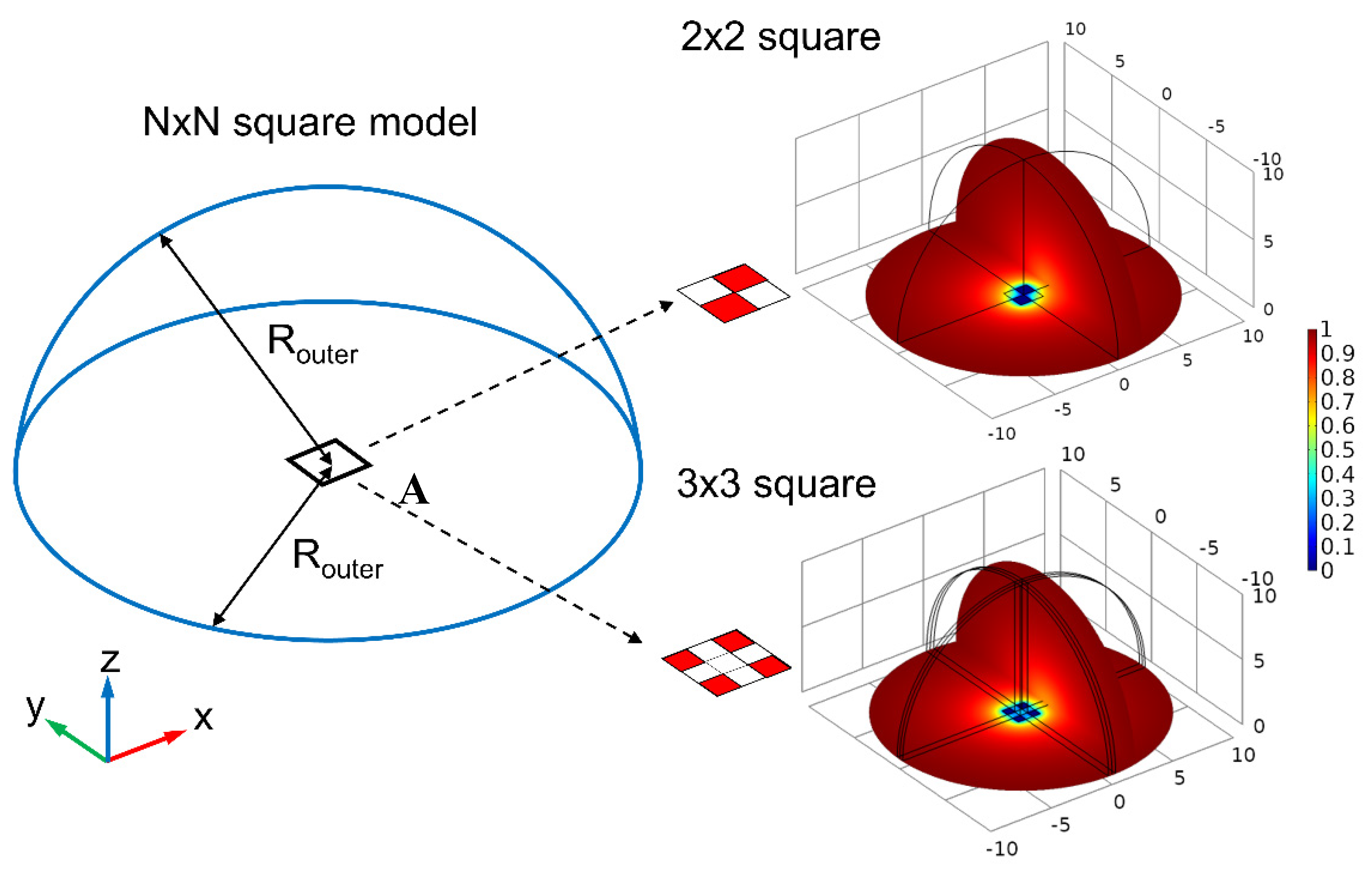
3.1. First Model Type: N× N SQUARE Reactant Model
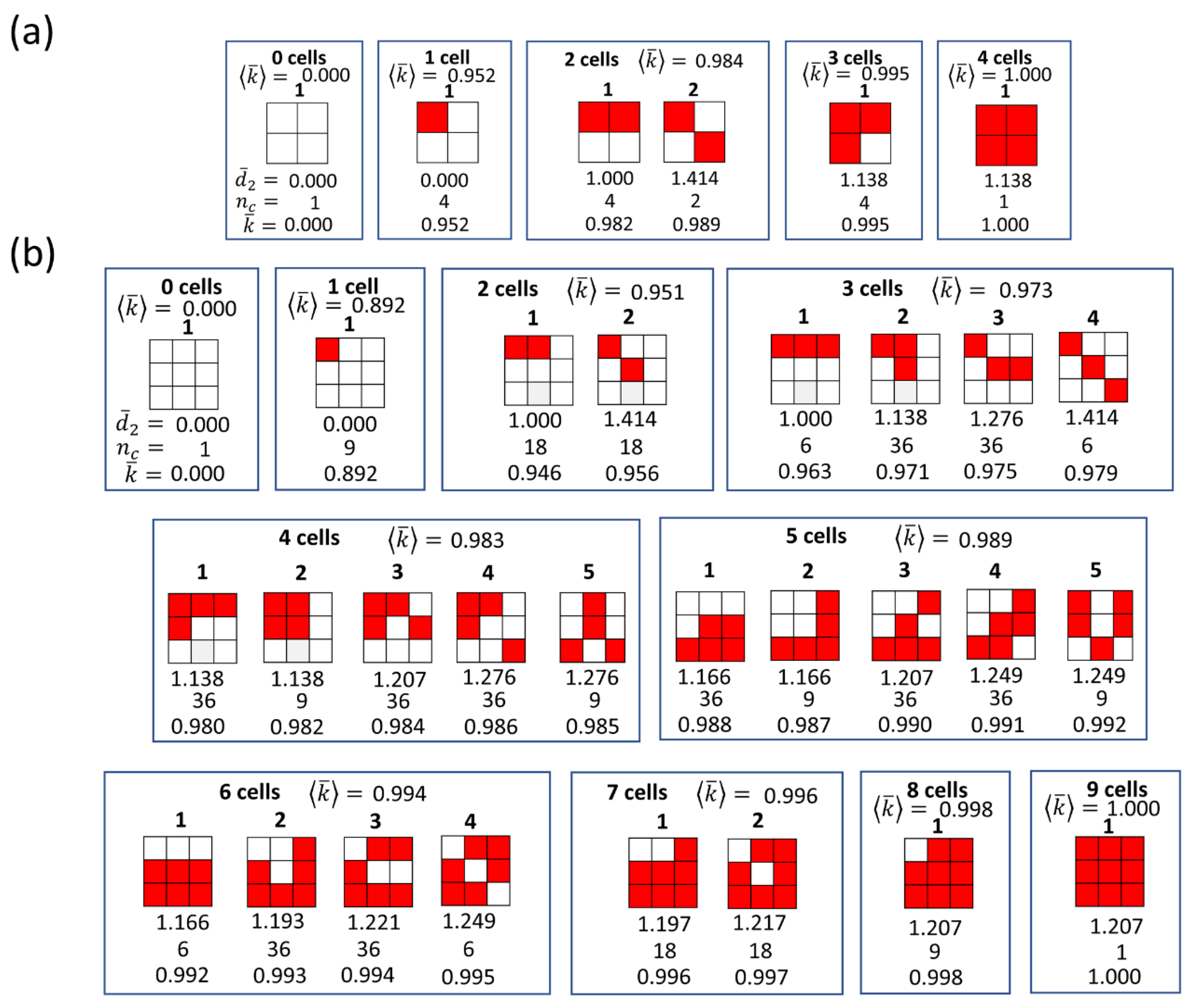
In the N × N square reactant model of the first type, to study the effects of the size, number, and arrangement of reactive patches on the kinetics, we first consider various N × N patch configurations generated by the model. Since the N × N square model has N × N cells and each cell can be a reactive patch or not, the total number of configurations for the N × N square model is
. For instance, for N = 2 and 3, the total number is
and
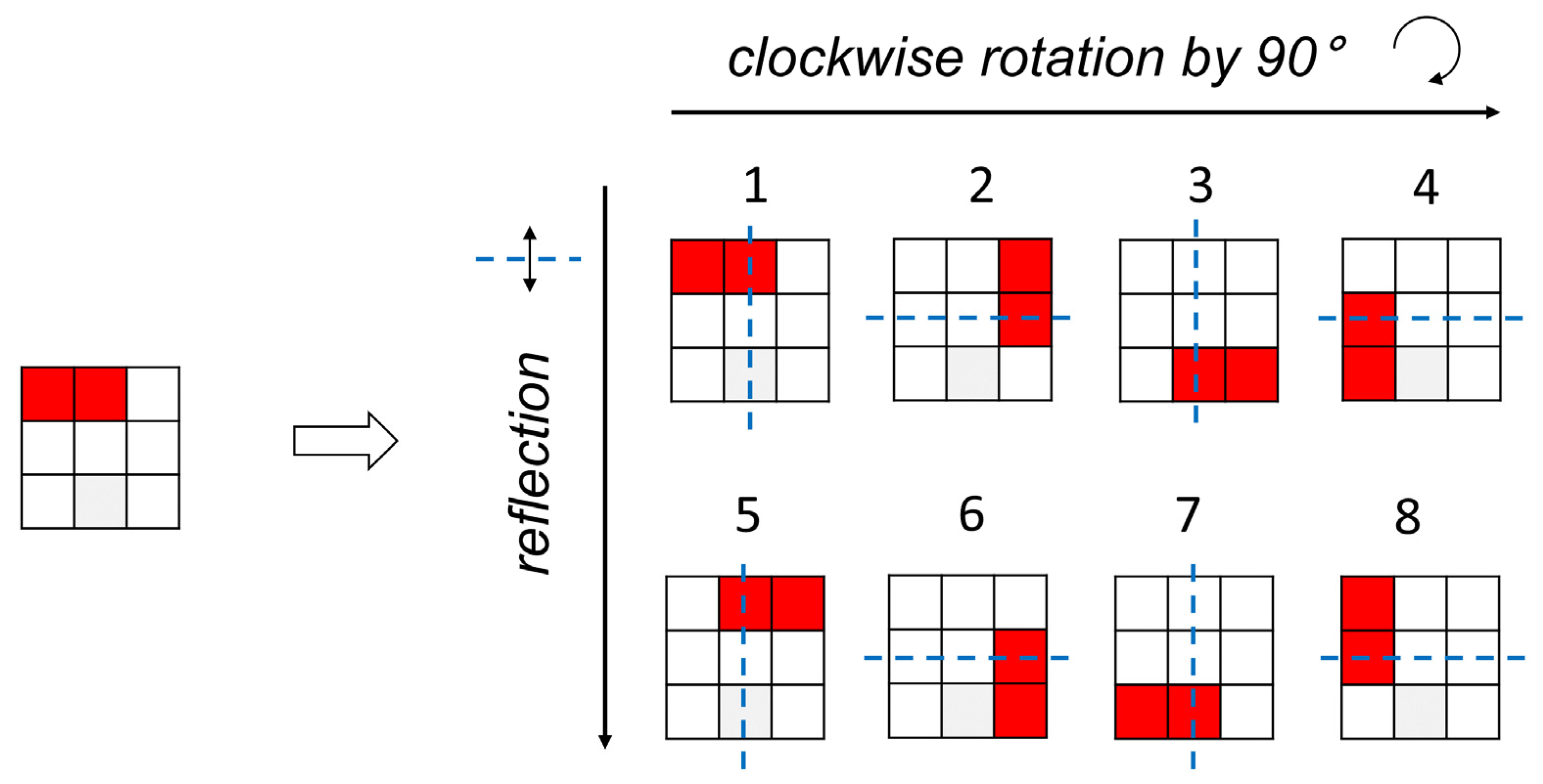
, respectively. In fact, in this work, we completely analyze all the configurations for N = 2, 3, applying symmetric operations to the configurations. Note that a configuration of reactive patches can generate eight kinetically equivalent configurations by rotations and reflections through planes, as shown in
Figure 3. However, when the configuration has symmetries in the arrangement of patches, the number of configurations generated is reduced because some configurations are duplicated. Therefore, we consider only symmetrically representative configurations with the number of equivalent configurations
.
In
Figure 4, we present all the symmetrically representative configurations of patches for N = 2 and 3 and the normalized rate constants
calculated from the solutions of the Smoluchowski equations. Since the rate constant is dependent on the distances between the reactive patches (cells), we calculate the average of the distances between all pairs of the reactive cells
. Note that a similar study based on the geometric mean pair distance between patches has been performed [
17]. The average pairwise distances are also displayed in
Figure 4. Here, we find a general trend that as
increases, the normalized rate constant
increases. Therefore, for a given number of reactive cells, the normalized rate constant
could differ depending on the distances between the patches or the configurations of the patches. Notably, in the 3 × 3 square model, the configurations giving the highest rate constant are mainly the configurations that have a symmetric arrangement of the reactive patches (configurations 8, 23, 22, 16, and 3 for 2, 4, 5, 6, and 8 reactive cells, respectively).
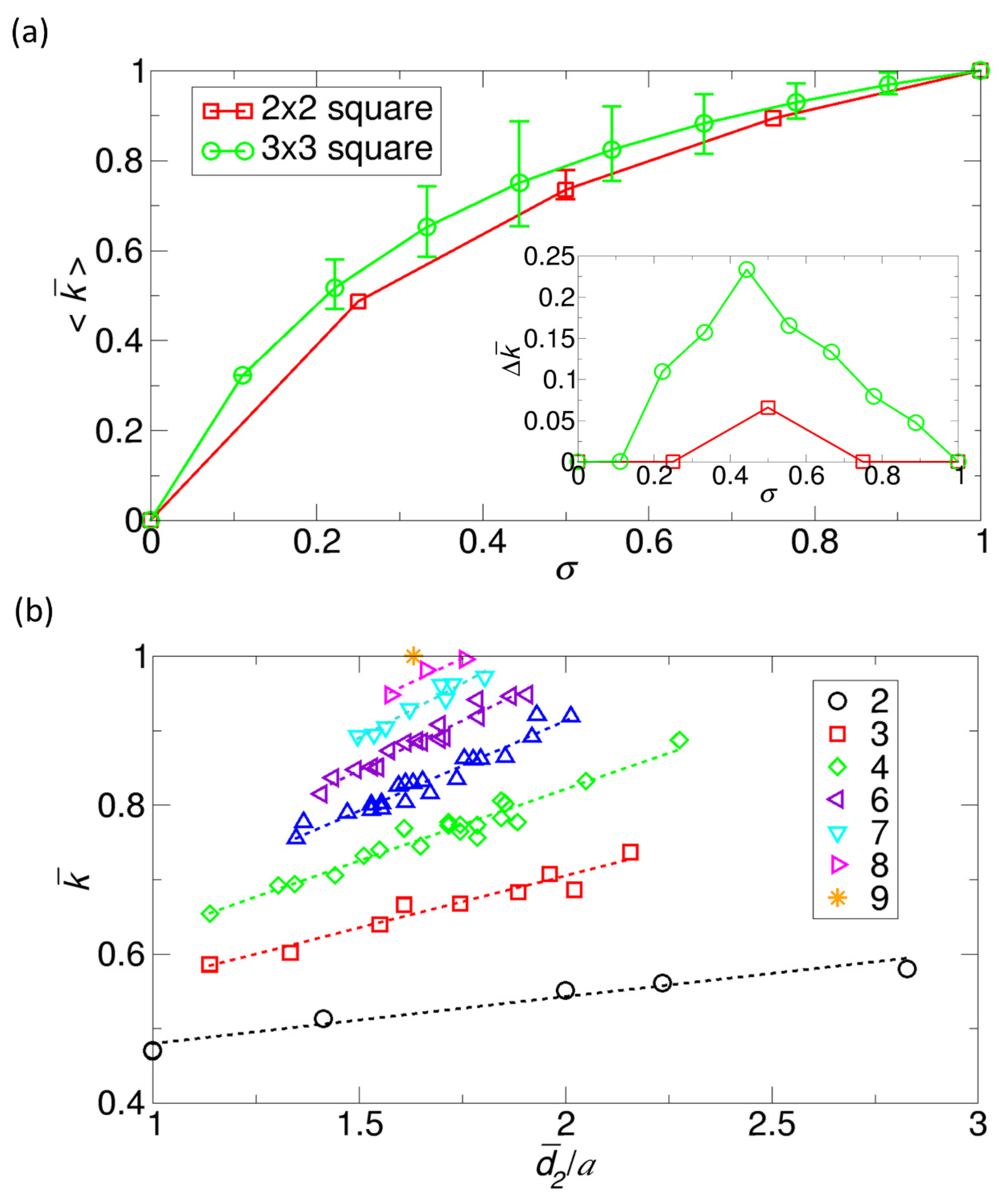
Additionally, we calculate the ensemble-averaged value of the normalized rate constants
for a given number of reactive cells, since we can determine the probability of each representative configuration from
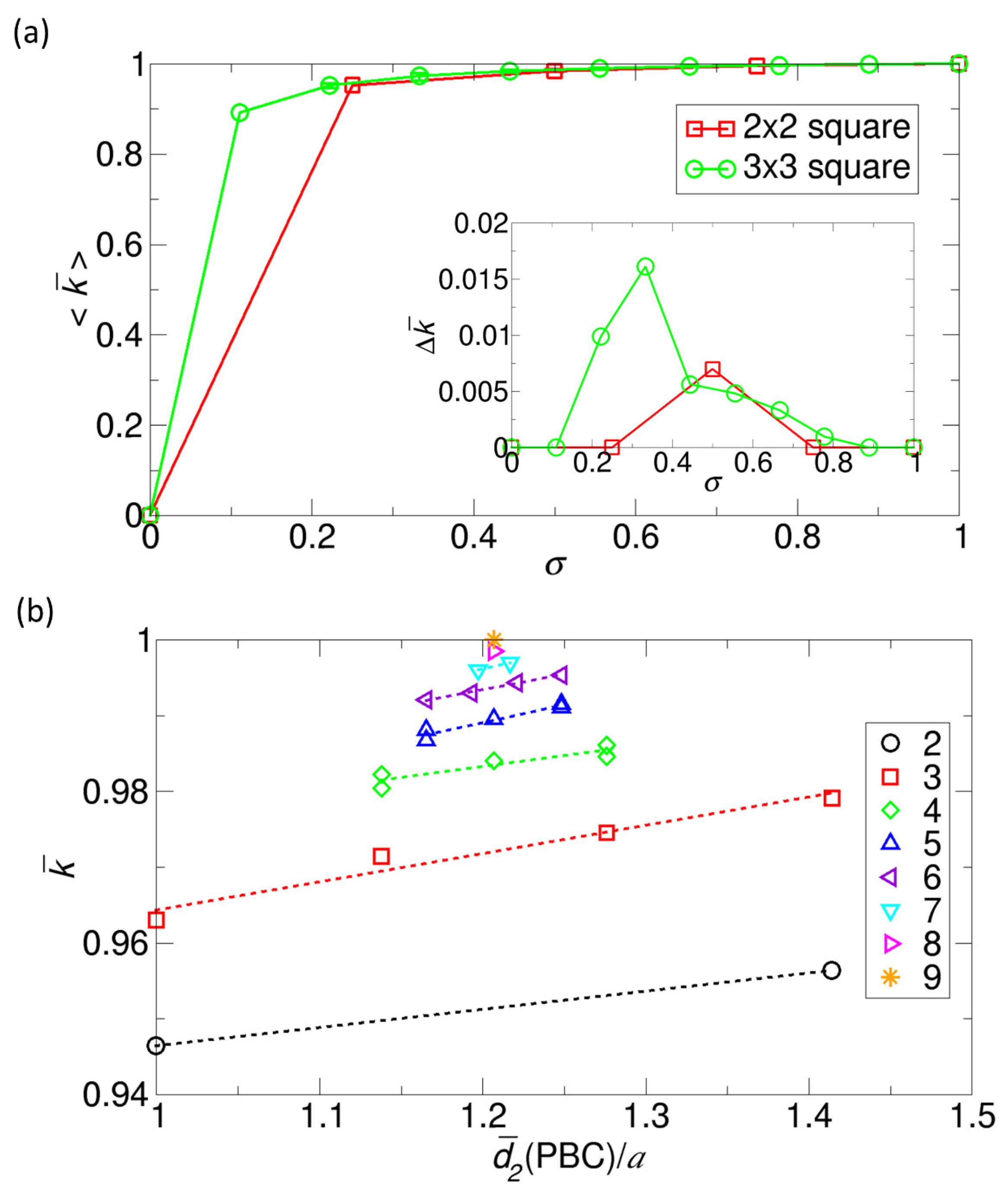
. From the calculation, we plot the ensemble-averaged rate constant against the surface coverage ratio of reactive cells over the entire reactant area
.
is easily calculated by counting the number of reactive cells; for example, in the 2 × 2 model, if only one cell is reactive,
is 0.25 because it is 1 over 4. The plot is shown in
Figure 5a. As one can expect, as
increases, the normalized rate constant
increases, but as
approaches 1, the slope of the rate constant against
decreases, which is due to the increase in the competition between reactive patches. We also show the maximum and the minimum values of the normalized rate constant for a given value of
. Interestingly, as is shown in the inset of
Figure 5a, the variation in the rate constant
, i.e., the difference between the maximum and minimum values increases at low values of
, reaches its maximum, and then decreases at large values. This characteristic behavior was also observed in the reactive patches of a spherical reactant [
7,
17].
Another feature from
Figure 5a is that for a given value of
, the ensemble-averaged normalized rate constant for the 3 × 3 model is larger than that for the 2 × 2 model. This outcome is consistent with the observation in a spherical reactant that a smaller patch gives a larger rate constant [
7,
17]. Basically, this occurrs because in the case of a higher value of N, more configurations exist in which the reactive patches are separated, which reduces the competition between patches. Therefore, one can expect that as N increases in the N × N model, one can obtain a higher ensemble-averaged rate constant.
In this work, we plot the normalized rate constant
as a function of the dimensionless distance
, where
is the length of the unit cell. The result is shown in
Figure 5b. Since the cases of the 2 × 2 square model are trivial, we present only the cases of the 3 × 3 square model. From the plot, we find a general trend that as
increases, the normalized rate constant
increases. Specifically, from linear regressions, the result shows that a strong correlation exists between the normalized rate constant
and
, but the linear lines are not monotonously increasing, which means that
is a good parameter but is not a perfect parameter for evaluating the competition between reactive patches in a given configuration.
3.2. Second Model Type: N × N Square Reactant Model
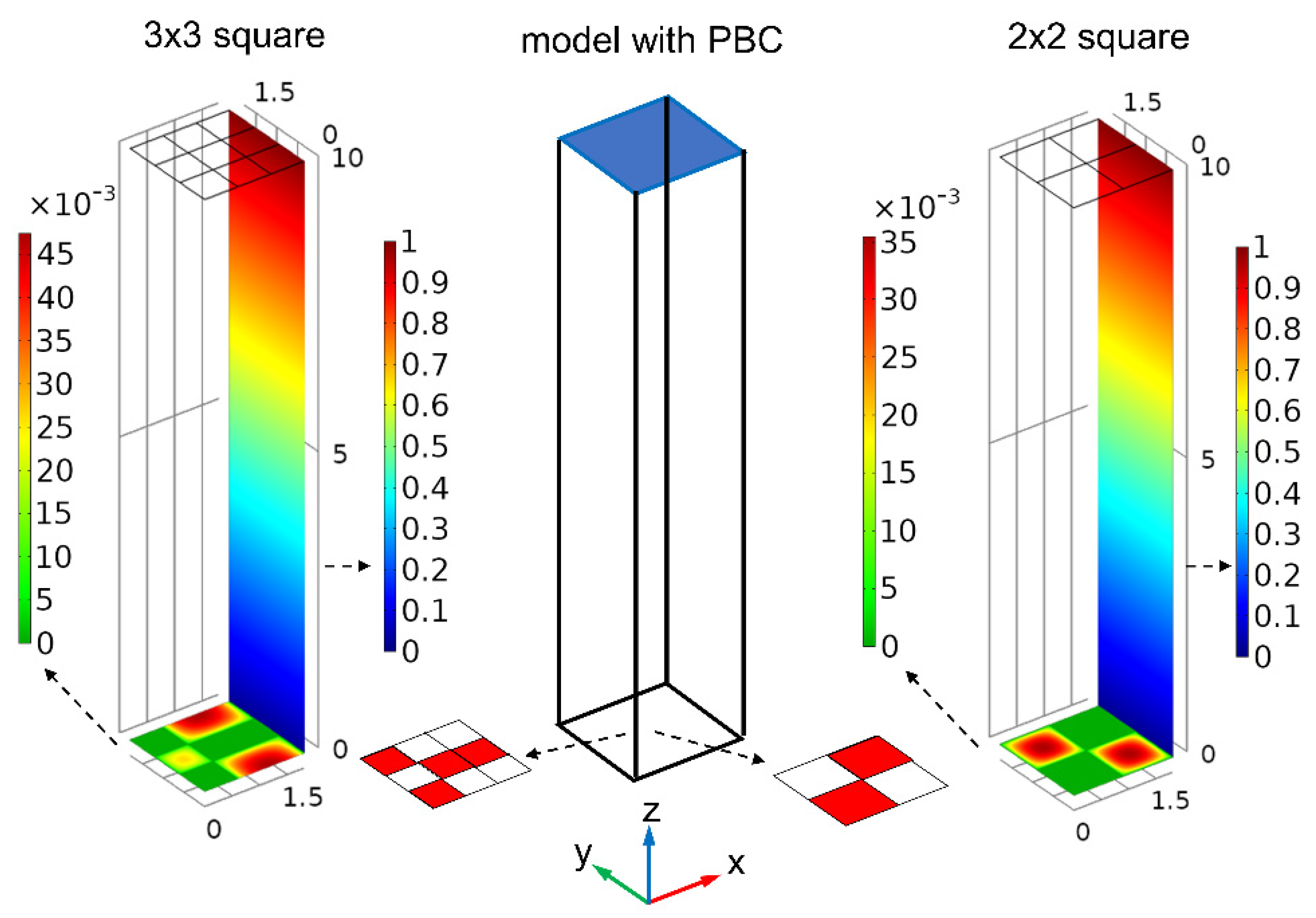
The main difference between the first and the second model types comes from whether PBCs are applied to the x and y dimensions. In this section, we discuss the second model type with PBCs. When we apply PBCs to the x-y plane, the number of symmetrically representative configurations that we have to consider is significantly reduced, as shown in
Figure 6. As in
Figure 4, we calculate
,
, and
for each representative configuration for the 2 × 2 and 3 × 3 square models. For a given number of reactive cells, we arrange the configurations in increasing order of
. As expected, the normalized rate constant
generally increases with
.
The ensemble-averaged normalized rate constant
is shown in
Figure 7a. We also observe that as
increases, the rate constant increases, which is the same trend observed in
Figure 5a. However, differences exist. Notably, the normalized rate constant
is very high even at low values of
. That is, even a small surface coverage of reactive patches can produce a high rate constant. This significant increase due to the boundary condition is discussed further with the dependence of the kinetics on
in
Section 3.3. Another noticeable property from
Figure 7a is that the variation in the rate constant is small, as indicated in the inset of
Figure 7a. These interesting properties with the PBCs were also found in the reaction systems of a spherical reactant with multiple reactive patches [
10]. For a spherical reactant, small patches can produce a large rate constant, and the distribution of rate constants is narrow, which means that the difference between the maximum and minimum values is relatively small. These common features may come from the fact that the reactant surface with PBCs in the second model type is topologically similar to the surface over a sphere in that they are closed surfaces and have no boundary; if one walks straight starting from a certain position on the surface, one will eventually return to the starting position. As in
Figure 5b, we also show a scatter plot of the normalized rate constant
and the dimensionless average pairwise distance
for symmetrically representative configurations in the 3 × 3 square reactant model. The linear regression lines show a strong correlation between them.
3.3. Dependence of Kinetics on the Fraction of the Total Reactive Patch Area
The results of the N × N square reactant models in
Section 3.1 and
Section 3.2 indicate that the normalized rate constant
is apparently dependent on the fraction of the total area of the reactive patches
. For example, let us consider the first model type without PBCs. From
Figure 4, if we consider Case 1 of the 3 × 3 model with one reactive cell (
), Case 1 of the 2 × 2 model with one reactive cell (
), Case 1 of the 3 × 3 model with four reactive cells (
), and Case 1 of the 2 × 2 model with four reactive cells (
), we understand the dependence of kinetics on
in that the rate constant for a single square increases in a nonlinear way as
increases;
= 0 (
), 0.323 (
), 0.486 (
), 0.654 (
), and 1 (
) (see the filled squares in
Figure 8). Similarly, for the PBC cases, from
Figure 6, if we consider Case 1 of the 3 × 3 model with one reactive cell (
), Case 1 of the 2 × 2 model with one reactive cell (
), Case 2 of the 3 × 3 model with four reactive cells (
), and Case 1 of the 2 × 2 model with four reactive cells (
), we see that the rate constant
increases with
in another nonlinear way;
= 0 (
), 0.892 (
), 0.952 (
), 0.982 (
), and 1 (
) (see the filled circles in
Figure 8).
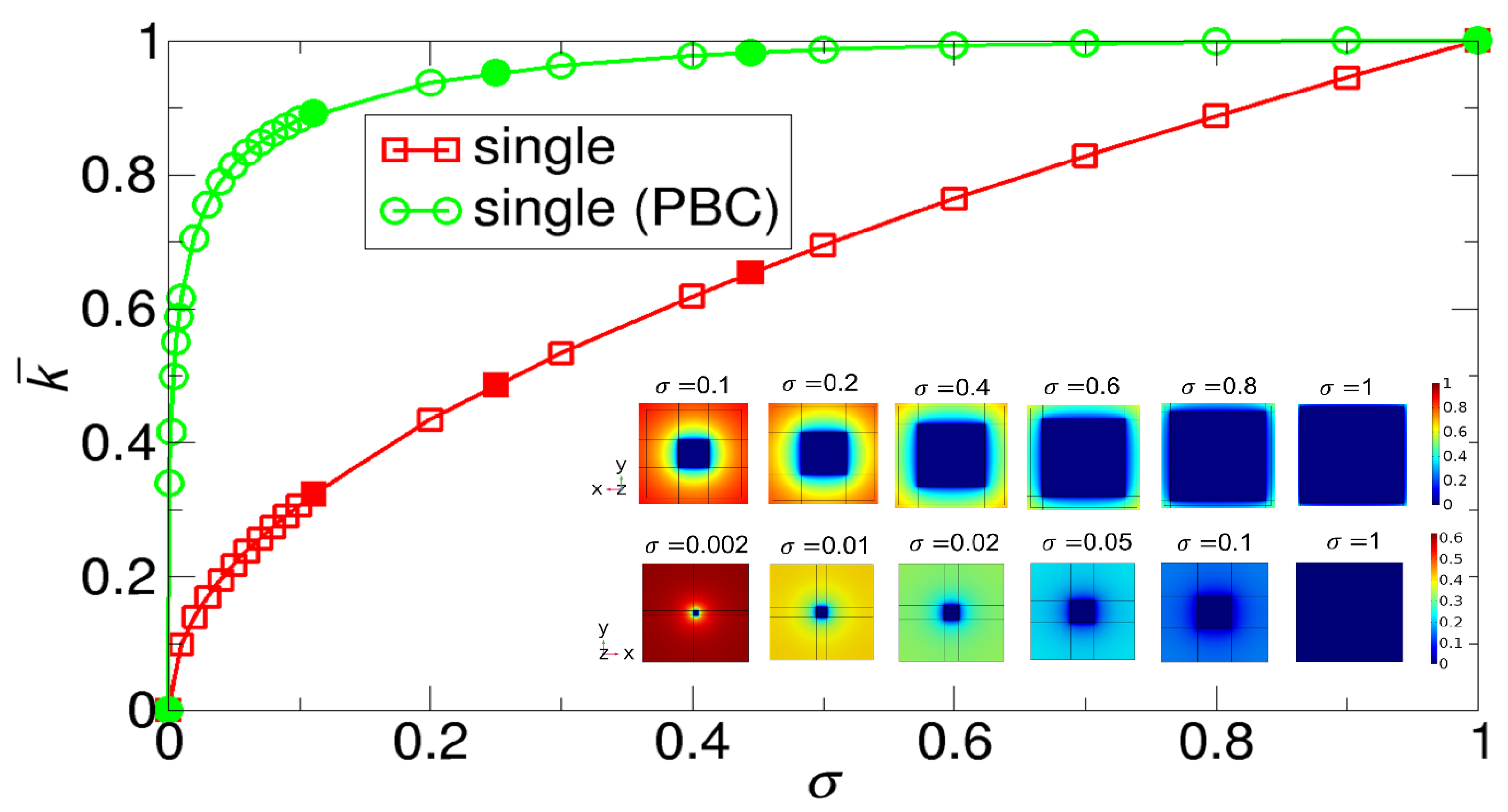
However, because of the limitations in exploring various cases with different values of
from the 2 × 2 and 3 × 3 square reactant models, we consider another square reactant model in which one reactive square cell is placed at the center of the square reactant. Here, we change the size of the reactive cell, such that we have different values of
. The result is shown in
Figure 8. We see that this result from the square model with one reactive cell is consistent with the results from the N × N square model from
Figure 4 and
Figure 6 (filled symbols). The main feature is that as
increases, the normalized rate constant
increases, and the effect is much more significant with PBCs. That is, for a given value of
, the rate constant in the presence of PBCs is larger than the corresponding rate constant without PBCs. In the presence of PBCs, even with
= 0.01, the normalized rate constant
is 61.7% of the maximum rate constant with
= 1, while the corresponding rate constant in the first model type without PBCs is 9.78%. Additionally, we notice that in the inset of
Figure 8, the concentration color at
= 0.1 is almost blue (concentration is near zero) for the case with PBCs; in this case, the normalized rate constant
is 88.2% of the maximum rate constant.
The high rate constants obtained with PBCs may suggest that in the first type of model, even in a single small patch in a reactant, if one breaks it into many smaller patches and arranges them such that any patch looks like the one with PBCs in
Figure 8, the overall rate constant can be significantly increased. To check this idea, we consider the division-separation procedure of reactive cells in
Section 3.5 and
Section 3.6 to see how the procedure enhances the rate constant.
Additionally, from the agreement of
between the square model of a single reactive cell and the 2 × 2 and 3 × 3 square models in
Figure 8, we note that the 2 × 2 and 3 × 3 square models are useful in obtaining a general trend of the dependence of the kinetics on
, although the results do not cover the full range of
. This result confirms the validity and usefulness of the simple N × N square reactant models.
3.4. Effect of the Reactive Patch Distribution on the Kinetics
The results of the N × N models in
Section 3.1 and
Section 3.2 show that the rate constant is dependent on the distribution of the reactive patches, as demonstrated by the variation in the rate constant
at a fixed value of
in the insets of
Figure 5a and
Figure 7a. The general trend is that when the patches (cells) are aggregated, the normalized rate constant
is lower than when the patches are largely separated. Here, we notice that the variation in the rate constant
is dependent on the fraction of the area of the unit cell
in the N × N model. That is, as N increases,
decreases, which allows more diverse arrangements of patches on a reactant and increases the variation of the rate constant. Note that in the 2 × 2 square reactant model,
is 1/4 and in the 3 × 3 model,
is 1/9.
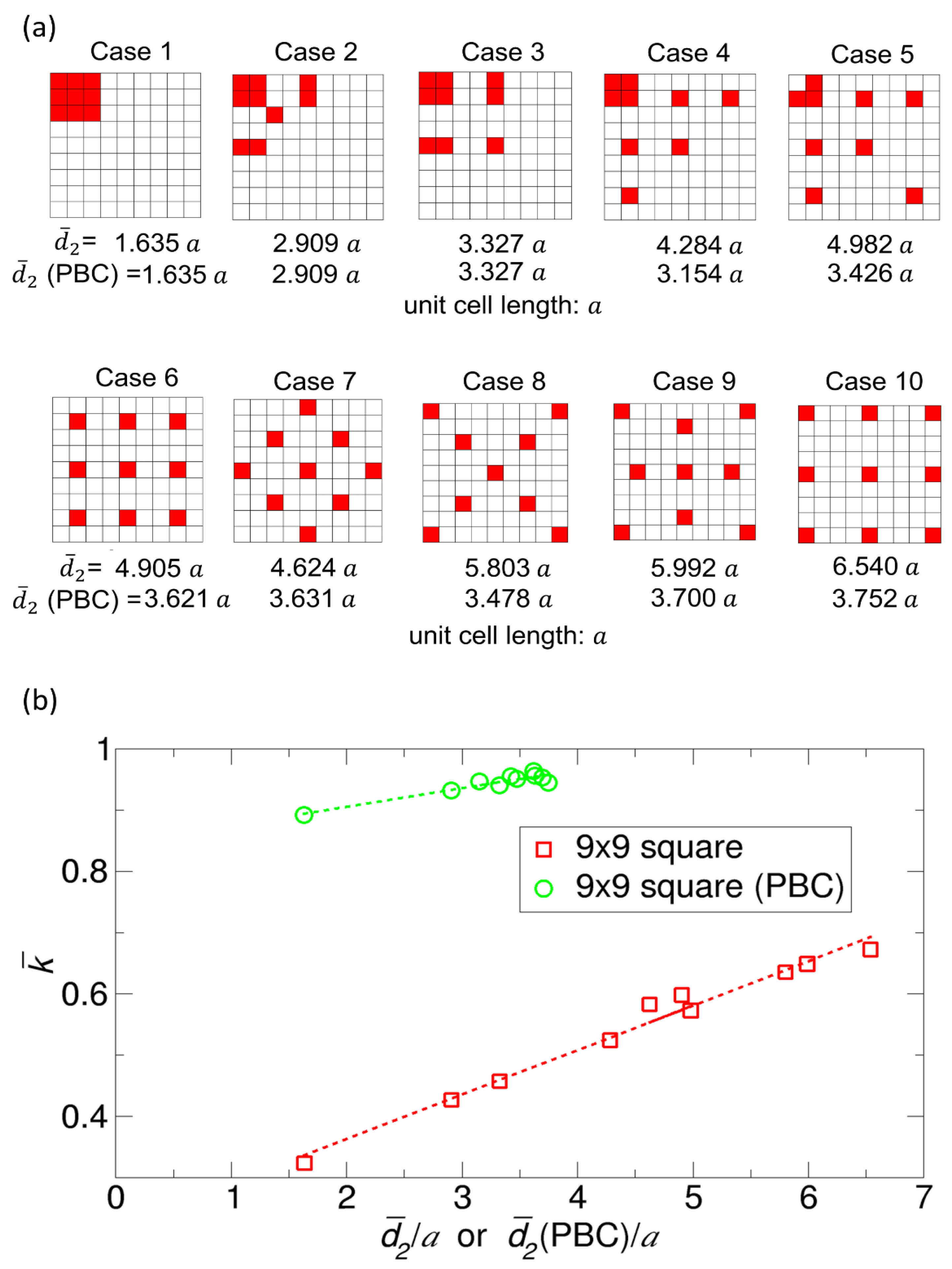
Since the 2 × 2 and 3 × 3 square reactant models do not provide a variety of patch arrangements, we consider the spatial arrangements of patches with
= 1/9 in the 9 × 9 square model with
= 1/81. In this case, the number of reactive cells is 9. Note that in the 3 × 3 square model, the number of reactive cells corresponding to
= 1/9 is 1. Moreover, note that in contrast to the 2 × 2 and 3 × 3 square models, in this case, considering all the possible patch configurations is practically impossible because the total number of arrangements of patches is enormous; when we ignore symmetrically equivalent patch arrangements and PBCs, the number of patch configurations is
81C
9; in fact, when we consider the symmetry of arrangements and PBCs, the actual number of symmetrically unique patch configurations is less than this number. Therefore, instead of considering all the cases, we consider 10 representative cases from the one with mostly aggregated patches to the one with largely separated patches, as shown in
Figure 9a. We also use the average value of the pairwise distance as a way to measure the degree of scattering of patches over the reactant surface. For each case, we calculate the normalized rate constant
for the first and second model types. We display the results as a plot of the normalized rate constant
versus the dimensionless average pairwise distance
or
, as shown in
Figure 9b.
In
Figure 9b, as one can expect from the competition between patches, as the reactive cells move away from each other or
increases, the normal rate constant
increases. This effect is more apparent in the first type of model without PBCs. Interestingly, for a given value of
= 1/9, by simply redistributing patches from the most aggregated patches (Case 1) to the maximally separated patches (Case 10), we can increase the normalized rate constant
by more than two times, from 0.323 to 0.671; the normalized rate constant
in Case 10 (
= 1/9) is comparable to the ensemble-averaged rate constant
for three reactive cells (
= 1/3) in the 3 × 3 model (see
Figure 4b; 0.653). Therefore, in addition to increasing the
value, another way to increase the rate constant is to arrange the patches such that they are more separated from each other.
In the second type of model with PBCs, we also observe the trend that the rate constant
increases with
, as is indicated by the linear regression line. However, with PBCs, except for Case 1 (the most aggregated case), the normalized rate constant
does not strongly depend on the details of the patch arrangements in that the values of
are more or less the same. Another interesting observation is that the case giving the highest rate constant is Case 6 (the most symmetrical arrangement), where the reactive cells are uniformly distributed in the presence of PBCs with equal distance between neighboring cells. This arrangement of reactive cells corresponds to the symmetric distribution minimizing their competitions in a sphere, which is related to the solutions of the Thomson problem or the Tammes problem [
7]. Specifically, our competition-minimization problem with
n reactive patches is similar to the Thomson problem aimed to find the spatial arrangement of
n electrons on a sphere giving the minimum potential energy and the Tammes problem aimed to find the spatial arrangement of circles maximizing the minimal distance between circles in that their solutions are generally uniformly distributed arrangements.
3.5. Symmetric Reactive Patch Distributions
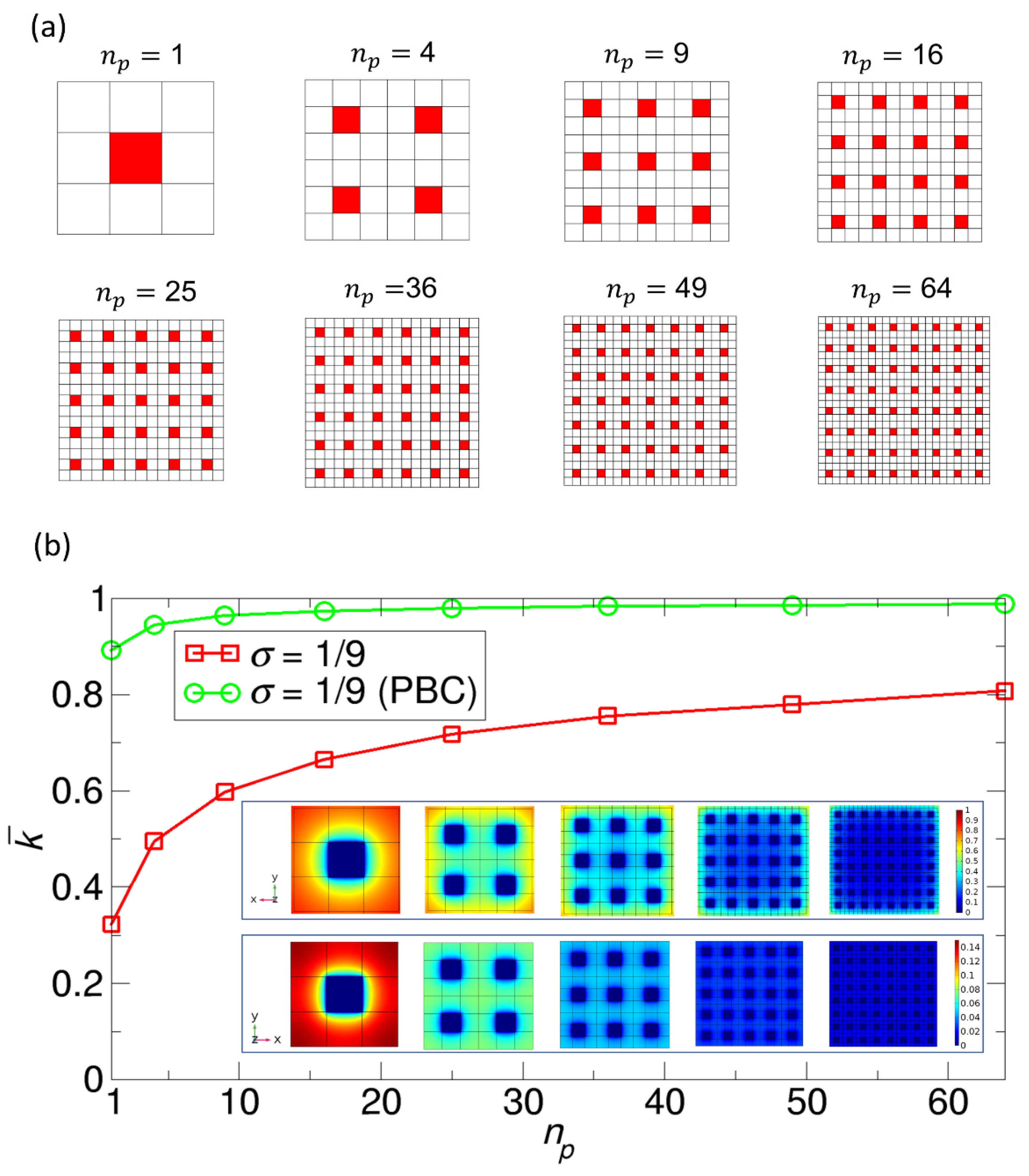
Based on the effect of the patch distribution in
Section 3.4, we further study the dependence of normalized rate constant
on the number of reactive patches
for a given value of
. For this study, we employ the square reactant models of
= 1/9 with symmetric patch distributions, in which the patches are uniformly distributed over the reactant surface (see Case 6 of
Figure 9a). In the patch distributions, we consider
= 1
2, 2
2, 3
2, 4
2, 5
2, 6
2, 7
2, and 8
2 and arrange the patches symmetrically (see
Figure 10a). Note that the case with
= 3
2 is exactly the same as Case 6 of
Figure 9a. For each case, we calculate the normalized rate constants
for the first and second model types, the results of which we present in
Figure 10b. The general trend is that the normalized rate constant
increases with
. As a result, for the first type of model, the case with
8
2 and
= 1/9 has a high rate constant (0.807), comparable to the rate constant (0.827) of the case with
1 and
= 0.7 (see
Figure 8). However, for the second type of model, even for
1, the normalized rate constant
is very high (0.891); thus, the enhancement of
due to the division and separation of patches is not as dramatic as that in the first type of model. Another feature in the plots of
Figure 10b is that as
increased, the effect of the enhancement of
is reduced; the enhancement is largest when
changed from 1 to 4.
3.6. Multiple Divisions of Patches and the Power–Law Relationship
For the square reactant model with symmetric patch distributions in
Section 3.5, we can further discuss the mathematical relationship between the normalized rate constant
and the number of reactive patches
for the cases with a fixed value of
. For the discussion, we consider sequential construction procedures for systematically generating the reactants with symmetric patch distributions of smaller patches. Precisely speaking, the procedures consist of N steps of division and symmetric arrangement of patches, and the procedures are sequential in that the reactant at the
Mth step is obtained from the reactant at the previous
M-1th step.
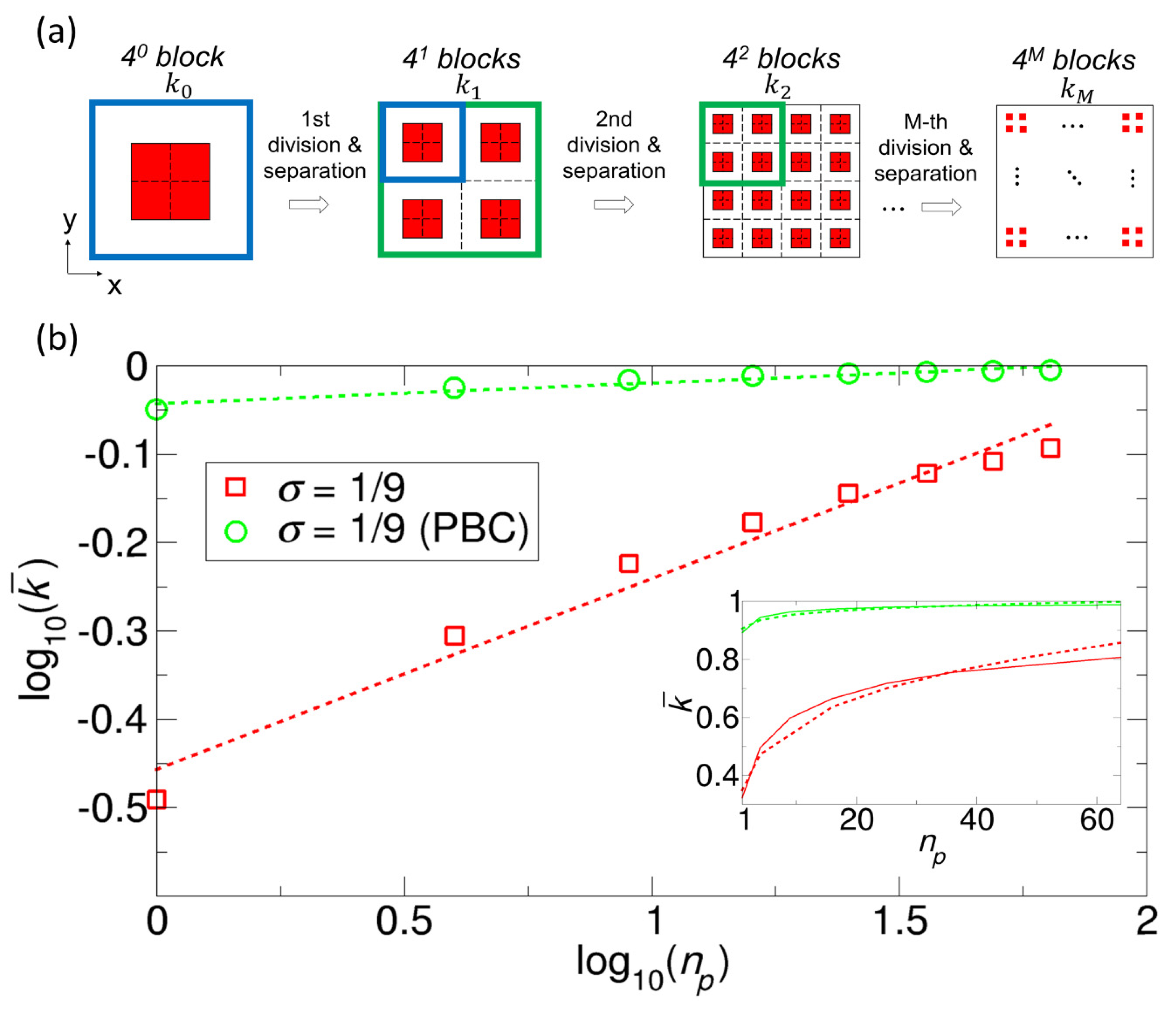
To explain the procedure in detail, we start with a single square reactive patch at the center of the square reactant, as shown in the leftmost reactant in
Figure 11a. In the first step, we divide the square reactive patch into four equal smaller patches. In
Figure 11a, the division of the patch is represented by the dotted lines. We also perform the same type of division for the entire square reactant, resulting in four smaller square blocks. For each smaller square block, we place one reactive patch at the center of the square block, resulting in the separation of the original reactive patch. The patch distribution obtained from this procedure is shown in the second reactant in
Figure 11a, which corresponds to the symmetric patch distribution with
=
=
in
Figure 10a. Note that each block with a smaller reactive patch has exactly the same shape as that of the original initial reactant. That is, if we select any one of the four blocks in the second reactant and enlarge its area by four times, the enlarge block will be exactly the same as the original reactant (see the blue square lines in
Figure 11a). Now, if we apply the same division-separation procedure to each of the four blocks in the second reactant in
Figure 11a, we generate another four smaller blocks for each block. As a result, the total number of patches is
=
=
; the overall patch distribution is shown in the third reactant in
Figure 11a. We can repeatedly apply this procedure to a reactant at each step.
Now, we consider how the overall normalized rate constant changes as we carry out the procedure repeatedly. For a quantitative discussion on the change in the rate constant due to the first division-separation procedure, we denote the rate constant before the procedure as , the rate constant after the procedure as , and the overall increasing factor of the rate constant due to the reduction in the competition by the first procedure as . Then, the overall rate constant is , where . Note that if the rate constant of each patch is simply proportional to its area, the overall rate constant is , since there are four patches with a rate constant of . Therefore, the reduction in competition is taken into account only through the factor , which may be different from system to system.
Similarly, from the second division-separation procedure, the competitions among the patches are further reduced. After the second procedure, we obtain the third patch distribution, in which 16 identical blocks are generated. Each block has a reactive square patch at its center. Because of the way we construct the reactant, a similarity symmetry exist between a four-block square in the third patch distribution and a four-block square (entire reactant) in the second patch distribution (see the green square lines in
Figure 11a). Because of the similarity symmetry appearing in the sequential procedures, we may assume that the increasing factor
due to the reduction in the competition by the second procedure is the same as the increasing factor
by the first procedure. Under the assumption that
, the overall rate constant after two divisions, or
, can be written as
. Together with
, we finally obtain
.
In this way, we can repeat the division-separation procedure under the similarity symmetry, the competition is continuously reduced, and as a result, the overall rate constant increases. Moreover, with the assumption that is constant, after an M-fold symmetric division and arrangement, we finally obtain the overall rate constant . That is, we obtain the power–law relationship between the rate constant and the number of division-separation procedures . Subsequently, we obtain the normalized rate constant , which is calculated by dividing by the rate constant for ( or ), and the same power law , where . However, note that this power–law scaling behavior has limitations. That is, we consider only the nearest neighbor competitions through the similarity symmetry, but if we take into account the competitions arising from all possible pairs of patches, the behavior of the rate constant will deviate from the power–law behavior as M or increases. Moreover, since the upper value of is 1 (normalized rate constant for ), we expect that as the number of procedures M increases, will eventually become saturated, which means that decreases; otherwise diverges as M increases.
In the case above of the division of patches by four, since the number of patches and the number of procedures are related by , we can represent in terms of as . That is, , which means that is proportional to . Additionally, note that from a logarithmic property, we can rewrite as . Therefore, the simple scaling argument provides a power law of for the rate constant , generally denoted by .
3.6.1. Analysis for the Case of 1/9
For the reactants with symmetric distributions in
Figure 10a, to see what the plot of
versus
looks like according to the above division-by-four procedure, we calculate
for the rate constant
shown in
Figure 10b and display the log-log plot in
Figure 11b. In the plot, the y-intercept and the slope correspond to
and
, respectively. Again, the physical interpretation of slope (
) as
means that if we increase
by
times (e.g.,
= 1, 4, 16, 64, …), the increasing factor
is given by
. However, the trend deviates from linearity as
increases. In fact, to find the slope, we fit the data with a linear equation for
versus
using the xmgrace program. The correlation coefficients for the first and the second model types in
Figure 10 are 0.985 and 0.960, respectively. These high values explain why the relation between
and
can be described by power laws (
or
). From the linear equations for the regressions, we can easily determine
for the division-by-four procedure; for a determined value of
,
is given by
. Note again that here, the factor of
is due to the division by four carried out in the procedure. In general, if we break a patch into
smaller patches at every step of the division,
. In this case, when each patch was divided into
patches in the procedures,
indicate how the normalized rate constant
scales with
(=
).
In fact, from
Figure 11b, we find power laws for
by determining the values of
and
; the slopes are 0.2158 and 0.02348 for the first and second model types, respectively, and accordingly, the
values are 1.349 and 1.033, respectively. In fact, in the inset of
Figure 11b, we plot the normalized rate constants
calculated by the power laws of
(dashed lines), along with the original ones shown in
Figure 10b (solid lines). The two curves are generally in good agreement, but the rate constant from the power–law deviates from the original rate constant as
increases.
Instead of using four patches in the division-separation procedure, we can break a single patch into a smaller number of patches. In this case, decreases since the competition decreases less; for example, in a division-by-two procedure, the values () for the first and second model types are 1.161 and 1.016, respectively. In contrast, if we break the patch into a larger number of patches, will increase since the competition decreases more. For example, in a division-by-eight procedure, the values () for the first and second model types are 1.566 and 1.050, respectively.
We now consider the general properties of the power laws observed in
Figure 11b. First, for all cases,
is greater than 1, which means that
always increases when the division and separation take place. Second, as
increases, we expect that the slope (
) decreases and eventually becomes zero (
) since
has an upper bound of 1; otherwise,
would be larger than 1 as
increases.
3.6.2. Analysis for the Cases of 0.01 and 0.001
In a reactant with symmetrically distributed reactive patches, we expect that as increases, the interference between a reactive patch and its other patches beyond the nearest neighboring patches is more significant. As a result, the increasing factor is more dependent on the number of patches, which means that the assumption that is constant, used to derive the power law of , becomes questionable.
In contrast, if
decreases, the interference is less significant and the assumption that the increasing factor
is constant makes more sense. To see if
shows more of a power–law behavior for small values of
, we consider the case of
= 0.01 for a reactant with symmetrically distributed patches for the first and second model types. The result is shown in
Figure 12. We also consider the case of
= 0.001, but it is only for the second type of model; moreover, we calculate the normalized rate constant
only up to
= 25 because of the difficulty in creating a very refined mesh for the first and second model types. In
Figure 12a, we display the normalized rate constant
as a function of
and in
Figure 12b, we show the log-log plot of
against
. Remarkably, the correlation coefficient for the case of the first model type with
= 0.01 is very high (0.997). In fact, the correlation coefficients for other cases are also high; 0.970 and 0.988 for the second model type with
= 0.01 and 0.001, respectively. From the slopes, we also determine the
values for the division-by-four procedure, i.e., 1.723 (first type,
= 0.01), 1.1494 (second type,
= 0.01), and 1.448 (second type,
= 0.001).