Abstract
Spectral singularities and coherent perfect absorption are two interrelated concepts that have originally been introduced and studied for linear waves interacting with complex potentials. In the meantime, the distinctive asymptotic behavior of perfectly absorbed waves suggests considering possible generalizations of these phenomena for nonlinear waves. Here, we address the perfect absorption of nonlinear waves by an idealized infinitely narrow dissipative potential modeled by a Dirac -function with an imaginary amplitude. Our main result is the existence of perfectly absorbed flows whose spatial amplitude distributions are asymmetric with respect to the position of the absorber. These asymmetric states do not have a linear counterpart. Their linear stability is verified numerically. The nonlinear waveguide also supports symmetric and constant-amplitude perfectly absorbed flows. The stability of solutions of the latter type can be confirmed analytically.
1. Introduction
The concept of spectral singularities (SSs) has already been known in mathematics for a long time [1,2]. The related physical phenomenon, known today as coherent perfect absorption (CPA) [3], was discovered independently [4,5,6] (see [7] for a chronological review on the topic) and is characterized by the asymptotic behavior of the field corresponding to only an incoming wave. The link between mathematical singularities and asymptotic behaviour of the respective solutions is established by the theorem due to Vainberg [8]. In the past decade, the interest in physical effects related to the SSs has been revitalized due do to a series of works [3,9,10] establishing direct links between mathematical properties of SSs and their relevance for physical applications, as well as due to the first experimental implementation of a CPA [11].
The early proposals of CPA addressed the absorption of the electromagnetic radiation by a layer with the complex-valued dielectric permittivity. This, in particular, can be implemented using a confined plasma layer [5]. More recently, CPA was reported for a variety of photonic systems, including plasmonic metasurfaces, graphene-based systems electromagnetic waves interacting with graphene and plasmonic metasurfaces, microcavities, etc.—see a recent review [12] on physical applications of photonic coherent perfect absorbers. Moreover, the paradigm of CPA was enriched by addressing the absorption of waves of various nature, such as acoustic waves interacting with a fluid absorber [13] and quantum superfluids depleted by a focused electron beam applied to an atomic Bose–Einstein condensate (BEC) [14].
By its definition, a SS is an essentially linear object. However, considering it from the physical point of view, i.e., focusing on the distinctive asymptotic behavior of the solutions associated with SSs, one can extend the paradigm to nonlinear setups. One of the ways to do this is by using nonlinear properties of a confined absorbing layer embedded in a linear medium [15,16]. Another possible way is to consider waves propagating in a nonlinear medium and interacting with a linear absorbing potential. This generalization of the concept of CPA was suggested in [17] and validated in experiments with atomic BECs [14]. Furthermore, the two types of nonlinearities (that of the potential and that of the medium) can be combined [18]. Strictly speaking, in the nonlinear case, there is no interference of states, and thus the coherence loses the meaning it has in the linear theory, but one can still consider perfect absorption.
These recent developments raise new questions in the theory of perfect absorption, such as the effects of eventual instabilities and nonlinearity-induced symmetry-breaking. The aim of this paper is to show that waveguides with a spatially uniform nonlinearity and a localized dissipation in the form of the idealized -function support perfectly absorbed modes with asymmetric amplitude distribution. In sharp contrast to constant-amplitude CPA solutions, nonlinear asymmetric currents cannot be reduced to the linear limit by decreasing the background solution intensity.
In a more general context of the nonlinear waves theory, the found asymmetric states are remarkable, because they are supported by only a single absorbing layer. This situation contrasts with the well-studied conventional spontaneous symmetry-breaking of nonlinear waves, which typically requires a double-well spatial potential (see e.g., [19,20,21,22]) or results from the competition between spatially inhomogeneous linear and nonlinear potentials [23].
2. The Model
We consider the spatially one-dimensional defocusing nonlinear Schrödinger equation (NLSE)
where is a real parameter which governs the strength of the dissipation (for ) or energy gain (for ), and is the Dirac delta function. The model (1) was introduced in Ref. [24] as a limiting case, modeling scanning electron microscopy of ultracold atomic gasses [25]. In such an experimental setting, a Bose–Einstein condensate is affected by a narrow electronic beam, which in the meanfield approximation is described by a localized dissipative potential in the Gross–Pitaevskii equation [26]. Similar scenarios with the spatially confined absorption of nonlinear waves can be implemented in other experimental setups, like nonlinear optical and magnon waveguides, plasmonic nanostructures, exciton-polariton condensates, etc. (see e.g., [17,27] for schematics of possible systems).
In what follows, we present our main results, mainly for the perfectly absorbed flows supported by a -function-shaped dissipation situated at , and therefore we assume . In the meantime, most of our results can be generalized straightforwardly on the case of a lasing potential, by inverting the sign of .
Looking for stationary states , where real has the meaning of the chemical potential of the condensate, we use the hydrodynamic representation of the time-independent wavefunction , where is the amplitude of the wavefunction, and is the hydrodynamics velocity. The respective current density, , is defined as . Now, Equation (1) reduces to the system
We are looking for perfectly absorbed flows directed from the left and the right infinities towards the center. The corresponding solutions are determined by the boundary conditions
where constants and set the background amplitude and the magnitude of the flow at the infinities. These boundary conditions fix the chemical potential
Since the perfectly absorbed flows are directed from the infinity to the center, the limiting (below also called background) current density is negative () for large positive x and positive () for large negative x. The case of lasing solutions emitted by a -function amplifying potential with can be addressed by assuming that . In this situation, it follows from (4) that the current is positive for and is negative for .
It follows from Equation (3) that the current density is the step function , and the background current density is related to the amplitude at as
Using the fact that is constant for , and integrating Equation (2) we obtain a first-order nonlinear differential equation, in which J plays the role of a parameter:
3. The Main Results
3.1. Symmetric and Asymmetric Perfectly Absorbed Flows
Let us now discuss possible types of perfectly absorbed solutions that can be found in the introduced model. First, we notice that there exists an immune to the dissipation solution in the form of a dark soliton pinned to [24]: . This solution does not correspond to a real physical absorber, since the corresponding current is identically zero: . Solutions of the second type correspond to the constant-amplitude nonlinear CPA modes and have uniform amplitudes . Such modes are characterized by the background current densities and represent the direct nonlinear generalization, parametrized by R, of the linear CPA corresponding to the SS of the absorbing -potential [28]. These nonlinear modes exist for arbitrarily strong dissipation .
Solutions of the third type are characterized by a spatially nonuniform amplitude with a dip. These solutions do not exist in the linear limit. They feature nonzero current density at the dissipative spot and have nontrivial and asymmetric amplitude landscapes. The possibility of existence of such currents becomes evident from the inspection of the phase space corresponding to the identity (7) which, for any J in the interval , features a homoclinic orbit connecting the saddle point to itself (according to the introduced boundary conditions, the latter saddle point corresponds to ). Further analysis of the differential Equation (7) shows that the homoclinic orbits exemplified in Figure 1 are associated with exact solutions of the form
where the new parameters D and are defined from the relations
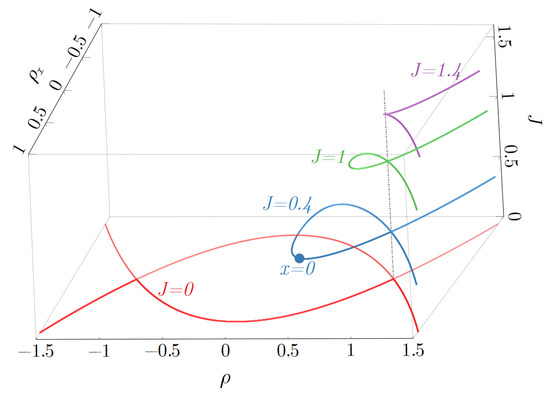
Figure 1.
Examples of orbits generated by the differential Equation (7) in the phase space for several different values of J. The heteroclinic orbits shown with red lines correspond to the dark soliton solution that is immune to the dissipation and bears zero background current . Homoclinic orbits with correspond to perfectly absorbed flows with a density dip in a uniform background. Each homoclinic orbit passes through the saddle point , where R is the background amplitude. Depending on the position of the point that corresponds to the dissipative spot, i.e., in our case, each orbit can represent either a symmetric or an asymmetric perfectly absorbed flow. In this figure, the background amplitude of nonlinear flows is fixed as .
Notice that the quantity which characterizes the depth of the dip in the squared amplitude is positive provided that . Additionally, for the solution to be meaningful, two more constraints must be imposed. The first condition reads
This condition is necessary to guarantee that the argument of in Equation (11) is real. In the asymptotic limit where J approaches from below, the argument of diverges, and the position of the intensity dip tends to . Another condition that needs to be imposed for the solutions to be meaningful reads
It implies that the right-hand side of (8) is nonnegative, and the argument of in Equation (11) is greater than or equal to unity.
Notice that found solutions are generically asymmetric, i.e., the minimum of amplitude is achieved at which is generically different from zero. Notice also that found states are essentially nonlinear, since they cannot be reduced to the linear limit by sending the nonlinearity coefficient to zero, i.e., they have no counterpart in the asymptotically linear limit of small background amplitudes . Such asymmetric perfectly absorbed states exist in pairs, with positive and negative , which is reflected by the ± sign in (11). To summarize the situation, in Figure 2 we show a representative existence diagram for perfectly absorbed solutions of different types. Since the main characteristic of a perfectly absorbed solution is the associated flux J, the existence diagram is presented in the plane J vs. for fixed background amplitude R. The emergence of asymmetric nonlinear states upon the increase of the dissipation strength is illustrated in Figure 3a for two fixed values of the background current J. Asymmetric states emerge when the dissipation strength exceeds (the latter value corresponds to the dissipation that is necessary to support the constant-amplitude CPA state with the given current J). Emerging nonlinear states are characterized by the infinitely large position of the amplitude dip (mathematically diverging is explained by the fact that the argument of in (11) is infinitely large). The further increase of the dissipation strength decreases and eventually, at , the amplitude distribution becomes symmetric with . Thus, symmetric perfectly absorbed states correspond to the equality sign in (13). The existence of symmetric dip solutions can be explained by the fact that in a realistic system that cannot support infinitely large background currents J, one should expect that the increase of the dissipation strength destroys the constant amplitude of the steadily absorbed state and eventually results in the decrease of the background current, rather than to its increase (compare red and green curves in Figure 2). This behavior can be attributed to the macroscopic Zeno effect studied previously in nonlinear waveguides with localized dissipation [27].
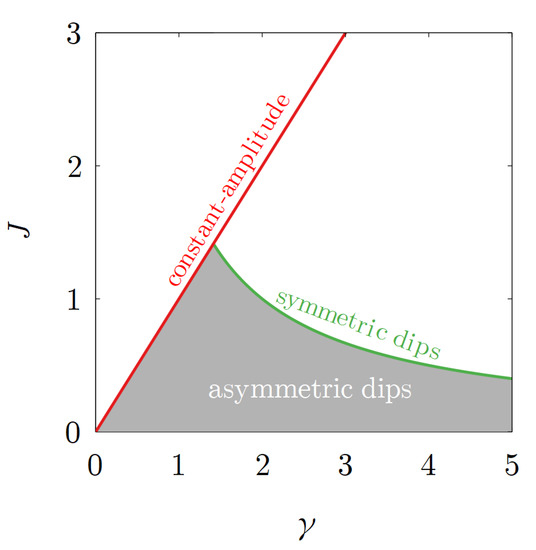
Figure 2.
The existence diagram for solutions of three different types discussed in Section 3.1. The diagram is shown in the plane J vs. for fixed background density . The gray domain corresponds to asymmetric dips, whereas red and green lines correspond to the constant-amplitude solutions and symmetric dips, respectively.
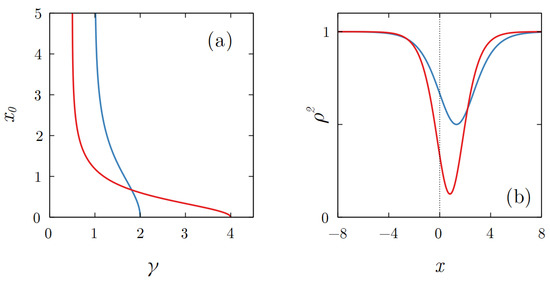
Figure 3.
(a) Dependencies of the position of the amplitude dip defined by (11) on the absorption strength for the fixed values of the background current: (red curve) and (blue curve). (b) Squared amplitude of asymmetric states that exist at with (red curve) and (blue curve). In both panels . Only solutions with are shown; there also coexist their mirror counterparts with .
3.2. Stability of Perfectly Absorbed Nonlinear Currents
In order to study spectral stability of the perfectly absorbed flows, we consider a perturbed stationary mode in the form , where u and v are small-amplitude perturbations. A linearization of the main Equation (1) with respect of u and v leads to the system
The spectrum of eigenvalues associated with bounded eigenfunctions and characterizes the stability of the stationary solution: the perfectly absorbed flow is unstable if there is an eigenvalue with negative imaginary part: . Since, for the defocusing nonlinearity, the modulational instability of the uniform background is absent, and it is intuitively clear that the thin absorbing layer cannot excite spatially unbounded unstable modes, we expect that the eventual instability can be caused only by spatially localized eigenmodes. We are therefore interested in eigenfunctions u, v that decay as .
In general, the eigenvalue problem (14) and (15) can only be solved numerically. However, for the constant-amplitude solutions, the analytical treatment is possible. Let us first consider this problem only in the right half-axis , where the stationary constant-amplitude wavefunction reads , and chemical potential reads . Using substitutions , , the stability equations take the form of a constant-coefficient ODE problem
where
Searching for solutions proportional to , the exponent k is determined from the characteristic equation for matrix :
For solutions, that decay at , roots k must belong to the right complex half-plane. Using the Routh–Hurwitz theorem [29], we conclude that for any with negative imaginary part, the characteristic Equation (18) has exactly two roots with positive real parts. Generically, those two roots are different, and the most general solution that decays at is a linear combination of two independent exponents. In terms of functions and , this solution has the form
where are complex-valued constant coefficients, and .
Next, we consider the eigenvalue problem (14) and (15) only in the left half-axis . The analysis can be performed in a similar way by replacing to and k with (because now we consider growing solutions ). As a result, the general solution reads
Applying the continuity conditions , and using that , we conclude that and . Integrating Equations (14) and (15) across , we obtain conditions for jumps of the derivatives:
It is easy to check that these conditions imply ; therefore no unstable localized mode is possible.
For the peculiar case when the characteristic Equation (18) has a double root in the right half-plane, inspecting the structure of this polynomial one can establish that the latter root is positive: , and, respectively, if the corresponding eigenvalue exists, then it is purely imaginary: , . In this case, without loss of generality, one can consider solutions of the form . The solution has the form , where upper and lower signs correspond to and , respectively, and are some coefficients. From the condition of the derivative jump, it follows that . On the other hand, from the ODE system (16) and (17), one can derive , which is impossible for real and . Therefore, in the case of the double root, the instability of constant-amplitude currents cannot take place.
Thus, we have demonstrated that no localized eigenmodes of the stability problem exist for any with nonzero real part. This implies the stability of constant-amplitude nonlinear CPA states.
For dark solitons and dip solutions, linear stability Equations (14) and (15) do not admit simple analytical treatment, but the spectrum of eigenvalues can be computed numerically. A systematic stability study demonstrates that these perfectly absorbed solutions are also stable for all parameters in their existence domain.
4. Conclusions
In this paper, we have studied nonlinear stationary flows perfectly absorbed by an idealized infinitely narrow dissipative spot of infinite strength, which can be modeled by a Dirac -function potential with a purely imaginary amplitude. The found solutions have been classified into three types. Solutions of the first type have the form of conventional dark solitons. Their amplitude is identically zero at the dissipative spot, and these solutions are therefore immune to dissipation and do not generate superfluid flows. Solutions of the second class have constant amplitude and represent a direct nonlinear generalization of linear coherently absorbed modes corresponding to the spectral singularities of the underlying -function potential. Solutions of the third type represent intensity dips in the uniform amplitude. Remarkably, these solutions do not have linear counterparts, and their amplitude distribution can be asymmetric. Constant-amplitude CPA flows and (a)symmetric dips are supported by superfluid flows directed towards the dissipation. Using the linear stability approach, we have demonstrated analytically that constant-amplitude flows are stable. The stability of dark solitons and dip solutions has been confirmed numerically.
Author Contributions
The authors claim to have contributed equally and significantly in this paper. All authors read and approved the final manuscript.
Funding
Work of D.A.Z. is funded by Russian Foundation for Basic Research (RFBR) according to the research project No. 19-02-00193. V.V.K. acknowledges support from the Portuguese Foundation for Science and Technology (FCT) under Contract no. UIDB/00618/2020.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEC | Bose–Einstein condensate |
| CPA | coherent perfect absorption |
| NLSE | nonlinear Scrödinger equation |
| SS | spectral singularity |
References
- Naimark, M.A. Investigation ofthe spectrum and the expansion in eigenfunctions of a nonselfadjoint operator of the second order on a semi-axis. Tr. Mosk. Mat. Obs. 1954, 3, 181–270. [Google Scholar]
- Schwartz, J. Some non-selfadjoint operators. Commun. Pure Appl. Math. 1960, 13, 609. [Google Scholar] [CrossRef]
- Chong, Y.D.; Ge, L.; Cao, H.; Stone, A.D. Coherent perfect absorbers: Time-reversed lasers. Phys. Rev. Lett. 2010, 105, 053901. [Google Scholar] [CrossRef] [PubMed]
- Khapalyuk, A.P. Electromagnetic field inside a plane-parallel plate in a resonance absorption regime. Dokl. Akad. Nauk BelSSR 1962, 6, 301. [Google Scholar]
- Zharov, A.A.; Zaboronkova, T.M. On the optimal absorption of electromagnetic waves by finite plasma structures. Fiz. Plazmy 1983, 9, 995. [Google Scholar]
- Poladian, L. Resonance mode expansions and exact solutions for nonuniform gratings. Phys. Rev. E 1996, 54, 2963. [Google Scholar] [CrossRef]
- Rosanov, N.N. Antilaser: Resonance absorption mode or coherent perfect absorption? Phys. Usp. 2017, 60, 818. [Google Scholar] [CrossRef]
- Vainberg, B. On the analytical properties of the resolvent for a certain class of operator-pencils. Math. USSR Sb. 1968, 6, 241. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Spectral singularities of complex scattering potentials and infinite reflection and transmission coefficients at real energies. Phys. Rev. Lett. 2009, 102, 220402. [Google Scholar] [CrossRef]
- Longhi, S. PT-symmetric laser absorber. Phys. Rev. A 2010, 82, 031801(R). [Google Scholar] [CrossRef]
- Wan, W.; Chong, Y.; Ge, L.; Noh, H.; Stone, A.D.; Cao, H. Time-reversed lasing and interferometric control of absorption. Science 2011, 331, 889. [Google Scholar] [CrossRef] [PubMed]
- Baranov, D.G.; Krasnok, A.; Shegai, T.; Alú, A.; Chong, Y. Coherent perfect absorbers: Linear control of light with light. Nat. Rev. Mater. 2017, 2, 17064. [Google Scholar] [CrossRef]
- Song, J.Z.; Bai, P.; Hang, Z.H.; Lai, Y. Acoustic coherent perfect absorbers. New J. Phys. 2014, 16, 033026. [Google Scholar] [CrossRef]
- Müllers, A.; Santra, B.; Baals, C.; Jiang, J.; Benary, J.; Labouvie, R.; Zezyulin, D.A.; Konotop, V.V.; Ott, H. Coherent perfect absorption of nonlinear matter waves. Sci. Adv. 2018, 4, eaat6539. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Nonlinear spectral singularities for confined nonlinearities. Phys. Rev. Lett. 2013, 110, 260402. [Google Scholar] [CrossRef]
- Reddy, K.N.; Dutta Gupta, S. Light-controlled perfect absorption of light. Opt. Lett. 2013, 38, 5252–5255. [Google Scholar] [CrossRef][Green Version]
- Zezyulin, D.A.; Konotop, V.V. Nonlinear currents in a ring-shaped waveguide with balanced gain and dissipation. Phys. Rev. A 2016, 94, 043853. [Google Scholar] [CrossRef]
- Zezyulin, D.A.; Ott, H.; Konotop, V.V. Coherent perfect absorber and laser for nonlinear waves in optical waveguide arrays. Opt. Lett. 2018, 43, 5901. [Google Scholar] [CrossRef]
- Gaididei, Y.B.; Mingaleev, S.F.; Christiansen, P.L. Curvature-induced symmetry breaking in nonlinear Schrödinger models. Phys. Rev. E 2000, 62, R53. [Google Scholar] [CrossRef]
- Jackson, R.K.; Weinstein, M.I. Geometric analysis of bifurcation and symmetry breaking in a Gross-Pitaevskii equation. J. Stat. Phys. 2004, 116, 881. [Google Scholar] [CrossRef]
- Theocharis, G.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Schmelcher, P. Symmetry breaking in symmetric and asymmetric double-well potentials. Phys. Rev. E 2006, 74, 056608. [Google Scholar] [CrossRef] [PubMed]
- Matuszewski, M.; Malomed, B.A.; Trippenbach, M. Spontaneous symmetry breaking of solitons trapped in a double-channel potential. Phys. Rev. A 2007, 75, 063621. [Google Scholar] [CrossRef]
- Zezyulin, D.A.; Lebedev, M.E.; Alfimov, G.L.; Malomed, B.A. Symmetry breaking in competing single-well linear-nonlinear potentials. Phys. Rev. E 2018, 98, 042209. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Konotop, V.V.; Pérez-García, V.M.; Ott, H. Dissipation-induced coherent structures in Bose-Einstein condensates. Phys. Rev. Lett. 2009, 102, 144101. [Google Scholar] [CrossRef]
- Gericke, T.; Würtz, P.; Reitz, D.; Langen, T.; Ott, H. High-resolution scanning electron microscopy of an ultracold quantum gas. Nature Phys. 2008, 4, 949–953. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Zezyulin, D.; Konotop, V.V.; Barontini, G.; Ott, H. Macroscopic Zeno Effect and Stationary Flows in Nonlinear Waveguides with Localized Dissipation. Phys. Rev. Lett. 2012, 109, 020405. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Delta-function potential with a complex coupling. J. Phys. A Math. Gen. 2006, 39, 13495. [Google Scholar] [CrossRef]
- Gantmacher, F.R. The Theory of Matrices; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).