Abstract
Turn-Milling Combined NC machine tool is different from traditional machine tools in structure and process realization. As an important means in the design stage, the analysis method of geometric accuracy error is also different from the traditional method. The actual errors and the error compensation values are a pair of "symmetry" data sets which are connected by the movement of machine tools. The authors try to make them more consistent through this work. The geometric error terms were firstly determined by topological structure analysis, then based on homogeneous coordinate transformation and multibody system theory, the geometric error model was established. With the interval theory, the function rule of sensitivity of geometric error sources to spatial errors was analyzed in detail, and the global maximum interval sensitivity of nine geometric error sources was extracted, providing a theoretical basis for error compensation and precision distribution. The geometric error sensitivity analysis method proposed in this paper can accurately evaluate the influence weights of each error term on the machining accuracy, and identify the important sensitive error terms with great influence on the machining accuracy from many error terms.
1. Introduction
Aimed at actual processing needs of the automotive, aerospace, military, and other industries, Turn-Milling combined NC machine tool can not only carry out turning, milling, drilling, grinding, and other multi-process compound processing, the use of multi-axis linkage function can also complete the inclined parts and complex space surface processing, which is greatly improving the processing efficiency and accuracy. At the same time, with the further development of processing technology, some scholars and researchers have carried out remarkable researches to improve the processing quality of workpieces. Radoslaw et al. [1] presented a comprehensive approach to surface formation after machining with different cooling/lubricating techniques. Nieslony et al. [2] used some physical and technological aspects of a precise turning with Self-Propelled Rotary Tool. Marta et al. [3] illustrated the influence of manufacturing technology, cutting speed, and feed ratio on selected surface parameters of samples was made. Wojciechowski et al. [4] proposed the prediction of cutting forces during micro end milling using a novel approach that takes into account the chip thickness accumulation phenomenon.
Geometric error modeling can significantly improve the performance of machine tools in the design process. The key to research in error modeling techniques is to find a more effective modeling method to accurately reflect the error of the machine tool through the established model. The research of machine tool error modeling method has been developed for a long time. Existing machine tool error modeling technology research toward multi-axis, multi-error, multi-factor direction, all kinds of research results and practical applications more closely integrated. Most of the existing techniques are based on the theory of multibody system theory (MBS) using the homogeneous coordinate transformation method.
Tao et al. [5] used matrix decomposition method to simplify the calculation of tool position error in the volumetric error model based on MBS. Further-more, Tao developed a geometric error model for the turning process on an ultra-precision lathe based on MBS [6], and the machining accuracy of workpieces can be improved by crucial geometric error compensation. Guo et al. [7] established a synthetic geometric error model for a five-axis machine tool with tilting head and turntable based on the MBS and the method of homogeneous coordinate transformation. Based on the theory of MBS, Chen et al. [8] established an error model of angular measurement with geometric errors of a torsional characteristic measurement system based on MBS, which can effectively predict the angular measurement error. Other new theories have been applied to modeling machine tool errors, such as screw theory. Zhang et al. [9] dealt with geometric error modeling and sensitivity analysis of an over-constrained parallel mechanism based on the screw theory. The proposed geometric error modeling method can also be applied to other types of parallel mechanisms. Zha et al. [10] modeled the geometric errors of the NC rotary table using the screw theory, and a three-point measurement method was proposed to realize the separation of these geometric errors. Chen et al. [11] used motion-axis differential operators to calculate the differential transformation matrix of each motion axis, and summed them to obtain the integrated error transformation matrix of the machine. Tang et al. [12] presented the process of transferring geometric errors in a multi-axis system using the stream of variation. (SOV). Fu et al. [13,14] used the product-of-exponential theory to establish an exponential product error model for CNC machine tools and proposed a geometric error compensation method based on Jacobian of twists. In addition, Fu et al. [15] applied differential motion relation to geometric error modeling, expressing the error model as the sum of the errors of the individual axes of motion.
Cheng et al. [16] used a variance-based Sobol global sensitivity analysis method to conduct sensitivity analysis of the geometric errors of three-axis ultra-precision turning machine tool. Los et al. [17] proposed an adaptive Monte Carlo method to analyze the uncertainty of geometric errors in 5-axis machine tools. Guo et al. used various methods for error sensitivity analysis and error optimization methods, such as the use of extended Fourier amplitude sensitivity test method to establish a quantitative global sensitivity analysis model for geometric error elements, which is suitable for identifying the key geometric errors and improving the precision of CNC machine tools effectively [18]. In addition, he used the global sensitivity analysis method to quantitatively analyzed the influence of uncertainty of geometric error on the multidimensional output simultaneously [19,20]. Cui et al. [21] took a 3-axis nano-machine as an example and used the MBS to establish a geometric error transfer model for the machine tool. Then, a sensitivity analysis method based on orthogonal experiments was proposed and sensitivity coefficients of error were calculated. Guo et al. [22] used the multiplication dimension reduction method to obtain a one-dimensional error model and performed a global sensitivity analysis of the three-axis CNC milling machine errors to identify important errors.
The sensitivity analysis method based on interval theory can effectively compensate for the deficiencies of traditional sensitivity calculation methods, especially for non-linear systems, with higher calculation efficiency and more accurate results [23]. Therefore, in the machine tool design and assembly process, it is possible to avoid the poor accuracy caused by the loose geometric accuracy or unnecessary costs due to the tight accuracy, so as to achieve the purpose of guiding the machine tool design and assembly.
Turn-Milling combined NC machine tool, compared to conventional machining tools, generally have at least three parallel axes and two rotary axes. These multi-axis machine tools change the directional vector of the tool during motion due to the presence of the rotary axes. In addition, the specific structure of the machine tool determines the kinematic relationship between the axes and the obverse and inverse solutions, but the different combinations of parallel axes and rotary axes and the sequence of combinations lead to a variety of configurations of multi-axis machines. Therefore, it is necessary to build geometric error models for machining tools and analyze their tool attitude changes to improve the effectiveness. At the same time, the sensitivity of each geometric error source will provide the weights for the geometric accuracy allocation. This method is less costly than the traditional geometric accuracy allocation, which not only has significant economic value, but also greatly extends the service life of the existing machine tools.
For machine centers, the actual errors and the error compensation values are a pair of “symmetry” data sets which are connected by the movement of machine tools. Through the establishment of error model and sensitivity analysis, the main influencing factors in the symmetric data set can be found. In this work, considering special characteristics of the structure and working mode of the Turn-Milling combined machine tool, its topological structure is described, and 45 geometric error terms are analyzed and determined. Moreover, the ideal and real kinematic models are established, and the geometric error models are derived with the unity coordinate transformation and multibody system theory. Based on the interval theory, the sensitivity of each geometric error source to its spatial error is analyzed. In practical applications, according to the actual error detecting results when the machine running, the key error terms that cause machining errors can be calculated through the proposed error model, and these errors can be compensated in advance by the CNC system. As a new type of machine tool, this work provides an effective method to improve the machining accuracy.
2. Geometric Error Terms for Turn-Milling Combined NC Machine Tool
2.1. The Topological Structure of Turn-Milling Combined NC Machine Tool
In terms of machine structure, the machine bed of the Turn-Milling Combined NC machine tool is T-shaped, which can effectively carry the weight of the column structure [24]. The column structure moves left and right on the bed to form Z-axis. The sliding plate moves up and down inside the column to form X-axis. The ram moves forward and backward inside the sliding plate to form Y-axis. The turning spindle is directly driven by a built-in electric spindle for C-axis function, and the B-axis is installed in Y-axis ram to drive the tool spindle to rotate within −30° to +210°. The tailstock adopts the upper and lower split tilting type, which is easy to assemble and adjust, and the tailstock of the upper body can be replaced by the second spindle according to the customer’s request. The tool magazine is arranged on the outside of the first spindle box.
The parts of the machine tool are considered to be composed of various rigid bodies, then the Turn-milling combined NC machine tool can be considered as a multibody system, which is containing multiple branching chains of open loops from the tool, the workpiece to the bed. The steps of the multibody system are described with low-order body array. Topological structure of the machine is shown in Figure 1. The base coordinate system, which is set on the bed of the machine, is first selected and numbered 0. Z-axis guide rail is mounted horizontally on the bed, numbered 1. X-axis guide is mounted vertically on Z-axis, numbered 2. Respectively, Y-axis guide is mounted on X-axis, numbered 3. And B-axis parallel to Y-axis, it is mounted on Y-axis, numbered 4. Tool is mounted on the B-axis, numbered 5. Turning spindle C is mounted on the bed, numbered 6, workpiece is mounted on the spindle, numbered 7. W-axis numbered 8 is mounted on the bed, the direction of motion is opposite to the positive direction of Z-axis, tailstock is mounted on W-axis, its number is 9.
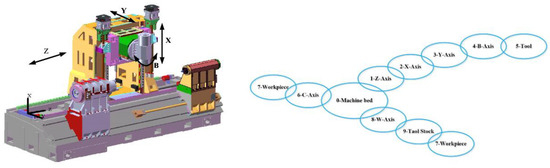
Figure 1.
The topological structure of Turn-Milling Combined NC machine tool.
The low-order body array of each classical body in the Turn-Milling Combined NC machine tool can be calculated according to the above relationship, and the low-order body array of its topological structure can be obtained, shown in Table 1.

Table 1.
Low-order body array of Turn-milling combined NC machine tool.
2.2. Determination of Geometric Error Terms
The geometric error can be divided into position-independent error and position-dependent error. Position-independent error has nothing to do with the position of the machine’s movement axes in space, generally due to manufacturing defects and wear of the machine tool itself, which is a constant value. Position-dependent error is mainly caused by assembling deviation between two motion axes and other transmission components, resulting in deviations in the movement of the axes in the process of movement. Therefore, position-dependent error is a variable about the position of the machine tool in the machining process.
Position-independent error mainly includes the perpendicularity error of the linear and rotary axes. According to the transmission order of movement axis, Z-axis is connected to the bed, so it does not have any position-independent error, X-axis is attached to Z-axis, the direction of X-axis is defined in the actual Z-axis and X-axis plane, the X-axis has a perpendicularity error around Y-axis in this plane. Similarly, there are two perpendicularity errors on the Y-axis. W-axis is an additional coordinate system, parallel to Z-axis, and there are two perpendicularity errors. Due to the installation error, the direction of the axis of rotation of axis B cannot be completely parallel to Y-axis, there are perpendicularity errors around the X-axis and around Z-axis, respectively, similarly there are two perpendicularity errors between C-axis and Z-axis.
Each machine tool component has six degrees of freedom in space, so there are six position-dependent errors, including three positional errors and three angular errors, denoted by and , respectively. The first of these subscript i denotes the direction of this error, along X-, Y-, and Z-axes and the direction of rotation around X-, Y-, and Z-axes, respectively. The second subscript j denotes the machine tool motion axis code, which can be X, Y, Z, B, W, C. For example, denotes the positioning error of motion X-axis in the x direction, and and denote the straightness error of motion X-axis in the y and z direction. The angular errors can be divided into yaw error, pitch error, and roll error according to the different directions. Therefore, according to the definition, the machine has a total of 45 geometry error terms listed in Table 2.

Table 2.
The geometric errors terms for Turn-milling combined NC machine tool.
3. Geometric Error Modeling Methods
Firstly, it is necessary to build a kinematic model to establish the kinematic relationship, considering the initial position of each axis and the position changes caused by the movement, between the tool coordinate system and the workpiece coordinate system according to the kinematic chain. Based on low-order body array of actual structure of a CNC machine according to MBS, homogeneous coordinate transformation matrix is used to calculate the position of the cutting point of the tool and the attitude of the tool axis in the workpiece coordinate system. Combined with constraints of the forming motion, the geometric error model can be built, deriving the motion position error of the spatial point and the motion attitude error of the spatial vector.
The kinematic model establishes the relationship between the tool and the workpiece, and the model is also the basis for kinematic obverse and inverse solutions, tool position analysis, and CNC instructions. However, the existence of relative static and motion errors between the axes leads to cumulative errors during actual motion, which have an impact on the theoretical tool path and machining accuracy.
3.1. Analysis of Ideal Kinematics Model of Turn-Milling Combined NC Machine Tool
The position relationship between machine tool coordinate system, workpiece coordinate system, and each moving body coordinate system of should first be determined. The machine bed coordinate system is located at the fixed position of the machine tool and used to determine the reference relationship between workpiece and machine tool, its direction is the same as the theoretical direction of the X-, Y-, and Z-axes. The workpiece coordinate system is the same as the programming coordinate system used in CAM. When the workpiece mounted to the machine, the deviation relationship between the workpiece and the machine coordinate system can be determined. The origin of the tool coordinate system is the position of the center point of the tool; the position of these three coordinate systems in space is shown in Figure 2.
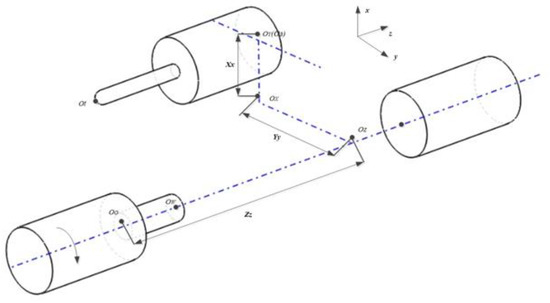
Figure 2.
Coordinate system in milling mode.
As shown in Figure 2, there are two kinematic chains in this Turn-Milling Combined NC machine tool.
The first chain: workpiece—C-axis—machine bed—Z-axis—Y-axis—X-axis—spindle—tool.
The second chain: workpiece—tailstock—W-axis—machine bed—Z-axis—X-axis—Y-axis—spindle—tool.
Using the bed as a boundary, the first kinematic chain is divided into a workpiece chain and a tool chain.
Workpiece chain: machine bed—C-axis—workpiece.
Tool chain: machine bed—Z-axis—X-axis—Y-axis—B-axis—tool.
To facilitate kinematic modeling, the coordinate system of each rigid body on the workpiece chain is set at , which is the intersection of the chuck endface and the rotary axis. The Z-axis coordinate system on the tool chain is established at distance from Z axis, the X-axis coordinate system is established at distance from Z-axis, and the Y-axis coordinate system and the tool coordinate system are established at the intersection of the tool axis and the B-axis. All coordinate system orientations are the same as .
3.2. Analysis of Actual Kinematics Model of Turn-Milling Combined NC Machine Tool
Firstly, move the distance of x, y, z along the coordinate axis, then rotate the axis of rotation around the X- Y-and Z-axis by angle A, B and C successively, the transformation matrix between the two coordinate systems can be obtained as Equation (1). Homogeneous coordinate transformations achieve the representation of points in different coordinate systems, and the order of translation transformation does not affect the coordinates after the movement of the composite transformation, but the change order of rotation transformation will influence the coordinates.
Since the errors are very small, the Taylor expansion of and can be replaced after neglecting the second and higher order terms, expressed as,
Therefore,
3.2.1. The Actual Kinematics Model in Milling Mode
The actual motion in space can be seen as adding an error motion to the theoretical motion. Therefore, the actual motion transformation between adjacent bodies a and b can be expressed as the actual coordinate transformation matrix between a and b.
In the actual turn-milling process, the motion error of each axis as well as the spatial geometric error between the axes always exists. Each geometric error is defined in Table 2, according to which the feature matrix is obtained, as shown in Table 3.

Table 3.
Position and motion error transformation matrices for adjacent bodies.
The actual position vector of the milling mode in the workpiece coordinate system, according to the transmission chain, can be solved as,
Since the motion of the linear axis does not change the orientation vector of the tool for the linear axis, and therefore only the effect of the position-independent error of the linear axis and the position-dependent error on the tool attitude is considered, the actual orientation vector of the milling mode of the tool in the workpiece coordinate system can be written as,
The position vector and the direction vector of the tooltip point can be obtained in the workpiece coordinate system by Equations (6) and (7).
3.2.2. The Actual Kinematics Model in Turning Mode
Based on the theoretical model of kinematics in the turning mode and the error-transformation matrix, the actual kinematics model with geometric errors can be solved as,
In this mode, since the orientation vector of the tool does not change, only the actual position vector needs to be analyzed.
3.3. Geometry Error Modeling of Turn-Milling Combined NC Machine Tool
With the low-order body analysis, the corresponding feature matrices are built according to of each adjacent body features in each error branch, which are represented by the main feature symbols and auxiliary feature symbols, and then the corresponding standard feature matrices are found according to the feature symbols of adjacent body.
The position vector error and the direction vector error can be written as,
3.3.1. Geometry Error Modeling in Milling Mode
According to Equation (9), the kinematic error in the milling mode can be written as,
3.3.2. Translation Axis Geometric Error Model
Parallel unit is an important component in the multi-axis CNC machine tool system, and the geometric error of the parallel unit accounts for a large proportion of the machine tool geometric error. As a specialized research, the parallel system geometric spatial error model should be built. This error model in the total geometric error modeling is easy to obtain.
Assuming that the rotary feed unit and spindle are fixed, can be written as,
Ignoring second-order and higher-order items, can be represented as,
4. Geometric Precision Error Analysis
Geometric error compensation can improve the machining accuracy to a certain extent, but when compensating each geometric error, there are problems such as heavy workload and poor compensation effect. To avoid the blindness of the error compensation, the sensitivity analysis of the geometric error should be carried out. The sensitivity coefficient of the error term can quantify the influence weight of each error term. Based on the sensitivity analysis result, the error terms that have a significant impact on accuracy can be identified. Targeted compensation and correction of important sensitive error terms can effectively improve machining accuracy.
4.1. Analysis of the Interval Sensitivity of Each Axis to Geometric Errors
The sensitivity of position error source to the spatial error component can be defined directly as,
In Equation (14), is the interval expansion factor of the angular error source on the spatial error component . When the instrument measurement axis does not coincide exactly with the actual motion axis, an error caused by the axis angle will be generated during movement of the parts, known as Abbe error. Therefore, for the angle error source, the interval dilation factor cannot be used directly as sensitivity due to the existence of Abbe error.
Based on the above considerations, the sensitivity of the angular error source to the spatial error component is,
In Equation (15), is the interval expansion factor of the angular error source for the spatial error component when the X-, Y-, and Z-axes are located at the origin and the tool length is 0.
According to the actual structure of the machine, the values of each body coordinate system in the basic coordinate system are: . are related to the actual workpiece coordinate system position of the part and the tool length. Substituting the structural parameter values into the spatial error Equation (13) for the Turn-milling combined NC machine tool, the simplified error model is obtained as,
4.1.1. Interval Sensitivity Analysis of X-Axis Geometric Error to Spatial Error
To describe the sensitivity coefficients and more clearly, the statistics and analysis of the data are carried out with the matplotlib module of Python. The sensitivity coefficients of the X-axis geometric errors are shown in Figure 3.
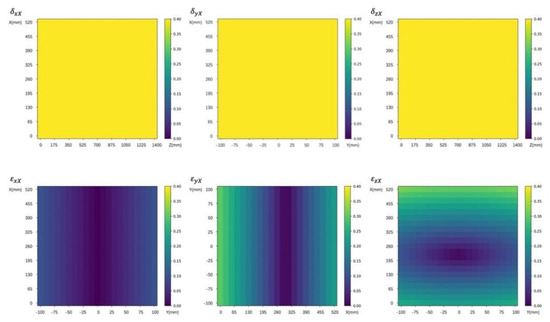
Figure 3.
Interval sensitivity of X-axis geometric error to spatial error.
The six geometric errors, on X-axis are sequentially analyzed. have the same effect on the spatial error; and their sensitivity does not change with the position movement, and the sensitivity to is always 1. The sensitivity of to terms does not exceed 0.1, and increases with the increase of Y coordinate. The sensitivity of to spatial error decreases first and then increases with the increase of the X coordinate, and the maximum value does not exceed 0.35. The sensitivity of to spatial error first decreases and then increases with the increase of X coordinate, which increases with the increase of Y coordinate, and the sensitivity changing along X-axis has a larger range.
4.1.2. Interval Sensitivity Analysis of Y-Axis Geometric Error to Spatial Error
The sensitivity analysis on the 6 geometric errors on Y-axis at above position points can be drawn from Figure 4. Three errors have the same effect on the spatial error. Their sensitivity does not change with the movement of the X-axis, Y-axis and Z-axis, and the sensitivity to the ∆r is always 1. Three items , have no effect on errors in ΔX, ΔY, and ΔZ directions, can be ignored.
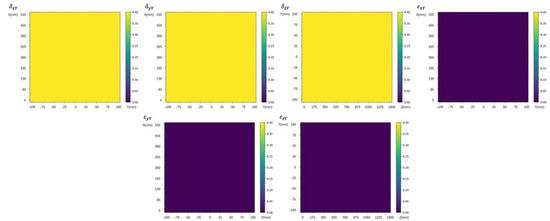
Figure 4.
Interval sensitivity of Y-axis geometric error to spatial error.
4.1.3. Interval Sensitivity Analysis of Z-axis Geometric Error to Spatial Error
The sensitivity of the six geometric errors on Z-axis at above position points can be drawn from Figure 5.
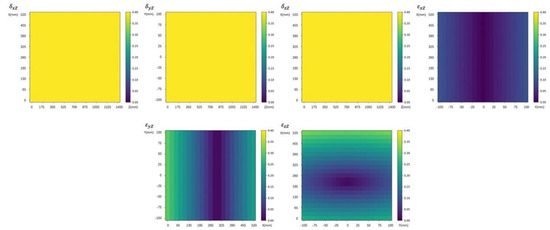
Figure 5.
Interval sensitivity of Z-axis geometric error to spatial error.
The influence of on the spatial error is the same as the position error of X-axis and Y-axis. Its sensitivity does not change with the movement of X-axis, Y-axis and Z-axis, and the sensitivity to ∆r point is always 1.
The sensitivity of shows an upward trend as Y coordinate moves away from the origin, but the maximum value is only 0.1. The sensitivity of increases first and then decreases with the increase of X coordinate, so the error sensitivity at both ends of X-axis is the highest, reaching about 0.3. The sensitivity of changes with the movement of both X-axis and Y-axis.
4.1.4. Interval Sensitivity Analysis of Perpendicularity Errors to Spatial Errors
As shown in Figure 6, three squareness errors all affect the spatial error. The sensitivity of error is relatively largest, and it changes slightly with the movement of Y-axis, basically stable at about 0.3. The sensitivity of is relatively small and has been stable below 0.1. The sensitivity changes with the movement of X-axis, and has the largest changing range.
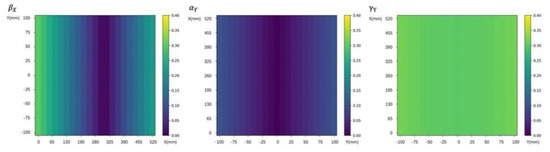
Figure 6.
Interval sensitivity of perpendicularity error to spatial error.
4.2. Global Maximum Interval Sensitivity Analysis to Spatial Error of Geometric Error Sources
The global maximum interval sensitivity can guide the accuracy design in the actual manufacturing assembly process. The global maximum interval sensitivity of the angular error source to the spatial error component is expressed as,
The global maximum interval sensitivity of the geometric error source to spatial error is expressed as,
The maximum interval sensitivity can be used directly as the sensitivity of the machine tool accuracy design index. Based on the sensitivity design, by assigning a tolerance interval to each error source, all geometric error sources of the machine tool can meet the design requirements in space. By Equation (18), each geometric error source to the spatial error of the global maximum interval sensitivity can be calculated, as shown in Figure 7.
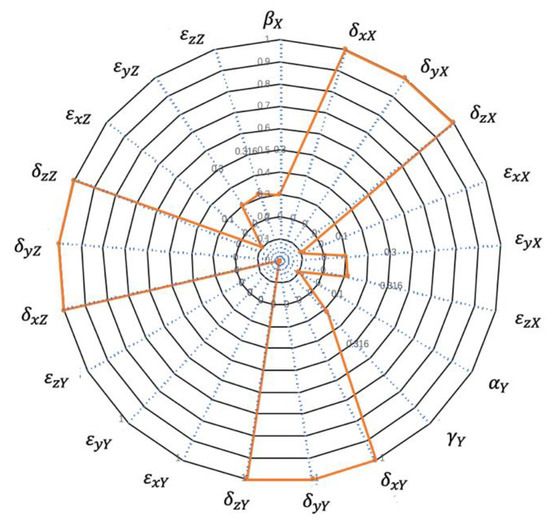
Figure 7.
Global maximum interval sensitivity to spatial error of geometric error sources.
Three angular errors result from the forward and backward movement of the slide ram have no effect on the spatial error, but the other geometric error sources have varying degrees of influence on the spatial error. The sensitivity of each position error, the axis positioning error and the straightness error to the global maximum interval of the spatial error, is the same value 1. For other error terms, the roll error of Z axis, the yaw error of X-axis, and the squareness error between X-axis and Z-axis have the greatest sensitivity to the global maximum interval. The pitch error of X-axis and Y-axis and the squareness error between X-axis and Y-axis have the second highest sensitivity. The yaw error of X-axis, the pitch error of Z-axis and the squareness error between Y-axis and Z-axis.
5. AN Experimental Study
In above analysis, proposed spatial geometric error model helps to describe the relationship between each geometric error term and the final machining error. The sensitivity analysis can effectively reflect influence degree of each error term on the final error under different machining conditions. With results of sensitivity analysis, can obtain the sensitive error term with great influence on the machine accuracy can be given. Based on the above work, this section carries out an experimental study on the sensitivity model of a Turn-milling combined NC machine tool. Without considering the comprehensiveness of errors, the experimental study is limited as follows: the machine components are considered as rigid bodies; and the machine parts have similar manufacturing accuracy are. The errors value can reflect the influence degree on the machine tool accuracy, namely the geometric error sensitivity of machining tool.
Taking Y-axis of a Turn-milling combined NC machine tool as an example, the experimental procedure of geometric error sensitivity model verification is shown in Figure 8. Firstly, the various error terms of the combined geometric accuracy of turning and milling, shown in Figure 9, are measured. Then, the typical error modeling, error separation method and experimental fitting method are used to separate the error terms of Y-axis, and values of all error terms are analyzed comparatively to verify the error sensitivity model established in this paper.
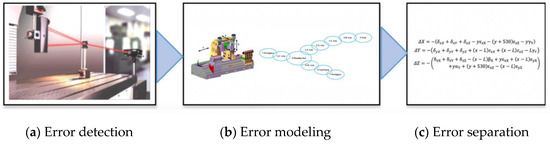
Figure 8.
The experimental procedure of geometric error sensitivity model verification.

Figure 9.
Error detection experiment.
With the geometric error sensitivity model of the Turn-milling combined NC machine tool, the typical error separation and experimental fitting methods are used to decompose various geometric errors. The decomposition results are shown in Table 4. The error values of are 1.0092, 4.2666 and 36.712, respectively. are 6.91 × 10−5, 0.04744, and 9.09 × 10−7, respectively, which are at least 2 orders of magnitude smaller than . Among them, the value of is larger due to the error caused by the weight of Y-axis and B axis. And the reason for a larger value of is synchronization error of Y-axis. The experimental results is close to the sensitivity analysis results of the geometric error mentioned above. That is, the positioning error and linearity error of Y-axis are highly sensitive, while the sensitivity of yaw error, pitch error, and roll error is low. The sensitivity analysis results of the turning-milling compound geometric error is consistent with the experimental error decomposition results, demonstrating the effectiveness of the sensitivity analysis method.

Table 4.
Measurement and separation results of geometric error term of Y-axis.
6. Conclusions and Discussion
6.1. Discussion
With the increasing application of multi-axis simultaneous machining machines, subsequent work can gradually extend the methodological basis of this Turn-Milling compounding research to different multi-axis machines. This paper establishes a mathematical model of the geometric error for the Turn-Milling combining and error compensation through the results of sensitivity analysis. The method is an efficient, economical, and practical way to improve the machining accuracy of machine tools. From the current state of development, there are still some aspects that need to be further studied and solved. Most of the existing geometric error model research is based on the case of no-load operation, when the Turn-Milling compound error modeling, the error model can increase in the actual machining process of cutting force, tool wear, and vibration and other factors. The geometric error, thermal error, and cutting force error of different parts and different machining speeds may vary greatly. Therefore, a comprehensive error model more in line with the actual machining conditions should be established in subsequent research. The accuracy and robustness of the error model must be considered to improve the machining accuracy.
The interval sensitivity analysis provides geometric accuracy allocation weights for the next study on the optimal allocation of geometric accuracy, but it needs to establish a dynamic feedback mechanism with the actual manufacturing and assembly process. In the process of this research, the analysis is only based on the spatial error accuracy index of machine tool. Subsequently, the dynamic changes of geometric errors in the actual manufacturing and assembly process should be fully considered to avoid too loose or too tight tolerances caused by some geometric error sources, which can increase the unnecessary assembly time and cost.
6.2. Conclusions
Turn-milling combined NC machine tool generally have at least three parallel axes and two rotary axes. With the existence of the rotary axes, the directional vector of the tool is also changed during the movement, and the trajectory of the tool cannot be imagined visually under the machine coordinate system. Therefore, the topological relations of the machine tool were established with the MBS. Furthermore, the position transformation matrices, the position error transformation matrices, the motion transformation matrices, and the motion error transformation matrices under ideal and actual motion conditions were deduced with the homogeneous coordinate transformations. Through the multiplication of the characteristic matrix, the spatial error model of the whole machine with five-axis linkage in milling mode and three-axis linkage in turning mode is obtained.
In previous, the error sensitivity in a particular state of the machine was usually analyzed, and the error sensitivity during machine movement was only analyzed qualitatively. In this paper, the error sensitivity in different positions of the machine tool is analyzed more precisely. Geometric error sensitivity coefficients are calculated for the spatial geometric error model of the machine tool. With interval theory, its error models along X, Y, and Z directions are built using an interval sensitivity analysis. Based on the results of the sensitivity analysis, it can be shown that the errors ; are important sensitive errors that have a significant impact on the machining accuracy. And the tolerance ranges related to the above factors should be strictly controlled in the optimization of machine geometry accuracy. The tolerance range can be relaxed to a larger range for geometric error sources with small global maximum interval sensitivity, such as . It is important to pay attention to the error terms that have a significant impact on machining accuracy and give priority to ensuring their accuracy in the machine design, manufacturing, assembly, and other stages.
The geometric error sensitivity analysis method proposed in this paper can accurately evaluate the influence weights of each error term on the machining accuracy of Turn-Milling Combined NC machine tool, and accurately identify the important sensitive error terms that have a great influence on the machining accuracy from many error terms. Geometric error sensitivity analysis can provide a theoretical basis for geometric error index distribution and geometric error accuracy optimization for Turn-Milling machine centers in precision design process, manufacturing, assembly, and debugging. At the same time, it can clarify the priority of the error compensation order in the error compensation stage.
Author Contributions
P.L.: Conceptualization and supervision, R.Z.: Methodology and data curation, L.L.: Validation and formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Chinese government Megaproject of High-grade NC Machine Tools and Basic Manufacturing Equipment (2019ZX04005-001-013).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maruda, R.W.; Krolczyk, G.M.; Wojciechowski, S.; Powalka, B.; Klos, S.; Szczotkarz, N.; Matuszak, M.; Khanna, N. Evaluation of turning with different cooling-lubricating techniques in terms of surface integrity and tribologic properties. Tribol. Int. 2020, 148, 106334. [Google Scholar] [CrossRef]
- Gong, L.; Bertolini, R.; Ghiotti, A.; He, N.; Bruschi, S. Sustainable turning of Inconel 718 nickel alloy using MQL strategy based on graphene nanofluids. Int. J. Adv. Manuf. Technol. 2020, 108, 3159–3174. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Matuszak, M.; Powałka, B.; Madajewski, M.; Maruda, R.W.; Królczyk, G.M. Prediction of cutting forces during micro end milling considering chip thickness accumulation. Int. J. Mach. Tools Manuf. 2019, 147, 103466. [Google Scholar] [CrossRef]
- Krawczyk, M.B.; Królikowski, M.A.; Grochała, D.; Powałka, B.; Figiel, P.; Wojciechowski, S. Evaluation of Surface Topography after Face Turning of CoCr Alloys Fabricated by Casting and Selective Laser Melting. Materials 2020, 13, 2448. [Google Scholar] [CrossRef]
- Tao, H.; Chen, R.; Xuan, J.; Xia, Q.; Yang, Z.; Zhang, X.; He, S.; Shi, T. A new approach to identify geometric errors directly from the surface topography of workpiece in ultra-precision machining. Int. J. Adv. Manuf. Technol. 2020, 106, 5159–5173. [Google Scholar] [CrossRef]
- Tao, H.; Chen, R.; Xuan, J.; Xia, Q.; Yang, Z.; Zhang, X.; He, S.; Shi, T. Prioritization analysis and compensation of geometric errors for ultra-precision lathe based on the random forest methodology. Precis. Eng. 2020, 61, 23–40. [Google Scholar] [CrossRef]
- Guo, S.; Mei, X.; Jiang, G. Geometric accuracy enhancement of five-axis machine tool based on error analysis. Int. J. Adv. Manuf. Technol. 2019, 105, 137–153. [Google Scholar] [CrossRef]
- Chen, B.; Peng, C.; Huang, J. A new error model and compensation strategy of angle encoder in torsional characteristic measurement system. Sensors 2019, 19, 3772. [Google Scholar] [CrossRef]
- Zhang, J.; Lian, B.; Song, Y. Geometric error analysis of an over-constrained parallel tracking mechanism using the screw theory. Chin. J. Aeronaut. 2019, 32, 1541–1554. [Google Scholar] [CrossRef]
- Zha, J.; Li, L.H.; Han, L.; Chen, Y.L. Four-station laser tracer-based geometric error measurement of rotary table. Meas. Sci. Technol. 2020, 31, 9. [Google Scholar] [CrossRef]
- Chen, J.; Lin, S.; He, B. Geometric error compensation for multi-axis CNC machines based on differential transformation. Int. J. Adv. Manuf. Technol. 2013, 71, 635–642. [Google Scholar] [CrossRef]
- Tang, H.; Duan, J.; Lan, S.; Shui, H. A new geometric error modeling approach for multi-axis system based on stream of variation theory. Int. J. Mach. Tools Manuf. 2015, 92, 41–51. [Google Scholar] [CrossRef]
- Fu, G.; Fu, J.; Xu, Y.; Chen, Z. Product of exponential model for geometric error integration of multi-axis machine tools. Int. J. Adv. Manuf. Technol. 2014, 71, 1653–1667. [Google Scholar] [CrossRef]
- Fu, G.; Fu, J.; Shen, H.; Xu, Y.; Jin, Y. Product-of-exponential formulas for precision enhancement of five-axis machine tools via geometric error modeling and compensation. Int. J. Adv. Manuf. Technol. 2015, 81, 289–305. [Google Scholar] [CrossRef]
- Fu, G.; Fu, J.; Xu, Y.; Chen, Z.; Lai, J. Accuracy enhancement of five-axis machine tool based on differential motion matrix: Geometric error modeling, identification and compensation. Int. J. Mach. Tools Manuf. 2015, 89, 170–181. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, H.; Zhang, G.; Gu, P.; Cai, L. An analytical approach for crucial geometric errors identification of multi-axis machine tool based on global sensitivity analysis. Int. J. Adv. Manuf. Technol. 2014, 75, 107–121. [Google Scholar] [CrossRef]
- Los, A.; Mayer, J.R.R. Application of the adaptive Monte Carlo method in a five-axis machine tool calibration uncertainty estimation including the thermal behavior. Precis. Eng. 2018, 53, 17–25. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, D.; Xi, Y. Global quantitative sensitivity analysis and compensation of geometric errors of CNC machine tool. Math. Probl. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, D. Geometric error analysis and compensation of rotary axes of five-axis machine tools. Adv. Eng. Sci. 2020, 52, 130–139. [Google Scholar]
- Li, Q.; Wang, W.; Jiang, Y.; Li, H.; Zhang, J.; Jiang, Z. A sensitivity method to analyze the volumetric error of five-axis machine tool. Int. J. Adv. Manuf. Technol. 2018, 98, 1791–1805. [Google Scholar] [CrossRef]
- Cui, W.; Li, B.; Yang, J. Optimization of machine error based on error sensitivity analysis for nano-machine. J. Donghua Univ. (Nat. Sci.) 2016, 42, 253–257. [Google Scholar]
- Guo, H.; Yang, X.; Wang, S.; Dai, Z. Research on the application of multiplication dimension reduction method in global sensitivity analysis of CNC machine tools. Aip Adv. 2020, 10, 015029. [Google Scholar] [CrossRef]
- Zhang, Q. Fully discrete convergence analysis of non-linear hyperbolic equations based on finite element analysis. Appl. Math. Nonlinear Sci. 2019, 4, 433–444. [Google Scholar] [CrossRef]
- Zhang, W.; Vollmer, H.M. Prediction model and compensation system of CNC machine tool thermal error. J. Mech. Eng. Res. Dev. 2016, 39, 387–393. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).