Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels
Abstract
:1. Introduction
2. Proposed Calculation Method
2.1. Method of Solving Additional Stress on Existing Tunnels at Any Angle
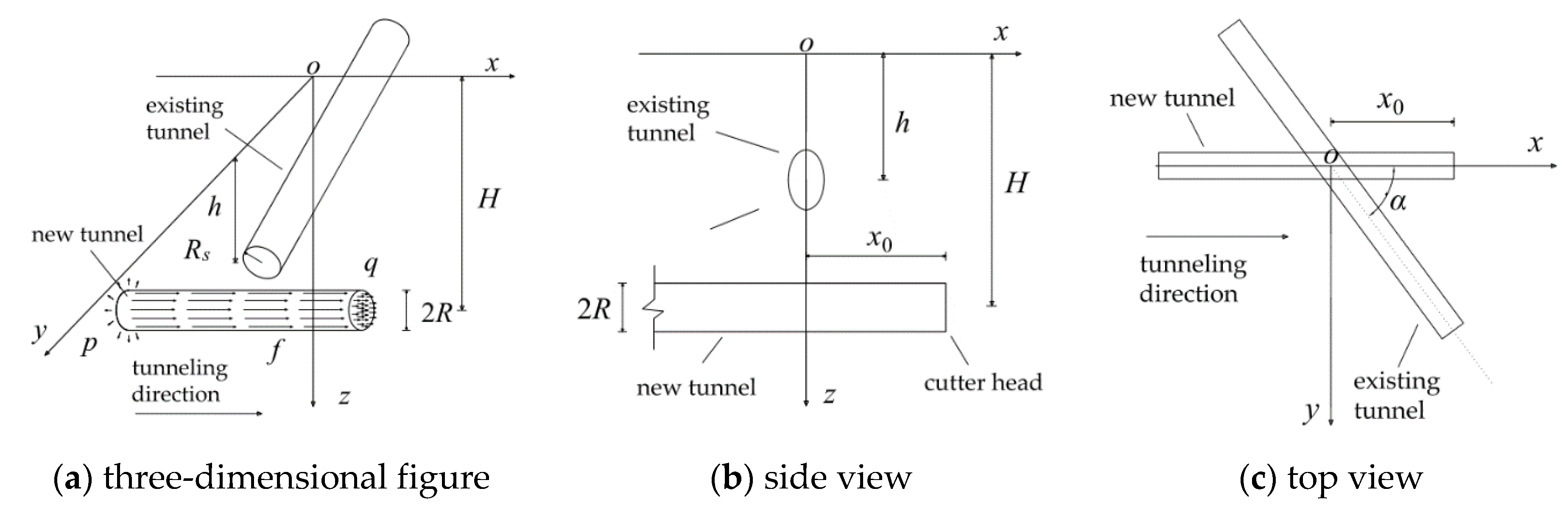
2.1.1. Establishment of a Mechanical Model
2.1.2. Solution for Additional Stress Caused by Shield Tunneling
- ,
- ,
- ,
- .
2.2. Analysis of the Principle of Circumferential Grouting and Its Influence on the Surroundings
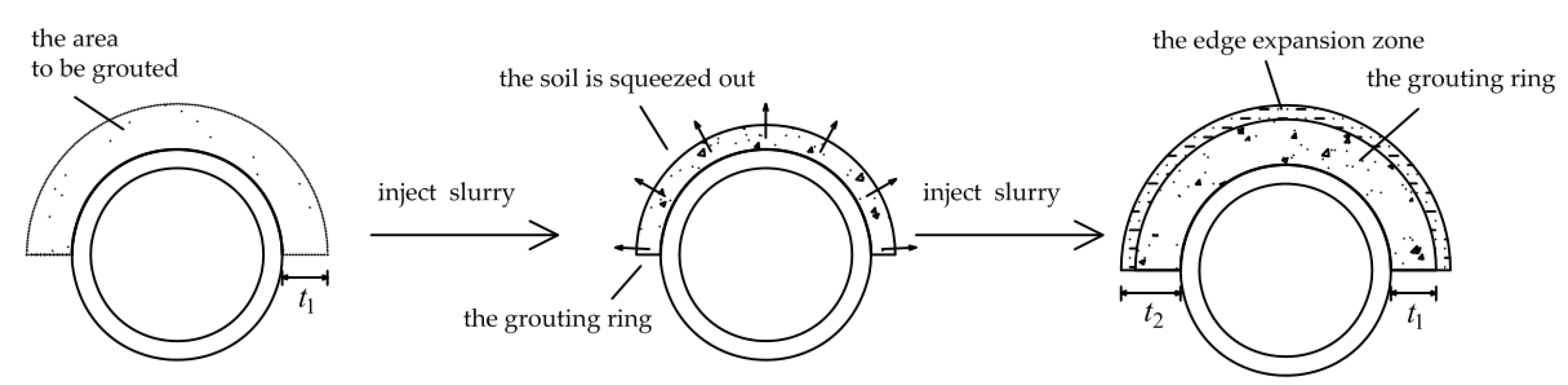
2.2.1. Analysis of the Principle of Circumferential Grouting
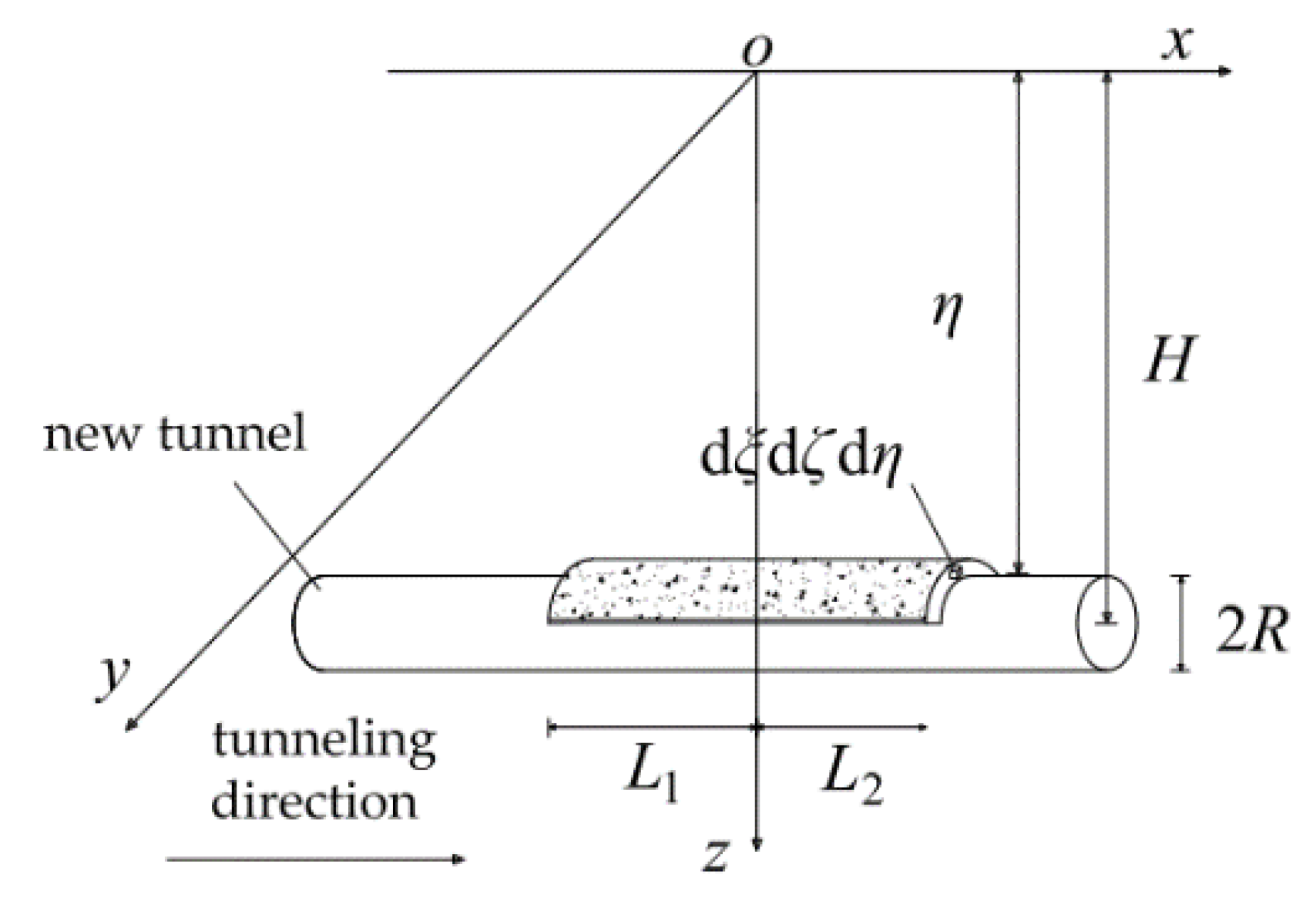
2.2.2. Establishment of the Grouting Ring Expansion Model and Calculation of Its Influence on the Surroundings
2.3. Calculation of the Vertical Displacement of Existing Tunnels
3. Analysis and Reliability Verification of an Engineering Case
3.1. Example Conditions
3.2. Theoretical Calculation Results
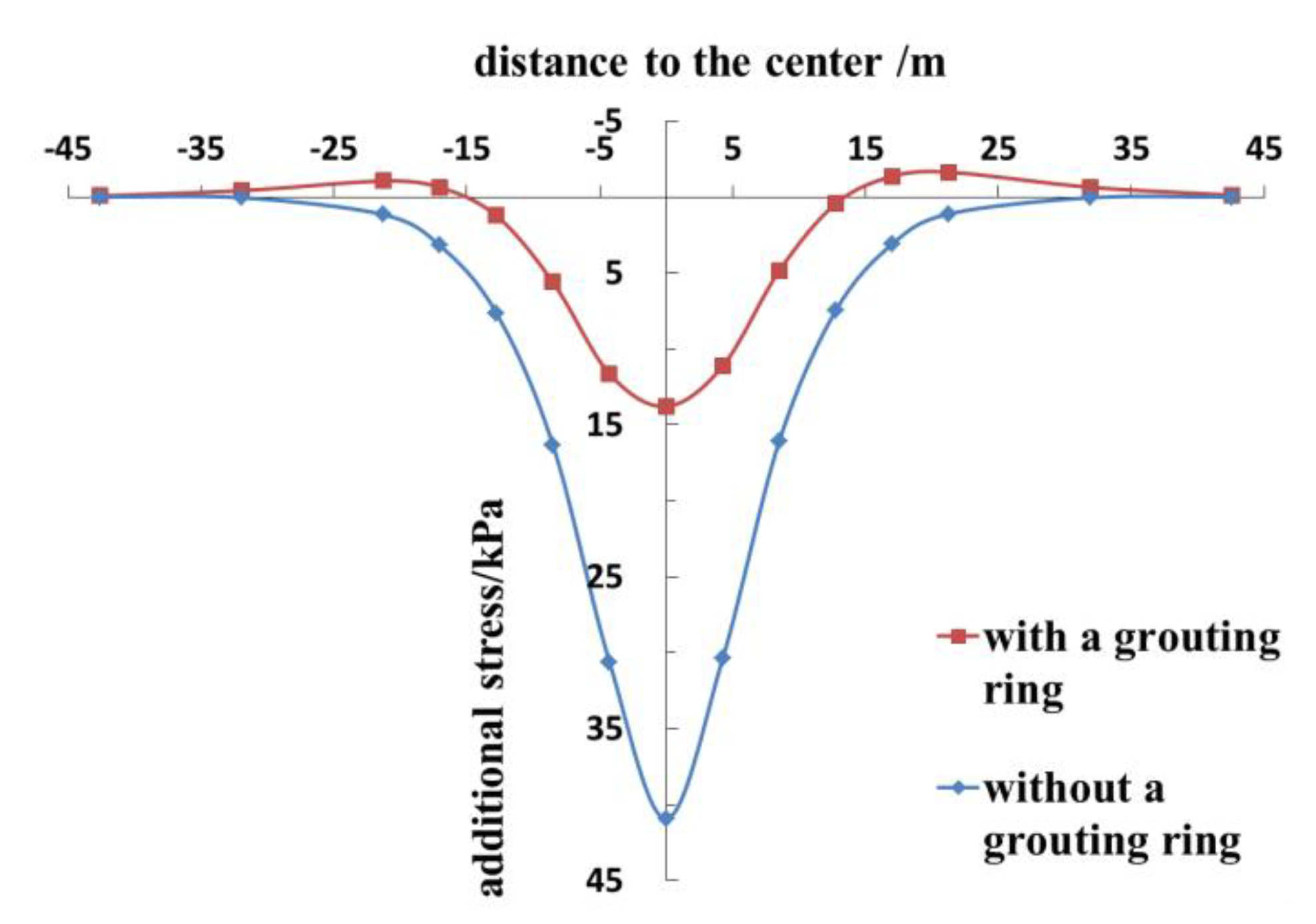
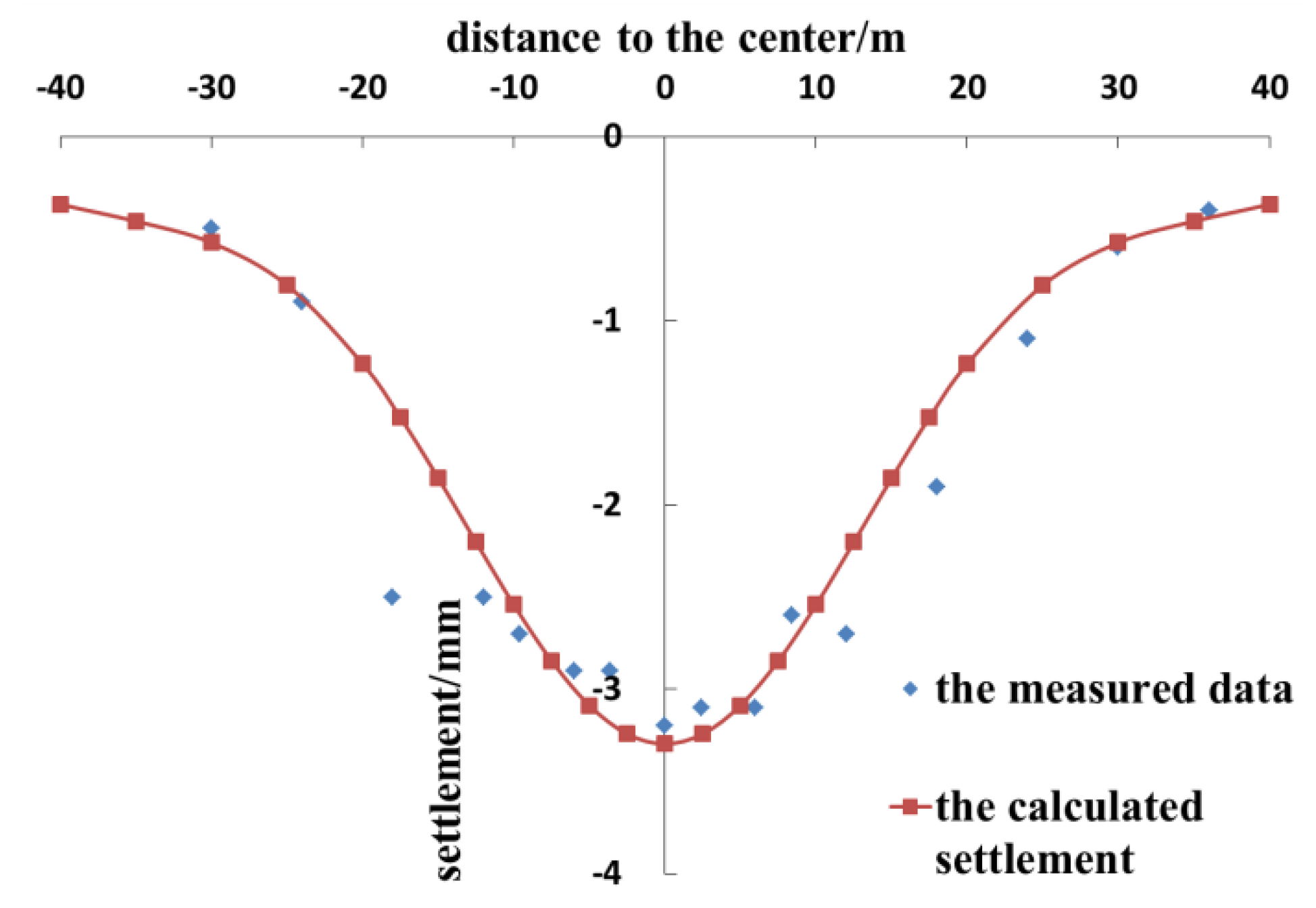
3.3. Reliability Verification
4. Influence of a Single Factor on Existing Tunnels
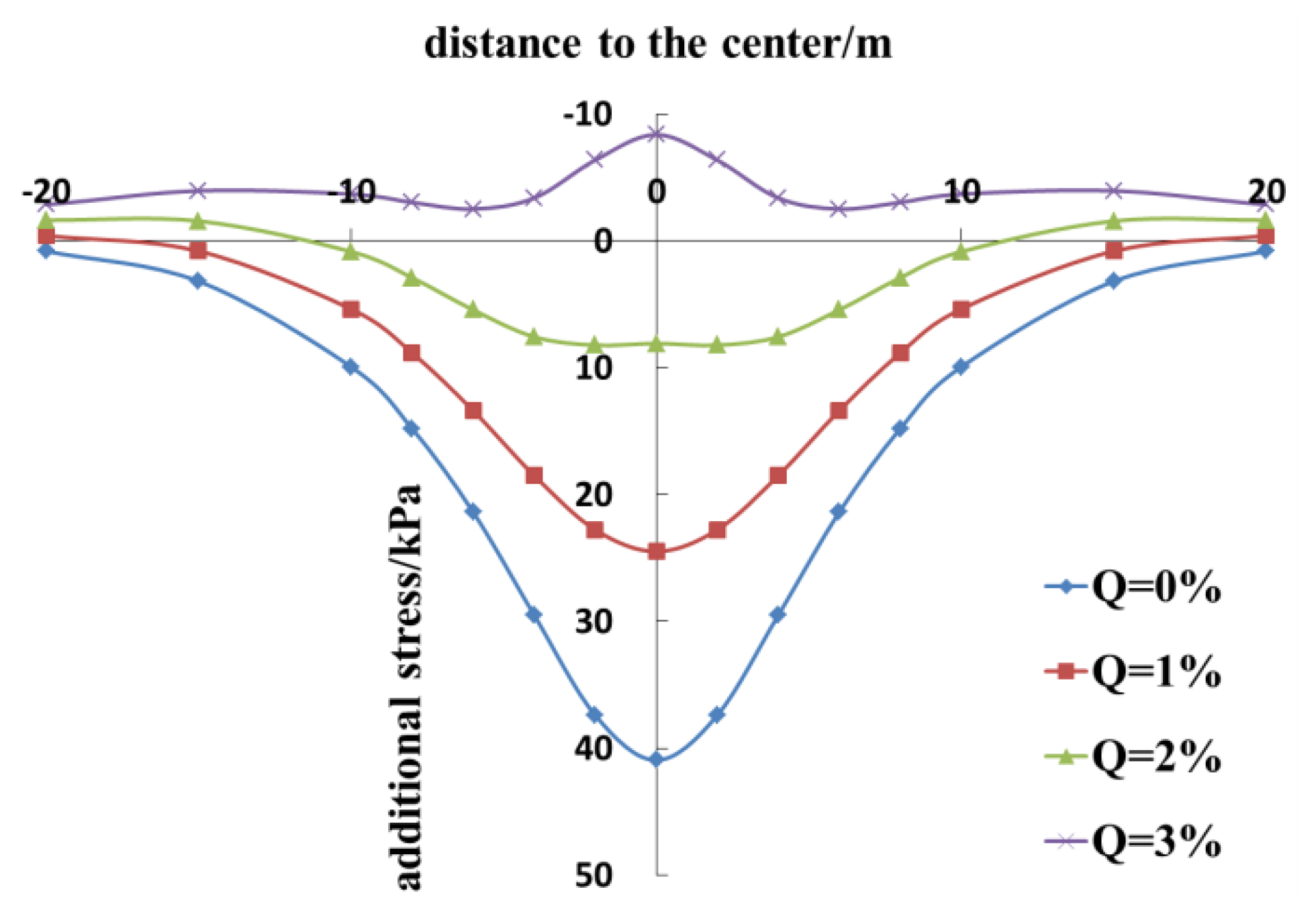
4.1. Volume Expansion Rate
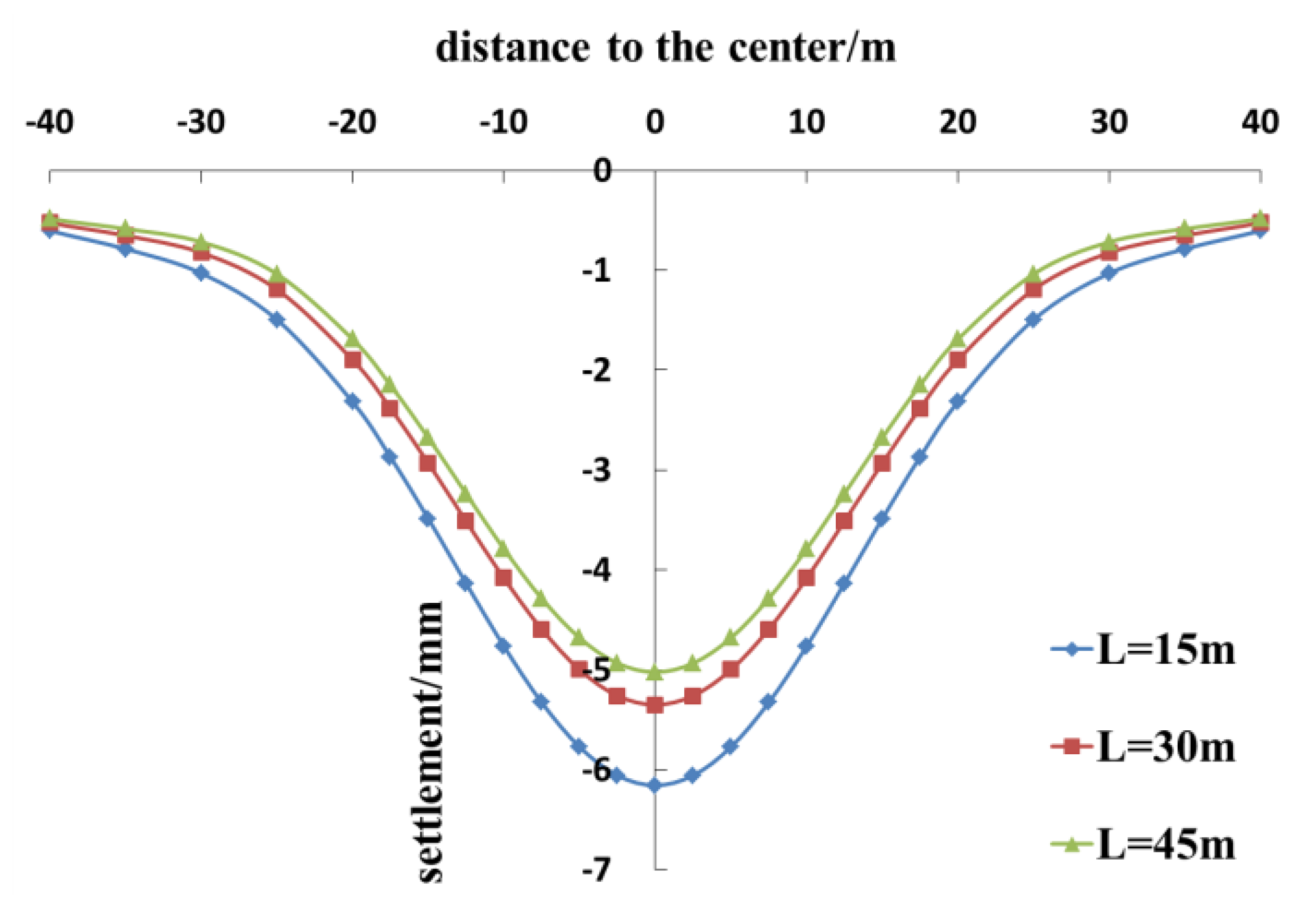
4.2. Length of Grouting Rings
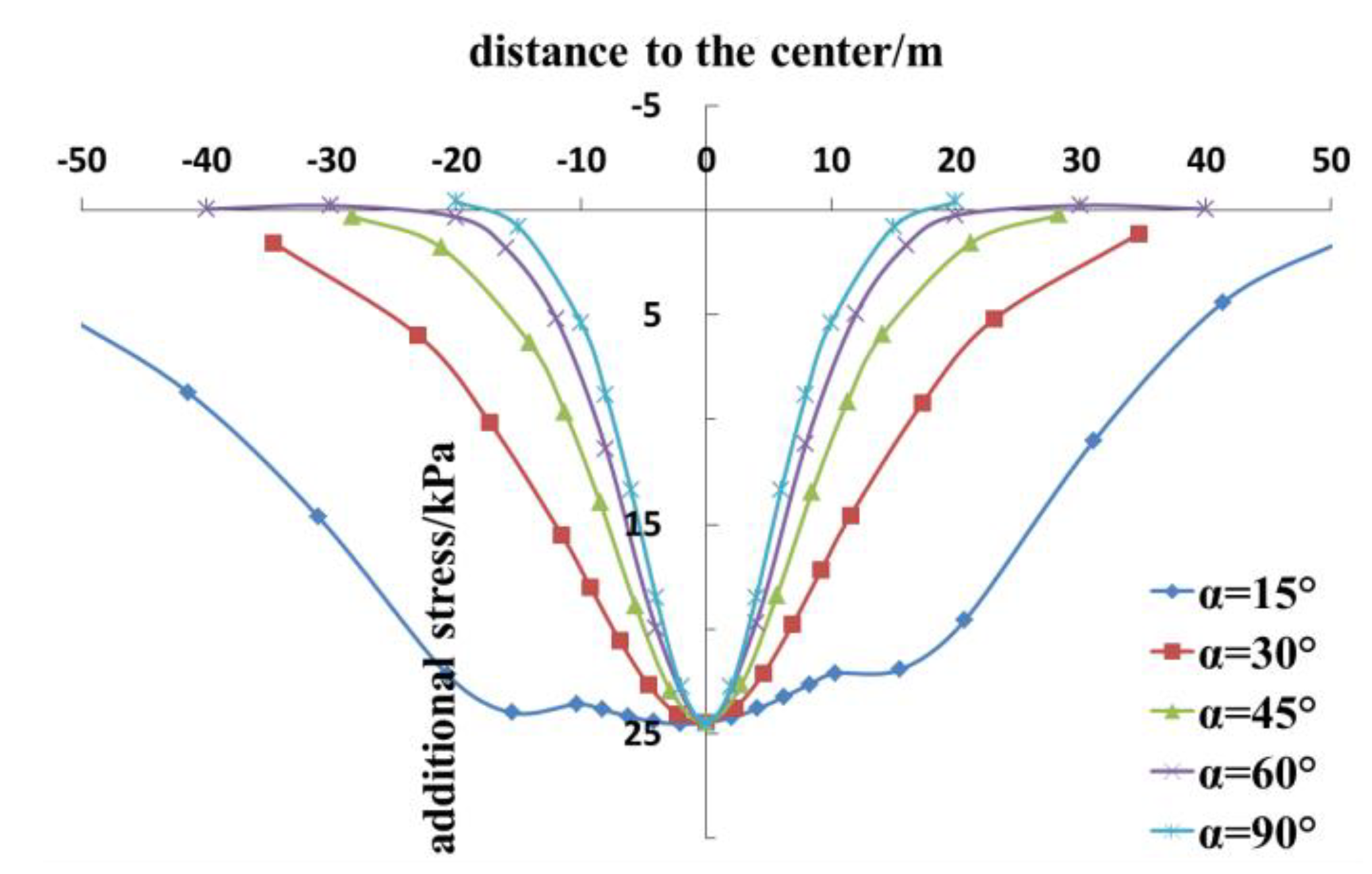
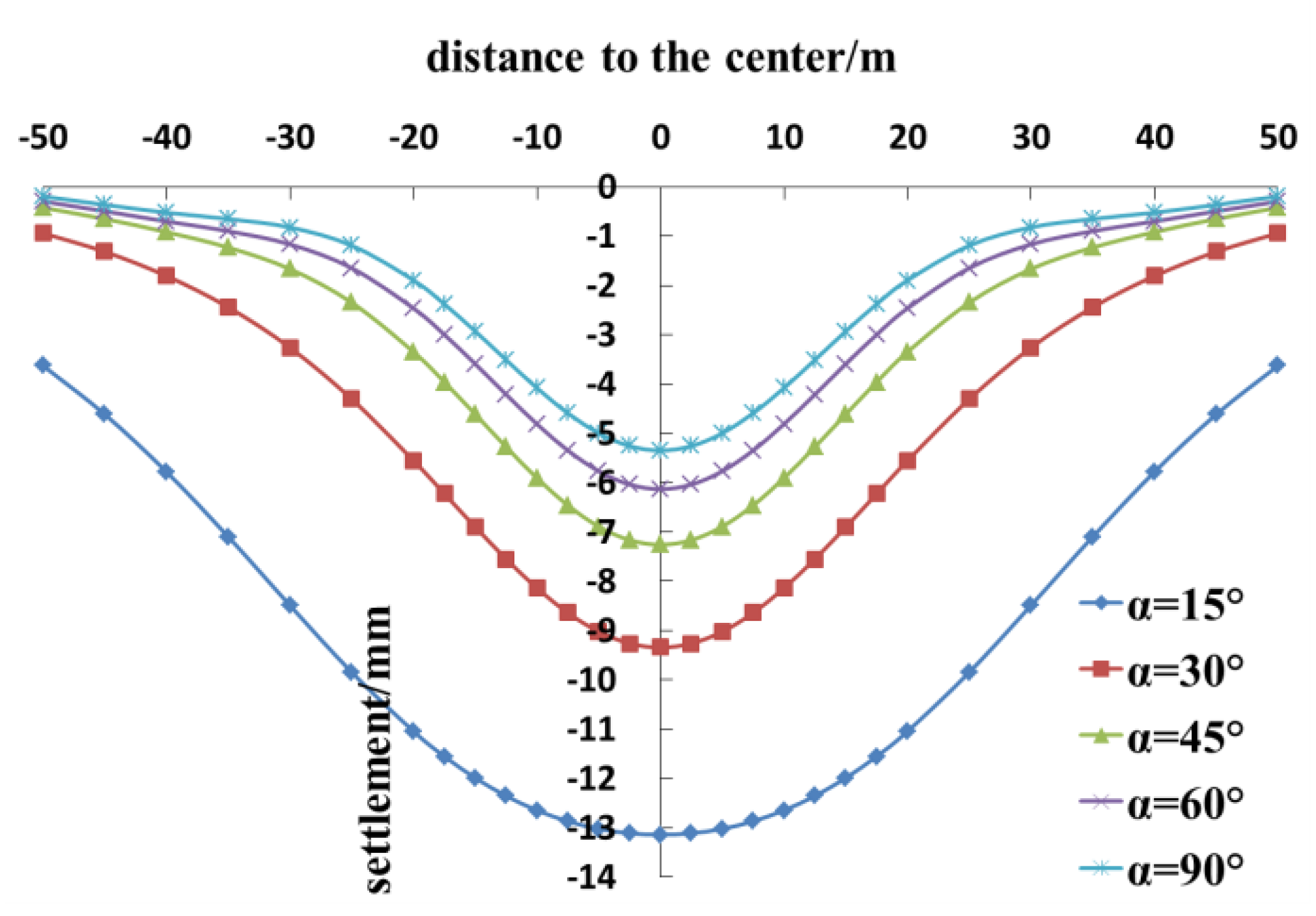
4.3. Tunnel Crossing Angle
5. Conclusions
- The results of this theoretical calculation method are in good agreement with the measured data. The proposed method can be used to calculate the vertical displacement of the existing tunnel caused by a new tunnel crossing, under the influence of the grouting rings.
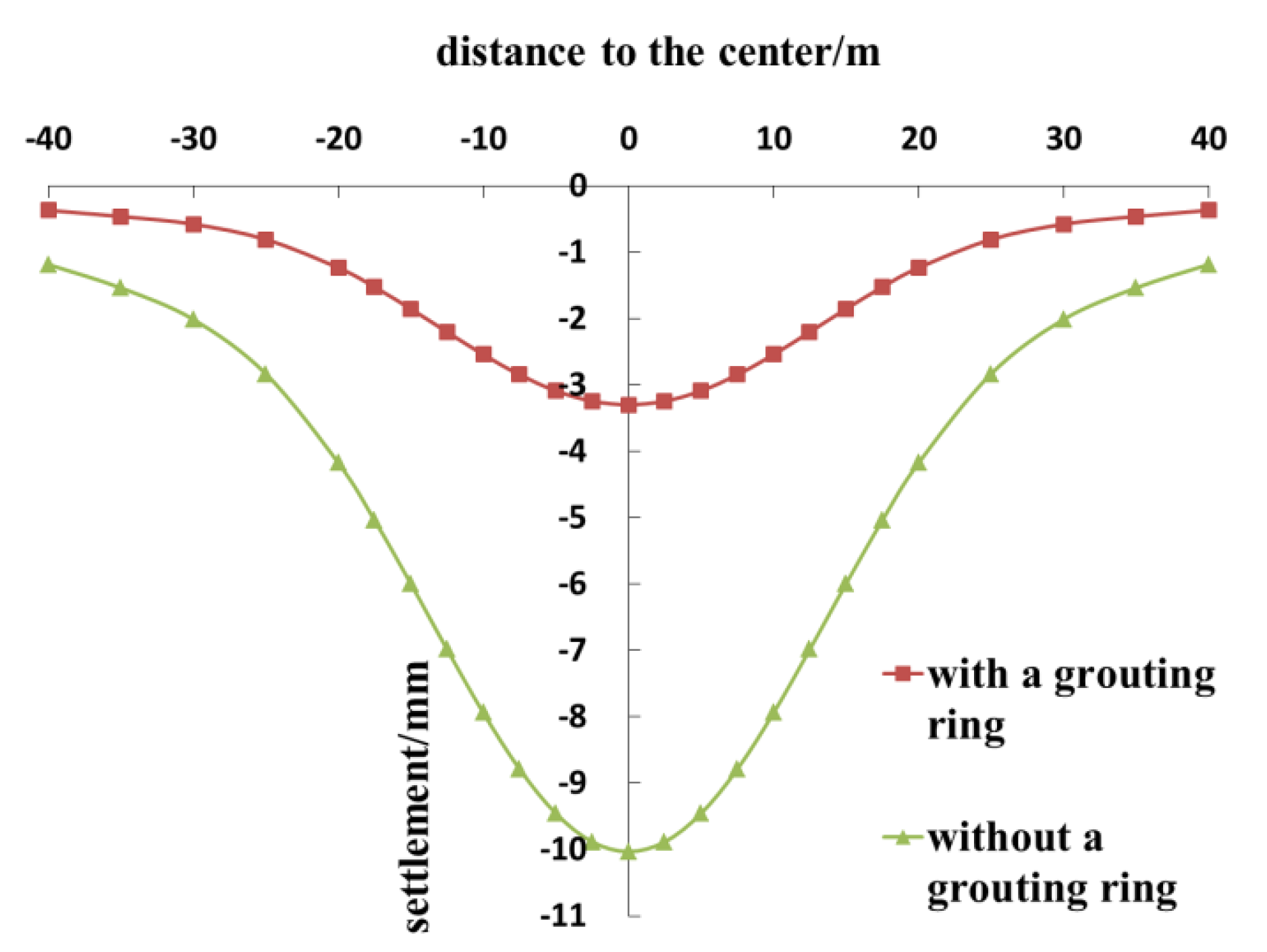
- Installing grouting rings on new tunnels can effectively reduce the disturbance to existing tunnels caused by tunnel crossing and can significantly decrease the additional stress on and the settlement of the existing tunnels.
- When the volume expansion of the grouted volume is within a certain range, increasing Q can effectively reduce the additional stress on and the settlement of the existing tunnel. When the volume expansion rate is too large, the impact of the grouting ring on the existing tunnel exceeds that of the tunnel excavation, and the variation in the additional stress on the existing tunnel shifts to a vertical upward trend; thus, the tunnel is bulged.
- Properly increasing the length of the grouting ring can decrease the additional stress on and the settlement of the existing tunnel, but the effect gradually lessens. As the tunnel crossing angle decreases, the range of the settlement and the settlement value of the existing tunnel gradually rise.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Liu, G.; Wang, Z.; Wu, S.; Hong, C. The shield tunnel obliquely crossing over an existing pipeline: A numerical analysis. Civ. Eng. Urban Plan. 2012, 748–754. Available online: https://ascelibrary.org/doi/abs/10.1061/9780784412435.136 (accessed on 10 September 2020).
- Yin, M.; Jiang, H.; Jiang, Y.; Sun, Z.; Wu, Q. Effect of the excavation clearance of an under-crossing shield tunnel on existing shield tunnels. Tunn. Undergr. Space Technol. 2018, 78, 245–258. [Google Scholar] [CrossRef]
- Sagaseta, C. Patterns of soil deformations around tunnels: Application to the extension of Madrid Metro. Comput. Geotech. 2001, 28, 445–468. [Google Scholar]
- Han, Y.; Ye, W.; Wei, Q. Research on the influence of new shield tunnel to adjacent existing tunnel. Appl. Mech. Mater. 2013, 295–298, 2985–2989. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Li, X.G.; Yuan, D.J. Response of a double-decked metro tunnel to shield driving of twin closely under-crossing tunnels. Tunn. Undergr. Space Technol. 2012, 28, 18–30. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Zhang, M.X.; Wu, H.M.; Xiao, X. 3D numerical simulation for mechanical influence of multi-line tunneling on existing tunnel in soft clay GB/T 7714. In Proceedings of the IET International Conference on Smart & Sustainable City, Shanghai, China, 6–8 July 2011. [Google Scholar]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Li, L. Research on construction disturbance caused by multi-line overlapped shield perpendicularly crossing. In Proceedings of the Tunneling & Underground Construction, Shanghai, China, 26–28 May 2014; ASCE: New York, NY, USA, 2014. [Google Scholar]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. An in-tunnel grouting protection method for excavating twin tunnels beneath an existing tunnel. Tunn. Undergr. Space Technol. 2018, 71, 27–35. [Google Scholar] [CrossRef]
- Peng, H.; Dong, Z.Y.; Liu, Y.L. Research on deformation influence of shield undercrossing the existing metro double shield tunnel. Adv. Mater. Res. 2015, 1065–1069, 378–382. [Google Scholar] [CrossRef]
- Au, S.K.A.; Soga, K.; Jafari, M.R.; Bolton, M.D.; Komiya, K. Factors affecting long-term efficiency of compensation grouting in clays. J. Geotech. Geoenviron. Eng. 2003, 129, 254–262. [Google Scholar] [CrossRef]
- Zhang, D.; Zou, W.; Yan, J. Effective control of large transverse deformation of shield tunnels using grouting in soft deposits. Chin. J. Geotech. Eng. 2014, 36, 2203–2212. [Google Scholar]
- Qi, J.; Xu, R.; Wei, G. Research on calculation method of soil 3D displacement due to shield tunnel construction. Rock Soil Mech. 2009, 30, 2442–2446. [Google Scholar]
- Wei, G.; Zhang, X. Calculation of rotation and shearing dislocation deformation of underlying shield tunnels due to foundation pit excavation. J. Cent. South Univ. (Sci. Technol.) 2019, 50, 2273–2284. [Google Scholar]
- Wei, G.; Yu, G.; Yang, B. Calculation of existing shield tunnel shearing dislocation platform deformation due to undercrossing new shield tunnel undercrossing. J. Hunan Univ. 2018, 45, 103–112. [Google Scholar]
- Mindlin, R.D. Force at a point in the interior of a semi-infinite soild. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Wei, G. 3-D analytical solution of ground deformation induced by shield tunneling construction. In Proceedings of the Second National Conference on Engineering Security and Protection, Beijing, China; Chinese Society for Rock Mechanics & Engineering: Beijing, China, 2010; pp. 369–374. Available online: https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGYJ201008003005.htm (accessed on 10 September 2020).
- Knothe, S. Observations of surface movements under influence of mining and their theoretical interpretation. In Proceedings of the European Congress on Ground Movement, Leeds, UK, 9–12 April 1957; University of Leeds: Leeds, UK, 1957; pp. 210–218. [Google Scholar]
- Zhou, S.; He, C.; Xiao, J. Energy method for calculation deformation of adjacent shield tunnels due to foundation pit excavation considering step between rings. China Railw. Sci. 2016, 37, 53–60. [Google Scholar]
- Wei, G.; Qi, Y.; Wu, H. Calculation of rotation and segment ring dislocation deformation caused by surcharge in shield tunnels. Tunn. Constr. 2019, 39, 1781–1789. [Google Scholar]





| Parameters | New Tunnel | |
|---|---|---|
| H | 17.6 m | |
| R | 3.35 m | |
| ηs | 2% | |
| q | 45 kPa | |
| f | 110 kPa | |
| p | 120 kPa | |
| d | 2.68 m | |
| Es | 10.47 MPa | |
| μ | 0.27 | |
| φ | 28° | |
| Parameters | Existing tunnels | |
| Upline | Downline | |
| h | 11.0 m | 11.1 m |
| α | 62° | 61° |
| L | L1 = 18.25 m L2 = 31.25 m | L1 = 31.25 m L2 = 18.25 m |
| Rs | 3.1 m | |
| Dt | 1.5 m | |
| EtIt (tunnel equivalent bending stiffness) | 1.1 × 108 kN·m2 | |
| ks (shear stiffness between rings) | 7.45 × 105 kN/m | |
| kt (tensile stiffness between rings) | 1.94 × 106 kN/m | |
| J (coefficient of rotation effect of rigid body) | 0.3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Wei, G.; Xie, Y. Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels. Symmetry 2020, 12, 1623. https://doi.org/10.3390/sym12101623
Qi Y, Wei G, Xie Y. Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels. Symmetry. 2020; 12(10):1623. https://doi.org/10.3390/sym12101623
Chicago/Turabian StyleQi, Yongjie, Gang Wei, and Yu Xie. 2020. "Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels" Symmetry 12, no. 10: 1623. https://doi.org/10.3390/sym12101623
APA StyleQi, Y., Wei, G., & Xie, Y. (2020). Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels. Symmetry, 12(10), 1623. https://doi.org/10.3390/sym12101623





