Abstract
The human brain is approximately a symmetric structure, although the functional brain does not exhibit symmetry. Functional brain aging process modelling is essential for the understanding of hypothesized generative mechanisms for human brain networks throughout one’s lifespan. We present a novel generative network model of the human functional brain network, which is the hybrid of the local naïve Bayes model and the anatomical similarity correction (LNBE). We use LNBE, as well as published generative network models to simulate the aging process of the functional brain network, to construct artificial brain networks and to reveal the generative mechanisms and evolutionary patterns of human functional brain across human lifespans. It is suggested that the idea of classifying common neighbours while considering anatomical distances during network formation can provide a much more similar generative mechanism of the human fMRI brain aging process as well as a more practical generative network model of it. We hold that studies on brain normal aging process modelling have the potential to improve the way in which early warnings for latent injury or disease are practised today and advance healthcare.
1. Introduction
1.1. Brain Ageing
Brain ageing, to some extent, is inevitable, in the sense it affects every brain. Throughout human lifespans, our brain changes like any other part of our body with each passing year. From the moment the brain starts to develop in gestation to old age, its structure changes and, therefore, its functions, networks and pathways as well. To date, brain ageing studies are applied to understanding the neuronal mechanisms underlying normal and pathological brain ageing. Pathological ageing, which is usually known as accelerated ageing, is an area with numerous studies aiming to improve our understanding of pathogenic mechanisms of pathological ageing, why the rate of ageing differs and to promote treatment strategy optimization [1,2,3,4]. While the normal ageing process is accompanied by cognitive decline, loss of nerve fibres, etc. [5,6], it has been concluded that there is no massive neuronal loss during normal ageing [7].
1.2. Brain Network Modelling
The human connectome is “a comprehensive presentation of the network of nodes and connections forming the human brain” [8,9,10]. In the context of complex networks, the connectome is a network with nodes and edges, a functional connection (an edge) between two cortical areas (nodes) segregated by anatomical distance [11,12]. The human brain network is a macro-scale map of connectivities of the brain, where nodes usually represent brain regions, while edges represent functional, anatomica or effective connections [13]. The functional connectome is the neural map of brain activity.
Within the framework of complex networks, generative network models simulate the mechanisms by which networks are generated. The computational models provide opportunities to investigate the hypothesized generative mechanisms to explore what structures those models could generate. If the topological structures are similar to those of networks observed in the real world, this implies that similar generative mechanisms may be at work in real brain networks. Studies of brain network modelling have led to important findings of how the functional and structural connectivities of the brain give rise to cognition [14,15,16,17,18,19]. Prior studies [20,21] considered anatomical distance as a major determinant of the connection between two ROIs (regions of interest) during network modelling. Studies showed that network topological factor, as well as the anatomical factor, have significant effects on network formation and performance [12,22,23]. It is generally confirmed that link prediction algorithms provide various rules for link establishment and network formation by quantifying the topological similarity between two unconnected nodes [24,25].
1.3. Contributions of the Research
In this paper, we aim to simulate the ageing process of the functional brain network, and construct similar enough artificial brain networks, in order to reveal the dynamic evolution patterns of human functional brain network across the human lifespan and gain a better knowledge of the generative mechanisms of it. We construct macro-scale functional brain networks using a novel generative network model, LNBE, with a basis of a common neighbour link prediction model (LNB) [26] which combines with the concept of anatomical distance similarity. During network formation, we innovatively evaluate whether the artificial network has the same status as a real functional brain network by assessing the artificial network every time a link is added. We evaluate and compare our proposed model to several possible generative network models. We find that the combination of the idea of classifying common neighbours and the anatomical distance similarity in the process of network formation provides a more practical generative network model, and also provides suggestions of generative mechanisms of the human brain ageing process.
2. Materials and Methods
2.1. Data Acquisition and Processing
Data applied in this work were obtained from International Consortium for Brain Mapping (ICBM) Subject, Centre for Biomedical Research Excellence (COBRE) and State Key Laboratory of Cognitive Neuroscience and Learning of Beijing Normal University (BNU) databases. A whole-brain, resting-state functional magnetic resonance imaging (fMRI) image was acquired from each participant. Imaging information of these datasets is freely accessible from the International Neuroimaging Data-Sharing Initiative (INDI) of the 1000 Functional Connectomes Project [27] Each candidate's ethics committee approved the submission of de-identified data. The institutional review boards of NYU Langone Medical Center and New Jersey Medical School approved the receipt and dissemination of the data [28]. Image pre-processing was performed using Data Processing Assistant for Resting-State fMRI (DPARSF) [29] which is based on Statistical Parametric Mapping (SPM, Department of Cognitive Neurology, Institute of Neurology, London, UK) software (SPM12) (http://www.fil.ion.ucl.ac.uk/spm/software).
In this study, a total of N = 90 healthy participants were selected, (age range: 19–79, mean age: 42.2, M/F = 41/49). All participants were full-brain coverage scanned. It was guaranteed that the 90 participants were selected from the whole age range (19–79) as evenly as possible. Participants were categorized by age into three groups: young (N = 30, ages 19–30, mean age = 22.7, M/F = 13/17), middle-age (N = 30, ages 31–53, mean age = 42.6, M/F = 16/14,), and old (N = 30, age range 54–79, mean age: 61.3, M/F = 12/18) (Table 1). Each group contains 30 participants and the mean age of each group remains around a 20-year gap.

Table 1.
Demographical statistics for participants of the study.
2.2. Construction of fMRI Brain Networks
Nodes and edges are fundamental elements of a network. In brain connectomics, the connectome is generally described as a graph or network. Nodes are usually defined as regions or structural or functional interacting units in the brain network, while between functional connections, interactive relationships may also exist between anatomically unconnected nodes. For each participant in this study, 90 regions of interest (ROIs) (45 for each hemisphere, as the whole brain approximately is a symmetric structure) of the cerebrum were further functionally parcelled and defined as 90 nodes of the functional brain network, by using the Automated Anatomical Labelling (AAL) atlas template. The AAL atlas template is a software package and digital atlas of the human brain [30]. Then functional connectivity was defined by the Pearson correlation coefficient between each pair of nodes based on BOLD fMRI time courses [31]. By this procedure, a weighted 90 × 90 symmetric correlation matrix was constructed for each participant. The elements of the matrix were the absolute values of correlation coefficients. Fisher’s r-to-z transformation was performed to improve the normality of correlation coefficients in the matrix. The correlation matrix was refined by setting threshold θ. If the absolute values of correlation coefficients in between two nodes reached the threshold θ, these elements were set to 1, otherwise to 0. Lastly, the correlation matrix was converted into binary adjacent matrix A, which represents a functional brain network for each participant, where aij, an element of the matrix A, represents the functional connection between node i and node j. Several studies proved different thresholds θ affect functional brain network [32,33], according to previous findings, θ was set to 0.5, as it is a relatively practical and optimized threshold.
2.3. Topological Measures in Functional MRI Brain Networks
Graph theoretical analysis for the functional brain network is performed in our study. Some of the widely used and practical topological measures are applied, including number of edges, average clustering coefficient, modularity, characteristic path length, global efficiency and local efficiency. Edges (E) denote either physical connections or activity levels between nodes. The average clustering coefficient (C) shows the popularity of clustered connectivity around individual nodes [34], it is a useful measurement for understanding the functional and structural associations within the brain. The modularity (Q) quantifies the tendency of a network to be decomposed into segregated module structures (community structures) [35,36]. Characteristic path length (L), also known as the average shortest path distance [37,38], describes the average of all shortest path lengths between all the node pairs. Lengths of paths indicate the potential for functional integration between brain regions. Shorter paths imply a stronger potential for integration [34], and facilitated information flow between nodes (brain regions) across the network. Global efficiency (Eglbl) implies how efficiently the information is transmitted within the network. Local efficiency (Elcl) is the efficiency of information transfers between a node and neighbouring network nodes, similar to global efficiency, but the former reflects network integration, while local efficiency reveals network segregation. Local efficiency decreases with age [39]. Both local and global efficiency is positively associated with executive function and information processing speed [40].
3. Generative Network Model of Functional Brain Network
Generative network models of link prediction provide a set of mathematically and algorithmically defined approaches, where simple connecting rules are being applied to generate artificial networks. These days, one of the well-known examples of generative network models is the Barabási–Albert (BA) model [41], which was proposed to simulate and explain network formation processes of various networks. Preferential attachment is the generative mechanism of the BA model, where nodes make preferential selection on high-degree nodes (the degree of a node is the number of its adjacent-links [42]) in the period of connecting. Notably, the aim of using a preferential attachment mechanism is to calculate the topological similarity between two given nodes. If two nodes both have larger degrees, they score higher topological similarity and, therefore, their connecting probability is higher. At present, both network topological features and anatomical distance are treated as essential impact factors in modelling brain networks [12,22,23]. Vértes et al. established a hemisphere-brain network by using an Economical Clustering Model (ECM) based on a link prediction algorithm of local topologies called common neighbours (CN) in order to simulate the formation mechanism of human brain networks [12,43]. In this study, we proposed a novel generative network model LNBE, inspired by the idea of preferential attachment. In our model, which considers both topological features and anatomical distance of the human brain, connections are established gradually according to the connection probability. The general formation process of artificial brain network develops gradually with age, and is realized by the increase of connections. Our model strives to simulate the generative mechanism of fMRI brain network evolution. By investigating the process of artificial brain network formation, we attempt to gain a better knowledge of the dynamic evolution pattern of the human functional brain network across the lifespan.
The simulation starts from the “Young” fMRI brain network of group by adding a new connection into the topology. The connection probability is calculated by the generative network model. Each artificial network will receive a two-sample t-test, after one link is generated in artificial network each time, in comparison of real fMRI brain networks of “Mid-age” and “Old” groups, respectively. The two-sample t-test is between artificial brain networks and fMRI brain networks in comparison of number of edges (edges), average clustering coefficient (C), modularity (Q), characteristic path length (L), global efficiency (Eglbl) and local efficiency (Elcl). One iteration is completed by the time when the p-value of the two-sample t-test is calculated. The network formation process takes iterations until p-value of the t-test stops increasing. In other words, the artificial network with a maximum p-value is considered as the accomplished artificial brain network. In Section 3.1, we give a full description of the formation process of the artificial brain network. In Section 3.2, we perform a preferential selection scheme which is used in the LNBE model.
3.1. Generative Scheme of Artificial Brain Network
It is particularly notable that artificial networks are generated by adding a certain amount of links at one time, and evaluations applied after all requested links are added [22,23]. In order for a clearer and more accurate observation on brain network formation, we apply a generative strategy as follows: For each given graph G (V, E), where V is the set of nodes, and E is the set of links. i,j ∈ V, while ei,j denotes the link between node i and j, ei,j ∈ E. The artificial brain network formation starts from the brain network of young adults (group Young), and it evolves either towards mid-age or old. Each initial brain network of group Young contains a fixed number of nodes, │V│ = 90. Each network contains different numbers of edges. In each iteration (growth and test), one node out of 90 is selected and one connection is established between two neighbours of the chosen node based on connection likelihood model.
The artificial brain network formation is an iterative process, which consists of the following three major steps:
- Initialization: Brain network extraction is started by image pre-processing. Experimental brain fMRI datasets of participants across all age groups (group Young, group Mid-age and group Old) are processed, and the relevant initial fMRI brain networks Gy = (gy1, gy2, …, gyn), Gm = (gm1, gm2, …, gmn) and Go = (go1, go2, …, gon) are obtained. Each initial network consists of a fixed number of nodes │V│ = 90. Edge sets of participants in groups young, mid-age and old are represented as Ey = (ey1, ey2, …, eyn), Em = (em1, em2, …, emn), Eo = (eo1, eo2, …, eon), with the threshold θ value is being set to 0.5.
- Growth: After initialization, artificial brain networks start to evolve from the status of young age. For each brain network, one interested node v out of 90 ROIs is selected according to probability pv-see Equation (1) below—and the degree of node v is requested no less than 2. A connection is expected to be established between node v′s two neighbour nodes i and j. Node i is selected firstly from v′s neighbour nodes set |Γ(v)|. Moreover, node i is not connected with at least one node in |Γ(v)|. Otherwise, a new interested node v must be selected again based on pv. The network evolution process will not progress until the new qualified node v is found. Connection probability pi,j of node i and the remaining neighbours (which are necessarily unconnected to node i) is calculated by the connection likelihood model. A link will then be established according to the highest connection likelihood, in between node i and j. This step continues to the next step when each brain network within the group succeeds in adding a link.
- Two-sample t-test: After a link is established in each network, the t-test is executed to test the difference between the artificial brain networks and the fMRI brain networks (group Mid-age and group Old, respectively), in comparing the number of edges, which is used to evaluate how significant the difference is.
- Process of iterations: Artificial brain networks formation is a process of iterations. Step 2 and step 3 constitute one iteration, which adds one link to the network and performs a two-sample t-test. As new links are being added to artificial brain networks, the p-value of t-test increases. Therefore, the formation process ends when p-value stops increasing. The artificial brain network with the greatest p-value at the current iteration is considered as the final artificial brain network.The selection probability pv of selecting an interested node v is expressed by Equation (1):where kv represents the degree of node v, the pv is positive correlated to the degree of node v. This strategy allows nodes with larger degrees to get a larger probability of being selected.
3.2. Connection Likelihood Model-LNBE
The link prediction mechanism of CN model treats each common neighbour equally. Nevertheless, common neighbours may have various degrees as well as other topological features, which implies different common neighbours function differently while connections are established. According to recent research, a local naïve Bayes model (LNB) has been proposed [26]. As a probabilistic model, the model makes a classification of common neighbours. In the LNB, two pairs of nodes with the same amount of common neighbours may reach different selection probabilities during connection establishment. Inspired by the idea of model LNB, we propose a probabilistic model LNBE. By combining naïve Bayes classifiers and the concept of anatomical distance similarity di,j, taking the CN model as a basis, we investigate whether classifying common neighbours of node i and node j can help with a more practical generative network model for human fMRI brain networks in the process of ageing.
In this study, topological features and anatomical distance of human brain are both considered. Connections are established progressively according to the probability given by Equation (2):
where Pi,j is the probability that nodes i and j are connected. Si,j denotes the contribution of topological similarity to connection probability, and is computed by model LNB. In this study, 1/di,j refers to the similarity of anatomical distance similarity of nodes i and j. A comprehensive illustration of how Si,j of the LNB works is shown in the following part.
Firstly, an illustration of the naïve Bayes classifier is given, as it will be used in calculation.
Naïve Bayes classifiers are a collection of probabilistic classifiers based on Bayes’ theorem. They are a family of classifiers which share a common principle. They are particularly well suited if the assumptions are met that every pair of features being classified are independent from each other. Abstractly, the conditional probability model of a classifier is written as p (C│x1, …, xn), in which C represents a dependent class, X = (x1, …, xn) denotes the features. By using Bayes’ theorem, the posterior probability P (C|X), can be calculated by P (C), P (X) and P (X|C), given by Equation (3):
Taking “naïve” conditional independence assumptions into consideration, each feature xi of a given class C is conditionally independent from any other features xj, for i ≠ j. Thus, posterior probability can be rewritten as Equation (4):
According to Bayesian theory, the posterior probability of node i and node j is connected is given by Equation (5):
while the posterior probability of node i and node j are unconnected is:
In Equations (5) and (6), Oi,j denotes a common neighbour node set of any pair of node i and j. is the probability of node i and j having any common neighbours. and denote prior probabilities of node i and node j being connected and unconnected, respectively. Both prior probabilities can be calculated according to a given graph G (V, E) as follows I Equations (7) and (8):
where |V| and |E| represent the number of existing nodes and edges of graph G, respectively.
Node ξ is a common neighbour of node i and j. For each node ξ, is the conditional probability that two connected nodes i and j having a neighbour node ξ in common, while is the conditional probability that two disconnected nodes i and j have a neighbour node ξ in common. According to Bayes′ theory, these two conditional probabilities are as follows:
where p(ξ) is the probability that a selected node ξ is also a common neighbour of one pair of nodes. For the common neighbour node set of any pair of nodes i and j, the posterior probability of node i and j being connected or unconnected is shown in Equations (11) and (12), respectively:
Moreover, for given node i and j, a comparison between the two posterior probabilities may be able to estimate whether the given nodes tend to connect. In order to capture the connection likelihood of node pairs, topological similarity Si,j of node i and node j is defined as the ratio of to in Equation (13):
p(Ci,j│ξ) can be calculated by the clustering coefficient of ξ, which is given by Equation (14):
where Nξ denotes the neighbour’s set of node ξ, |Eξ| represents the number of existing edges among Nξ, |Nξ|(|Nξ| − 1)/2 is the number of edges could possibly exist among Nξ. As , we have:
Therefore, topological similarity can be written as Equation (16):
where and . As s is a constant for the given network, therefore, itself as well as s−1 can both be neglected in the calculation. It is obvious, if Rξ = 1, the contribution of topological similarity to connection probability, which is computed by the LNBE model, is equal to the CN model.
In network topology, each node has its own local topological performance, i.e., degree () and connections (), therefore, different common neighbours ξ ∈ Oi,j obtain different values of , which means they make a different contribution to the topological similarity while the connection likelihood of nodes i and j are being calculated.
Additionally, to obtain a linear formula of the topological similarity, a logarithmic function is used on both sides of Equation (16). Then, topological similarity of a linear function is given by Equation (17) [26]:
4. Statistical Evaluation of Generative Network Models
Goodness-of-fit of each generative network model is theoretically evaluated by how well the generated networks fit the fMRI brain data by comparing the overall network performance of generated networks and fMRI brain networks. Inspired by previous studies on the evaluation of generative network models [12,22,23], the Likeness is calculated via Equation (18) to measure the significance of the difference between a generated artificial brain network and the fMRI brain network, according to an overall condition. This function is defined based on the p-values associated with the two-sample t-test of the difference in the number of edges (edges), average clustering coefficient (C), modularity (Q), characteristic path length (L), global efficiency (Eglbl) and local efficiency (Elcl):
where Pedges is the p-value associated with two-samples t-test for the difference in the number of network edges of a set of 90 model-generated artificial brain networks vs. a set of 90 fMRI brain networks. Similarly, PC, PQ, PL, PEglbl and PElcl are the p-values of two-sample t-tests for the difference in average clustering coefficient, modularity, characteristic path length, global efficiency and local efficiency between artificial brain networks vs. fMRI brain networks, respectively. A high Likeness value indicates a high similarity between the generated artificial brain networks and the observed fMRI brain networks. The Likeness function applied to those artificial networks when the p-values stop increasing. In other words, the Likeness function is applied to mid-age artificial brain networks and to old artificial brain networks.
5. Results
5.1. Ageing of the Functional Brain Network
Ninety fMRI brain networks were obtained in total and were divided into three different age groups. We took the average of each group and demonstrated network topologies, as shown in Figure 1. Figure 1a is brain network topologies of group young, Figure 1b is for group mid-age, while Figure 1c is for group old. All 90 nodes were ordered by node ID. The layout direction was counter-clockwise. Nodes were coloured according to the node′s modularity classes, while sizes vary with nodes’ degree. Node no. 1 of each brain network was marked in Figure 1. Nodes interacted with other nodes through all the network, accordingly, the topological structure of brain network changes constantly. Taking node-1 as an example, it connected to seven out of 90 nodes in the same community (black nodes) during young phase (Figure 1a). The node-1 community aligned itself with more nodes and built a larger community during the mid-age phase (light grey nodes) (Figure 1b), as all the black nodes and some of the other nodes joined them. The edges visibly increased in the old phase, and the node-1 community shuffled a little yet kept enlarging. Some of the nodes from 19–34, as well as most of the nodes from 57–72 (light grey nodes, both subgroups were marked by arcs), joined into the observing community (Figure 1c).
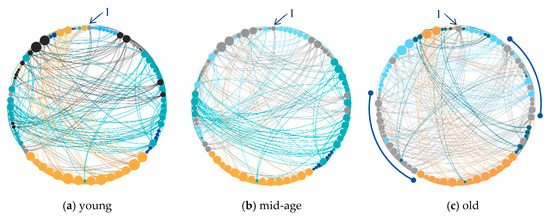
Figure 1.
Illustration of the real fMRI brain network topology. (a) Brain network topology of group young, (b) brain network topology of group mid-age, (c) brain network topology of group old. The colours of nodes vary with the node′s modularity classes. Node sizes vary with the node′s degree. Node no. 1 of each brain network was marked.
Several topological network measurements (i.e., number of edges, average clustering coefficient, modularity, characteristic path length, global efficiency and local efficiency) were applied on the observed fMRI dataset to capture the functional brain network’s dynamical performance as well as topological features. The results were demonstrated by boxplots (Figure 2). Potential unusual observations (outliers) were eliminated from the dataset (Figure 2). To achieve further insight of the normal brain aging process, a linear regression analysis was applied to capture the general evolution tendency of the functional brain network, especially in terms of network topological features, i.e., the number of edges, average clustering coefficient, modularity, characteristic path length, global efficiency and local efficiency (small windows in Figure 2). Colours of elements in the illustration represent the evolving trend of topological property. It is shown that edges and the value of average clustering coefficient, global efficiency and local efficiency increased with age, which was demonstrated by orange colour (Figure 2a,b,e,f). It is also found that the value of modularity and characteristic path length both decreased with age, as demonstrated by blue in Figure 2c,d. Median and mean value of each property evolved among different age groups (from young through mid-age to old), and obeyed the evolving trend of scatters and fitting lines in small windows. Boxplots and linear regression plots showed the consistency of the evolution trend of each topological property of the functional brain network in the aging process.
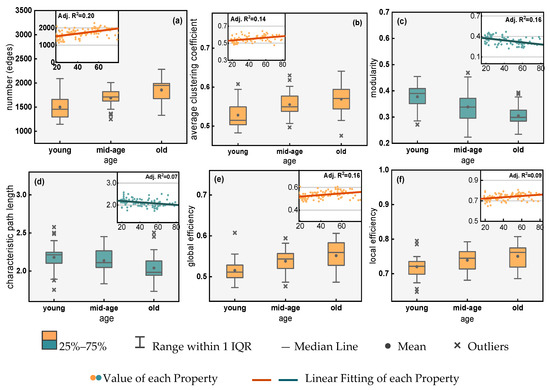
Figure 2.
Illustration of six observed topological properties of fMRI brain network. Subfigure (a) is the number of edges of functional brain network, while (b) is for average clustering coefficient, (c) is modularity, (d) characteristic path length, (e) global efficiency and (f) local efficiency. Each subfigure is demonstrated by boxplot, where the comparison is made among different groups, from young through mid-age to old. Small windows within each illustration is a linear regression plot of property value, which represents a general evolution trend of each topological property. Orange and blue represent the increase and decrease of the property value, respectively.
5.2. Evaluation Results—Comparison of the LNBE Model Versus Mechanistic Generative Network Models
In order to test the LNBE model we proposed, we compared LNBE versus five state-of-the-art mechanistic models for link-prediction and link-based network growth. Additionally, we also considered the performance of a random predictor. Three of these models are based on classical mechanistic modelling: common neighbours (CN) [43], Barabasi–Albert (BA) [40] and Jaccard (JC) [44]. Whereas, two of the tested mechanistic models are the Cannistraci–Alanis–Ravasi model (CAR) and the Cannistraci–Alanis–Ravasi Resource Allocation model (CRA) [45]. The comparison was implemented by performing two-sample t-test between artificial networks and functional brain networks and by analysing the energy index. We drew a comparison between each generated networks and fMRI brain networks, the results were demonstrated in the heatmap, Table 2 represents the obtained p-value and energy index. In Table 2, lower values were demonstrated by tinted tones, while higher values were by shaded tones. It was found that the artificial brain network generated by the LNBE model outperformed those generated by other models. For the LNBE model, apart from average clustering coefficient of group old (C, p-value = 0.0215), p-values of two-sample t-test of the other five topological properties were highly non-significant in both group mid-age and group old. The other three noticeably well-performed models were CN, CAR and CRA. Their p-values were mostly above 0.05. For the CN model, similar to the LNBE, the average clustering coefficient of group old showed a significant difference to functional brain network (C, p-value = 0.0104 < 0.05). Yet interestingly, speaking of the average clustering coefficient, CAR and CRA had outstanding performance instead (CCAR, p-value = 0.7095 > 0.05, while CCRA, p-value = 0.5151 > 0.05). For model CAR, p-values were all above 0.05 in group mid-age. In contrast, among group old, it performed poorly in the index of modularity (Q, p-value = 0.0442 < 0.05) as well as local efficiency (Elcl, p-value = 0.0162 < 0.05), but had a considerably good performance in characteristic path length (L, p-value = 0.9599 > 0.05). For the CRA model, all the observed topological properties showed acceptable performance, as their p-values are above 0.05, apart from the index of local efficiency in both group mid-age (Elcl, p-value = 0.0041 < 0.05) and group old (Elcl, p-value = 0.0298 < 0.05). The Likeness value of the artificial brain network generated by the LNBE model was 4.4794 in group mid-age, and 3.4021 among group old, with both higher than the other models.

Table 2.
A comparison between artificial brain networks and fMRI brain networks among group mid-age and group old.
5.3. Model LNBE—In Comparison with Functional Brain Networks
As the LNBE was proved to be the most relatively optimized generative network model, a series of topological analysis was applied to artificial networks which were simulated by the LNBE. The boxplots below (Figure 3) illustrated an overview of the comparison between functional brain network and artificial network generated by the LNBE on dynamical performance and topological features. In each diagram, two boxes were plotted in both mid-age phase and old phase along the x-axis, showing the comparison of functional brain network and artificial network on each topological property with age. A few potentially unusual observations were marked as outliers so that the analysis results would not be affected by extreme deviations. Apart from the evolution trend of each topological property of functional brain network shown above (i.e., edges, and the value of average clustering coefficient, global efficiency and local efficiency increased with age, while the value of modularity and characteristic path length both decreased with age), it was found that all indices of the artificial network mainly performed in accordance with those of the functional brain network, especially in terms of the general evolution trend, which implies the generative network model does mimic the aging process and the evolution pattern of human functional brain networks.
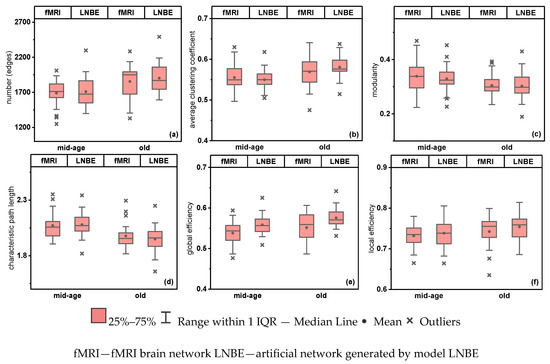
Figure 3.
Comparison of artificial networks generated by LNBE and fMRI brain networks on six studied topological properties. Subfigure (a) is the comparison of the number of edges between artificial network and functional brain network, while subfigure (b) is for average clustering coefficient, (c) is modularity, (d) characteristic path length, (e) global efficiency and (f) local efficiency. The shaded part is for the fMRI brain network, while the non-shaded part is for the LNBE generated network.
6. Discussion
The results strongly indicated the concept that the topology of functional brain network and its topological features evolved progressively and constantly while aging. It is found that all the indices of artificial networks (generated by the LNBE) performed in accordance with those of functional brain networks, especially the centre, spread and overall range of each pair of datasets. Growth of edges demonstrated either physical connections or activity level between nodes (brain regions) raised. An increase of the average clustering coefficient indicated that the nodes in the network are more likely to have highly-connected neighbours, which can be considered as an expected consequence of growing edges. The results showed global efficiency and local efficiency increased with age, which indicated that global and local behaviour improved, that information is exchanged more efficiently within the brain network, and that the executive function and information processing speed both increase with age. The decrease of modularity and characteristic path length implied the stronger potential for integration between brain regions and presence of significant community structure in the network and, therefore, the information flow between nodes (brain regions) across the network is facilitated. This result might seem controversial in the sense that it is known that the brain performance diminishes with aging. However, the brain performance is not only the function of the functional connectome organization, but there are also other molecular factors which are not taken into consideration in this study.
p-values and Likeness revealed how significant the differences between artificial brain networks generated by the LNBE and the six other studied models were to functional brains. It is apparent that the overall performance of model LNBE stands out among others, in the sense that the artificial brain network generated by the LNBE model behaves and evolves more alike to fMRI brain networks than the other artificial networks generated by the rest of the models throughout the lifespan. We also observed that the average clustering coefficient of LNBE artificial network has a significant difference to it of functional brain network among group old. The comparison results also suggested three out of six models performed well. These models are CN, CAR and CRA. The CN model operates similarly to the LNBE, as artificial networks generated by the CN model are mostly similar to functional brain networks but the average clustering coefficient is shows a statistically significant difference, while it is found that CAR and CRA models had good concrete performance on this index. The results showed that the CAR artificial networks had significant differences associated with the comparison of modularity and local efficiency with those of functional brain networks among group old. It is also noticeable that local efficiency of artificial networks which are generated by CRA showed a significant difference to it of functional brain networks among both groups of mid-age and old, which indicated a different local behaviour of artificial networks and functional networks. Considering the value of Likeness, the LNBE performed as the best model in comparison of the six models. Both CRA and CN can be considered as the second-best models in comparison, they both performed better than CAR in general, and CRA is the second best (better than CN) in comparison among group old.
By proposing a novel generative network model, LNBE, for human functional brain networks, we simulated the ageing process of functional brain networks, generated similar enough artificial brain networks and attempted to obtain a better understanding of the generative mechanisms and evolution patterns of the human brain throughout the human lifespan. By comparing the LNBE to the different generative models, we revealed that the idea of classifying common neighbours in the process of network formation provides a similar generative mechanism of human brain ageing process as well as a more practical generative network model. The functional brain ageing process modelling is essential for understanding how cognitive processes develop and evolve across the lifespan. We hold that this study will have the potential to improve the way in which early warnings for latent injury or disease is practiced today and advance healthcare.
Author Contributions
X.L. and S.S. proposed the fundamental idea of the study. X.L. conceived and conducted the experiments. S.S. selected the data B.H. and S.S. wrote and performed the program. X.L. analysed the results. X.L. wrote the article. H.Z. and J.Z. led the project. All authors reviewed and validated the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Fundamental Research Funds for the Central Universities (no. N161608001) and the grant from Major Project of the National Social Science Fund of China (NSSFC) (no. 18ZD23). Financial support for the data used in this project was provided by a grant from the National Natural Science Foundation of China (30770594) and a grant from the National High Technology Program of China (863) (2008AA02Z405).
Acknowledgments
X.L. would like to thank Vania Carolina Fonseca da Silva and Menno de Jong for helpful suggestions.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Isaev, N.K.; Genrikhs, E.E.; Oborina, M.V.; Stelmashook, E.V. Accelerated aging and aging process in the brain. Rev. Neurosci. 2018, 29, 233–240. [Google Scholar] [CrossRef]
- Martin, G.M. Genetic syndromes in man with potential relevance to the pathobiology of aging. Birth Defects Orig Artic. Ser. 1978, 14, 5–39. [Google Scholar] [PubMed]
- Martin, G.M. Genetics and aging; the Werner syndrome as a segmental progeroid syndrome. Adv. Exp. Med. Biol. 1985, 190, 161. [Google Scholar] [PubMed]
- He, Y.; Chen, Z.; Evans, A. Structural Insights into Aberrant Topological Patterns of Large-Scale Cortical Networks in Alzheimer’s Disease. J. Neurosci. 2008, 28, 4756–4766. [Google Scholar] [CrossRef] [PubMed]
- Isaev, N.K.; Stelmashook, E.V.; Stelmashook, N.N.; Sharonova, I.N.; Skrebitsky, V.G. Brain aging and mitochondria-targeted plastoquinone antioxidants of SkQ-type. Biochemistry 2013, 78, 295–300. [Google Scholar] [CrossRef]
- Xekardaki, A.; Eniko, K.; Gold, G. Neuropathological changes in aging brain. Adv. Exp. Med. Biol. 2015, 821, 11. [Google Scholar]
- Pannese, E. Morphological changes in nerve cells during normal aging. Brain Struct. Funct. 2011, 216, 85–89. [Google Scholar] [CrossRef]
- Sporns, O.; Tononi, G.; Kötter, R. The human connectome: A structural description of the human brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef]
- Hagmann, P. From Diffusion MRI to Brain Connectomics. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2005. [Google Scholar]
- Yap, P.T.; Wu, G.; Shen, D. Human Brain Connectomics: Networks, Techniques, and Applications [Life Sciences]. IEEE Signal Process. Mag. 2010, 27, 131–134. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Vértes, P.E.; Alexander-Bloch, A.F.; Gogtay, N.; Giedd, J.N.; Rapoport, J.L.; Bullmore, E.T. Simple models of human brain functional networks. Proc. Natl. Acad. Sci. USA 2012, 109, 5868–5873. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Functional and effective connectivity, Neuroimaging: A synthesis. Hum. Brain Map. 1994, 2, 56–78. [Google Scholar] [CrossRef]
- Mesulam, M. Large-scale neurocognitive networks and distributed processing for attention, language, and memory. Ann. Neurol. 1900, 28, 597–613. [Google Scholar] [CrossRef] [PubMed]
- McIntosh, A.R. Towards a network theory of cognition. Neural Netw. 2000, 13, 861–870. [Google Scholar] [CrossRef]
- Bressler, S.L.; Menon, V. Large-scale brain networks in cognition: Emerging methods and principles. Trends Cogn. Sci. 2010, 14, 277–290. [Google Scholar] [CrossRef]
- Sporns, O. Contributions and challenges for network models in cognitive neuroscience. Nat. Neurosci. 2014, 17, 652–660. [Google Scholar] [CrossRef]
- Medaglia, J.D.; Lynall, M.-E.; Bassett, D.S. Cognitive network neuroscience. J. Cogn. Neurosci. 2015, 27, 1471–1491. [Google Scholar] [CrossRef]
- Stillman, P.E.; Wilson, J.D.; Denny, M.J.; Desmarais, B.A.; Bhamidi, S.; Cranmer, S.J.; Lu, Z.L. Statistical Modeling of the Default Mode Brain Network Reveals a Segregated Highway Structure. Sci. Rep. 2017, 7, 11694. [Google Scholar] [CrossRef]
- Kaiser, M. Modelling the development of cortical networks. Neurocomputing 2004, 58–60, 297–302. [Google Scholar] [CrossRef]
- Zhao, Q.-B.; Feng, H.-B.; Tang, Y.-Y. Modelling human cortical network in real brain space. Chin. Phys. Lett. 2007, 24, 3582. [Google Scholar]
- Cheng, C.; Chen, J.; Cao, X.; Guo, H. Comparison of local information indices applied in resting state functional brain network connectivity prediction. Front. Neurosci. 2016, 10, 585–599. [Google Scholar] [CrossRef] [PubMed]
- Betzel, R.F.; Avena-Koenigsberger, A.; Goñi, J. Generative models of the human connectome. Neuroimage 2016, 124, 1054–1064. [Google Scholar] [CrossRef] [PubMed]
- Liben-Nowell, D.; Kleinberg, J. The Link Prediction Problem for Social Networks. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1019–1031. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Q.M.; Lü, L. Link prediction in complex networks: A local naïve Bayes model. Europhys. Lett. 2011, 96, 48007. [Google Scholar] [CrossRef]
- Available online: http://fcon_1000.projects.nitrc.org/ (accessed on 1 January 2019).
- Biswal, B.B.; Mennes, M.; Zuo, X.N. Toward discovery science of human brain function. Proc. Natl. Acad. Sci. USA 2010, 107, 4734–4739. [Google Scholar] [CrossRef]
- Yan, C.; Zang, Y. DPARSF: A MATLAB toolbox for “pipeline” data analysis of resting-state fMRI. Front. Syst. Neurosci. 2010, 4, 13. [Google Scholar] [CrossRef]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazyoer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef]
- Betzel, R.F.; Fukushima, M.; He, Y. Dynamic fluctuations coincide with periods of high and low modularity in resting-state functional brain networks. NeuroImage 2016, 127, 287–297. [Google Scholar] [CrossRef]
- Hayasaka, S.; Laurienti, P.J. Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage 2009, 50, 499–508. [Google Scholar] [CrossRef]
- Garrison, K.A.; Scheinost, D.; Finn, E.S.; Shen, X.; Constable, R.T. The (in)stability of functional brain network measures across thresholds. Neuroimage 2015, 118, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 66133. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small-world” networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Telesford, Q.K.; Joyce, K.E.; Hayasaka, S. The ubiquity of small-world networks. Brain Connect. 2011, 1, 367–375. [Google Scholar] [CrossRef]
- Ajilore, O.; Lamar, M.; Kumar, A. Association of brain network efficiency with aging, depression, and cognition. Am. J. Geriatr. Psychiatry 2013, 22, 102–110. [Google Scholar] [CrossRef]
- Wen, W.; Zhu, W.; He, Y. Discrete neuroanatomical networks are associated with specific cognitive abilities in old age. J. Neurosci. 2011, 31, 1204–1212. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010; p. 8. [Google Scholar]
- Newman, M.E.J. Clustering and preferential attachment in growing networks. Phys. Rev. E 2001, 64, 025102. [Google Scholar] [CrossRef]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 241–272. [Google Scholar]
- Cannistraci, C.V.; Alanis-Lobato, G.; Ravasi, T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Sci. Rep. 2013, 3, 1613. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

