Abstract
The preference ranking organization method for enrichment of evaluations (PROMETHEE) method considers a significant outranking class of multi-criteria decision analysis (MCDA), as it is easy to deal with its simple computations. In the PROMETHEE, different preference functions are used according to the type and nature of attributes or criteria that demonstrate the clearness and reliability of this method. This study provides a new version of the PROMETHEE method using bipolar fuzzy information, named the bipolar fuzzy PROMETHEE method. Bipolar fuzzy sets or numbers constitute an asymmetrical relationship between two judgmental factors of human reasoning. Vague and imprecise knowledge is characterized by bipolar fuzzy linguistic terms which are further represented in the form of trapezoidal bipolar fuzzy numbers. The trapezoidal bipolar fuzzy numbers are used by analysts to assign the preferences of alternatives on the basis of criteria. Further, a ranking function of bipolar fuzzy numbers is considered to access the crisp real preferences of alternatives. The entropy weighting information is employed to calculate the weights of attributes by considering the condition of normality. A numerical example such as the selection of green suppliers by using the bipolar fuzzy PROMETHEE is performed on the basis of the usual criterion preference function in order to explain the procedure of the proposed method. Comparable results are derived by using the combination of linear and level preference functions. The results obtained by using different types of preference functions are the same, representing the authenticity of the proposed bipolar fuzzy PROMETHEE method.
1. Introduction
In the modern era, companies and organizations need to integrate their techniques and services to meet customer requirements and survive in the competitive environment. On the other hand, customers are demanding high-quality products which should be delivered on time at a low cost. Therefore, the selection of suppliers becomes an important strategic decision for supply chain management, which affects the satisfaction of customers and the market value of products. The manufacturers are strained to pay attention to the environmental competencies because of the critical environmental issues such as increasing public awareness, global warming, and pressure from consumers, organizations, and governments. For this purpose, green supplier selection is structured with green packaging to avoid pollution and for the safety of the environment. This has become an important research topic in recent years that is very popular among researchers. The green supplier selection problem is based on multiple conflicting criteria, as it is not a single-criterion problem. In this respect, multi-criteria decision analysis (MCDA) techniques or tools can be used to investigate this problem in a better way. MCDA methods are used to rank suppliers or to choose the most appropriate and favorable supplier on the basis of multiple conflicting criteria. Many researchers have employed different techniques to select suppliers, such as Awasthi et al. [] by fuzzy TOPSIS, Handfield et al. [] by AHP, Mousakhani et al. [] using interval type-2 fuzzy information, and Yeh and Chuang [] by MOGA. Hou and Yanrong [] applied entropy weight information to calculate the weights of criteria and then used the TOPSIS technique to choose a suitable supplier under a green environment. Yazdani et al. [] introduced a new hybrid MCDA model to investigate supply chain management through the quality function deployment (QFD) and step-wise weight assessment ratio analysis (SWARA) models, which are used to derive the inputs of problems. Further, weighted aggregated sum product assessment (WASPA) is applied to obtain the ordering of green suppliers.
In the last several decades, a number of MCDA techniques and their different versions or extensions have been introduced, including the analytical hierarchy process (AHP) [], the preference ranking organization method for enrichment of evaluations (PROMETHEE) [], the elimination and choice translating reality (ELECTRE) [], VIekriterijumsko KOmpromisno Rangiranje (VIKOR, meaning multi-criteria optimization and compromise solution) [], and technique for the order of preference by similarity to an ideal solution (TOPSIS) [], to solve and structure multi-criteria decision making (MCDM) problems. The MCDA methods are used to rank a set of actions or alternatives on the basis of conflicting criteria or to obtain the optimal solution of MCDM problems. Initially, these MCDA methods were introduced to investigate problems having exact data and numeric information. However, many real-life problems have vague and uncertain information that cannot be addressed with the help of exact or crisp data. For this reason, Bellman and Zadeh [] originated the concept of fuzzy MCDA methods to structure and evaluate problems having inexact and imprecise information. After that, many researchers used fuzzy sets and their different extensions to solve decision-making problems having imprecision and uncertainties. Furthermore, multi-criteria group decision analysis (MCGDA) is developed when a group of several decision makers is involved to analyze problems that consist of multiple criteria. Moreover, linguistic variables are used to address vagueness when it is not possible to determine the crisp numeric values of alternatives. These linguistic variables are then converted to the numerical values of respective sets in order to compare the alternatives for further evaluation. A number of MCGDA methods are utilized to investigate supply chain management and to assess the most suitable supplier using fuzzy information. For example, Chiou et al. [] investigated green suppliers and presented a comparative analysis of the electronics industry in China using a fuzzy AHP. Sanayei et al. [] used fuzzy VIKOR for the group assessment of suppliers. Liu et al. [] proposed multi-operators based on intuitionistic fuzzy sets and used it for the evaluation of urban-infrastructure-based projects. Kannan et al. [] utilized fuzzy TOPSIS for green supplier selection by considering a Brazilian electronics company. Further, Awasthi and Kannan [] worked on a development program of green suppliers by using the nominal group technique (NGT) and VIKOR method under a fuzzy environment. Hamdan and Cheaitou [] used fuzzy AHP and TOPSIS to evaluate suppliers and developed a mathematical technique to allocate orders. Recently, Shumaiza et al. [] presented the bipolar fuzzy ELECTRE II technique to obtain the ranking of suppliers using an optimization technique to calculate the weights of criteria. Ziemba et al. [] introduced the method of criteria selection and the calculation of weights in the process of web projects evaluation.
The PROMETHEE is an outranking approach of MCDA methods introduced by Brans and Vincle [] in 1985 to obtain the partial ranking (PROMETHEE I) and complete ranking (PROMETHEE II) of alternatives depending on multiple attributes or criteria. Moreover, Brans and Mareschal [] presented two new extensions of the PROMETHEE method—PROMETHEE III, in which ranking is based on intervals, and PROMETHEE IV which is a continuous case of ranking. Abdullah et al. [] used the PROMETHEE method for the selection of green suppliers and provided a comparative study on the basis of preference functions. Behzadian et al. [] provided a comprehensive study of PROMETHEE methodologies and applications. Govindan et al. [] presented an application of a PROMETHEE-based method for the ranking of green suppliers in a food supply chain. Goumas and Lygerou [] extended the PROMETHEE for decision-making in fuzzy environment. Krishankumar et al. [] introduced a new extension of PROMETHEE using intuitionistic fuzzy information with the help of linguistic variables. Ziemba [] provided a new multi-criteria decision-making approach by introducing the NEAT F-PROMETHEE technique in which the decision is made on the basis of mapping trapezoidal fuzzy numbers. YinYang bipolar fuzzy set theory (or bipolar fuzzy set theory) was initiated by Zhang [,] as a generalization of fuzzy set theory [] to deal with the bipolar judgmental thinking of human reasoning. Akram and Arshad [] introduced bipolar fuzzy linguistic variables and bipolar fuzzy numbers as an extended version of bipolar fuzzy sets. Alghamdiet al. [] proposed multi-criteria decision-making methods using bipolar fuzzy information. Akram et al. [] applied TOPSIS and ELECTRE I models using bipolar fuzzy information for medical diagnosis. Shumaiza et al. [] introduced a group decision-making approach based on the VIKOR method using trapezoidal bipolar fuzzy numbers. The existing versions and extensions of the PROMETHEE technique can be successfully adopted to examine the problems when the information is provided in the form of crisp or fuzzy values, but they cannot assess the problems which have bipolar uncertainties. Crisp or fuzzy sets only provide one-sided information, or we can say we have only the information about the satisfaction degree of alternatives. In these sets, we are unable to provide any information about the dissatisfaction degree of alternatives. Therefore, this study provides an extension of the PROMETHEE method to solve problems having two-sided information. We use bipolar fuzzy linguistic terms to assign the preferences of alternatives relative to conflicting criteria. Further, we parameterize the bipolar fuzzy linguistic variables in terms of bipolar fuzzy numbers for the numeric preferences of alternatives []. We calculate the normalized weights of criteria based on entropy weight measuring technique [,]. We compute a decision matrix consisting of crisp real values using the ranking function of bipolar fuzzy numbers presented in []. We find the partial ranking of alternatives using PROMETHEE I by considering the positive and negative outranking flows. Further, we determine the net flows and rank the alternatives using PROMETHEE II. We also make a comparison of net results obtained by applying different preference functions.
The main contributions of this research study are as follows:
- The PROMETHEE method is extended to a bipolar fuzzy PROMETHEE method to deal with the double-sided information of human reasoning. More generally, trapezoidal bipolar fuzzy numbers are used to obtain more accurate results.
- The personal interest or influence of decision makers towards the criteria is minimized by using the Shannon entropy weighting technique to calculate the normalized weights of criteria.
- The partial and complete ranking of alternatives are determined by applying the PROMETHEE I and PROMETHEE II, respectively.
- A numerical example for the selection of green suppliers is presented that shows the validity and authenticity of the proposed method.
The outline of this paper is as follows: Section 1 contains the basic definitions and concepts, and also provides the methodology of the bipolar fuzzy PROMETHEE method. Section 3 contains the numerical application of green supplier selection under the usual criterion preference function. Section 4 provides a comparative analysis by using linear and level preference functions. Section 5 concludes the whole discussion.
2. Methodology of the Bipolar Fuzzy PROMETHEE Method
This section contains the basic definitions relevant to bipolar fuzzy sets and numbers. Further, the step-by-step procedure of the bipolar fuzzy PROMETHEE method is presented. A YinYang bipolar fuzzy set (or bipolar fuzzy set) is defined as follows.
Definition 1
([]). Consider a non-empty universe of discourse X. A bipolar fuzzy set on X is defined as
where and represent the satisfaction and dissatisfaction degrees of bipolar fuzzy set , respectively.
Particularly, the bipolar fuzzy numbers as a generalization of bipolar fuzzy sets are defined as follows.
Definition 2
([]). A bipolar fuzzy number is defined on real line R having the form
such that the satisfaction degree of is defined as
and dissatisfaction degree of is defined as
where and represent the left and right membership degrees of , respectively. Similarly, and represent the left and right membership degrees of , respectively.
Just like the trapezoidal fuzzy numbers are an important and useful type of fuzzy number [], bipolar fuzzy numbers are easy for computations if they have the following form.
Definition 3
([]). A bipolar fuzzy number is called the trapezoidal bipolar fuzzy number, denoted by , if its satisfaction and dissatisfaction degrees are described as follows:
and
Ranking or score functions are used to simplify the given information in the form of real crisp values. The ranking function of trapezoidal bipolar fuzzy numbers is given as:
Definition 4
([]). Consider a trapezoidal bipolar fuzzy number , which can be converted into a real number by applying the ranking function as:
where and are the mean values of respective sets.
2.1. Procedure of Bipolar Fuzzy PROMETHEE Method
This section provides a new extension of an outranking method PROMETHEE using bipolar fuzzy information, namely, the bipolar fuzzy PROMETHEE method, to evaluate multi-criteria group decision-making problems. The procedure of this method is established as follows: specify the problem area and select a suitable and relevant group of decision-makers; define the linguistic terms or variables and their corresponding values; construct a decision matrix for each decision maker and then aggregate their decision values; calculate the normalized weights of criteria using the entropy weight method []; define some preference function for pairwise comparison of alternatives, find the multi-criteria preference index of alternatives; determine the partial ranking of alternatives (PROMETHEE I); and determine the complete ranking of alternatives (PROMETHEE II).
Consider a multi-criteria decision-making problem involving a set of p alternatives , which is evaluated on the basis of q conflicting criteria . A group of r decision-makers , is selected for the assessment of feasible alternatives with respect to different criteria. The preference values of alternatives with respect to each criterion are used to construct a decision matrix for every decision maker . The procedure of the bipolar fuzzy PROMETHEE technique is summarized in the following steps:
- Step 1.
- Identify the linguistic variables.Linguistic variables are used by decision-makers to determine the ratings of an alternative with respect to different criteria. It is most important to identify the relevant and appropriate set of linguistic variables and define their respective values. In this method, a set of seven linguistic variables in the form of trapezoidal bipolar fuzzy numbers are considered and shown in Figure 1. The values of these trapezoidal bipolar fuzzy numbers are taken from the numerical domain [0,1].
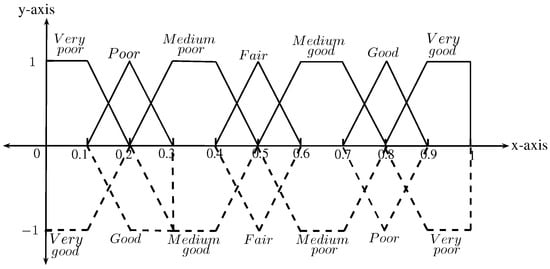 Figure 1. Linguistic variables for criteria.
Figure 1. Linguistic variables for criteria. - Step 2.
- Construct a decision matrix.Suppose that the alternatives are evaluated on the basis of conflicting criteria which are assessed by every decision maker . Then, r decision matrices are constructed containing the rating values of linguistic variables given by r decision-makers in the following manner:where each entry represents a trapezoidal bipolar fuzzy number. The aggregated bipolar fuzzy decision value of each alternative with respect to the criteria , denoted by is computed by using the averaging operator as follows:These aggregated values are used to construct an aggregated decision matrix as follows:
- Step 3.
- Rank the bipolar fuzzy numbers.The bipolar fuzzy numbers of aggregated values are then converted into the crisp values of real numbers by using the ranking function of bipolar fuzzy numbers as follows:and these crisp values are used to construct a simple decision matrix for further calculation.
- Step 4.
- Determine the deviation by pairwise comparison.The deviation of alternatives is computed by the pairwise comparison of alternatives on the basis of criteria by using the following expression:where represents the difference or deviation of any two alternatives and with respect to each criterion. The terms and denote the crisp ratings of alternatives and , respectively, with respect to some criterion .
- Step 5.
- Define the preference function.A preference function is defined to evaluate the preference of alternative regarding alternative on the basis of each criterion and has a value ranging from 0 to 1. If the value of the preference function is zero or negative then there is the indifference of the decision maker between the alternatives with respect to that criterion. On the other hand, a value closer to 1 shows a greater preference. This preference function represents the intensity of preference of an alternative over another alternative and is categorized as follows:
- -
- shows an indifference between and , or no preference of over ;
- -
- represents a weak preference of over ;
- -
- represents a strong preference of over ;
- -
- shows a strict preference of over .
- Step 6.
- Calculate the normalized weights.The weight value of each criterion shows the relative importance of that criterion towards the other criteria of that problem. These weight values may be completely or partially unknown for decision makers, and can be calculated by using various techniques or methods. If all the criteria have the same importance for a decision maker, then all weights can be assigned equal value. In this methodology, the entropy weight measuring information is used to enumerate the normalized weights of conflicting criteria. In order to calculate the weights by entropy measure, first we should normalize the decision values of each criterion and obtain the projection values of criteria as follows:These projection values are then used to calculate the entropy value for each criterion as follows:where is a constant. Afterward, the degree of divergence of the intrinsic information for each criterion is calculated by using the following expression:The divergence value denotes the inherent contrast intensity of criteria . The higher value of shows that the criterion is considered as more important for that problem. Then, the weights of criteria are calculated as:such that, and
- Step 7.
- Determine the multi-criteria preference index.When a preference function and weight is assigned to each criterion by a decision maker for the considered problem, then the multi-criteria preference index of alternatives is determined. The multi-criteria preference index ∏ is calculated as the weighted average of the preference functions :Since the normalized weights are used in this method, Equation (12) is reduced as follows:The multi-criteria preference index ∏ has a value between 0 and 1, such that
- -
- represents the weak preference of alternative over with respect to all criteria;
- -
- represents the strong preference of alternative over with respect to all criteria.
This preference index induces an outranking relation on the set of alternatives which is further represented by an outranking graph. The nodes of this outranking graph are the alternatives and, between any two nodes and , there are two arcs with values , and which have no particular relation. - Step 8.
- Find the preference order.The outranking relation is then used to obtain the ranking of alternatives, which may be partial or complete. The alternatives are ranked partially by using the PROMETHEE I, whereas complete ranking can be obtain by proceeding one more step of PROMETHEE II.
- (i)
- Ordering the alternatives by partial ranking or PROMETHEE I.For each alternative in the outranking graph, the leaving or outgoing flow is defined as:which is the sum of values of outward arcs of alternative and thus gives the outgoing flow of as shown in Figure 2. This positive outranking flow measures how an alternative dominates all other alternatives.
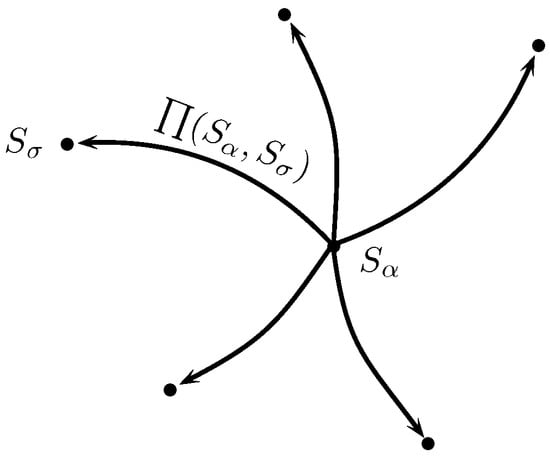 Figure 2. Outgoing flow of .Similarly, for each alternative in outranking graph, the entering or incoming flow is defined as:which is the sum of values of inward arcs of alternative and thus gives the incoming flow of as shown in Figure 3. This negative outranking flow determines how an alternative is dominated by all other alternatives.
Figure 2. Outgoing flow of .Similarly, for each alternative in outranking graph, the entering or incoming flow is defined as:which is the sum of values of inward arcs of alternative and thus gives the incoming flow of as shown in Figure 3. This negative outranking flow determines how an alternative is dominated by all other alternatives.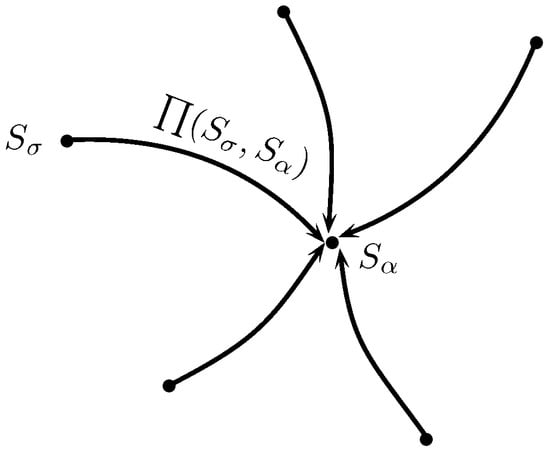 Figure 3. Incoming flow of .The alternative which has the greater value of and the lower value of is chosen as the most suitable alternative. The outgoing and incoming flows determine the preferences as given in Equations (12) and (13), respectively.The PROMETHEE I partial ordering is then obtained by taking the intersection of the two previously mentioned preferences as:Since all the alternatives are not comparable in PROMETHEE I, the computation of the net outranking flow of alternatives is as follows.
Figure 3. Incoming flow of .The alternative which has the greater value of and the lower value of is chosen as the most suitable alternative. The outgoing and incoming flows determine the preferences as given in Equations (12) and (13), respectively.The PROMETHEE I partial ordering is then obtained by taking the intersection of the two previously mentioned preferences as:Since all the alternatives are not comparable in PROMETHEE I, the computation of the net outranking flow of alternatives is as follows. - (ii)
- Ordering the alternatives by complete ranking or PROMETHEE II.The net flow of each alternative is the difference of outgoing and incoming flows, which is computed as:The net flow provides the complete ordering of alternatives by avoiding any incomparability, the PROMETHEE II complete ranking is given in Equation (16).Thus, all the alternatives can be compared on the basis of net flows . The alternative with maximum net flow is observed as the most suitable alternative.The framework of the procedure of the bipolar fuzzy PROMETHEE method is provided in Figure 4. This framework consists of the goal of the selection procedure, the environmental and economical criteria, the alternatives for evaluation, the preference functions, and the net outranking flows of PROMETHEE I and PROMETHEE II in the form of partial and complete ranking, respectively.
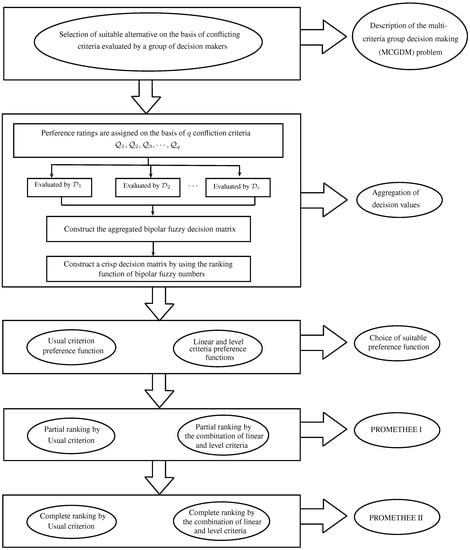 Figure 4. Framework of the bipolar fuzzy preference ranking organization method for enrichment of evaluations (PROMETHEE).
Figure 4. Framework of the bipolar fuzzy preference ranking organization method for enrichment of evaluations (PROMETHEE).
This multi-criteria outranking approach is based on a series of computations, in which all steps remain the same other than the definition of the preference function and the computation of normalized weights. The normalized weights can be calculated by using an appropriate method according to the choice of decision values or the preference of the decision makers. The preference function defined in Step 5 is an irrational choice of preference function which depends on the nature of the criteria or the desire of the decision-makers. The choice of types of preference function is very important as it may change the net outranking flow or the ranking of alternatives.
2.2. Preference Function
The PROMETHEE technique requires the relevant and suitable preference functions for its implementation. A preference function is a function which defines the deviation between alternatives for each criterion. Different types of preference function are defined and used by Brans et al. [,]. In this article, the preference functions are defined to accomplish the condition of the PROMETHEE algorithm that will be applied to a case study. With reference to Step 5, three types of preference functions are used, given as follows.
Definition 5.
Type 1: The usual criterion preference function is defined as,
where d represents the difference or deviation between alternatives. In this type of preference function, there is an indifference between two alternatives a and b if only if . The usual criteria function works on the formula “the more the better” and is used when decision makers cannot assign importance to different criteria values.
Definition 6.
Type III: The linear criterion preference function is defined as
where is the preference value given by the decision maker. When the difference or deviation d is lower than m, the preference of the decision maker increases linearly with d. When d is greater than m, a strict preference of an alternative is achieved with respect to that criteria.
Definition 7.
Type IV: The level criterion preference function is defined as
where m and n are the preference and indifference values, respectively, taken from . There is an indifference between alternatives on the interval . This preference function is always used for qualitative or benefit type criteria.
3. Green Supplier Selection
The advancement of economic globalization has increased the challenges of survival and development for manufacturers and companies. Manufacturing companies can efficiently improve their competitiveness if they have an impressive supply chain management system. Supplier selection is a basic key for supply chain management systems, and so has become the most popular research area for practitioners and scholars, both nationally and globally. The development of the economy has a great impact on the ecological environment, which threatens the survival of humans on Earth. As economic development has become an important factor, manufacturers should be more socially responsible while maintaining the development of their companies. Manufacturers have also introduced the concept of “Green suppliers” in the supply chain management system. Green supplier selection plays a vital role in green supply management, and is the key to the success of any business or company.
In this research article, we evaluate green suppliers using bipolar fuzzy information in the form of trapezoidal bipolar fuzzy numbers. For this case study, criteria and alternatives were considered based on the work of Abdullah et al. [] and Gurel et al. []. After initial screening, the following four alternatives denoted by , and were selected for further evaluation.
- MVG Food Marketing Sdn Bhd;
- CF Org Noodle Sdn Bhd;
- Hexa Food Sdn Bhd;
- SCS Food Manufacturing Sdn Bhd.
A group of three decision-makers was appointed to evaluate these companies for the selection of a green supplier on the basis of seven criteria, denoted by , and , which were as follows:
- Cost of products (consists of transportation, purchasing, inventory, maintenance, holding, security etc.);
- Quality of products (indicated by the principles, techniques, and practices of companies);
- Service provided (low costs, high productivity, quick response, minimum wastage, no damage, etc.);
- Delivery (at the correct time, at the right place, and in good condition);
- Pollution control (an important criterion, as pollution is obtained as a byproduct of energy use in the production procedures);
- Environmental management system (the environmental dimension has been recently added in assessment procedures);
- Green packaging (a type of packaging which aims protect the environment by using environmentally friendly material).
The computations of the PROMETHEE method by using the usual criterion preference function are described and computed in the following steps:
- Step 1.
- The group of decision-makers decided to use linguistic variables to rate the alternatives with respect to different criteria for evaluation. A set of seven linguistic variables is presented in Figure 1. These linguistic variables and their corresponding bipolar fuzzy numbers are given in Table 1.
 Table 1. Linguistic variables and values of criteria.
Table 1. Linguistic variables and values of criteria. - Step 2.
- The preference ratings of alternatives with respect to conflicting criteria given by decisions makers in the form of linguistic terms are shown in Table 2.
 Table 2. Performance ratings by decision-makers (linguistic terms).The rating values of these linguistic variables in the form of trapezoidal bipolar fuzzy numbers were used as defined in Table 1, and the results are given in Table 3. The aggregated decision values of these trapezoidal bipolar fuzzy numbers were computed by employing the Equation (1), and an aggregated decision matrix was constructed as shown in Table 4.
Table 2. Performance ratings by decision-makers (linguistic terms).The rating values of these linguistic variables in the form of trapezoidal bipolar fuzzy numbers were used as defined in Table 1, and the results are given in Table 3. The aggregated decision values of these trapezoidal bipolar fuzzy numbers were computed by employing the Equation (1), and an aggregated decision matrix was constructed as shown in Table 4. Table 3. Performance ratings by decision makers (bipolar fuzzy numbers).
Table 3. Performance ratings by decision makers (bipolar fuzzy numbers). Table 4. Aggregated decision matrix.For example, the aggregated decision value of supplier with respect to criterion was computed by arithmetic mean as,
Table 4. Aggregated decision matrix.For example, the aggregated decision value of supplier with respect to criterion was computed by arithmetic mean as, - Step 3.
- In this step, a simple decision matrix consisting of real numbers as entries was constructed for further calculations by using the ranking function of bipolar fuzzy numbers. Equation (2) was applied to the entries of Table 1, and the bipolar fuzzy numbers were converted to crisp values, which are shown in matrix T.For instance, is the performance value of supplier on the basis of criterion , which was calculated as follows:
- Step 4.
- The decision matrix T was used to determine the deviation of each alternative towards the other alternatives with respect to all criteria. The deviations were calculated by using Equation (3), and the results are shown in Table 5.
 Table 5. Deviation of alternatives with respect to criteria.
Table 5. Deviation of alternatives with respect to criteria. - Step 5.
- A preference function is required for the implementation of the PROMETHEE method. The preference function was used to define the deviation of any pair of alternatives on the basis of each criterion. In this step, the usual criterion preference function was used as defined in Definition 5, and the results are summarized in Table 6.
 Table 6. Usual criterion preference function.
Table 6. Usual criterion preference function. - Step 6.
- The weights of criteria specify the importance of each criterion towards the alternatives of the problem. In this method, the entropy weight information technique is used to calculate the normalized weights of criteria. The first step of this technique is the computation of projection values of criteria in order to normalize the decision values of criteria. The projection values for all criteria were calculated using Equation (4), and the results shown in Table 7. For example, is the projection value of criterion regarding the supplier and was calculated as follows:
 Table 7. Projection values of criteria.The entropy value and the degree of divergence for each criterion were calculated by using the projection values given in Table 7, and deploying Equations (5) and (6), respectively, which were further utilized to determine the normalized weights of criteria. The results of entropy values, degrees of divergence, and weights of criteria are respectively shown in Table 8.
Table 7. Projection values of criteria.The entropy value and the degree of divergence for each criterion were calculated by using the projection values given in Table 7, and deploying Equations (5) and (6), respectively, which were further utilized to determine the normalized weights of criteria. The results of entropy values, degrees of divergence, and weights of criteria are respectively shown in Table 8. Table 8. Entropy value, divergence, and weights of criteria.
Table 8. Entropy value, divergence, and weights of criteria. - Step 7.
- In this step, the multi-criteria preference index of each alternative is calculated, taking into account the weight criteria. The preference index of each alternative shows the value of preference of a supplier over other suppliers. The values of multi-criteria preference index were computed using Equation (9), and the results are summarized in Table 9.
 Table 9. Multi-criteria preference index.
Table 9. Multi-criteria preference index. - Step 8.
- This step concludes the whole procedure and the partial as well as net flows of alternatives are computed.
- (i)
- Positive and negative flows of alternatives (PROMETHEE I).The outgoing and incoming flows of alternatives are obtained which are positive and negative outranking flows, respectively. The positive outranking flow of an alternative determines how an alternative dominates all other alternatives and the negative flow shows how an alternative is dominated by all other alternatives. Equations (10) and (11) were used to calculate the outgoing and incoming flows of each alternative, and the results are given in Table 10. The partial ordering of suppliers was then obtained by taking the intersection of preorders and , which is given as follows:and the partial results of PROMETHEE I are illustrated in Figure 5.
 Table 10. Outgoing and incoming flow.
Table 10. Outgoing and incoming flow.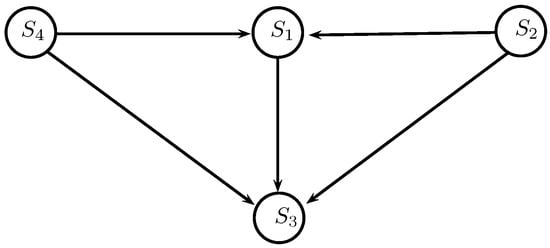 Figure 5. Partial PROMETHEE I relations.The results of positive outranking flow show that the supplier is most preferable with greatest outgoing flow rate and determine that the supplier is more dominant over all other suppliers. On the other hand, the negative outranking flow shows that the supplier is less dominated by all other suppliers with minimum incoming flow value. These results are not able to compare all the alternatives nor to determine the most suitable supplier. For this reason, we need to calculate the net outranking flow of suppliers to obtain the complete preference of suppliers in the next step.
Figure 5. Partial PROMETHEE I relations.The results of positive outranking flow show that the supplier is most preferable with greatest outgoing flow rate and determine that the supplier is more dominant over all other suppliers. On the other hand, the negative outranking flow shows that the supplier is less dominated by all other suppliers with minimum incoming flow value. These results are not able to compare all the alternatives nor to determine the most suitable supplier. For this reason, we need to calculate the net outranking flow of suppliers to obtain the complete preference of suppliers in the next step. - (ii)
- Net flow of alternatives (PROMETHEE II).The net flow of each alternative was calculated by using Equation (15), which is the combination of positive and negative flows. The net outranking flow provides the complete ranking of alternatives by avoiding the incomparability. The results of the net flow of alternatives are shown in Table 11. These results can be justified by sketching the PROMETHEE diamond, which is a chart used to elaborate the results of PROMETHEE I and PROMETHEE II simultaneously. The positions of suppliers or complete ranking (PROMETHEE II) as well as the outgoing and incoming flows are also displayed in Figure 6.
 Table 11. Net flow of suppliers.
Table 11. Net flow of suppliers.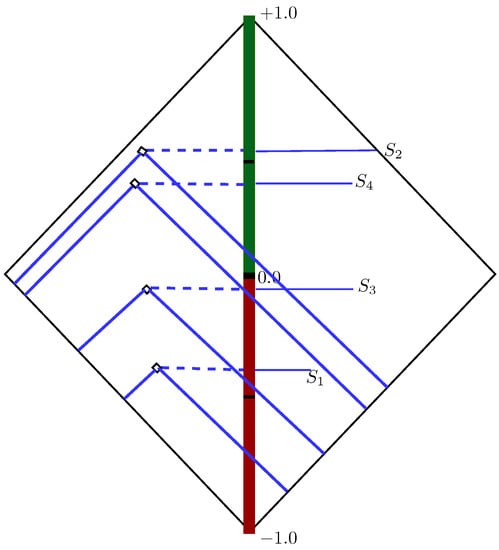 Figure 6. PROMETHEE diamond.
Figure 6. PROMETHEE diamond.
4. Comparative Study
The PROMETHEE method has the advantage of choosing or adopting different preference functions for all criteria. In Section 3, the usual criterion preference function was applied to all criteria and the ordering of green suppliers was obtained. In this section, the level and linear criteria preference functions are used for green supplier selection in order to make a comparison of the results of the PROMETHEE method. The preference functions were selected according to the nature or type of criteria. For example, the linear preference function was adopted for criterion (Cost of products), as the linear function is best adapted for quantitative criteria. The level criterion preference function is suitable for benefit or qualitative criteria, that is, (Quality of products). The construction of the decision matrix and the calculation of weights were the same as computed in Section 3, so we move on to Step 5.
- Step 5.
- In this step, the combination of level and linear preference functions were adopted for conflicting criteria. The list of all criteria and their corresponding preference functions is given in Table 12.
 Table 12. Preference functions corresponding to criteria.The linear preference function has a preference threshold value and the level function evaluates the criteria on the basis of preference and indifference threshold values, which are given by decision makers. In this multi-criteria decision-making problem, the indifference and preference threshold values were considered as and , respectively, for both linear and level preference functions. The deviations between every pair of alternatives were obtained using Equations (6) and (7), and the results are shown in Table 13.
Table 12. Preference functions corresponding to criteria.The linear preference function has a preference threshold value and the level function evaluates the criteria on the basis of preference and indifference threshold values, which are given by decision makers. In this multi-criteria decision-making problem, the indifference and preference threshold values were considered as and , respectively, for both linear and level preference functions. The deviations between every pair of alternatives were obtained using Equations (6) and (7), and the results are shown in Table 13. Table 13. Linear and level criteria preference function.
Table 13. Linear and level criteria preference function. - Step 6.
- Step 7.
- The multi-criteria preference indices were calculated using Equation (9), and the outcomes are shown in Table 14.
 Table 14. Multi-criteria preference index.
Table 14. Multi-criteria preference index. - Step 8.
- The partial and net flows are determined in this step.
- (i)
- The positive and negative outranking flows of the suppliers were computed by deploying the Equations (10) and (11), respectively. The respective results of outgoing and incoming flows for PROMETHEE I are shown in Table 15.
 Table 15. Outgoing and incoming flow.The partial ordering of suppliers was then obtained by taking the intersection of preorders and , which is given as follows:and the partial results of PROMETHEE I are illustrated in Figure 7.
Table 15. Outgoing and incoming flow.The partial ordering of suppliers was then obtained by taking the intersection of preorders and , which is given as follows:and the partial results of PROMETHEE I are illustrated in Figure 7.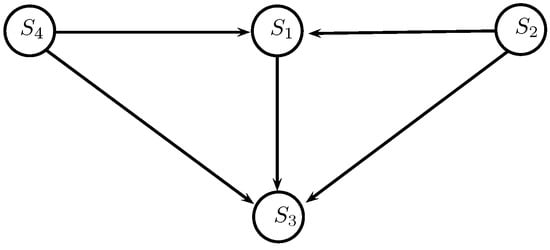 Figure 7. Partial PROMETHEE I relations.
Figure 7. Partial PROMETHEE I relations. - (ii)
- The net outranking flow of each alternative was calculated by deploying Equation (15), and the results of PROMETHEE II are given in Table 16.
 Table 16. Net flow of suppliers.It can be clearly seen that supplier is chosen as the most preferable alternative under the combination of linear and level preference functions and the suppliers can be ordered as
Table 16. Net flow of suppliers.It can be clearly seen that supplier is chosen as the most preferable alternative under the combination of linear and level preference functions and the suppliers can be ordered as
5. Discussion and Conclusions
In this article, an outranking technique was proposed to obtain the partial and complete ordering of suppliers using green packaging. Different types of preference functions were used for computations in order to make a comparison of PROMETHEE behavior under different preference functions. Firstly, the usual criterion preference function was used to find the net flows and ranking of alternatives, as it is considered as the simplest function and is easy to apply. Then, the combination of linear and level preference functions was employed to obtain the net outranking flows and the ordering of alternatives. The final ranking of suppliers by PROMETHEE using different preference functions are given in Table 17. It can be easily seen that the supplier was chosen as best for both functions. Furthermore, the results or net outranking flows of suppliers under both preference functions are summarized and shown in Figure 8.

Table 17.
Final ranking of suppliers.
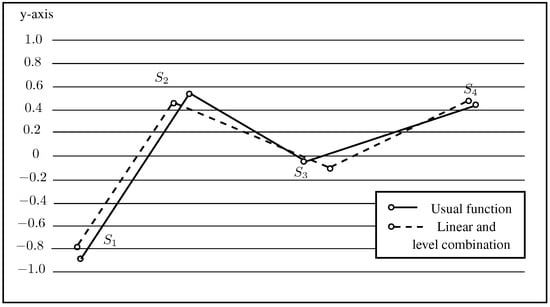
Figure 8.
Comparison between the net flows of different preference functions.
The PROMETHEE is an outranking class of multi-criteria decision analysis methods which rank alternatives on the basis of conflicting criteria. PROMETHEE is easy to apply and understand due to its simple conception and computations. The PROMETHEE I gives the partial ordering of alternatives based on the positive and negative outranking flows, as it contains the preferences, indifferences, and incomparabilities. Whereas, the PROMETHEE II provides the complete ordering of alternatives in the descending order of net flow values. In the literature, different types of preference functions of criteria have been defined and utilized according to the nature of the criteria. In this study, we investigated the green suppliers on the basis of seven types of environmental and economical criteria by a group of three decision makers. We used different preference functions to examine the influence and impact of these preference functions on ranking. The results clearly show that there was no significant impact of these preference functions on the final selection or ranking.
This research analysis has some limitations, especially in the choice of preference functions and their arithmetic functions. This study is restricted to three types of preference function. In future work, it could be extended to other types of preferences or with a modified preference function. The subtraction arithmetic function was used to calculate the net flows of alternatives, which is very simple and straightforward. Different types of arithmetic operations or distances could be implied in the future.
Author Contributions
Investigation, M.A., S., and A.N.A.-K.; writing—original draft, M.A. and S.; writing—review and editing, A.N.A.-K. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (D1441-107-130). The authors therefore gratefully acknowledge DSR technical and financial support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Awasthi, A.; Chauhan, S.S.; Goyal, S.K. A fuzzy multicriteria approach for evaluating environmental performance of suppliers. Int. J. Prod. Econ. 2010, 126, 370–378. [Google Scholar] [CrossRef]
- Handfield, R.; Walton, S.V.; Sroufe, R.; Melnyk, S.A. Applying environmental criteria to supplier assessment: A study in the application of the Analytical Hierarchy Process. Eur. J. Oper. Res. 2002, 141, 70–87. [Google Scholar] [CrossRef]
- Mousakhani, S.; Nazari-Shirkouhi, S.; Bozorgi-Amiri, A. A novel interval type-2 fuzzy evaluation model based group decision analysis for green supplier selection problems: A case study of battery industry. J. Clean. Prod. 2017, 168, 205–218. [Google Scholar] [CrossRef]
- Yeh, W.C.; Chuang, M.C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Hou, B.; Yanrong, W. Supplier evaluation and selection based on improved TOPSIS method in green supply chain. J. Hunan Univ. Technol. 2014, 2, 17–25. [Google Scholar]
- Yazdani, M.; Zolfani, S.H.; Zavadskas, E.K. New integration of MCDM methods and QFD in the selection of green suppliers. J. Bus. Econ. Manag. 2016, 17, 1097–1113. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic foundation of the analytic hierarchy process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincle, P.V. A Preference Ranking Organization Method. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Benayoun, R.; Roy, B.; Sussman, B. ELECTRE: Une Methode pour Guider le Choix en Presence de Points de vue Multiples; Note de Travail, 49, SEMA-METRA International, Direction Scientifique; SEMA: Montrouge, France, 1966; 43p. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 4, 141–164. [Google Scholar] [CrossRef]
- Chiou, C.Y.; Hsu, C.W.; Hwang, W.Y. Comparative investigation on green supplier selection of the American, Japanese and Taiwanese electronics industry in China. In Proceedings of the 2008 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008; pp. 1909–1914. [Google Scholar]
- Sanayei, A.; Mousavi, S.F.; Yazdankhah, A. Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst. Appl. 2010, 37, 24–30. [Google Scholar] [CrossRef]
- Liu, B.; Huo, T.; Wang, X.; Shen, Q.; Chen, Y. The decision model of the intuitionistic fuzzy group bid evaluation for urban infrastructure projects considering social costs. Can. J. Civil Eng. 2013, 40, 263–273. [Google Scholar] [CrossRef]
- Kannan, D.; Jabbour, A.B.L.d.; Jabbour, C.J.C. Selecting green suppliers based on GSCM practices: Using fuzzy TOPSIS applied to a Brazilian electronics company. Eur. J. Oper. Res. 2014, 233, 432–447. [Google Scholar] [CrossRef]
- Awasthi, A.; Kannan, G. Green supplier development program selection using NGT and VIKOR under fuzzy environment. Comput. Ind. Eng. 2016, 91, 100–108. [Google Scholar] [CrossRef]
- Hamdan, S.; Cheaitou, A. Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach. Comput. Oper. Res. 2017, 81, 282–304. [Google Scholar] [CrossRef]
- Akram, M.; Al-Kenani, A.N. Multiple-Attribute Decision Making ELECTRE II Method under Bipolar Fuzzy Model. Algorithms 2019, 12, 226. [Google Scholar]
- Ziemba, P.; Piwowarski, M.; Jankowski, J.; Watrobski, J. Method of criteria selection and weights calculation in the process of web projects evaluation. In Proceedings of the International Conference on Computational Collective Intelligence, Seoul, Korea, 24–26 September 2014; pp. 684–693. [Google Scholar]
- Brans, J.P.; Vincle, P.; Mareschal, B. How to select and how to rank projects: The PROMETHEE method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Brans, J.P.; Mareschal, B. PROMETHEE methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin, Germany, 2005; pp. 163–186. [Google Scholar]
- Abdullah, L.; Chan, W.; Afshari, A. Application of PROMETHEE method for green supplier selection: A comparative result based on preference functions. J. Ind. Eng. Int. 2019, 15, 271–285. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Govindan, K.; Kadzinski, M.; Sivakumar, R. Application of a novel PROMETHEE-based method for construction of a group compromise ranking to prioritization of green suppliers in food supply chain. Omega 2017, 71, 129–145. [Google Scholar] [CrossRef]
- Goumas, M.; Lygerou, V. An extension of the PROMETHEE method for decision making in fuzzy environment: Ranking of alternative energy exploitation projects. Eur. J. Oper. Res. 2000, 123, 606–613. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Saeid, A.B. A new extension to PROMETHEE under intuitionistic fuzzy environment for solving supplier selection problem with linguistic preferences. Appl. Soft Comput. 2017, 60, 564–576. [Google Scholar]
- Ziemba, P. NEAT F-PROMETHEE-A new fuzzy multiple criteria decision making method based on the adjustment of mapping trapezoidal fuzzy numbers. Expert Syst. Appl. 2018, 110, 363–380. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. In Proceedings of the IEEE Conference Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Zhang, W.R. (Yin)(Yang) bipolar fuzzy sets. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems Proceedings, IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228), Anchorage, AK, USA, 4–9 May 1998; Volume 1, pp. 835–840. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Akram, M.; Arshad, M. A novel trapezoidal bipolar fuzzy TOPSIS method for group decision-making. Group Decis. Negot. 2019, 28, 565–584. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Alshehri, N.O.; Akram, M. Multi-criteria decision-making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 2018, 20, 2057–2064. [Google Scholar] [CrossRef]
- Akram, M.; Shumaiza; Arshad, M. Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 2020, 39, 1–23. [Google Scholar] [CrossRef]
- Akram, M.; Al-Kenani, A.N.; Alcantud, J.C.R. Group decision-making based on the VIKOR method with trapezoidal bipolar fuzzy information. Symmetry 2019, 11, 1313. [Google Scholar]
- Lihong, M.; Yanping, Z.; Zhiwei, Z. Improved VIKOR algorithm based on AHP and Shannon entropy in the selection of thermal power enterprise’s coal suppliers. In Proceedings of the International Conference on Information Management, Innovation Management and Industrial Engineering, Taipei, Taiwan, 19–21 December 2008; Volume 2, pp. 129–133. [Google Scholar]
- Shemshadi, A.; Shirazi, H.; Toreihi, M.; Tarokh, M.J. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst. Appl. 2011, 38, 12160–12167. [Google Scholar] [CrossRef]
- Alcantud, J.C.R.; Biondo, A.E.; Giarlotta, A. Fuzzy politics I: The genesis of parties. Fuzzy Sets Syst. 2018, 349, 71–98. [Google Scholar] [CrossRef]
- Gurel, O.; Acar, A.Z.; Onden, I.; Gumus, I. Determinants of the green supplier selection. Procedia-Soc. Behav. Sci. 2015, 181, 131–139. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).