Abstract
The present study accentuates the heat transfer characteristics of a convective condition of micropolar nanofluid on a permeable shrinking/stretching inclined surface. Brownian and thermophoresis effects are also involved to incorporate energy and concentration equations. Moreover, linear similarity transformation has been used to transform the system of governing partial differential equations (PDEs) into a set of nonlinear ordinary differential equations (ODEs). The numerical comparison has been done with the previously published results and found in good agreement graphically and tabular form by using the shooting method in MAPLE software. Dual solutions have been found in the specific range of shrinking/stretching surface parameters and the mass suction parameter for the opposing flow case. Moreover, the skin friction coefficient, the heat transfer coefficient, the couple stress coefficient, and the concentration transfer rate decelerate in both solutions against the mass suction parameter for the augmentation of the micropolar parameter respectively. The first (second) solution is the stable (unstable) solution and can (not) be considered as a real solution as the values of the smallest eigenvalues are positive (negative).
1. Introduction
During the past two decades researchers have constructed or modified the models of fluid where gyrating micro-components is the necessary factor. There exists such a model known as the micropolar fluid model. Initially, this model was introduced by Eringen [1] in which he added microscopic velocity field and atomic rotating motion in the fluid. These kinds of fluids contain rigid/spherical particles, nonsymmetric stress tensor, and micro rotational characteristics during the flow. Some common daily life examples of micropolar fluids are ferrofluids, bubbly fluids, animal blood, liquid crystals, mixture of red and white cells, etc. [2,3]. Lukaszewicz [4] wrote a detailed book on micropolar fluid in which he explained that micropolar fluid contains five more viscosities of coefficients. It can be concluded from the survey of the past published literature that micropolar nanofluid has received much attention from many researchers. Micropolar nanofluid is the extension of Buongiorno’s model [5] by considering the angular momentum effect on the fluid flow model. Hsiao et al. [6] examined micropolar nanofluid by using Buongiorno’s model and found that the intensity of the thermophoresis enhanced the temperature of the fluid. Hayat et al. [7] considered the micropolar nanofluid over the stretching surface and found a single solution. Micropolar nanofluid over the vertical surface was investigated by Noor et al. [8]. They successfully obtained one solution. Haq et al. [9] studied the stagnation point flow of the micropolar nanofluid over the vertical sheet in which they considered the model of Buongiorno. Furthermore, only one solution was obtained successfully even in the opposing case. Recently, micropolar nanofluid in the presence of magnetic force was investigated by Patel et al. [10] in which they also noticed a single solution. Rafique et al. [11] considered micropolar nanofluid on the inclined stretching plane where they obtained a single local similarity solution. Moreover, they claimed that the effect of the Brownian motion is then inversely proportional to the rate of heat transfer. The same authors published an article of the local similarity solution (all parameters are not truly similar) in which they examined the stagnation point flow of micropolar nanofluid on the inclined plane with the effect of magnetohydrodynamic (MHD) and chemical reaction [12]. They successfully obtained only one solution. Some advances of the micropolar nanofluid can be seen in these articles in which researchers obtained a single solution [13,14,15,16,17,18,19,20]. Further, the dual solutions of micropolar nanofluid on the vertical surface were investigated by Lund et al. [21] in which they found that dual solutions are only possible in some ranges of the suction parameter. Dero et al. [22] found triple solutions during the examination of micropolar nanofluid over the stretching and shrinking surfaces. It was noticed that thermophoresis and Brownian motion are good agents to increase the thickness of thermal boundary layer and temperature of the fluid. However, they did not perform a stability analysis. Dual solutions, without performing the stability analysis, of micropolar nanofluid over the shrinking/stretching surface was found by Magodora et al. [23] in the presence of thermal effect. Triple solutions of micropolar nanofluid over the shrinking surface with the effect of the velocity slip was obtained by Ali et al. [24] in which they performed the analysis of stability in order to determine the stable solution. A few more related research articles of the micropolar fluid and nanofluid for the multiple solutions can be seen in References [25,26,27,28,29,30]. A vast analysis of the published works reveals that no one has considered micropolar nanofluid model over the inclined plane for multiple solutions. Further, stability analysis is performed which also can be considered as one of the prime objectives of the current study. Therefore, the effect of the inclined angle on the steady flow of the micropolar nanofluid over the linear plane is being examined. It is expected that this investigation would add an innovative approach for those researchers who are interested to find the characteristics of the multiple solutions of the micropolar nanofluid.
The boundary layer flow of fluids attracts numerous researchers due to its vast applications over stretching/shrinking surface on different fields of sciences such as mechanical, aeronautical, and civil engineering. Some applications of boundary layer flows are tinning and strengthening of copper wires, elastic sheets, non-stop cooling, fiber turning, wire drawing, expulsion of polymer, paper, and food processing, etc. It seems that Sakiadis [31] was the first who examined the boundary layer flow. Later on, many researchers considered boundary layer flow of Newtonian and non-Newtonian fluids. It should be noted that a lot of works have been done on boundary layer flow. However, we considered recently published works of boundary layer flow of nanofluids over stretching/shrinking surface for multiple solutions. Raju et al. [32] investigated nanofluid over non-linear stretching surface and found dual solutions. Oblique stagnation point flow of nanofluid on shrinking surface was examined by Li et al. [33] and successfully noticed dual solutions in the range of stretching/shrinking parameter. Nanofluid with the effect of Soret and Dufour was investigated and noticed a dual solution without performing the analysis of the stability of the solutions [34]. Dero et al. [35] studied the unsteady flow of nanofluid on stretching/shrinking surface by considering various slip effects. Zaib et al. [36] used a single-phase nanofluids model for micropolar fluid and found dual solutions. The model of single-phase nanofluid in the presence of binary chemical reaction of the cross-flow of nanofluid over the stretching/shrinking surface was studied by Khan et al. [37]. They noticed dual solutions in various ranges of the physical parameters. Lund et al. [38] considered nanofluid over non-linear shrinking surface with the effect of viscous dissipation and found two solutions. They stated that the first solution can be realizable as compared to the second solution by performing the analysis of stability on the solutions. The advance works on boundary layer flow of various fluids can be seen in these articles [39,40,41,42,43,44,45]. In light of the above-mentioned references and literature survey, it is concluded that micropolar nanofluid over the inclined shrinking/stretching surface has not yet been studied for multiple solutions and these results are novel. Therefore, we attempt to examine micropolar nanofluid due to its rising desires in various areas of engineering and industries.
2. Problem Formulation
Two-dimensional steady flow of incompressible micropolar nanofluid on the linear inclined shrinking surface has been considered. Physical model and coordinate system of the problem is explained in Figure 1. Under the consideration of velocity and angular velocity field, temperature and nanoparticles volume fraction of the boundary layer equations for the flow of micropolar nanofluid can be written in the Buongiorno model [5] as below
in which is the velocity vector, is the microrotation vector, the spin gradient viscosity is , micro-rotation viscosity coefficient is , the gravitational acceleration is , is micro-inertia density, , ,,, , , and stand for dynamic viscosity of base fluid, the densities of base fluid, pressure, the coefficient of Brownian motion, the thermal conductivity of base fluid, the thermophoretic diffusion coefficient, and the effective heat capacity of the base fluid, the effective heat capacity of the nanoparticle material, angle respectively. Further, and are the respective temperature and concentration, and are the respective coefficient of thermal and nanoparticle volumetric expansion.
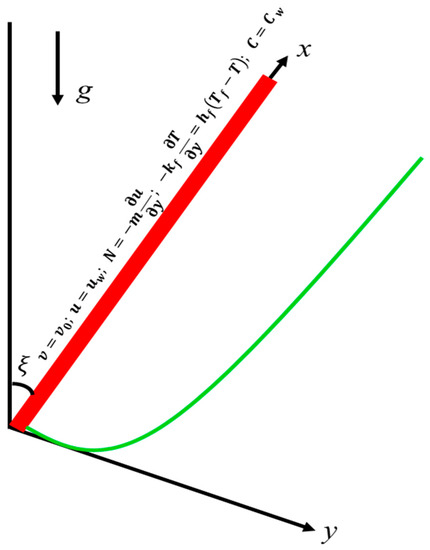
Figure 1.
Physical model and coordinate system.
According to scale analysis, we have the following boundary layer equations:
subject to boundary condition
where is the velocity of sheet and is the constant, is the thermal diffusivity, is the ratio of effective heat capacity, is the suction/injection parameter, and are the ambient concentration and temperature respectively, such that and . Following similarity will be used to get similarity solution of Equations (7)–(10) with subject to boundary conditions Equation (11). Moreover, is the constant, where which means that microelements are unable to rotate, when .5 which implies that antisymmetric part of the stress tensor is vanishing and where m = 1 which indicates the model of the turbulent flow.
By applying above relations and Equation (12) in Equations (7)–(10), we have
along boundary conditions
Here prime denotes the differentiation with respect to , is the micropolar parameter, is the Buoyancy constraint where , is the buoyancy force due to concentration difference where , is the Prandtl number, are the Brownian motion and thermophoresis parameters. Moreover, is the Schmidt number, is the Suction/Blowing parameter, is the stretching and shrinking parameter, and Biot number or convective parameter is .
The physically quantity of interest are Skin friction coefficient, local Nusselt number and local Sherwood number, which can be expressed as
Using Equation (12) in Equation (18), we have
where is local Reynolds number.
3. Stability Analysis
The analysis of the stability of the solutions is a significant analysis to check the consistency of the multiple similarities as well as local similarity solutions. It is worth mentioning that a boundary layer problem might have one, zero, or multiple solutions. For instance, if there exist non-unique solutions in any boundary layer problem but the investigators succeed in obtaining one solution only, that solution may be the second solution (not real/unstable). It may prompt the distortion of the heat transfer attributes and flow. For dual solutions, the double set of initial suppositions (one (second) set for first (second) solution) are required to get two disparate profiles (solutions) of the velocity, temperature and concentration in the numerical method subject to condition that both the first and second profiles must asymptotically fulfill the boundary conditions. The following researchers have considered this analysis in their studies [46,47,48,49,50].
According to Merkin [51] and Dero et al. [52], the first stage in the stability analysis is to change the system of governing equations into a system of an unsteady problem by introducing where is the time since the disturbance may decay or grow with time. Thus, we have now following system of equations
The new similarity transformation with can be expressed as
Using Equation (24) into Equations (20)–(23), we get
with the following boundary conditions
The following functions are used to obtain the behavior of the solution’s stability by perturbing with the disturbance [53].
where , , and are small relative to , , and respectively. Further, , , and are the steady state solutions of the problem and is the unknown eigenvalue. Now, by substituting Equation (30) in Equations (25)–(28), we get following system of linearized eigenvalue problem
with the boundary conditions
According to Haris et al. [54], one boundary condition should be relaxed in the BVP4C solver to obtain the values of the smallest eigenvalue . Here, is relaxed to .
4. Numerical Method
It is very difficult to find the exact solutions for ODEs system when it contains non-linearity. In this case, researchers opted for numerical approach. Since we are dealing with highly non-linear system of ODEs Equations (13)–(16) subject to boundary conditions Equation (17), shooting method is adopted to solve the system. However, this system needs to be reduced to the equivalent system of first order ODEs as follows
subject to initial conditions
In order to solve Equations (36)–(39) subject to initial conditions Equation (40), the initial values and are required. These values are approximated by using the shooting method. Then, the resultant system of first order ODEs is solved by employing Runge–Kutta of 4th order. By assuming , the calculated values of are compared with given boundary condition and the estimated values of and , are adjusted to obtain a better approximate solution.
5. Results and Discussion
In this section, the results of the considered problems are discussed. In this analysis, we have taken the Prandtl number for the water is Pr = 6.2 in order to check the effect of micropolar parameters over the inclined plane. The comparison and the authenticity of our numerical solution for the skin friction with the results of Bhattacharyya et al. [55] is portrayed in Figure 2 in which the latter solution is highlighted with the solid lines while the new solution is shown with the dashed lines. Further, our results are compared numerically for some selected values of and and found in a good agreement with Khan and Pop [56] as highlighted in Table 1. Table 2 displays the values of the smallest eigenvalue with fixed parameters . It is noticed that the positive (negative) values of smallest eigenvalues indicates that the first (second) solution is stable (unstable). The solution in this paper is obtained for both branches which we refer as dual solutions. Throughout the paper, the first solution is represented by the solid blue lines, while the second solution is represented by the dashed red lines. The critical points in all the figures is marked by the small green dot where both the solution behavior is changed at this position. These multiple solutions were found for different parameters and their results are plotted in distinct graphs.
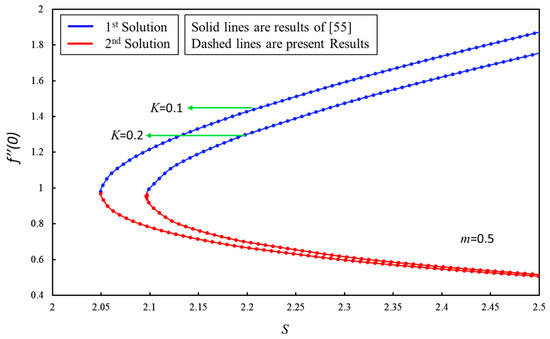
Figure 2.
Comparison of with results of Bhattacharyya et al., when

Table 1.
Comparison of results for the reduced Nusselt and Sherwood numbers when 10.

Table 2.
Smallest eigen values for different values of and .
Figure 3 was drawn for the skin friction coefficient along x-axis against the parameter or various values of non-Newtonian parameter . The critical points of are , and where dual solutions exist. Moreover, after these points, there is no solution range. Absolute viscosity reduces for the higher values of the micropolar parameter due to this reduction, the first solution decreases. On the other hand, the dual trend is noticed in the second solution. Figure 4 shows the behavior of against for various values of angle . The coefficient of skin friction is higher at the inclined plane in the first solution. Moreover, the dual solutions can be found in the shrinking case only. It is also noticed that has an inverse relation with the profile of . The impacts of the material parameter on the for are demonstrated in Figure 5. It is noticed that the couple’s stress coefficient is higher in the first solution for the higher values of the suction as resistance is created in the fluid flow. On the other hand, dual behavior is noticed in the second solution. Figure 6 is plotted to show the effect of on the for the various values of . The behavior is revealed in Figure 4. Figure 7 depicts a decreasing behavior in both branches of the solution as the non-Newtonian parameter is increased. It can be explained as a material parameter enhances the heat transfer rate due to the reduction in the absolute viscosity. As a result, the thickness of the thermal boundary layer becomes thinner. The impact of angle on the against the parameter is highlighted in Figure 8. The heat transfer rate reduces in both solutions when increases.
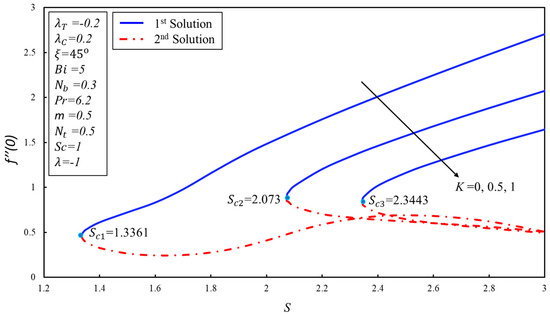
Figure 3.
versus the suction for varying material parameter .
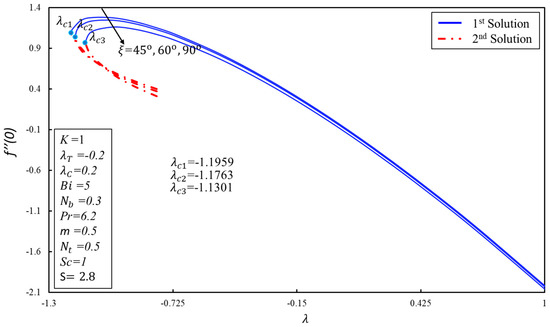
Figure 4.
versus the stretching/shrinking parameter for varying angle .
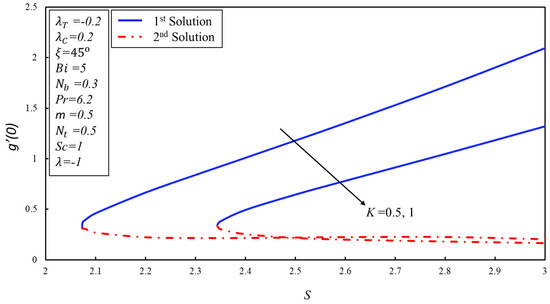
Figure 5.
versus the suction S for varying material parameter .
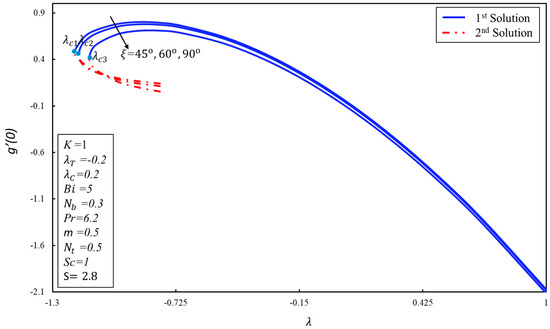
Figure 6.
versus the stretching/shrinking parameter for varying angle .
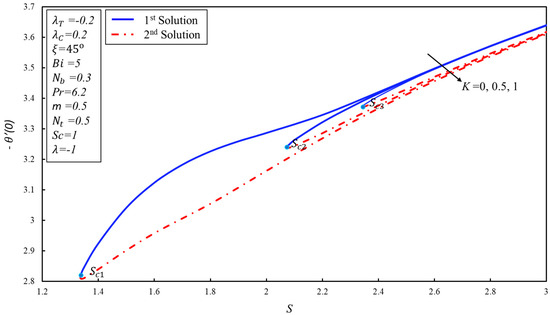
Figure 7.
versus the suction S for varying material parameter .
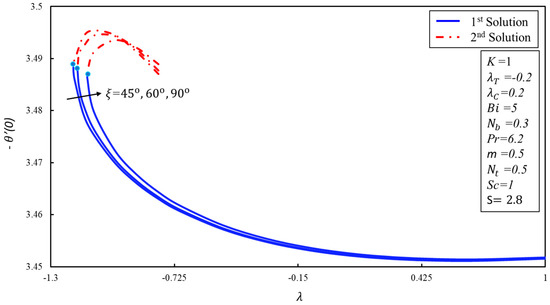
Figure 8.
versus the stretching/shrinking parameter for varying angle .
Figure 9 displays the influences of on the rate of mass transfer against . It elucidates that both solutions are decelerating for the larger values of . In general, it can be noticed that the concentration boundary layer is moving down when is increased. The effects of the angle parameter on the rate of mass transfer against the parameter is captured in Figure 10. The similar behavior of solutions is observed in Figure 10 as is noticed in Figure 9.
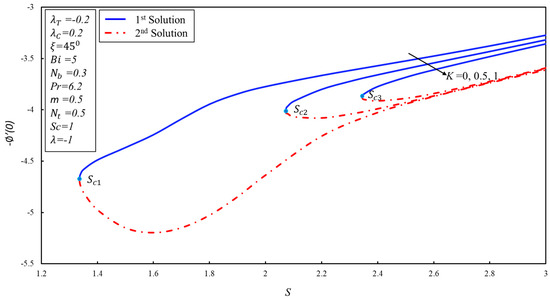
Figure 9.
versus the suction S for varying material parameter .
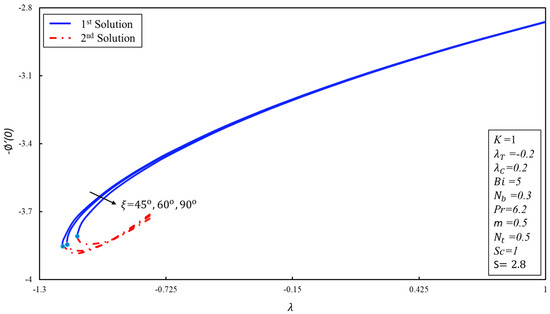
Figure 10.
versus the stretching/shrinking parameter for varying angle .
Figure 11 and Figure 12 show the behavior of the profiles for the and for the various values of the material parameter , respectively. Figure 11 demonstrated that the momentum boundary layer is declined in the first solution and inclined in the second solution as is increased for some fixed angle value as highlighted in the above figure, while the impact of the same corresponding parameter on the is plotted in Figure 12 where the identical behavior is seen in the upper branch solution and the total reverse behavior is observed in the second branch solution. Figure 13, Figure 14 and Figure 15 are plotted in order to expose the behavior of temperature profile for various values of thermophoresis parameter, the Biot number and the Brownian motion parameter , respectively. More exactly, it is scrutinized from Figure 13, Figure 14 and Figure 15 that when we are augmenting the values of , and , the temperature profile is boosted up in all the figures in both solutions, respectively.
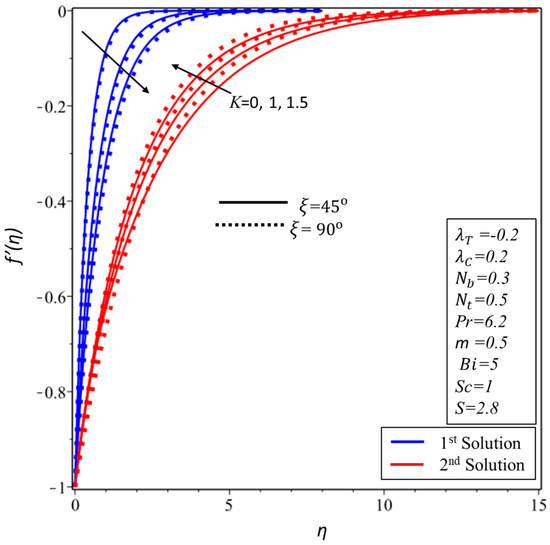
Figure 11.
for various values of material parameter .
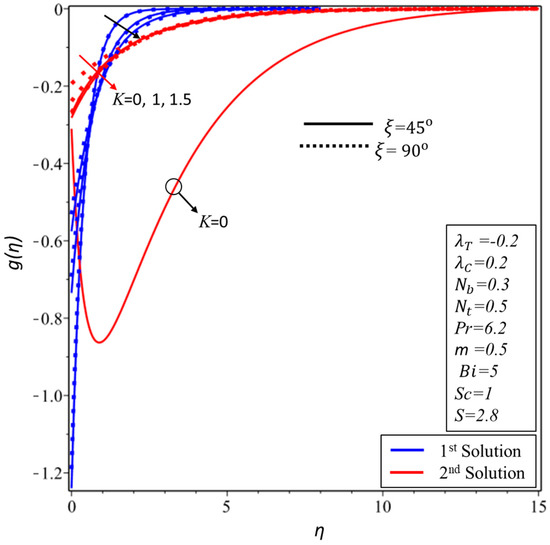
Figure 12.
for various values of material parameter .
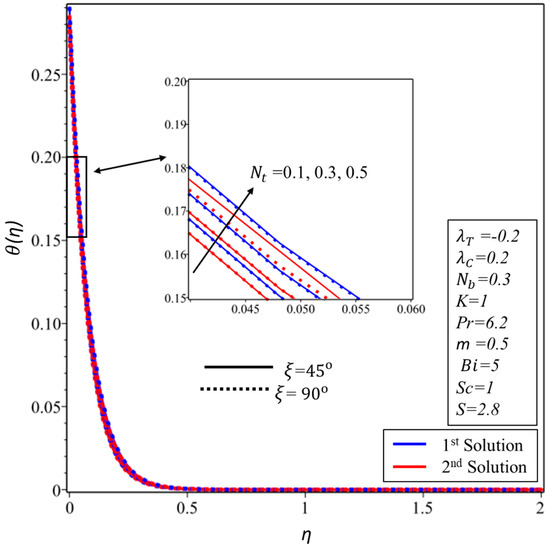
Figure 13.
for various values of thermophoresis parameter .
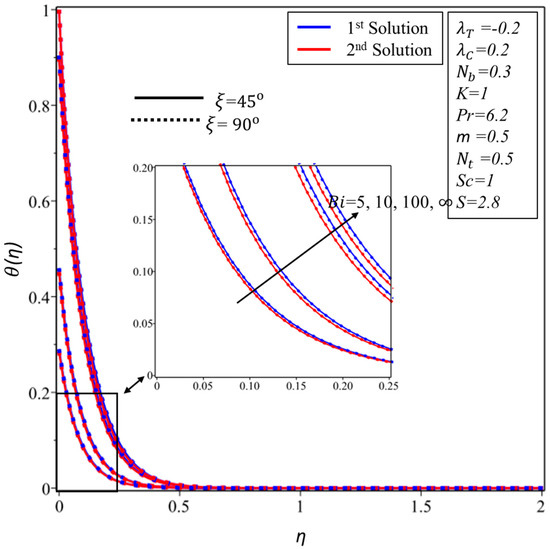
Figure 14.
for various values of Biot number .
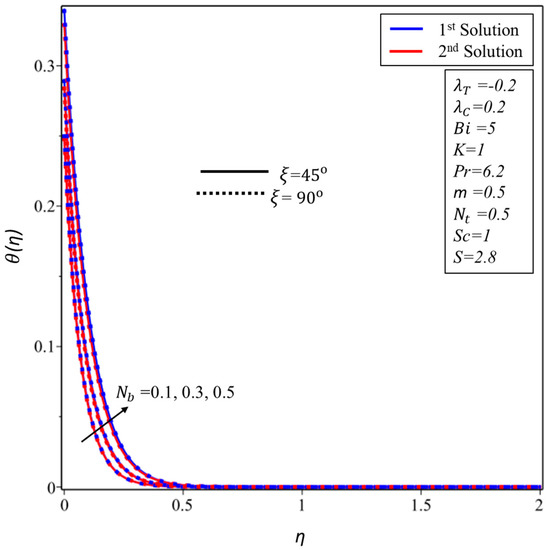
Figure 15.
for various values of Brownian motion parameter .
Figure 16, Figure 17 and Figure 18 are designed in order to interpret the behavior of concentration profile for various values of thermophoresis parameter, the Biot number and the Brownian motion parameter , respectively. Thus, it is investigated further, from Figure 16 and Figure 17 that when we augment the values of and the concentration boundary layer is larger in both branches of solutions, respectively, whilst the total reverse behavior is observed in Figure 18 for the augmentation of the Brownian motion parameter .
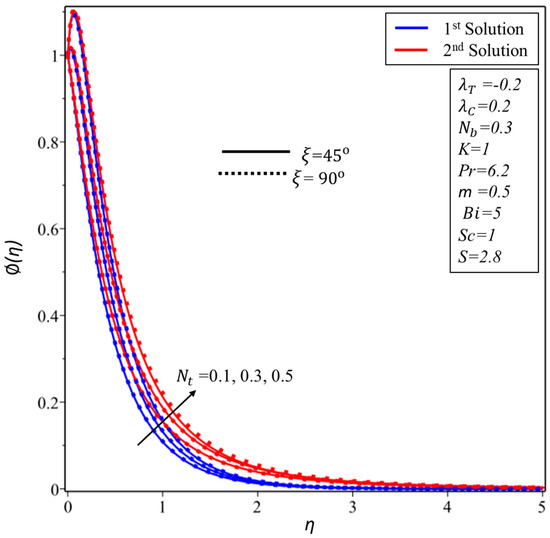
Figure 16.
for various values of thermophoresis parameter .
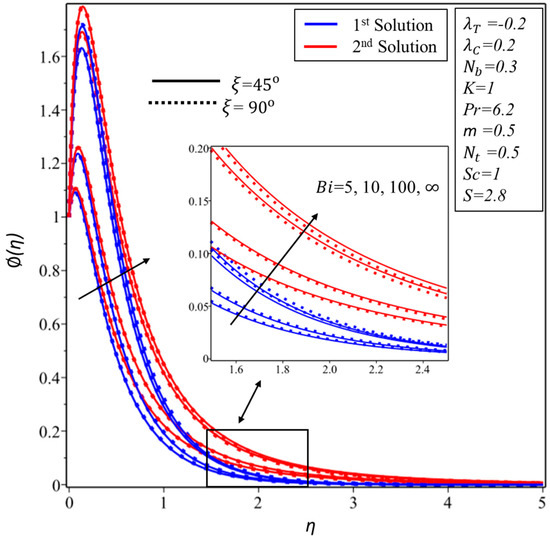
Figure 17.
for various values of Biot number .
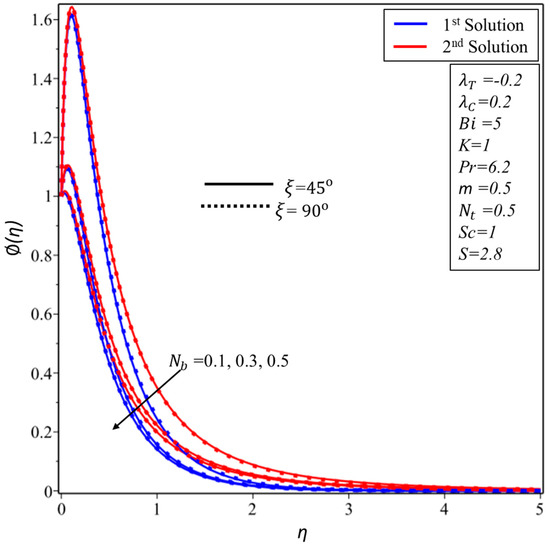
Figure 18.
for various values of Brownian motion parameter .
6. Conclusions
The two-dimensional steady flow of incompressible micropolar nanofluid on the linear inclined shrinking/stretching surface has been considered in the presence of convective condition. The self-similar equations are solved numerically. The microrotation and the angle effect on the flow implements when the material parameter vagaries. It is observed that due to the augmentation in the micropolar parameter the steady flow needs more amount of mass suction and the stretching and shrinking parameter. More exactly, in all the phenomenon the dual similarity solutions for velocity, temperature and concentration exist. The skin friction coefficient, the heat transfer coefficient, the and the mass transfer rate decelerate in both solutions (first and second solution) against the mass suction parameter for the augmentation of the material parameter , respectively. On the other hand, the impact of the angle parameter against the parameter on the skin friction, mass transfer rate and shows an increasing behavior in both solutions whilst the reverse flow is observed for the heat transfer rate.
Author Contributions
Conceptualization, L.A.L. and Z.O.; Funding acquisition, D.B.; Investigation, U.K. and I.K.; Methodology, L.A.L., U.K. and I.K.; Project administration, I.K.; Software, L.A.L., I.K., Z.O., U.K. and K.S.N.; Supervision, I.K.; Review and Revision: D.B. and K.S.N.; Formal Analysis: D.B. and K.S.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are thankful to the Universiti Utara Malaysia (UUM) for supporting this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eringen, A.C. Simple micropolar fluids. Int. J. Eng. Sci. 1964, 2, 205–207. [Google Scholar] [CrossRef]
- Koriko, O.K.; Animasaun, I.L.; Omowaye, A.J.; Oreyeni, T. The combined influence of nonlinear thermal radiation and thermal stratification on the dynamics of micropolar fluid along a vertical surface. Multidiscip. Model. Mater. Struct. 2019, 15, 133–155. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Dawar, A.; Alzahrani, E.O.; Thounthong, P. Study of the Couple Stress Convective Micropolar Fluid Flow in a Hall MHD Generator System. Front. Phys. 2019, 7, 171. [Google Scholar] [CrossRef]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications; Brikhauser: Basel, Switzerland, 1999. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Khan, M.I. Radiative flow of micropolar nanofluid accounting thermophoresis and Brownian moment. Int. J. Hydrogen Energy 2017, 42, 16821–16833. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Nadeem, S.; Hashim, I. Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects. Meccanica 2015, 50, 2007–2022. [Google Scholar] [CrossRef]
- Haq, R.U.; Nadeem, S.; Akbar, N.S.; Khan, Z.H. Buoyancy and radiation effect on stagnation point flow of micropolar nanofluid along a vertically convective stretching surface. IEEE Trans. Nanotechnol. 2014, 14, 42–50. [Google Scholar]
- Patel, H.R.; Mittal, A.S.; Darji, R.R. MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 2019, 108, 104322. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 1–21. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Nisar, K.S. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1379. [Google Scholar] [CrossRef]
- Sithole, H.; Mondal, H.; Magagula, V.M.; Sibanda, P.; Motsa, S. Bivariate Spectral Local Linearisation Method (BSLLM) for unsteady MHD Micropolar-nanofluids with Homogeneous–Heterogeneous chemical reactions over a stretching surface. Int. J. Appl. Comput. Math. 2019, 5, 12. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Elmasry, Y.; Malik, M.Y. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Progr. Biomed. 2020, 186, 105194. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gadisa, G. Finite element analysis of couple stress micropolar nanofluid flow by non-Fourier’s law heat flux model past stretching surface. Heat Transf. Asian Res. 2019. [Google Scholar] [CrossRef]
- Abbas, Z.; Mushtaq, T.; Shehzad, S.A.; Rauf, A.; Kumar, R. Slip flow of hydromagnetic micropolar nanofluid between two disks with characterization of porous medium. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 465. [Google Scholar] [CrossRef]
- Alzahrani, E.O.; Shah, Z.; Alghamdi, W.; Ullah, M.Z. Darcy–Forchheimer Radiative Flow of Micropoler CNT Nanofluid in Rotating Frame with Convective Heat Generation/Consumption. Processes 2019, 7, 666. [Google Scholar] [CrossRef]
- Abidi, A.; Raizah, Z.; Madiouli, J. Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid. Appl. Sci. 2018, 8, 2342. [Google Scholar] [CrossRef]
- Raslan, K.; Mohamadain, S.; Abdel-wahed, M.; Abedel-aal, E. MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface. Appl. Sci. 2018, 8, 736. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Magodora, M.; Mondal, H.; Sibanda, P. Dual solutions of a micropolar nanofluid flow with radiative heat mass transfer over stretching/shrinking sheet using spectral quasilinearization method. Multidiscip. Model. Mater. Struct. 2019. [Google Scholar] [CrossRef]
- Ali Lund, L.; Ching, D.L.C.; Omar, Z.; Khan, I.; Nisar, K.S. Triple local similarity solutions of Darcy-Forchheimer Magnetohydrodynamic (MHD) flow of micropolar nanofluid over an exponential shrinking surface: Stability analysis. Coatings 2019, 9, 527. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. Int. J. Non-Linear Mech. 2016, 83, 59–64. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: Exact solutions. Int. J. Heat Mass Transf. 2017, 106, 127–134. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Ishak, A.; Pop, I. Oblique stagnation slip flow of a micropolar fluid towards a stretching/shrinking surface: A stability analysis. Chin. J. Phys. 2018, 56, 3062–3072. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Dero, S.; Khan, I. Linear stability analysis of MHD flow of micropolar fluid with thermal radiation and convective boundary condition: Exact solution. Heat Transf. Asian Res. 2019, 49. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. Rheology of micropolar fluid in a channel with changing walls: Investigation of multiple solutions. J. Mol. Liq. 2016, 223, 890–902. [Google Scholar] [CrossRef]
- Mahmood, A.; Chen, B.; Ghaffari, A. Hydromagnetic Hiemenz flow of micropolar fluid over a nonlinearly stretching/shrinking sheet: Dual solutions by using Chebyshev Spectral Newton Iterative Scheme. J. Magn. Magn. Mater. 2016, 416, 329–334. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar]
- Raju, C.S.K.; Sandeep, N.; Babu, M.J.; Sugunamma, V. Dual solutions for three-dimensional MHD flow of a nanofluid over a nonlinearly permeable stretching sheet. Alex. Eng. J. 2016, 55, 151–162. [Google Scholar] [CrossRef]
- Li, X.; Khan, A.U.; Khan, M.R.; Nadeem, S.; Khan, S.U. Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution. Symmetry 2019, 11, 1070. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Dual solutions for nanofluid flow past a curved surface with nonlinear radiation, Soret and Dufour effects. J. Phys. Conf. Ser. 2018, 1000, 012152. [Google Scholar] [CrossRef]
- Dero, S.; Uddin, M.J.; Rohni, A.M. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Transf. Asian Res. 2019, 48, 2047–2066. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U.; Sheikholeslami, M.; Khan, U. Numerical analysis of effective Prandtl model on mixed convection flow of γAl 2 O 3-H 2 O nanoliquids with micropolar liquid driven through wedge. Phys. Scr. 2019. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Nisar, K.S. Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation: Dual Solutions. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu-C 6 H 9 NaO 7 and Ag-C 6 H 9 NaO 7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J. Dual solutions for unsteady stagnation-point flow of Prandtl nanofluid past a stretching/shrinking plate. Defect Diffus. Forum 2018, 388, 124–134, Trans Tech Publications. [Google Scholar] [CrossRef]
- Ali Lund, L.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of Viscous Dissipation in Heat Transfer of MHD Flow of Micropolar Fluid Partial Slip Conditions: Dual Solutions and Stability Analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef]
- Junoh, M.M.; Md Ali, F.; Pop, I. Magnetohydrodynamics Stagnation-Point Flow of a Nanofluid Past a Stretching/Shrinking Sheet with Induced Magnetic Field: A Revised Model. Symmetry 2019, 11, 1078. [Google Scholar] [CrossRef]
- Revnic, C.; Ghalambaz, M.; Groşan, T.; Sheremet, M.; Pop, I. Impacts of Non-Uniform Border Temperature Variations on Time-Dependent Nanofluid Free Convection within a Trapezium: Buongiorno’s Nanofluid Model. Energies 2019, 12, 1461. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Md Arifin, N.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. A Stability Analysis for Magnetohydrodynamics Stagnation Point Flow with Zero Nanoparticles Flux Condition and Anisotropic Slip. Energies 2019, 12, 1268. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K.; Vajravelu, K.; Van Gorder, R.A. Stability analysis of the dual solutions for stagnation-point flow over a non-linearly stretching surface. Meccanica 2012, 47, 1623–1632. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Stability of dual solutions in stagnation-point flow and heat transfer over a porous shrinking sheet with thermal radiation. Meccanica 2013, 48, 23–32. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Stability analysis of dual adiabatic flows in a horizontal porous layer. Int. J. Heat Mass Transf. 2009, 52, 2300–2310. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Quadruple solutions of mixed convection flow of magnetohydrodynamic nanofluid over exponentially vertical shrinking and stretching surfaces: Stability analysis. Comput. Method. Program. Biomed. 2019, 182, 105044. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Dual Solutions and Stability Analysis of Micropolar Nanofluid Flow with Slip Effect on Stretching/Shrinking Surfaces. Energies 2019, 12, 4529. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Med. 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C.; Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2945–2952. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).