Abstract
Disk milling strategy has been applied in grooving for decades for its capacity to provide huge milling force on difficult-to-cut material. However, basic research on the tool orientation of the disk milling cutter for the disk milling process on the milling free surface, especially on the free surface of the blisk, is still lacking in previous studies. In this study, the minimum residual amount after the disc milling process is used as an optimization target to obtain the optimal tool orientation of the disc cutter. To address the problem mentioned above, a torque balance method, including a torque balance algorithm and concentric circle ray point (CCRP) method is proposed. The torque calculation and torque balance problem are solved by the torque balance algorithm and the problem of generating random points to cause torque symmetry is solved in the CCRP method. Based on the secondary development of UG NX software, a series of tool orientation of disk milling cutter are calculated. Finally, the torque balance method is compared with steepest descent method, Newton method, and conjugate gradient method in the aspects of calculation accuracy, operation speed, and convergence speed. However, both the calculation speed and the convergence speed are better than the other three algorithms. Compared with the other three methods, the operation speed of the torque balance method is reduced by 0.35 times, 1.5 times, and 2.25 times. The results prove the feasibility of the torque balance method in solving the problem of tool orientation optimization of the disk milling cutter.
1. Introduction
The blisk is combined by the rotor blade with the wheel disk to reduce the weight of the engine, simplify the structure of the engine, improve the reliability of the engine, and extend the service life of the engine. Therefore, it has become an important component of aero-engines and has been widely used in modern high performance aero-engines [1,2,3]. The blisk is usually manufactured by difficult-to-cut material such as titanium alloy or high temperature alloy [4,5]. At present, the CNC (Computer Numerical Control) milling such as plunge milling process and side milling process is usually used in the slotting process of blisk channel. However, due to the low processing efficiency and high processing cost of the above processing methods, the development of aero-engines is seriously restricted. In recent years, a new type of disc milling process has been found in my laboratory and has been widely used in machining aero-engine blisk tunnels because of its high efficiency and reliability. Disk milling cutter orientation has a vital influence on the machining efficiency of blisk tunnels. At the same time, reasonable tool orientation of the disk milling cutter can not only effectively avoid the interference between the disk milling cutter and the workpiece, but also help to improve the material removal rate, so as to further shorten the processing time of the blisk. In the disk milling process, the shape of the workpiece and the parameters of the disk milling cutter are usually invariable. However, it is feasible to optimize the tool orientation of the disk milling cutter to obtain higher material removal rate.
In recent years, the machining process of titanium alloy for blisk channels has been studied by many scholars in many literatures. By analyzing the shapes of channel profiles and the distribution of the electrochemical machining lateral gap, the trajectory of three stainless steel tools is optimized, and three channels are processed simultaneously by Xu et al. [6]. The processing efficiency has been improved to a certain extent. On the other hand, a rational electrolyte flow mode for electrochemical machining was proposed by Xu et al. [7]. At the same time, the problems of poor stability and low efficiency in electrochemical machining were solved. The two methods mentioned above have improved the processing efficiency to some extent. However, due to the materials of blisk being difficult-to-cut materials, and comparing with CNC machining, the efficiency of the electrochemical machining process is obviously insufficient. Zhang et al. [8] proposed a three-dimensional (3-D) instantaneous cutting force (ICF) forecasting model for an indexable disc milling cutter considering cutter run-out. It turns out that the presented model can successfully and precisely predict the 3-D ICF of an indexable disc milling cutter under a variety of processing parameters. From the study of Zhang et al. [9], the relationship between feed position and rotation angle is presented in the form of a mathematical model. Through experimental comparison, it is found that spiral feeding ECM (Electro Chemical Machining) is feasible and efficient. Ren et al. [10] proposed a new tool axis orientation planning method based on the fixed axis in each cutting line machining for closed blisk tunnel finish machining. The basic concept of the method is discussed from the machining principle, and the five-axis machining features of the closed blisk tunnel are analyzed. Experimental results demonstrate that, compared with the five-axis linkage machining method, the fixed axis in each cutting line not only significantly improves the stability of machining and the quality of the machined blade surface, but also improves the blade finish machining efficiency. In multi-axis plunge milling, tool orientations are usually determined conservatively as the normal or tangent direction of a face to prevent extravagant cutting and unanticipated tool breakage. To address this issue, Chiou et al. [11] presented a swept envelope approach to determining the optimal tool orientation for five-axis tool-end machining. By analyzing the swept profile against the part geometry, four types of machining errors (local gouge, side gouge, rear gouge, and global collision) were identified. At same time, an explicit solution for the swept profile of a general cutter in five-axis tool-end machining was proposed in this paper. Through the analysis of simulation results, the method can accurately determine the optimal tool orientation and efficiently avoid machining errors for five-axis tool-end machining. It is one of the challenging problems to determine the tool orientation when plunge milling or side milling, so that the material left on the blade after rough machining is close to the specified value [12]. Ho et al. [13] verified through experiments that the quaternion interpolation algorithm (QIA method) has better machining efficiency, better surface quality, and no interferences between the tool and part surfaces. Yu et al. [14] proposed a new optimization method to select a tool orientation for machining a sculptured surface by the 3 + 2-axis machining strategy. The method presented could also be applied on the trimmed surface, the surface with a boss, and the blade on a blisk. Luo [15] proposed a kinematic method to solve the problem that tool positioning between adjacent contact points cannot be changed rapidly in reality. At the same time, according to their report [16], my laboratory proposed a processing method integrating the disc milling process, plunge milling, and side milling process. At the same time, a special machine tool for processing the integral blade plate was designed to improve the machining efficiency.
According to the above research, researchers usually focus on the optimization of the process parameters and the optimization of the tool orientation of plunge milling and flank milling during the processing of the blisk channel. It is a new method of fast material removal to use the disk milling cutter for the processing of the blisk channel, so research on the optimization of tool orientation of the disk milling cutter in the slotting process of the disk channel is rarely carried out by scholars. A torque balance method is proposed to calculate the tool orientation of the disk milling cutter for the disk milling process. Finally, the torque balance method is compared with steepest descent method, Newton method, and conjugate gradient method in terms of calculation accuracy, operation speed, and convergence speed. The results showed that the calculation accuracy of the torque balance method is not much different from the other three methods, but the operation speed and convergence speed are obviously better than the other three methods, which proves the feasibility of the torque balance method in solving the problem of tool orientation optimization of the disk milling cutter.
2. Torque Balance Method
The torque balance method adjusts the position of the bar or plane according to the difference of the torque values on both sides or around the rotation center, so that the torque values on both sides or around the plane of the adjusted bar or plane can reach the symmetrical state. In two-dimensional space, if we choose a rotation center, the object will turn to the direction of the high torque value until the torque values on both sides of the rotation center is symmetric. Similarly, to achieve torque balance in three-dimensional space, the torque values on both sides of the fulcrum in any direction must be symmetric. The torque balance method has two main requirements, one is the torque balance problem, the other is the point generation problem. The torque balance algorithm mainly realizes the requirement of torque balance, while the concentric circle ray point (CCRP) method mainly realizes the point generation of the torque balance algorithm. Therefore, the torque balance method is divided into the torque balance algorithm and CCRP method.
2.1. Introduction of High-Efficiency and Powerful Compound Milling Process
Due to the characteristics of thin blade, large bending and torqueing, and poor openness of the blisk, processing of the blisk becomes difficult. Therefore, the production efficiency cannot meet the demand of the current aero-engine production. Disk milling-plunge milling-side combined milling technology has been proposed to solve the problems mentioned above. At the same time, a high efficiency and powerful compound milling machine has been developed, as shown in Figure 1. Firstly, using the characteristics of the high cutting efficiency of disc milling, the blank material of the blisk was slotted to achieve the effect of large material removal. Then, in order to save cutting time, the plunge milling process is applied to milling off the cutting area after the disc milling process. At the plunge process, the profile of the blade is shaped roughly. Finally, cylindrical or ball-end milling cutters are used to finish the side milling to the blisk, in order to complete rough machining and semi-finishing of blisk blade. In the process of machining, the disc milling process and plunge milling process cooperate with each other to complete the efficient grooving milling process. The optimization of tool orientation of the disc cutter for the disk milling process is related to the machining efficiency and needs to be further researched in-depth. This paper will mainly be based on the theory of disc milling for reasoning and analysis, the corresponding method is calculated, so as to obtain the optimal tool orientation of the disc cutter.
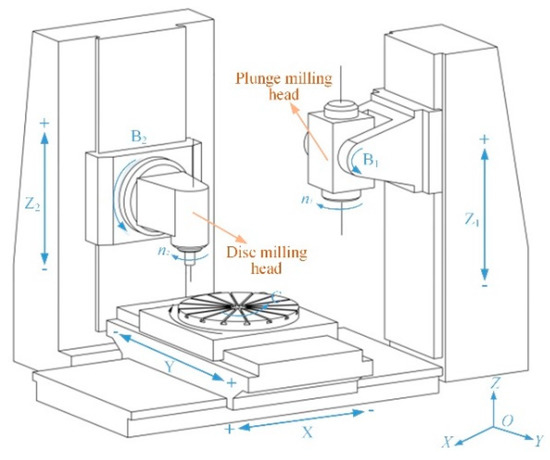
Figure 1.
Schematic diagram of efficient and powerful CNC (Computer Numerical Control) milling machine.
2.2. Torque Balance Algrithm Derivation Based on Minimum Residual Amount
According the characteristic of the disk milling cutter, the cutting edge is distributed in the circumferential direction of the disk milling cutter as shown in Figure 2. Therefore, the cutter feed direction can only be milling along the radial edge direction, in the process of disk milling. At the same time, due to the lack of cutting edge on the side of the disk milling cutter, the tool orientation of the disk milling cutter cannot be changed during the milling process. So, the surface after the disk milling cutter milling is a plane.

Figure 2.
Schematic diagram of the disc milling cutter.
The problem of calculating the tool orientation of the disk milling cutter to improving the milling efficiency is changed to the problem of how to get a plane that minimizes the volume between the plane and the free surface. In other words, the final plane is calculated, and the normal vector of the final plane is used as the tool orientation of the disk milling cutter. According to the Figure 2, the residual material can be formulated as follows:
where D is the integral region on the surface, as shown in Figure 3a; a, b, , and are the lower limit and upper limit of the integral region in the x-axis and y-axis, respectively; f(x,y) is the distance of the integral surface to the zero plane on a small area (dS) formatted as a rectangular coordinate.
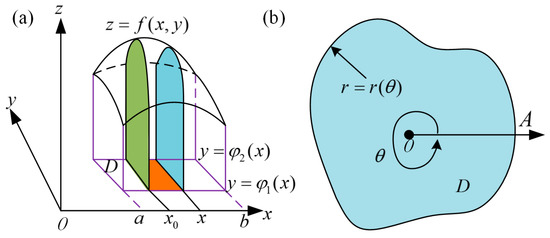
Figure 3.
Schematic diagram of integral. (a) Diagram of surface integral; (b) Schematic diagram of polar integral region.
The integral in rectangular coordinate form is transformed into the integral in polar coordinate form as follows:
where f(rcosθ,rsinθ) is the distance of the integral surface to the zero plane on a small area (dS) formatted as polar coordinates; r is the distance from the pole to the edge of the integral region (D). At the same time, the integral region D also changes correspondingly.
The pole is inside of the integral region (D), so the expression of I can be changed to the form as follows:
It is feasible to use Equation (3) to calculate the residual material when the mathematical expression of the surface is known. However, it is difficult to get the mathematical expression for free-form surface, and the boundary conditions (r(θ)) of the integral surface are not easy to be determined. So, the residual material is approximated by the method of differential and then summing, so the formula of residual material can be defined as:
where is the distance between the integration region of infinite subdivision D and the plane.
When the variables ∆θ, ∆r, and i satisfy the condition , , and , the variable is approximately equal to and the variable is approximately equal to . So Equation (4) can be changed to the type as follows:
Based on the definition, if we can get a flat surface through optimization with the least residual material, the problem of optimizing the tool orientation of the disk milling cutter can be perfectly solved and formulated as the following minimization model
The minimization problem described in Equation (6) is difficult to straightly solve, since the uniqueness of the free surface and the large calculation caused by the variable number. In order to solve the problem presented by Equation (6), torque is introduced in this paper. Torque, as known to us, is a physical quantity for rotation of the object. According the torque formula: M = Fl, is transformed into the elastic extension quantity. So Equation (6) can be transformed as follows:
where the stiffness coefficient k is given in the length direction of .
Based on the definition in Equation (7), the minimization problem of I(r, θ) can be transformed to the minimization problem of M(r, θ)
2.3. Concentric Circle Ray Point (CCRP) Method
As described in Equation (8), in the torque balance algorithm, in order to obtain a more accurate simulation result, numerous points must be generated, so that the result of the discrete sum is equal to the result of the integral. However, it is impossible to generate an infinite number of random points to realize the algorithm based on the computing speed of the computer. Therefore, in the simulation operation, it is necessary to determine a simple point mesh method to ensure the accuracy of the calculation results while reducing the computational load of the computer.
According the torque balance algorithm, the product of two variables, force and distance, forms the expression for torque. In other words, the values of torque are related to the two variables mentioned above. If one side’s torque magnitude has been determined, there are multiple torques on the other side to match it, which means that even if the plane is not rotated, a series of points can be found to implement the torque balance algorithm. Refer to Figure 4 for analysis of various matching situations described above.
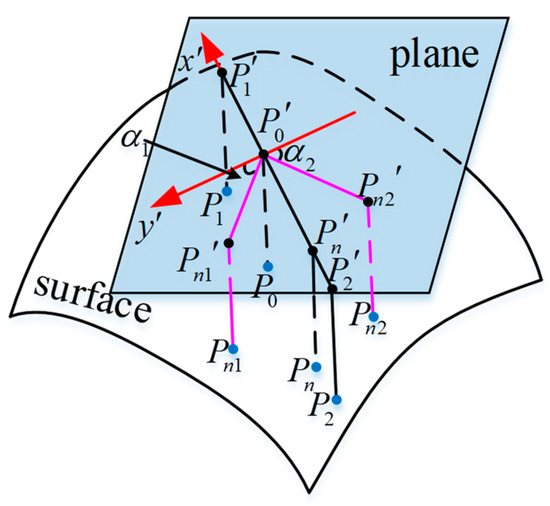
Figure 4.
The asymmetry of random points in the torque balancing algorithm.
Assuming that the first point P1′ on the plane has been generated, the torque M1 can be easily calculated according to Equation (7), .
There are two ways to get infinite number of torque values that match M1.
Way 1: points on the line of P0P2′.
There are an infinite number of points on the line corresponding to an infinite number of torque values. Due to the irregular torque values, there may be a non-unique solution matching M1 on line P0P2′.
Way 2: points on the plane.
This means that a new torque is synthesized on the line P0P2′ to match M1, if n points can be found on the plane to satisfy the formula . Since the number of n is not unique, it indicates that there may be more than one such newly synthesized torque matching M1. Obviously, the newly generated torque may not be the same as the torque generated by the point on the line.
At the same time, as mentioned above, the generation of infinite points can realize the balance algorithm even if the plane does not rotate. The phenomenon described above is defined as the asymmetry of random points in the torque balancing algorithm. Obviously, the algorithm has certain risks, making the results inaccurate. In order to solve the problems mentioned above, a concentric circle ray point (CCRP) method was proposed to solve the problem above. As can be seen from Figure 4, the free surface is a four-sided surface, rather than a circle. Therefore, it is necessary to extend the surface so that the points generated by this method are all on the surface. However, the algorithm of extended surface has been studied by many scholars, so we will not elaborate on the algorithm in this paper. Now we specifically describe how to generate the free surface points with CCRP method and how to get the variables in torque balance algorithm.
- Step 1:
- Extend the free surface. The method to extend the surface is shown in Figure 5a.
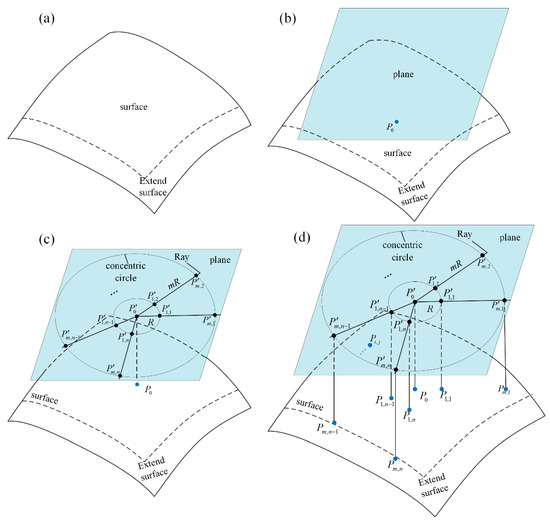 Figure 5. Concentric circle ray point (CCRP) method. (a) Extend the free surface; (b) Create the plane and find the rotate center; (c) Create a point with concentric circles and rays on the plane; (d) Project the points on the plane to the free surface.
Figure 5. Concentric circle ray point (CCRP) method. (a) Extend the free surface; (b) Create the plane and find the rotate center; (c) Create a point with concentric circles and rays on the plane; (d) Project the points on the plane to the free surface. - Step 2:
- Create a plane that does not intersect the existing free surface. As shown in Figure 5b, find a point on the free surface closest to the plane and defined as P0.
- Step 3:
- Project the point P0 on to the plane, defined as P0′. As shown on the plane in Figure 5c, R, 2R, …, mR are the radii of the concentric circles centered on the P0′, and n rays are created with P0′ as the start point and 2π/n radian adjacent to the two rays. After that, m concentric circles generate m × n intersection points with n rays, defined as .
- Step 4:
- Project the points on the extended free surface, which are defined as . The projection method is shown in Figure 5d.
- Step 5:
- Get the distance of and , then multiply the stiffness factor k before , and change the distance variable into the mechanical variable .
- Step 6:
- Get the distance of and , then multiply the mechanical variable and the distance variable , calculate the torque value of Mm,n.
- Step 7:
- Find the angle value αn between the nth ray and the x axis, then get the torque value of each point which was generated by the concentric circles and rays, defined as .
2.4. The Calculation of the Optimal Tool Orientation of the Blisk Milling Cutter Based on the Torque Balance Method
Through analyzing the characteristics of the disk milling, the maximum cutting amount of the disk milling is transformed into the minimum volume between the free surface and the plane, and it is feasible to transform the volume minimization problem into the torque solution of discrete region after inference. In this section, the torque balance method is used to obtain a radian value that minimizes the residual between the free surface and the plane.
As shown in Section 2.3, the torque value of of each point on the free surface in each direction can be figured out. Since the parameter contains two pieces of information, one is the information of torque value and the other is the position information of the point. Thereafter, the torque balance method is displayed as follows:
Step 1: Decompose the torque vector . According to Equation (9), there are innumerable points on the plane and free surface. Since a point corresponds to a torque vector, that means there are an infinite number of torque vectors. Based on the uncertainty of the torque vector value and direction, it is difficult to achieve balance through the calculation method. Therefore, it is necessary to decompose an infinite number of torque vectors in rectangular coordinates for unity. So, all the vectors included can be decomposed into a vector along the x direction and y direction by using the formula as follows:
where is the projection in x direction of torque at some point on the plane; is the projection in y direction of torque at some point on the plane. If the decomposed vectors are the same as x or y direction, take the positive direction; instead, take the negative.
Step 2: Accumulate torque values in the x and y directions. Through the calculation method of Equation (9), all the vectors after decomposed are concentrated in the x and y directions. Meanwhile, the vectors, after being decomposed, can be added and subtracted in either x direction or y direction. The torque values in x direction and y direction should be accumulated respectively to facilitate the torque balancing algorithm by using the following formula
where is the total torque value after accumulation along the x direction; is the total torque value after accumulation along the y direction.
Step 3: Calculate the total torque and the radian. According to Equations (9) and (10), the un-neutralized part of the torque of the free surface and plane should be calculated after the decomposition and accumulation effect, so as to calculate the rotation radian of the plane and realize the torque balance method between the plane and the free surface. Since all the initial torque vectors are decomposed into the x direction and y direction, so that all the accumulated torque vectors are located in the x direction and y direction, the total torque and angle value are calculated as shown in Equation (11).
where the total torque value is the remaining torque which is not neutralized after Equation (10). It is also the torque that needs to be neutralized by adjusting the position of the plane. The radian α in Equation (11) is the radian between the x direction and the direction of the total torque value as shown in Figure 6a.
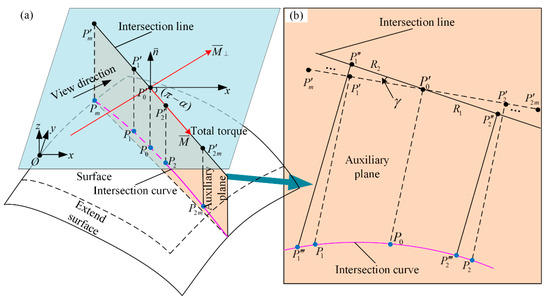
Figure 6.
The schematic diagram for searching the optimal machining plane. (a) The schematic diagram for calculating the final torque and search the rotation axis of the plane; (b) The schematic diagram for calculating the radians of a plane rotation.
Step 4: Calculate the rotation axis of the final plane. According to Equation (11), the total torque value and the direction in which the total torque is located have been calculated. It follows that the sum of the components of all torque values in the perpendicular direction of the total torque vector is zero. As shown in Figure 6a, we define the direction perpendicular to the total torque vector as . Therefore, the line that vector sits on is the axis of rotation of the final plane.
Step 5: Calculate the rotation direction. According to the definition of symmetry, if the plane is rotated along the vector by a certain radian γ, the components of the torque value on both sides of in the direction of increase or decrease at the same time, without affecting its symmetry. Since the total torque value is obtained after generating countless points between the plane and the free surface, in order to achieve the state of balance and symmetry, the total torque increase and decrease of all points must be equal to the total torque value after the plane rotates a certain radian γ around axis . To facilitate calculation, points on the plane are divided into two parts along the rotation axis - the right part (RP) and the left part (LP). If the torque values on the right part (RP) are decreasing, the plane is rotated clockwise along axis , and if the torque values on the left part (LP) are increasing, on the contrary, the plane changes accordingly.
Step 6: Calculate the rotation radian of the final plane. As shown in Figure 6b, the new plane is formed in the normal of the plane () and total torque directions (), and the intersecting lines and intersecting curves are generated respectively with the plane and the free plane. As shown in Figure 6b, a certain number of points are generated on the intersecting line and intersecting curve, so as to illustrate the relationship between the change of torque and the position of points when the plane rotates radian γ along axis , and the formula is calculated as follows:
where Ri is the distance from point Pi to axis . When the points belong to the LP, the torque values are negative; otherwise, they are positive.
Because of the application of the CCRP method, the distance variable in the torque formula becomes a controllable variable, so as to control the point mesh method. In the process of implementing torque balance method, the distance variables of each point are dimensionally unified to avoid the problem of torque balance without plane rotation.
The Equations (9)–(11) are used to calculate the points generated by the CCPR method to get the remaining torque and the radian α. At the same time, Equation (12) is changed into another form as follows:
where k is the kth concentric circle where the point is and i is the ith ray where the point is. The radian α is the radian between x direction and the direction of the total torque value as shown in Figure 6b.
Expand and sum each parameter in Equation (13) and get Equation (14) as follows:
We can get the radians γ as follows:
Through the above six steps, a center of rotation (P0′), an axis of rotation (), and a rotation radian (γ) are calculated. If a plane is rotated according to these parameters, the optimal cutting plane of disk milling cutter will be obtained. In the other words, the normal direction of the rotated optimal plane is the optimal tool orientation of the disk milling cutter.
3. Simulation and Calculation
3.1. Secondary Development for Torque Balance Method on UG NX
With the development of software, UG NX software provides a series of secondary development functions and interfaces. Among them, the most widely used are the API (Application Programming Interface) functions provided by the software, which can access the core applications of NX and realize relevant UG operations [16]. At the same time, UG NX also provides the auxiliary tools such as interface making, to realize the needs of secondary development customers [17].
In this paper, the second development of the torque balance method based on the torque balance algorithm and the CCRP method, is carried out through the API function which is provided in the UG NX software. Moreover, the implementation of the secondary development of the torque balance method based on the torque balance algorithm and the CCRP method in UG NX must follow the steps in Figure 7.
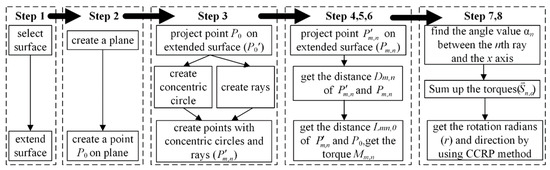
Figure 7.
Step diagram of the torque balance method by using UG NX secondary development.
In order to successfully realize the secondary development of UG NX and integrate it into functional sub-software, customizing the menu toolbar, creating the dialog box, writing corresponding method code, generating a dynamic link library, and other functions, will be realized in the process of software creation. In this article, the “torque balance algorithm” dialog as shown in Figure 8a is created with the MenuScript and UIStyler custom menu toolbars supported by UG NX software, and the “torque balance algoritm.dll” program based on the torque balancing algorithm is generated. Finally, the torque balance method realized by combining UG NX, the torque balance algorithm and the CCRP method is as follows:
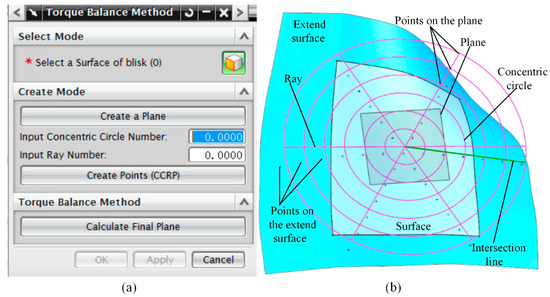
Figure 8.
Realizing the torque balance method by using UG NX secondary development. (a) The interface created by UG NX; (b) The effect diagram of the torque balance method is realized.
- (1)
- Creating menu tools and dialogue box. The files “torquebalancemethod.men” and “torquebalancemethod.dlg” were created by using the models of MenuScript and UIStyler supported by UG NX software. After that, saving the two files into a specific folder.
- (2)
- Loading the generated C++ file. The app and CPP (C++ language prepared by the source code file suffix) files corresponding to the UG NX version number are created by using Visual Studio 2008 and named “torqueblancemethod.app” and “torqueblancemethod.cpp”.
- (3)
- Writing the torque balance method code based on the toque balance algorithm and the CCRP method. The file named “torquebalancealgorithm.dll” is created after compiling the program, and then putting the dll in the startup folder in a special position.
The second development for the disk milling process could be finished following the steps above. The UG NX will call the dll and dlx automatically when it starts, and the interface after running the program is shown in Figure 8a. At this time, the customer can use the menu to enter any number of rays and concentric circles, and finally, the property information of the final plane can be seen from the interface. When there are six concentric circles and rays in the secondary development for the torque balance method based on UG NX, the results presented are shown in Figure 8b. Among them, the light blue surface is the free surface, the blue surface is the expanded surface, the rose-red objects are concentric circles and rays, and the green line is the line where the total torque is.
3.2. Simulation and Measurement Results
As described in the torque balance method, the combined torque balance algorithm and CCRP point mesh method, an infinite number of points are created, that is, the number of concentric circles and rays should be infinite. However, due to the limited computing speed of the CPU (Central Processing Unit), the torque balance method with infinite points can only be in the theoretical stage.
The simulation data results, including angle value between the tool orientation of the disk milling cutter and the x axis (αx), angle value between the tool orientation of the disk milling cutter and the y axis (αy), and angle value between the tool orientation of the disk milling cutter and the z axis (αz) are gathered together as shown in Table 1. In the table, point number denotes the number of points where concentric circles intersect with rays. In this simulation experiment, the same number of concentric circles and number of rays are used, and the range is 9 to 31. For the angle value between the tool orientation of the disk milling cutter and the x axis (αx), the maximum and minimum values are 91.1938° and 88.3465°, respectively. For the angle value between the tool orientation of the disk milling cutter and the y axis (αy), the maximum and minimum values are 42.1519° and 36.4559°, respectively. Lastly, for the angle value between the tool orientation of the disk milling cutter and the z axis (αz), the maximum and minimum values are 53.5567° and 47.8486°, respectively.

Table 1.
Simulation and measurement results.
Table 1 provides the results of the simulation and measurement for the tool orientation of the disk milling cutter. According to the results of the simulation and measurement, the angle values between the tool orientation of the disk milling cutter and the x, y, and z axis are about 90°, 41°, and 49°. However, it is impossible to get the specific distribution of the tool orientations of the disk milling cutter from the table, which leads to the difficulty of subsequent analysis of the tool orientation. In view of this, 23 groups of tool orientations of the disk milling cutter are displayed in a gauss sphere in Figure 9 to analyze the distribution rule of the tool orientation of the disk milling cutter with the increase in the number of generated points.
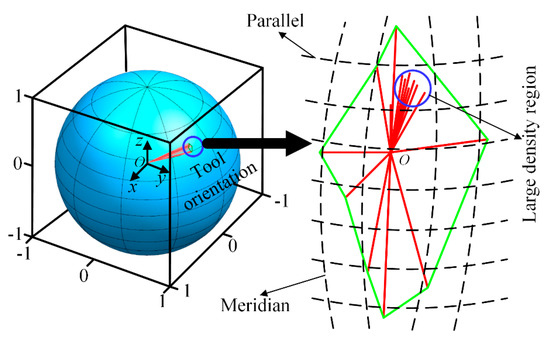
Figure 9.
Schematic diagram of the direction of the tool orientation in a gauss sphere.
According to the tool orientation of the disk milling cutter results shown in Figure 9, the intersection points between the tool orientations of the disk milling cutter and the gauss sphere generated by the torque balance method (torque balance algorithm and CCRP point mesh method) is concentrated in a certain area of the sphere (blue area in the gauss sphere). Meanwhile, when zooming in on this region, it is found that the tool orientations of the disk milling cutter become more and more concentrated as the number of generated points increases (large density region and black area). Thus, it can be boldly inferred that, if the number of generated points tends to be infinity, the tool orientation of disk milling cutter must be tend to a certain fixed value.
3.3. Calculation of Tool Orientation of the Disk Milling Cutter
Although Table 1 and Figure 9 in Section 3.2 respectively show the measurement results and the distribution of the tool orientations of disk milling cutter after using the torque balance method (torque balance algorithm and CCRP point mesh method), the correlation between the number of production points and the distribution of the tool orientations of the disk milling cutter is unknown. In order to intuitively describe the relationship between the above two factors (number of production points and the distribution of the tool orientations of disk milling cutter), the rule of the angle values between the tool orientation of the disk milling cutter and the x-axis, y-axis, and z-axis with the number of production points is shown in Figure 10.
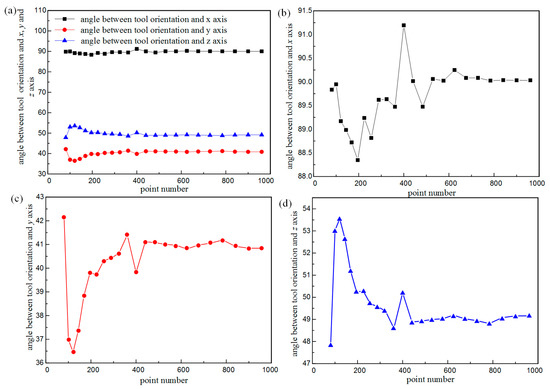
Figure 10.
Simulation results of torque balancing algorithm (a) The angle between tool orientation and the x, y, and z axis. (b) The angle between the tool orientation and x axis; (c) The angle between the tool orientation and y axis; (d) The angle between the tool orientation and z axis.
As shown in Figure 10b–d, when the number of generation points is less than 500, the angle values generated by the tool orientations of the disk milling cutter and the x, y, and z axis change greatly, which are basically irregular. However, when the number of production points is greater than 500, the angle values between the tool orientations of the disk milling cutter and the x, y, and z axis change extremely little. At the same time, as the number of points generated increases, the change range of the angle between the tool orientation of the disk milling cutter and the x, y, and z axis becomes smaller and smaller. It can be inferred that the more points that are generated, the closer the final cutter axis vector is to the optimal value. Based on the limitation of computer operation speed, the tool orientation of the disk milling cutter calculated when the number of points is 961 is taken as the optimal calculation result in this paper, as shown in Equation (16), to compare the authenticity and validity of its value with other optimization methods.
4. Algorithm Verification and Experimental Verification
4.1. Comparison Algorithm and Model
In the process of solving the optimization problem, there are three methods: steepest descent method, Newton method, and conjugate gradient method. The convergence paths of the steepest descent method, Newton method, and conjugate gradient method is shown in Figure 11a [18,19,20,21]. In order to compare and analyze the tool orientation of the disk milling cutter obtained by the optimization algorithm proposed in this paper, the blank model of the blade needs to be established first. As shown in Figure 11b, the model contains a blade and the material to be removed between the blades.
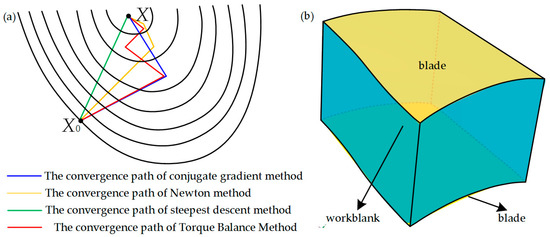
Figure 11.
Comparison algorithm and model. (a) The convergence path of four methods; (b) The blank model of the blade.
4.2. Algorithm Contrast
In the steepest descent method, Newton method, and conjugate gradient method, the values of three independent variables need to be continuously transformed to obtain the optimal solution. Therefore, many intermediate solutions are obtained. However, in the torque balance algorithm proposed in this paper, the optimal result is calculated once, so there is no intermediate solution. In order to reduce the comparison parameters in the algorithm comparison, the residual amount in Section 2.2 is taken as the main comparison parameter. Finally, the tool orientation of the disk milling cutter corresponding to the minimum residual amount is taken as the optimal calculation result.
4.2.1. Calculation Accuracy
In order to realize the comparison of optimization algorithms, all algorithms must meet the requirements in accuracy. Meanwhile, calculation accuracy refers to whether the algorithm can satisfy the accuracy requirements of machine tool processing in the case of unlimited time and convergence speed. In the numerical control system of modern digital machine tools, the accuracy in the angle is mostly accurate to the level of 10−4. As shown in Table 2, after comparing the simulation results, it is found that the four methods—the steepest descent method, Newton method, conjugate gradient method, and torque balance algorithm can reach the level of 10−5 without the simulation time. At the same time, the simulation results can meet the precision requirements of the CNC system of the machine tool. Therefore, the conclusion can be inferred that these four methods meet the requirements in terms of calculation accuracy.

Table 2.
Calculation accuracy results.
4.2.2. Operation Speed
In the optimization algorithm, the convergence speed is defined as the speed of an iterative sequence approaching its local optimal value, which is an important index to evaluate the performance of an iterative method in this problem. The residual amount is used instead of the tool orientation of the disk milling cutter in this paper, that is, the change of the residual amount as the evaluation standard of convergence speed with the increase of time. The residual amount of disk milling progress generated with time is shown in Figure 12 through the application of the steepest descent method, Newton method, conjugate gradient method, and torque balance method.
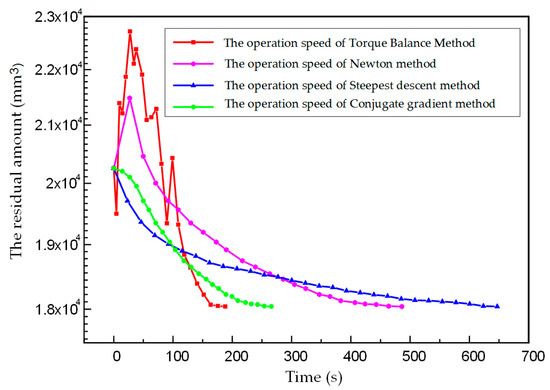
Figure 12.
The operation speed of the torque balance method, Newton method, steepest descent method, and conjugate gradient method.
The negative gradient direction of the current position is used as the search direction of the steepest descent method. Meanwhile, the Newton method needs to provide the first derivative information of the function to find the next search direction, and needs to store and calculate the Hesse matrix and find the inverse. However, the conjugate gradient method is a method between the steepest descent method and Newton method. It only needs to use the information of the first derivative, which not only avoids the disadvantages of the Newton method that the Hesse matrix needs to be stored and calculated and inverted, but also overcomes the deficiencies of the slow convergence of the steepest descent method. However, there is no available optimization function in the process of the disk milling progress. Therefore, when the negative gradient direction or the direction of the first derivative is taken as the convergence direction, the point near the current position and its corresponding residual amount must be calculated. Every residual amount calculation needs to be re-modeled in the model of the blisk, which takes a long time to calculate. It takes about 270 s, 500 s, and 650 s by using the conjugate gradient method, Newton method, and steepest descent method, respectively.
Different from the three optimization algorithms mentioned above, the corresponding points on the surface and plane are added in the torque balance method (torque balance algorithm and CCRP point mesh method) instead of computing the first derivative information. Therefore, the time spent in repeated modeling is avoided in the whole process, and the computing speed is accelerated. It takes less than 200 s to achieve the machining accuracy of the machine tool by using the torque algorithm, and compared with the three algorithms, conjugate gradient method, Newton method, and steepest descent method, the operation speed of the torque balance algorithm is reduced by 0.35 times, 1.5 times, and 2.25 times, respectively.
4.2.3. Convergence Speed
The convergence speed is an important index to evaluate the merits of an optimization algorithm. In this paper, the variation of the residual amount in per unit time is defined as the convergence rate. Meanwhile, it can be defined by the difference between two calculations in two sampling times. Figure 13 shows the rule that the convergence speed of the four optimization algorithms (steepest descent method, Newton method, conjugate gradient method, and torque balance method) changes with time.
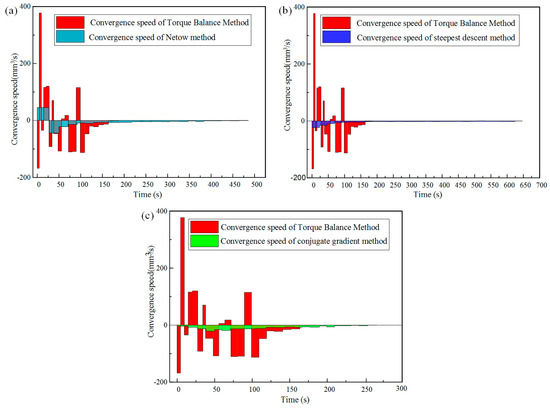
Figure 13.
Convergence speed comparison. (a) Convergence speed comparison of the torque balance method and Newton method; (b) Convergence speed comparison of the torque balance method and steepest descent method; (c) Convergence speed comparison of the torque balance method and conjugate gradient method.
Figure 13a–c are respectively the trapezoidal diagrams of the convergence speed of the torque balance method and the Newton method, steepest descent method, and conjugate gradient method. According to the integral theorem, the larger the area enclosed by the trapezoidal diagram of the convergence rate and the zero axis, the faster the convergence rate is. It can be observed intuitively from Figure 13 that the convergence speed of the torque balance method is obviously faster than the other three optimization algorithms, especially when the running time exceeds 100 s.
4.3. Experimental Verification
In order to verify the feasibility of the torque balance method, the optimized tool orientation of the disc cutter was edited into the corresponding tool path file, and this file was applied to the powerful compound milling machine. The whole process of machining is shown in Figure 14.

Figure 14.
The process of blisk milling. (a) Contact segment of the blisk milling process; (b) Milling section of the blisk milling process; (c) The effect drawing after the blisk milling process.
The blisk channel after grooving is shown in Figure 14c. In order to verify the accuracy of the machine tool and the correctness of the method, the processed part was removed from the machine tool and put into the CMM (Coordinates Measuring Machine) for data measurement. The measured data were imported into UG NX software and analyzed. The analysis results are shown in Table 3. The maximum and minimum machining errors of the three channels (Channel 1, Channel 2, and Channel 3) were 0.184 mm and 0.014 mm, which verified that the machine’s repeated positioning accuracy was good. In terms of the tool orientation of the disc cutter optimized by the torque balance method, the section after machining was 0.238 mm and 0.040 mm, compared with the section simulated by UG NX software, and this error is within the allowable range of the disk milling process.

Table 3.
Analysis results after measurement.
5. Conclusions
The advantages and disadvantages of the tool orientation of the disk milling cutter determine whether more materials can be removed by the disk milling cutter in the disk milling process of the titanium alloy blisk channels. In this paper, the torque balance method, combining the torque balance algorithm and the CCRP method, is used to obtain the optimal tool orientation of the disk milling cutter under the condition of generating as few points as possible. The upshots can be concluded as follows:
- (1)
- By analyzing the main principle of disc milling and the position of the cutting edge of the disc milling cutter, the maximum cutting amount is converted to the minimum residual amount. Through the calculus formula, the torque balance algorithm is deduced.
- (2)
- Because of the asymmetry of random points in the torque balance algorithm, the generation of random points is controlled by the CCRP method (concentric circle ray point method). On the basis of the CCRP method, the suitable formula for the torque balance algorithm is deduced. At the same time, a torque balance method including the torque balance algorithm and CCRP method is formed.
- (3)
- After comparison with the other three algorithms (steepest descent method, Newton method, and conjugate gradient method) the operation speed and the convergence of the torque balance method are better than the others. In particular, the operation speed of torque balance method was reduced by 0.35 times, 1.5 times, and 2.25 times compared to the other three methods.
The simulation of the torque balance method based on UG NX second development shows that the torque balance method has been greatly improved in terms of operation speed and convergence speed on the premise of satisfying the machining accuracy of the machine. The torque balancing method can save computing cost. Furthermore, the optimized tool orientation of the disk milling cutter can effectively reduce the processing cost of the blisk.
Author Contributions
Z.L. presented the conception of this article and collected the corresponding data. Then he carried out the experimental work and participated in the acquisition of data. Finally, Z.L. completed the rough draft for the manuscript. Y.S. reviewed this article and put forward some constructive suggestions for the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Numerical Control Major Projects Foundation of China] grant number [2013ZX04001081].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hoenisch, P.; Kiihhorn, A.; Beirow, B. Experimental and Numerical Analyses of Radial Turbine Blisks with Regard to Mistuning. In Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011; pp. 971–980. [Google Scholar]
- Calleja, A.; Fernandez, A.; Campa, F.J.; Lamikiz, A.; de Lacalle, L.N.L. Reliable Manufacturing Process in Turbine Blisks and Compressors. In Manufacturing Engineering Society International Conference; University of Zaragoza: Zaragoza, Spain, 2013; pp. 57–63. [Google Scholar]
- Klocke, F.; Schmitt, R.; Zeis, M.; Heidemanns, L.; Kerkhoff, J.; Heinen, D.; Klink, A. Technological and Economical Assessment of Alternative Process Chains for Blisk Manufacture. Procedia CIRP 2015, 35, 67–72. [Google Scholar] [CrossRef]
- Yang, J.; Chen, T.; Cheng, Y.; Xu, M. Design and wear analysis of tool for high-efficiency disk milling roughing of aero-engine blisk channels. Int. J. Adv. Manuf. Technol. 2018, 96, 1305–1317. [Google Scholar]
- Denkena, B.; Boess, V.; Nespor, D.; Floeter, F.; Rust, F. Engine blade regeneration: A literature review on common technologies in terms of machining. Int. J. Adv. Manuf. Technol. 2015, 81, 917–924. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Xu, Q.; Zhu, D.; Gong, T. A high efficiency electrochemical machining method of blisk channels. CIRP Ann. 2013, 62, 187–190. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, L.; Hu, Y.; Zhang, J. Flow field design and experimental investigation of electrochemical machining on blisk cascade passage. Int. J. Adv. Manuf. Technol. 2014, 71, 459–469. [Google Scholar] [CrossRef]
- Zhang, N.; Shi, Y. A 3-D instantaneous cutting force prediction model of indexable disc milling cutter for manufacturing blisk-tunnels considering run-out. Int. J. Adv. Manuf. Technol. 2019, 103, 4029–4039. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Zhu, D.; Su, W.; Zhu, D. Study of tool trajectory in blisk channel ECM with spiral feeding. Mater. Manuf. Process. 2017, 32, 333–338. [Google Scholar] [CrossRef]
- Ren, J.; He, Q.; Yao, C.; Liang, Y.; Liu, B. Tool Axis Orientation Planning Method of Fixed Axis in Each Cutting Line for Closed Blisk Tunnel Five-axis Machining. Acta Aeronaut. Astronaut. Sin. 2012, 33, 1923–1930. [Google Scholar]
- Chiou, J.C.J.; Lee, Y.S. Optimal Tool Orientation for Five-Axis Tool-End Machining by Swept Envelope Approach. J. Manuf. Sci. Eng. Trans. ASME 2005, 127, 810–818. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, D.; Chen, Z.C.; Ren, J.; Li, X. Tool orientation optimization and location determination for four-axis plunge milling of open blisks. Int. J. Adv. Manuf. Technol. 2014, 70, 2249–2261. [Google Scholar] [CrossRef]
- Hu, C.; Hwang, Y.; Ho, M. Five-axis tool orientation smoothing using quaternion interpolation algorithm. Int. J. Mach. Tools Manuf. Des. Res. Appl. 2003, 43, 1259–1267. [Google Scholar]
- Zhao, P.; Shi, Y. Posture adaptive control of the flexible grinding head for blisk manufacturing. Int. J. Adv. Manuf. Technol. 2014, 70, 1989–2001. [Google Scholar] [CrossRef]
- Luo, M. Five-axis Tool Orientation Optimization Based on Kinematical Method. J. Mech. Eng. 2009, 45, 158–163. [Google Scholar] [CrossRef]
- Zhao, P.; Huang, J.; Shi, Y. Structure design and rotation control of the disc milling head in blisk manufacturing. Int. J. Adv. Manuf. Technol. 2017, 88, 2121–2133. [Google Scholar] [CrossRef]
- UGS Corp. NX 5 Help Library 2007, NX Open for NET Programmer’s Guide; UGS Corp: Plano, TX, USA, 2007. [Google Scholar]
- Jie, T.; Xianglin, Z. Research about the Further Develop of UG Based on C++. Modern Mach. 2007, 10, 80–92. [Google Scholar]
- Nazareth, J.L. Wiley Interdisciplinary Reviews: Computational Statistics. Conjug. Gradient Method 2009, 1, 348–353. [Google Scholar]
- Chan, R.H.; Ng, M.K. Conjugate gradient methods for toeplitz systems. SIAM Rev. 1996, 38, 427–482. [Google Scholar] [CrossRef]
- Battiti, R. First- and Second-Order Methods for Learning: Between Steepest Descent and Newton’s Method. Neural Comput. 1992, 4, 141–166. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).