Abstract
We report evidence that the experimentally observed small deformation of antiferromagnetic NiO modifies the symmetry of the crystal in such a way that the antiferromagnetic state becomes an eigenstate of the electronic Hamiltonian. This deformation closely resembles a rhombohedral contraction, but does not possess the perfect symmetry of a trigonal (rhombohedral) space group. We determine the monoclinic base centered magnetic space group of the antiferromagnetic structure within the deformed crystal which is strongly influenced by the time-inversion symmetry of the Hamiltonian. The antiferromagnetic state is evidently stabilized by a nonadiabatic atomic-like motion of the electrons near the Fermi level. This atomic-like motion is characterized by the symmetry of the Bloch functions near the Fermi level and provides in NiO a perfect basis for a Mott insulator in the antiferromagnetic phase.
1. Introduction
Nickel monoxide is antiferromagnetic with the relatively high Néel temperature K. Above , NiO possesses the fcc structure bearing the international number 225 [1]. Cracknell and Joshua [2] found that, below , the magnetic structure is invariant under the magnetic group (Number 90 in Table 7.4 of [3]), which will be given explicitly in Equation (1). The antiferromagnetic state is accompanied by a small contraction of the crystal along one of the triad axes often referred to as a rhombohedral deformation. However, the magnetic group does not possess any trigonal (rhombohedral) subgroup. Thus, this interpretation, if taken literally, seems to imply that the ground state of NiO does not possess any symmetry because, clearly, it cannot have two space groups.
In Section 4, this paper treats a new path in interpreting the experimental observation of Rooksby [1]: the time-inversion symmetry of the electron system suggests that the crystal is deformed by a small contraction closely resembling a rhombohedral deformation of the oxygen atoms in such a way that both the magnetic structure and the rhombohedral-like deformation have a common magnetic space group, namely the group , which will be defined in Section 3. Now, having determined explicitly the magnetic group of the ground state of NiO, the group-theoretical nonadiabatic Heisenberg model (NHM) [4] becomes applicable. The NHM defines a nonadiabatic atomic-like motion briefly described in Section 5.1. On the basis of the symmetry of the Bloch functions in the band structure of NiO, the NHM predicts that, indeed, a magnetic structure with the magnetic group may be stable in NiO (Section 5.2).
NiO has a second very interesting feature: it is an antiferromagnetic Mott insulator [5,6]. Furthermore, this observation may be understood within the NHM. In Section 6 we will show that the atomic-like motion of the electrons in antiferromagnetic NiO stabilizes not only the antiferromagnetic state, but, in addition, provides an ideal precondition for the Mott condition to be effective in NiO.
In order to understand the interesting features of NiO, the paper formulates three conditions of stability. The first two conditions in Section 3 and Section 5.1, respectively, concerning the stability of a magnetic state, have already been published in former papers. They are reformulated in order to facilitate the reading of the paper. The third condition in Section 6, concerning the existence of a Mott insulator, is given for the first time in this paper.
2. Group-Theoretical and Computational Methods Used in the Paper
The band structure of paramagnetic NiO in Figure 1 is calculated by the FHI-aims (“Fritz Haber Institute ab initio molecular simulations”) computer program using the density functional theory (DFT) [7,8] to compute the total energy in the electronic ground state. The NHM does require the exact total curves of the electrons, but only a more qualitative run of the energy bands. It starts from the symmetry of the Bloch states in the points of symmetry in the respective Brillouin zone. The FHI-aims program uses spherical harmonics as eigenvectors and provides the possibility of an output of the eigenvectors at any wave vector . Thus, I was able to write a C++ program to determine the symmetry of the Bloch functions at the points of symmetry in the Brillouin zone for the fcc Bravais lattice using the symmetry of the spherical harmonics as given in [3]. The results are given in Figure 1.
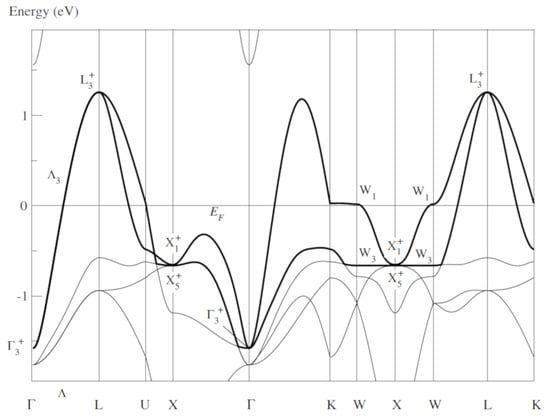
Figure 1.
Conventional band structure of paramagnetic fcc NiO as calculated by the FHI-aims program [7,8], using the structure parameters given in [1], with symmetry labels determined by the author. The notations of the points of symmetry in the Brillouin zone for follow Figure 3.14 of [3], and the symmetry labels are defined in Table A1 in Appendix B. The “active” band highlighted by the bold line becomes a magnetic super band when folded into the Brillouin zone for the magnetic structure; see Figure 3.
In Table A2, I give the symmetry of those Bloch functions, which can be unitarily transformed into optimally localized Wannier functions adapted to the symmetry of the magnetic group of antiferromagnetic NiO. The determination of these “magnetic bands” (Section 5.2) is a complex process described in [9] (see Theorems 5 and 7 ibidem), which is also performed by a C++ computer program. The notes to Table A2 give short remarks on the (symmetry) properties of the Wannier functions.
3. Magnetic Group of the Antiferromagnetic State: First Stability Condition
The antiferromagnetic structure of NiO is invariant under the symmetry operations of the type IV Shubnikov space group [2], which may be written as [3]:
where K denotes the anti-unitary operator of time-inversion. The unitary subgroup has the monoclinic base centered Bravais lattice and contains (besides the pure translations) four elements,
when the magnetic structure is orientated as given in Figure 2 (and in [2]).
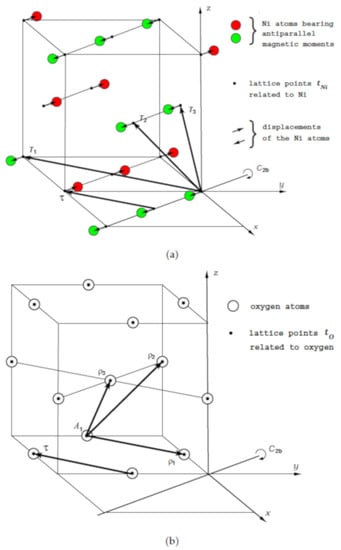
Figure 2.
Nickel (a) and oxygen (b) atoms in distorted antiferromagnetic NiO with the magnetic group in Equation (12) possessing the monoclinic base centered Bravais lattice . The Ni atoms represented by red circles bear a magnetic moment parallel or antiparallel to and the atoms represented by green circles the opposite moment. The magnetic structure is orientated as in [2]. The vectors are the basic translations of .
As in our former papers, we write the symmetry operations in the Seitz notation: R is a point group operation and the subsequent translation. In this paper, R stands for the identity E, the inversion I, the rotation through indicated in Figure 2, or the reflection ; the translation is or , where:
stands for the non-primitive translation in the group indicated in Figure 2. In what follows, the magnetic group is referred to as because the unitary subgroup bears the international number 15,
Though the magnetic group leaves the antiferromagnetic structure of NiO invariant, it need not be the magnetic group of antiferromagnetic NiO. This statement can be understood as follows: Consider a magnetic material, and let:
be a magnetic group leaving invariant the magnetic structure in this material. S is the unitary subgroup of M; K is still the operator of time-inversion; and R a point group operation. M includes all magnetic groups whether they are of type II, III, or IV [3]. Further, let be the exact magnetic ground state of the electronic Hamiltonian . Since commutes with the symmetry operators assigned to the symmetry operations a of M,
the magnetic state is the basis function of a one-dimensional co-representation D of M,
where . The operators and the operator K of time-inversion are defined in [9]; in the present paper, there definition is omitted.
The time-inverted state represents the opposite magnetic structure and, hence, is different from ,
is also an eigenstate of since commutes with K,
Hence, the states and form a basis of a two-dimensional co-representation of the overgroup:
of M, where D is subduced from . Now, we can formulate a stability condition for magnetic states: the states and are eigenstates of (i.e., and represent stable magnetic structures) if and only if the two-dimensional co-representation is irreducible [10]. This statement is well known in the theory of ordinary (unitary) groups [11].
Fortunately, it is not very complicated to decide whether or not the magnetic group has at least one co-representation complying with these conditions [12]:
Condition 1.
The group M in Equation (5) may be the magnetic group of a stable magnetic structure if the unitary subgroup S has at least one one-dimensional single valued representation:
- (i)
- following Case (a) with respect to the magnetic group in Equation (5) and
- (ii)
- following Case (c) with respect to the magnetic group .
The cases (a) and (c) are defined by Equations (7.3.45) and (7.3.47), respectively, of [3].
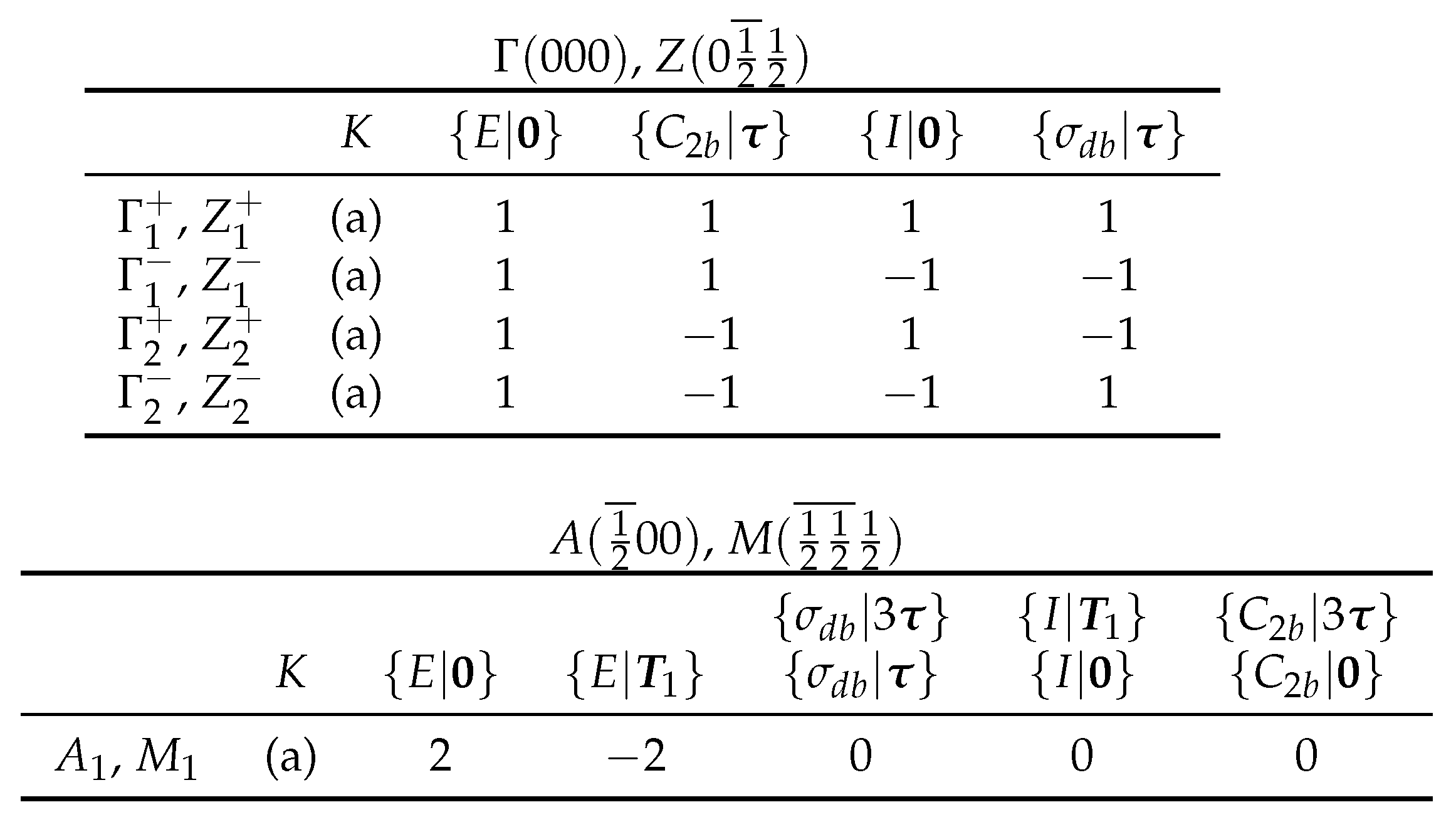
Table A3 and Table A4 provide all the information we now need for antiferromagnetic NiO: First, Table A3 shows that the space group (15) has only real one-dimensional representations, and hence, no representation meets the second condition (ii). Consequently, a spin structure with the magnetic group cannot be stable in NiO.
Removing from the two symmetry operations and , we receive the space group (9) containing (besides the pure translations) two elements,
Table A4 shows that the representations at points A and M in the Brillouin zone of (9) meet Condition (ii). In addition, the first condition (i) is satisfied for the magnetic group:
while it is not satisfied for . Consequently, the group is the only magnetic group in antiferromagnetic NiO representing a stable antiferromagnetic structure. Just as , the group has the monoclinic base centered Bravais lattice [3].
Magnetostriction alone produces the magnetic group in NiO. Consequently, in addition to the magnetostriction, the crystal must be distorted in such a way that the Hamiltonian still commutes with the elements of:
but does not commute with the symmetry operations of:
This is achieved by exactly the one distortion of the crystal illustrated in Figure 2: The Ni atoms are shifted in the direction from their positions at the lattice points in Equation (17), realizing in this way the group in the sense that the two commutator relations (14) and (16) are satisfied. With our group-theoretical methods, we cannot determine the magnitude of the displacements; however, they are clearly not so large as plotted (for the sake of clarity) in Figure 2a. The oxygen atoms, on the other hand, are not shifted from their positions at the lattice points in Equation (18) since any dislocation of the oxygen atoms would destroy the symmetry of the group . These statements on the atomic positions in the group may be understood by inspection of Figure 2. However, they may also be justified in terms of the Wyckoff positions of Ni and O in the group ; see Appendix A.
4. Rhombohedral-Like Distortion
Antiferromagnetic NiO becomes slightly deformed by a small contraction along one of the triad axes [1]. This deformation is often referred to as distortion from the cubic structure in the paramagnetic state to a rhombohedral one in the antiferromagnetic state [13]. On the basis of Figure 2, this important and interesting experimental observation can be understood as follows.
Figure 2 shows exhaustively the distorted antiferromagnetic structure of NiO with the magnetic group . However, it should be noted that, for the sake of clarity, the basic vectors of the Bravais lattice of are embedded in the paramagnetic fcc lattice of NiO. However, the fcc lattice may be distorted as a whole on the condition that the vectors , , and stay basic vectors of . The lattice points and plotted in Figure 2a,b, respectively, are no longer the positions of Ni and O in the fcc lattice, but are defined by the equations:
and:
where , , and are the basic vectors of and , , and are integers. Thus, the vectors and are solely given in terms of the basic vectors of detached from the paramagnetic fcc lattice.
In the stable antiferromagnetic structure, the Ni atoms are shifted in the ± () direction from their positions at the lattice points , while the oxygen atoms stay at the positions (Section 3). Within a ferromagnetic sheet, all the Ni atoms are dislocated in the same direction. Hence, the atomic distances within a sheet are the same as in the paramagnetic fcc phase. In adjacent sheets, on the other hand, the dislocations have different directions, and consequently, the distances between the Ni atoms in adjacent sheets become slightly greater than in the paramagnetic phase. Hence, the initial fcc structure is mostly disturbed in the <111> direction. It is conceivable that the antiferromagnetic structure is slightly contracted along the <111> axis because no symmetry operation of forbids such a contraction.
Figure 2b shows the position vectors , , and of three oxygen atoms in relation to the atom at position . In the paramagnetic fcc phase, the form a basis of the trigonal (rhombohedral) lattice orientated in the <111> direction. Within the Bravais lattice of , however, they are no longer translational symmetry operations. Thus, in the antiferromagnetic state of NiO, the no longer define a trigonal space group, but only define the positions of the oxygen atoms in the lattice . A (slight) contraction of the crystal along <111> has the consequence that the three position vectors are modified. However, they can only be modified in such a way that the magnetic group is preserved, which means that the vectors , , and stay basic vectors of . Thus, the directions and the lengths of the vectors , , and are modified on the condition that:
- still passes through the plain and
- in relation of this plane, and stay symmetrical to one another.
The and the are connected by the equations:
see Figure 2. From the last the two equations, it follows that:
Let be P the plane parallel to containing the point in Figure 2b. Equations (19) and (22) immediately show that , , and still are basic vectors of in the disturbed system if:
- (i)
- passes through P and
- (ii)
- and are symmetrical to each other with respect to P.
These two conditions are satisfied when still the modified vectors comply with a trigonal basis orientated in the direction. Hence, the magnetic group with the monoclinic base centered Bravais lattice is preserved when the modified define a rhombohedral-like array of the oxygen atoms within the antiferromagnetic state. The rhombohedral-like array of the oxygen atoms forms an “inner” deformation of the oxygen atoms within the monoclinic base centered Bravais lattice .
In summary: In the forgoing Section 3, we report evidence that the antiferromagnetic ground state of NiO is stable only if in Equation (12) is the magnetic group of the antiferromagnetic structure. Thus, the experimentally observed “rhombohedral structure” is evidently the described rhombohedral-like contraction of the crystal in the direction producing a rhombohedral-like array of the oxygen atoms preserving the magnetic group with the monoclinic base centered Bravais lattice . Since this contraction is small, the direction only differs slightly from the <111> direction.
The above conditions (i) and (ii) do not require that the vectors comply exactly with a trigonal basis. Thus, the oxygen atoms will not form an exact trigonal array within the antiferromagnetic system because there is no symmetry operation in requiring such an exact array. Nevertheless, the conditions (i) and (ii) allow only small deviations from an ideal trigonal array in the antiferromagnetic system, in particular also since the vectors form an exact trigonal basis in the paramagnetic phase of the crystal.
5. Wannier Functions Symmetry Adapted to M: Second Stability Condition
5.1. Atomic-Like Motion
The nonadiabatic Heisenberg model (NHM) [4] is based on three immediately obvious postulates defining an atomic-like motion [14,15] in narrow, partly filled bands, which cannot be described within the adiabatic approximation. This nonadiabatic atomic-like motion is a strongly correlated electronic motion clearly separated from any adiabatic band-like motion because the electrons gain the nonadiabatic condensation energy (Equation (2.20) of [4]) at the transition from the adiabatic band-like to the nonadiabatic atomic-like motion.
The nonadiabatic localized states belonging to the atomic-like motion are represented by hypothetical nonadiabatic localized functions. They are adapted to the symmetry of the crystal in order that the nonadiabatic Hamiltonian of the atomic-like system has the correct symmetry, i.e., the correct commutation properties [4]. Their existence, their spin dependence, and their symmetry are fixed by the postulates of the NHM. Therefore, they have the same symmetry and the same spin dependence as the exact symmetry adapted optimally localized Wannier functions related to one of the narrowest, partly filled bands in the conventional band structure of the considered metal. The adjective “exact” means that the Wannier functions are an exact unitary transformation of the actual Bloch functions of the considered band. Particularly, any modification of the symmetry of the Bloch functions in order to obtain closed bands is not allowed because we would lose important physical information. “Optimally localized” and “symmetry adapted” Wannier functions were defined in Definitions 5 and 7, respectively, of [9]. By “conventional band structure”, I mean a pure one electron band structure not taking into account any correlation effect. Correlation effects enter into the theory by the postulates of the NHM since the nonadiabatic atomic-like motion is strongly correlated.
The known complication that the narrowest bands of the metals are generally not closed may be solved in specific cases by allowing the Wannier functions to have a reduced symmetry [9]. So far, we found narrow, partly filled bands with optimally localized symmetry adapted Wannier functions in the band structures of magnetic materials and of superconductors by allowing the Wannier functions:
- (i)
- to be adapted only to the magnetic group M of the magnetic structure or
- (ii)
- to be spin dependent,
respectively. An energy band with Wannier functions of the first type (i) and the second type (ii) we called “magnetic band related the the magnetic group M” and “superconducting band”, respectively (Definitions 16 and 22 of [9]), because the strongly correlated nonadiabatic atomic-like motion in a magnetic band and in a superconducting band evidently stabilizes magnetism [10,16,17] and superconductivity [18,19], respectively. While superconducting bands are not the subject of this paper, the meaning of magnetic bands shall be clarified as follows:
Condition 2.
A magnetic structure with the magnetic group M may be stable in a material if and only if there exists a narrow, roughly half filled magnetic band related to M in the conventional band structure of this material. The Wannier functions are centered at the positions of the atoms bearing the magnetic moments.
5.2. Magnetic Band of NiO
All the information we now need is given in Figure 3 and in Table A2. When folding the band structure of paramagnetic NiO given in Figure 1 into the Brillouin zone of the monoclinic base centered magnetic structure, we receive the bands plotted in Figure 3. The band highlighted in the paramagnetic band structure by the bold lines is still highlighted in Figure 3. In what follows, it is referred to as the “active band”. In the same manner as in [9] (see Definition 2 ibidem), we call the active band a “single band” consisting of two (Figure 1) or four (Figure 3) branches. The active band in Figure 3 is a magnetic band related to the magnetic group because the Bloch functions of two branches of this band bear the symmetry labels of Band 1 in Table A2a. Thus, we can unitarily transform the Bloch functions of two branches of the active band into optimally localized Wannier functions symmetry adapted to and centered at the Ni atoms. Thus, the active band provides localized states allowing the electrons to perform a nonadiabatic atomic-like motion stabilized by the nonadiabatic condensation energy . However, a prerequisite is that a magnetic structure with the magnetic group is actually realized in the crystal. Therefore, the electron system activates a spin dependent exchange mechanism producing the magnetic structure with the magnetic group . Such a mechanism is possible within the nonadiabatic system; see Section 2 of [20]. The group is reduced to the group by the dislocations of the Ni atoms.
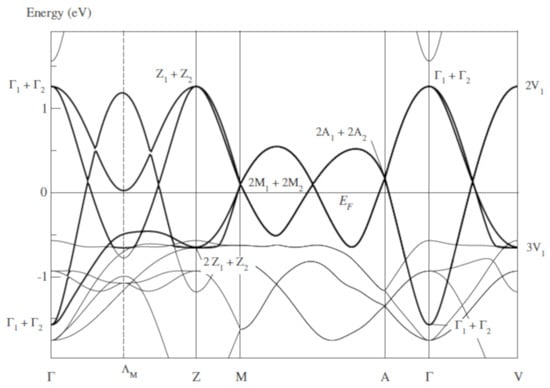
Figure 3.
The band structure of NiO given in Figure 1 folded into the Brillouin zone for the monoclinic base centered Bravais lattice of the magnetic group . The band highlighted in Figure 1 by the bold lines is still highlighted by bold lines in the folded band structure. It now forms a magnetic “super” band consisting of four branches assigned to the two nickel and the two oxygen atoms. The symmetry labels are defined in Table A4 and are determined from Figure 1 by means of Table A5. The notations of the points of symmetry follow Figure 3.4 of [3]. The midpoint of the line is equivalent to the points and in the Brillouin zone for the paramagnetic fcc lattice.
In summary, the electrons produce the magnetic structure with the magnetic group , so that the symmetry of the crystal is modified in such a way that the active band becomes a closed band [9]. This allows the electrons at the Fermi level to occupy an atomic-like state stabilized by the nonadiabatic condensation energy [4].
6. Mott Insulator: Third Condition of Stability
The active band of NiO does not only contain a magnetic band, but has in addition two remarkable features:
- (i)
- The magnetic band with the symmetry in Table A2a occurs twice in the active band. Since Band 1 in Table A2b has the same symmetry, we can unitarily transform the Bloch functions of two branches of the active band into optimally localized Wannier functions centered at the Ni atoms, and the Bloch functions of the two remaining branches into optimally localized Wannier functions centered at the O atoms. Thus, the electrons perform an atomic-like motion with localized states situated at both the Ni and the O atoms.
- (ii)
- All the electrons at the Fermi level take part in the atomic-like motion because the active band comprises all the branches crossing the Fermi level.
Such an active band I already found in the band structure of BaMnAs [17] and called it the “magnetic super band”:
Definition 1.
The Bloch functions of a magnetic super band related to the magnetic group M can be unitarily transformed into optimally localized Wannier functions symmetry adapted to M in such a way that the Wannier functions are not only centered at the atoms bearing the magnetic moments, but are centered at all the atoms of the material. Moreover, each Bloch function at the Fermi level belongs to the super band.
Thus, a magnetic super band produces a nonadiabatic atomic-like motion not only between the atoms bearing the magnetic moments, but between all the atoms of the material, whereby all the electrons at the Fermi level take part in the atomic-like motion. A magnetic super band contains just as many branches as there are atoms in the unit cell, and only branches belonging to the super band cross the Fermi level.
If the magnetic super band of NiO is half filled, it produces not only the magnetic structure, but may produce an atomic-like state with exactly one electron on each atom. If such a state has the lowest Coulomb repulsion energy, the crystal is a Mott insulator, because there are no further electrons at the Fermi level that would be able to carry an electrical current.
Because NiO is a prototype Mott insulator [5,6,21], the magnetic super band of NiO is evidently half filled, and the Mott condition is evidently satisfied in this band. As mentioned, I already found a magnetic super band in the band structure of BaMnAs [17]. In fact, also BaMnAs is a band gap insulator, often referred to as a small band gap semiconductor [22,23]. These observations on NiO and BaMnAs suggest that the nonadiabatic atomic-like motion in these materials, involving all the atoms and all the electrons at the Fermi level, is a cause for the insulating ground state. On the basis of these observations, I try to formulate a third condition of stability:
Condition 3.
Let a magnetic material be given with the magnetic space group M that possesses bands crossing the Fermi level in its conventional band structure (i.e., the material should be metallic under conventional band theory). This material may be in fact a band gap or Mott insulator, if there exists a half filled narrow magnetic super band related to M in its band structure.
If in any material, the non-adiabatic atomic-like motion in a magnetic super band stabilizes both a magnetic structure and an insulating ground state, then the atomic-like motion breaks down in the paramagnetic phase, and hence, the material becomes metallic. Therefore, there is evidence that both NiO and BaMnAs are metallic above the Néel temperature.
7. Results
The paper is concerned with three features of antiferromagnetic NiO, where two of them are very special:
- The rhombohedral-like deformation of antiferromagnetic NiO,
- the stability of the antiferromagnetic state, and
- the insulating ground state.
7.1. The Rhombohedral-Like Deformation
The time-inversion symmetry of the electronic Hamiltonian requires that the magnetic group of the antiferromagnetic state possesses special irreducible co-representations (Condition 1 in Section 3) so that the antiferromagnetic state is stable. The maximal group leaving the magnetic structure of NiO invariant, however, does not possess such suitable irreducible co-representations. It is the subgroup of that has co-representations allowing a stable magnetic structure.
Thus, the Ni atoms are shifted from their positions in the space group as indicated in Figure 2 (a) in order that is realized, i.e., in order that , but not , is the magnetic space group of the crystal. This distortion creates a deformation of the crystal closely resembling a rhombohedral deformation, but, clearly, cannot produce a rhombohedral space group because the magnetic space group of NiO still is the monoclinic base centered group . The rhombohedral-like deformation may be called an “inner” deformation of .
7.2. The Stability of the Antiferromagnetic State
In Section 5.2, we show that NiO possesses a narrow, roughly half filled magnetic band related to the magnetic group in its band structure. Thus, the electrons may perform a nonadiabatic atomic-like motion with the localized states centered at the Ni atoms. This atomic-like motion stabilizes the antiferromagnetic structure of NiO.
7.3. The Insulating Ground State
Moreover, the magnetic band of NiO is a magnetic super band. This means that the electrons even perform a nonadiabatic atomic-like motion with the localized states centered at both the Ni and the O atoms and that all the electrons at the Fermi level take part in the atomic-like motion. This is an optimal precondition for antiferromagnetic NiO to be a Mott insulator.
8. Discussion
The nonadiabatic Heisenberg model (NHM) defines a nonadiabatic atomic-like motion in NiO (Section 5.1) and claims that this motion is physically existent. It provides evidence that this really existing electronic motion causes the interesting properties of NiO, namely the stability of the antiferromagnetic structure and of the insulating ground state. The antiferromagnetic structure, however, can only be stable when the crystal is slightly distorted. This distortion creates a deformation of the crystal closely resembling a rhombohedral deformation.
The NHM provides the group-theoretical framework of the atomic-like motion of the electrons in NiO. It considers the exact atomic-like motion with hypothetical nonadiabatic localized functions being not suited for the calculation of matrix elements. For this purpose, we still must approximately represent the nonadiabatic localized states by atomic functions or (if they are known) by adiabatic Wannier functions. This “adiabatic approximation” of the nonadiabatic atomic-like state should yield physically relevant results in NiO because the electrons actually perform a nonadiabatic atomic-like motion. Thus, our results conflict neither with band structure calculations taking correlation effects into account [24,25] nor with the proven concept of correlation effects in narrow d bands being responsible for the nonmetallic behavior in NiO [6,14,21,26].
9. Conclusions
The results of this paper corroborate that the nonadiabatic atomic-like motion defined within the NHM is physically existent if the considered metal possesses a narrow, partly filled band with suitable Wannier functions (Section 5.1). The success in the last 40 years in identifying narrow, roughly half filled superconducting [9,27] and magnetic [9,17] bands in the conventional band structures of superconducting and magnetic materials provides evidence that the nonadiabatic atomic-like motion as defined in the NHM actually has physical reality and stabilizes the superconducting and magnetic states, respectively, in these materials. In addition, our results on NiO and BaMnAs [17] suggested that “magnetic super bands” (Section 6) may stabilize insulating ground states in a magnetic phase.
Funding
This publication was supported by the Open Access Publishing Fund of the University of Stuttgart.
Acknowledgments
I am very indebted to Guido Schmitz for his support of my work.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Nonadiabatic condensation energy as defined in Equation (2.20) of [4] | |
| NHM | Nonadiabatic Heisenberg model |
| E | Identity operation |
| I | Inversion |
| Rotation through as indicated in Figure 2 | |
| Reflection | |
| K | Anti-unitary operator of time inversion |
Appendix A. Wyckoff Positions
The magnetic group of the antiferromagnetic state of NiO is a type III Shubnikov space group, which also may be written in the form [3]:
where the unitary space group contains (besides the translations) the elements:
Though the symmetry operations of the group are different from the operations contained in (see Equation (2)), both groups bear the same international number 15 because the elements of are changed into the elements of when the origin of is translated by [3]:
Keeping this in mind, we may determine the Wyckoff positions of the atoms in the space group by means of the Bilbao Crystallographic Server [28] yielding the Wyckoff positions :
in the space group . In the coordinate system given in Figure 2a, the two Wyckoff positions may be written as:
and in the case , we have (for ):
since (in Equation (A4)) and .
Thus, the vectors and in Equations (17) and (18) represent the Wyckoff positions and of . Equation (A4) confirms that in the magnetic group , the nickel atoms may be shifted by in the direction from their positions , while the oxygen atoms are fixed at their positions .
Appendix B. Group-Theoretical Tables
This Appendix provides Table A1,
Table A2, Table A3, Table A4,
Table A5 along with notes to the tables.

Table A1.
Character tables of the single valued irreducible representations of the cubic space group (225) of paramagnetic NiO.
Table A1.
Character tables of the single valued irreducible representations of the cubic space group (225) of paramagnetic NiO.

Notes to Table A1:
- (i)
- The point group operations are related to the coordinate system in Figure 2.
- (ii)
- The notations of the points of symmetry follow Figure 3.14 of [3].
- (iii)
- The character tables are determined from Table 5.7 of [3].
- (iv)
- The point R lies in the plane .

Table A2.
Symmetry labels of the Bloch functions at the points of symmetry in the Brillouin zone for (9) of all the energy bands with symmetry adapted and optimally localized Wannier functions centered at the Ni (Table (a)) and O (Table (b)) atoms, respectively.
Table A2.
Symmetry labels of the Bloch functions at the points of symmetry in the Brillouin zone for (9) of all the energy bands with symmetry adapted and optimally localized Wannier functions centered at the Ni (Table (a)) and O (Table (b)) atoms, respectively.
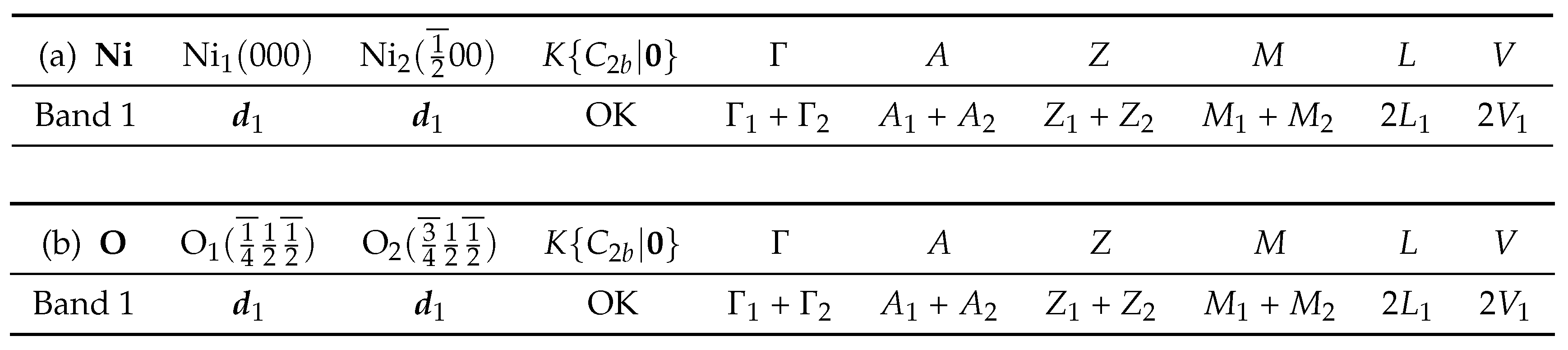
Notes to Table A2:
- (i)
- The space group is the unitary subgroup of the magnetic group leaving invariant both the experimentally observed [2,29,30,31,32] antiferromagnetic structure and the dislocations of the Ni atoms shown in Figure 2a. K still denotes the operator of time-inversion.
- (ii)
- Each band consists of two branches (Definition 2 of [9]) since there are two Ni and two O atoms in the unit cell.
- (iii)
- Band 1 of Ni forms the magnetic band responsible for the antiferromagnetic structure of NiO.
- (iv)
- Band 1 of Ni and Band 1 of O form together the magnetic super band responsible for the Mott insulator.
- (v)
- The notations of the points of symmetry in the Brillouin zone for follow Figure 3.4 of [3].
- (vi)
- The symmetry notations of the Bloch functions are defined in Table A4.
- (vii)
- The bands are determined following Theorem 5 of [9].
- (viii)
- Table (a) is valid irrespective of whether or not the Ni atoms are dislocated as shown in Figure 2a.
- (ix)
- The Wannier functions at the Ni or O atoms listed in the upper row belong to the representation included below the atom.
- (x)
- Applying Theorem 5, we need the representation of the point groups and of the positions of the Ni and O atoms, respectively (Definition 12 of [9]). In NiO, both groups contain only the identity operation,Thus, the Wannier functions belong to the simple representation defined by:
1 - (xi)
- Each row defines a band with Bloch functions that can be unitarily transformed into Wannier functions being:
- as well localized as possible (according to Definition 5 of [9]);
- centered at the Ni (Table (a)) or O (Table (b)) atoms; and
- symmetry adapted to ; that means (Definition 7 of [9]) that they satisfy Equation (15) of [9], reading in NiO as:where , and denote the Wannier functions centered at the Ni and O atoms, respectively.
- (xii)
- The entry “OK” indicates that the Wannier functions follow also Theorem 7 of [9] with in Table (a) and in Table (b). That means that the Wannier functions may even be chosen symmetry adapted to the magnetic group . Thus, Equation (62) of [9] is valid, reading in NiO as:in addition to Equations (A8).
- (xiii)
- Within the NHM, Equations (A8) and (A9) have only one, but an important meaning: they ensure that the nonadiabatic Hamiltonian of the atomic-like electrons commutes with the symmetry operators of [4].

Table A3.
Character tables of the single valued irreducible representations of the monoclinic base centered space group (15).
Table A3.
Character tables of the single valued irreducible representations of the monoclinic base centered space group (15).
Notes to Table A3:
- (i)
- The notations of the points of symmetry follow Figure 3.4 of [3].
- (ii)
- Only the points of symmetry invariant under the complete space group are listed.
- (iii)
- The character tables are determined from Table 5.7 in [3].
- (iv)
- K denotes the operator of time inversion. The entry (a) is determined by Equation (7.3.51) of [3] and indicates that the related co-representations of the magnetic group follow Case (a) as defined in Equation (7.3.45) of [3].

Table A4.
Character tables of the single valued irreducible representations of the monoclinic base centered space group (9).
Table A4.
Character tables of the single valued irreducible representations of the monoclinic base centered space group (9).
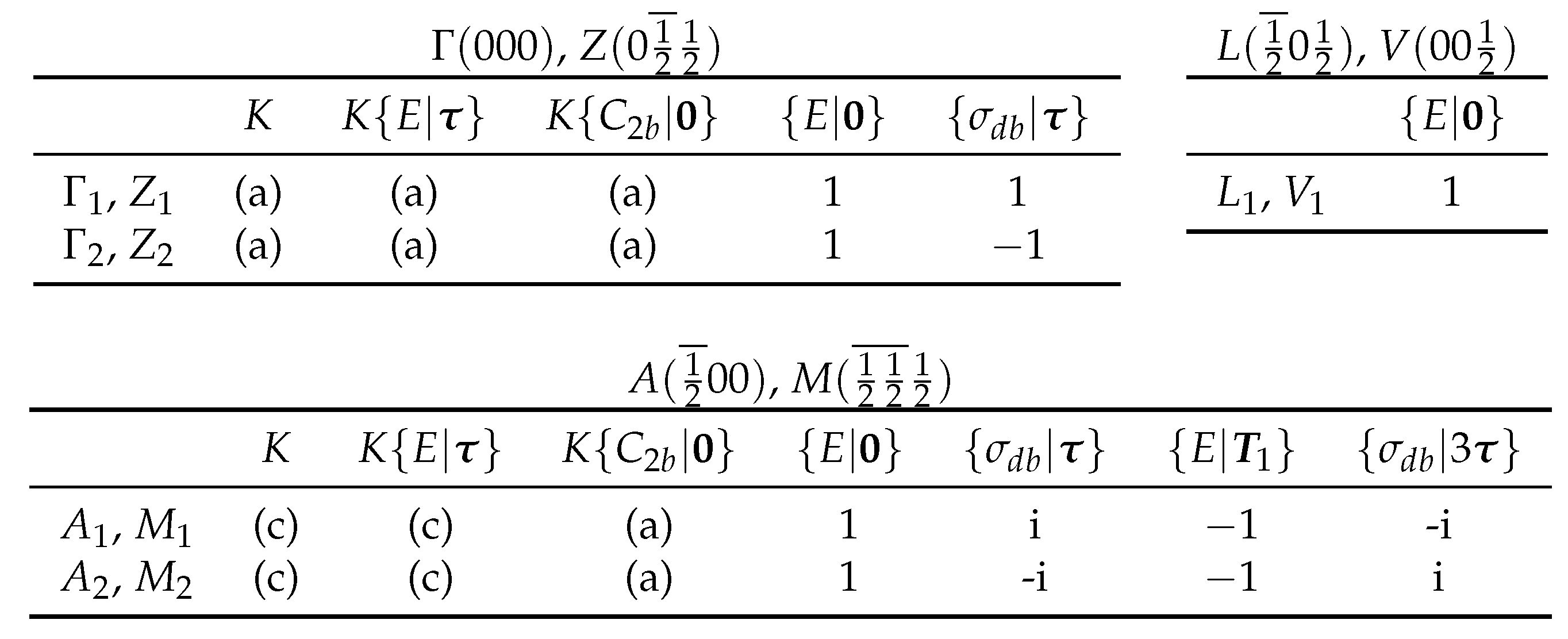
Notes to Table A4:
- (i)
- The notations of the points of symmetry follow Figure 3.4 of [3].
- (ii)
- The character tables are determined from Table 5.7 in [3].
- (iii)
- K denotes the operator of time inversion. The entries (a) and (c) are determined by Equation (7.3.51) of [3]. They indicate whether the related co-representations of the magnetic groups , , and follow Case (a) or Case (c) as defined in Equations (7.3.45) and (7.3.47), respectively, of [3].

Table A5.
Compatibility relations between the Brillouin zone for the fcc space group (225) of paramagnetic NiO and the Brillouin zone for the space group (9) of the antiferromagnetic structure in distorted NiO.
Table A5.
Compatibility relations between the Brillouin zone for the fcc space group (225) of paramagnetic NiO and the Brillouin zone for the space group (9) of the antiferromagnetic structure in distorted NiO.
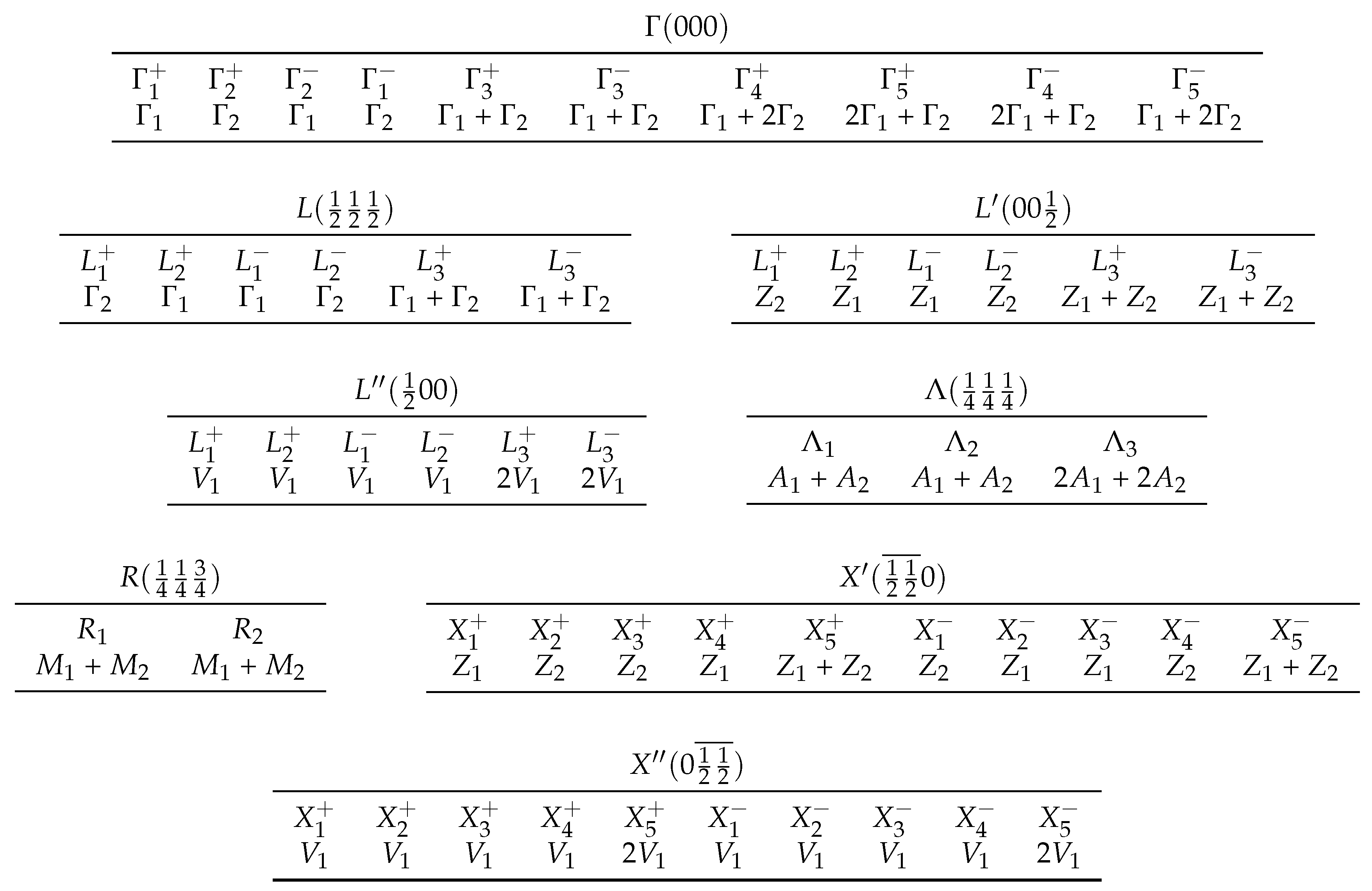
Notes to Table A5:
- (i)
- The Brillouin zone for (9) lies diagonally within the Brillouin zone for (225).
- (ii)
- The upper rows list the representations of the little groups of the points of symmetry in the Brillouin zone for , and the lower rows list representations of the little groups of the related points of symmetry in the Brillouin zone for .The representations in the same column are compatible in the following sense: Bloch functions that are basis functions of a representation in the upper row can be unitarily transformed into the basis functions of the representation given below .
- (iii)
- The notations of the points of symmetry follow Figures 3.14 and 3.4, respectively, of [3].
- (iv)
- (v)
- Within the Brillouin zone for , the primed points are equivalent to the unprimed point.
- (vi)
- The compatibility relations are determined by a C++ computer program in the way described in great detail in [33].
References
- Rooksby, H. A note on the structure of nickel oxide at subnormal AND elevated temperatures. Acta Crystallogr. 1948, 1, 226. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Joshua, S.J. The space group corepresentations of antiferromagnetic NiO. Math. Proc. Camb. Philos. Soc. 1969, 66, 493–504. [Google Scholar] [CrossRef]
- Bradley, C.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B 2001, 63, 144403. [Google Scholar] [CrossRef]
- Gavriliuk, A.G.; Trojan, I.A.; Struzhkin, V.V. Insulator-Metal Transition in Highly Compressed NiO. Phys. Rev. Lett. 2012, 109, 086402. [Google Scholar] [CrossRef] [PubMed]
- Mott, N.F. The Basis of the Electron Theory of Metals, with Special Reference to the Transition Metals. Proc. Phys. Soc. Sect. A 1949, 62, 416–422. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient O(N)O(N) integration for all-electron electronic structure calculation using numeric basis functions. Comput. Phys. Commun. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Krüger, E.; Strunk, H.P. Group Theory of Wannier Functions Providing the Basis for a Deeper Understanding of Magnetism and Superconductivity. Symmetry 2015, 7, 561–598. [Google Scholar] [CrossRef]
- Krüger, E. Stability and symmetry of the spin-density-wave-state in chromium. Phys. Rev. B 1989, 40, 11090–11103. [Google Scholar] [CrossRef]
- Wigner, E.P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra; Acad. Press: New York, NY, USA, 1964. [Google Scholar]
- Krüger, E.; Strunk, H.P. Structural Distortion in Antiferromagnetic BaFe2As2 as a Result of Time-Inversion Symmetry. J. Supercond. 2014, 27, 601–612. [Google Scholar] [CrossRef]
- Slack, G.A. Crystallography and Domain Walls in Antiferromagnetic NiO Crystals. J. Appl. Phys. 1960, 31. [Google Scholar] [CrossRef]
- Mott, N.F. On the transition to metallic conduction in semiconductors. Can. J. Phys. 1956, 34, 1356–1368. [Google Scholar] [CrossRef]
- Hubbard, J. Elelectron correlations in narrow energy bands. Proc. R. Soc. Lond. Ser. A 1963, 276, 238–257. [Google Scholar]
- Krüger, E. Energy band with Wannier functions of ferromagnetic symmetry as the cause of ferromagnetism in iron. Phys. Rev. B 1999, 59, 13795–13805. [Google Scholar] [CrossRef]
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Semiconducting Ground State of BaMn2As2. Symmetry 2016, 8, 99. [Google Scholar] [CrossRef]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry I. Band Structure of Niobium. J. Supercond. 2001, 14, 469–489, Please note that in this paper the term “superconducting band” was abbreviated by “σ band”. [Google Scholar] [CrossRef]
- Krüger, E. k-Space Magnetism as the Origin of Superconductivity. Symmetry 2018, 10, 259. [Google Scholar] [CrossRef]
- Krüger, E. Theoretical investigation of the magnetic structure in YBa2Cu3O6. Phys. Rev. B 2007, 75, 024408. [Google Scholar] [CrossRef]
- Austin, I.G.; Mott, N.F. Metallic and Nonmetallic Behavior in Transition Metal Oxides. Science 1970, 168, 71–77. [Google Scholar] [CrossRef]
- An, J.; Sefat, A.S.; Singh, D.J.; Du, M.H. Electronic structure and magnetism in BaMn2As2 and BaMn2Sb2. Phys. Rev. B 2009, 79, 075120. [Google Scholar] [CrossRef]
- Singh, Y.; Ellern, A.; Johnston, D.C. Magnetic, transport, and thermal properties of single crystals of the layered arsenide BaMn2As2. Phys. Rev. B 2009, 79, 094519. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Korotin, M.A.; Kurmaev, E.Z. Band-structure description of Mott insulators (NiO, MnO, FeO, CoO). J. Phys. Condens. Matter 1990, 2, 3973–3987. [Google Scholar] [CrossRef]
- Gillen, R.; Robertson, J. Accurate screened exchange band structures for the transition metal monoxides MnO, FeO, CoO and NiO. J. Phys. Condens. Matter 2013, 25, 165502. [Google Scholar] [CrossRef]
- Mott, N.F. The transition to the metallic state. Philos. Mag. 1961, 6, 287–309. [Google Scholar] [CrossRef]
- Krüger, E. Constraining Forces Stabilizing Superconductivity in Bismuth. Symmetry 2018, 10, 44. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Perez-Mato, J.M.; Capillas, C.; Kroumova, E.; Ivantchev, S.; Madariaga, G.; Kirov, A.; Wondratschek, H. Bilbao Crystallographic Server I: Databases and crystallographic computing programs. Z. Krist. 2006, 221, 15–27. [Google Scholar] [CrossRef]
- Roth, W.L. Magnetic Structures of MnO, FeO, CoO, and NiO. Phys. Rev. 1958, 110, 1333–1341. [Google Scholar] [CrossRef]
- Roth, W.L. Multispin Axis Structures for Antiferromagnets. Phys. Rev. 1958, 111, 772–781. [Google Scholar] [CrossRef]
- Yamada, T. Magnetic Anisotropy, Magnetostriction, and Magnetic Domain Walls in NiO. I. Theory. J. Phys. Soc. Jpn. 1966, 21, 664–671. [Google Scholar] [CrossRef]
- Yamada, T.; Saito, S.; Shimomura, Y. Magnetic Anisotropy, Magnetostriction, and Magnetic Domain Walls in NiO. II. Experiment. J. Phys. Soc. Jpn. 1966, 21, 672–680. [Google Scholar] [CrossRef]
- Krüger, E. Symmetry of Bloch functions in the space group of perfect antiferromagnetic chromium. Phys. Rev. B 1985, 32, 7493–7501. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).