Abstract
Quantum droplets are ultradilute liquid states that emerge from the competitive interplay of two Hamiltonian terms, the mean-field energy and beyond-mean-field correction, in a weakly interacting binary Bose gas. We relate the formation of droplets in symmetric and asymmetric two-component one-dimensional boson systems to the modulational instability of a spatially uniform state driven by the beyond-mean-field term. Asymmetry between the components may be caused by their unequal populations or unequal intra-component interaction strengths. Stability of both symmetric and asymmetric droplets is investigated. Robustness of the symmetric solutions against symmetry-breaking perturbations is confirmed.
1. Introduction
The mean-field (MF) theory of weakly interacting dilute atomic gases rules out formation of a liquid state [1,2]. However, it has been recently shown that a liquid phase arises if one takes into account beyond-MF effects originating from quantum fluctuations around the MF ground state of weakly interacting binary (two-component) Bose gases [3]. A fundamental property that allows one to interpret this phase as a fluid is incompressibility: It maintains a limit density which cannot be made larger (see details below), hence adding more atoms leads to spatial expansion of the state. Another fundamental feature of this quantum-fluid phase is that it facilitates self-trapping of quantum droplets (QDs), which are stabilized by the interplay between the contact MF interaction and the beyond-MF Lee–Huang–Yang (LHY) correction [4]. Binary Bose–Einstein condensates (BECs) with competing intra- and inter-component MF interactions of opposite signs offer a remarkable possibility for the generation of QDs, as proposed by Petrov [3]. This possibility was further elaborated in various settings, including different effective dimensions [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In particular, the dynamics of QDs with the flat-top (FT) or Gaussian shape, which correspond to large or relatively small numbers of particles, respectively, was addressed in the framework of the one-dimensional (1D) reduction of the model [20]. The theoretical prediction was followed by experimental creation of QDs in mixtures of two different atomic states of K, with quasi-2D [21,22] and fully 3D [23,24] shapes (see also recent reviews [25,26]). Very recently, the creation of especially long-lived QDs was reported in a heteronuclear K-Rb system [27]. Another theoretically predicted and experimentally realized option for the creation of QDs makes use of the single-component condensate with dipole–dipole interactions [28,29,30,31,32,33,34,35]. It is relevant to mention that the formation of multiple droplets was also predicted and experimentally observed as an MF effect in strongly nonequilibrium (turbulent) states of BECs [36].
Collective modes of QDs are a subject of special interest, as they reveal internal dynamics of the droplets [20,24,32,37,38]. In particular, the stable existence of the QDs is secured if the particle-emission threshold lies below all excitation modes, hence a perturbation in the form of such modes will not cause decay of the droplet.
We aim to address issues that are related to the creation of QDs in the 1D setting and were not addressed in previous works. First, we consider modulational instability (MI) of spatially uniform plane-wave (PW) states, in the framework of the coupled system of Gross–Pitaevskii (GP) equations with the LHY corrections, for the two-component MF wave function of the binary condensate. This is the system which was originally derived in [5]. Recently, MI has been experimentally demonstrated in BECs with attractive interactions [39,40,41]. Other examples of the MI are provided by the binary BEC with the linear Rabi coupling or the spin-orbit coupling [41,42], and by a system combining the MF and LHY terms [43]. The linear-stability analysis, followed by direct simulations of the corresponding GP equations, shows that the lower branch of the PW states exhibits MI, the instability splitting the PW into a chain of localized droplet-like structures. Secondly, we address properties of the QDs in the binary condensate in the framework of the two-component GP system, without assuming effective inter-component symmetry, which reduces the system to a single-component GP equation. The asymmetry implies different MF self-repulsion coefficients in the two components, and/or unequal norms in them. Although properties of QDs have been studied by using the two-component GP system in some papers [6,11,14,15,17,18], the explicit asymmetry of the system parameters has not been addressed, except for [14] in which the situation for K-K and Na-Rb atomic mixtures have been considered. We conclude that the population difference between the components does not significantly affect density profiles of QDs in the system with equal MF self-repulsion strengths in the two components. On the other hand, we find that profiles of the QD solutions are essentially asymmetric when the self-repulsion coefficients are different in the components. Generally, the numerical findings corroborate stability of the known symmetric states against symmetry-breaking perturbations. We also address the MI of the two-component system, and demonstrate that chains of asymmetric QDs can be generated by the MI-induced nonlinear evolution.
The paper is organized as follows. In Section 2 we introduce the model and discuss conditions necessary for the formation of the droplets. Section 3.1 deals with the single-component version of the symmetric system. We consider various solutions admitted by it (PW, FT, periodic, etc.), and apply the linear-stability analysis of the PW solution to assess the MI, in a combination with direct simulations. In Section 3.2, we address the stability of asymmetric droplets, as well as the formation of droplets in the two-component asymmetric system via the MI. The paper is concluded by Section 4. Additional symmetric and asymmetric exact and approximate analytical solutions are presented in Appendices.
2. Model and Methods
We consider the 1D model of the two-component condensate with coefficients of the intra-component repulsion, and , and inter-component attraction, . In the weak-interaction limit, the corresponding energy density, which includes the MF terms and LHY correction, was derived in [5]:
where m is the atomic mass (the same for both components), is the density of the j-th component, represented by the MF wave function , and
The last term in Equation (1) represents the LHY correction. Derivation of Equation (1) assumes that the binary BEC is close to the point of the MF repulsion-attraction balance, with . In experiments, may be tuned to be both positive and negative [21,22,23].
Equation (1) is valid in the case of tight confinement applied in the transverse dimensions, which makes the setting effectively one-dimensional. In the 3D case, the LHY term (for ) is replaced by one . A detailed consideration of the crossover from 3D to 1D [12,44,45] in the two-component system is a problem which may be a subject of a separate work. Here, it is relevant to compare the symmetric version of Equation (1) for the energy density with that recently presented in [12]. It demonstrates that an accurately derived LHY contribution to the energy density of the 1D system contains, in addition to the term which was derived in [5], a term , which can be absorbed into the mean-field energy density, and a higher-order term , which was omitted in the analysis reported in [12]. A conclusion formulated in that work is that the energy density originally derived in [5] is literally valid if the ratio of the mean-field energy to that of the transverse confinement takes values . For typical experimental parameters, this implies that the difference between absolute values of scattering lengths of the mean-field intra-component repulsion and inter-component attraction should be nm, which may be achieved in the experiment. The 1D QDs originate from the balance of the second term in Equation (1), corresponding to the weakly repulsive MF interaction, with , and the LHY term, which introduces effective attraction in the 1D setting, on the contrary to the repulsion in the 3D setting [5,20].
The energy functional, , gives rise to the system of GP equations, which include the LHY correction,
where T and Z are the time and coordinate measured in physical units, and parameter
measures the deviation from the MF repulsion–attraction balance point, see Equation (2). The normalization of the components of the wave function is determined by numbers of bosons in each component:
Further, rescaling
casts Equation (3) in the normalized form,
where parameter
determines the asymmetry of the system, in the case of . Note that, as concerns stationary solutions with chemical potentials , sought for as
states with mutually proportional components, , are only possible in the fully symmetric case with , , and . In previous works [5,20], 1D solutions for QDs were considered only in the framework of the single GP equation which corresponds to symmetric system Equation (7) with and .
3. Modulation Instability Versus QDs
In this section, we address MI of PWs in both symmetric and asymmetric GP systems, and relate it to formation of the QDs in the binary bosonic gas. To the best of our knowledge, this is the first work aiming to associate the MI with the formation of the 1D droplets in the system with unequal components. We first consider MI in the framework of the single-component reduction of the symmetric version of Equation (7), after briefly reviewing stationary solutions of the GP equation. Next, we extend the analysis for the two-component GP system, which makes it possible to produce asymmetric QDs, starting from the MI of asymmetric PW states.
3.1. The Single-Component GP Model
Under the single-component reduction of the binary system, with and , Equation (1) simplifies to [5]
with the single dimensionless density, . Assuming a spatially uniform state, the equilibrium density and the corresponding chemical potential are given by
Density corresponds to the minimum of the energy per particle, , and is negative for . The corresponding single GP equation is
with normalization condition , where is the number of atoms in each component.
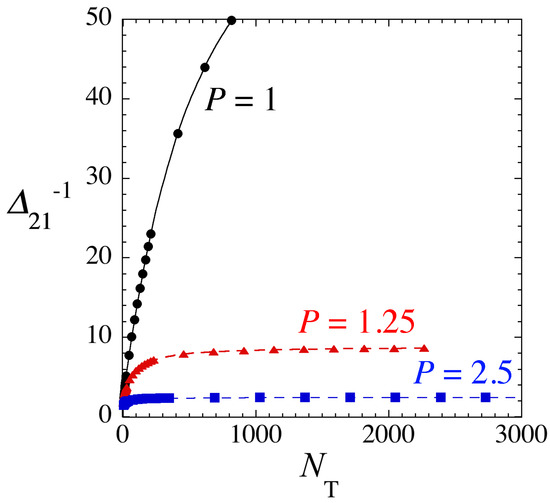
Although coefficient can be scaled out in Equation (12), as done in [20], we keep it here as a free parameter. This option is convenient for the subsequent consideration of the MI, treating and density n as independent constants, which may be matched to experimentally relevant parameters.
Below, we address two stationary solutions of Equation (12). One is the QD bound state of a finite size, which was studied in detail in [5,20]. The other solution is the PW with uniform density. Here, we briefly recapitulated basic properties of these solutions for the completeness of the presentation. In Section 3.1.3 we address the MI of the PWs and associate it with the spontaneous generation of chains of localized modes. Additional families of exact analytical solutions of Equation (12) are given in Appendix A.
3.1.1. The Droplet Solution
As shown in [5,20,46], at Equation (12) gives rise to an exact soliton-like solution representing a QD, maintained by the balance between the effective cubic self-repulsion and quadratic attraction:
This solution exists in a finite range of negative values of the chemical potential , featuring the FT shape at , with size [5,20]. A typical density profile of the FT solution is displayed in the inset of Figure 1. At , the size of the droplet diverges, and the solution carries over into the delocalized PW with uniform density, . The fact that the density of the condensate filling the FT state cannot exceed the largest value, , implies its incompressibility. For this reason, the condensate may be considered as a fluid, as mentioned above. With the increase of from towards , the maximum density of the localized mode,
monotonously decreases from to 0. The QD’s FWHM size, defined by condition , also shrinks at first with increasing , attaining a minimum value at . Further increase of towards makes the QD broader, its width diverging as at .
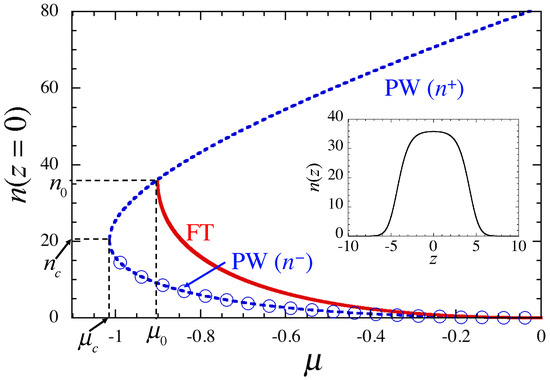
Figure 1.
The maximum density in the FT (flat-top) state, as per Equation (14), and the PW (plane-wave)/density are displayed as functions of by the red-solid and blue-dashed curves, respectively, for . In this case, Equation (11) yields and . The PW solution includes upper and lower branches corresponding to , as given by Equation (20), the lower one (marked by circles) being subject to the MI (modulational instability). The spinodal point is one with coordinates . For other values of , the plot can be generated from the present one by rescaling. The inset shows the density profile of the FT solution for and , very close to the delocalization limit (the transition to PW).
The norm of the exact QD solutions given by Equation (13) is
It satisfies the well-known Vakhitov–Kolokolov (VK) necessary stability criterion [47],
due to and
Full stability of the QD family has been verified by direct simulations of the evolution of perturbed QDs in the framework of Equation (12).
It is relevant to mention that the exact solution of Equation (13) is valid too at , when the cubic term in Equation (12) is self-attractive, like the quadratic one. In that case, is positive, as per Equation (11), while the chemical potential of the self-trapped state remains negative, as the solution of Equation (13) may exist only at . Then, it follows from Equation (13) that the soliton-like mode exists for all values of (unlike the finite interval Equation (17), in which the solution exists for ), and it does not feature the FT shape. Rather, with the increase of , it demonstrates a crossover between the KdV-soliton shape and the nonlinear-Schrödinger one, . For , the dependence for the soliton family carries over into the following form,
which is an analytical continuation of Equation (15). This dependence also satisfies the VK criterion.
3.1.2. The Plane-Wave Solution
The PW solution of Equation (12) can be presented in a form with wavenumber and constant density n, which determine the corresponding chemical potential:
The Galilean invariance of Equation (12) implies that any quiescent solution generates a family of moving ones, with arbitrary velocity c. Therefore, may be canceled by means of transformation with .
For given , Equation (19) produces two different branches of the density as a function of (here, is set):
For , these branches are shown in Figure 1. As follows from Equation (20), they exist (for ) above a minimum value of : , the respective density being
Values and correspond to the spinodal point [5], and (see Equation (13)). Note that the above-mentioned existence region of the soliton solution in terms of the chemical potential, , lies completely inside that of the PW state, which is . Thus, the soliton always coexists with the PW (this fact is also obvious in Figure 1).
3.1.3. Modulational Instability of the Plane Waves
Here, we aim to analyze the MI of PW solutions in the framework of the single-component GP Equation (12) and demonstrate how the development of the MI can help to generate QDs. We perform the analysis for the PWs with zero wavenumber , which is sufficient due to the aforementioned Galilean invariance of the underlying equation.
A small perturbation is added to the stationary PW state as
The substitution of this expression in Equation (12) and linearization with respect to perturbation leads to the corresponding Bogoliubov–de Gennes equation,
By looking for perturbation eigenmodes with wavenumber k and frequency ,
and real infinitesimal amplitudes and , Equation (23) yields a dispersion relation for the eigenfrequencies:
The MI takes place when acquires an imaginary part. As follows from Equation (25), this occurs when the density satisfies condition see (Equation (21)), which corresponds to branch of the PW state. The instability region in terms of k is given by
The MI gain is plotted in Figure 2 versus and , for given density in panel (a), and versus and n, for given in (b). It is easy to find from Equation (25) that the largest gain is attained at wavenumber
with defined as per Equation (26). Note that Figure 2a includes the case of the self-attractive cubic nonlinearity, with , which naturally displays much stronger MI, as in this case it is driven by both the quadratic and cubic nonlinear terms. In fact, the extension of the MI chart to makes it possible to compare the MI in the present system and its well-known counterpart in the setting with the fully attractive nonlinearity.
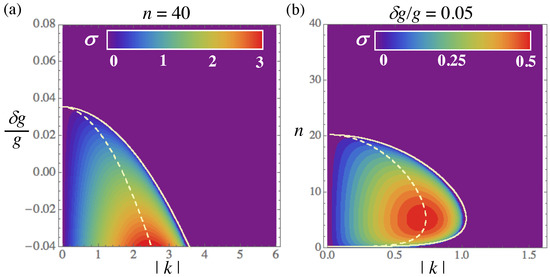
Figure 2.
Color-coded values of the MI gain, , are displayed for fixed in (a), and for fixed in (b). Note that panel (a) covers both signs of the cubic nonlinearity, and . Solid and dashed white curves represent the MI boundary (Equation (26)) and the peak value of the MI gain (Equation (27)), respectively.
Comparing parameter values at which the QD solutions are predicted to appear, and the MI condition for the PW with the corresponding density, the MI is expected to provide a mechanism for the creation of the QDs. This is confirmed by direct simulations of the GP Equation (12), as shown in Figure 3. The PW with is taken as the input, so that it is subject to the MI for , as seen in Figure 2b. As shown in Figure 3, small initial perturbations trigger the emergence of multiple-QD patterns (chains) at . For these parameters, we get and , which determines the wavelength of the fastest growing modulation, , and the growth-time scale, . The number of the generated droplets in Figure 3 is consistent with estimate , where is the size of the simulation domain. We have checked that the number of generated droplets is approximately given by for other values of parameters as well. This dynamical scenario is similar to those observed in other models in the course of the formation of soliton chains by MI of PWs [39,40]. The long-time evolution in Figure 3a shows that the number of the droplets becomes smaller due to merger of colliding droplets into a single one, which agrees with dynamical properties of 1D QDs reported in [20].
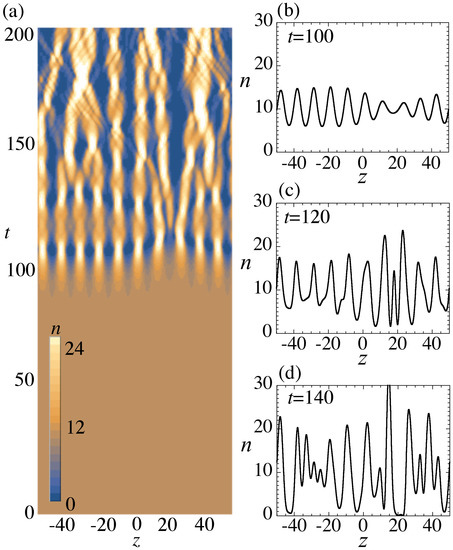
Figure 3.
A typical example of the MI development, starting from an unstable PW state, with density and , which is subject to the MI, pursuant to Figure 2. In (a), the spatiotemporal pattern of the evolution of the condensate density is shown. In the right-hand panels, cross sections of the density profiles are displayed at (b), (c), and (d). The simulations were performed in domain with 2500 grid points and periodic boundary conditions.
To implement this mechanism of the generation of a chain of solitons in the experiment, i.e., make the density smaller than the critical value , one may either apply interaction quench (by means of the Feshbach resonance), suddenly decreasing , as was done in recent experimental works for different purposes [21,22,23,48]. Another option, which is specific to the 1D setting, is sudden decrease of density n by relaxing the transverse trapping.
3.2. The Two-Component Gross–Pitaevskii Model
In this section, we revert to the full two-component GP system Equation (7), aiming to explore the formation of QD states in it. The two-component setting may include parameter imbalance between the two components, as indicated theoretically [3] and observed experimentally [21,22,23,27]. Here, we present the analysis of asymmetric QDs in two cases: (i) the two-component GP system with different populations, , and equal intra-component coupling strength, (i.e., , see Equation (8)), and (ii) the system with different intra-component coupling strengths, (i.e., ). These options suggest a possibility to check the stability of the solutions of the symmetric system, reduced to the single-component form, against symmetry-breaking perturbations. That objective is relevant because, in the real experiment, scattering lengths of the self-interaction in the two components are never exactly equal [21,22,23,24]. We address, first, an asymmetric single-droplet solution, and, subsequently, MI of the PW states in the two-component system.
Because, as said above, solutions with mutually proportional components (written as ) are possible solely in the strictly symmetric setting, asymmetric QDs cannot be found in an exact analytical form. As shown in Appendix B (see Equations (A6)–(A12)), asymptotic analytical solutions can be obtained for strongly asymmetric states, with one equation replaced by its linearized version. In this section, we chiefly rely on numerical solution of Equation (7).
3.2.1. Asymmetric QDs with Unequal Populations () for ()
In the system with (see Equation (8)), we calculated the droplet states as stationary solutions of Equation (7) by means of the imaginary-time-evolution method with the Neumann’s boundary conditions, under the constraint that the norm is fixed in the first component, , while chemical potential is fixed in the other one, allowing its norm to vary.
Figure 4 displays essential features of weakly asymmetric droplets for and fixed . The symmetric (completely overlapping) solution with is found at . When deviates from this value, profiles of the two components become slightly different, as shown in Figure 4a. The profiles of the droplet solution hardly change for different values of , but Figure 4b demonstrates that, at , develops small-amplitude extended tails, which are absent in . Due to the contribution of the tails, the approach of towards zero leads to the increase of norm , as seen in Figure 4c. Note that the growth of at is opposite to the decay of the QD’s norm in the single-component model at , cf. Equation (15). At , the component undergoes delocalization, with its tails developing a nonzero background at , as seen in the density profile displayed in Figure 4b for , and norm diverging at in Figure 4c.
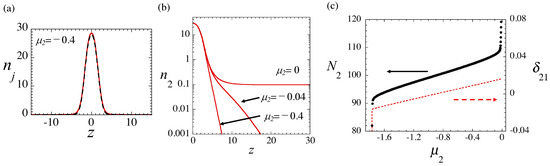
Figure 4.
(a) Stationary weakly asymmetric (with respect to the two components) solutions of Equation (7), obtained for with fixed . Dashed and solid curves display density profiles of the first () and second () components, respectively. (b) The semi-log plot of the density profiles of for , , and 0 at . (c) Dependences of (black dots: the left vertical axis) and asymmetry parameter , defined as per Equation (28) (the red dashed line pertaining to the right vertical axis), on for fixed . The parameters are and . The symmetric point with and corresponds to .
In Figure 4c, we also plot the parameter of the asymmetry between the two components, defined as
It increases almost linearly with , although its absolute value does not exceed . Thus, the droplet tends to keep a nearly symmetric profile, with respect to the two components, in the symmetric system, even if the population imbalance is admitted. In fact, this circumstance makes the analysis self-consistent, as the use of the GP system with the LHY correction implies that the MF intra- and inter-component interactions nearly cancel each other, which is possible only if shapes of the two components are nearly identical.
3.2.2. Asymmetric QDs in the System with ()
Next, we consider the QDs for , setting without loss of generality. Then, the MF energy is minimized for ; the situation with can be considered too, replacing P by .
Following the procedure similar to that employed in Section 3.2.1, we produce QD solutions for , , and several different values of P, varying . In Figure 5a, we plot density profiles for three different values of P. Naturally, the difference of the two components increases with the increase of P. In Figure 5b we display and parameter (see Equation (28)) of the asymmetric QDs for and . All these states have been checked to be stable in time-dependent simulations.
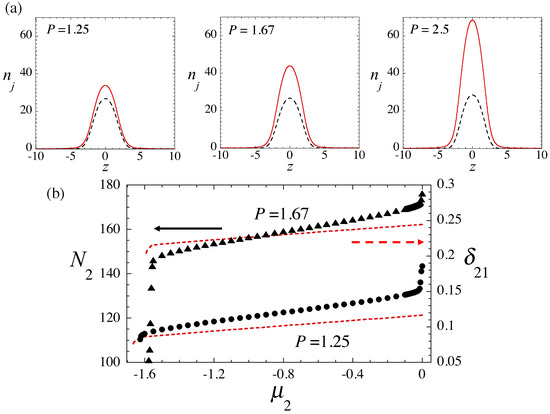
Figure 5.
(a) Stationary solutions of Equation (7), obtained for and . From the left panel to the right one, the parameter in Equation (8) is , , and , and the chemical potential for the second component is , , and , respectively, just below the threshold above which the tails of extend to infinity. Dashed and solid curves represent the density of the first () and second () components. (b) Dependences of (black dots: the left vertical axis) and asymmetry parameter , defined as per Equation (28) (the red dashed line pertaining to the right vertical axis), on for fixed and or .
The density difference at the center of the droplet can be determined by the condition of the existence of the liquid phase in the free space. This condition is obtained by minimizing the grand-potential density [5,14], which leads to the zero-pressure condition,
From this, we obtain relation
which can be rewritten in the scaled form as
For given , we solved Equation (31) to find the respective value of , which is shown in Figure 6 for and several values of P. There are two branches of the solutions, that enclose the negative-pressure region, in which QDs may exist. The maximum value of at the tip of the negative-pressure region corresponds to the density in the droplet’s FT segment. The ascending negative-pressure region for each P nearly follows relation , which is derived by the minimization condition for the dominant first term in Equation (30) It is seen that a larger difference in the profiles of the two components occurs for larger P, as expected. Also, for given , the negative-pressure region becomes wider with respect to for larger P (note that the figure displays a log–log plot).
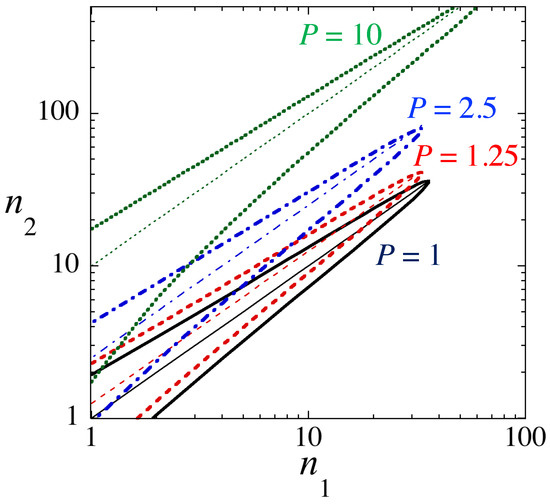
Figure 6.
The negative-pressure region in the plane for and values of asymmetry parameter in Equation (8) (the solid curve), (dashed), (dashed-dotted), and 10 (dotted). Boundaries are determined by the zero-pressure condition, as given by Equation (31). The negative pressure, at which localized states may exist, occurs inside the boundaries. Thin lines represent relation .
As the QDs have a finite norm, it is relevant to characterize the asymmetry in terms of the norm, rather than density. Here, we aim to find a largest value of the norm difference,
where is the total norm, which admits the existence of the QDs. For given , we obtain the upper bound for above which the solution becomes delocalized, and calculate the corresponding critical value of . The results are shown in Figure 7. For the system with , the curve demonstrates an empirical dependence with exponent . Accordingly, the asymmetry tends to vanish asymptotically for very “heavy” droplets, at . As the system becomes slightly asymmetric, with , exponent is significantly reduced for small , and converges to a certain finite value at . Thus, it is again confirmed that values maintain conspicuous asymmetry between the QD’s components. Finally, strongly asymmetric non-FT (Gaussian-shaped [20]) solutions can be obtained in an approximate analytical form for any value of P, as shown in Appendix C.
3.2.3. The MI of the Asymmetric PW States
The MI of two-component asymmetric PWs is a relevant subject too. Such solutions are written as . The substitution of this in Equation (7) yields
Accordingly, in the symmetric system with , densities of the asymmetric PW state are expressed in terms of the chemical potentials as
We introduce the perturbation around the PW states as
with infinitesimal amplitudes and , cf. Equation (24). The substitution of this in Equation (7) and the linearization with respect to and yields the dispersion equation for the perturbation:
where
For and , these results reproduce Equation (25) for the branch. A parameter region in which at least one squared eigenfrequency is negative gives rise to the MI of the two-component state.
3.2.4. The MI for
In Figure 8, we plot the gain spectrum for the asymmetric PWs in the symmetric system with and , in the plane of wavenumber k and density ratio . For the consistency with the single-component situation displayed in Figure 3, we here fix the total density as . For given , the MI occurs at , and the gain attains its maximum at . The largest gain is obtained at equal densities, . Both the k-band of the instability and magnitude of the gain slowly decrease as the deviation of from unity increases. This means that the MI occurs in the PW states with a large density difference, thus giving rise to the formation of solitons with large asymmetry even for equal intra-component MF interaction strengths, (see Equation (8)).
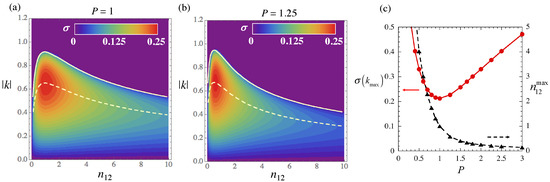
Figure 8.
Color-coded values of the MI gain, , for asymmetric PWs, as calculated from Equation (36) in the plane of wave number and density ratio , are displayed for (a) and (b) with fixed and . The solid and dashed white curves represent the MI boundary and the peak value of the MI gain at , respectively. In (c), we plot (circles) and (triangles) versus P.
In Figure 9 we display typical examples of the numerically simulated development of the MI in the symmetric two-component system with and population imbalance. Figure 9a shows the evolution of central-point values of the density of the first component, , for different values of the density ratio, . Time required for the actual onset of the instability increases with the increase in , as is clearly shown by the density-plot evolution in Figure 9d,e for and Figure 9f,g for . This observation can be understood in terms of the MI gain , as shown in Figure 8c, where at becomes smaller with increasing .
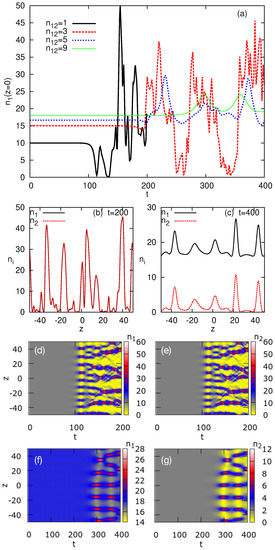
Figure 9.
Numerically simulated development of the MI of asymmetric PW states in the two-component system, with and . The initial PW states are taken with fixed total density, . (a) The evolution of the central density of the first component, , for different density ratios in the two components, . (b,c) Snapshots of density profiles for the cases of (b) at and (c) at . Panels (d,e) and (f,g) are top views of the spatiotemporal evolution of the densities, and , for and , respectively. Simulations were performed in the domain with 2048 grid points, subject to periodic boundary conditions. In this figure and in Figure 10, the scaled time unit corresponds to s in physical units.
Spatial profiles at fixed time, which are plotted in Figure 9b,c for these two cases, show fragmentation of the profiles into sets of localized structures. The decrease in the number of fragments with the increase of is explained by the decrease of , see Figure 8a. For , the results are the same as in the single-component case, as coinciding profiles in the two components of the symmetric system are stable against spontaneous symmetry breaking. On the other hand, when an in-phase two-component localized structure appears, keeping the initial density imbalance. Since one can select an arbitrary ratio of densities of the two components for the initial PW state, a highly asymmetric structure, like the one displayed in Figure 9c, may emerge even for , as a result of the MI-induced nonlinear evolution.
3.2.5. The MI for
Figure 8b represents the MI gain for and a fixed total density, , in the case of slightly different strengths of the intra-component repulsion. The peak value of the MI gain is attained at , below the equal-densities point . This is consistent with the fact that, at , unequal values are suitable to the formation of an asymmetric soliton structure, as seen in Figure 5a. In Figure 8c, we plot the peak MI gain, , along with the respective value of the density ratio, , as a function of P. Value monotonously decreases as a function of P, while the peak gain attains a minimum at .
In Figure 10, we present the development of the MI in the two-component system for and a fixed total density, . Figure 10a displays the evolution of the central-point density of the first component, , for different values of the density ratio, . It shows that time required for the development of the MI increases with the increase in the asymmetry of the density. This is also made evident by the density plots of the temporal evolution of the first component, shown in Figure 10e–g. This result is consistent with Equation (36), which shows a decrease of the MI gain with the increase of the asymmetry even for . Spatial profiles at fixed time, displayed in Figure 10b–d, show fragmentation of the profiles. Figure 10c clearly indicates that, even for , the MI generates asymmetric droplet-like structures similar to Figure 5a, where the complete overlapping of the two densities does not occur.
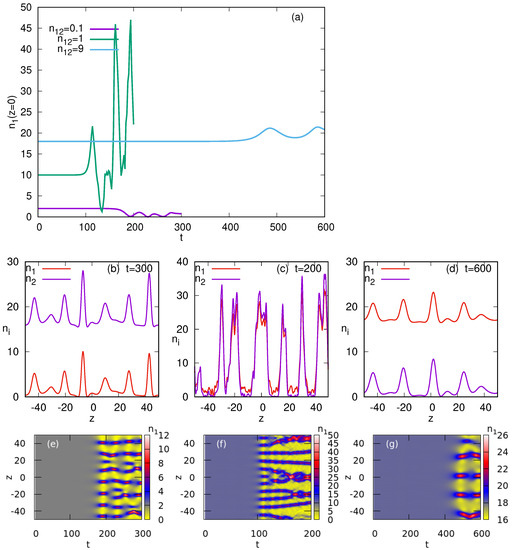
Figure 10.
Numerically simulated development of the modulational instability in the two-component system with and . The initial PW states are taken with a fixed total density, . (a) The evolution of the central density of the first component, , for different density ratios in the two components, . (b–d) Snapshots of density profiles for the cases of (b) at , (c) at and (d) at . Panels (e–g) represent the top view of the spatiotemporal evolution of the densities, , corresponding to (b–d), respectively (the evolution of shows similar patterns). Simulations were performed in the domain with 2048 grid points, subject to periodic boundary conditions.
4. Conclusions
The main purpose of this work is to associate the MI (modulation instability) of plane waves (PWs) to the mechanism of the creation of QDs (quantum droplets) in the system described by the coupled GP (Gross–Pitaevskii) equations including the LHY (Lee–Huang–Yang) terms in the 1D setting. This system is the model of weakly interacting binary Bose gases with approximately balanced interactions between the intra-component self-repulsion and the inter-component attraction. We have investigated, analytically and numerically, the MI of the lower branch of PW states in both symmetric (effectively single-component) and asymmetric (two-component) GP systems, and ensuing formation of a chain of droplet-like states. In particular, numerical solution for QDs which are asymmetric with respect to the two components are obtained, both in the system with equal repulsion strengths but unequal populations in the two components, and in the one with different self-repulsion strengths. The results corroborate that the previously known symmetric states are robust against symmetry-breaking disturbances.
These predictions can be tested experimentally by preparing uniform binary Bose gases with equal or different densities of two components, and suddenly reducing the strength of the effective MF (mean-field) interaction by means of the Feshbach-resonance quench, in order to enhance the relative strength of the LHY terms. In particular, for typical values of physical parameters, an estimate of the characteristic time of the modulation instability growth for typical values of the physical parameters is ∼1 s. This time is much smaller than a typical lifetime of the droplet, which is ≳100 s [21,22,23,27], thus making the observation of the MI feasible. The present analysis being restricted to the 1D setting, effects of the tight transverse confinement and crossover to the 3D configuration [12,44,45] deserves further consideration.
Author Contributions
Conceptualization and investigation, T.M., A.M., K.K., B.A.M., and A.K.; analytics, A.K. and B.A.M.; numerics, T.M., K.K., and A.M.; writing—original draft preparation, T.M.; writing—review and editing, A.M., K.K., B.A.M., and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We appreciate valuable comments received from M. Modugno. T.M. acknowledges support from IBS (Project Code IBS-R024-D1). A.M. acknowledges support from the Ministry of Education, Science, and Technological Development of Republic of Serbia (project III45010) and the COST Action CA 16221. The work of K.K. is partly supported by the Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for Scientific Research (KAKENHI Grant No. 18K03472). B.A.M. appreciates support from the Israel Science Foundation through grant No. 1287/17. A.K. thanks the Indian National Science Academy for the grant of INSA Scientist Position at Physics Department, Savitribai Phule Pune University).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Other Exact Solutions for the Single-Component GP Equation
Here we briefly list other types of exact solutions of the single-component Equation (12), in addition to the FT and PW solutions in Equations (13) and (22) which were considered in detail above (solutions to Equation (12) in the form of dark and anti-dark solitons were reported in [46]).The stability of a majority of these solutions is not addressed here, as it should be a subject for a separate work.
Appendix A.1. δg/g>0
In the case of comparable quadratic self-attraction and cubic repulsion in Equation (12) with , exact spatially-periodic solutions with odd parity can be expressed in terms of the Jacobi’s elliptic sine, whose modulus q is an intrinsic parameter of the family:
where
In the limit of , Equation (A1) goes over into the kink (the same as found in [46]),
with parameters
Appendix A.2. δg/g<0
In the case when the inter-species MF attraction is stronger than the intra-species repulsion, resulting in , spatially-periodic solutions are expressed in terms of even Jacobi’s elliptic functions, and . First, it is
with the elliptic modulus taking all values , other parameters being
The second solution is expressed in terms of the elliptic cosine, with :
Appendix B. Analytical Solutions for Strongly Asymmetric Fundamental and Dipole States
Here we consider analytical solutions of Equation (7) with strong asymmetry, which can be found under small-amplitude conditions, . Then, cubic terms may be neglected in Equation (7), and approximation is used to simplify Equation (7) to the following equations for stationary states in Equation (9):
Although this case is somewhat formal, in terms of the underlying concept of the quantum droplets, which is essentially based on the competition of residual MF and LHY terms, it is interesting to consider it too.
The soliton solution of Equation (A7) is obvious,
where the solution in Equation (13) takes essentially the same form in the limit of . Then, the substitution of Equation (A8) in Equation (A6) makes it tantamount to the linear Schrödinger equation with the Pöschl-Teller potential [50]. The ground-state (GS) solution of Equation (A6) for , with arbitrary amplitude ,
exists with
and eigenvalue
In this case, the QD solutions are quasi-Gaussian objects [20]. Note that, in the symmetric system with , Equations (A10) and (A11) yield and , i.e., the eigenmode and eigenvalue coincide with their counterparts in the soliton solution in Equation (A8), while they are different in the asymmetric system, the GS level lying below or above the chemical potential of soliton in Equation (A8) at and , respectively.
In Figure A1 we compare a typical asymptotic solution given by Equations (A8) and (A9) with a numerically obtained GS solution for the same values of the parameters. It is seen that the analytical and numerical results match well.
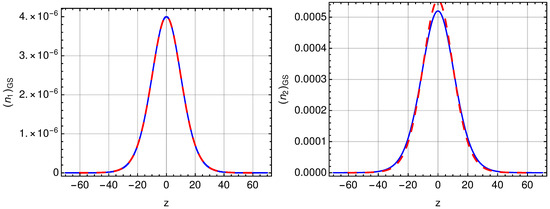
Figure A1.
Comparison of the asymptotic analytical solutions, given by Equations (A8) and (A9), with their numerically obtained counterparts. The density of the first () and second () components are displayed in top and bottom panels, respectively. Solid blue lines represent the numerical results, while dashed red lines represent the analytical solution. Here, parameters are , , and .
Further, it is also possible to produce the first excited state of Equation (A6) in the form of the dipole (antisymmetric) mode with an arbitrary amplitude:
where is the same as in Equation (A10), the respective eigenvalue being
which is obviously higher than its GS counterpart in Equation (A11) (at , Equation (A13) yields , and falls below for ). Unlike the GS, the dipole mode exists not at all values of P, but only for . Exactly at , one has , and the dipole mode in Equation (A12), with , is a delocalized one, .
Linear Schrödinger Equation (A6) with the Pöschl-Teller potential may give rise to higher bound states of integer order as well, with eigenvalues
where and 1 correspond to Equations (A11) and (A13), respectively, the -th spate existing at . The number of such solutions is always finite.
Unlike solutions considered in Appendix A and Appendix C, the stability of the solutions given by Equations (A8)–(A14) is obvious.
Appendix C. Other Exact Solutions in the Case of N1 ≪ N2
Here we provide periodic solutions to the semi-linear system of Equations (A6) and (A7) in terms of Jacobi elliptic functions. In the limit of , they go over into solutions given in the main text, in the form of Equations (A8), (A9), and (A12).
Appendix C.1. Solution of Equation (A7)
Appendix C.2. Solutions of Equation (A6)
We now show that, with given by Equation (A15), linear Equation (A6) has several particular solutions depending on the value of P.
Solutions For
Appendix C.2.1. Solution I
Appendix C.2.2. Solution II
Appendix C.2.3. Solution III
Solutions for .
Appendix C.2.4. Solution IV
Appendix C.2.5. Solution V
Appendix C.2.6. Solution VI
Appendix C.2.7. Solution VII
References
- Pitaevskii, L.; Stringari, S. Bose–Einstein Condensation and Superfluidity; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Pethick, C.; Smith, H. Bose–Einstein Condensation in dilute Gases; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Luo, Z.; Lio, Y.; Chen, Z.; Huang, C.; Fu, S.; Tan, H.; Malomed, B.A. Two-dimensional solitons and quantum droplets supported by competing self-and cross-interactions in spin-orbit-coupled condensates. New J. Phys. 2017, 19, 113043. [Google Scholar] [CrossRef]
- Cappellaro, A.; Macrí, T.; Bertacco, G.F.; Salasnich, L. Equation of state and self-bound droplet in Rabi-coupled Bose mixtures. Sci. Rep. 2017, 7, 13358. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, N.B.; Bruun, G.M.; Arlt, J.J. Dilute fluid governed by quantum fluctuations. Phys. Rev. Lett. 2018, 121, 173403. [Google Scholar] [CrossRef] [PubMed]
- Cikojević, V.; Dželalija, K.; Stipanović, P.; Markić, L.V.; Boronat, J. Ultradilute quantum liquid drops. Phys. Rev. B 2018, 97, 140502(R). [Google Scholar]
- Cappellaro, A.; Macrí, T.; Salasnich, L. Collective modes across the soliton-droplet crossover in binary Bose mixtures. Phys. Rev. A 2018, 97, 053623. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Tarruell, L.; Torner, L. Three-dimensional droplets of swirling superfluids. Phys. Rev. 2018, 98, 013612. [Google Scholar] [CrossRef]
- Zin, P.; Pylak, M.; Wasak, T.; Gajda, M.; Idziaszek, Z. Quantum Bose-Bose droplets at a dimensional crossover. Phys. Rev. A 2018, 98, 051603(R). [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Luo, Z.; Huang, C.; Tan, H.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Ancilotto, F.; Barranco, M.; Guilleumas, M.; Pi, M. Self-bound ultradilute Bose mixtures within local density approximation. Phys. Rev. A 2018, 98, 053623. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, H.-F.; Zhong, R.-X.; Zhang, X.-L.; Qin, X.-Z.; Huang, C.; Li, Y.-Y.; Malomed, B.A. Symmetry breaking of quantum droplets in a dual-core trap. Phys. Rev. A 2019, 99, 053602. [Google Scholar] [CrossRef]
- Chiquillo, E. Low-dimensional self-bound quantum Rabi-coupled bosonic droplets. Phys. Rev. A 2019, 99, 051601(R). [Google Scholar] [CrossRef]
- Tononi, A.; Wang, Y.; Salasnich, L. Quantum solitons in spin-orbit-coupled Bose-Bose mixtures. Phys. Rev. A 2019, 99, 063618. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Metastability of Quantum Droplet Clusters. Phys. Rev. Lett. 2019, 122, 193902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, X.; Zheng, Y.; Chen, Z.; Liu, B.; Huang, C.; Malomed, B.A.; Li, Y. Semidiscrete quantum droplets and vortices. Phys. Rev. Lett. 2019, 123, 133901. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Dynamics of one-dimensional quantum droplets. Phys. Rev. A 2018, 98, 013631. [Google Scholar] [CrossRef]
- Cabrera, C.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose–Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright Soliton to Quantum Droplet Transition in a Mixture of Bose–Einstein Condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-Bound Quantum Droplets of Atomic Mixtures in Free Space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef] [PubMed]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemi, A.; Recati, A.; Fattori, M. Collisions of self-bound quantum droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.; Astrakharchik, G.; Malomed, B.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I. Ultradilute Quantum Droplets. Phys. Today 2019, 72, 46–52. [Google Scholar] [CrossRef]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Research 2019, 1, 033155. [Google Scholar] [CrossRef]
- Kadau, H.; Schmitt, M.; Wentzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosenzweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Quantum filaments in dipolar Bose–Einstein condensates. Phys. Rev. A 2016, 93, 061603(R). [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Ground-state properties and elementary excitations of quantum droplets in dipolar Bose–Einstein condensates. Phys. Rev. A 2016, 94, 043618. [Google Scholar] [CrossRef]
- Baillie, D.; Blakie, P.B. Droplet Crystal Ground States of a Dipolar Bose Gas. Phys. Rev. Lett. 2018, 121, 195301. [Google Scholar] [CrossRef] [PubMed]
- Ferrier-Barbut, I.; Wenzel, M.; Schmitt, M.; Böttcher, F.; Pfau, T. Onset of a modulational instability in trapped dipolar Bose–Einstein condensates. Phys. Rev. A 2018, 97, 011604(R). [Google Scholar] [CrossRef]
- Cidrim, A.; Santos, F.E.A.d.; Henn, E.A.L.; Macrí, T. Vortices in self-bound dipolar droplets. Phys. Rev. A 2018, 98, 023618. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Novikov, A.N.; Bagnato, V.S. Formation of granular structures in trapped Bose–Einstein condensates under oscillatory excitations. Laser Phys. Lett. 2014, 11, 095501. [Google Scholar] [CrossRef]
- Bulgac, A. Dilute Quantum Droplets. Phys. Rev. Lett. 2002, 89, 050402. [Google Scholar] [CrossRef]
- Baillie, D.; Wilson, R.M.; Blakie, P.B. Collective Excitations of Self-Bound Droplets of a Dipolar Quantum Fluid. Phys. Rev. Lett. 2017, 119, 255302. [Google Scholar] [CrossRef]
- Nguyen, J.H.V.; Luo, D.; Hulet, R.G. Formation of matter-wave soliton trains by modulational instability. Science 2018, 356, 422–426. [Google Scholar] [CrossRef]
- Everitt, P.J.; Sooriyabandara, M.A.; Guasoni, M.; Wigley, P.B.; Wei, C.H.; McDonald, G.D.; Hardman, K.S.; Manju, P.; Close, J.D.; Kuhn, C.C.N.; et al. Observation of a modulational instability in Bose–Einstein condensates. Phys. Rev. A 2017, 96, 041601. [Google Scholar] [CrossRef]
- Sanz, J.; Frölian, A.; Chisholm, C.S.; Cabrera, C.R.; Tarruell, L. Interaction control and bright solitons in coherently-coupled Bose–Einstein condensates. arXiv 2019, arXiv:1912.06041. [Google Scholar]
- Bhat, I.A.; Mithun, T.; Malomed, B.A.; Porsezian, K. Modulational instability in binary spin-orbit-coupled Bose–Einstein condensates. Phys. Rev. A 2015, 92, 063606. [Google Scholar] [CrossRef]
- Singh, D.; Parit, M.K.; Raju, T.S.; Panigrahi, P.K. Modulational instability in one-dimensional quantum droplets. Res. Gate Prepr. 2019. [Google Scholar] [CrossRef]
- Ilg, T.; Kumlin, J.; Santos, L.; Petrov, D.S.; Büchler, H.P. Dimensional crossover for the beyond-mean-field correction in Bose gases. Phys. Rev. A 2018, 98, 051604. [Google Scholar] [CrossRef]
- Edler, D.; Mishra, C.; Wächtler, F.; Nath, R.; Sinha, S.; Santos, L. Quantum Fluctuations in Quasi-One-Dimensional Dipolar Bose–Einstein Condensates. Phys. Rev. Lett. 2017, 119, 050403. [Google Scholar] [CrossRef]
- Triki, H.; Biswas, A.; Moshokoa, S.P.; Belić, M. Optical solitons and conservation laws with quadratic-cubic nonlinearity. Optik 2017, 128, 63–70. [Google Scholar] [CrossRef]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Di Carli, A.; Colquhoun, C.D.; Henderson, G.; Flannigan, S.; Oppo, G.-L.; Daley, A.J.; Kuhr, S.; Haller, E. Excitation modes of bright matter-wave solitons. Phys. Rev. Lett. 2019, 123, 123602. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Panova, E.Y. Stability and evolution of the quiescent and travelling solitonic bubbles. Phys. D Nonlinear Phenom. 1993, 69, 114–134. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Nauka Publishers: Moscow, Russia, 1989. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).