Abstract
Aviation bearing assembled detection is the final barrier to quality and safety. Therefore, an accurate detection method of aviation bearing that is based on local characteristics is designed to solve the detection problem of mis-assembly and miss-assembly of balls in aviation bearing assembled. When considering the spatial limitation of aviation bearing assembled image acquisition, the dynamic distribution of balls and the interference of lubricating grease on the surface, a dynamic local ball segmentation model that is based on U-Net network with symmetrical structure is designed to achieve the accurate segmentation of the local ball region of aviation bearing. Subsequently, an incomplete circle fitting algorithm is designed based on the segmented local ball image and Hough transform principle. These two algorithms make the measurement error of aviation bearing ball size less than 100 μm. Using bearings validates the algorithm. The results show that the accuracy of dynamic local ball segmentation model that is based on U-Net network with symmetrical structure is over 99%. At the same time, on the basis of accurate segmentation in aviation bearing local ball, the designed Hough circle algorithm is used for circle detection. The experimental results show that the false detection rate of mis-assembly and miss-assembly of balls is less than 3%. Further, the goal of zero-missed detection of mis-assembly and miss-assembly of balls in aviation bearing is achieved. The accurate segmentation of aviation bearing local ball and the effective identification of mis-assembly and miss-assembly of balls are realized. This method can provide a theory for the improvement of mis-assembly and miss-assembly of balls detection in aviation bearing. Furthermore, it has high application value.
1. Introduction
High precision aviation bearing, as an important part of aircraft, is easy to lead to mis-assembly and miss-assembly of balls in the process of automatic production equipment because of the large number of balls and the small size difference. Therefore, it is necessary to accurately detect the mis-assembly and miss-assembly of balls accurately in order to achieve strict quality control of aviation bearing after the assembly of bearing.
After the assembly of high-precision aviation bearings, the bearing cage occludes the balls. Additionally, the local image of bearing ball can only be obtained from the micro-level dynamic slit. Therefore, the segmentation of bearing balls is of great significance in the detection of mis-assembly and miss-assembly of balls in aviation bearings. Bearing is one of the core components of modern mechanical equipment. Additionally, the corresponding research on bearing quality problems has been carried out. In Ref. [1], Wang et al. proposed a non-destructive testing method for the surface defect of bearing ball to be assembled. The target area was segmented by the circular outer rectangular redrawing algorithm. Following this, the surface defect of ball was detected by the method of subtration image. The defect recognition rate reached more than 97%. However, it is impossible to segment the local dynamic balls without obvious features. In Ref. [2], Chen et al. used the thresholding method based on Otsu’s method to separate the character area and non-character area of bearing dust cover. Subsequently, the template matching method detects the defect of dust cover. The defect recognition rate is over 96%. The defect detection on the surface of dust cover can be automatically achieved. In Ref. [3], firstly, Hao Yong used circular Hough transform to locate the bearing. Afterwards, the image of deep groove ball bearing is normalized and expanded into rectangle by Cartesian polar coordinate expansion method. Finally, the mistaken ball is detected and identified by the thresholding segmentation method. The recognition rate is over 93.3%. However, the two methods mentioned above are not effective for ball segmentation, which is not obviously different from the gray values of other parts of the bearing. The above image segmentation methods achieve a high recognition rate for the segmentation and extraction of general bearing target features. However, the methods that are mentioned above are not ideal for the image segmentation of bearing local balls with small targets and inconspicuous features.
In Refs. [4,5], CNN (Convolutional Neural Network) has strong ability of feature learning and feature expression. CNN can further express high-level abstract features by learning low-level features, which makes CNN achieve remarkable results in image segmentation. CNN can learn target features from collected data as compared with traditional methods. The segmentation problem is automatically solved according to the learning results. In Refs. [6,7], various target segmentation algorithms that are based on CNN have been proposed. In 2015, Rommeber et al. in [8] proposed a U-Net convolution neural network to segment the biomedical cells. The kind of CNN uses multi-scale feature information to improve the accuracy of pixel location and image segmentation. In Refs. [9,10], Falk and Daniel verified that the U-Net neural network can be used for cell segmentation, counting, and morphological detection accurately in a large number of images of arbitrary quality. In Refs. [11], based on the structure of U-Net convolution neural network, Sevastopolsky repeatedly added visual geometry group (VGG) classification convolution network to the structure of contraction path to reduce the amount of pooling and the loss of image information. This improvement shortens the prediction time of optic disc cup segmentation in glaucoma detection. Therefore, the U-Net convolution neural network is used to accurately segment the dynamic local ball of aviation bearing. U-Net uses symmetrical U-shaped network and skip connection structure to fuse deep low-resolution and shallow high-resolution information, so as to improve the precise location of the target area. When compared with traditional bearing detection methods, target features can be learned from a small amount of data to solve the problem of ball segmentation for aviation bearings with small targets and obscure features. The Batch Normalization (BN) layer is used to optimize the U-Net network, which solves the problem that the time and space complexity increases with the deepening of the layers of the convolutional neural network. It further improves the expressive ability and segmentation accuracy of the network.
In summary, this paper comprehensively analyses the problem of mis-assembly and the miss-assembly of balls in aviation bearing assembled by using common methods of bearing detection and combining with the successful experience of U-Net convolution neural network in biomedical detection. An accurate detection method of aviation bearing that is based on local characteristicsis designed. This method uses the pre-trained U-Net network model to automatically segment the dynamic local ball of aviation bearing. This method improves the segmentation accuracy. Subsequently, Hough circle detection is used to detect the circle of the segmented ball, so as to achieve the accurate detection of the mis-assembly and miss-assembly of bearing balls.
2. Overall Scheme Design and Principle Analysis
2.1. Overall Scheme Design of Ball Detection in Aviation Bearing
This paper is about the detection of mis-assembly and miss-assembly of balls of high precision aviation bearing assembled. The bearing image is shown in Figure 1, below. The local information of the bearing ball can only be obtained through the local space of micro-level because the bearing balls are occluded by cages. Moreover, the difference between adjacent grades of ball is 1/61 inches, which requires the high segmentation accuracy of bearing ball. Therefore, an accurate detection algorithm of bearing ball based on the combination of U-Net network and Hough detection is designed to solve the problem of small target and unclear characteristics of balls in aviation bearing on the basis of the imaging characteristics of aviation bearing ball shown in Figure 1 and the requirements of ball detection accuracy.
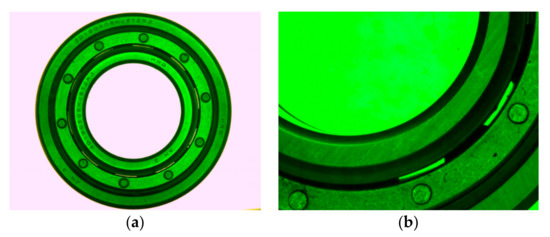
Figure 1.
Aviation bearing image: (a) Aviation bearing complete image; (b) Aviation bearing part image.
Figure 2 shows the overall structure. It mainly consists of two parts: image segmentation and recognition.
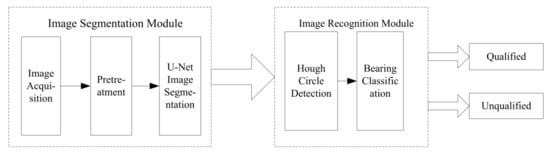
Figure 2.
Overall structure block diagram.
In the image segmentation part, the U-Net convolution neural network is used to segment the image. Subsequently, the batch normalization (BN) layer is added to optimize the bearing ball segmentation model. In the image recognition part, based on the traditional Hough circle detection, the detection range of bearing ball image is limited by the known bearing size and the edge gradient. Afterwards, this optimization not only reduces the cumulative times of detection, but also improves the adaptability and accuracy of detection.
2.2. U-Net Network
In 2015, the U-Net Convolutional Neural Network is a full-convolution network (FCN) model that was proposed by Rommeber in the ISBI Cell Tracking Challenge, which achieves accurate segmentation of cell images. The network structure is similar to the structure of FCN. In the network structure, there are only convolution layer and pooling layer. There is no full connection layer [12,13]. The difference of the two network structures is that up-sampling and down-sampling in U-Net network adopt the same level of convolution operation. The skip connection structure is used to link up the up-sampling layers and down-sampling layers to obtain multi-scale feature information, which further improves the accuracy of pixel location and segmentation [14,15]. The U-Net network adopts left-right symmetry structure. Contraction path (left) is used to obtain context information. Additionally, extension path (right) is used to locate accurately. In the contraction path, feature extraction is mainly carried out by down-sampling. The resolution of each down-sampling image is reduced to half of the original one. At the same time, the number of sampling channels will be doubled in order to retain more image feature information. In the up-sampling of extension path, the U-Net network restores image and spatial dimension by deconvolution. At the same time, the number of sampling channels will be reduced by half [16,17]. In order to further improve the accuracy of positioning, the skip connection structure is used to fuse the up-sampling results and the shallow high-resolution information of the contraction path to obtain the accurate location of the target area [18].
The original U-Net network is used to segment the aviation bearing ball. Figure 3 shows the segmentation results. From the segmentation results, it can be seen that the bearing balls are obviously segmented, which proves that this method is feasible.
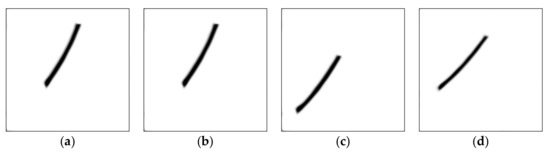
Figure 3.
Results of original U-Net network segmentation: (a) First segmentation result; (b) Second segmentation result; (c) Third segmentation result; (d) Forth segmentation result.
2.3. Hough Transform Principle
Hough transform is a method for shape detection of region boundary, which is often used for line, circle, and ellipse detection. Hough also has a good detection effect to incomplete circles [19]. The principle of circle detection that is based on Hough transform [20] is as follows. The circle with (a,b) as the center and r as the radius in the X-Y plane is transformed into a three-dimensional space with (a,b,r) as the parameter. The following equation is obtained:
where, the circle at any point in the image X-Y plane space corresponds to a three-dimensional cone in the parameter (a,b,r) space. The points on the same circle in the image space are mapped to all the cones in the parameter space, where the intersection points correspond to the center and radius of the circle in the image space. As shown in Figure 4.
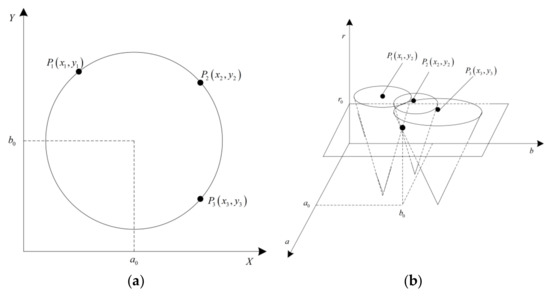
Figure 4.
Relationship between a binary image plan and the Hough space: (a) The circle in the image X-Y plane space; (b) Representation of parametric space.
The parameters of a circle can be obtained by detecting this point. The specific solution processes is as follows:
- (1)
- An accumulator array with parameter is obtained by quantifying the three-dimensional parameter space appropriately.
- (2)
- After edge extraction, all points whose distance from each pixel on the edge is r are calculated.
- (3)
- Let r change from 0 to 256, and then repeat the above steps.
- (4)
- The values of all accumulators of a three-dimensional array are checked. The coordinates of their peaks correspond to the center of the circle.
3. Segmentation Method Based on U-Net Network and Hough Circle Detection Algorithms
Although the original U-Net network can achieve the segmentation of bearing ball, it can be seen from Figure 3 that not only the boundary of the segmentation is not clear, but there are also problems of over-segmentation and under-segmentation of the boundary. The segmentation accuracy is not high. The reasons are as follows: (1) The gray scale of the boundary is not uniform because of the existence of industrial lubricating oil on the bearing surface, which leads to unclear boundaries. (2) U-Net network does not satisfy the assumption of independent and identical distribution for convolutional neural networks [21]. In the actual training process, the output of the upper layer is the input of the next layer. As the weight of each layer is updated, the output of each layer is also updated, so the independent and identical distribution relationship of each layer cannot be guaranteed. As a result, the difference of network activation value distribution will become larger and larger with the deepening of the network, which makes the network model difficult to train. Hough circle detection is used to find multiple circles in an image, but only one circle is needed to find in this paper. Additionally, from the above Hough circle detection process, the calculation is large and cumbersome. Hence, there are many unnecessary calculations for the detection of aviation bearing ball [22].
3.1. Improved U-Net Network
3.1.1. BN Layer
The BN layer is a network layer with parameters and learnable. Its practical function is to standardize the output of the former layer, that is, the input of the next layer [23]. The BN layer is set before the activation function. The input of each layer of U-Net network is normalized to optimize the network. Suppose that a layer of U-Net network has m-dimensional input , where is the input value of the activation function(that is referred to as the activation value behind).The first step of BN layer: The activation values are regularized to a Gaussian distribution with an average of 0 and a variance of 1 in order to sparse the parameters. The formula is expressed, as follows:
where, is the average of m activation values. is the standard deviation calculated from the average and m activation values. The second step of BN layer: the normalized activation value is fine-tuned to achieve re-parameterization by introducing the learnable parameters . The formula of activation value after introducing parameter is as follows:
After reconstructing parameters through BN layer, the reliability and predictability of gradient descent and the expressive ability of the network are improved. The specific advantages include:
- (1)
- The sensitivity to parameter selection is reduced. The network can choose a larger learning rate to improve the training speed.
- (2)
- The loss process is smoother to prevent the disappearance of gradient and gradient explosion.
- (3)
- Reduce the need for dropout while resolving the over-fitting problem.
- (4)
- The noise mixed in the training process can not only regularize the model parameters, but also improve the generalization ability of the network.
3.1.2. Network Structure
As shown in Figure 5, the U-Net network structure for ball segmentation of aviation bearing consists of 10 layers. Each layer contains two repeated convolutions, which are used to linearly map the image to extract image features. The U-Net network consists of a contraction path and expansion path. In the contraction path, the convolution of is used for pooling to obtain contextual information. In the extended path, the deconvolution of is used for up-sampling to recover image information. The output image can be restored to the original image size when the network extends to the end. However, the time and space complexity of the whole model training is increased with the deepening of network layers. Therefore, each convolution is followed by a BN layer, which is used to normalize the output data of convolution in batches (that is to say, the input of the next convolution is normalized in batches). The non-linear activation function ReLU [24] is used to activate the normalized batch values. Subsequently, the network expression ability is improved. At the end of the network, the U-Net network uses a convolution layer to reduce the number of feature maps to 1. The sigmoid function is used to activate, so that the value of each pixel in the image corresponds to 0–1. Finally, the graph is taken as the final output probability graph of the network, that is, the probability of whether each pixel belongs to the bearing ball.
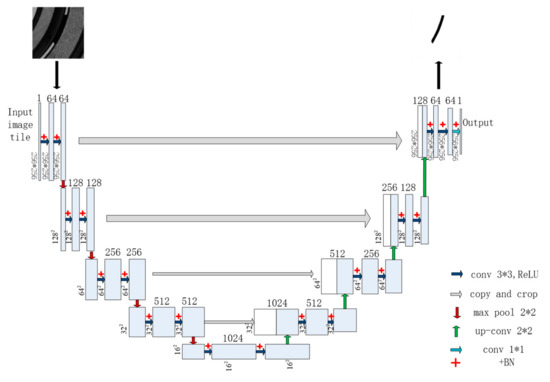
Figure 5.
U-Net network structure diagram.
3.2. Hough Circle Detection of Aviation Bearing Ball Based on Segmentation
In order to improve the efficiency of Hough circle detection, some restrictions that are based on the principle of Hough circle detection are added to the process of Hough circle detection to reduce the accounts of calculation and improve the speed. The difference of radius is only 1/64 inches in case of assembling wrongly because the radius of bearing ball to be tested is known, so the range of radius change is limited to R. For each point on the edge, times need to be calculated when and change, respectively. Assuming that each such calculation takes t seconds, an edge point takes seconds. When R changes from 0 to 256, the time that is consumed for each edge point is:
For the image in this paper, the order of magnitude is reduced from 106 to 104, but the amount of calculation is also very large. Therefore, the gradient information of edge points can be used to change r along the normal direction of the edge point , which not only reduces the invalid search of Hough circle detection, but also improves the accuracy of circle detection. The formula for calculating the center of a circle is as follows:
where, the formula for calculating a is . and are gradients in two directions, respectively. In this way, when R changes from 0 to 256, the time that is consumed at each edge point of Hough transform is , which further reduces the time consumed by Hough transform.
4. Experiments and Results Analysis
4.1. Sample Creation
It is difficult to obtain a clear image due to the limitation of shooting space and the interference of lubricating grease on the surface of the aviation bearing assembled. Therefore, the device shown in Figure 6 below is designed as the acquisition system. The coaxial light source is used as the shooting light source. The coaxial light source is composed of red, green, and blue light-emitting diode (LED) lamps. Additionally, the light rays are vertically illuminated on the bearings. The coaxial light source can solve the problem of reflecting light on bearing metal surface and lubricating oil. Five million charge coupled device (CCD) camera captures images. The strategy of shooting a ball is adopted to obtain high-definition local bearing image because of the limitation of the shot space of bearing ball image. Bearings of type 3D180506KJ8T2R3 were taken photographs. The inner diameter of bearing is 61.78 mm. The outer diameter of bearing is 29.92 mm. The ball diameter of bearing is 9.79 mm. The photographed image is shown in Figure 7a, below.

Figure 6.
Acquisition system diagram: (a) Front view; (b) Gray diagram.

Figure 7.
Bearing diagram: (a) Original diagram of acquisition; (b) Gray diagram.
The image is grayed in order to reduce the time of image processing and U-Net network training and recognition. However, important information of the image must be preserved to ensure the subsequent image segmentation, recognition, and other operations. From Figure 7a, not only the light and color of the bearing picture are uniform, but also the color of the bearing and the background are very different. The gray level is enough to express the feature information. Therefore, the habitual gray level that is acceptable to the human eye is selected for graying. The graying formula is as follows:
Figure 7b is a gray image of the corresponding image of Figure 7a. From Figure 7b, only the information that is near the ball is useful. Therefore, region of interest (ROI) needs to be extracted from 7b. The position of the ball area in the original image is relatively fixed. Therefore, a fixed size region is extracted from each original image sample as the region of interest, which completely contains the position of the bearing ball.
Opencv3.0, which is configured under Visual Studio 2013, is used to make data sets for Figure 8a,b. The bearing ball area is manually segmented by the least square method to construct the training U-Net network model samples that are based on the known bearing inner diameter, outer diameter, and ball diameter. There are 500 pictures of aviation bearings, of which 60% are trained and 40% are tested. Figure 8 is a sample of the aviation bearing data set.

Figure 8.
Training sample diagram: (a) Sample diagram; (b) Segmented diagram; (c) Sample diagram; (d) Segmented diagram.
4.2. Comparison of Ball Segmentation Algorithms for Aviation Bearing Based on Improved U-Net Network
Loss function and accuracy are used to evaluate the improved U-Net algorithm and the original U-Net network.
The blue curve in Figure 9 above is the loss function and accuracy change curve of training set under the original U-Net network. The red curve is the loss function and accuracy change curve of training set of U-Net network with a BN layer (hereinafter referred to as the improved U-Net network).As can be seen from Figure 9a, the loss curves of the two networks rapidly dropped from 0.9 to less than 0.3 in the first 20 iteration cycles. In the process of network model training, the improved U-Net network not only has a smooth loss curve, but it also tends to be stable after 200 iteration cycles. The loss process of the original U-Net network fluctuates greatly. The loss curve not only tends to be stable after 300 iteration cycles, but it also tends to increase after 350 iteration cycles. The network shows over-fitting phenomenon. Similarly, as shown in Figure 9b, the accuracy curves of the two networks are over 80% after several iteration cycles. After 200 iterations, the accuracy of the improved U-Net network is over 99%, while the accuracy of the original U-Net network is 92%. In general, after adding the BN layer, the loss and accuracy curves of the network are not only smoother, but the convergence speed is also faster in the training process. The performance of the network as a whole has been greatly improved. Gradient descent is more predictable, which can prevent the network from falling into local minimum. At the same time, a larger learning rate can be chosen to improve the training speed and generalization ability. The network segmentation performance is better.
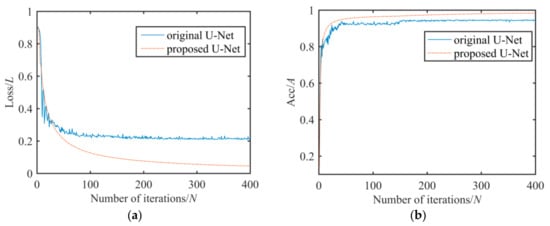
Figure 9.
Training curve: (a) Loss curve; (b) Accuracy curve.
4.3. Experimental Result
In this experiment, different types of aviation bearing are tested. Figure 10 is the result of ball segmentation that is based on U-Net network. Table 1 is the result of Hough circle detection after ball segmentation of aviation bearing.

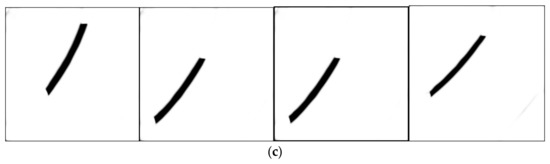
Figure 10.
Experimental result: (a) test diagram; (b) original U-Net network segmentation result diagram; (c) improved algorithm segmentation result diagram.

Table 1.
Table of Hough test results after two kinds of network segmentation.
As shown in Figure 10b, above, this is the result of the original U-Net network partition. The result shows that the original U-Net network is not ideal for boundary detection. This result is not only the objective reason of uneven gray scale and unclear boundary that is caused by industrial oil on the bearing surface, but also the subjective reason that the CNN does not satisfy the assumption of independent and identical distribution, which makes the network model difficult to train with the increase of network layers. It leads to blurred boundary and inaccurate results of original U-Net network segmentation. At the same time, the background near the ball boundary is taken as the target area, or the target area with a close gray value to the background is taken as the background. The phenomenon of over-segmentation and under-segmentation appears in the network. After adding the BN layer, batch normalization is carried out for each layer of U-Net network to make each layer as independent as possible. At the same time, new learning parameters are added to re-parameterize the network further improve the learning and expression ability of the network. As shown in Figure 10c above, the improved U-Net network has a higher degree of discrimination between background and bearing ball target area, and more accurate edge segmentation. The accuracy of bearing ball segmentation is further improved.
From Table 1, the radius error of Hough circle detection after segmentation of the original U-Net network model is concentrated in (30–80) microns. The mean error of measurement is 49.87 micron. The standard variance is 24.22 microns. Each radius error of the improved U-Net network is within 100 microns. The measurement errors are concentrated in (0–30) microns. The average measurement error is 29.48 microns. The standard variance is 20.50 microns. Therefore, the reliability and predictability of gradient descent are improved after using the BN layer to improve the U-Net network. Moreover, the segmentation accuracy is higher and more stable. It is necessary to ensure zero leakage detection rate of aviation bearing because the detection of aviation bearing assembled is the last barrier of quality and safety assurance. Therefore, when the detection radius error is greater than 80 microns after Hough circle detection, the bearing balls are determined to be unqualified. Under this setting, on the basis of accurate segmentation of the local ball area of aviation bearing by improved U-Net network and Hough circle detection, the false detection rate is reduced from 10% of the original U-Net network segmentation algorithm to less than 3%, which greatly improves the detection accuracy.
5. Conclusions
An accurate detection method of aviation bearing ball that is based on local characteristics is designed in order to solve the problem of mis-assembly and miss-assembly of balls in aviation bearing assembled, including a dynamic local ball segmentation model that is based on U-Net network and a Hough circle detection algorithm. The dynamic local ball segmentation model based on U-Net network with BN layer can achieve a good segmentation effect for local and dynamic ball. It not only overcomes the disadvantageous influence of blurred edge and uneven gray level of balls, but it also avoids the problems of over-segmentation, under-segmentation, and over-fitting. The training speed and generalization ability of the network are improved. At same time, the sensitivity of the network to parameter selection is weakened. The accuracy of segmentation is over 99%. Hough circle detection algorithm that is based on radius size and radius edge gradient information greatly improves the detection speed and accuracy. Accurate detection method of aviation bearing based on local characteristics makes the error detection rate of mis-assembly and miss-assembly of balls less than 3%. Thus, the zero-miss detection target for mistaken and leaky ball of aviation bearing can be achieved. Finally, the accurate segmentation of local ball in aviation bearing and the effective identification of mis-assembly and miss-assembly of balls are achieved. This method is suitable for the detection of known dimensions of aviation bearings, but not for the unknown dimensions of aviation bearings. How to realize the detection of unknown dimension aviation bearings is the focus of future research.
Author Contributions
P.X. and Y.J. conceived and designed the experiments; Y.J. and H.H. performed the experiments; Y.J. and H.W. analyzed the data; Y.J. wrote the paper.
Funding
This work is supported by the Natural Science Foundation of Heilongjiang Province (No. F201310), and Science and Technology Innovation Talents Project of Harbin (No:2016RAQXJ037).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.W.; Qu, G.T.; Liu, X.L.; Fu, P.Q.; Li, B. Image Subtraction Detection Algorithm for Surface Defect of Steel Ball. J. Comput. Aided Des. Comput. Graph. 2016, 28, 1699–1704. [Google Scholar]
- Chen, W.D.; Bai, R.L.; Ji, F.; Wen, Z.S. Bearing Shield Surface Defect Detection Based on Machine Vision. Comput. Eng.Appl. 2014, 50, 250–254. [Google Scholar]
- Hao, Y.; Zhao, X.; Wen, Q.; Shang, Q.; Chen, B. Roller Missing Detection in Deep Groove Ball Bearings Based on Machine Vision. Laser Optoelectron. Prog. 2018, 55, 380–385. [Google Scholar]
- Chen, J.; Liu, Q.; Gao, L. Visual Tea Leaf Disease Recognition Using a Convolutional Neural Network Model. Symmetry 2019, 11, 343. [Google Scholar] [CrossRef]
- Ju, J.Y.; Luo, Z.B.; Wang, Z.B.; He, M.; Chang, Z.; Hui, B. An Improved YOLO V3 and Its Application in Small Target Detection. Acta Opt. Sin. 2019, 39, 1–13. [Google Scholar]
- Hua, X.; Wang, X.Q.; Wang, D.; Ma, Z.Y.; Shao, F.M. Multi-Objective Detection of Traffic Based on Improved SSD. Acta Opt. Sin. 2018, 38, 221–231. [Google Scholar]
- Wang, W.X.; Fu, Y.T.; Dong, F.; Li, F. Infrared ship target detection method based on deep convolution neural network. Acta Opt. Sin. 2018, 38, 160–166. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Daniel, M.C.; Atzrodt, L.; Bucher, F.; Wacker, K.; Böhringer, S.; Reinhard, T.; Böhringer, D. Automated segmentation of the corneal endothelium in a large set of ‘real-world’ specular microscopy images using the U-Net architecture. Sci. Rep. 2019, 1, 4752–4758. [Google Scholar] [CrossRef] [PubMed]
- Falk, T.; Mai, D.; Bensch, R.; Çiçek, Ö.; Abdulkadir, A.; Marrakchi, Y.; Böhm, A.; Deubner, J.; Jäckel, Z.; Seiwald, K.; et al. U-Net:deep learning for cell counting, detection, and morphometry. Nat. Methods 2019, 16, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Sevastopolsky, A. Optic disc and cup segmentation methods for glaucoma detection with modification of U-Net convolutional neural network. Pattern Recognit. Image Anal. 2017, 27, 618–624. [Google Scholar] [CrossRef]
- Lu, J.; Xu, Y.; Chen, M.; Luo, Y. A Coarse-to-Fine Fully Convolutional Neural Network for Fundus Vessel Segmentation. Symmetry 2018, 10, 607. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, H.; Sun, Q. A Multiorgan Segmentation Model for CT Volumes via Full Convolution-Deconvolution Network. BioMed Res. Int. 2017, 2017, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Thiemann, F.; Sester, M. Learning Cartographic Building Generalization with Deep Convolutional Neural Networks. ISPRS Int. J. Geo-Inf. 2019, 8, 258. [Google Scholar] [CrossRef]
- He, H.; Yang, D.; Wang, S.; Wang, S.; Li, Y. Road Extraction by Using Atrous Spatial Pyramid Pooling Integrated Encoder-Decoder Network and Structural Similarity Loss. Remote Sens. 2019, 11, 1015. [Google Scholar] [CrossRef]
- Guo, Z.; Shengoku, H.; Wu, G.; Chen, Q.; Yuan, W.; Shi, X.; Shao, X.; Xu, Y.; Shibasaki, R. Semantic Segmentation for Urban Planning Maps based on U-Net. In Proceedings of the International Symposium on Geoscience and Remote Sensing (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 6187–6190. [Google Scholar]
- Wang, C.; Zhao, Z.; Ren, Q.; Xu, Y.; Yu, Y. Dense U-net Based on Patch-Based Learning for Retinal Vessel Segmentation. Entropy 2019, 21, 168. [Google Scholar] [CrossRef]
- Yoseob, H.; Jongchul, Y. Framing U-Net via Deep Convolutional Framelets: Application to Sparse-View CT. IEEE Trans. Med. Imaging 2018, 37, 1418–1429. [Google Scholar]
- Yao, Z.; Yi, W. Curvature aided Hough transform for circle detection. Expert Syst. Appl. 2016, 51, 26–33. [Google Scholar] [CrossRef]
- Djekoune, A.O.; Messaoudi, K.; Amara, K. Incremental Circle Hough Transform: An Improved Method for Circle Detection. Opt. Int. J. Light Electron Opt. 2017, 133, 17–31. [Google Scholar] [CrossRef]
- Sergey, I.; Christian, S. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Comput. Sci. 2015, arXiv:1502.03167v3. [Google Scholar]
- Bing, Z. Using Vector Quantization of Hough Transform for Circle Detection. In Proceedings of the IEEE International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 447–450. [Google Scholar]
- Shibani, S.; Dimitris, T.; Andrew, I.; Aleksander, M. How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift). Statistics 2018, 2, 2483–2493. [Google Scholar]
- Xu, L.; Choy, C.-S.; Li, Y.-W. Deep sparse rectifier neural networks for speech denoising. In Proceedings of the International Workshop on Acoustic Signal Enhancement (IWAENC), Xi’an, China, 13–16 September 2016; pp. 13–16. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).