Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution
Abstract
1. Introduction
2. Basic Equations
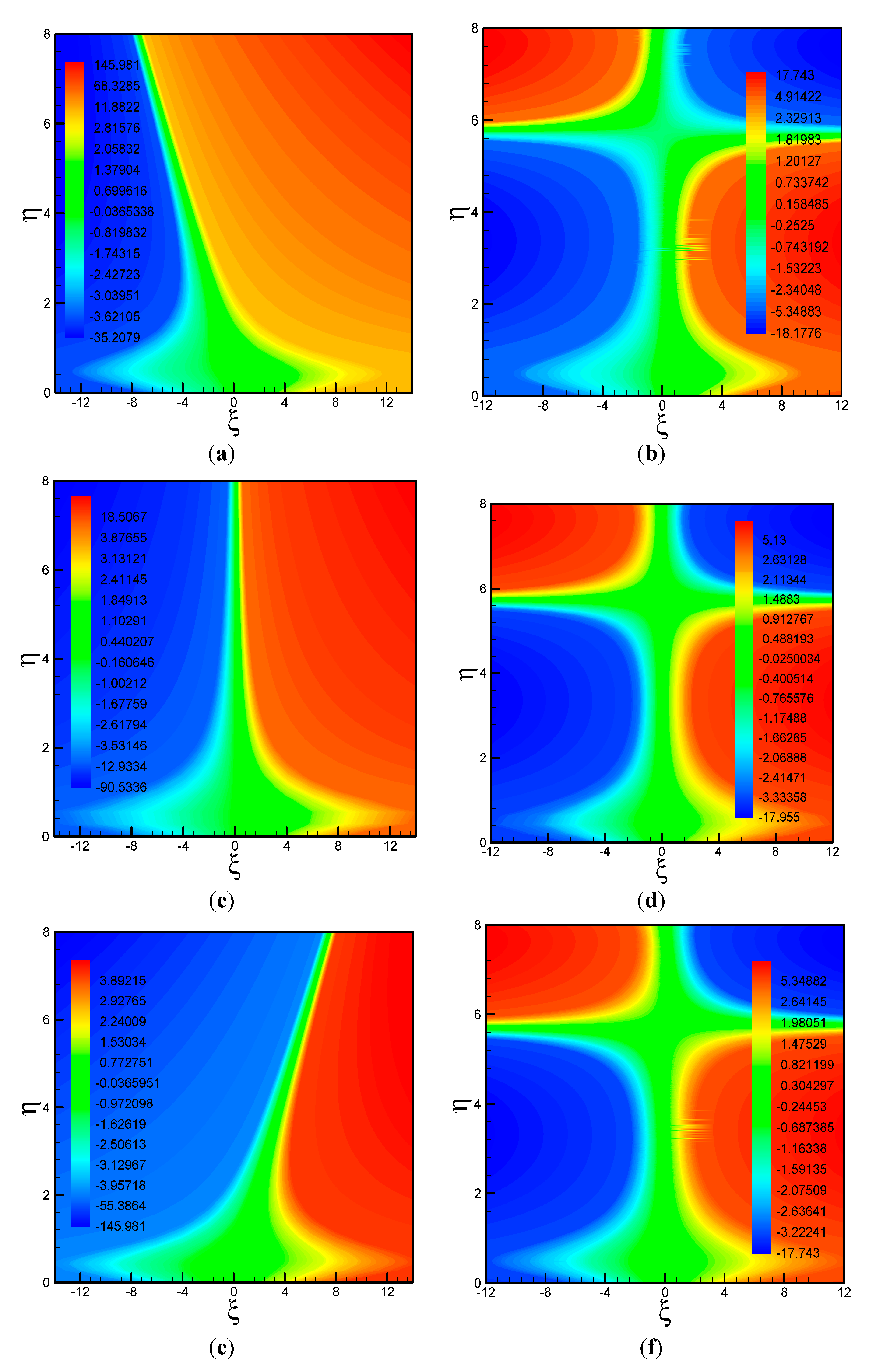
3. Results and Discussion
4. Conclusions
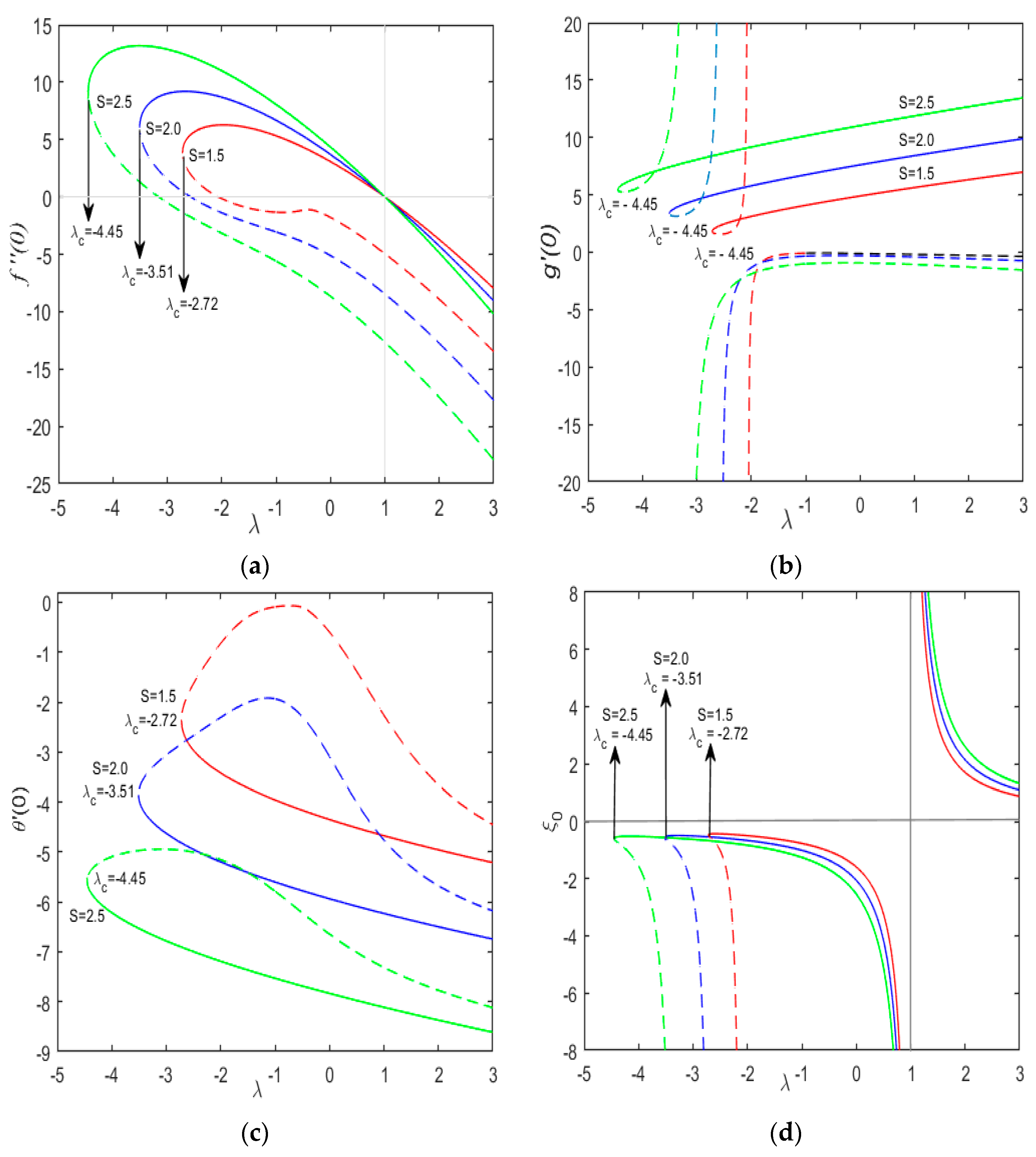
- Increasing the values of suction parameter gradually decreases the rate of heat transfer in a fluid both for first and second solutions. This rate is maximum when the sheet is shrunken and minimum when sheet is stretched.
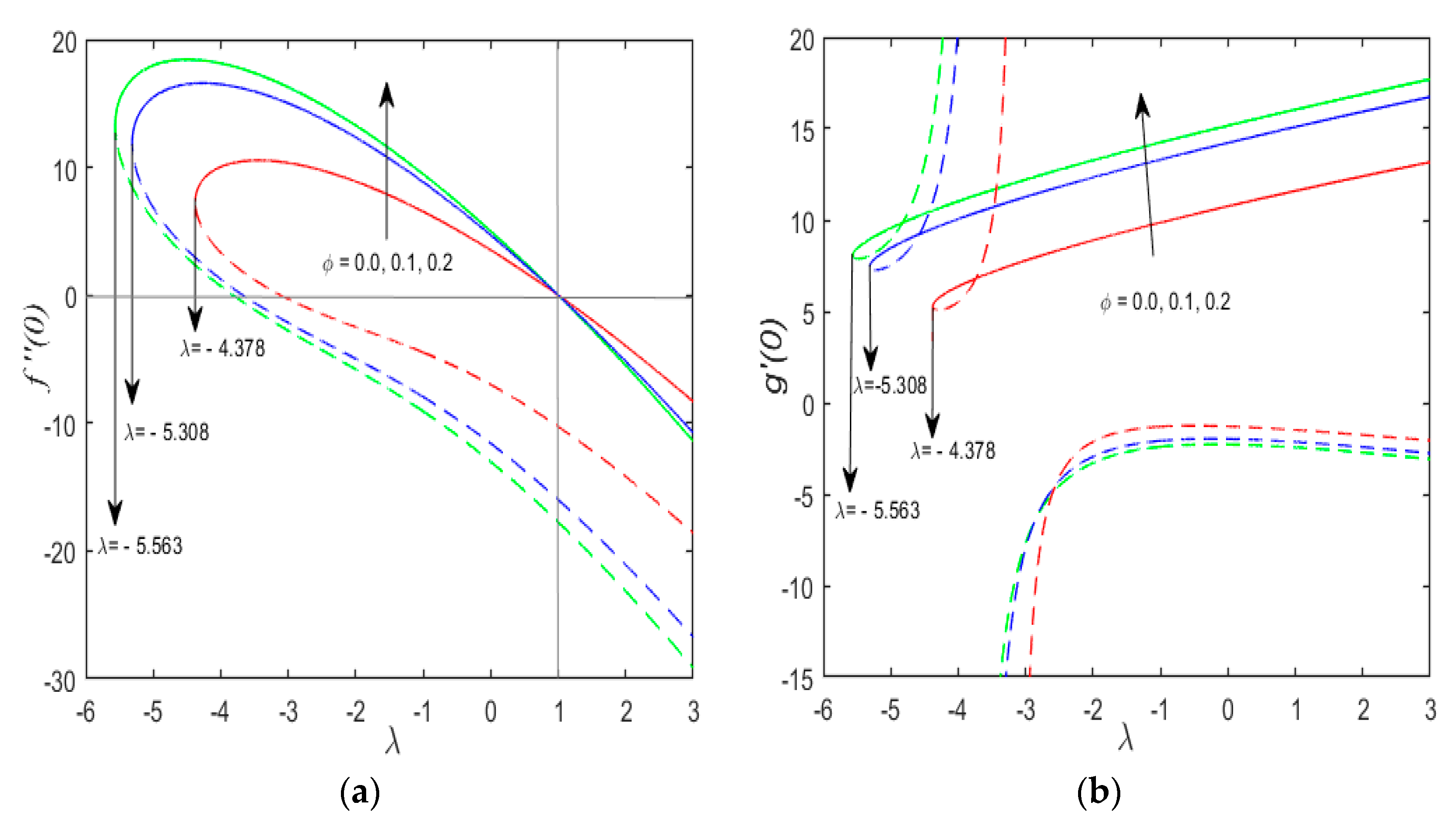
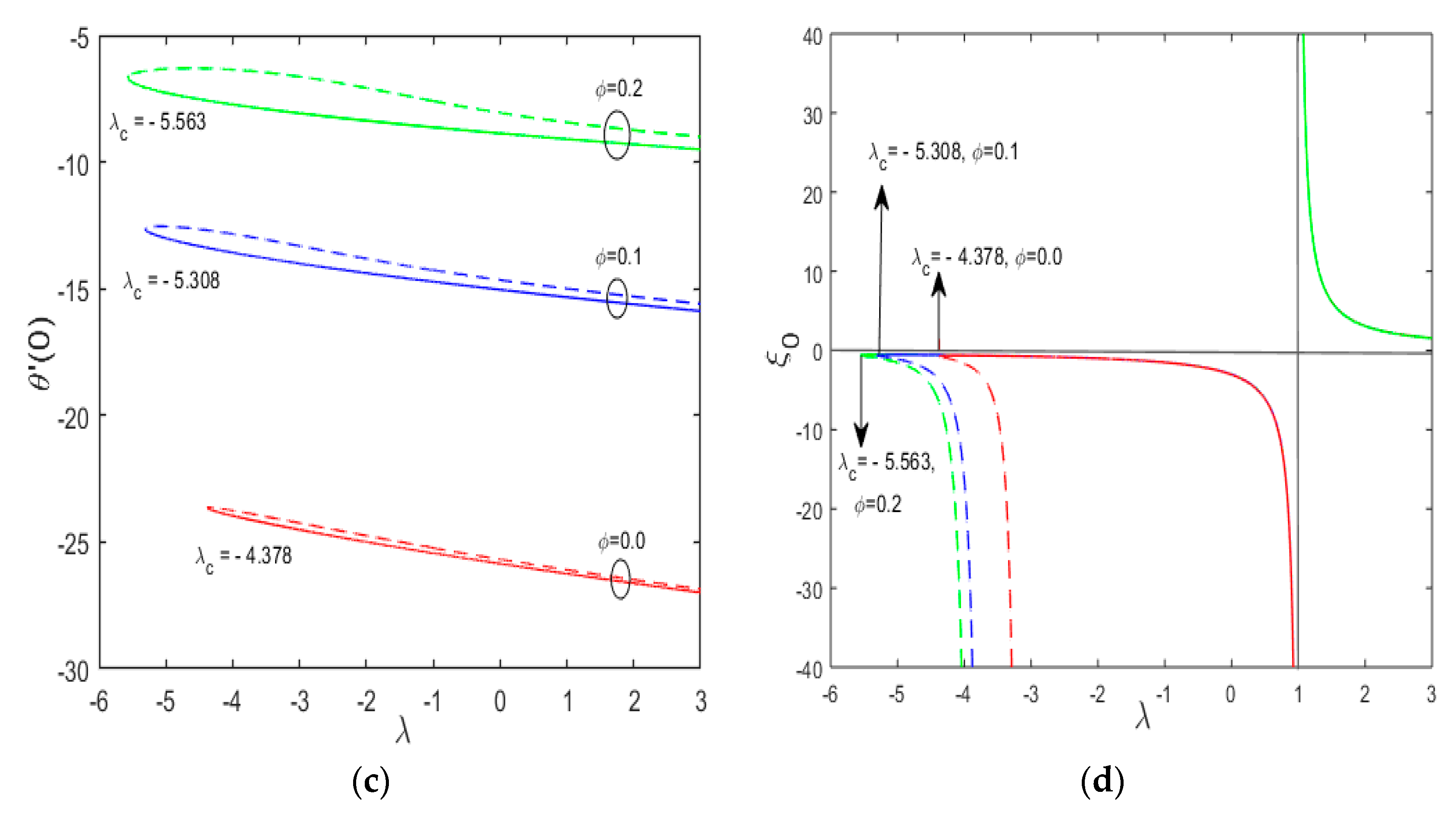
- Increasing the concentration of nanoparticles increases the rate of heat transfer in a fluid. Here has same effect both on first and second solution and is maximum for shrinking sheet as compared to stretching sheet.
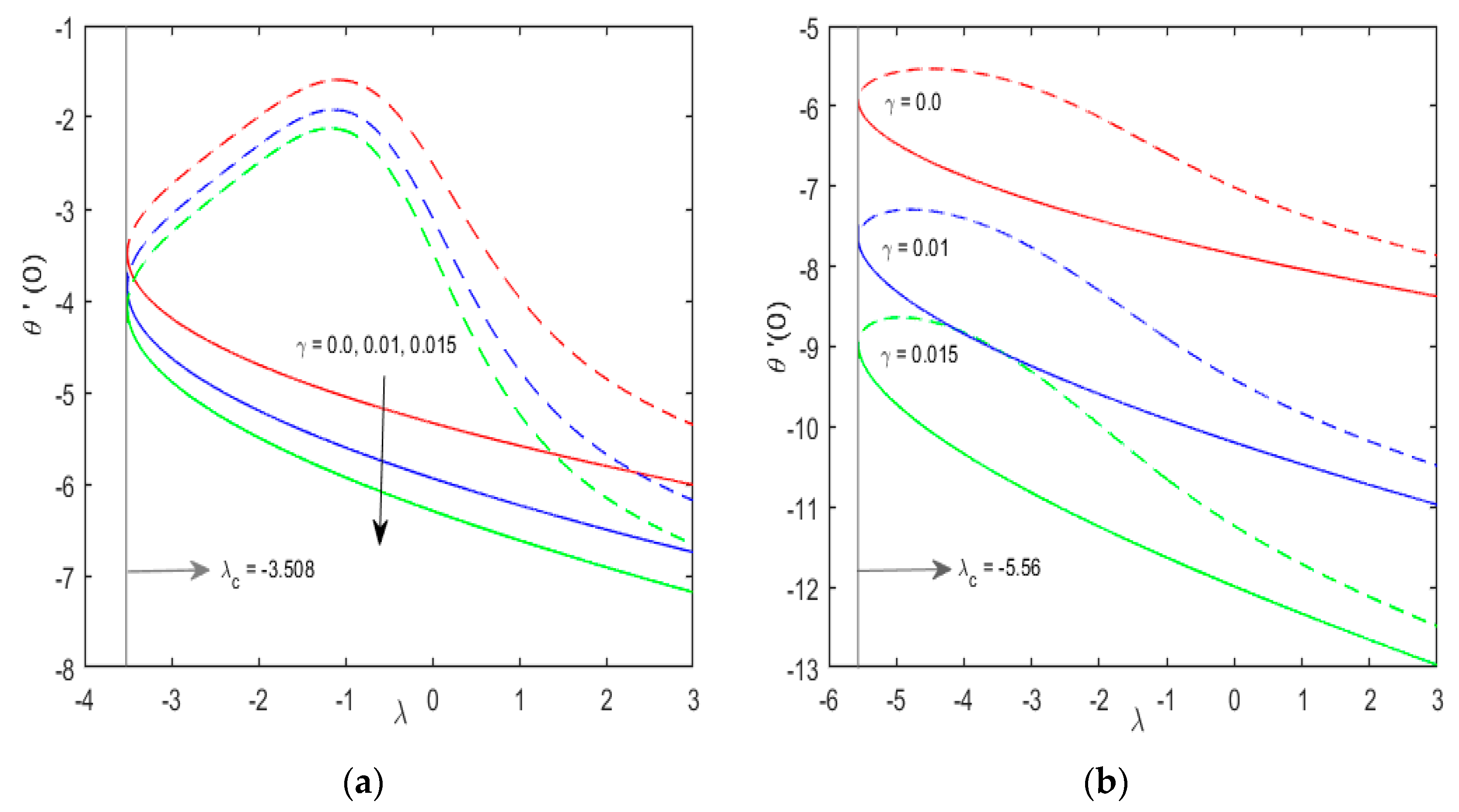
- It is notified that magnifying values of thermal relaxation parameter , only leads to a decrease in the rate of heat transfer and vice versa. Since we have one way coupling of momentum equation and temperature equation, therefore, thermal relaxation parameter γ, does not influence the skin friction coefficient, also it has no effect on the critical values of stretching/shrinking parameter, i.e., .
- The increasing values of and leads to an increase of .
- The local Nusselt number decreases with positive values of (stretching sheet), however it increases with the negative values of (shrinking sheet).
- decreases with high values of mass suction .
- The streamlines pattern for three different values of free stream parameter over a shrinking surface shows that both positive and negative values of increases the obliquity of flow toward the left or right of the origin, but for orthogonal stagnation flow has been realized.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | Meaning and Dimensions | Dimensionless |
| x, y | Spatial coordinates (L) | |
| u, v | Velocity components (L/T) | , |
| p | Pressure field (ML/ | p |
| Stream function (/ | ||
| Normal component of the flow | ||
| Shear component of flow | ||
| Density of nanofluids | _ | |
| Density of base fluid and solid fraction ( | _ | |
| Dynamic viscosity of nanofluid | ||
| Dynamic viscosity of base fluid and solid fraction ( | _ | |
| Thermal relaxation time | ||
| Kinematic viscosity of nanofluid | _ | |
| Kinematic viscosity of base fluid and solid fraction ( | _ | |
| Thermal conductivity of nanofluids | _ | |
| Thermal conductivity of nanoparticles and base fluid () | _ | |
| Heat capacity of nanofluids | _ | |
| _ | Prandtl number | |
| Heat capacity of nanoparticles and base fluid | _ | |
| Thermal diffusivity of nanofluids | _ | |
| Thermal diffusivity of nanoparticle and base fluid ( | _ | |
| Electrical conductivity of nanofluids | _ | |
| Electrical conductivity solid fraction and base fluid ( | _ | |
| _ | Skin friction coefficient | |
| _ | Nusselt’s number | Nu |
| Boundary layer control parameters (L) | , | |
| Reference and ambient temperature | _ | |
| _ | Reynolds number | |
| _ | Stretching/shrinking parameter | |
| _ | Nanoparticles concentration |
References
- Vo, T.Q.; Kim, B. Transport Phenomena of Water in Molecular Fluidic Channels. Sci. Rep. 2016, 6, 33881. [Google Scholar]
- Ge, Z.; Cahill, D.G.; Braun, P.V. Thermal conductance of hydrophilic and hydrophobic interfaces. Phys. Rev. Lett. 2006, 96, 186101. [Google Scholar] [CrossRef] [PubMed]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena. 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–79. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Shahid, A.; Bhatti, M.M.; Bég, O.A.; Kadir, A. Numerical study of radiative Maxwell viscoelastic magnetized flow from a stretching permeable sheet with the Cattaneo–Christov heat flux model. Neural Comput. Appl. 2018, 30, 3467–3478. [Google Scholar] [CrossRef]
- Khan, M.; Khan, W.A. Three-dimensional flow and heat transfer to burgers fluid using Cattaneo-Christov heat flux model. J. Mol. Liq. 2016, 221, 651–657. [Google Scholar] [CrossRef]
- Ciarletta, M.; Straughan, B. Uniqueness and structural stability for the Cattaneo–Christov equations. Mech. Res. Commun. 2010, 37, 445–447. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Zhang, X. Fractional anomalous diffusion with Cattaneo–Christov flux effects in a comb-like structure. Appl. Math. Model. 2016, 40, 6663–6675. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Bilal, S.; Awais, M. MHD flow of Cattanneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Stuart, J.T. The Viscous Flow Near a Stagnation Point When the External Flow Has Uniform Vorticity. J. Aerosp. Sci. 1959, 26, 124–125. [Google Scholar] [CrossRef]
- Tamada, K. Two-Dimensional Stagnation-Point Flow Impinging Obliquely on a Plane Wall. J. Phys. Soc. Jpn. 1979, 46, 310–311. [Google Scholar] [CrossRef]
- Dorrepaal, J.M. An exact solution of the Navier-Stokes equation which describes non-orthogonal stagnation-point flow in two dimensions. J. Fluid Mech. 1986, 163, 141. [Google Scholar] [CrossRef]
- Reza, M.; Gupta, A.S. Steady two-dimensional oblique stagnation-point flow towards a stretching surface. Fluid Dyn. Res. 2005, 37, 334–340. [Google Scholar] [CrossRef]
- Chaim, T.C. Stagnation-point flow towards a stretching plate. J. Phys. Soc. Jpn. 1994, 63, 2443–2444. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Pop, I. Non-orthogonal stagnation point flow towards a stretching sheet. Int. J. Non-Linear Mech. 2006, 41, 622–627. [Google Scholar] [CrossRef]
- Drazin, P.G.; Riley, N. The Navier-Stokes Equations: A Classification of Flows and Exact Solutions; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Weidman, P.D.; Putkaradze, V. Axisymmetric stagnation flow obliquely impinging on a circular cylinder. Eur. J. Mech. B/Fluids 2003, 22, 123–131. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.R.; Khan, A.U. MHD oblique stagnation point flow of nanofluid over an oscillatory stretching/shrinking sheet: Existence of dual solutions. Phys. Scr. 2019, 94, 7. [Google Scholar] [CrossRef]
- Ariel, P.D. Hiemenz flow in hydromagnetics. Acta Mech. 1994, 103, 31–43. [Google Scholar] [CrossRef]
- Xu, H.; Liao, S.-J.; Pop, I. Series solutions of unsteady three-dimensional MHD flow and heat transfer in the boundary layer over an impulsively stretching plate. Eur. J. Mech. B/Fluids 2007, 26, 15–27. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Carragher, P.; Crane, L.J. Heat Transfer on a Continuous Stretching Sheet. ZAMM Zeitschrift für Angewandte Mathematik und Mechanik 1982, 62, 564–565. [Google Scholar] [CrossRef]
- Dutta, B.K.; Roy, P.; Gupta, A.S. Temperature field in flow over a stretching sheet with uniform heat flux. Int. Commun. Heat Mass Transf. 1985, 12, 89–94. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AIChE J. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für Angewandte Mathematik und Physik ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Ellahi, R.; Riaz, A. Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Math. Comput. Model. 2010, 52, 1783–1793. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Lee, C.; Khan, Z.H. Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet. PLoS ONE 2013, 8, e69811. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solutions of Magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 2013, 87, 1121–1124. [Google Scholar] [CrossRef]
- Wang, Y.C. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef]
- Miklavčič, M.; Wang, C. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non. Linear. Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Kechil, S.A.; Hashim, I. Simple non-perturbative solution for MHD viscous flow due to a shrinking sheet. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 144–148. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. Thermal boundary layers over a shrinking sheet: An analytical solution. Acta Mech. 2010, 209, 325–343. [Google Scholar] [CrossRef]
- Midya, C. Hydromagnetic boundary layer flow and heat transfer over a linearly shrinking permeable surface. Int. J. Appl. Math. Mech. 2012, 8, 57–68. [Google Scholar]
- Muhaimin; Kandasamy, R.; Hashim, I. Effect of chemical reaction, heat and mass transfer on nonlinear boundary layer past a porous shrinking sheet in the presence of suction. Nucl. Eng. Des. 2010, 240, 933–939. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Lemont, IL, USA, 1995. [Google Scholar]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Wang, C.Y. Analysis of viscous flow due to a stretching sheet with surface slip and suction. Nonlinear Anal. Real World Appl. 2009, 10, 375–380. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transfer. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Hassani, M.; Tabar, M.M.; Nemati, H.; Domairry, G.; Noori, F. An analytical solution for boundary layer flow of a nanofluid past a stretching sheet. Int. J. Therm. Sci. 2011, 50, 2256–2263. [Google Scholar] [CrossRef]
- Akyildiz, F.T.; Bellout, H.; Vajravelu, K.; van Gorder, R.A. Existence results for third order nonlinear boundary value problems arising in nano boundary layer fluid flows over stretching surfaces. Nonlinear Anal. Real World Appl. 2011, 12, 2919–2930. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ganji, D.D. Effect of Cattaneo–Christov heat flux on buoyancy MHD nanofluid flow and heat transfer over a stretching sheet in the presence of Joule heating and thermal radiation impacts. Indian, J. Phys. 2018, 92, 757–766. [Google Scholar] [CrossRef]
- Kefayati, G.H.R.; Sidik, N.A.C. Simulation of natural convection and entropy generation of non-Newtonian nanofluid in an inclined cavity using Buongiorno’s mathematical model (Part II, entropy generation). Powder Technol. 2017, 305, 679–703. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of natural convection and entropy generation of non-Newtonian nanofluid in a porous cavity using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2017, 112, 709–744. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Mixed convection of non-Newtonian nanofluid in an enclosure using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2017, 108, 1481–1500. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Lattice Boltzmann simulation of natural convection in a nanofluid-filled inclined square cavity at presence of magnetic field. Sci. Iran. Trans. B. Mech. Eng. 2013, 20, 1517. [Google Scholar]
- Borrelli, A.; Giantesio, G.; Patria, M.C. MHD oblique stagnation-point flow of a micropolar fluid. Appl. Math. Model. 2012, 36, 3949–3970. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Khan, Z.H. Numerical investigation of Cattanneo-Christov heat flux in CNT suspended nanofluid flow over a stretching porous surface with suction and injection. Discret. Contin. Dyn. Syst. 2018, 11, 583–594. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Heat transfer analysis of water-based nanofluid over an exponentially stretching sheet. Alex. Eng. J. 2014, 53, 219–224. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2000, 2000, 1–27. [Google Scholar]
- Borrelli, A.; Giantesio, G.; Patria, M.C. MHD oblique stagnation-point flow of a Newtonian fluid. Zeitschrift für Angewandte Mathematik und Physik 2012, 63, 271–294. [Google Scholar] [CrossRef]
| Thermophysical Properties | Cu | Pure Water |
|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Khan, A.U.; Khan, M.R.; Nadeem, S.; Khan, S.U. Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution. Symmetry 2019, 11, 1070. https://doi.org/10.3390/sym11091070
Li X, Khan AU, Khan MR, Nadeem S, Khan SU. Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution. Symmetry. 2019; 11(9):1070. https://doi.org/10.3390/sym11091070
Chicago/Turabian StyleLi, Xiangling, Arif Ullah Khan, Muhammad Riaz Khan, Sohail Nadeem, and Sami Ullah Khan. 2019. "Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution" Symmetry 11, no. 9: 1070. https://doi.org/10.3390/sym11091070
APA StyleLi, X., Khan, A. U., Khan, M. R., Nadeem, S., & Khan, S. U. (2019). Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution. Symmetry, 11(9), 1070. https://doi.org/10.3390/sym11091070




