Abstract
We define a family of observables for abelian Yang-Mills fields associated to compact regions with smooth boundary in Riemannian manifolds. Each observable is parametrized by a first variation of solutions and arises as the integration of gauge invariant conserved current along admissible hypersurfaces contained in the region. The Poisson bracket uses the integration of a canonical multisymplectic current.
MSC:
70S10; 70S15; 58Z05; 49S05
1. Introduction
In Classical Covariant Field Theory two desirable conditions are required for a family of observables: In one side we require this function to separate solutions of the Euler-Lagrange equations. On the other hand, we need the Jacobi identity in order to have a Lie (Poisson) bracket. It is a known problem to characterize those theories accomplishing these two requirements, as pointed out in [1,2] and others. There are two main difficulties. On one hand, under locality assumptions, Jacobi identity is well established but generically there are few observables associated with conservation laws given by Noether’s First Theorem, see for instance [3]. On the other hand, extending to non-locality of variations of solutions, we may provide enough observables, see for instance [4,5], nevertheless the Jacobi identity does not necessarily hold, see [6].
For linear theories there are no such difficulties, and vector fields in the space of solutions can be modeled as in Theorem 2, see also [7]. For instance, in Lorentzian globally hyperbolic spacetimes, Maxwell equations [8] exhibit a family of observables, related to the Aharomov-Bohm effect, and a Poisson bracket constructed with Peierls method for local variables. We provide a similar set of observables for the abelian Yang-Mills (YM) fields on Riemannian manifolds. This could be mentioned as the novelty introduced in this work, although our aim is to prepare the scenario for non-abelian (non-linear) YM fields. We adopt the Lagrangian approach of the variational bicomplex formalism, see [9,10,11] rather than the Hamiltonian multysimplectic formalism approach to describe non abelian YM fields, see [12,13].
We consider regions U with smooth boundary both contained in a n-dimensional Riemannian manifold, usually . Here we avoid the complications of corners in which will be treated elsewhere. For a principal bundle we take solutions of the Yang-Mills (YM) equations for the abelian structure group. We are interested in defining a family of observables for YM solutions in U, , of the integral form
defined for a 3-dimensional compact Riemannian admissible smooth hypersurface with volume form , where admissibility means , see [14]. Observable currents, are horizontal -forms, , in the jet bundle associated to sections of the affine bundle of connections. The local invariance condition is then assumed by imposing , when restricted to the locus of the YM equations . is the horizontal differential, see the notation of the variational bicomplex formalism in Appendix A. We adapt helicity for hypersurfaces embedded properly in general compact regions U, rather than considering cylinder regions with space-like slices, , this is related to the General Boundary Formalism for field theories, see [15] and references therein.
The idea is to define the relative helicity from hydrodynamics properly adapted to YM fields as a local observable. In order to motivate this definition we recall the notion of helicity from magneto-hydrodynamics. For a divergence (non-autonomous) free vector field, in a three-dimensional Riemannian manifold tangent to the boundary , helicity is defined as
where one considers the vector field , as a potential in . Helicity of measures globally the degree of self-linking of its flow. Helicity remains an invariant for every -preserving diffeomorphism of that carries the boundary into itself, where is given by the volume form on . The situation can be dually described in terms of 1-forms. If where is the Riemannian metric on , then under the additional topological condition, , there exists a potential such that . Here helicity reads as
It does depend just on the vorticity although for its definition the potential 1-form or the vector field v, respectively, may intervene.
If we adopt divergence-free or respectively, then the property of isovorticity holds for for the magnetic potential, as well as for any solution of the Euler equation of hydrodynamics. This means that can be constructed as the image of under a diffeomorphism and if we consider a space-time domain , then helicity does not depend on the parameter t of the non-autonomous flow. To review this concepts see for instance [16,17].
Under the assumption of simple connectednes of , then the Lie algebra of divergence-free vector fields, have a bilinear form, relative helicity, defined as
Notice that helicity is and also that is a symmetric bilinear form under the assumption of closedness for .
Considering YM solutions , where is a fixed connection and is a 1-form in M, we would like to define the field strength helicity as in (2). Choose a tubular neighborhood of with exponential coordinates , with embedding . We take an axial gauge fixing, that is a 1-form such that in has no normal component. In addition, we may suppose that , as well as are divergence-free. See Appendix on the geometry of abelian YM fields in [15].
Then the helicity for abelian YM fields could be defined as
where is the Hodge operator associated to the induced Riemannian metric on . Hence we could define helicity as in (1) for the vector fields defined as
Nevertheless, this notion of helicity would depend on the gauge fixing choice, therefore cannot be generalized as a gauge invariant observable. Moreover, we do not get a local -closedness condition for an observable current: if is an open region such that , then
where L is the Lagrangian density. We will rather try to define the relative helicity of YM fields. Take any other solution. Take a first variation of solutions , let us define
Then for gauge translations we would have . Moreover, if is an open region such that , then Thus for every couple where and is a first variations of solutions, we consider the antisymmetric component of the relative helicity or simply -helicity,
In Section 4 we formalize this construction in the language of the variational bicomplex, see Appendix A.
2. Variational Bicomplex Formalism for Abelian YM Fields
Along this section we adopt the terminology and notation of the variational bicomplex formalism, for the readers convenience we give a brief presentation and references for this in Appendix A. Let be a principal bundle on a Riemannian manifold with structure group and a region with smooth boundary. Let with be the affine bundle whose sections are the G-covariant connections on .
For abelian YM, the Lagrangian density is defined by the Lagrangian
where this expresion corresponds to local coordinates in , is a fixed volume form in the base and , with the Riemannian metric in U.
Then denote the Euler-Lagrange equations, where stands for the basis for the vertical —forms in . Thus YM equations have locus which is the prolongation of . In the local coordinate chart,
The space of solutions over U is
Thus solutions satisfy .
The linearized equations for any (local) evolutionary vector field, are
where is the integration by parts operator, see its definition in [18]. In local coordinates this linearized equation reads as
Let be the Lie subalgebra of those evolutionary vector fields satisfying the linearized Euler-Lagrange equations. The Lie algebra will turn out to be our model for variations of YM solutions. For example, the radial evolutionary vector field whose prolongation is
is a symmetry of the YM PDE, i.e. . This is a general constructions of symmetries for linear PDEs, see [5].
The presymplectic current
with , has the property stated in the following general Lemma.
Lemma 1 (Multysimplectic formula).
For every we have
Definition 1 (Gauge).
- 1.
- Those first variations of solutions satisfyingdefine the Lie subalgebra of locally Hamiltonian first variations as .
- 2.
- We define the Lie algebra of gauge first variations as those satisfying locally the presymplectic degeneracy condition, i.e.,
For instance, the radial vector defined in (6) is not locally hamiltonian, since it satisfies the Liouville condition rather than condition (7).
In the second part of Definition 1 we may also have adopted instead of and
as is stated in the following assertion.
Proposition 1.
Suppose that satisfies
for every variation of solutions . Then .
Notice that the locally Hamiltonian condition is stronger than the property exhibited in Proposition 1 for every variation of solutions. Thus .
Lemma 2.
is a Lie ideal.
Proof.
If then
which by hypothesis and by anticommutativity of is -exact, hence and therefore is a Lie subalgebra. To see that , apply vertical derivation to (8).
Take , then apply vertical derivation to Equation (9) with and the condition of -exactness for implies the -exactness of holds. Therefore . □
Form Proposition 1 it follows also the following assertion.
Lemma 3.
is a Lie ideal, hence
Lemma 4.
If for every
holds, then in local coordinates holds in for each where .
Definition 2 (Gauge with boundary condition).
- 1.
- The Lie subalgebraof locally Hamiltonian first variations with null boundary conditions, consists of those satisfying (7) andwhen evaluated in . In particular .
- 2.
- The Lie ideal of gauge variations with null boundary conditionsconsists of those such that (8) holds together withWhich means that there is no gauge action in the boundary.
The following assertions are used in the definition.
Lemma 5.
The following inclusions are Lie ideal inclusions into Lie algebras:
Proof.
imply that hence is indeed a Lie algebra. To see that it is an ideal in we just consider the fact that for every .
To see that is an ideal in , derive vertically (8) and notice that is null along thanks to Lemma 4, in particular is -exact.
We claim that is an ideal of . For if then vanishes.
Finally, to see that is an ideal, is -exact by (9). □
3. Linear Theory
Recall that each fiber of is an affine bundle modeled over a linear bundle with .
Since the space of YM solutions is an affine space, take a fixed connection , then is such that . Here ★ denotes the Hodge star operator. In addition, there exists such that
Even though Equation (5) imposes a condition on-shell, i.e., on for , the linearized equations, , induce that satisfies (5) off-shell, that is in .
As a complementary definition to (10) we may define for every solution, , and every first variation of solutions, the section
Here we use the isomorphism, depending on a fixed connection, , between the pullback of the vertical bundle , and the linear bundle .
For the previous definitions the following properties hold
The following assertion holds as an observation that will follow from Lemma 9.
Lemma 6.
We have that for every solution of the linearized equation . Hence, for every .
The following assertion holds for linear theories.
Lemma 7.
For every solution, , and every first variation of solutions, , in a linear theory, there exists such that or equivalently
If we want to consider the gauge classes on we can consider the gauge representatives consisting of Lorentz gauge fixing conditions, i.e., for every there exists a gauge related
where being a gauge translation by exact 1-forms in .
Recall the Hodge-Morrey-Friedrichs -ortogonal decomposition, see [19]. For null normal components we have,
where
Given a fixed point, , the linear space of Lorentz gauge fixing, , defines a linear subspace
of linearized solutions, , such that there is a covering, ,
of the -componentspace of solutions modulo gauge,.
The following results of this section recover the usual characterizations of gauge symmetries in as translations by exact forms.
Lemma 8.
For every and , .
Proof.
If we calculate the square of the -norm, of where ★ stands for the Hodge star operator for the Riemannian metric g, then we get
If , then due to Lemma 4, the norm can be calculated as
Recall (8) and that . Hence
Therefore . □
Proposition 2.
For every solution, and every gauge first variation with null boundary condition, , the induced 1-form in the base, , defined as in (11), is exact. Therefore, .
Proof.
We solve the Poisson BVP for with Dirichlet boundary conditions
Notice that the necessary integral condition for the Poisson equation follows from the boundary condition .
Thus is a solution of with Lorentz gauge fixing condition and Dirichlet boundary condition.
Recall (13). Since , according to Lemma 8, and .
There are two cases:
Case 1. The normal component does not vanish. Here in local coordinates, . Then is harmonic and ). Therefore, it belongs to i.e., it is exact.
Case 2. , that is, . Then , i.e., where
In any case is exact and so is . □
Proposition 3.
Take any solution η, and any gauge symmetry, . Then there exists such that . Hence is exact.
Proof.
Take . According to the argument given in Proposition 2 we just need to show that the pullback is null for the inclusion . Then would have null Dirichlet condition and would be exact for suitable .
Notice that the following boundary conditions are in general different objects:
Since , then we are assuming a boundary condition on X, namely , with , when evaluating in . Due to Lemma 4 we have that does not depend on vertical coordinates, when evaluating in .
We claim that indeed . Recall that, according to Lemma 4, for every we have
Therefore, for , hence null Dirichlet boundary conditions hold for . There exists a smooth function such that , and . If
then has null both Neumann and Dirichlet conditions on . We just need to refine the choice of f, so that . Hence . □
Theorem 1.
There is an inclusion of the gauge quotients of Lie algebras,
Proof.
By the Second Isomorphism Theorem for Lie algebras
Notice that
where is the Lie algebra morphism defined as the composition in the diagram below.


By the first isomorphism theorem, there exists an induced monomorphism and a commutative diagram


There is an inclusion . Hence . By Proposition 3, the inclusion is a section of the projection 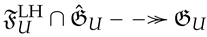 , given by .
, given by .
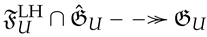 , given by .
, given by .Therefore, we have the required inclusion
 □
□

Recall that in the exact sequence,
Hence, the demand in the proof of Proposition 3 for to be null is equivalent to demanding to lie into . Thus, defines a relative cohomology class . Further considerations actually explain that .
Proposition 4.
If , then .
Proof.
For every we have that with . Take any YM solution. For , we solve the Poisson BVP
then may be gauge translated by an exact form so that has no normal components along and satisfies as well as the linearized YM equation, .
Notice that the induced linearized solution in fact belongs to .
By (13) . For the coclosed projection of , we have the orthogonal decomposition, .
Consider the boundary conditions linear map, , such that
where the codomain is the linear space of Dirichlet-Neumann boundary conditions modulo gauge,
See [15] for further considerations of this space. Recall the isomorphisms
Since then by (16) we have . Hence, the closed projection of would have cohomology class in induced by . Therefore, is injective.
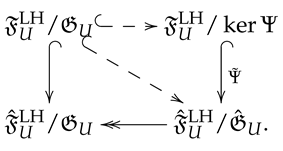
If we proceed as in the previous argument with we can define an injective map such that the following diagram commutes

Notice that and have the same image. □
Remark that we have the commutative diagram
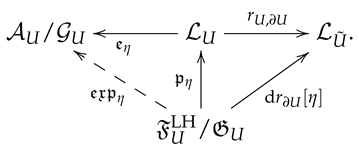 where
with the map of boundary conditions of solutions modulo gauge, see [15] for further properties of this map. Here we use axial gauge fixing in a tubular neighborhood of as well as the linear map is defined in (17). The linear map is induced by where is a coclosed linearized solution, such that , see notation (11).
where
with the map of boundary conditions of solutions modulo gauge, see [15] for further properties of this map. Here we use axial gauge fixing in a tubular neighborhood of as well as the linear map is defined in (17). The linear map is induced by where is a coclosed linearized solution, such that , see notation (11).

By composing the projection with the map we get the map . Diagram (18) suggests that Hamiltonian first variation modulo gauge, is a Lie algebra isomorphic as linear space to the tangent space of the moduli space at .
The following assertion related to Proposition 4 explains how the relative cohomology codifies the description of with respect to the boundary conditions, see also [15].
Proposition 5.
if and only if is injective and is a linear isomorphism.
4. Poisson-Lie Algebra of Hamiltonian Observables
Definition 3 (Hamiltonian observable currents).
We say that an observable current is a Hamiltonian observable current if there exist and a residual form such that the following relation holds when restricted to and evaluated on ,
We denote the space of Hamiltonian observable currents over U as . The evolutionary vector field V, is actually a locally Hamiltonian first variation, i.e., . If in addition in (19) we have the boundary condition
then we call F a Hamiltonian observable current with boundary condition. Here . We denote the space of these kind of observable currents as .
Definition 4 (Helicity current).
Suppose that is a solution of the linearized YM equation, . Define the φ-helicity current as
where was defined in (6). More explicitly
Form the very definition and the multysimplectic formula it can be seen that .
Remark that we could have defined observable currents, , for any divergence-free in U, , with evolutionary Hamiltonian vector field, , rather than in restricting ourselves to Hamiltonians first variations in , just as the observables considered in [8]. Nevertheless, if we had adopted this definition, then we would have to restrict the domain of and evaluate only ob solutions with Lorentz gauge fixing (12), in order to have local invariance .
From the following assertion it follows that helicity currents are Hamiltonian observable currents restricted to U, that is .
Lemma 9.
The φ-helicity current, defines a locally Hamiltonian observable current with Hamiltonian whenever .
Proof.
Recall the notation in (10). Notice that the relation is valid off-shell. Therefore we have
in particular when evaluated on . □
Lemma 10.
If are solutions of , then the Lie derivative, lies in with Hamiltonian . Under integration over Σ, it yields the symplectic product observable, associated to ,
Proof.
Therefore Recall that , see for instance [20] por the explicit form of the Lie bracket of evolutionary vector fields. Hence is Hamiltonian first variation for . □
Define the family of -helicity observables as
We see that is related to the anti-symmetric component of the helicity as bilinear form, see Section 1, in the sense of (3). Notice also that is not necessarily symmetric, unless . Hence not necessarily equals 0.
We say that is a Hamiltonian observable with Hamiltonian first variation so that the following formal identity holds:
Let us explain the formal notation of (21). Any first variation of solutions, encodes a variation of any fixed solution , which we denote as ,
for a one-parameter family of smooth solutions This means that .
In the r.h.s. we have an evaluation of a symplectic form,
While in the l.h.s. we have
With this notation we suggest that we are modeling a Lie derivative in the tangent space of the moduli space , while corresponds to local vector fields near .
If corresponds to a first variation of a one-parametric family of gauge equivalent solutions, , then which follows from . Thus is well defined for the gauge class .
Lemma 11.
Consider the linear space
where is a constant function iff represent the same -class. Then is a Lie algebra with bracket
which means
Proof.
Let be 1-forms as in the hypothesis. As in the proof of Lemma 10, recall that
There are gauge translations such that the gauge translations are divergence-free, see for instance the Appendix [15]. Recall that are defined by respectively. Hence and . By (9)
Hence
with
Denote as the a 1-form such that . In local coordinates:
Recall that divergence-free vector fields form a Lie algebra, that is . Then
Therefore,
for every variation of solutions w associated to every . See the explanation of the notation in (21). Hence □
We claim that yields a family of local observables sufficiently rich to separate solutions, see also [7]. Suppose that we consider a non-gauge variation of a solution . More precisely, take a one-parametric family of solutions encoded by the symmetry , that is Without loss of generality we can also suppose that with . Hence, for any , there exists such that in a suitable open n-dimensional ball . We choose an embedded -dimensional ball, such that
for associated to a non trivial solution to linearized equations in that also vanishes in the exterior of .
We then extend to such that . The variation of along w in the space of YM solutions is
Remark that for every YM solution and for every variation , if , then and Thus we could change notation and index the family as where we take V in .
We summarize the results exposed in this section in the following result and regard the family of observables as a “Darboux local coordinate system” for our gauge field theory.
Theorem 2 (Darboux’s Theorem).
Given a fixed YM solution. For each an admissible hypersurface, , with relative homology class , there exists an infinite dimensional gauge invariant Lie algebra (modulo constant functions)
such that the following assertions hold:
- 1.
- is gauge invariant: If X is a variation of one-parametric family of gauge equivalent solutions then Moreover, depends just on the gauge -class, .
- 2.
- Each variation V is in fact locally Hamiltonian, hence is an observable that satisfies the Hamilton’s equation (recall notation in (21)):
- 3.
- , locally separates solutions near η: For every non-gauge variation modeled by , there exists a locally Hamiltonian variation w modeled by and with
The following commutative diagram of Lie algebra morphisms and vertical exact sequences summarizes our results
 where denote subset of the the constant observable currents
with the additional boundary condition , .
where denote subset of the the constant observable currents
with the additional boundary condition , .

Definition 5 (Poisson algebra).
Let Σ be any admissible hypersurface . The (polynomial) Poisson algebra of helicity Hamiltonian observables,
is generated by the Lie algebra
The proof of the following assertion follows from the fact that the space of boundary conditions of solutions, , is a Lagrangian subspace with respect to the symplectic form , see [21].
Proposition 6.
For a hypersurface (such that and for its complement, the corresponding observables uniquely define an observable
associated to the oriented and closed -dimensional boundary .
The Lie algebra
will suffice to separate boundary conditions of solutions, while the Lie algebras corresponding to will be necessary if we want to separate solutions yielding the same boundary conditions, hence in the fibers of . This happens when according to Proposition 5. This also allows us to consider the fibers of as the symplectic leafs the coisotropic linear space . This image has been described in detail for the moduli space of non-abelian YM solutions in the two dimensional case, see for instance [22].
5. Gluing Observable Currents
Suppose that a region U is obtained by gluing along the closed hypersurfaces , to avoid corners case we suppose . This includes an isometry of with together with the compatibility of normal derivatives of the metric. We also suppose that the principal bundle over U is induced by the corresponding principal bundle over . From the projection map we fix base points obtained by gluing .
Suppose that satisfy the continuity gluing condition along
and denote those couples satisfying (26) as , where . It is a Lie subalgebra of . The continuity gluing condition (26) is trivially satisfied for the gauge Lie algebras so that , hence there is a well defined Lie algebra
Let denote those gauge variations whose jet vanish along the boundary components of except for . Similarly define . If we define
then by an Isomorphism Theorem for Lie algebras,
There is a commutative diagram of linear maps as follows. Recall the gluing procedure for abelian YM, see [15]. The doted arrow is a Lie algebra morphism.
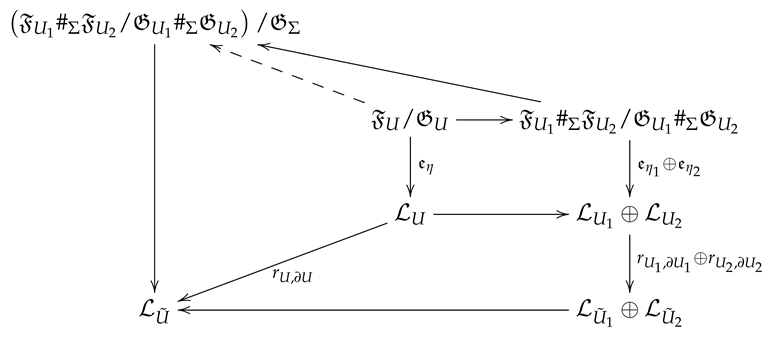

From the Lagrangian embedding of with respect to the symplectic structure, it follows that the Dirichlet conditions along and completely determine the Neumann conditions in and respectively. Here we consider an axial gauge fixing for solutions in satisfying also the Lorentz gauge fixing condition in , see Appendix in [15]. This means that the continuous gluing condition (26) will suffice to reconstruct modulo gauge the first variation for disregarding the normal derivatives along . This proves the following assertion.
Theorem 3 (Gluing of symmetries modulo gauge).
There is an isomorpmhism of Lie algebras
6. Outlook: Further Problems
We just remark that in further directions of research. In the first place, it is highly desirable to see whether or not observables can be defined for non abelian (non-linear) YM equations and if it will suffice to separate solutions just as in Theorem 2. Extension of the variationa bicomplex ttreatment need to be extended to non-local first variations to get enough observables to separate solutions. The existence of a Jacobi bracket needs also to be verified in this case. Gluing properties for observables need also to be developed and explained in detail. Namely the continuous gluing of currents in relation to as well as the gluing for hypersurfaces intersecting transversally the gluing boundary component . Finally, considerations of Riemannian manifolds with corners may introduce further difficulties in the results we have established for the smooth boundary case.
Funding
This research was funded by CONACYT-MEXICO, grant number 58132.
Acknowledgments
The author thanks J. A. Zapata since most of the results of this article arise as a particular application of the results sketched in a joint work [23] see also [7]. Along the review of [23] many clarifications came from correspondence with Luca Vitagliano and notes from an anonymous referee who provided many clarifications for the difficulties arising in non-linear field theories.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PDE | PArtial differential equation |
| YM | Yang-Mills |
| BVP | Boundary value problem |
Appendix A. Variational Bicomplex Formalism
For the convenience of the reader, in this section we fix notation by recalling basic definitions of the variational formalism for variational PDEs taken from [3,11,18,20,24,25].
Let M be an n-dimensional manifold, and let be a fiber bundle with m-dimensional fiber . Denote its sections or histories as where is a compact domain with piecewise smooth boundary.
The k-jet bundle , . On take the local coordinates
where and denotes a multiindex of degree , . For , we define . We denote the projection of the -jet onto the k-jet as . For a section , we denote its k-jet as , where
Denote the space of p-forms on as . For the decomposition , denote the space of r-horizontal and s-vertical forms on as , have as basis the -forms , where
The Cartan distribution on is generated by the basis of contact 1-forms (A1)
The vertical differential for defined as
then we are forced to consider the horizontal differential with range in the -forms in
where
The injective limit , models the p forms in the infinite jet space . We have the identities
Hence, the following diagram commutes
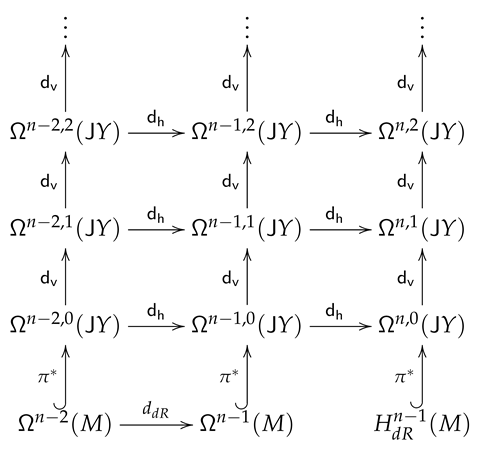
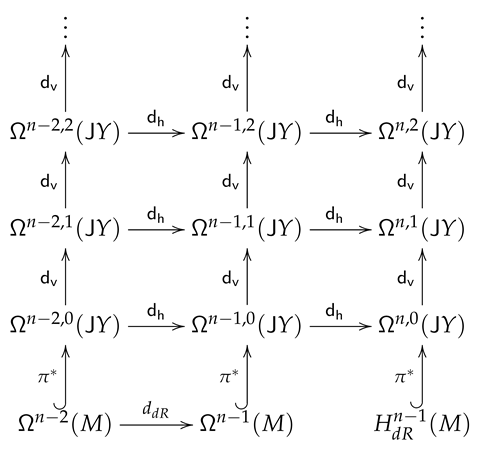
Derivations in the algebra of smooth functions on ,
are in correspondence with sections , where is the pullback under of the vertical (vector) bundle, , whose fiber at each is consists of the vertical fibers . In fact, its prolongations
where , , act as infinitesimal symmetries of the Cartan distribution in in the sense that
Here the horizontal derivative operator equals with
We will assume that has no horizontal component. Hence and
We call this space the space of evolutionary vector fields,
where the functions are local in the sense that they depend on a finite number of derivatives of u.
For a first-order Lagrangian variational problem in a region , the space of first variations of histories, , for a fixed , can be modeled as
where is a neighborhood of the graph .
Let be a fixed volume n-form on M, and consider the Lagrangian density, , with Lagrangian
Consider the action functional on ,
if we take the vertical derivative
and then the Euler-Lagrange equations are
Recall that . Another way of obtaining the Euler-Lagrange equations is by where we use the integration by parts operator for , satisfying and that is -exact. In coordinates it is given by
Meanwhile, the locus of the Euler-Lagrange PDEs
The space of solutions of the Euler-Lagrange equations
On the other hand, if we define the form , or
For a first variation modeled by , let us consider the Cartan formula for vertical derivation
see [18] Proposition 1.16. Then
Therefore,
or
In particular . Hence the variation for the action is
Proposition A1.
Let be for the Poincarè-Cartan form, which is also the principal Lepage equivalent of , and let ϕ be a section. The following assertions are equivalent
- 1.
- .
- 2.
- For every vertical vector field, , the n-form in , vanishes.
- 3.
- The Euler-Lagrange equations hold for every
Notice that in the Euler-Lagrange equations arising from , the total horizontal derivations are involved. Meanwhile, the Euler-Lagrange equations mentioned in Proposition A1 deal with partial horizontal derivations, , see [1,14].
In general for an -dimensional manifold , we can define the 1-form
where the variation corresponds to . For ,
Define the presymplectic structure , so that we have
From it follows that .
References
- Goldschmidt, H.; Sternberg, S. The Hamilton-Cartan formalism in the calculus of variations. Annales de l’Institut Fourier 1973, 23, 203–267. [Google Scholar] [CrossRef]
- Kijowski, J. A finite-dimensional canonical formalism in the classical field theory. Commun. Math. Phys. 1973, 30, 99–128. [Google Scholar] [CrossRef]
- Deligne, P.; Freed, D.S. Classical field theory. In Quantum Fields and Strings: A Course for Mathematicians; American Mathematical Society: Providence, RI, USA; Princeton, NJ, USA, 1999; Volume 1, Chapter 1; pp. 137–225. [Google Scholar]
- Lunev, F.A. An analogue of the Noether theorem for non-Noether and nonlocal symmetries. Akademiya Nauk SSSR Teoreticheskaya i Matematicheskaya Fizika 1990, 84, 205–210. [Google Scholar]
- Anco, S.C.; Bluman, G. Derivation of conservation laws from nonlocal symmetries of differential equations. J. Math. Phys. 1996, 37, 2361–2375. [Google Scholar] [CrossRef]
- Olver, P.J.; Sanders, J.A.; Wang, J.P. Ghost symmetries. J. Nonlinear Math. Phys. 2002, 9 (Suppl. 1), 164–172. [Google Scholar] [CrossRef]
- Zapata, J.A. Gauge from Holography and Holographic Gravitational Observables. Adv. High Energy Phys. 2019, 2019. [Google Scholar] [CrossRef]
- Sanders, K.; Dappiaggi, C.; Hack, T.P. Electromagnetism, local covariance, the Aharonov-Bohm effect and Gauss’ law. Commun. Math. Phys. 2014, 328, 625–667. [Google Scholar] [CrossRef]
- Reyes, E.G. On covariant phase space and the variational bicomplex. Int. J. Theor. Phys. 2004, 43, 1267–1286. [Google Scholar] [CrossRef]
- Vitagliano, L. Secondary calculus and the covariant phase space. J. Geom. Phys. 2009, 59, 426–447. [Google Scholar] [CrossRef]
- Zuckerman, G.J. Action principles and global geometry. In Proceedings of the Conference on Mathematical Aspects of String Theory, San Diego, CA, USA, 21 July–2 August 1986; World Science Publishing: Singapore, 1986; Volume 1. [Google Scholar]
- Hélein, F. Multisymplectic formulation of Yang-Mills equations and Ehresmann connections. Adv. Theor. Math. Phys. 2015, 19, 805–835. [Google Scholar] [CrossRef]
- Hélein, F.; Kouneiher, J. The notion of observable in the covariant Hamiltonian formalism for the calculus of variations with several variables. Adv. Theor. Math. Phys. 2004, 8, 735–777. [Google Scholar] [CrossRef]
- Forger, M.; Romero, S.V. Covariant poisson brackets in geometric field theory. Commun. Math. Phys. 2005, 256, 375–410. [Google Scholar] [CrossRef]
- Díaz-Marín, H.G.; Oeckl, R. Quantum abelian Yang-Mills theory on Riemannian manifolds with boundary. SIGMA Symmetry Integr. Geom. Methods Appl. 2018, 14. Paper No. 105, 31. [Google Scholar] [CrossRef]
- Arnold, V.I.; Khesin, B.A. Topological Methods in Hydrodynamics; Springer: New York, NY, USA, 1998; Volume 125. [Google Scholar]
- Khesin, B.; Wendt, R. The Geometry of Infinite-Dimensional Groups; Springer: Berlin, Germany, 2009; Volume 51. [Google Scholar]
- Anderson, I.M. The Variational Bicomplex. Book Draft, Free Web Version Edition, 2004. Available online: https://ncatlab.org/nlab/files/AndersonVariationalBicomplex.pdf (accessed on 7 June 2019).
- Schwarz, G. Hodge Decomposition—A Method for Solving Boundary Value Problems; Springer: Berlin, Germany, 1995; Volume 1607. [Google Scholar]
- Krasilshchik, I.S.; Vinogradov, A.M. Symmetries and Conservation Laws for Differential Equations of Mathematical Physics; Translations of Mathematical Monographs, AMS, Draft Edition; American Mathematical Society: Providence, RI, USA, 1999. [Google Scholar]
- Cattaneo, A.S.; Mnev, P.; Reshetikhin, N. Semiclassical quantization of classical field theories. In Mathematical Aspects of Quantum Field Theories; Calaque, D., Strobl, T., Eds.; Mathematical Physics Studies, Chapter Part III: (Semi-)Classical Field Theories; Springer: Cham, Switerland, 2015; pp. 275–314. [Google Scholar]
- Sengupta, A.N. The moduli space of flat connections on oriented surfaces with boundary. J. Funct. Anal. 2002, 190, 179–232. [Google Scholar] [CrossRef][Green Version]
- Díaz-Marín, H.G.; Zapata, J.A. Observable currents and a covariant poisson algebra of physical observables. arXiv 2018, arXiv:1704.07955. [Google Scholar]
- Krupka, D. Introduction to Global Variational Geometry; Atlantis Press: Paris, France, 2015; Volume 1. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1986; Volume 107. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).