Abstract
In this study we compared the biomonitoring potential of various types of flower asymmetry indices in Iris pumila (Dwarf Bearded Iris). We chose 197 naturally growing clones from the arid steppe habitat in the largest sandy area in Europe (Deliblato Sands Nature Reserve), and we transplanted two replicates of each clone to a polluted highway site with a heavy traffic flow. After a period of acclimatization, lower levels of photosynthetic pigment concentrations and higher stomatal density and specific leaf area in transplants verified that the chosen highway site was indeed more stressful and therefore suitable for estimation of the flower asymmetry biomonitoring potential. We analyzed radially and bilaterally symmetrical flower structures (radial fluctuating asymmetry (RA) and bilateral fluctuating asymmetry (FA)) on three perianth parts—falls, standards, and styles—and calculated various asymmetry indices based on linear and geometric morphometrics. Despite utilizing a heavily polluted environment and fairly large sample sizes, only one asymmetry index was significantly higher on the polluted site with demonstrated stressful effects on utilized plants, indicating that flower asymmetry was not an efficient method for biomonitoring in the case of I. pumila RA and FA indices.
1. Introduction
Every individual has a unique capability to preserve developmental precision during ontogeny. Developmental instability (DI) is an estimation of that capability [1]. Evaluation of DI through asymmetry measurements assesses small, random deviations from perfect symmetry. Those deviations are a consequence of subtle cellular processes that separately affect sides or repeated parts of a symmetrical organ or a structure that share the same genome and the same, or very similar, environmental conditions [2,3,4]. DI is most often susceptible to genetic or environmental stresses and can be measured by a variety of indices [2,5,6]. This method could be advantageous in biomonitoring compared to other methods because it is noninvasive, does not need expensive equipment, and the optimal level (i.e., perfect symmetry) is already known [2,6].
Plants as sessile organisms are considerably influenced by different environmental factors including light intensity and light quality, availability of water and nutrients, and pollution. Biologically relevant and frequently used biomarkers in plants are biomass, growth rate, productivity, population, and community dynamics [7,8,9,10]. As we go down to the morphological, anatomical, or physiological levels, the biomarker spectrum expands to the specific leaf area, stomatal density, stomatal pore surface, photosynthetic pigment concentrations, etc. [11,12,13]. Unfortunately, these methods are often time-consuming, need specific equipment, and, above all, require estimation of the ‘normal state’, or referent measure, which is often not predefined [14]. A variety of vegetative and reproductive organ symmetries make plants excellent candidates for biomonitoring through the application of various asymmetry indices. DI could be estimated both in vegetative and in reproductive plant organs. Previous studies usually used vegetative organs because of the larger sample sizes, longer seasons, and much simpler handling during sampling and measuring, but DI estimation of flowers should be utilized more because DI of sexual traits are demonstrated to be susceptible to the effects of environmental stress [15,16,17,18,19,20].
Angiosperm flowers show great diversity in morphology and coloration. As attractants for pollinators with the main function to advertise floral rewards, they display various types of symmetries, or even more than one, depending on the complexity of the corolla structure [21,22]. Patterns of symmetry are controlled by natural and sexual selection [23,24,25]. In general, the level of DI should increase with stress [10,16,26,27]. For bilaterally symmetrical flower structures, DI estimation is based on the measurements of their left- and right-side dimensions (bilateral fluctuating asymmetry (FA)), while for radially symmetrical structures, measurements are taken from homologous flower parts (radial fluctuating asymmetry (RA)). Most studies are based on measuring FA, but measuring RA of multiple morphological structures that develop as a result of the same developmental program, the same genotype, and (almost) identical environments could reflect individual DI more reliably because of the smaller sampling error and more than one degree of freedom when more than two measures are used [2,28].
Iris pumila (Dwarf Bearded Iris) is a monocotyledonous species well studied in every aspect of its biology with a wide range of traits surveyed under versatile abiotic and biotic influences [29]. It has large, hermaphroditic, entomophilous, and overall actinomorphic flowers. The bilaterally symmetrical parts (pollinator tunnels) are nested within the radially symmetrical flower, which makes it suitable for asymmetry morphometric analysis, as performed previously in natural habitats [29,30,31,32]. It is, therefore, a good choice for testing the suitability of various asymmetry indices for detection of environmental stress.
Anthropogenic stresses usually have larger effects on DI compared to naturally occurring ones [33]. Therefore, we measured if I. pumila flower RA and FA changed significantly with anthropogenic pollution in a heavily polluted highway site and whether these univariate and multivariate asymmetry indices could be used for detecting environmental stress. For verification of the polluted site’s environmental stress effect on I. pumila plants, we utilized leaf photosynthetic pigment concentrations (PPCs) and their ratios (physiological), stomatal density (SD) (anatomical), and specific leaf area (SLA) (morphological). All three measured traits are proven to be sensitive to different types of urban and traffic pollution [13,34,35,36,37,38,39,40]. Plants growing in a polluted environment usually show a decrease in chlorophyll a, chlorophyll b, and total chlorophyll content, while the directions of anatomical and morphological changes for SD and SLA depend on the factor affecting the plant, whether it is a monocot or a dicot, and on the species itself [41].
The goal of this study was to assess the environmental stress detection potential of different types of estimated flower asymmetries (RA and FA, indices from linear and geometric morphometrics) and their applicability in biomonitoring.
2. Materials and Methods
2.1. Species Description
Iris pumila (Dwarf Bearded Iris) is a species of the Iridaceae family, with Pontic–Pannonian distribution—from Austria in the west, through southeastern Europe, to the Caucasus Mountains on the east [42,43]. In Serbia this species inhabits northern and eastern parts, mostly the Special Nature Reserve Deliblato Sands [44]. I. pumila is classified as an endangered species; it is on the Red List and in the Red Book of Serbia [45].
Dwarf Bearded Iris is a perennial, clonal monocot and xerophyte that inhabits arid steppe habitats. This species’ blooming phase starts in the early spring and lasts for a few weeks. It is pollinated by Hymenoptera, mostly bumblebees [29,46,47]. I. pumila has spreading, underground rhizomes with short or absent stems. Leaves are ascending, alternate, basal, and up to 15–20 cm in length with unifacial leaf blades and sunken anomocytic stomata [48].
The inflorescence has only one large, hermaphroditic and radially symmetrical flower [49]. The flower composition allows entomophilous pollination where insects enter the so-called pollinator tunnels. The perianth is composed of three pollinator tunnels. Above every tunnel stands the vertical inner tepal—the standard (Figure 1A). The tunnel itself consists of three floral organs. At the bottom, there is the outer tepal serving as a landing place for pollinators—the fall (Figure 1B). The female sex organ—the style (Figure 1C)—is above the fall. The style ends with the stigmatic lip and a crest at the top. The male sex organ—the stamen—is placed tightly under the style. I. pumila flowers display great color polymorphisms, which enables easy identification of genetically distinct clones [29].

Figure 1.
Linear measures of Iris pumila flower traits for three perianth parts—standard (A), fall (B), and style (C). Length—standard length (SL), fall length (FL), and style length (StL) (1–5); width —standard width (SW), fall width (FW), and style width (StW) (2–4); left—L (2–3); and right—R (3–4).
2.2. Study Sites
The Special Nature Reserve of Deliblato Sands, the largest sandy area in Serbia and Europe, was studied as the unpolluted native site for Dwarf Bearded Iris (Deliblato Sands, Figure 2). This nature reserve, as an important habitat for in situ conservation of biological diversity that contains threatened species “of outstanding universal value”, was also listed on the tentative list of UNESCO’s World Heritage Sites, since 2002 [50].
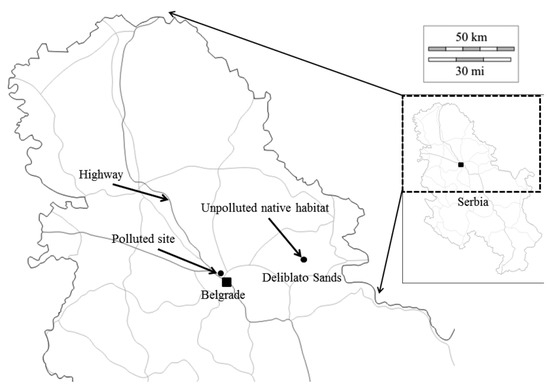
Figure 2.
Locations of the unpolluted Deliblato Sands site (44°47′39″ N, 21°20′00″ E; 45°13′10″ N, 21°26′08″ E) and the polluted highway site (44°51′15.7″ N, 20°21′58.4″ E; 44°51′26.0″ N, 20°21′38.1″ E).
For a polluted site, we selected the access road connecting A1 category State road Horgoš-Preševo (the longest highway route in Serbia and a part of the European route E75) with Zemun—the second most populous municipality of the Serbian capital Belgrade [51] (highway, Figure 2). This urban motorway is surrounded by industrial facilities, with three high-traffic lanes in each direction. The arterial road was chosen because access roads usually have greater pollutant emissions than the main highways carrying the same vehicle volume. This is explained by vehicular flows with frequent stops and starts that often generate emissions higher than constant-speed traffic [52].
2.3. Sampling Design
During flowering time in early spring, we selected and marked 197 I. pumila clones in the native Deliblato Sands site using flower color as an indicator of different genotypes. In the autumn of the same year, we transplanted two replicates for each clone to the polluted highway site (Figure 2). Plants were planted under the fence edging the median dividing island (area that separates opposing lanes of traffic), not more than 0.5 m from the fast motorway lane. Previous studies on flowering time [53] and on several morphological traits, including perianth parts of Iris pumila [54,55], showed that the patterns obtained on transplants and replants after one year were consistent with the patterns observed after more years of acclimatization, and they were consistent with the patterns on naturally growing clones, indicating that one year of acclimatization was sufficient. In addition, taking small parts of the large clones of Iris pumila for transplantation elsewhere is considered less invasive compared to placing transplants of this protected species in their natural habitat in the Special Nature Reserve Deliblato Sands and disturbing natural environment and population structures. Therefore, we requested special permission from the Serbian Environmental Agency only for taking parts of I. pumila clones and not for replantation in the reserve.
After one year of acclimatization, we collected the last fully developed leaf per clone. We used their upper half for the SD analysis. Leaves were also used to estimate SLA and PPC. During the spring period, several flowers per clone were also sampled from both sites. Transplants to the polluted site had fewer flowers than the clones at the Deliblato Sands site. For the study of radially and bilaterally symmetrical flower structures (i.e., RA and FA), we utilized only clones that flowered at both sites (57 clones).
For RA and FA analyses, flowers were cut just above the floral tube end, and perianth parts for every flower were placed between two glass plates, flattened, and embedded in glycerol in order to preserve their basic shape. Perianth parts were scanned by an optical scanner (CanoScan 5200F, Canon) at a resolution of 300 ppi.
2.3.1. Photosynthetic Pigment Concentrations, Stomatal Density, and Specific Leaf Area
Quantification of PPC was done according to Hiscox and Israelstam [56] and Minocha et al. [57]. Circles of 0.5 cm diameter were cut out, weighted, placed in a vial (Eppendorf Safe Lock, 2 mL) containing 1.5 mL of dimethylsulfoxide, and incubated for 5 h at 65 °C. After incubation, we measured optical density, an estimation of the quantity of the extracted pigments, at wavelengths 480, 649, and 665 nm (Multiskan Spectrum v1. 2, SkanIt Software 2.2, Vantaa, Finland). Concentrations of chlorophyll a (Chla), chlorophyll b (Chlb), and Carotenoids (Car) were estimated using Minocha et al. [57] formulas and presented in mg/g.
Stomatal density was estimated by a microrelief method [58]. Both sides of each leaf were painted at the upper half with see-through nail polish, about 0.5 cm wide. After drying, a strip of dry nail polish with stomatal imprints was peeled off using a transparent adhesive tape and placed on the microscope slide. Ten randomly chosen microscopic fields per side were photographed under a light microscope at 40 × 2.5 magnification (Canon digital camera Power shoot AQ7 attached to the Olympus ‘Vanox’ microscope, Tokyo, Japan). Stomata were counted for every photograph. SD was presented as the number of stomata per mm2 (#/mm2).
The specific leaf area was measured as the ratio of the leaf area and dry leaf biomass (cm2/g) [59]. The area of the fresh leaf was scanned (CanoScan 5200F, Canon, Tokyo, Japan) and then measured in Digimizer (Version 4.6.1). After drying in the oven for 48 h at 60 °C, dry mass was measured on a Chyio JL-200 scale (Chyio Balance Corporation, Kyoto, Japan).
2.3.2. Radial and Bilateral Fluctuating Asymmetry
Linear Morphometrics
For the traditional linear measures, for the standard and the fall, we measured the distance from the base to the top through the midaxis—the standard length (SL (1–5), Figure 1A) and the fall length (FL (1–5), Figure 1B). For the style, we measured the distance between the base and the top point of the stigmatic lip—the style length (StL (1–5), Figure 1C). We also measured the distance between the left and the right margins in the widest part of all three perianth parts—the standard width (SW (2–4), Figure 1A), the fall width (FW (2–4), Figure 1B), and the style width (StW (2–4), Figure 1C). The distances from the midrib to the left and the right margins at the widest part of all three flower parts (L—left and R—right) were also measured (L (2–3) and R (3–4) (Figure 1A–C)). Interlandmark distances were calculated by the TMorphGen6 program [60] from landmark coordinate data previously obtained by tpsDIG 2.16 [61]. Measurements were taken blind (without knowing their origin), by the same person, twice, on different dates and in a random order to reduce bias.
Geometric Morphometrics
For geometric morphometric analyses, we randomly selected a subset of all utilized clones that flowered on both sites, with every clone represented by a single flower (57 clones/flowers per site). Bearded Iris petals lack distinct anatomical landmarks that could enable extraction of appropriate shape information. Therefore, we first applied MakeFan6 software from the Integrated Morphometric Package [62] to place five (or seven) lines on every flower part in order to ensure uniformity in additional landmarks positioning. For the standard and the fall, the distance between two landmarks placed at the base and at the top, was divided into six equal parts (Figure 3A,B). For the style, between-landmark distance was divided into four equal parts because the style is generally shorter and has less complex shape than the other two flower parts (Figure 3C). Besides two landmarks at the base and at the top, we placed ten additional landmarks at the margins of the standard and the fall and an unpaired thirteenth additional landmark at the midaxis between points four and ten. The layout was similar for the style, with two landmarks at the base and at the top of the stigmatic lip, six additional landmarks on the margins of this flower part, and one unpaired additional landmark at the midaxis between points three and seven (Figure 3A–C). Landmarks and additional landmarks were digitized by TpsDig in the same manner as the linear measures [61].
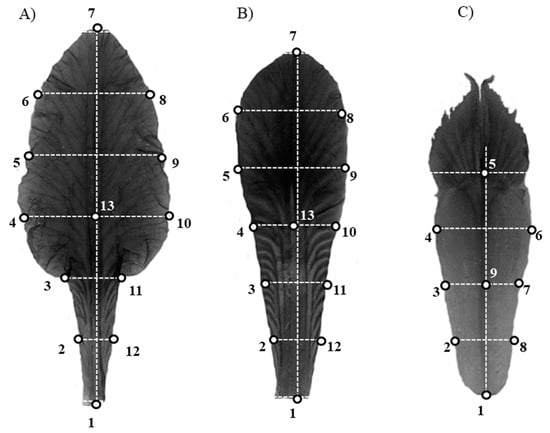
Figure 3.
Landmarks and additional landmarks digitized on three perianth parts of Iris pumila flower—standard (A), fall (B), and style (C). (A) Landmarks (1 and 7) and additional landmarks (2–6, 8–12, and 13); (B) landmarks (1 and 7) and additional landmarks (2–6, 8–12, and 13); (C) landmarks (1 and 5) and additional landmarks (2–4, 6–8, and 9).
After digitizing of landmarks and additional landmarks, variations in flower parts shape were analyzed using MorphoJ [63]. The fall, the standard, and the style all had bilateral object symmetry; therefore, the original configurations of landmarks and additional landmarks were first reflected and relabeled along the first principal axes. This preliminary procedure is needed for Procrustes superimposition, a method that performs scaling, translation, and rotation of the structures obtained by landmark positioning. This procedure minimizes the squared deviations between positioned landmarks and their averages in order to extract only shape information as a primary descriptor of analyzed flower parts [64].
2.4. Statistical Analyses
2.4.1. Photosynthetic Pigment Concentrations, Stomatal Density, and Specific Leaf Area
After calculation of PPC, SD, and SLA mean values for every clone at both sites, we performed a two-way analysis of variance (ANOVA) without replication with site and clone as factors in order to test for differences in SD, SLA, Chla, Chlb, ChlT (Chla + Chlb), Car, Chla/Chlb, and Chla/Car between the polluted highway site and unpolluted Deliblato Sands site, as well as between clones. We applied the GLM procedure of the SAS statistical package [65,66].
2.4.2. Radial and Bilateral Fluctuating Asymmetry
Linear Morphometrics
Statistical analyses of fluctuating asymmetry for the traditional linear measures were performed following Palmer and Strobeck’s recommendations considering data preparation and examination [2,6,67] and respecting the order of statistical procedures in a step-by-step example [68].
We estimated RA as the deviation of the individual fall, standard, and style trait values (length and width of the Standard—SL and SW, the Fall—FL, and FW and the Style—StL and StW) from the average for the flower. We calculated two univariate RA indices, standard deviation (sd) and coefficient of variation (cv), for all measured traits (Table 1). In order to estimate DI more accurately, information from lengths and widths were combined in the multivariate indices—multivariate standard deviations (MVsd) and multivariate coefficients of variation (MVcv) for lengths and widths for all three perianth parts together (Table 1). Length and width are different measurements of the same structure, and in our study these two measurements were significantly correlated (Pearson correlation coefficients ranging from 0.19–0.59 and p < 0.0001 for all); therefore, they did not evaluate DI independently and should not be combined in multivariate indices [2].

Table 1.
Description of radial fluctuating asymmetry (FA) indices (univariate and multivariate) and bilateral fluctuating asymmetry indices (univariate and composite). All abbreviations and formulas for FA indices are proposed by Palmer and Strobeck [2], except for composite index proposed by Leung [69]. Acronyms R and L stand for distances from the midrib to the left and the right margins of the flower parts (see Figure 1).
For all RA indices we performed mixed analysis of variance (ANOVA) with site as the fixed and clone as the random factor in order to test for differences in RA between polluted and unpolluted sites and between clones [65,66]. According to Zars’ [70] Model III computation of the F statistic in a two-factor ANOVA with replication, site as the fixed factor was tested over an interaction (site × clone), while clone and interaction (site × clone) were tested over the error. For these analyses, we used the PROC GLM procedure test statement.
After the inspection for outliers accompanied by Grubb’s test [68], we tested if the side × individual variance was equal to zero for each site and for each trait. To test the effect of the side (directional asymmetry), effect of the clone (difference in size and shape), and nondirectional asymmetry (side × part(flower(clone)) interaction), we performed the two-way mixed model ANOVA with side (fixed) and clone (random) as main factors [2,68,71]. Data were also tested for normality (skewness and kurtosis) [72] and for directional asymmetry (paired t-test of R vs. L) [73]. Because the level of fluctuating asymmetry depends on the size of the measured structure [71,73], we tested for correlation between absolute asymmetry and character size for each site studied by calculating Pearson correlation coefficients [72].
Based on these results, we selected four univariate bilateral asymmetry indices. The first index enabled estimation of FA on untransformed data with measurement error [2] (FA1, Table 1). The second enabled estimation of FA on untransformed data but without measurement error [2] (FA10a, Table 1). The third was calculated on logarithm transformed data with measurement error [2] (FA8a, Table 1), and fourth was also calculated on logarithm transformed data but without measurement error [2] (FA10b, Table 1). We also utilized the composite bilateral asymmetry index standardized by the averaged bilateral asymmetry for the whole sample, which removed size-dependent differences in FA among traits [69] (CFA2, Table 1).
For FA1 and FA8a indices, we performed mixed model ANOVA for the site and the clone effect. Site as fixed factor was tested over the interaction (site × clone), while clone, interaction (site × clone), and flower nested within (site × clone) interaction were tested over the error. For CFA2 index, we utilized two-factor ANOVA with replication with site as the fixed factor, and we tested over the interaction (site × clone) and clone as the random factor, which was tested over the error. For these analyses, we used the PROC GLM procedure test statement. To estimate differences between the polluted and the unpolluted site for FA10a and FA10b indices, we performed F-tests for pairwise comparisons [73].
Geometric Morphometrics
The raw landmark coordinates were superimposed by generalized Procrustes analysis (GPA) [74] to remove the variation from the isometric effect of size, position, and orientation. After Procrustes superimposition, we performed Procrustes ANOVA in MorphoJ with clone and side (reflection) as the main factors and replicate measurements as the error term [64]. Procrustes ANOVA estimates the amount of measurement error compared to other sources of variation. Based on the results of this analysis we calculated FA10a index (Table 1). The differences between the polluted and unpolluted site for FA10a index were estimated by F-tests for pairwise comparisons [73].
For the estimation of radial fluctuating asymmetry for flower part shapes we utilized Procrustes FA scores, which were calculated as deviations of the asymmetries of every repeated piece of every flower part (F, S, and St) from the mean asymmetry for the flower [75]. We also calculated average RA for Procrustes FA scores as the mean value for all three flower parts. For each separate flower part FA score (shape RA), as well as for average shape RA for all three parts together, we performed one-way ANOVA for the site effect.
3. Results
3.1. Photosynthetic Pigment Concentrations, Stomatal Density, and Specific Leaf Area
Chla, Chlb, ChlT, Car, and the ratio Chla/Car were significantly higher at the native Deliblato Sands site. Only the values of the Chla/Chlb ratio showed the opposite direction—significantly higher values were detected at the polluted highway site (Table 2, Figure 4A).

Table 2.
The results of analyses of variance (ANOVA) for the site and clone effect in photosynthetic pigment concentrations (PPCs), stomatal density (SD), and specific leaf area (SLA).
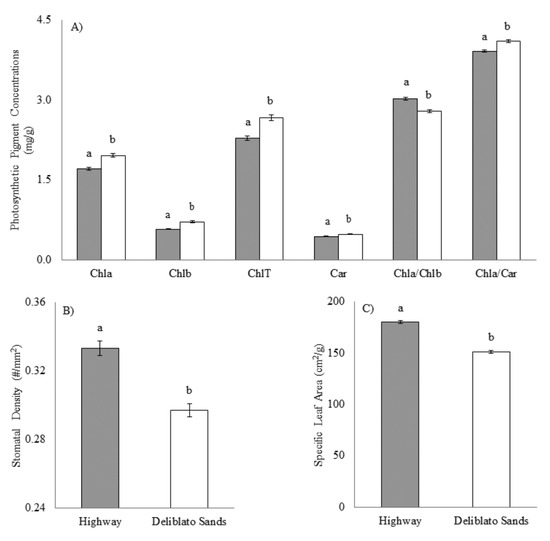
Figure 4.
Mean values and standard errors for (A) photosynthetic pigment concentrations (Chla, Chlb, ChlT, Car, Chla/Chlb, and Chla/Car), (B) stomatal density, and (C) specific leaf area in plants originating from the polluted highway site (gray bars) and the unpolluted Deliblato Sands site (white bars). Significantly different mean values are presented in different letters (p < 0.05).
Both SD and SLA values were higher at the polluted highway site, and this difference was statistically significant (Table 2, Figure 4B,C).
ANOVA for all PPCs and SDs did not detect statistically significant differences between clones, contrary to SLA where statistically significant differences between clones were detected.
3.2. Radial and Bilateral Fluctuating Asymmetry
3.2.1. Linear Morphometrics
The mixed ANOVA models for univariate RA indices (sd and cv) for almost all flower traits (length and width of the standard and the fall and length of the style) as well as for all multivariate RA indices were not statistically significant. The only exception was the univariate RA index standard deviation of the style width (sdStW). The effect of the clone as well as interaction (site × clone) were statistically significant (Table 3). Estimated RA was greater in plants that originated from the polluted highway site, but analysis did not detect statistically significant differences (Table 3). Mean values for sdStW with standard errors and pairwise comparisons between sites are presented in Figure 5.

Table 3.
The results of analyses of variance (ANOVA) for univariate FA (FA1 and FA8a) and univariate RA (sd) indices and the results of the F-test for univariate FA indices (FA10a and FA10b). The site (S) and the clone (C) effect, their interaction (S × C) and flower nested within interaction effect (F(S × C)) for FA1 (fall width (FW), style width (StW)), and FA8a (FW). The results of the F-test for site effect for fall width (FW), standard width (SW), and style width (StW). The site and the clone effect and their interaction for sd (StW).
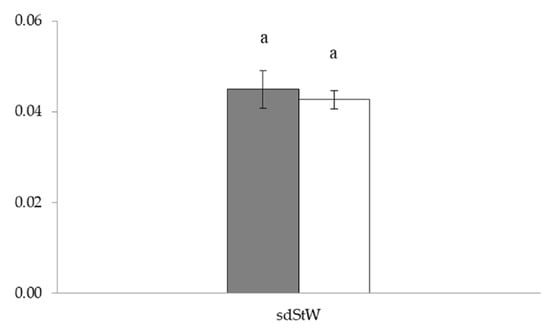
Figure 5.
Mean values and standard errors for the univariate radial asymmetry index sd for style width (StW) in plants originating from the polluted highway site (gray bars) and the unpolluted Deliblato Sands site (white bars). Significantly different mean values are presented in different letters (p < 0.05).
Prior to estimating the fluctuating asymmetry indices, factorial two-way mixed ANOVAs with side (fixed) and clone (random) as main factors showed that for all traits and both studied sites, the between-sides variation was significantly greater than zero. The Pearson correlation coefficients for correlations between fluctuating asymmetry and size showed significant, but low, size dependencies for FW and SW (FW r = 0.07, p < 0.023 and SW r = 0.09, p < 0.008). Correlation coefficients for StW were not statistically significant. Because of the low, but statistically significant, correlations, we calculated both size corrected (FA8a and FA10b, Table 1) and size uncorrected (FA1 and FA10a, Table 1) indices for FW and SW. For StW, we calculated only size uncorrected indices FA1 and FA10a (Table 1) because there were no significant correlations. The t-test revealed significant differences between left and right sides for FW and SW, indicating presence of directional asymmetry (FW, t = 3.32 and p < 0.0009; SW, t = 3.04 and p < 0.0024). According to Palmer and Strobeck [2], directional asymmetry complicates estimation of DI because of the genetic basis, and they suggest that those traits should be excluded from the further analysis. Graham et al. [76], on the other hand, propose that antisymmetry and directional asymmetry can be the consequence of symmetry-breaking phase transitions on right and left sides of a measured structure rather than the consequence of genetic differences. Keeping in mind that our study was testing possible methods for detecting environmental stress by asymmetry estimation, we decided to utilize all three measured traits in the bilateral fluctuating asymmetry analysis and critically consider all the results.
The results of analyses of variance (ANOVA) for the univariate FA index FA1 for FW and StW, univariate size corrected index FA8a for FW, and the results of the F-test for univariate FA indices with measurement error correction (FA10a and FA10b) are presented in Table 3. The ANOVA results presented in Table 3 showed a statistically significant model statement. For all other traits, as well as for composite index, the CFA2 model statement in the mixed ANOVA analysis was statistically nonsignificant and therefore not included in the further study. Plants originating from the polluted highway site had higher asymmetry values in comparison to the plants originating from the unpolluted Deliblato Sands site for almost all indices, but these differences were not statistically significant (Figure 6). For FA1 index for FW, ANOVA detected statistically significant differences between clones, while significant (site × clone) interaction was detected for FA8a index for FW.
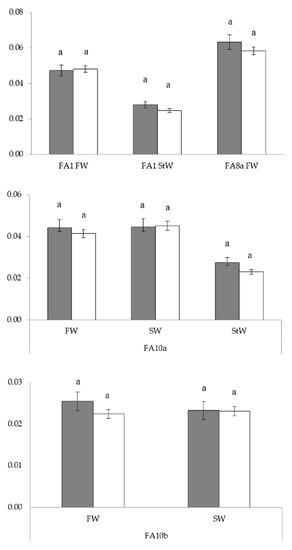
Figure 6.
Mean values and standard errors for univariate bilateral asymmetry indices (FA1, FA8a, FA10a, and FA10b) in plants originating from the polluted highway site (gray bars) and the unpolluted native Deliblato Sands site (white bars). Significantly different mean values are presented in different letters (p < 0.05).
3.2.2. Geometric Morphometrics
Procrustes ANOVA detected significant effects of all factors (p < 0.0001). A significant clone effect was indicated between individual differences in the shape of every floral organ, while a significant side (reflection) effect showed the presence of directional asymmetry. ANOVA for RA calculated on FA scores for the shape for every flower part separately (F, S, and St) and all parts together showed a statistically significant model effect only for style. For style, the shape site showed statistically significant effect, with shape RA being higher at the polluted highway site (Figure 7).
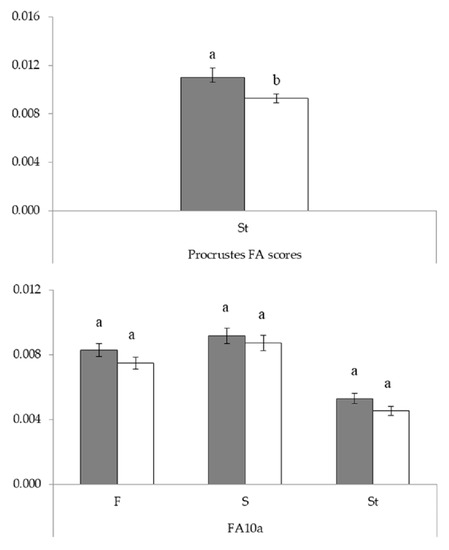
Figure 7.
Mean values and standard errors for shape RA (FA scores) and shape FA index (FA10a) in plants originating from the polluted highway site (gray bars) and the unpolluted native Deliblato Sands site (white bars). Significantly different mean values are presented in different letters (p < 0.05).
After calculation of FA10a shape FA indices for all three floral parts (F, S, and St), we conducted F-tests for the site effect (Table 4). Shape FA of floral parts showed higher values at the polluted highway site, but these differences were not statistically significant (Figure 7).

Table 4.
The results of the F-test for shape FA index FA10a and analysis of variance (ANOVA) for shape RA index calculated on FA scores from the Procrustes ANOVA. The results of the F-test for site effect for fall (F), standard (S), and style (St). The results of analysis of variance for the site effect for Style (St).
4. Discussion
For testing of various flower asymmetry indices suitable for detecting environmental stress, we selected a site that should be stressful to plants for obvious reasons. The chosen highway site is an urban motorway surrounded by industrial facilities with three high-traffic lanes in each direction. It is exposed to the type of anthropogenic pollution that presents a major problem for biodiversity and habitat conservationists [77,78]. Gaseous pollutants and airborne coarse particulate matter, for example, often could have a negative impact, in the range from tens of meters to kilometers, and reach even remote regions [79]. The presence of heavy metals, especially Pb and other pollutants, could cause production of reactive oxygen species (ROS) in plant tissues. ROS provoke damage to different cell components and degradation of photosynthetic pigments, primarily chlorophylls [80,81,82]. In addition, the suitability of the chosen site for testing the applicability of asymmetry indices in environmental stress detection was further corroborated by analyses of photosynthetic pigments, stomatal density, and specific leaf area. Concentrations of photosynthetic pigments—Chla, Chlb, ChlT, and Car—and the ratio Chla/Car showed significantly lower values at the polluted highway site. Lower values of the Chla/Car ratio suggest that the carotenoid content decreased slower than the Chla concentration, reflecting a higher contribution of photoprotective carotenoids under the pollution impact. The Chla/Chlb ratio showed significantly higher values at the polluted highway site. This is a typical response of plants exposed to polycyclic aromatic hydrocarbons (PAHs), a group of compounds that are released, among others, as products of vehicular traffic and agricultural burning [83]. Both SLA and SD showed significantly higher values at the polluted highway site. A morphological shift towards the leaves with a larger surface and lower thickness could be a consequence of a compensatory growth in order to reduce the possible inhibition of photosynthesis in polluted sites [84]. Stomata are responsible for gas exchange [85] and higher or lower SD, under air pollution impact, is a species-specific strategy to finely adjust between the gain of CO2 and consequent enhancement in photosynthesis, on one side, and the risk of faster penetration and absorption of pollutants on the other [86]. These results showed that the chosen polluted site was indeed stressful for I. pumila plants and therefore suitable for the estimation of flower asymmetry on biomonitoring potential.
The species utilized in our study, Iris pumila, had previously shown sensitivity to airborne fluoride around aluminum smelters and phosphate fertilizer plants. This kind of exposure resulted in the appearance of necrotic regions on leaf blades [87]. Leaves of Dwarf Bearded Iris also accumulated Pb and Ni in concentrations six times higher in the plants grown at the polluted site (Belgrade urban area) than in those from the unpolluted site (Deliblato Sands Nature Reserve) [88].
In previous studies, FA measurements on I. pumila lacked the power of distinction between more and less stressful environments. For instance, the effect of higher light intensity, as a more stressful environment, was reflected in higher flower bilateral fluctuating asymmetry only in natural habitats but not in a common garden experiment [27,30]. In congeneric species Iris germanica with a matching flower composition, the estimated FA indices did not show any significant differences between unpolluted rural and polluted urban sites, while almost all RA indices detected significantly higher DI in the polluted sites [89]. The studies on other genera showed similar results regarding RA. In Cistus ladanifer, the flower radial asymmetry of petal traits was significantly larger in the contact zone between serpentine and siliceous soils in the presence of increased concentrations of Ni [90].
In this study we failed to detect significant effects of polluted environment on all univariate bilateral fluctuating asymmetry indices obtained on linear morphometrics. All but one radial fluctuating asymmetry index, obtained on linear morphometrics, had an insignificant whole model effect, even~though these indices had higher power because of the larger number of replicated parts (three instead of two). The remaining index also had an insignificant site effect. The same situation occurred with FA10a, FA10b, and the composite indices. Among asymmetry indices based on geometric morphometrics, only one detected a significant site effect with higher asymmetry and, therefore, a higher developmental instability in the heavily polluted highway site. Sample sizes in this experiment were high, and levels of pollution were extremely high, compared to situations in which we would need reliable detection of environmental degradation by bioindicator species. A constant pattern of observed, nonsignificant differences indicated that with increased power of performed tests, some additional significant effects of the environmental stress caused by pollution could be probably detected. However, much larger sample sizes would be needed for that detection, especially if changes in the pollution level are not as drastic as in this study (undisturbed natural environment in the reserve vs. highly polluted highway). Therefore, I. pumila and its flower asymmetry cannot be efficiently utilized in bioindication of environmental pollution.
5. Conclusions
- The chosen site was proven stressful and, therefore, appropriate for testing the suitability of various flower asymmetry indices, as demonstrated by lower levels of photosynthetic pigment concentrations and higher stomatal density and specific leaf area, in transplanted plants.
- All but one of the analyzed asymmetry indices failed to detect a significant effect of a heavily polluted environment, with a demonstrated stressful effect on Iris pumila plants.
- Iris pumila flower asymmetry is not suitable for biomonitoring purposes.
Author Contributions
Conceptualization, Methodology, Formal Analysis, Investigation, Writing-Original draft preparation, Visualization, N.B.K.; Methodology, Investigation, Writing-Review and Editing, Visualization, D.M.; Investigation, Writing-Review and Editing, S.A.; Investigation, Writing-Review and Editing, U.Ž.; Conceptualization, Methodology, Investigation, Writing-Review and Editing, Supervision, A.T.
Funding
This work is supported by 173025 Research Grant of the Ministry for Education, Science and Technology of the Republic of Serbia.
Acknowledgments
The authors wish to thank the English language editor Krinka Vidaković Petrov, as well as Darka Šešlija Jovanović and Vida Jojić for their comments that improved the quality of the paper. We also would like to sincerely thank the anonymous referees for the helpful suggestions for the improvement of an earlier draft of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Møller, A.P.; Shykoff, J.A. Morphological developmental stability in plants: Patterns and causes. Int. J. Plant Sci. 1999, 160, S135–S146. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry analyses revisited. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: Oxford, UK, 2003; pp. 279–319. [Google Scholar]
- Clarke, G.M. The genetic basis of developmental stability. V. Inter- and intra-individual character variation. Heredity 1998, 80, 562–567. [Google Scholar] [CrossRef][Green Version]
- Van Dongen, S. How repeatable is the estimation of developmental stability by fluctuating asymmetry? Proc. R. Soc. B Biol. Sci. 1998, 265, 1423–1427. [Google Scholar] [CrossRef]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory, and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef]
- Palmer, A.R. Fluctuating asymmetry analyses: A primer. In Developmental Instability: Its Origins and Evolutionary Implications; Markow, T.A., Ed.; Kluwer: Dordrecht, The Netherlands, 1994; pp. 335–364. [Google Scholar]
- Angold, P.G. The impact of a road upon adjacent heathland vegetation: Effects on plant species composition. J. Appl. Ecol. 1997, 34, 409–417. [Google Scholar] [CrossRef]
- Cottingham, K.L.; Carpenter, S.R. Population, community, and ecosystem variates as ecological indicators: Phytoplankton responses to whole-lake enrichment. Ecol. Appl. 1998, 8, 508–530. [Google Scholar] [CrossRef]
- Komac, B.; Alados, C.L. Fluctuating asymmetry and Echinospartum horridum fitness components. Ecol. Indic. 2012, 18, 252–258. [Google Scholar] [CrossRef]
- Alados, C.L.; Navarro, T.; Escós, J.; Cabezudo, B.; Emlen, J.M. Translational and fluctuating asymmetry as tools to detect stress in stress-adapted and nonadapted plants. Int. J. Plant Sci. 2001, 162, 607–616. [Google Scholar] [CrossRef]
- Balasooriya, B.L.W.K.; Samson, R.; Mbikwa, F.; Vitharana, U.W.A.; Boeckx, P.; Van Meirvenne, M. Biomonitoring of urban habitat quality by anatomical and chemical leaf characteristics. Environ. Exp. Bot. 2009, 65, 386–394. [Google Scholar] [CrossRef]
- Cañas, M.S.; Carreras, H.A.; Orellana, L.; Pignata, M.L. Correlation between environmental conditions and foliar chemical parameters in Ligustrum lucidum Ait. exposed to urban air pollutants. J. Environ. Manag. 1997, 49, 167–181. [Google Scholar]
- Carreras, H.A.; Cañas, M.S.; Pignata, M.L. Differences in responses to urban air pollutants by Ligustrum lucidum Ait. and Ligustrum lucidum Ait. f. tricolor (Rehd.) Rehd. Environ. Pollut. 1996, 93, 211–218. [Google Scholar] [CrossRef]
- Markert, B. Definitions and principles for bioindication and biomonitoring of trace metals in the environment. J. Trace Elem. Med. Biol. 2007, 21, 77–82. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Duda, J.J.; Brown, M.L.; Kitchen, S.; Emlen, J.M.; Malol, J.; Bankstahl, E.; Krzysik, A.J.; Balbach, H.; Freeman, D.C. The effects of drought and disturbance on the growth and developmental instability of loblolly pine (Pinus taeda L.). Ecol. Indic. 2012, 20, 143–150. [Google Scholar] [CrossRef]
- Raz, S.; Graham, J.H.; Hel-Or, H.; Pavlíček, T.; Nevo, E. Developmental instability of vascular plants in contrasting microclimates at ‘Evolution Canyon’. Biol. J. Linn. Soc. 2011, 102, 786–797. [Google Scholar] [CrossRef]
- Barišić Klisarić, N.; Miljković, D.; Avramov, S.; Živković, U.; Tarasjev, A. Fluctuating asymmetry in Robinia pseudoacacia leaves—Possible in situ biomarker? Environ. Sci. Pollut. Res. 2014, 21, 12928–12940. [Google Scholar] [CrossRef] [PubMed]
- Venâncio, H.; Alves-Silva, E.; Santos, J.C. Leaf phenotypic variation and developmental instability in relation to different light regimes. Acta Bot. Bras. 2016, 30, 296–303. [Google Scholar] [CrossRef]
- Kozlov, M.V.; Wilsey, B.J.; Koricheva, J.; Haukioja, E. Fluctuating asymmetry of birch leaves increases under pollution impact. J. Appl. Ecol. 1996, 33, 1489–1495. [Google Scholar] [CrossRef]
- Watson, P.J.; Thornhill, R. Fluctuating asymmetry and sexual selection. Trends Ecol. Evol. 1994, 9, 21–25. [Google Scholar] [CrossRef]
- Citerne, H.; Jabbour, F.; Nadot, S.; Damerval, C. The Evolution of Floral Symmetry. Adv. Bot. Res. 2010, 54, 85–137. [Google Scholar]
- Klingenberg, C.P. Analyzing fluctuating asymmetry with geometric morphometrics: Concepts, methods, and applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Endress, P.K. Symmetry in Flowers: Diversity and Evolution. Int. J. Plant Sci. 1999, 160, S3–S23. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P.; Sorci, G. Insect preference for symmetrical artificial flowers. Oecologia 1998, 114, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Møller, A.P.; Eriksson, M. Pollinator preference for symmetrical flowers and sexual selection in plants. Oikos 1995, 73, 15–22. [Google Scholar] [CrossRef]
- Alados, C.L.; Giner, M.L.; Dehesa, L.; Escos, J.; Barroso, F.G.; Emlen, J.M.; Freeman, D.C. Developmental instability and fitness in Periploca laevigata experiencing grazing disturbance. Int. J. Plant Sci. 2002, 163, 969–978. [Google Scholar] [CrossRef]
- Tucić, B.; Miljković, D. Fluctuating asymmetry of floral organ traits in natural populations of Iris pumila from contrasting light habitats. Plant Species Biol. 2010, 25, 173–184. [Google Scholar] [CrossRef]
- Helsen, P.; Van Dongen, S. Associations between floral asymmetry and individual genetic variability differ among three Prickly Pear (Opuntia echios) populations. Symmetry 2016, 8, 116. [Google Scholar] [CrossRef]
- Tarasjev, A.; Avramov, S.; Miljković, D. Evolutionary biology studies on the Iris pumila clonal plant: Advantages of a good model system, main findings and directions for further research. Arch. Biol. Sci. 2012, 64, 159–174. [Google Scholar] [CrossRef]
- Miljković, D. Developmental stability of Iris pumila flower traits: A common garden experiment. Arch. Biol. Sci. 2012, 64, 123–133. [Google Scholar] [CrossRef]
- Radović, S.; Urosević, A.; Hočevar, K.; Vuleta, A.; Manitasević-Jovanović, S.; Tucić, B. Geometric morphometrics of functionally distinct floral organs in Iris pumila: Analyzing patterns of symmetric and asymmetric shape variations. Arch. Biol. Sci. 2017, 69, 223–231. [Google Scholar] [CrossRef]
- Tarasjev, A. Relationship between phenotypic plasticity and developmental instability in Iris pumila L. Russ. J. Genet. 1995, 31, 1409–1416. [Google Scholar]
- Hogg, I.D.; Eadie, J.M.; Dudley Williams, D.; Turner, D. Evaluating fluctuating asymmetry in a stream-dwelling insect as an indicator of low-level thermal stress: A large-scale field experiment. J. Appl. Ecol. 2001, 38, 1326–1339. [Google Scholar] [CrossRef]
- Gostin, I.N. Air pollution effects on the leaf structure of some Fabaceae species. Not. Bot. Horti Agrobot. Cluj-Napoca 2009, 37, 57–63. [Google Scholar]
- Arellano, P.; Tansey, K.; Balzter, H.; Tellkamp, M.; Martin, R.; Bidel, L. Plant family-specific impacts of petroleum pollution on biodiversity and leaf chlorophyll content in the Amazon rainforest of Ecuador. PLoS ONE 2017, 12, e0169867. [Google Scholar] [CrossRef]
- Pignata, M.L.; Gudifio, G.L.; Cafiasa, M.S.; Orellanab, L. Relationship between foliar chemical parameters measured in Melia azedarach L. and environmental conditions in urban areas. Sci. Total Environ. 1999, 243–244, 85–96. [Google Scholar] [CrossRef]
- Haruna, H.; Aliko, A.A.; Ahmad, F.A.; Abubakar, A.W. Effect of automobile exhaust on some leaf micromorphological characteristics of some members of Verbanaceae, Annonaceae and Euphorbiaceae families. Bayero J. Pure Appl. Sci. 2017, 10, 251–258. [Google Scholar] [CrossRef][Green Version]
- Shiv, K.; Ila, P. Stomatal analysis in Cassia occidentalis L. in response to automobile pollution along roadsides in Meerut city, India. Int. Res. J. Sci. Eng. 2014, 2, 167–170. [Google Scholar]
- Dineva, S.B. Comparative studies of the leaf morphology and structure of white ash Fraxinus americana L. and London plane tree Platanus acerifolia Willd. growing in polluted area. Dendrobiology 2004, 52, 3–8. [Google Scholar]
- Wuytack, T.; Wuyts, K.; Van Dongen, S.; Baeten, L.; Kardel, F.; Verheyen, K.; Samson, R. The effect of air pollution and other environmental stressors on leaf fluctuating asymmetry and specific leaf area of Salix alba L. Environ. Pollut. 2011, 159, 2405–2411. [Google Scholar] [CrossRef]
- Poorter, H.; Niinemets, Ü.; Poorter, L.; Wright, I.J.; Villar, R. Causes and consequences of variation in leaf mass per area (LMA): A meta-analysis. New Phytol. 2009, 182, 565–588. [Google Scholar] [CrossRef]
- Mitra, J. Karyotype Analysis of Bearded Iris. Bot. Gaz. 1955, 117, 265–293. [Google Scholar] [CrossRef]
- Purger, D.; Csiky, J.; Topić, J. Dwarf iris, Iris pumila L. (Iridaceae), a new species of the Croatian flora. Acta Bot. Croat. 2008, 67, 97–102. [Google Scholar]
- Randolph, L.F. The geographic distribution of European and Eastern Mediterranean species of bearded Iris. In Iris Year Book; British Iris Society: Tunbridge Wells, UK, 1955; pp. 35–46. [Google Scholar]
- Stevanović, V. The Red Data Book of Flora of Serbia 1. Extinct and Extremely Endangered Taxa; Stevanović, V., Tatić, B., Eds.; Ministry of the Environment of the Republic of Serbia, Faculty of Biology, University of Belgrade, Institute for Protection of Nature of the Republic of Serbia: Belgrade, Serbia, 1999. [Google Scholar]
- Stjepanović-Veseličić, L. Vegetation of the Deliblato Sands; Institute for Ecology and Biogeography: Belgrade, Serbia, 1953. [Google Scholar]
- Goldblatt, P.; Manning, J.C. The Iris Family: Natural History and Classification; Timber Press: Portland, OR, USA, 2008; ISBN 0881928976. [Google Scholar]
- Wu, Q.-G.; Cutler, D.F. Taxonomic, evolutionary and ecological implications of the leaf anatomy of rhizomatous Iris species. Bot. J. Linn. Soc. 1985, 90, 253–303. [Google Scholar] [CrossRef]
- Neal, P.R.; Dafni, A.; Giurfa, M. Floral symmetry and its role in plant-pollinator systems: Terminology, distribution, and hypotheses. Annu. Rev. Ecol. Syst. 1998, 29, 345–373. [Google Scholar] [CrossRef]
- UNESCO. WHC Tentative List; UNESCO World Heritage Centre: Paris, France, 2002. [Google Scholar]
- The Government of the Republic of Serbia. Decree on Criteria for State Road Categorization; Official Gazette of the Republic of Serbia: Belgrade, Serbia, 2013.
- Jayaratne, E.R.; Wang, L.; Heuff, D.; Morawska, L.; Ferreira, L. Increase in particle number emissions from motor vehicles due to interruption of steady traffic flow. Transp. Res. Part D Transp. Environ. 2009, 14, 521–526. [Google Scholar] [CrossRef]
- Tarasjev, A. Flowering phenology in natural populations of Iris pumila. Ecography 1997, 20, 48–54. [Google Scholar] [CrossRef]
- Tarasjev, A.; Barisić Klisarić, N.; Stojković, B.; Avramov, S. Phenotypic plasticity and between population differentiation in Iris pumila transplants between native open and anthropogenic shade habitats. Russ. J. Genet. 2009, 45, 944–952. [Google Scholar] [CrossRef]
- Tarasjev, A.; Tucić, B. Morphological differentiation of Iris pumila populations in Deliblato sands. In Proceedings of the Deliblato Sands Conference, Belgrade, Serbia, January 1994; Volume 6, pp. 289–297. [Google Scholar]
- Hiscox, J.D.; Israelstam, G.F. A method for the extraction of chlorophyll from leaf tissue without maceration. Can. J. Bot. 1979, 57, 1332–1334. [Google Scholar] [CrossRef]
- Minocha, R.; Martinez, G.; Lyons, B.; Long, S. Development of a standardized methodology for quantifying total chlorophyll and carotenoids from foliage of hardwood and conifer tree species. Can. J. Res. 2009, 39, 849–861. [Google Scholar] [CrossRef]
- Pazourek, J. The effect of light intensity on stomatal frequency in leaves of Iris hollandica hort., var. wedgwood. Biol. Plant. 1970, 12, 208–215. [Google Scholar] [CrossRef]
- Wilson, P.J.; Thompson, K.; Hodgson, J.G. Specific leaf area and leaf dry matter content as alternative predictors of plant strategies. New Phytol. 1999, 143, 155–162. [Google Scholar] [CrossRef]
- Sheets, H.D.; Zelditch, M. TMorphGen6. 2003. Available online: http://www3.canisiuse.du/~sheets/ morphsofthtml (accessed on 15 December 2013).
- Rohlf, F.J. TpsDIG 2.16. 2010. Available online: http://life.bio.sunysb.edu/morph/soft- dataacq.html (accessed on 15 December 2013).
- Sheets, H.D. Imp, Integrated Morphometric Package. 2000. Available online: http://www.canisius.edu/~sheets/morphsoft.html (accessed on 15 December 2003).
- Klingenberg, C.P. MorphoJ: An integrated software package for geometric morphometrics. Mol. Ecol. Resour. 2011, 11, 353–357. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- SAS Institute SAS 9.1.3 2011. Statistical Analysis System Institute, Inc. 2011. The SAS System for Windows (release 9.3.). Cary, North Carolina, USA. Available online: http://support.sas.com/software/93/ (accessed on 17 June 2019).
- Scheffe, H. A Method for judging all contrasts in the analysis of variance. Biometrika 1953, 40, 87–104. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Palmer, A.R.; Strobeck, C. Appendix V. Fluctuating-asymmetry analysis: A step-by-step example. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Leung, B.; Forbes, M.R.; Houle, D. Fluctuating asymmetry as a bioindicator of stress: Comparing efficacy of analyses involving multiple traits. Am. Nat. 2000, 155, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Zar, J.H. Biostatistical Analysis, 5th ed.; Lynch, D., Ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry as a measure of developmental stability: Implications of non-normal distributions and power of statistical tests. Acta Zool. Fenn. 1992, 191, 57–72. [Google Scholar]
- Day, R.W.; Quinn, G.P. Comparisons of treatments after an analysis of variance in ecology. Ecol. Monogr. 1989, 59, 433–463. [Google Scholar] [CrossRef]
- Sokal, R.; Rohlf, F. Biometry; Freeman and Company: New York, NY, USA, 1995. [Google Scholar]
- Rohlf, F.J.; Slice, D. Extensions of the Procrustes method for the optimal superimposition of landmarks. Syst. Zool. 1990, 39, 40–59. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Monteiro, L.R. Distances and directions in multidimensional shape spaces: Implications for morphometric applications. Syst. Biol. 2005, 54, 678–688. [Google Scholar] [CrossRef]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Antisymmetry, directional asymmetry, and dynamic morphogenesis. Genetica 1993, 89, 121–137. [Google Scholar] [CrossRef]
- Jozic, M.; Peer, T.; Türk, R. The impact of the tunnel exhausts in terms of heavy metals to the surrounding ecosystem. Environ. Monit. Assess. 2009, 150, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Gajić, G.; Mitrović, M.; Pavlović, P.; Stevanović, B.; Djurdjević, L.; Kostić, O. An assessment of the tolerance of Ligustrum ovalifolium Hassk. to traffic-generated Pb using physiological and biochemical markers. Ecotoxicol. Environ. Saf. 2009, 72, 1090–1101. [Google Scholar]
- Seiler, A. Ecological Effects of Roads: A Review; Swedish University of Agricultural Sciences: Uppsala, Sweden, 2001. [Google Scholar]
- Rai, R.; Rajput, M.; Agrawal, M.; Agrawal, S.B. Gaseous air pollutants: A review on current and future trends of emissions and impact on agriculture. J. Sci. Res. 2011, 55, 77–102. [Google Scholar]
- Giri, S.; Shrivastava, D.; Deshmukh, K.; Dubey, P. Effect of air pollution on chlorophyll content of leaves. Curr. Agric. Res. J. 2013, 1, 93–98. [Google Scholar] [CrossRef]
- Sharma, P.; Dubey, R.S. Lead toxicity in plants. Braz. J. Plant Physiol. 2005, 17, 35–52. [Google Scholar] [CrossRef]
- Ratola, N.; Amigo, J.M.; Oliveira, M.S.N.; Araújo, R.; Silva, J.A.; Alves, A. Differences between Pinus pinea and Pinus pinaster as bioindicators of polycyclic aromatic hydrocarbons. Environ. Exp. Bot. 2011, 72, 339–347. [Google Scholar] [CrossRef]
- Wolfenden, J.; Mansfield, T.A. Physiological disturbances in plants caused by air pollutants. Proc. R. Soc. Edinb. Sect. B Biol. Sci. 1991, 97, 117–138. [Google Scholar] [CrossRef]
- Gutschick, V.P. Biotic and abiotic consequences of differences in leaf structure. New Phytol. 1999, 143, 3–18. [Google Scholar] [CrossRef]
- Unsworth, M.H.; Black, V.J. Stomatal responses to pollutants. In Stomatal Physiology; Jarvis, P.G., Manfield, T.A., Eds.; Cambridge University Press: Cambridge, UK, 1981; Volume 191. [Google Scholar]
- Weinstein, L.H.; Davison, A.W. Native plant species suitable as bioindicators and biomonitors for airborne fluoride. Environ. Pollut. 2003, 125, 3–11. [Google Scholar] [CrossRef]
- Miljković, D.; Avramov, S.; Vujić, V.; Rubinjoni, L.; Barišić Klisarić, N.; Živković, U.; Tarasjev, A. Lead and nickel accumulation in Iris pumila: Consideration of its usefulness as a potential bioindicator in the natural protected area of Deliblato sands, Serbia. Arch. Biol. Sci. 2014, 66, 331–336. [Google Scholar] [CrossRef]
- Barišić Klisarić, N.; Miljković, D.; Avramov, S.; Živković, U.; Tarasjev, A. Developmental instability in German Iris flower as a potential biomonitoring method. Arch. Biol. Sci. 2016, 68, 837–844. [Google Scholar] [CrossRef]
- Alados, C.L.; Navarro, T.; Cabezudo, B. Tolerance assessment of Cistus ladanifer to serpentine soils by developmental stability analysis. Plant Ecol. 1999, 143, 51–66. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).