Abstract
Space-filling curves (SFCs) represent an efficient and straightforward method for sparse-space indexing to transform an n-dimensional space into a one-dimensional representation. This is often applied for multidimensional point indexing which brings a better perspective for data analysis, visualization and queries. SFCs are involved in many areas such as big data analysis and visualization, image decomposition, computer graphics and geographic information systems (GISs). The indexing methods subdivide the space into logic clusters of close points and they differ in various parameters including the cluster order, the distance metrics, and the pattern shape. Beside the simple and highly preferred triangular and square uniform grids, the hexagonal uniform grids have gained high interest especially in areas such as GISs, image processing and data visualization for the uniform distance between cells and high effectiveness of circle coverage. While the linearization of hexagons is an obvious approach for memory representation, it seems there is no hexagonal SFC indexing method generally used in practice. The main limitation of hexagons lies in lacking infinite decomposition into sub-hexagons and similarity of tiles on different levels of hierarchy. Our research aims at defining a fast and robust hexagonal SFC method. The Gosper fractal is utilized to preserve the benefits of hexagonal grids and to efficiently and hierarchically linearize points in a hexagonal grid while solving the non-convex shape and recursive transformation issues of the fractal. A comparison to other SFCs and grids is conducted to verify the robustness and effectiveness of our hexagonal method.
1. Introduction
A space-filling curve (SFC) represents a bijective transformation of multidimensional points onto 1D representation by computing an index (hash code) for each point defining the linear order of points in the space []. A SFC hashing algorithm usually follows a pattern of some tree or pyramid structure. SFCs are utilized, e.g., for space indexing and range querying [,,] and also for building spatial hierarchies especially for parallel platforms [,]. While the SFCs based on orthogonal and triangular uniform grids are well investigated and preferred in the applications, we propose an effective and robust hexagonal Node-Gosper SFC based on the Gosper fractal [] (Figure 1). This paper analyzes the problems of hierarchical hexagonal indexing and proposes solutions of issues related to transformations of multi-resolution hexagonal grids and fractal shape of Gosper tiles. Our novel method overcomes the lacks of naive Gosper-based approaches [,] and competes well with other non-hexagonal SFCs.
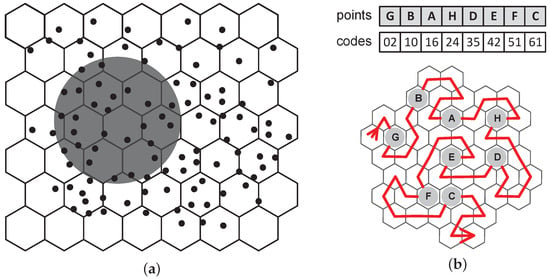
Figure 1.
Hexagonal clustering: (a) Circular disc query. (b) Points ordered along the Node-Gosper space-filling curve according to the corresponding cluster codes.
A point cloud (PC) is a collection of points of the same type (2-3D real points) [] representing a discrete form of real objects. Beside traditional PCs produced mostly by 3D scanners [], a set of points can also represent general spatial information [] such as location, GPS coordinates on the map [], swarm particles [], nodes of graph generated by visualization algorithms [], etc. We focus on 2D point clouds as they are highly investigated in the areas such as data mining [,,], computer graphics [,], image analysis [,,], geographic information systems (GISs) [,,,,], sensor networks [,], triangulation [,,,] and data visualization []. In the mentioned application fields, the point indexing/clustering algorithms are crucial, e.g., for efficient organization of data in the memory, analyzing their properties, visualization of clusters, computation of forces in particle systems and searching near neighbors. Point indexing algorithms decompose the space into subspaces or tiles [,] containing a subset and create structures for effective addressing of the points. Usually, the structures utilize the uniform regular grids that are represented by list of clusters [], or the clusters are organized in the hierarchical manner to reduce the costs of point queries [,] by omitting irrelevant clusters such as empty or distant ones (Figure 1a). The hierarchies offer good query times, esp. for sparse datasets, but they are often memory consuming and unbalanced [,]. Linear methods save memory usage and provide constant query time for uniformly distributed datasets []. However, they are inefficient for sparse point clouds.
The space-filling curves combine both approaches as they define the linear order of clusters and preserve the hierarchical information about points in the hash codes. To compute an index uniquely addressing a point in a hierarchy covering the whole space, the multi-resolution grids are often used. Most widely used SFCs including Peano, Z-order, Hilbert and Sierpiński SFC [,,,] are for orthogonal or triangular grids. The multi-resolution hexagonal grids were utilized for image processing [,,,]. Burt [] proposed a structure for coding binary images with hexagonal grids and Gibson and Lucas [] extended this structure to the more sophisticated Generalized Balanced Ternary (GBT). Those methods serve to decompose and represent images with pixels having positive coordinates, but they do not offer any general method for real points indexing and querying. Several papers discussed the problems of different grid systems and their mutual conversion to combine their best properties [,,], but they all miss the correct hierarchical 1-to-7 refinement in the hexagonal grid (Figure 2) for a correct hexagonal SFC. During the last years, the hexagons have gained increased interest in scientific areas including geographic information systems [,,,,,,], data clustering and querying [,,,,], data visualization [,], computer graphics [] and computer or sensor networks [,]. Recently, the transportation network company Uber Technologies Inc. introduced a discrete global grid system [] based on multi-resolution hexagonal grids. They use it to localize cars and customers on the map, to efficiently optimize ride pricing and dispatch and to visualize and explore spatial data. The GPS coordinates of locations on the map represent the points that are indexed by hexagonal grids. The hexagons also form the basis for analysis of the Uber marketplace, they can easily approximate zones defined by edges of required area on the map and they minimize the quantization error []. Unlike squares and triangles, hexagons have uniform distance between neighboring cells and they have the optimal perimeter/area ratio which leads to good approximation of circles [].
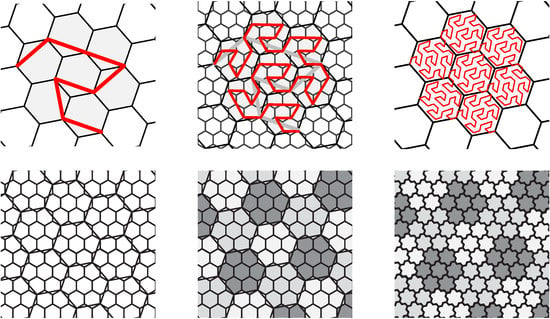
Figure 2.
Row 1: Three iterations of the Gosper curve. Row 2: Tiling with Gosper islands. Seven joined hexagons represent the basic level-1 island.
While the hexagonal grids have a wide range of applications and a convenient linear representation could simplify performing point indexing, the hexagonal SFCs are not utilized very often. The main obstacle is that a hexagon is not a rep-tile. A rep-tile is a tile which is infinitely decomposable into similar tiles. A hexagon can be decomposed only into triangles, thus the hierarchy has to be defined by bottom-up composition of hexagons creating a system of multi-resolution grids []. After exploring different hexagonal patterns, we decided to follow the concept of the Gosper fractal (or Flowsnake) which is a self-similar recursive fractal discovered by William Gosper in 1973 and introduced by Martin Gardner in 1976 [,] (Figure 2). The fractal connects the vertices of hexagonal lattice and creates a pattern of 7 hexagons called the Gosper island. These islands can be composed again into 7-pattern to create an island of greater level (Figure 2). We define a procedure extending the Gosper fractal to its node form (Node-Gosper curve) for point indexing in the manner of SFCs. The key tasks are: point localization in the hierarchy and inverse point mapping algorithm. The first published method [] simply decomposes the points into 7 disjoint areas in the top-down manner to approximate the hexagonal 7-pattern. The paper [] shows that the top-down decomposition is not reliable and it cannot produce a correct hexagonal hierarchy. The Gosper islands are non-convex fractal tiles (Figure 2) with jagged edges that are fitted into surrounding ones. This leads to point mislocalization in the hierarchy (esp. at the edges) which produces many non-hexagonal clusters in the lower levels of decomposition. Thus, the hexagonal properties are not preserved. Later, the inverse bottom-up mapping procedure fixing those problems was theoretically proposed [], but its mapping algorithm is inaccurate and inefficient. To the best of our knowledge, there is no straightforward hashing algorithm mapping the points onto the Gosper curve.
This paper summarizes a background about hexagonal grids and Gosper fractal to understand the advantages and lacks of hexagons and hexagonal multi-resolution grids. The main contribution of this work lies in the derivation of the hexagonal space-filling curve solving the lacks by using the pattern of the Gosper fractal to make a hexagonal linearization available to wide range of applications. We focus on correct point localization in the Gosper islands, stable point mapping onto the Gosper curve, fast determination of related hexagonal pattern, its rotation and indexation and efficient design of these algorithms. Our Gosper SFC method is supported by several theoretical metrics, e.g., Honeycomb conjecture [] proving good coverage of a circle by hexagonal grid, distance metrics [] declaring good real distance between points neighboring along the curve and construction times comparison. The metrics are verified by practical experiments comparing different grids and SFCs which show that our Node-Gosper SFC is robust and it produces the correct hexagonal hierarchy without mislocalization much faster than previous approaches [,].
The paper is organized as follows. Section 2 describes the related theoretical background we need for hierarchical hexagonal clustering. Section 3 gives the details of our hierarchical hexagonal composition and the corresponding Node-Gosper SFC construction. Finally, Section 4 evaluates our SFC by comparing against other grids and space-filling curves.
2. Background of Hierarchical Hexagonal Clustering
This section summarizes the theoretical and mathematical background needed to define and understand our Node-Gosper SFC. At first, we state why we prefer hexagonal grids over orthogonal and triangular ones (Section 2.1) and briefly survey selected properties of hexagonal grids. Section 2.2 overviews the existing SFCs and defines the criteria that we generally expect from a good SFC. Afterwards, we include a brief analysis of hexagonal multi-resolution grids and explanation why the Gosper fractal is selected for point indexing (Section 2.3).
2.1. Hexagonal Grids
In mathematics, a tiling means decomposition of the space into collection of geometric shapes representing some logical subspaces covering the whole space. There are only three types of regular tilings []: Triangular, square and hexagonal (Figure 3). Unlike other tilings, hexagons have uniform distances between tiles, a hexagon is the regular shape closest to the circle and one lattice vertex is shared by only three hexagons. The outstanding circular coverage by hexagonal grids is supported by several theoretical metrics including isoperimetric inequality [], Honeycomb conjecture [] and circle packing problem solution [] which show that the best regular shape having the maximal area with the least perimeter is the hexagon. The chart in Figure 4 confirms experimentally the predominance of the hexagonal grid over the orthogonal grid. These properties are useful for disc queries and nearest neighbors search as the number of tested tiles should be minimized []. On the other hand, hexagons are not infinitely decomposable. We solve this by following the principles of Gosper fractal that gives hexagons a hierarchical organization.
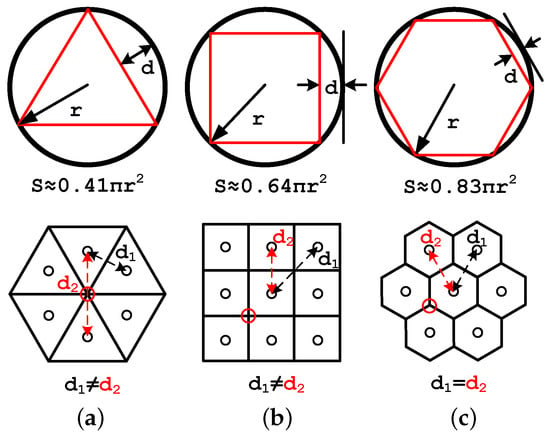
Figure 3.
A comparison of properties of regular grids: (a) Triangular, (b) orthogonal, (c) hexagonal.
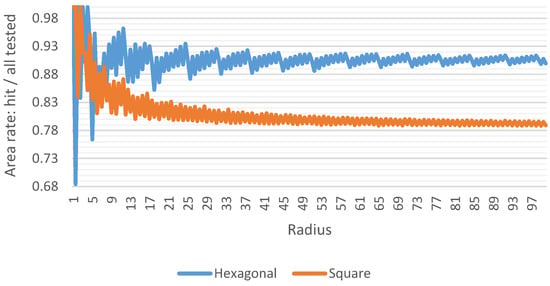
Figure 4.
For a disc of radius from 1 to 100, the graph represents the rate between the area of hit clusters and all tested clusters. The area of each cluster (hexagon or square) is unitary. The tested clusters represent the corresponding complete cluster rings covering the query disc.
As the points in a PC are real points, the discrete hexagonal coordinate system has to be defined to localize them in the hexagonal grid and give them integer coordinates of the corresponding tile. The axial and cube coordinates are used to address the hexagons. The cube coordinates extend the axial ones by one redundant coordinate to get the six-directional system simplifying some calculations. If the condition is met, the axial coordinates are calculated simply by neglecting the redundant y coordinate . We refer to papers [,] for more details and visualizations.
2.2. Space-Filling Curves
Space-filling curves represent a family of point hashing algorithms which define the basic standards of space linearization []. These standards are carefully taken into account when designing our Node-Gosper SFC (see, e.g., Figure 1b). Space-filling curves transform a general n-dimensional point into a one-dimensional (1D) index by localizing it in multi-resolution grids (Figure 5). For each point, a set of hierarchical indices addressing the sub-clusters containing the hashed point is computed. The hash code is usually a bit string merged from the indices in the top-down manner so that the root index occupies the most significant bits []. After sorting the points by codes an SFC is constructed and the points from the same cluster (with the same hash) are aligned in the memory. An SFC order of clusters represents the depth first passage of the corresponding tree (Figure 5). The nearby points are stored close to each other in the memory. However, there can be some points lying very close on the curve, but in reality, they are far away (see, e.g., Figure 5a). The shape of clusters and their indexation are varied, and thus, there are many different curves. The popular ones are Z-order, Hilbert or Sierpinski space-filling curves [,,,]. SFCs are very straightforward and efficient methods for sparse-space clustering. Such a structure design is also much more convenient for massive parallel processing of clusters [,,,,].
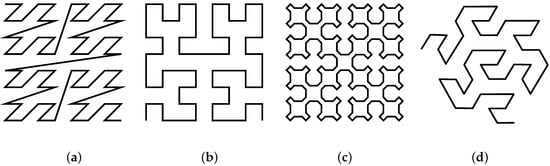
Figure 5.
The examples of space-filling curves: (a) Z-order, (b) Hilbert, (c) Sierpiński, (d) Gosper.
The linear point memory representation is used, e.g., for space indexing and range querying [,,] or sophisticated triangulation algorithms [,]. SFCs are often utilized for building spatial hierarchies especially for parallel platforms [,]. The linearly stored points can be grouped together in parallel to build a space tree (e.q. Octree) instead of a sequential particle insertion []. Papers [,] discuss the utilization of SFCs for speeding up the nearest neighbors (NNs) algorithm and real time graph layout visualization. To bring a solid hexagonal method, we define the general criteria for good SFCs [] in Section 2.2.
Space-Filling Curves Criteria
The SFCs differ in their properties, so that there is no SFC that works efficiently for all kinds of applications. However, several criteria should be met to define a high-quality SFC []. The conditions 1–3 are mandatory followed by quality criteria:
- Mapping between a point and SFC code is bijective—each point is assigned a unique hash code defining the cluster along the SFC. This has to be possible for greater depths of hierarchy.
- The curve is space-filling—every point of space lies on the curve.
- Total ordering—each cluster is visited by an SFC only once.
- Mapping between points and codes should be easy to compute.
- Two points close along the curve should be also close in the multidimensional space.
- Sequentialisation of a contiguous data set should also lead to a contiguous sequence of code numbers. This is handy for efficient memory addressing.
2.3. Hexagonal Curve Selection
To best fulfill the requirements for good SFCs, many hexagonal and combined fractal tiling patterns have been studied (see, e.g., [,,,]). The fractal patterns usually have very complex shapes, and thus, they are not appropriate for point clustering. There are three reasonable variants of multi-resolution hexagonal grids often used in the Discrete Global Grid Systems [,,,,]. Generally, the grids of aperture 3 and 4 are preferred (see Figure 6) to avoid the problems with fractal shapes. While these grids can be used for localization, they do not preserve the basic properties of the regular hexagonal grids. A grid of level divides the hexagons of level into non-hexagonal polygons, which have to be joined together on the level . These hierarchies are incongruent, and therefore, the classical tree-based algorithms cannot be utilized with them. Thus, only the hexagonal grid of aperture 7 (Figure 6C) is applicable for an SFC construction (Figure 2) because the composites are completely disjoint (not overlapping). As a result, the points of each island can be aligned and linearly stored in the memory in the manner of an SFC.
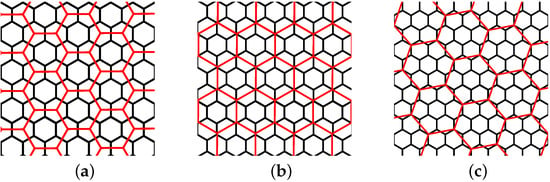
Figure 6.
Multi-resolution hexagonal grids: (a) aperture 3, (b) aperture 4, (c) aperture 7.
As mentioned before, the Gosper curve is a curve based on such a hierarchy. The space filled by the i-th recursion of this curve is bounded by the level-i Gosper island (Figure 2). The Gosper curve and its islands have many notable properties deriving from the essence of the hexagonal grid and its distance characteristics (see Figure 3) [,,]. The Gosper curve satisfies the conditions of the good SFCs such as the continuity, uniformity, scale invariance, etc. [,] (see Section 2.2). Each point in the space is visited just once, and the distance between adjacent clusters along the curve is uniform. Any hexagon (or Gosper island) shares edges with six other identical shapes so that the Gosper islands can be simply addressed by the same coordinate system as the regular hexagons. All the points of the dataset lie on the curve. The whole point cloud just has to be fitted into the circle inscribed into the Gosper island. The mapping is bijective for sufficiently deep hierarchies. The specific indexation of clusters and mapping complexity depend on the final algorithm. The Gosper curve is also held up by several theoretical metrics. The worst-case locality value () [] (smaller is better) examines the rate between the Euclidean distance of two points in the real 2D space and the distance along an SFC. The Gosper curve () is comparable with sophisticated non-hexagonal SFCs, e.g., Hilbert () or Sierpiński () curve. The number [] (smaller is better) represents the maximum tiles hit by reasonably small radius and judges the suitability of a tiling (or an SFC) for a circular neighborhood querying. The Gosper curve has optimal while other named SFCs have at least .
3. Node-Gosper Space-Filling Curve
We mentioned the main issues related to hexagonal hierarchy such as impossibility of recursive decomposition and fractal shape of Gosper islands that make it difficult to design a correct point mapping algorithm. The solutions proposed by previous work are insufficient. The approximative top-down decomposition [] following the fractal drawing algorithm produces deformed polygons and obviously incorrect point localization. The naive bottom-up approach [] solving the issue with point localization and producing the correct Node-Gosper SFC proposes only a theoretical pipeline with bad accuracy and performance.
This section represents the main contribution of the paper addressing all the named issues related to hierarchical hexagonal point indexing. We improve the existing simple concepts from papers [,] and define the complete hexagon-based system in detail with mathematical definitions and pseudocodes.
At first, the mathematical definition and the recursive construction of the Gosper fractal is reminded in Section 3.1. Following the transformations defined for the Gosper fractal, we introduce our Node-Gosper indexation model in Section 3.2 which gives the right order to the hashed points. Next, we define the procedure computing a hexagon centroid according to its hash code based on the indexation model and top-down drawing algorithm of the Gosper fractal. Section 3.4 defines our novel mapping algorithm representing the hashing function which correctly maps a point onto the Node-Gosper curve and returns the corresponding hash code.
3.1. Gosper Fractal
Our Node-Gosper SFC is inspired by the Gosper fractal drawing algorithm which is reminded here. The Gosper fractal is based on the pattern of seven hexagons (Figure 7a). The fractal is recursively constructed by replacing the oriented red arrows with the properly rotated and scaled pattern in the top-down manner (Figure 7b). The arrows connect the vertices of the hexagonal grid, and thus, this iterative method secures the geometrical continuity of the patterns and draws the correct image of the fractal. Alternatively, the same procedure can be applied to the node-based pattern (Figure 7c) connecting the hexagon centers which was probably first mentioned by Ventrella [] and its design is better for point indexing than the vertex one. The derivation of exact mathematical properties of the Gosper fractal is crucial for the Node-Gosper SFC definition and we briefly remind them here. See papers [,,,] for details.
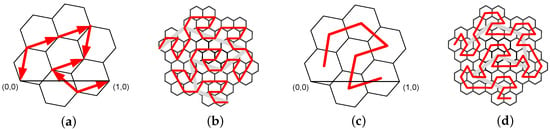
Figure 7.
The basic patterns of the Gosper curve: (a) 7-pattern of vertex representation, (b) the second iteration of vertex representation, (c) 7-pattern of node representation, (d) the second iteration of node representation.
Figure 8 describes the transformation of the pattern replacing the base hexagon inscribed in the unit circle of (black dashes) by seven smaller hexagons (level-1 Gosper island). A hexagon itself practically represents a level-0 Gosper island. The figure also shows two features of the Gosper islands: The Gosper island preserves the area of the parent hexagon, but its perimeter limit is infinity. The scale factor can be computed according to the blue triangle (Figure 8) using the Law of Cosine and it also represents the size of child hexagons. The angle can be computed using the Law of Sine and the scale factor r. Figure 7a shows that the patterns replacing differently oriented arrows have to be additionally rotated. The angles of orientation are defined by function in (1). Going through the basic Gosper pattern (Figure 7a) from the first vertex to the last vertex , the hexagons 0 and 3 are rotated by and the hexagon 5 by . The transformations can be easily computed using the well-known matrices for rotation (2), scale and translation.
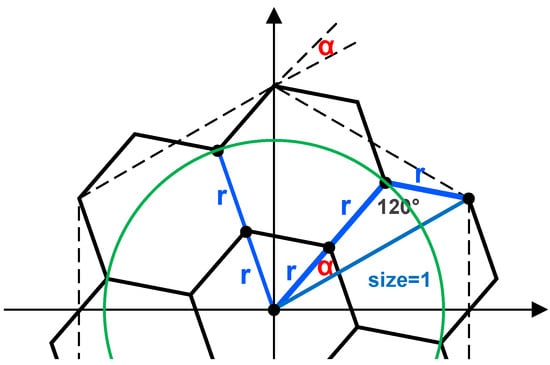
Figure 8.
Grid transformation for Gosper islands construction.
3.2. Node-Gosper Indexation
While the recursive method described in the previous section serves only to draw an image of the Gosper fractal with geometrical continuity, the indexation model must precisely state the order of the clusters along the SFC. Each point of the point cloud is localized in the hexagonal grid and the corresponding hexagon is assigned a bit hash code representing its serial number. This section explains our indexation model of the hexagons ordered by the Node-Gosper SFC.
The basic patterns defining rotation and indexation are shown in Figure 9. The main point is that the subordinate patterns have different order of indices depending on the indexation of the parent pattern. For the indexation model, the geometrical continuity is insufficient.
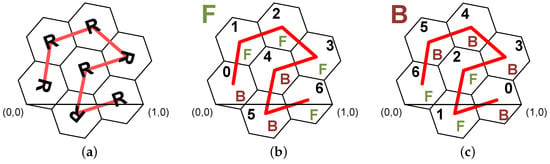
Figure 9.
Indexation and passage order of the Node-Gosper pattern. Figure (a) shows the basic rotation of subordinate patterns. The other two figures represent the patterns with (b) forward (F) and (c) backward (B) indexation.
Thus, two structural patterns are described in Figure 9b,c. They define both forward (F) and backward (B) indexing variants. The F-pattern is initial and the curve indexation is calculated in the top-down manner. Each hexagon is recursively replaced by a corresponding subordinate pattern depending on the designation of its parent. Notice that the F/B designation in the backward indexation is just the opposite direction to the forward indexation. This secures the smooth passage of all hexagons along the curve without any large leaps and crossings. The final hierarchical indexation based on the patterns from Figure 9 is displayed in Figure 10. A hash code consists of indices , where , addressing the Gosper islands containing a query point on each level of the hexagonal hierarchy. The indices of the upper hierarchical levels are represented by more significant trinities and the lower ones by less significant trinities. The hash code is computed as . Inversely, an index can be obtained from by simple bit operations. An index is a number from 0 to 6, but the three bits can represent maximally the number 7. Thus, there is unfortunately a numerical gap breaking the requirement of a contiguous sequence of indices (codes) stated in Section 2.2. However, it does not have to be a crucial problem. While having a 64-bit unsigned integer, a 21-level hexagonal indexation can be defined.
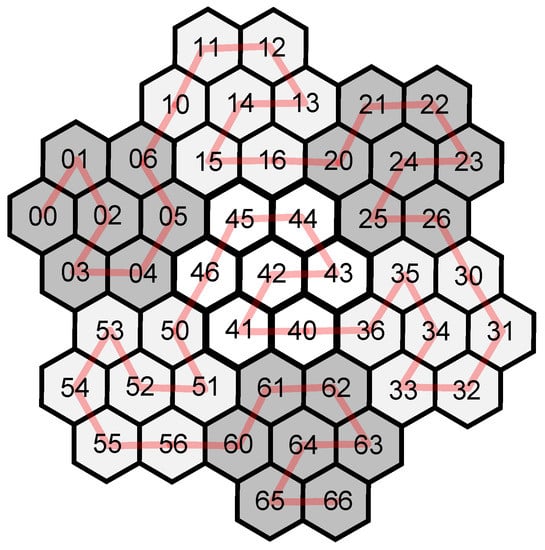
Figure 10.
Indexation of the level-2 Node-Gosper curve.
3.3. Localization with Node-Gosper Curves
As emphasized before, the hexagons are not hierarchically decomposable. However, the Gosper fractal (Section 3.1) and Node-Gosper indexation (Section 3.2) are defined recursively in the top-down manner. At first, we define a top-down algorithm computing a centroid of hexagon hierarchically addressed by indices . In the next section, we use this method to define the inverse algorithm mapping the points onto the Node-Gosper SFC.
Let us consider the case of the base hexagon with (Figure 11), which is recursively replaced by the Node-Gosper patterns (Figure 9) up to the level n. Given a vector of indices addressing a hexagon in a level-n Gosper island, a center point of such a hexagon is computed. This algorithm represents the backward mapping which verifies the bijectivity of the Gosper mapping.
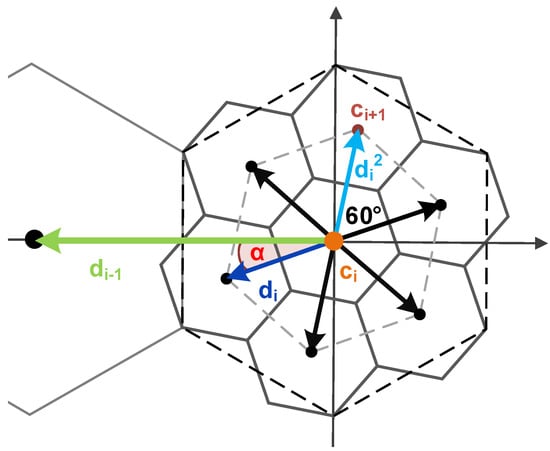
Figure 11.
The transformation of directional and position vectors.
The subordinate patterns can be indexed in the forward (F) or backward (B) manner (Figure 9), which affects the addressing order of the hexagons by . A pattern passing order F/B of the i-th recursion can be determined depending on as follows:
Each index has to be recalculated to index in the F order (Figure 9) to unify addressing of the corresponding Gosper islands in the top-down manner. The calculation of is defined as follows:
For example, a point hashed onto indices according to the level-2 Node-Gosper curve (Figure 10) belongs to the hexagon 5 () on the first hexagonal level (), whose subordinate island thus has reverse indexation of hexagons. Therefore, the corresponding index is 1 on the second level of recursion and not 5, as it would be according to the F order, which means . A pattern rotation is considered in the following transformations.
is used to compute the center point of the addressed hexagon. The algorithm recursively transforms two vectors: Position vector and directional vector (see Figure 11), where i is the current level of recursion. A vector represents the initial center position of the current Gosper island. The vector represents the rotation and scale of the grid on the i-th level of recursion. The initial directional vector is pointing to the neighboring hexagon and it is defined as , where w is the width of the base hexagon. The defines the basic orientation and distance between two neighboring hexagon centers before the first transformation. Depending on , is defined by the recurrent formula:
where represents the scale by and rotation by the angle (Section 3.1), and the represents the additional rotation defined by (1). The grid transformation can be simply defined by the following matrix:
Next, a vector pointing to the specific neighboring hexagon addressed by is defined as:
where represents the corresponding angle by which has to be rotated, so that the points to the hexagon addressed by the index. is defined as:
where equals to a multiple of . The hexagon with is initial, and therefore, . For example, is rotated by to obtain the second hexagon center (see Figure 11).
The center point is computed by a translation of by the properly rotated directional vector as:
The center point represents the final hexagon center addressed by indices .
3.4. Node-Gosper Point Mapping
In the previous section, we described the algorithm computing a hexagon center according to . In this section, we define the inverse mapping of a point onto the Node-Gosper curve, so that is computed and the corresponding hash is generated.
The mapping onto the Node-Gosper curve can be done only in the bottom-up manner, because hexagons cannot be decomposed into sub-hexagons (Figure 12). As it was explained in the previous sections, the hexagonal 7-pattern (Gosper island) is rotated and scaled to replace a parent hexagon which defines the required hierarchy of hexagons. The constructed Gosper islands are non-convex fractal tiles, so that they have to be fitted into neighboring islands to tile the plane. The top-down point localization is incorrect, because the jagged edges of islands overstep the borders of parent hexagons, so that a point previously localized in the hexagon (especially close to the edges) may belong to different branch of hierarchy in the next iteration (Figure 12). An important fact about the hexagonal hierarchy is that seven hexagon centers of each Node-Gosper pattern are always located inside their parent hexagon. It means that the upward hexagon centers localization defines numerically stable inverse procedure to the top-down algorithm and it secures the correct hierarchical assignment regardless of the jagged edges. There are still several problems that have to be solved:
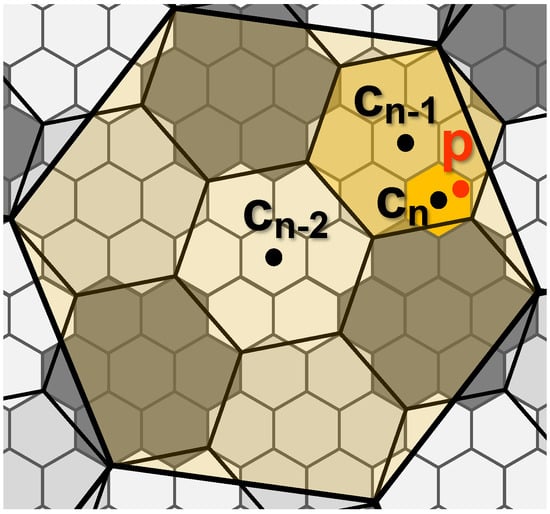
Figure 12.
The localization of in level-n Gosper island and the search of the corresponding centers.
- The relative position of hexagons of two subsequent grids at level i and is not obvious, because information of the complete parental hierarchy is unknown at level i (Figure 12).
- The grid rotation varies in the different branches of hierarchy. The specific grid transformation has recursive character and is unknown at level i (Section 3.2).
- For the same reason, the indexation and passage order are unknown at level i too.
To achieve both the correctness of hierarchical localization and recursive principles of the Gosper fractal, we separate the hashing algorithm into two phases. At first, we localize a point in the multi-resolution hexagonal grid in the bottom-up manner using the inverse formulas for the Gosper fractal construction (Figure 12). The hierarchical localization gives us just a vector of indices defining the relative location of a point in the multi-resolution grid. This step secures the correct localization inside the fractal shape of Gosper islands and we describe the procedure in detail in Section 3.4.1. As the Gosper fractal is defined recursively, the specific pattern transformation and indexation for the different recursive branches can be computed only in the top-down manner. Thus, the indices returned by the first part of the algorithm have to be recursively recalculated in the top-down manner (see Section 3.4.2). The second part of the algorithm returns the correct indices that are used to compute the final hash code defining the point order along the Node-Gosper SFC.
3.4.1. Gosper Hierarchical Localization
The task is to determine the relative position of the current hexagon in the context of the parent hexagon. We ignore the difficulties with rotation and passage order in different branches of recursion for start. First, a point is localized in the level-n hexagonal grid (details in [,,]) using the matrix (12) which returns the axial coordinates of the hexagon containing the point . The next procedure computes only the relative transformation between axial coordinates which is independent on the specific of hexagons. As mentioned before, the center points of hexagons can be reliably localized inside the parent hexagon. Thus, our transformation between levels i and consists of three steps:
- Calculation of hexagon center according to axial coordinates .
- Transformation of the according to the orientation of the parent grid.
- Localization of the transformed center point in the parent grid and calculation of the new axial coordinates .
The superior grid of level- should be scaled by and rotated by . However, it is easier to preserve the same transformation matrix for calculation of all indices and alternatively transform the center point (scaled by , rotated by ), so the matrix G (6) is used instead. The transformation between levels i and can be written as follows:
where C is the matrix (11) computing the center of a hexagon according to the axial coordinates, is the inverse matrix (12) computing the axial coordinates from the center point and G is the forward transformation matrix (6) (read [,,] for details).
The final constant matrix T is calculated as:
and are the integer axial coordinates of hierarchically corresponding hexagons at level i and . As the transformation matrix T produces real unrounded coordinates, we denote the parent real axial coordinates as that have to be rounded to the closest integers . Their hierarchical relationship with child axial coordinates can be derived as:
The Equation (14) computes the transformed axial coordinates, but we also need to compute the hexagon index corresponding to the Node-Gosper pattern described in Section 3.2. Let the parent axial coordinates denote as . They are recalculated to the cube coordinates as according to the condition . The decimal part of coordinates represents the relative position between the child and parent hexagon. The relative decimal coordinates , , are computed as:
As each hexagon center is close to one vertex and edge of the parent grid (see Figure 12), the dominant axis and its sign determine the index of the child hexagon in the view of the parent hexagon. The advantage is that this numeric transfer takes into account the negative coordinates of points, so that the dataset can be positioned anywhere in the space. The relative decimal coordinates can be recalculated to the index of the default pattern (Figure 13 P1), where is defined as:
The threshold constant represents some small decimal number ( works well). As the coordinate transformation works on the level of a unitary grid, the method is numerically stable. The optimized algorithm is summarized in Algorithm 1.
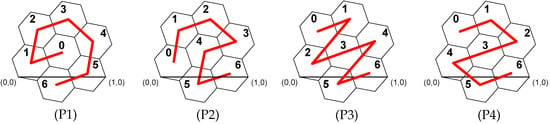
Figure 13.
Four different hexagonal indexation patterns. The pattern (P1) is the default one.
| Algorithm 1 Hierarchical point mapping |
|
3.4.2. Index Conversion
Section 3.4.1 described a general method for hierarchical localization of a point in the level-n Gosper island. This section shows how to recalculate the default indexation model to other models. Especially, it defines a method solving the difficulties like pattern rotation and passage order to construct the correct Node-Gosper SFC.
Let be a vector of indices returned by Algorithm 1, where n is the number of hierarchical levels. Each can be further transfered to final index , where is the function defined in Table 1. The different indexation patterns are shown in Figure 13 and their conversion is very simple. The final vector of indices defines the hierarchical address of a hexagon in the Gosper island to define the final order of hexagons. Each can be represented by three bits, so all the indices are masked to the corresponding bits of hash according to the index significance (read Section 3.2).

Table 1.
Table defining the transfer function between default index of pattern (P1) and patterns (P2), (P3) and (P4) according to types in Figure 13, where .
The procedure computing the correct Node-Gosper curve is more complicated. There are two tasks:
These properties have recursive nature and they cannot be solved by bottom-up localization. The has to be recalculated to obtain the indexation model described in Section 3.2. The whole method is described in Algorithm 2. Here, we summarize it in two steps:
- As the patterns are rotated only by (1), the rotation can be done by index shifting. The default indexation has the index 0 on the central hexagon and the indices 1–6 form a ring of hexagons. Let the be a number symbolizing the pattern rotation on the i-th level by . The shifted index is computed as explained in Algorithm 2 (lines 2–11).
- The passage order is reversed depending on the current pattern as explained in Section 3.3. The algorithm is described in Algorithm 2 (lines 12–16).
| Algorithm 2 Node-Gosper index computation |
|
4. Experiments and Discussion
This section evaluates our novel Node-Gosper SFC based on the hexagonal grid defined in Section 3. SubSection 4.1 compares the complexity and distance metrics of our algorithm with older methods and SFCs. SubSection 4.2 evaluates the pros and cons of the presented curve.
4.1. Comparison
Our method is compared with the older approximative top-down Gosper SFC [], the naive bottom-up approach [] and several widely used triangular and orthogonal SFCs. After extensive research, we have not found any other Gosper-based SFC method for comparison. The section is divided into three subsections comparing correctness of point localization, execution time and distance metrics.
All experiments run on the following hardware: Intel Core i7-7700HQ @ 2.8 GHz, 16 GB RAM, Windows 10 64-bit
4.1.1. Jagged Edges
Incorrect hierarchical point localization during the construction of the Node-Gosper SFC induces wrong point mapping along the curve []. The general Gosper islands are non-convex fractal tiles, so that the jagged edges of islands overstep the borders of parent hexagons. The previous algorithms [,] could not efficiently deal with jagged edges (Figure 14). The experiment presented in Figure 14 uses a point cloud representing the nodes of the level-5 Node-Gosper curve that are hashed according to the top-down and bottom-up methods. The figure confirms that the correct Node-Gosper SFC cannot be constructed by top-down decomposition of hexagons [], because it produces different types of polygonal clusters that do not preserve the features of the hexagonal grids. The misclassified points are accumulated close to the solid hexagonal edges between the Gosper islands (Figure 14A). Our method uses the bottom-up approach (Figure 14B) composing the Gosper islands from subordinate hexagons, which secures right point localization in the hexagonal hierarchy and produces the correct Node-Gosper SFC passing through the nodes of a regular hexagonal grid. The Gosper islands are undamaged and respecting the jagged edges (Figure 14B).
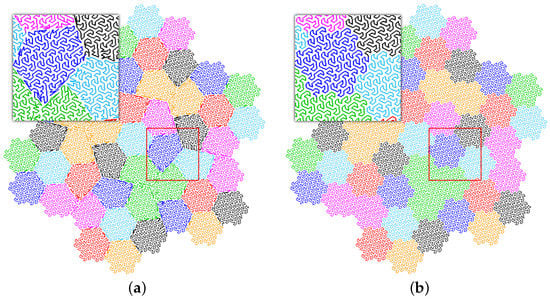
Figure 14.
The comparison of (a) top-down and(b) bottom-up level-5 Node-Gosper SFC. The top-down method obviously cannot solve the problem with jagged edges, because it produces non-hexagonal sub-clusters.
4.1.2. Efficiency
The efficiency of the curve construction is also a crucial problem, because an SFC with expensive hashing function is not suitable for practical usage regardless of the outstanding theoretical metrics. Next experiment is conducted to compare the execution times of our new optimized Node-Gosper method with other algorithms including the naive implementation of Node-Gosper curve [] and the Node-Gosper simple curve, which uses our new mapping algorithm (Algorithm 1) without additional index conversion (second recursive part) required for the correct Node-Gosper SFC. The simple variant is faster and can be used for general hierarchical hexagonal model without quality requirements on the final SFC. As the complexity of a hashing function is considered to be constant, the construction times are measured using a randomly generated dataset of uniformly distributed points. The chart in Figure 15 shows that our new algorithm is four times faster than the naive old one. In rough comparison with non-hexagonal SFCs (Z-order, Hilbert, Sierpińsky), the Node-Gosper hashing algorithm is approximately two times slower. However, this is a logical consequence of applied tiling. Unlike with quads (4-pattern) or triangles (2-pattern), seven sub-clusters have to be considered at each level, thus the number of clusters generated by Node-Gosper curve is much greater for the same hierarchical level than the number of quads, e.g., for a complete SFC contains triangles, quads and hexagons. It means that the hashing function of Node-Gosper curve is more time consuming but the construction time covers much greater number of sub-clusters creating finer tessellation of the space. To compare SFCs based on different grids, we compute the total construction time per cluster:
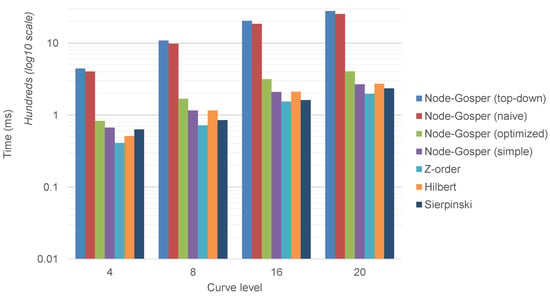
Figure 15.
The graph shows a comparison of construction times of our Node-Gosper (optimized) method with selected space-filling curves including the previous naive Node-Gosper algorithm [], top-down Node-Gosper algorithm [] and simple Node-Gosper (Figure 13 P2) algorithm grouping the hexagons into Gosper islands without additional pattern rotation and clusters reordering. Each measurement was performed on a random dataset with points for different levels of clustering.
Definition 1.
Letbe the total construction time of the SFC, letbe the hierarchical level until which the SFC is generated and letbe the number of sub-clusters of the tiling pattern, the time per cluster is computed as:
The metric in Definition 1 takes into account the number of clusters that have to be checked during the evaluation of hashing function which is applicable for any SFC based on the different types of grids. This metric is computed and compared for all SFCs in the chart in Figure 16. The chart shows that our optimized Node-Gosper SFC is actually faster than other good SFCs such as Hilbert and Sierpińsky curve and way faster than older variants of the Node-Gosper SFC. Moreover, the tiling with Gosper islands has Arrwwid number [], which means that a sufficiently small disc hits at most 3 tiles at each level, while for orthogonal and for triangular grids. This feature can be successfully utilized to define an efficient query structure based on the Node-Gosper curve in the future.
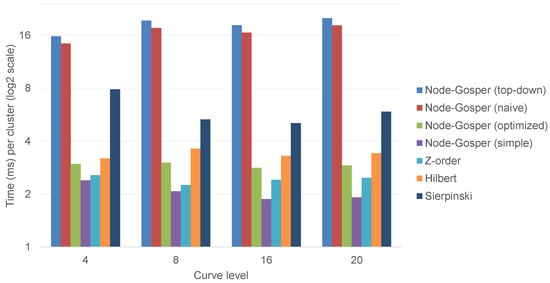
Figure 16.
The graph shows total construction times per cluster. Each method has a different number of sub-clusters per pattern (triangular Sierpińsky: 2, orthogonal Z-order and Hilbert: 4, hexagonal Node-Gosper: 7), and thus, produces different number of clusters on the same hierarchical level. This metric is computed as (total time/(sub-clusters × curve level)) and it helps to compare the real time complexity of different point indexing methods. The graph compares of our novel Node-Gosper (optimized) method with the older ones [,] and other SFCs. Each measurement was performed on a random dataset with points for different levels of clustering.
4.1.3. Distance Metrics
The last test is focused on the distance metrics of SFCs. The basic requirement for a good SFC is that two points along a curve should be close in the multidimensional space as well. The principal metric here is the sum of distances between the query point and 64 closest points along the curve (32 antecedent, 32 following). The metric average of all the points in the dataset is displayed in the charts in Figure 17. The charts compare four variants of the Node-Gosper curve (patterns Figure 13 P1–P4) and other 3 commonly used SFCs tested with six different datasets summarized in Table 2. The first three ones are randomly generated datasets with uniform or Gaussian distribution. The Gaussian islands is a dataset containing several clusters with Gaussian distribution. The datasets S1, S2 and S3 were downloaded from the web page []. Experiments show that the Node-Gosper curve is comparable with Hilbert or Sierpiński curves, its metrics are stable according to the standard deviation and its much better than other simple variants of SFCs. The top-down variant seems to have comparable metrics, but points are not localized correctly along the curve, so that it is not a good option.
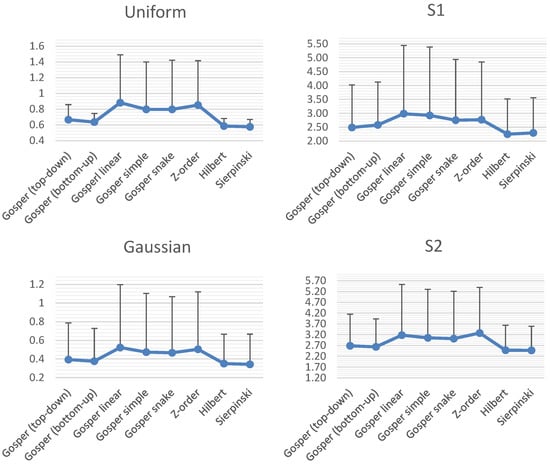
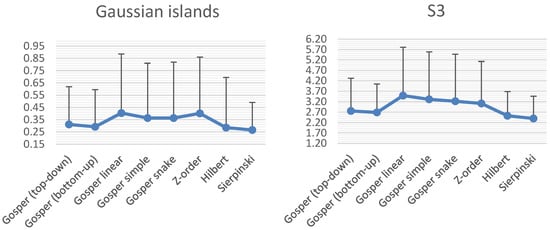
Figure 17.
The comparison of distance metrics of different curves. For each point the sum of distances to the closest 64 neighbors lying along the curve represents the principal metric value. The graph shows average and standard deviation of values of all points from a dataset. The distances were normalized by length of the bounding box diagonal. The Gosper SFCs represent the Node-Gosper type of the curve.

Table 2.
The list of tested datasets with corresponding point number and the length of the bounding box diagonal. The datasets were obtained from website [].
4.2. Properties
Finally, we summarize the main properties of our proposed curve which fulfill the requirements for a good SFC.
- Bijective mapping—Section 3.2, Section 3.3 and Section 3.4 defined how to map a point onto the Node-Gosper curve and how to compute a cluster point according to the given code.
- The curve is space-filling—every point of space lies on the curve. The dataset has to be fitted into the circle inscribed into the Gosper island.
- Total ordering—there are no pattern crossings, thus each cluster is visited by SFC only once.
- Localization— points close on the curve are also spatially close (see Figure 17).
- Sequentialisation—the Node-Gosper SFC does not lead to continuous sequence of code numbers.
The only trouble here is the sequentialisation, because our SFC is based on the 7-pattern, so there is a code gap between the cluster levels. However, it does not have to be a real problem for general clustering purposes. Sparse datasets lead to an incomplete SFC anyway, because the empty areas make an indexation gap along the curve, so most of the clustering methods do not rely on it. Overall, the Node-Gosper curve is a very good hexagonal SFC.
5. Conclusions
The main contribution of this paper is the new hexagonal space-filling curve (SFC) algorithm called the Node-Gosper SFC based on the recursive Gosper fractal. To the best of our knowledge, there is no paper defining a Gosper-based point indexing method except our previous naive proposals. As the multi-resolution hexagonal grids are highly required in various scientific fields such as computer graphics, image processing, data visualization and geographic information systems (GISs), our hexagonal Node-Gosper SFC represents an effective point indexing method applicable in those areas. This paper summarizes the background about the hierarchical hexagonal point clustering and the corresponding theory. It shows that the multi-resolution hexagonal grids have several outstanding properties including uniform distance between cells and the best coverage of circular queries. The paper surveys the existing SFC methods and highlights the current problems of the hexagonal clustering including the issues with hierarchical decomposition of hexagons, fractal shape of hexagonal composites and their reasonable indexation. Our method solves all those issues. In comparison with our older approaches, the novel method can deal with jagged edges and it is four times faster. The tests showed that the curve has similar distance properties as widely preferred non-hexagonal SFCs (Hilbert, Sierpinski, etc.) and its construction is even faster. Thus, our Node-Gosper SFC represents a scalable, rapid and stable method for hexagonal hierarchical indexing with good quality parameters.
The future work aims at hierarchical hexagonal structures construction and their application for the practical tasks including data visualization or location indexing in GISs. The discussed metrics and measurements already bring us promising results in areas like nearest neighbors search or range query.
Author Contributions
Conceptualization, V.U. and P.G.; methodology, V.U.; software, V.U.; validation, V.U., M.R. and Y.-C.L.; formal analysis, V.U. and P.G.; investigation, V.U.; resources, V.U., V.S. and Y.-C.L.; data curation, V.U., P.G. and V.S.; writing—original draft preparation, V.U.; writing—review and editing, P.G., V.S., M.R. and Y.-C.L.; visualization, V.U.; supervision, V.S. and Y.-C.L.; project administration, V.U. and V.S.; funding acquisition, V.S.
Funding
This work was supported by SGS project, VSB-Technical University of Ostrava, under the grant no. SP2019/141.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GIS | Geographic Information System |
| NN | Nearest Neighbor |
| PC | Point Cloud |
| SFC | Space-Filling Curve |
References
- Bader, M. Space-Filling Curves: An Introduction with Applications in Scientific Computing; Springer Publishing Company, Incorporated: Heidelberg/Berlin, Germany, 2012. [Google Scholar]
- Lawder, J.K.; King, P.J.H. Using Space-Filling Curves for Multi-dimensional Indexing. In Proceedings of the 17th British National Conferenc on Databases: Advances in Databases; Springer: London, UK, 2000; pp. 20–35. [Google Scholar]
- Skopal, T.; Krátký, M.; Pokorný, J.; Snášel, V. A New Range Query Algorithm for Universal B-trees. Inf. Syst. 2006, 31, 489–511. [Google Scholar] [CrossRef][Green Version]
- Lauterbach, C.; Garland, M.; Sengupta, S.; Luebke, D.; Manocha, D. Fast BVH Construction on GPUs. Comput. Graph. Forum 2009, 28, 375–384. [Google Scholar] [CrossRef]
- Isaac, T.; Burstedde, C.; Ghattas, O. Low-Cost Parallel Algorithms for 2:1 Octree Balance. In Proceedings of the 2012 IEEE 26th International Parallel Distributed Processing Symposium (IPDPS), Shanghai, China, 21–25 May 2012; pp. 426–437. [Google Scholar]
- Gardner, M. Mathematical Games—In which “monster” curves force redefinition of the word “curve”. Sci. Am. 1976, 235, 124–133. [Google Scholar] [CrossRef]
- Uher, V.; Gajdoš, P.; Radecký, M.; Snášel, V. A proposal of hierarchical vertex clustering based on the Gosper curve. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 632–637. [Google Scholar]
- Uher, V.; Gajdoš, P.; Snášel, V. Towards the Gosper Space Filling Curve Implementation. In Proceedings of the 2017 3rd IEEE International Conference on Cybernetics (CYBCONF), Exeter, UK, 21–23 June 2017; pp. 1–8. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Samet, H. Foundations of Multidimensional and Metric Data Structures; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2005. [Google Scholar]
- Brodsky, I. H3: Uber’s Hexagonal Hierarchical Spatial Index. 2019. Available online: https://eng.uber.com/h3/ (accessed on 20 April 2019).
- Gajdoš, P.; Ježowicz, T.; Uher, V.; Dohnálek, P. A parallel Fruchterman–Reingold algorithm optimized for fast visualization of large graphs and swarms of data. Swarm Evol. Comput. 2016, 26, 56–63. [Google Scholar] [CrossRef]
- Uher, V.; Gajdoš, P.; Ježowicz, T. Solving nearest neighbors problem on GPU to speed up the Fruchterman-Reingold graph layout algorithm. In Proceedings of the 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015; pp. 305–310. [Google Scholar]
- Pharr, M.; Jakob, W.; Humphreys, G. Physically Based Rendering: From Theory to Implementation; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Langetepe, E.; Zachmann, G. Geometric Data Structures for Computer Graphics; AK Peters, Ltd.: Natick, MA, USA, 2006. [Google Scholar]
- Sonka, M.; Hlaváč, V.; Boyle, R. Image Processing, Analysis, and Machine Vision; Cengage Learning: Boston, MA, USA, 2014. [Google Scholar]
- Ahuja, N. On approaches to polygonal decomposition for hierarchical image representation. Comput. Vis. Graph. Image Process. 1983, 24, 200–214. [Google Scholar] [CrossRef]
- Middleton, L.; Sivaswamy, J. Hexagonal Image Processing: A practical Approach; Advances in Computer Vision and Pattern Recognitio; Springer: London, UK, 2006. [Google Scholar]
- Sahr, K. Hexagonal discrete global grid systems for geospatial computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Ben, J.; Tong, X.; Chen, R. A spatial indexing method for the hexagon discrete global grid system. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–5. [Google Scholar]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hexagonal connectivity maps for Digital Earth. Int. J. Digit. Earth 2015, 8, 750–769. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Samavati, F.; Peterson, P. Categorization and Conversions for Indexing Methods of Discrete Global Grid Systems. ISPRS Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hierarchical Grid Conversion. Comput. Aided Des. 2016, 79, 12–26. [Google Scholar] [CrossRef]
- Wang, D.; Xu, L.; Peng, J.; Robila, S. Subdividing Hexagon-Clustered Wireless Sensor Networks for Power-Efficiency. In Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing, Kunming, China, 6–8 January 2009; Volume 2, pp. 454–458. [Google Scholar]
- Bandara, H.M.N.D.; Jayasumana, A.P.; Illangasekare, T.H. A Top-Down Clustering and Cluster-Tree-Based Routing Scheme for Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2011, 7, 1–17. [Google Scholar] [CrossRef]
- Márquez, A.; Plaza, Á.; Suárez, J.P. Hamiltonian triangular refinements and space-filling curves. J. Comput. Appl. Math. 2019, 346, 18–25. [Google Scholar] [CrossRef]
- Su, T.; Wang, W.; Lv, Z.; Wu, W.; Li, X. Rapid Delaunay triangulation for randomly distributed point cloud data using adaptive Hilbert curve. Comput. Graph. 2016, 54, 65–74. [Google Scholar] [CrossRef]
- Ivrissimtzis, I.; Dodgson, N.; Sabin, M. A generative classification of mesh refinement rules with lattice transformations. Comput. Aided Geom. Des. 2004, 21, 99–109. [Google Scholar] [CrossRef][Green Version]
- Alexa, M. Refinement operators for triangle meshes. Comput. Aided Geom. Des. 2002, 19, 169–172. [Google Scholar] [CrossRef]
- Franklin, W.R. Nearest Point Query on 184M Points in E3 with a Uniform Grid. In Proceedings of the 17th Canadian Conference on Computational Geometry (CCCG’05), Windsor, ON, Canada, 10–12 August 2005; pp. 239–242. [Google Scholar]
- Vitter, J.S. External Memory Algorithms and Data Structures: Dealing with Massive Data. ACM Comput. Surv. (CSUR) 2001, 33, 209–271. [Google Scholar] [CrossRef]
- Butz, A.R. Convergence with Hilbert’s Space Filling Curve. J. Comput. Syst. Sci. 1969, 3, 128–146. [Google Scholar] [CrossRef]
- Lam, W.M.; Shapiro, J.M. A Class of Fast Algorithms for the Peano-Hilbert Space-Filling Curve. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; Volume 1, pp. 638–641. [Google Scholar]
- Breinholt, G.; Schierz, C. Algorithm 781: Generating Hilbert’s Space-Filling Curve by Recursion. ACM Trans. Math. Softw. 1998, 24, 184–189. [Google Scholar] [CrossRef]
- Middleton, L.; Sivaswamy, J. Edge detection in a hexagonal-image processing framework. Image Vis. Comput. 2001, 19, 1071–1081. [Google Scholar] [CrossRef]
- Ohn, S.Y. Neighborhood Decomposition of Convex Structuring Elements for Mathematical Morphology on Hexagonal Grid. In Proceedings of the 21st International Conference on Computer and Information Sciences; Springer: Berlin/Heidelberg, Germnay, 2006; pp. 511–521. [Google Scholar]
- Bell, S.; Diaz, B.; Holroyd, F.; Jackson, M. Spatially referenced methods of processing raster and vector data. Image Vis. Comput. 1983, 1, 211–220. [Google Scholar] [CrossRef]
- Burt, P.J. Tree and pyramid structures for coding hexagonally sampled binary images. Comput. Graph. Image Process. 1980, 14, 271–280. [Google Scholar] [CrossRef]
- Gibson, L.; Lucas, D. Vectorization of raster images using hierarchical methods. Comput. Graph. Image Process. 1982, 20, 82–89. [Google Scholar] [CrossRef]
- Vince, A. Indexing the aperture 3 hexagonal discrete global grid. J. Vis. Commun. Image Represent. 2006, 17, 1227–1236. [Google Scholar] [CrossRef]
- Sahr, K. On the Optimal Representation of Vector Location using Fixed-Width Multi-Precision Quantizers. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-4/W2, 1–8. [Google Scholar] [CrossRef]
- Haverkort, H.J. Recursive tilings and space-filling curves with little fragmentation. J. Comput. Geom. 2011, 2, 92–127. [Google Scholar]
- Uher, V.; Gajdoš, P.; Ježowicz, T.; Snášel, V. Application of Hexagonal Coordinate Systems for Searching the K-NN in 2D Space. In Innovations in Bio-Inspired Computing and Applications; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 424, pp. 209–220. [Google Scholar]
- Muelder, C.; Ma, K.L. Rapid Graph Layout Using Space Filling Curves. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1301–1308. [Google Scholar] [CrossRef] [PubMed]
- Auber, D.; Huet, C.; Lambert, A.; Renoust, B.; Sallaberry, A.; Saulnier, A. GosperMap: Using a Gosper Curve for Laying Out Hierarchical Data. Vis. Comput. Graph. IEEE Trans. 2013, 19, 1820–1832. [Google Scholar] [CrossRef] [PubMed]
- Wyvill, B. Painting with Flowsnakes. In Proceedings of the Workshop on Computational Aesthetics; Eurographics Association: Aire-la-Ville, Switzerland, 2015; pp. 171–182. [Google Scholar]
- Hales, T.C. The honeycomb conjecture. Discret. Comput. Geom. 2001, 25, 1–22. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Co.: New York, NY, USA, 1983. [Google Scholar]
- Haverkort, H.; van Walderveen, F. Locality and bounding-box quality of two-dimensional space-filling curves. Comput. Geom. 2010, 43, 131–147. [Google Scholar] [CrossRef]
- Blåsjö, V. The Isoperimetric Problem. Am. Math. Mon. 2005, 112, 526–566. [Google Scholar] [CrossRef]
- Chang, H.C.; Wang, L.C. A simple proof of Thue’s Theorem on circle packing. arXiv 2010, arXiv:1009.4322. [Google Scholar]
- Patel, A.J. Red Blob Games—Hexagonal Grids. 2019. Available online: http://www.redblobgames.com/grids/hexagons/ (accessed on 20 March 2019).
- Bédorf, J.; Gaburov, E.; Portegies Zwart, S. A Sparse Octree Gravitational N-body Code That Runs Entirely on the GPU Processor. J. Comput. Phys. 2012, 231, 2825–2839. [Google Scholar] [CrossRef]
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic Discrete Global Grid Systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Smith, W.D. Space-filling curves, Randomness, and Geometry Problems. 2019. Available online: http://rangevoting.org/SpaceFillCurve.html (accessed on 20 March 2019).
- Ventrella, J. Brainfilling Curves—The Root 7 Family. 2019. Available online: http://www.fractalcurves.com/Root7.html (accessed on 20 March 2019).
- Riddle, L. Classic Iterated Function Systems—Flowsnake. 2019. Available online: http://ecademy.agnesscott.edu/~lriddle/ifs/ksnow/flowsnake.htm (accessed on 20 March 2019).
- Bishop, C.J.; Jones, P.W.; Pemantle, R.; Peres, Y. The Dimension of the Brownian Frontier is Greater Than 1. J. Funct. Anal. 1997, 143, 309–336. [Google Scholar] [CrossRef][Green Version]
- Fränti, P. Clustering Basic Benchmark. 2019. Available online: https://cs.joensuu.fi/sipu/datasets/ (accessed on 20 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).