Abstract
Pilot contamination is the reuse of pilot signals, which is a bottleneck in massive multi-input multi-output (MIMO) systems as it varies directly with the numerous antennas, which are utilized by massive MIMO. This adversely impacts the channel state information (CSI) due to too large pilot overhead outdated feedback CSI. To solve this problem, a compressed sensing scheme is used. The existing algorithms based on compressed sensing require that the channel sparsity should be known, which in the real channel environment is not the case. To deal with the unknown channel sparsity of the massive MIMO channel, this paper proposes a structured sparse adaptive coding sampling matching pursuit (SSA-CoSaMP) algorithm that utilizes the space–time common sparsity specific to massive MIMO channels and improves the CoSaMP algorithm from the perspective of dynamic sparsity adaptive and structural sparsity aspects. It has a unique feature of threshold-based iteration control, which in turn depends on the SNR level. This approach enables us to determine the sparsity in an indirect manner. The proposed algorithm not only optimizes the channel estimation performance but also reduces the pilot overhead, which saves the spectrum and energy resources. Simulation results show that the proposed algorithm has improved channel performance compared with the existing algorithm, in both low SNR and low pilot overhead.
1. Introduction
A massive multi-input multi-output (MIMO) system utilizes a large number of transmitting antennas on the base station and simultaneously serves multiple single receiver antenna users [1]. Therefore, massive MIMO shows good anti-noise and anti-narrowband fading ability, so as to make better use of increasingly precious spectrum and energy resources, and is poised to become the key technology for the future development of 5G [2,3]. In massive MIMO systems, accurate channel state information (CSI) is required for signal detection, beamforming, resource allocation, and channel allocation. Therefore, the channel estimation scheme with outstanding performance has become the supporting technology for massive MIMO. Pilot contamination, on the other hand, is considered as a bottleneck as the pilot sequence is limited and it is reused in massive MIMO and varies with the number of antennas [1,2]. Therefore, such pilot signal reuse causes contamination which reduces the accuracy of CSI. Moreover, pilot contamination puts asymptotic limits on the spectral efficiency, creates coherent interference, and also results from many users using the pilot signals in different cells in massive MIMO systems [3]. At present, most of the research on massive MIMO is carried out in time division duplex (TDD) mode, with the aim of utilizing the reciprocity of uplink and downlink channels. The CSI of the downlink channel is obtained by channel estimation for the uplink [4]. However, the frequency division duplex (FDD) mode has lower latency and higher communication efficiency than the TDD mode, and the current cellular systems in most countries in the world use FDD mode [5]. Therefore, research on channel estimation for massive MIMO in FDD mode has far-reaching significance.
However, in FDD mode, an accurate estimation of the downlink is very difficult [6]. A large number of antennas are distributed on the base station, and these transmissions are simultaneously sent to the user. Therefore, the data requires the user side to accurately estimate the CSI formed by each of the transmitting antennas and the single receiving antenna on the user side. It is also very difficult to satisfy both high accuracy and low pilot overhead.
OFDM systems have many advantages, such as higher spectrum utilization, good resistance to multipath interference, and the ability to resist narrowband fading [7]. In today’s surge in wireless communication users, more system capacity needs to be upgraded. Therefore, the OFDM system is combined with massive MIMO systems to achieve antenna diversity and spatial multiplexing [7]. In the current communication environment, the available wireless bandwidth is becoming more and more scarce. Combining the two systems can greatly improve the utilization of the spectrum resource, and can also effectively deal with the selective fading environment of the wireless channel frequency.
In the typical broadband wireless transmission environment, frequency-selective fading occurs. Therefore, in order to solve this problem, we use massive MIMO in combination with OFDM systems to establish a massive MIMO-OFDM system [8]. In a massive MIMO-OFDM transmission environment, a large number of scatters are distributed to form a Rayleigh multipath transmission channel, and most of the energy of the wireless channel is concentrated on the very small component of the channel impulse response (CIR) [9], so that the CSI formed by the user side and the base station naturally exhibit sparsity [10,11].
Based on the sparsity of the channel, the channel can be estimated using compressed sensing (CS) [12]. However, in the actual environment, the sparseness of the wireless channel is unknown as in the above literature. Then, the algorithms itself cannot estimate the channel without knowing the sparsity [13]. Therefore, this paper proposes the structured sparse adaptive coding sampling matching pursuit (SSA-CoSaMP) algorithm. The use of spatial common sparsity can not only improve the estimation performance, but also save the pilot overhead, and enable the algorithm to obtain the sparsity adaptive ability.
The main contributions of this paper are:
- (a)
- It improves the existing CoSaMP [14] algorithm from the dynamic sparsity adaptive and structural aspects.
- (b)
- The proposed algorithm has a feature to estimate the channel without unknown sparsity. This is realized by the threshold parameter which provides information on when to stop the iterations to get the required sparsity of channel.
- (c)
- Based on the adaptive sparsity, the massive MIMO channel space–time common sparse characteristics are used for structural processing. This not only makes the acquisition of sparsity faster but also improves estimation performance and accuracy.
- (d)
- A simulation program verifies the accuracy and performance comparison of the proposed channel estimation algorithm with the existing CoSaMP [14], structured CoSaMP (S-CoSaMP) [9], and structured turbo-CS [14] algorithms.
Furthermore, the proposed method utilizes the unique feature of threshold -based iteration control, which in turn depends on the SNR level. This approach enables us to determine the unknown sparsity in an indirect manner.
2. Space–Time Common Sparsity Modeling
2.1. The Spatial Common Sparsity
In the actual environment of signal transmission in massive MIMO-OFDM systems, a large number of scatterers are distributed to form a Rayleigh multipath transmission channel, and most of the energy of the wireless channel is concentrated on the very small components of the CIR [14], so that the CSIs formed by the user side and the base station naturally exhibit sparsity [15]. At the same time, when the signal from each transmitting antenna on the base station reaches the receiving antenna on the user side, the scatters passing through are very similar and almost identical. That is, the single antenna on the user has the characteristics of the spatial sparsity of all antennas on the base station. In addition, since the path delay varies much more slowly than the gain associated with the time channel, this sparsity is almost constant during the coherence time [16], forming a temporal correlation.
A typical single-cell downlink multi-user massive MIMO-OFDM wireless communication system has common spatial sparsity, which is caused by many factors, such as multipath effect, antenna physical characteristics, and wireless transmission environment. In a wireless transmission environment, the scatterer causes the signal to form multiple paths from the same transmit antenna to the receive antenna, creating a multipath effect. However, in these paths, the time from the transmitting antenna to the receiving antenna is also inconsistent [17]. Therefore, most of the energy with CIR is concentrated on a very small part of the multipath component; that is, the CIR energy is not evenly distributed over all the taps of the channel, which exhibits sparsity. In particular, the CIR formed between the transmit antenna of a massive MIMO and the user of a single antenna can be expressed as:
where represents the OFDM symbol and represent the equivalent channel length, .
The support set of can be expressed as:
where represents the minimum noise in the channel. The sparsity is affected by the actual propagation environment and the sparse nature of multipath propagation. In general, .
In a typical massive MIMO, the antenna array on the base station is dense, and the spacing between the antennas is relatively small compared to the distance traveled by the signals arriving at the user-side single antenna, so that is negligible, and there is a common scatterer in the channel between each transmitting and receiving antenna. Therefore, each antenna on the base station exhibits a highly similar path delay to the user’s single antenna [18,19], as shown in Figure 1.
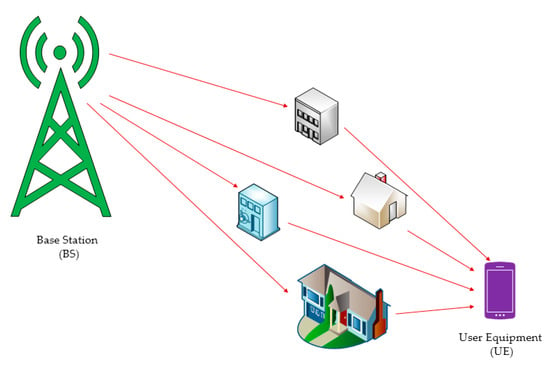
Figure 1.
Massive multi-input multi-output (MIMO) space common sparsity model.
The sparse characteristics of the CIR between different pairs of transmitting antennas are mostly coincident. This is the common spatial sparsity of massive MIMO channels. That is, for the OFDM symbol, different transmit antennas maintain the same sparsity, which can be expressed as:
2.2. Time Correlation
In terms of time, the path gains of the channel change much more slowly [20], thus showing the characteristics of time correlation, even in the case of fast time-varying channels. In other words, although the path gain varies greatly from one OFDM symbol to the next OFDM symbol, the path delay in successive OFDM symbols remains almost unchanged. This is because, in time-varying channels, the path delay time is inversely proportional to the system bandwidth, while the path gain coherence time is inversely proportional to the system carrier frequency [21]. That is, in the coherence time of the path gain, since the path delay remains almost unchanged, the CIR of the consecutive OFDM symbols remains the same as the common sparsity, as shown in Figure 2, i.e.,
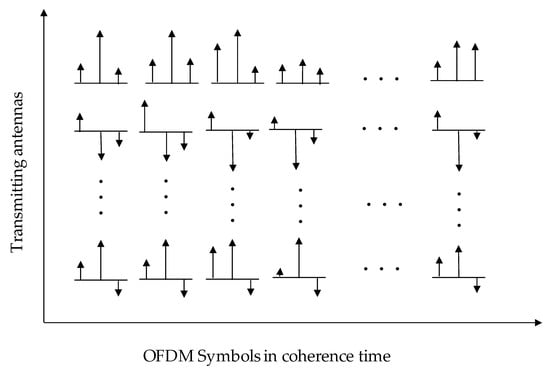
Figure 2.
Space–time common sparseness diagram.
In summary, the spatial sparsity and time correlation are collectively referred to as space–time common sparseness [22,23,24,25,26].
3. System Model
A typical FDD mode massive MIMO-OFDM system was established. The number of base station antennas in the cell was , and the number of single antenna users was , and , as shown in Figure 3. The total number of subcarriers of the OFDM symbol was , and the signal (including data and pilot) transmitted by the antenna of the base station was .
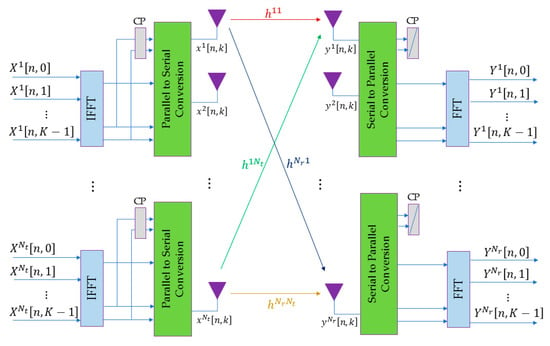
Figure 3.
Massive MIMO-OFDM framework.
Then, the signal received by the user side can be expressed as:
After removing the guard interval and performing the DFT transform, the user side extracts the pilot information in the OFDM symbol from the received information according to the pilot allocation scheme, and can be expressed as:
where denotes the position information of the subcarriers occupied by the pilot in one OFDM symbol.
In this paper, the pilot scheme is a non-orthogonal pilot allocation scheme (see Section 4 for details) = , where represents the set of pilot amplitudes of the antenna. denotes a DFT matrix of size , denotes the first rows of , denotes a submatrix according to , and denotes an additive white Gaussian noise (AWGN) noise vector of the OFDM symbol in the channel. Simplifying Equation (6) gives:
where and .
In massive MIMO-OFDM systems, . Therefore, Equation (7) is an undetermined equation, which cannot be reliably estimated using a traditional channel estimation method such as least squares (LS). However, after the above analysis, it is known that is a high-dimensional sparse signal. Therefore, the compressed sensing theory can be used to reconstruct from the low-dimensional . In addition, the spatial common sparseness inherent in massive MIMO mentioned in Section 2.1 can improve the reconstruction performance of the CS algorithm.
Let , and then arrange to get:
Similarly, let , then can be expressed as:
Therefore, Equation (9) can be organized as:
After the above-mentioned transformation deformation using the common sparsity of the wireless massive MIMO system, the sparsity of is structured to enhance the sparsity.
Using the temporal correlations mentioned in Section 2.2, the spatial common sparsity of a massive MIMO system is nearly constant over several consecutive OFDM symbols of coherence time. Therefore, under the pilot allocation scheme, the continuous OFDM symbols in the coherence time are processed, and Equation (10) can be organized as:
where , , and . can also be expressed as . Based on the time correlation of the wireless massive MIMO channel, based on Equation (10), the channel CIR matrix is further structured to obtain Equation (11), which improves the sparsity and improves the estimation performance of the CS algorithm.
4. Proposed Algorithm
4.1. Sparse Degree Adaptive Principle
In an actual communication environment, the sparsity of a channel is unknown, and the channel state changes with time or space. Therefore, in order to better apply in engineering, we propose a dynamic sparsity adaptive improvement scheme based on the threshold idea. Different from the traditional reconstructing algorithm, the number of iterations is determined according to the sparsity degree. The proposed scheme determines the number of iterations by setting a threshold, that is, the algorithm stops iterating when the residual value and the observed value are in the ratio relationship required to stop the iterative parameter. Moreover, the stop iteration parameter is not a fixed value, and it stops the iteration parameters differently under different channel states. The channel state is characterized by SNR. According to this, it can be expressed as:
where represents the residual and represent the observed value. means the stop iteration parameter, which is not of fixed value but is different under different SNR.
In summary, it can be known that the proposed dynamic sparsity adaptive scheme has the following characteristics:
- (a)
- Sparseness adaptation: In the case of unknown sparsity, the number of iterations can still be controlled by Equation (12), and finally the iteration is stopped, and the sparsity is obtained, thereby improving the ability of the algorithm in practical engineering applications.
- (b)
- Stop the dynamic setting of the iteration parameter : The influence of noise on the observation value will be different under different channel states, so the stop iteration parameter cannot be set to a fixed value but should be in different channel states. It is different, and the channel state is characterized by SNR, that is, the stop iteration parameter is different under different SNRs.
In [27], the method of using the threshold is also mentioned to make the algorithm adaptively obtain the sparsity, but the set stop iteration parameter is a fixed value, and the iterative parameters cannot be stopped according to the channel state change, and the proposed algorithm can dynamically get sparsity.
4.2. Proposed SSA-CoSaMP Algorithm
By exploiting the characteristics of the sparse channel, the reconstruction performance is improved from the aspects of structuring and dynamic sparsity adaptation. The specific steps of the sparse adaptive CoSaMP (SSA-CoSaMP) is proposed in Algorithm 1.
| Algorithm 1. SSA-CoSaMP |
| Input: Signal observation value , observation matrix , maximum channel length , number of antenas configured on the base station , number of consecutive OFDM symbols , algorithm stop parameter . |
| Output: Estimated CIR matrix . |
| 1: Initialization: Initial residual ; sparsity ; number of cycles ; support set (Equations (1) and (2)) |
| 2: (using the method of Reference [14]) |
| 3: Combine multiple vectors of the remainder into a vector using massive MIMO common space–time sparsity, i.e., , where , is the row and n column of (using Equation (6) and Reference [9]) |
| 4: merged set (from Equation (2) and References [9,14,15]) |
| 5: merged set |
| 6: |
| 7: updates the margin (using the method of References [8,9,10,11,12,28]) |
| 8: Stop iteration if is satisfied (using Equation (12)); otherwise let, , goto Step 2. |
From the improved SSA-CoSaMP algorithm flow, the SSA-CoSaMP algorithm does not stop the iteration according to the sparsity given in advance but establishes the relationship between the residual and the observation matrix. When the set condition is met, the iteration is automatically stopped. Therefore, the algorithm can adaptively acquire the sparsity, which provides the possibility of engineering application of the algorithm in actual channel estimation. From the SSA-CoSaMP process, it is mainly divided into two parts. The first part is the determination of the sparsity . The algorithm sets the sparsity in the initialization phase, and then uses the loop iteration method to finally obtain the sparsity that satisfies the stop iteration. See Steps 1 and 8 in Algorithm 1. The second part is to use the space–time common sparsity feature of the wireless massive MIMO channel in the case of the preset sparsity . In the process of reconstructing and estimating , multiple sparse vectors can be simultaneously applied to each iteration. The update corresponds to Steps 2–7 in the SSA-CoSaMP algorithm.
If the CoSaMP algorithm only uses space–time common sparsity without considering the sparsity adaptive environment, we call it the structured CoSaMP (i.e., S-CoSaMP) algorithm. The S-CoSaMP algorithm can only perform the number of iterations according to the given sparsity, instead of judging whether to end the algorithm by the actual channel state. There are two consequences of this:
- (a)
- The algorithm has reconstructed the result, but the algorithm itself needs to continue the loop iteration in order to satisfy the given sparsity, resulting in a waste of time and energy.
- (b)
- The result of the algorithm reconstruction is not accurate enough, but the given sparsity has already met the number of loop iterations, and the iteration stops, resulting in an insufficient accuracy of the estimation.
Section 5 compares the performance of S-CoSaMP and SSA-CoSaMP algorithms. In the SSA-CoSaMP algorithm, is different under different SNRs. If the value of is fixed, rather than dynamically changing according to the channel state, it will directly have a very serious impact on the reconstruction result. If the setting is too small, the number of iterations of the algorithm will increase, which will cause the algorithm to take too long, which is not conducive to engineering applications. Conversely, if the value is too large, it will cause the algorithm iteration to end prematurely. The reconstructed result is too large, which reduces the reconstruction accuracy of the algorithm. Hence, the setting of has a crucial impact on the reconstruction accuracy and iteration time. Therefore, in the next section, we determine the parameter through simulation experiments, which will reduce the computation time while satisfying the reconstruction accuracy.
4.3. Computational Complexity
The proposed SSA-CoSaMP algorithm requires complex multiplications to complete the calculation of threshold-based channel estimation, and also requires complex multiplication to obtain the final estimate of the CIR. The complexity of the proposed channel estimation algorithm is mainly related to the LS algorithm and the number of iterations. Therefore, the total complexity of the proposed algorithm is .
5. Simulation Results
Massive MIMO wireless channel estimation techniques primarily evaluate their performance using mean square error (MSE). This can be demonstrated from the following three aspects:
- (a)
- Estimation accuracy comparison experiment: The estimated multipath component is compared with the actual modeling, and the estimation performance is characterized by an intuitive method.
- (b)
- Performance simulation experiment with the change of pilot frequency: The decrease of the number of pilots will inevitably affect the estimation performance, and the number of pilot changes to characterize the estimation performance can better reflect whether the estimation algorithm can reduce the pilot overhead, without affecting the estimation performance.
- (c)
- Performance simulation experiment with SNR variation: SNR can reflect the channel state well, and SNR variation to characterize the estimation performance can well reflect the estimation of estimation algorithm under different channel conditions.
Therefore, this program mainly demonstrates the superiority of the proposed algorithm from the above three aspects of the experiments.
This section uses MATLAB simulation software to verify the performance of the proposed SSA-CoSaMP algorithm in a massive MIMO-OFDM wireless communication system. The system simulation parameters are in Table 1.

Table 1.
Simulation parameters.
In terms of performance measurement, normalized mean square error (NMSE) is used as an indicator. The smaller the NMSE, the smaller the error of the estimated result, indicating that the estimated performance is better. In this paper, the mean square error (MSE) is normalized, that is, NMSE, and is defined as follows to be used as a measure of channel estimation performance.
As a comparison algorithm, the CoSaMP algorithm [27] and the S-CoSaMP algorithm [28] are considered.
5.1. Stop Iteration Parameter
As the SNR continues to decrease, the effect of noise on the observed value of the signal will increase, so will change accordingly at different SNRs. In this section, from the perspective of comparative analysis, the exact LS algorithm is used to obtain the values of under different SNRs.
The channel estimation algorithm can generally be divided into two stages. In the first stage, the estimated position of the tap is reconstructed. In the second stage, the value of the position tap is estimated. The exact LS algorithm directly gives the exact position of the tap and only needs to estimate the value of the tap at that position. Thus, the exact LS algorithm represents the performance benchmark of the CS estimation. Therefore, in this experiment, the SSA-CoSaMP algorithm with a gradual change of is compared with the exact LS algorithm for NMSE, where , which just makes the two NMSEs equal, is the value of under the SNR.
In Figure 4a, when , the NMSEs of the two algorithms are exactly equal. When is greater than 0.058, the two NMSEs are inconsistent. When is less than 0.058, although the two NMSEs are equal, they do not reach an equal critical value. Similarly, according to the experimental simulation results of Figure 4b,c, the range of values can be summarized, as shown in Table 2.
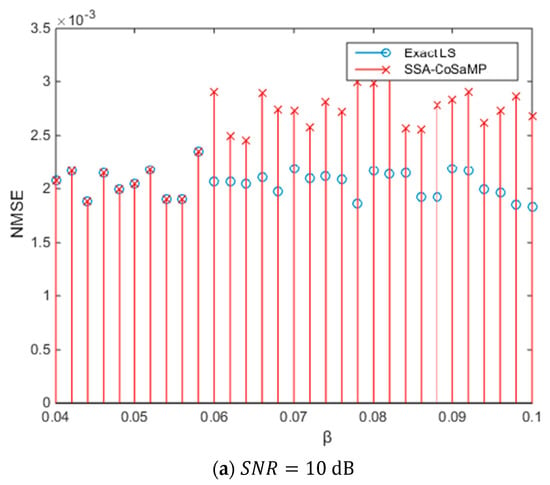
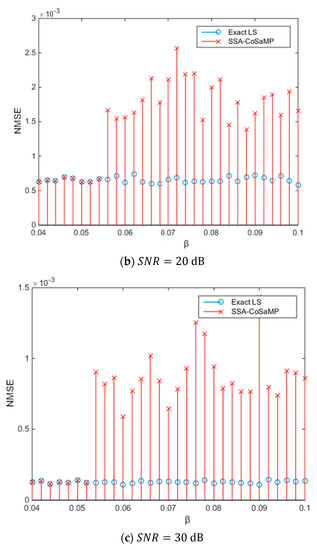
Figure 4.
Stop iteration parameter β under different SNR.

Table 2.
Proposed algorithm stop parameter, β corresponding to SNR.
5.2. Accuracy Comparison
The judgment of the merits and demerits of the estimated results of the algorithm can be considered from two aspects, namely, the estimated position and amplitude of the tap. Therefore, this section compares the results estimated by the algorithm with the channel model constructed by the experiment to verify its performance.
Figure 5a is a simulation diagram of the test performed when and the number of pilots . According to the experimental results, the results estimated by the CoSaMP algorithm are not accurate in both the position and the amplitude of the tap; while the results of the S-CoSaMP algorithm are only accurate in the position of some taps, and the tap positions and amplitudes of other results are not accurate. In contrast, the proposed SSA-CoSaMP algorithm is much more accurate, and the estimated taps are accurate both in position and amplitude.
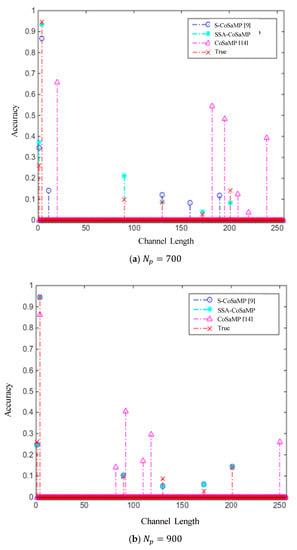
Figure 5.
Accuracy comparison of different channel estimation algorithms when .
When and the number of pilots , we compare the estimated results of the algorithms with experimental modeling, and we can get Figure 5b. According to the experimental results, the CoSaMP [14] algorithm still cannot accurately estimate, while the estimation performances of the SSA-CoSaMP algorithm and the S-CoSaMP [9] algorithm are basically the same, which are very accurate.
.
5.3. Channel Estimation Comparison with Number of Pilots
The pilot is special data that is arranged on a specific subcarrier of a certain part of the OFDM symbol on the base station, and the receiving end estimates the channel according to the received pilot. The pilot data occupies a certain transmission resource. In order to improve the spectral efficiency of the system, it is inevitable to reduce the proportion of pilot data in each frame of OFDM symbols and reducing the number of pilots will inevitably affect the estimation performance. Therefore, it is necessary to carry out simulation experiments on the influence of the number of pilots on the performance of the channel estimation algorithm.
Figure 6 shows that the NMSE of the SSA-CoSaMP algorithm, the S-CoSaMP algorithm, and the CoSaMP algorithm varies with the number of pilots when the SNR is and dB, respectively. It can be concluded from the experimental results that under different SNRs, the estimation performance of the three algorithms is improved as the number of pilots increases. When the number of pilots is lower than 750, the performance of the proposed SSA-CoSaMP is the best, followed by the S-CoSaMP algorithm, and the estimation performance of the CoSaMP algorithm is the worst. When the number of pilots is higher than 750, the estimated performance of the S-CoSaMP and the SSA-CoSaMP algorithms is basically the same.
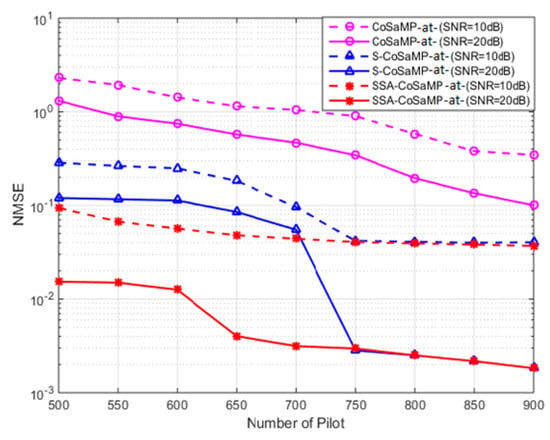
Figure 6.
Normalized mean square error (NMSE) performance comparison of algorithms under a different number of pilots.
5.4. Channel Estimation Comparison with SNR Variation
In addition to the influence of the number of pilot variation simulated in Section 5.3 on the performance of the estimation algorithm, there is also a parameter that has a great influence on the performance of the estimation algorithm, that is, the SNR. In order to further verify the relationship between the performance of the algorithm and the change of SNR, this section experiments with the performance simulation of the channel estimation algorithm with SNR. Figure 7 is an NMSE simulation of the channel estimation algorithm as a function of SNR. When the number of pilots is 650, 750, and 850, the experimental results are clearer and more accurate.
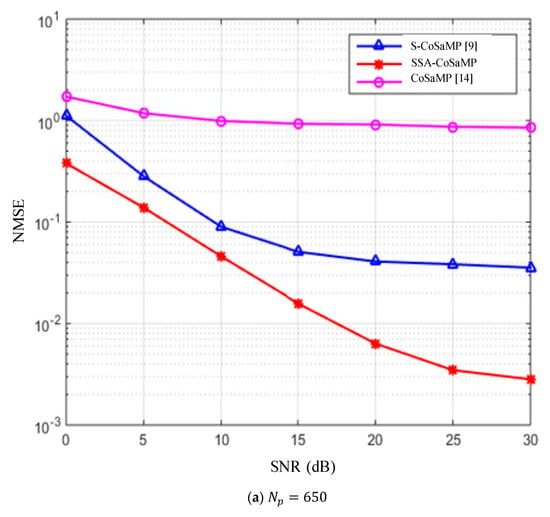
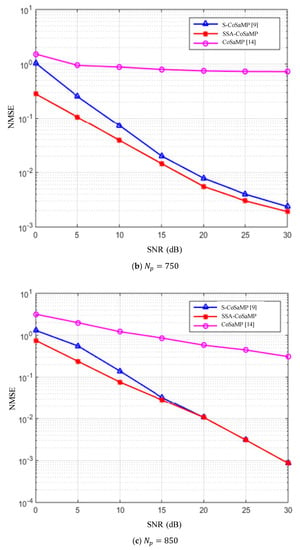
Figure 7.
NMSE performance comparison under different SNR and pilots.
It can be seen from Figure 7a that when the number of pilots is 650, the performance of the SSA-CoSaMP algorithm is much better than that of the S-CoSaMP algorithm. However, the CoSaMP algorithm does not change significantly with the increase of SNR, and it is in a state in which efficient operation cannot be performed. The experimental results show that the improved algorithm can still estimate the channel state well under low pilot conditions. In other words, when lower pilot overhead is required, only the SSA-CoSaMP algorithm can better estimate the channel state. From Figure 7b, when the number of pilots is increased to 750, the SSA-CoSaMP algorithm is slightly better than S-CoSaMP. However, for the CoSaMP algorithm, increasing the number of pilots to 750 still does not allow it to perform efficient operations. Figure 7c is a simulation when the number of pilots is up to 850. When the SNR is below 15 dB, the proposed SSA-CoSaMP algorithm is still superior to the S-CoSaMP algorithm; when the SNR is higher than 15 dB, the estimated performance of the SSA-CoSaMP and S-CoSaMP algorithms are basically the same.
Combining the simulation data in this section, in any case, the performance of the CoSaMP algorithm is far less than those of the S-CoSaMP algorithm and the SSA-CoSaMP algorithm. When the number of pilots is less than 750, the performance of the SSA-CoSaMP algorithm is better than that of the S-CoSaMP algorithm, and the SSA-CoSaMP algorithm is adaptive to sparsity and is more suitable for real environments where sparsity is unknown. The experimental results show that the SSA-CoSaMP algorithm enhances the sparsity. Under the same estimation performance conditions, the pilot overhead is reduced and the spectrum resources are saved. In the case of low pilot overhead, SSA-CoSaMP has advantages.
Figure 8 compares the bit error rate (BER) of the proposed algorithm with the other state-of-the-art algorithms [9,14,15] for the system configured parameters of Table 1. As can be seen from Figure 8, the proposed SSA-CoSaMP algorithm gives better overall BER performance than the other competing alternatives for different SNR levels which makes it superior for utilization in massive MIMO channel estimation. On the other hand, the traditional CoSaMP of [14] has poor BER performance compared to all the rest of competing alternatives and its channel estimation performance gets worse for increasing SNR values which makes it impractical to be deployed in such systems. The structured turbo-CS algorithm in [15] has better performance than S-CoSaMP [9] but is less efficient than the proposed algorithm for low and high SNR levels. Therefore, the proposed scheme is more effective than the other existing algorithms.
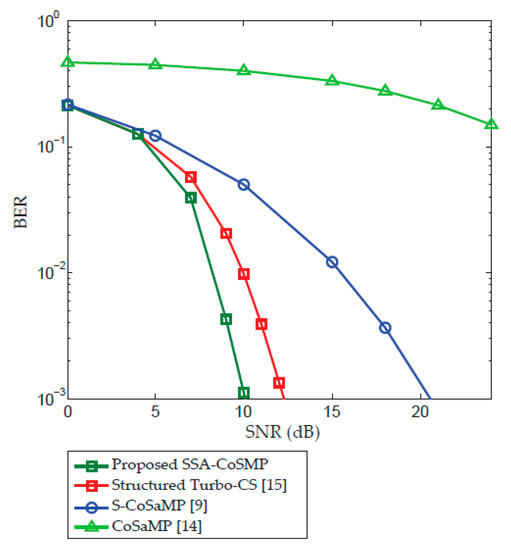
Figure 8.
Bit error rate (BER) performance comparison of the proposed algorithm with other existing algorithms [9,14,15] for different SNR levels.
6. Conclusions
This paper starts with the important feature of space–time common sparsity specific to massive MIMO channels and improves the CoSaMP algorithm [14] from the dynamic sparsity adaptive and structural aspects. The SSA-CoSaMP algorithm is proposed. The proposed algorithm not only optimizes the channel estimation performance but also reduces the pilot overhead, saving spectrum resources and energy consumption. The simulation result shows that the proposed algorithm has obvious performance gain compared with the traditional pilot-based channel estimation algorithms [9,14,15] in both low SNR and smaller number of pilot conditions. In the wireless communication environment, the structural characteristics are not only in the actual delay multipath domain but also in the virtual angle delay domain. Therefore, the next research work is mainly for massive MIMO antenna arrays where the problem of sparse structuring in the virtual angle domain enables the structural improvement scheme to be applied in the virtual angle domain, deeply exploring the scope of structured use and improving the applicability of the scheme.
Author Contributions
Conceptualization, I.K. and S.K.; data curation, I.K., Q.A., and S.A.; formal analysis, I.K. and S.K.; funding acquisition, I.K. and S.K.; investigation, I.K., O.A.S. and Q.A.; methodology, O.A.S., Q.A., and S.K.; project administration, I.K. and O.A.S.; software, O.A.S., I.K., and S.A.; writing—original draft, S.A., I.K., and S.K.; writing—review and editing, I.K., S.K., and S.A.
Funding
This research was supported by the Research Program through the National Research Foundation of Korea (NRF-2016R1D1A1B03934653, NRF-2019R1A2C1005920).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khan, I.; Singh, D. Efficient Compressive Sensing Based Sparse Channel Estimation for 5G Massive MIMO Systems. AEU Int. J. Electron. Commun. 2018, 89, 181–190. [Google Scholar] [CrossRef]
- Khan, I. A Robust Signal Detection Scheme for 5G Massive Multiuser MIMO Systems. IEEE Trans. Veh. Technol. 2018, 67, 9597–9604. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.H.; Jan, M.T.; Lloret, J.; Basheri, M.; Singh, D. Spectral and Energy Efficient Low-Overhead Uplink and Downlink Channel Estimations for 5G Massive MIMO Systems. Entropy 2018, 20, 92. [Google Scholar] [CrossRef]
- Khan, I.; Singh, M.; Singh, D. Compressive Sensing-Based Sparsity Adaptive Channel Estimation for 5G Massive MIMO Systems. Appl. Sci. 2018, 8, 754. [Google Scholar] [CrossRef]
- Khan, I. Channel modeling and analysis of OWC-massive MIMO Systems. Opt. Commun. 2018, 434, 209–217. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.H.; Ashraf, M.; Bayati, A.K.S. Computationally Efficient Channel Estimation for 5G Massive Multiple-Input Multiple-Output Systems. Electronics 2018, 7, 382. [Google Scholar]
- Hu, D.; He, L. Channel Estimation for FDD Massive MIMO OFDM Systems. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference, Toronto, ON, Canada, 4–27 September 2017; pp. 1–5. [Google Scholar]
- Dai, L.; Wang, Z.; Yang, Z. Spectrally efficient time-frequency training OFDM for mobile large-scale MIMO systems. IEEE J. Sel. Areas Commun. 2013, 31, 251–263. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; Shi, Y.; Shim, B.; Wang, Z. Joint channel training and feedback for FDD massive MIMO systems. IEEE Trans. Veh. Technol. 2016, 65, 8762–8767. [Google Scholar] [CrossRef]
- Weikun, H.; Lim, C.W. Structured compressive channel estimation for large-scale MISO-OFDM Systems. IEEE Commun. Lett. 2014, 18, 765–768. [Google Scholar]
- Shen, W.; Dai, L.; Shi, Y.; Zhu, X.; Wang, Z. Compressive sensing-based differential channel feedback for massive MIMO. Electron. Lett. 2015, 51, 1824–1826. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, L.; Gui, G.; Dai, W.; Wang, Z.; Adachi, F. Structured matching pursuit for the reconstruction of dynamic sparse channels. In Proceedings of the 2015 IEEE Global Communications Conference, San Diego, CA, USA, 6–10 December 2015; pp. 1–5. [Google Scholar]
- Gao, Z.; Dai, L.; Wang, Z.; Chen, S. Spatially common sparsity adaptive channel estimation and feedback for FDD massive MIMO. IEEE Trans. Signal Process. 2015, 63, 6169–6183. [Google Scholar] [CrossRef]
- Duarte, M.F.; Eldar, Y.C. Structured Compressed Sensing: From Theory to Applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Chen, L.; Liu, A.; Yuan, X. Structured Turbo Compressed Sensing for Massive MIMO Channel Estimation Using a Markov Prior. IEEE Trans. Veh. Technol. 2018, 67, 4635–4639. [Google Scholar] [CrossRef]
- Qin, Q.; Gui, L.; Gong, B.; Ren, X.; Chen, W. Structured distributed compressive channel estimation over doubly selective channels. IEEE Trans. Broadcast. 2016, 62, 521–531. [Google Scholar] [CrossRef]
- Uwaechia, A.N.; Mahyudding, N.M. A review on sparse channel estimation in OFDM system using compressed sensing. IETE Tech. Rev. 2017, 34, 514–531. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, C.; Wang, Z.; Chen, S. Priori-information aided iterative hard threshold: A low-complexity high-accuracy compressive sensing based channel estimation for TDS-OFDM. IEEE Trans. Wirel. Commun. 2015, 14, 242–251. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Chen, S.; Mu, X.; El-Hajjar, M.; Hanz, L. Pilot contamination elimination for large-scale multiple antenna aided OFDM systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 759–772. [Google Scholar] [CrossRef]
- Santos, T.; Karedal, J.; Almers, P.; Tufvesson, F.; Molisch, A.F. Modeling the ultra-wideband outdoor channel: Measurements and parameter extraction method. IEEE Trans. Wirel. Commun. 2010, 9, 282–290. [Google Scholar] [CrossRef]
- Telatar, I.E.; Tse, D.N. Capacity and mutual information of wideband multipath fading channels. IEEE Trans. Inf. Theory 1998, 46, 1384–1400. [Google Scholar] [CrossRef]
- Dai, L.; Gao, Z.; Wang, Z.; Yang, Z. Spectrum-efficient superimposed pilot design based on structured compressive sensing for downlink large-scale MIMO systems. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Gao, Z.; Dai, L.; Yuen, C.; Wang, Z. Asymptotic orthogonality analysis of time-domain sparse massive MIMO channels. IEEE Commun. Lett. 2015, 19, 1826–1829. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Dai, W.; Shim, B.; Wang, Z. Structured compressive sensing-based spatio-temporal joint channel estimation for FDD massive MIMO. IEEE Trans. Commun. 2015, 64, 601–617. [Google Scholar] [CrossRef]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tutor. 2017, 19, 204–238. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed sensing: A new approach to estimating sparse multipath channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Ye, X.; Zhu, W.P.; Zhang, A.; Yan, J. Sparse channel estimation of MIMO-OFDM systems with unconstrained smoothed lo-norm-regularized least squares compressed sensing. EURASIP J. Wirel. Commun. Netw. 2013, 2013, 282. [Google Scholar] [CrossRef]
- Mourad, N.; Sharkas, M.; Elsherbeny, M.M. Orthogonal Matching Pursuit with correction. In Proceedings of the IEEE 12th International Colloquium on Signal Processing & Its Applications (CSPA), Malacca City, Malaysia, 4–6 March 2016; pp. 247–252. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).