1. Introduction
Despite the success of fuzzy sets [
1], imprecise information cannot always be well represented by fuzzy values. Therefore, extensions or alternative models have proliferated [
2,
3,
4,
5] (see [
6] for an account of types of fuzzy sets with their relationships). In particular, there are situations in the fuzzy setting where the practitioner inputs more information than a unique membership degree, either because she receives a set of possible input values (hesitancy [
7], also with necessary and possible information [
8]), additional non-membership values (intuitionistic fuzzy sets [
9]), or both (dual hesitant fuzzy sets [
10]).
Let us dwell on the models that motivate our investigation. Hesitant fuzzy sets (HFSs) use many-valued sets of membership degrees [
11,
12,
13,
14]. Real applications validate this model, and decision-making approaches of various forms permit to act flexibly with data under hesitancy [
15]. If we can also avail ourselves of hesitant information on non-membership degrees, then dual hesitant fuzzy sets (DHFSs) provide a natural extension of both HFSs and intuitionistic fuzzy sets.
In this paper, we go beyond the latter model. We are concerned with a multi-person setting. In this context we propose a rich model that permits using non-membership degrees, hesitancy (in both membership and non-membership degrees), as well as the possibility of discriminating the information depending on the person that submitted it. We achieve our purpose by a suitable hybridization of two recent extensions of HFSs, namely, extended HFSs [
16] and dual HFSs. The fundamental algebraic properties of the concept that we call “dual extended hesitant fuzzy sets” are proven. We also define scores for the purpose of comparing the basic ingredients in this definition, which are extended hesitant fuzzy elements. We show how our model generalizes various existing models, which ensures its good performance in practice. Moreover, for solving the application of dual extended hesitant fuzzy problem, we develop a multi-attribute decision making (MADM) method based on weight score function, which is defined for that specific purpose. Finally, the effectiveness of the proposed algorithm is verified by the recourse to the criteria in Wang and Triantaphyllou [
17].
This paper is organized as follows.
Section 2 gives the necessary background about hesitant fuzzy sets and their extensions.
Section 3 defines and develops our model, inclusive of basic algebraic properties and a comparison law, and frames it in relation with existing models.
Section 4 presents a MADM method with its application in big data evaluation. We conclude in
Section 5.
2. Background about Hesitant Fuzzy Sets and Extensions
Let us fix a non-empty set of alternatives
. To define hesitant fuzzy set on
, the concept of hesitant fuzzy element from Xia and Xu [
18] is helpful:
Definition 1. A hesitant fuzzy element (HFE) is a non-empty subset of . Hence, is the set of all HFEs. A typical HFE (THFE) is a non-empty, finite subset of . denotes the set of all THFEs.
THFEs can be expressed as with . In this case, and are the minimum and maximum of the HFE, respectively. In general, we define and for (non-typical) HFEs.
Several tools help the researchers to investigate the main features of HFEs. Scores are provided in [
19] and the references therein. A critical review of the literature on entropy measures for HFEs is given in [
20].
Definition 2. A hesitant fuzzy set on is . A typical hesitant fuzzy set on is .
Definition 2 is attributed to Torra [
7] and Bedregal et al. [
21]. Each HFS on
associates a set of membership values to every element of
, and if it is typical then such set is always finite.
The HFS in Definition 2 can be expressed in a more practical notation: .
In typical HFSs on , we also write where . The cardinality of the HFE is . Repetitions are excluded in by definition (since it is a set).
Several recent papers give updated details about developments in the theory of HFSs [
13,
22,
23,
24]. In particular, we highlight that they can be hybridized with other structures. For example, hesitant fuzzy soft sets [
25] arise when we import the spirit of parameterized descriptions as defined by soft sets. The concept of interval-transformed HFE [
20] links HFEs and interval-valued fuzzy sets. D-intuitionistic hesitant fuzzy sets [
26] combine D numbers and generalized HFSs. Hesitant probabilistic fuzzy sets [
27,
28] incorporate probabilities corresponding to decision maker’s preferences associated with feasible values in HFSs.
In the rest of this section, we proceed to give a concise introduction to some enhancements of the concept of HFS in various lines, which we need for presenting our model.
2.1. Some Improvements of the HFS Model
Although Torra’s design of HFS has been successfully applied in many instances, it can be improved to account for a better informational basis or uncertainty in other senses beyond hesitancy:
- (1)
Whenever possible, it is interesting to keep track of who expressed which opinion, for example because the seniority of the agents is significant in the decision making.
- (2)
It is frequently the case that the agents are hesitant about membership degrees but also about the non-membership degrees of some options.
We recall the solutions that the literature has offered to incorporate both possibilities
separately in
Section 2.2 and
Section 2.3. Then, in
Section 3, we propose a novel model that
simultaneously benefits from both improvements.
2.2. Extended Hesitant Fuzzy Sets (EHFSs)
Zhu and Xu [
16] defined extended hesitant fuzzy sets (EHFSs) so that the values provided by the agents can be collected by value-groups. They also gave some fundamental operations for EHFEs, which are defined as the Cartesian product of HFSs. Therefore, HFSs can be used to generate EHFSs. In the other direction, particular EHFSs become HFSs. As in the case of HFSs, the constituents of the extended hesitant fuzzy sets are called extended hesitant fuzzy elements (EHFEs). The related notion of expanded hesitant fuzzy set [
29] (XHFS) can be used for similar purposes.
The necessary concepts can be defined in the following way which seems more amenable than the original definition:
Definition 3. An extended hesitant fuzzy element of degree
m is the Cartesian product of m non-empty subsets of . An extended hesitant fuzzy set of degree
m on is The next example illustrates the ideas of EHFE and EHFS.
Example 1. Two agents give their evaluations of options x and y.
- (a)
Agent 1 provides the membership set for x, and Agent 2 submits . It corresponds to the EHFE of degree 2 .
- (b)
Agent 2 provides the membership set for y, and Agent 2 submits . It corresponds to the EHFE of degree 2 .
Such information produces the EHFS of degree 2 on 2.3. Dual Hesitant Fuzzy Sets (DHFSs)
Zhu, Xu and Xia [
10] introduced the following two concepts:
Definition 4. A dual hesitant fuzzy element (DHFE) is a pair with , such that for all , , .
The restriction about the elements from h and g means that a DHFE is such that and (where , and .)
Definition 5. A dual hesitant fuzzy set (DHFS) on the set is such that each is a DHFE.
Typical DHFEs (also T-DHFEs [
30]) are such that
in Definition 4 are typical. Observe that when both
h and
g are singletons, we obtain intuitionistic fuzzy numbers [
31]: see Section 3.1 of [
30]. Precisely for this reason, we avoid the constraint [
30] that both
h and
g should have cardinality 2 or greater. Typical DHFSs are naturally defined too [
29].
In a DHFS, each agent evaluates each element by means of two respective sets of membership and non-membership values. Typically, these sets are always finite and of cardinality 2 or greater. To compare typical DHFEs, the following procedure is used [
10]:
Definition 6. Let and be typical DHFEs. Define for - (1)
When , we say that is superior to . We denote .
- (2)
When , we say that:
- (2.1)
is superior to when . We denote .
- (2.2)
is equivalent to when . We denote .
The researcher now has a nice toolbox to operate with this extension of HFSs. Correlation coefficients of DHFSs appear in [
32,
33,
34], and we also find an application to multiple attribute decision making in [
33]. Applications in pattern recognition that benefit from distance and similarity measures for DHFSs appear in [
35]. Quite recently, Chen et al. [
36] defined novel distances between DHFSs through the mean and standard deviations of its constituents DHFEs. Finally, Wang et al. [
37] produced dual hesitant fuzzy aggregation operators and showed their applicability in MADM.
Again, the spirit of parameterized descriptions can also be merged with this model. Dual hesitant fuzzy soft sets are the outcome of this combination [
38]. Their aggregation operators and corresponding applications to decision-making appear in [
39].
3. The Model: Dual Extended Hesitant Fuzzy Sets
Definition 7. A dual extended hesitant fuzzy element (DEHFE) of degree m is an element such that is a DHFE for . If such DHFEs are typical, then we say that the DEHFE is typical.
A dual extended hesitant fuzzy set
(DEHFS) of degree m on the set issuch that for each , is a DEHFE of degree m. If all such DEHFEs are typical, then we say that the DEHFS is typical. Example 2. Two agents evaluate options x and y by respective DHFEs:
- (a)
Agent 1 provides the evaluations and
- (b)
Agent 2 provides the evaluations and
Such information can be collected by one item, which is the DEHFS of degree 2 on defined as 3.1. Relationships with Existing Models
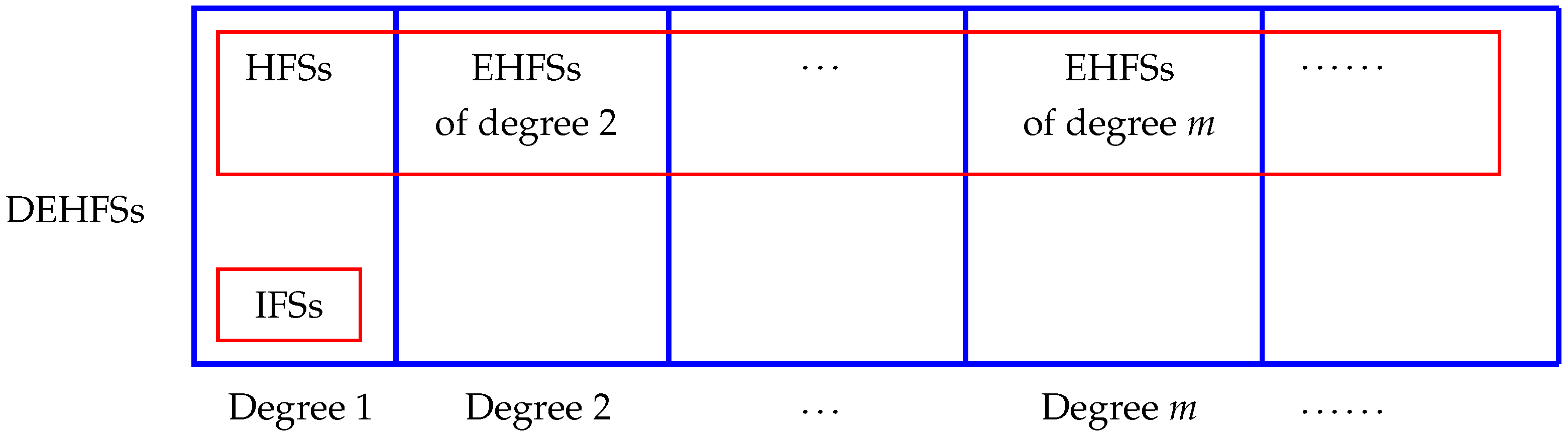
Clearly, DEHFEs of degree 1 are DHFEs. Therefore, our model subsumes other models that were already extended by DHFEs:
(1) When the DHFE
is such that
, it is an intuitionistic fuzzy number. Therefore, DHFSs
with
for all
are intuitionistic fuzzy sets (IFSs) [
9].
(2) When the DHFE is such that either or , it can be identified with a HFE. Therefore, DHFSs such that either for all , or for all , can be identified with HFSs.
In addition, if is a DEHFE of degree m such that either for all i, or for all i, then D can be identified with an EHFE of degree m. Hence, one can naturally embed EHFSs into DEHFSs too. As stated above, EHFSs of degree 1 are HFSs.
The diagram in
Figure 1 summarizes these relationships.
3.2. Algebra of Dual Extended Hesitant Fuzzy Sets
In Section 3.2 of [
10], some basic operators and operations on DHFEs are defined. We can take advantage of these elements to give a first insight into the algebra of our model.
The complement of DHFEs is an involutive operator defined as follows [
10]:
We can use this operator for the following purpose:
Definition 8. Let be a DEHFE of degree m, such that are DHFEs. Then, is the complement of D.
Similarly, the complement of the DEHFS of degree m on the set is the DEHFE of degree m given as .
The union and intersection of two DHFEs
and
are, respectively, defined as follows [
10]:
We can use these operations to define:
Definition 9. Let , be two DEHFEs of degree m. Then, is their union, and is their intersection.
Example 3. With respect to the DEHFS of degree 2 on defined in Example 2, 3.3. Comparison of Dual Extended Hesitant Fuzzy Elements
We adhere to the comparison procedure in
Section 2.3 to define a flexible procedure for the prioritization of typical DEHFEs with the same degree. The basic elements that we need are as follows:
Definition 10. Let be a vector of numbers in such that . Let be a DEHFE such that are typical DHFEs of degree m. With the help of Definition 6, we formulate We say that is the ω-score of the (typical) dual extended hesitant fuzzy element D, and is its w-accuracy function.
We are now ready to compare DEHFEs:
Definition 11. Let be a vector of numbers in such that . Let , be typical DEHFEs of degree m.
- (1)
When either , or and , we say that is superior to . We denote .
- (2)
When and , we say that is equivalent to . We denote .
Example 4. With , let us compare the DEHFEs of degree 2: Some direct computations produce , , , .
Therefore, and .
We conclude that D is superior to (i.e., ).
4. Approach to Dual Extended Hesitant Fuzzy MADM Based on Weight Score Function
In this section, we define the structure of the problems where the alternatives are described in terms of our newly defined notions. We also propose a decision-making mechanism that is adaptable, because it relies on the flexible concept of weights (associated with the relevant characteristics). Then, we illustrate the procedure with an example, and, finally, we check for its effectiveness.
4.1. Problem Description
Let
be a discrete set of alternatives,
be a collection of
n attributes, and
be a weight vector assigned to the attributes by the decision makers with the standard constraints
. We assume that the global evaluation of the alternatives with respect to attributes is represented by a dual extended hesitant fuzzy matrix
. By this we mean that the values associated with the alternatives for the modelization of MADM problems can be shown as in
Table 1.
The next subsection formalizes the flexible decision methodology that benefits from weight score functions, a concept that we introduce to give a comprehensive evaluation of the alternatives.
4.2. The Weight Score Function Method
To make decisions in the setting described above, the following algorithm is self-explanatory:
Observe that Equation (
8) defines a
weight score function . At the end of the process, any alternative such that
can be recommended.
We proceed to illustrate the steps of this decision-making procedure by an example.
Example 5. Assume that there are four companies to be considered for the assessment of big data industry. The expert panel chooses the decision attribute set to be (denoted as Volume), (denoted as Variety) and (denoted as Velocity). Based on the characteristics of the big data industry, we can determine that all these attributes are desirable attributes. Suppose that the experts agree on the following set of weights according to their prior experience or expertise: . The assessments arising from questionnaire investigation allow the experts to construct a dual extended hesitant fuzzy matrix with its tabular form given by Table 2. In what follows, we utilize Algorithm 1 to select the most suitable big data company under dual extended hesitant fuzzy information:
Step 1: The input is already available, namely, the dual extended hesitant fuzzy matrix
, which is shown in
Table 2, and the weights vector
w.
Step 2: The score value
of each alternative
under attribute
is shown in
Table 3.
Step 3: We calculate the assessment score of alternative
as follows:
Step 4: The ranking ordering is , hence is the optimal big data company.
| Algorithm 1 The weight score function mechanism |
- 1:
Identify the alternatives and attributes, and then input the dual extended hesitant fuzzy matrix which is shown in the format of Table 1. Input the weigths associated with the set of relevant attributes. - 2:
Compute the w-score value of each alternative under attribute by Definition 10, for each possible i and j. We denote it as . - 3:
Calculate the assessment score of alternative by the following expression, which produces its weight score:
- 4:
Select the optimal alternative(s) by maximization of their weight scores, i.e., any alternative whose weight score is at least as great as any other alternative’s can be chosen.
|
4.3. Effectiveness Test
This section justifies the adequacy of Algorithm 1 for making decisions in the context of dual extended hesitant fuzzy information. Certain test criteria that were proposed by Wang and Triantaphyllou [
17] are applied in the following terms:
Test Criterion 1: If we replace the decision values of a non-optimal alternative by those of the worst case, then the optimal alternative should not change.
Test Criterion 2: the MADM method should comply with the transitive property.
Test Criterion 3: When an appointed issue is disassembled into smaller ones and the same MADM method is employed, then the assorted ordering of the alternatives should be the same as the ranking of the original one.
In the next subsections, we confirm the verification of these test criteria for our developed dual extended hesitant fuzzy MADM method based on weight score function.
4.3.1. Effectiveness Test by Criterion 1
One can easily observe that Algorithm 1 verifies this criterion. The reason is that the assessment score of any alternative is independent of the structure of the other alternatives. Therefore, any exchange among the values of the remaining options still produces the highest evaluation at the same alternative.
For example, in the situation of
Section 4.2, if we exchange the membership and non-membership degrees of alternatives
(non-optimal option) and
(worst option) in the matrix
P, then the switched decision matrix turns into
, which is shown in
Table 4.
According to the information above, the presented weight score function has been applied, and the optimal alternative is which is same as that of the original ranking. Therefore, the proposed algorithm verifies the test Criterion 1.
4.3.2. Effectiveness test by Criteria 2 and 3
According to these tests, if we decompose the appointed problem into the sub-issues , , and and the procedure steps of the algorithm are employed, then we obtain that the ranking of these smaller issues is , , and , respectively. Hence, by combining Criteria 2 and 3 above, we obtain that the overall ranking order of the alternatives is , which is equal to that of the original ranking order. Therefore, the developed algorithm agrees with the test Criteria 2 and 3.