Abstract
In this article, the non-Newtonian fluid model named Casson fluid is considered. The semi-infinite domain of disk is fitted out with magnetized Casson liquid. The role of both thermophoresis and Brownian motion is inspected by considering nanosized particles in a Casson liquid spaced above the rotating disk. The magnetized flow field is framed with Navier’s slip assumption. The Von Karman scheme is adopted to transform flow narrating equations in terms of reduced system. For better depiction a self-coded computational algorithm is executed rather than to move-on with build-in array. Numerical observations via magnetic, Lewis numbers, Casson, slip, Brownian motion, and thermophoresis parameters subject to radial, tangential velocities, temperature, and nanoparticles concentration are reported. The validation of numerical method being used is given through comparison with existing work. Comparative values of local Nusselt number and local Sherwood number are provided for involved flow controlling parameters.
1. Introduction
The examination of non-Newtonian fluids has received remarkable attention from researchers and scientists because of their extensive use in industrial and technological areas. For instance, paints, synthetic lubricants, sugar solutions, certain oils, clay coating, drilling muds, and blood as a biological fluid are common examples of non-Newtonian fluids, just to mention a few. The fundamental mathematical equations given by Navier–Stokes cannot briefly delineate the flow field characteristics of non-Newtonian fluids because of the complex mathematical expression involved in the formulation of flow problem. In addition, the relation between strain rate and shear stress is non-linear so the single constitutive expressions are fruitless to report complete description of flows subject to non-Newtonian fluids. Numerous non-Newtonian fluid models are exposed to explore rheological characteristics, namely Bingham Herschel–Bulkley fluid model, Seely, Carreau Carreau–Yasuda, Sisko, Eyring, Cross, Ellis, Williamson, tangent hyperbolic, Generalized Burgers, Burgers, Oldroyd-8 constants, Oldroyd-A, Oldroyd-B fluid model, Maxwell, Jeffrey, Casson fluid model, etc. Researchers discussed flow characteristics of non-Newtonian fluid models via stretching surfaces by incorporating pertinent physical effects. Among these, Casson fluid model has many advantages as compared to rest of fluid models. This model can be used to approximate the properties of blood and daily life suspensions. One can assessed recent developments in this direction in References [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].
The centrifugal filtration, gas turbine rotors, rotating air cleaning machines, food processing, medical equipment, system of electric-power generation, crystal growth processes, and many others are the practical applications of rotational fluids flow. Therefore, analysis of flows due to rotation of solid surfaces is widely recognized by scientists, and researchers like Karman [16] firstly report viscous fluid flow induced by rotating solid disk. A special transformation named as Karman transformation given by him for the first time in this attempt. These transformations are utilized for conversion of fundamental equations termed as Naviers–Stokes equations in terms of ordinary differential system. Later on, a number of studies were given by researchers to depict the flow characteristics of both Newtonian and non-Newtonian fluids model over a rotating disk. Preceding these analyses in 2013, the extension of Karman problem was given by Turkyilmazoglu and Senel [17]. In this attempt they discussed numerical results for heat transfer properties of rotating partial slip fluid flow. In 2014, the magnetized slip flow via porous disk was reported by Rashidi et al. [18]. In addition, they discussed entropy measurements for this case. The flow properties in the presence of nano-size particles were discussed by Turkyilmazoglu [19]. He used numerical algorithm for solution purpose. In fact, he dealt comparative execution to report the impact of various nanoparticles suspended in fluid flow regime. Afterwards, tremendous attempts are given in this direction by way of both analytical and numerical approach. One can find the concern developments on rotating flows in References [20,21,22,23,24,25,26,27,28,29,30,31].
The present article contains analysis of Casson liquid towards rotating rigid disk. The Casson flow field is magnetized and has nanoparticles. Further, slip effects are also taken into account. The physical model is translated in terms of mathematical model. For solution purposes, the van Karman way of study is adopted. A computational algorithm is applied and the obtained results of involved parameters of concerned quantities are discussed via graphs and tables. Further, the current attempt is compared with existing literature and we found a good agreement which leads to the surety of the present work.
2. Problem Formulation
The Casson liquid is quipped above the disk for . The constant frequency () is constant. The semi bounded magnetized flow regime contains suspended nanoparticles. The surface is taken with velocity slip condition. The quantities (,,) are in (,,) directions. The ultimate differential system of said problem is:
for order reduction one can use the variables [16],
We get:
and:
the surface quantities are defined as:
3. Computational Outline
To transform the system of Equations (10)–(13) into an initial value problem one can use the dummy substitutions:
so we have
with
here, are initial guess values.
4. Analysis
The Casson fluid (CF) flow is considered on a rigid disk. The flow field is magnetized with suspended nanoparticles. The said problem is controlled mathematically and a numerical solution is offered through the shooting method. In detail, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 are used to highlight the variations of both CF velocities () via physical parameters, namely , , and Figure 1 and Figure 2 are plotted to examine the impact of on CF velocity. It is clear from Figure 1 and Figure 2 that the CF velocity decreases against .
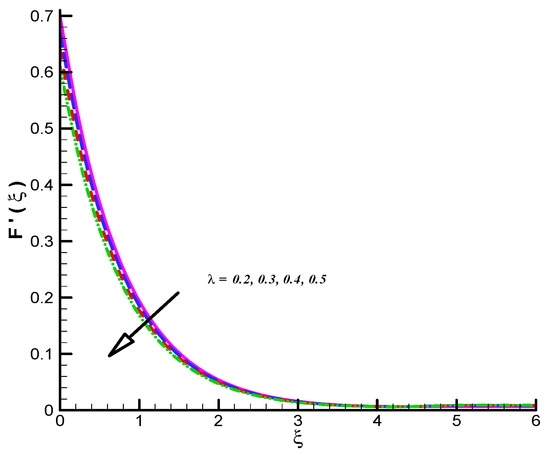
Figure 1.
Effect of on .
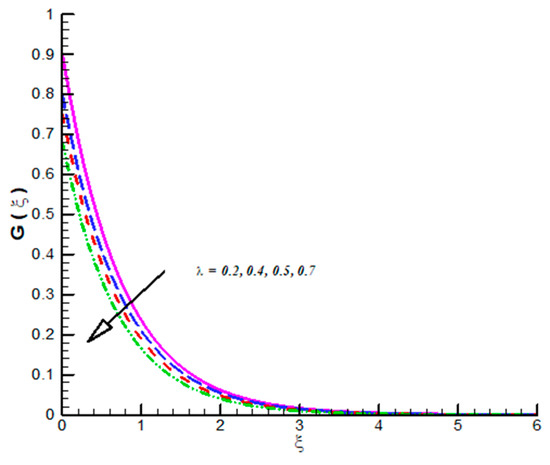
Figure 2.
Effect of on .
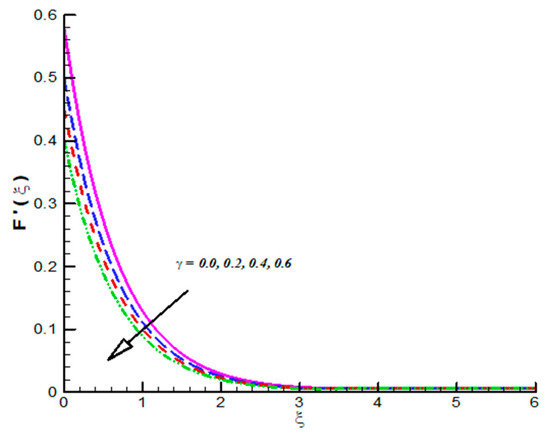
Figure 3.
Effect of on .
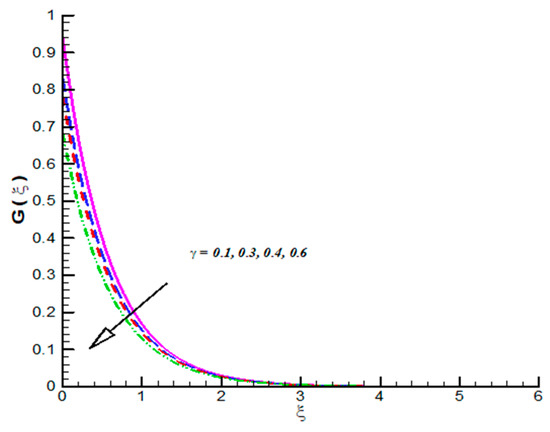
Figure 4.
Effect of on .
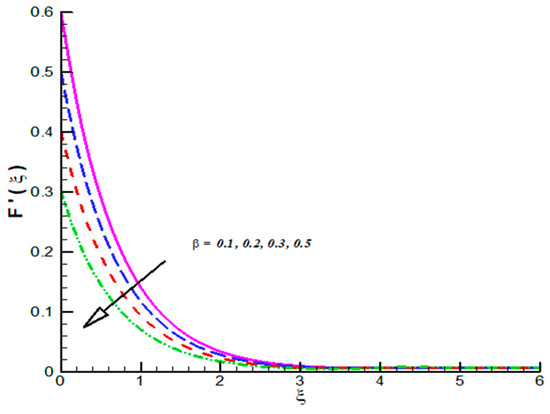
Figure 5.
Effect of on .
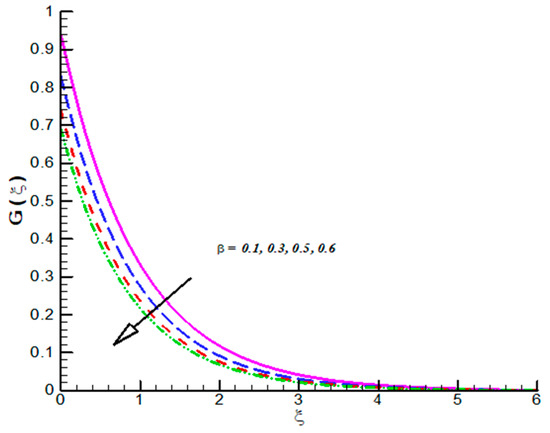
Figure 6.
Effect of on .
The impact of on CF velocity is examined and provided via Figure 3. The CF velocity decreases for higher values of . This is due to activation of Lorentz force via increasing . Similarly, the effect of on tangential velocity is examined and given by means of Figure 4. It is important to note that the tangential velocity decreases for like radial one. The effect of on radial velocity is offer in Figure 5. It is noticed that the radial velocity reflects a diminishing nature for positive values of and the corresponding momentum boundary layer is also effected and admits decline values. Figure 6 gives the effect of on tangential velocity of Casson fluid parameter. It is observed that the tangential velocity decreases for slip parameter. The Casson fluid temperature is examined and provided via Figure 7, Figure 8 and Figure 9. Particularly, Figure 7 is plotted against while Figure 8 is used to identify the influence of Pr on . Figure 9 reports influence of on . From these figures we observed that Casson fluid temperature increases towards , but opposite trend is testified for Pr. Figure 10, Figure 11 and Figure 12 reports the impact of on . In detail, Figure 10 paints the effect of on . The Casson concertation decreases for positive variations in Le. The effected significantly towards . Figure 11 is evident that the results decline values in for both zero and non-zero values of . Such decreasing trend is due to higher values of Brownian force. The change in is observed towards and offer in Figure 12. The higher values of corresponds increasing trends in and related momentum boundary layer. In this attempt the MHD Casson nanofluid flow brought by rotating solid disk in the presence of slip conditions is examined. For comparison purpose, when Casson fluid parameter approaches to infinity our problem absolutely match with Hayat et al. [32]. In this work they studied nanoparticle aspects on viscous fluid flow due to rotating disk along with slip effects numerically. We have compared the variation of both Nusselt and Sherwood numbers with their findings as shown in Table 1 and Table 2. One can see from these tables our finding match with existing values in a limiting sense. The trifling difference is due to choice of numerical method used in both attempts. Their values are obtained by build in command in Mathematica while we have used self-coded algorithm (shooting method with R-K scheme) subject to Casson nanofluid flow induced by solid rotating disk. Beside this one can extend idea to computational fluid dynamics in context of industrial and standpoints, see References [32,33,34,35,36,37,38,39,40,41,42].
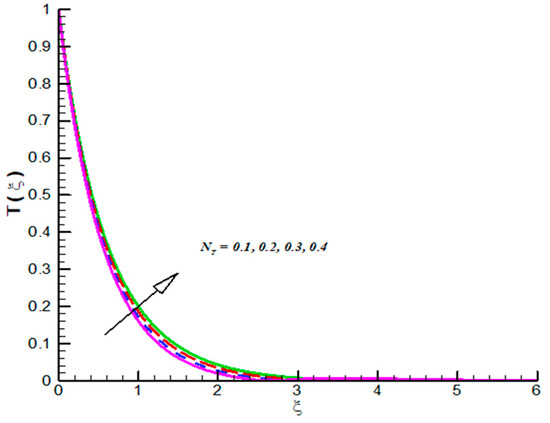
Figure 7.
Effect of on .
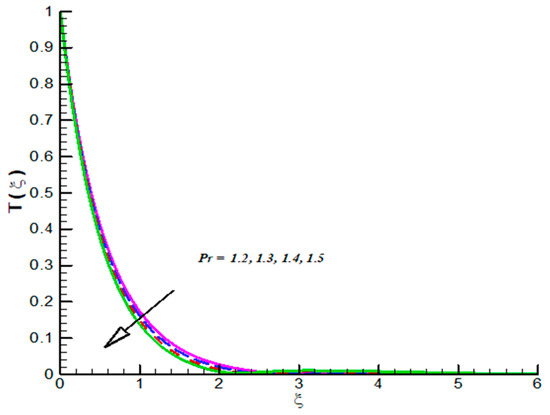
Figure 8.
Effect of on .
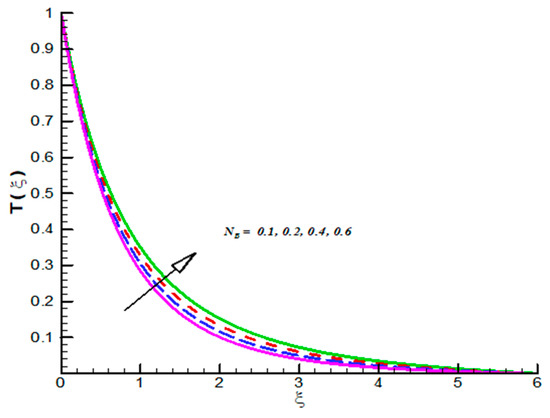
Figure 9.
Effect of on .
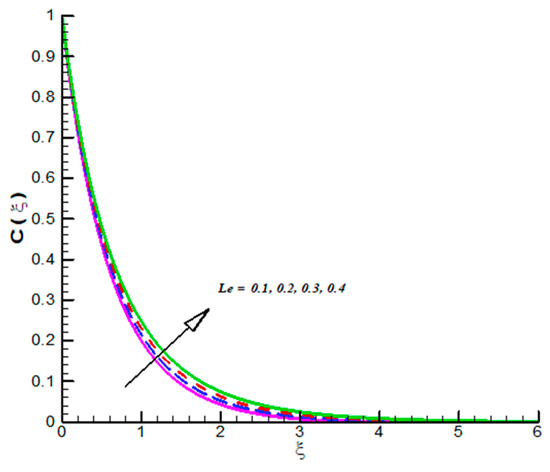
Figure 10.
Effect of on
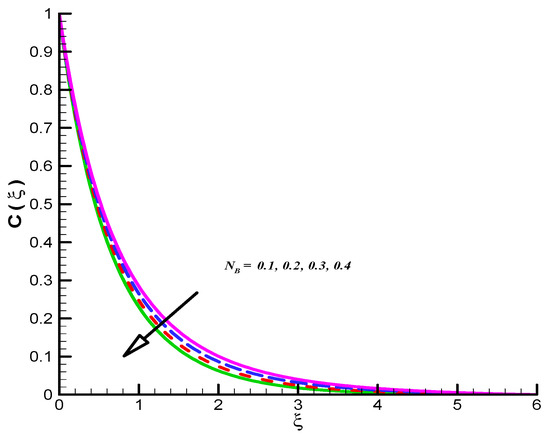
Figure 11.
Effect of on
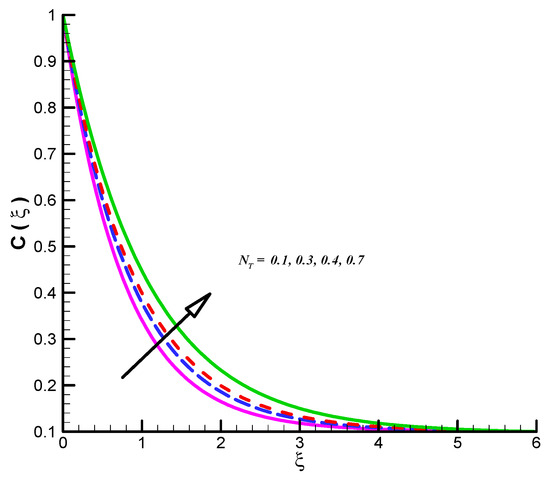
Figure 12.
Effect of on

Table 1.
Local Nusselt number comparison with Hayat et al. [32].

Table 2.
Local Sherwood number comparison with Hayat et al. [32].
5. Closing Remarks
A Casson fluid (CF) flow yield by rotating rigid disk is considered. Both the Brownian and thermophoresis aspects are entertained by incorporating nanoparticles. The flow characteristics are reported numerically with the support of computational algorithm. The summary is as follows:
- CF velocities which includes reflects decline trend towards .
- CF velocities are decreasing function of and .
- CFT admits inciting nature towards both and but opposite trend is observed for Pr.
- CFC shows decline values for both Le, and .
- CFC reflect inciting trend for .
- Comparative values of HTR and MTR are provided for involved flow controlling parameters.
Author Contributions
Conceptualization, K.U.R. and M.Y.M.; methodology, W.A.K.; software, I.K.; validation K.U.R. and M.Y.M. and W.A.K.; formal analysis, I.K.; investigation, W.A.K.; resources, K.U.R. and M.Y.M; writing original draft preparation, W.A.K. and I.K.; writing review and editing, I.K.; visualization, K.U.R. and M.Y.M; supervision, W.A.K.; project administration, W.A.K; funding acquisition, S.O.A.
Funding
This research was funded by Deanship of Scientific Research at King Khalid University, Abha 61413, Saudi Arabia grant number R.G.P-2/29/40.
Acknowledgment
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha 61413, Saudi Arabia for funding this work through research groups program under grant number R.G.P-2/29/40.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Velocity field | |
| (, , ) | Polar coordinates |
| Kinematic viscosity | |
| Casson fluid parameter | |
| Fluid density | |
| Electrical conductivity | |
| Uniform applied magnetic field | |
| Thermal diffusivity | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient | |
| Ambient temperature | |
| Velocity slip parameter | |
| Surface temperature | |
| Surface concentration | |
| Concentration | |
| Dimensionless velocities | |
| Dimensionless temperature | |
| Dimensionless concentration | |
| Magnetic field parameter | |
| Prandtl number | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Lewis number | |
| Velocity slip parameter | |
| Reynolds number |
References
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transf. Asian Res. 2011, 6, 563–576. [Google Scholar] [CrossRef]
- Nadeem, S.; Rizwan, U.H.; Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 2012, 19, 1550–1553. [Google Scholar] [CrossRef]
- Mustafa, M.; Tasawar, H.; Pop, I.; Awatif, H. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet. Z. Naturforsch. A 2012, 67, 70–76. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Iswar, C.M.; Tasawar, H. MHD boundary layer flow of Casson fluid passing through an exponentially stretching permeable surface with thermal radiation. Chin. Phys. B 2014, 23, 104701. [Google Scholar] [CrossRef]
- Mustafa, M.; Junaid, A.K. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv. 2015, 5, 077148. [Google Scholar] [CrossRef]
- Ramesh, K.; Devakar, M. Some analytical solutions for flows of Casson fluid with slip boundary conditions. Ain Shams Eng. J. 2015, 6, 967–975. [Google Scholar] [CrossRef]
- Sandeep, N.; Olubode, K.K.; Isaac, L.A. Modified kinematic viscosity model for 3D-Casson fluid flow within boundary layer formed on a surface at absolute zero. J. Mol. Liq. 2016, 221, 1197–1206. [Google Scholar] [CrossRef]
- Qing, J.; Muhammad, M.B.; Munawwar, A.A.; Mohammad, M.R.; Mohamed, E.-S.A. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Ali, M.E.; Sandeep, N. Cattaneo-christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: A numerical study. Results Phys. 2017, 7, 21–30. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Enhanced heat transfer in the flow of dissipative non-Newtonian Casson fluid flow over a convectively heated upper surface of a paraboloid of revolution. J. Mol. Liq. 2017, 229, 380–388. [Google Scholar] [CrossRef]
- Rehman, K.U.; Aneeqa, A.M.; Malik, M.Y.; Sandeep, N.; Saba, N.U. Numerical study of double stratification in Casson fluid flow in the presence of mixed convection and chemical reaction. Results Phys. 2017, 7, 2997–3006. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017, 233, 262–269. [Google Scholar] [CrossRef]
- Ali, F.; Nadeem, A.S.; Ilyas, K.; Muhammad, S. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Mohammad, M.H.; Sivasankar, T. Radiative flow of Casson fluid over a moving wedge filled with gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 575–583. [Google Scholar] [CrossRef]
- Kármán, T.V. Über laminare und turbulente Reibung. ZAMM 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Therm. Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Griffiths, P.T.; Stephen, J.G.; Stephen, S.O. The neutral curve for stationary disturbances in rotating disk flow for power-law fluids. J. Non Newton. Fluid Mech. 2014, 213, 73–81. [Google Scholar] [CrossRef][Green Version]
- Mustafa, M.; Junaid, A.K.; Hayat, T.; Alsaedi, A. On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J. Mol. Liq. 2015, 211, 119–125. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Numerical investigation of nanofluid spraying on an inclined rotating disk for cooling process. J. Mol. Liq. 2015, 211, 577–583. [Google Scholar] [CrossRef]
- Xun, S.; Zhao, J.; Zheng, L.; Chen, X.; Zhang, X. Flow and heat transfer of Ostwald-de Waele fluid over a variable thickness rotating disk with index decreasing. Int. J. Heat Mass Transf. 2016, 103, 1214–1224. [Google Scholar] [CrossRef]
- Latiff, N.A.; Uddin, M.J.; Ismail, A.M. Stefan blowing effect on bioconvective flow of nanofluid over a solid rotating stretchable disk. Propuls. Power Res. 2016, 5, 267–278. [Google Scholar] [CrossRef]
- Ming, C.; Zheng, L.; Zhang, X.; Liu, F.; Anh, V. Flow and heat transfer of power-law fluid over a rotating disk with generalized diffusion. Int. Commun. Heat Mass Transf. 2016, 79, 81–88. [Google Scholar] [CrossRef]
- Imtiaz, M.; Tasawar, H.; Ahmed, A.; Saleem, A. Slip flow by a variable thickness rotating disk subject to magnetohydrodynamics. Results Phys. 2017, 7, 503–509. [Google Scholar] [CrossRef]
- Doh, D.H.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Hayat, T.; Madiha, R.; Maria, I.; Ahmed, A. Nanofluid flow due to rotating disk with variable thickness and homogeneous-heterogeneous reactions. Int. J. Heat Mass Transf. 2017, 113, 96–105. [Google Scholar] [CrossRef]
- Devi, M.; Chitra, L.; Rajendran, A.B.Y.; Fernandez, C. Non-linear differential equations and rotating disc electrodes: Padé approximationtechnique. Electrochim. Acta 2017, 243, 1–6. [Google Scholar] [CrossRef]
- Guha, A.; Sayantan, S. Non-linear interaction of buoyancy with von Kármán’s swirling flow in mixed convection above a heated rotating disc. Int. J. Heat Mass Transf. 2017, 108, 402–416. [Google Scholar] [CrossRef]
- Ellahi, R.; Ahmed, Z.; Farooq, H.; Tehseen, A. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Hayat, T.; Taseer, M.; Sabir, A.S.; Ahmed, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comput. Methods Appl. Mech. Eng. 2017, 315, 467–477. [Google Scholar] [CrossRef]
- Vo, T.Q.; Park, B.S.; Park, C.H.; Kim, B.H. Nano-scale liquid film sheared between strong wetting surfaces: Effects of interface region on the flow. J. Mech. Sci. Technol. 2015, 29, 1681–1688. [Google Scholar] [CrossRef]
- Kherbeet, A.; Sh, H.A.; Mohammed, B.H.; Salman, H.E.; Ahmed, O.; Alawi, A.; Rashidi, M.M. Experimental study of nanofluid flow and heat transfer over microscale backward-and forward-facing steps. Exp. Therm. Fluid Sci. 2015, 65, 13–21. [Google Scholar] [CrossRef]
- Abbas, T.; Muhammad, A.; Muhammad, B.; Mohammad, R.; Mohamed, A. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Numerical study of entropy generation with nonlinear thermal radiation on magnetohydrodynamics non-Newtonian nanofluid through a porous shrinking sheet. J. Magn. 2016, 21, 468–475. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Alper, T.C.; Beskok, A. A phenomenological continuum model for force-driven nano-channel liquid flows. J. Chem. Phys. 2016, 145, 184109. [Google Scholar] [CrossRef]
- Bao, L.; Priezjev, N.V.; Hu, H.; Luo, K. Effects of viscous heating and wall-fluid interaction energy on rate-dependent slip behavior of simple fluids. Phys. Rev. E 2017, 96, 033110. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Beskok, A. Temperature profiles and heat fluxes observed in molecular dynamics simulations of force-driven liquid flows. Phys. Chem. Chem. Phys. 2017, 19, 10317–10325. [Google Scholar] [CrossRef]
- Mohebbi, R.; Rashidi, M.M.; Mohsen, I.; Nor, A.C.S.; Hong, W.X. Forced convection of nanofluids in an extended surfaces channel using lattice Boltzmann method. Int. J. Heat Mass Transf. 2018, 117, 1291–1303. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Iffat, Z.; Alqarni, M.S. Group theoretical analysis for MHD flow fields: A numerical result. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 156. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Mahmood, R.; Kousar, N.; Zehra, I. A potential alternative CFD simulation for steady Carreau–Bird law-based shear thickening model: Part-I. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 176. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).