Abstract
In the network operation stage of urban mass transit, the connection relations between lines can effectively improve travel accessibility. As the last opportunity to travel on the same day, whether the last train can achieve transfer will directly affect passengers’ travel experiences. It is an important work to make the connection scheme of the last train, which needs to take the network structure, the trend, and the volume of passenger flow into overall consideration. This paper analyzes the characters of the last train connection, including the connection structure and the accessible form. Then, we establish a scheme model and define the objectives, the constraints, and the decision data source, and transform it into a graph theory problem. Taking an urban mass transit network as an example, we demonstrate the solution process by using an improved Prim algorithm. Finally, the main aspects and methods of initial scheme optimization are proposed.
1. Introduction
Punctuality of urban rail transit and rationality of transfer connection are important factors in improving service quality and attracting passengers to travel by public transport [1]. The last train is the last opportunity for passengers to travel on the same day. The transfer connection sequence and the departure time of the last train have more direct impacts on passengers’ travel experiences. Influenced by the transfer relations between lines, the connection scheme should not be aimed at a single line but should consider the whole network and implement overall coordination. Therefore, the objective and the basis of decision-making are the first issues to be considered.
1.1. Related Works on Last Train Connection Scheme
The last train connection scheme problem belongs to the category of transportation system planning and optimization. Transportation system planning and optimization can usually be solved by operational research approaches, which include linear and nonlinear programming, nonsmooth and no convex optimization, integer programming, solving problems on graphs or with mixed variables, and heuristic approaches such as genetic algorithms [2,3,4]. At present, the connection scheme of the last train in the network has received extensive attention in the industry, and some scholars have carried out relevant research.
Aiming at the transfer connection problem, the existing research mainly sets the scheme objective to reduce the total waiting time of passengers at the transfer station. The research methods used include a mixed integer programming model [5,6,7,8,9], a non-linear mathematical programming model [10], and a genetic algorithm [11,12,13,14]. The main influencing factors for decision-making to be considered in the model construction include transfer forms, walking distance, and passenger volume at the transfer station [15]. In addition, some scholars have proposed multi-objective programming models. In literature [16], the authors take the minimized transfer waiting times and transfer dissatisfaction as the objectives and give priority to major passengers. In literatures [17,18], the authors propose to reduce passengers’ transfer waiting times and inaccessible passenger volume of all origin-destination as well as to improve passengers’ accessible reliability for the last trains. In literature [19], the authors take the maximized passenger satisfaction, the minimized train trip time, and the network energy consumption as objectives. Timetable or real-time control can be adopted in the transfer connection coordination mode of the last train [20]. Timetable coordination should first determine the departure time domain of the last train [21], and then, by optimizing the timetables of the last train on each line, it can achieve a good connection at transfer stations, thus achieving the optimal scheme objectives [22,23,24,25]. Real-time control coordination is mainly aimed at train delay under unexpected events and proposes a dispatch coordination model of the last train. By adjusting the arrival and the departure time of the last train on the affected lines and transfer lines, it minimizes the impact of emergencies [26,27,28,29]. In addition, taking service quality as the starting point, some scholars put forward last train passenger travel guidance to provide decision-making reference for the accessibility of Origin-Destination and the choice of transfer routes [30,31,32].
1.2. Novelties and Contributions
We comprehensively compare various research viewpoints in the industry and put forward the last train connection scheme model aimed at achieving maximum transfer passenger volume. In the process of model building, we consider the factors of transfer passenger volume, transfer connection structure, category of operating days, and non-passenger flow constraints. We put forward the calculation method of the last train connection sequence and departure time of each line in the timetable planning stage. This model has good applicability for various types of network structures. The main novelties and contributions of our works are listed below.
- (1)
- This paper transforms the last train connection scheme problem into a graph theory problem and constructs a scheme model aimed at maximizing the last train transfer volume, thus the practical scheme requirements can be solved mathematically.
- (2)
- This paper proposes to use a Prim algorithm to solve the maximum spanning tree and proposes a table operation method in the process of solving.
- (3)
- This paper applies big data. The big historical data of transfer volume in the last train time domain are used as the basis of solving the maximum spanning tree.
- (4)
- From the aspects of model building, algorithm selection, and application of basic data, we believe that we propose a new method about last train connection scheme.
2. Characteristics of Last Train Transfer Connection
2.1. Connection Structure of Urban Mass Transit Network
For transfer stations, there may be different situations, such as double-line or multi-line transfer. However, in any case, a transfer connection relation is generated by only two lines. The overall connection structure is the combination of connection structures between two lines. The connection structure between two lines mainly includes the following basic types.
2.1.1. Transfer at Single Station
As shown in Figure 1a–c, the two lines are connected by only one transfer station. Case (a) shows the cross transfer, and the transfer station is the intermediate station of both lines. Case (b) shows the T-shaped transfer, and the transfer station is the terminal station of one line and the intermediate station of the other line. Case (c) shows the L-shaped transfer, and the transfer station is the terminal station of both lines.
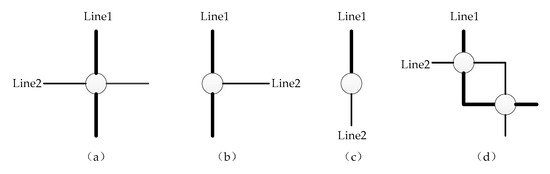
Figure 1.
Connection structure type between two lines.
2.1.2. Transfer at Multiple Stations
As shown in Figure 1d, there are multiple transfer stations between two lines. At each transfer station, the form of transfer may be cross, T or L.
2.2. Accessibility Form of Last Train Transfer
In the urban mass transit network, lines are connected by transfer stations. Every transfer connection relation is formed by any two directions passing through the transfer station, and we define it as a transfer connection pair. Because of the two directions of each line, multiple connection pairs can be formed between two lines. For the accessibility of last train transfer, there are three situations: double connection, single connection, and no connection.
2.2.1. Double Connection
Double connection means that, in a transfer connection pair, the passengers of the last train in both directions can transfer to the other direction. Taking Figure 2a as an example, the down directions of line A and line B can transfer to each other. To achieve double connection of the last train, both the station dwell times of the two last trains at the transfer station should not be less than the sum of the arrival time difference and the passenger’s transfer time. This situation has higher requirements on the structure of transfer corridor and station dwell time. In the actual operation of urban rail transit, it is mainly suitable for some special situations, such as one-platform transfer.
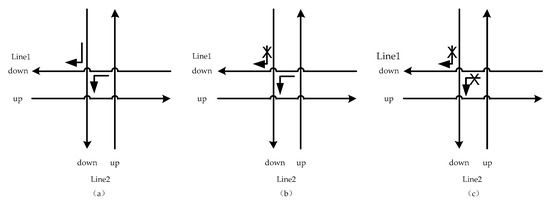
Figure 2.
Three accessibility forms of last train transfer.
2.2.2. Single Connection
Single connection means that, in a transfer connection pair, only one transfer can be achieved between the two last trains, as shown in Figure 2b. It is a normal situation of transfer connection.
2.2.3. No Connection
No connection means that, in a transfer connection pair, no transfer can be achieved between the two last trains, as shown in Figure 2c. When the station dwell time difference between the two last trains is less than the passenger’s transfer time, this situation will occur. This situation should be avoided in the planning of a timetable.
2.3. Major Considerations in Connection Scheme of Last Train
2.3.1. Scheme Objective of Last Train Connection
Due to the diversity of passenger Origin-Destination, there may be transfer needs between any two directions in the network. As mentioned in Section 2.2, the normal accessibility form of last train transfer is single connection. Therefore, no matter how the last train timetable is developed, there will be passenger flow of successful transfer and failure transfer. To improve service quality, operators should make a reasonable connection scheme for last train to maximize the passenger transfer and to guide passengers to avoid failure transfer.
Considering the actual demand above, this paper puts forward the goal of achieving the maximum transfer passenger volume within the network.
2.3.2. Constraints on the Connection Scheme of Last Train
The last train connection scheme is based on transfer passenger flow and is also constrained by a variety of conditions. For example, due to the demands of passengers’ night travel and maintenance time after operation, the last train time should not be earlier than 22:30 or later than 24:00. The lines extending from urban areas to suburbs, especially those connecting large residential areas, should first guaranty transport of passengers on the last train. This determines that some connection relations need to be prioritized. When there are planned large-scale night events, considering the location of the exercise yard, we should temporarily adjust the last train connection scheme and timetable for the whole network.
2.3.3. Data Source for Transfer Passenger Flow of Last Train
In a narrow sense, the transfer passenger flow of the last train is composed of passengers who take the last train and achieve transfer. However, the formation of the passenger flow is affected by the existing connection sequence of the last train, and that cannot accurately reflect the passengers’ demand for last train travel. Based on the facts, we assume that passengers have the ability to make rational decisions. When passengers have last train travel demand and Origin-Destination is not accessible, they will adopt flexible schemes, such as early travel. That is to say, the passenger flow in the last train time domain can be regarded as the potential passenger flow of the last train. Therefore, in a broad sense, the transfer passenger flow in the last train time domain is taken as the transfer passenger flow of the last train. This can be the decision basis of the last train connection scheme.
3. Graph Theory Representation and Algorithm for Connection Scheme of Last Train
3.1. Minimum Spanning Tree Problem
Graph theory is an important research method for traffic planning. A graph is a typical non-linear structure. Its essential content is the connection relations between vertices and edges, also known as the topological structure relationship. Given an undirected and a connected graph, , is a finite non-empty set of vertices, is a finite non-empty set of edges, represents the edges connecting vertices and , and represents the weights of the edges. Assuming that the total number of vertices of graph is , if a subgraph containing − 1 edges can connect its vertices without forming a loop, it is said that the subgraph is the spanning tree of graph . The spanning tree with the minimal weight is the minimal spanning tree of the connected graph, or for short [30]. The equation is as follows:
3.2. Graph Theory Representation for Connection Scheme of Last Train
To achieve the optimal objective, firstly, we transform the last train connection scheme problem into a graph theory problem. The key lies in converting the connection structure of the network into a connected graph and expressing the connection as the relationship between vertices and edges.
3.2.1. Representation of Vertices and Edges
As mentioned in Section 2.2, every transfer connection relation is formed by any two directions passing through the transfer station. In a connected graph, two vertices join to form an edge. We define the up and down directions of each line as vertices and the connection pairs as edges of the connected graph. When applied to the whole network, the connection structure of the network can be transformed into a connected graph, , where is the set of vertices, is the set of edges, the up or down direction of each line is the vertex, recorded as and , and the connection pair is the edge, recorded as and .
3.2.2. Representation of Weights
The weights of edges are the basis for solving the minimum spanning tree problem. The connection scheme of the last train is based on the transfer passenger volume. It should be defined as the weight of each edge, recorded as .
3.2.3. Representation of Scheme Objective
To solve the minimum spanning tree of a connected graph, − 1 edges are needed to connect vertices. To solve the connection scheme of the last train, it is necessary to define − 1 connection sequences for directions. For a weighted undirected graph, the principle of solving a minimum spanning tree is the same as that of a maximum spanning tree. The objective of the last train connection scheme is to achieve maximum transfer passenger volume. It can be expressed as solving the maximum spanning tree problem with transfer passenger volume as the weight. The equation is as follows:
where and represent the line number, and represent the line direction, and its value is 1 or 2. When the value is 1, it represents the up direction; when the value is 2, it represents the down direction. is the spanning tree of the connected graph, .
3.3. Algorithms for Solving Minimum Spanning Tree Problem
For the minimum spanning tree problem, the commonly used algorithms include a Kruskal algorithm, a Prim algorithm, and so on [33,34,35].
3.3.1. Prim Algorithm
A Prim algorithm is a construction algorithm. The idea of constructing a minimum spanning tree is as follows.
Suppose that , is a set of selected points in a connected graph, and is a set of points waiting to be selected.
Step 1. Initialize and take the edges from to all other vertices as candidate edges.
Step 2. Repeat Step (3) and execute − 1 times until other − 1 vertices join .
Step 3. Select the edge with the minimum weight from the candidate edges, and ensure that it does not constitute a loop. Define the other vertex of the minimum edge as , and add it to . . The edges from each vertex in to each vertex in are modified as candidate edges.
3.3.2. Kruskal Algorithm
A Kruskal algorithm selects appropriate edges to construct the minimum spanning tree according to the increasing order of weights. Its basic idea is as follows.
Suppose that the minimum spanning tree of a connected graph is , its set of vertices is , and its set of edges is .
Step 1. The set of all vertices in the connected graph is defined as the initial value of V, and the initial value of E is defined as empty.
Step 2. All edges in the connected graph are selected in order of weight from small to large. If the selected edge does not make form a loop, then the edge is added to . Otherwise, it is discarded until the number of edges in reaches .
3.3.3. Comparisons of the Applicability of Algorithms
In terms of algorithm efficiency, especially computer program execution efficiency, a Prim algorithm is suitable for dense graphs with fewer vertices and more edges. For a connected graph with vertices, the time complexity of a Prim algorithm is , independent of the number of edges. A Kruskal algorithm is suitable for sparse graphs with more vertices and fewer edges. For a connected graph with edges, its time complexity is , independent of the number of vertices.
In an urban mass transit network, if the total number of lines is , then the total number of vertices in the connected graph is , and the number of edges is equal to the total number of connection pairs. Taking a transfer station as an example, if there are lines passing through the station and lines terminating at the station, then there are connection pairs at the transfer station [36]. Generally, the planning and the construction of urban mass transit network consider linking the lines as much as possible to improve the overall accessibility, thus the total number of connection pairs in the network operation stage is much larger than the number of lines. Therefore, its connected graph has the characteristics of fewer vertices and more edges. A Prim algorithm is suitable for solving the Minimum Spanning Tree problem.
4. Model Construction and Solution
In this chapter, we take an urban rail transit network as an example to discuss the construction and the solution of the model. Figure 3 shows the structure of the urban mass transit network, which consists of six lines and 13 transfer stations. Among them, station is a three-line transfer station, and the others are two-line transfer stations.
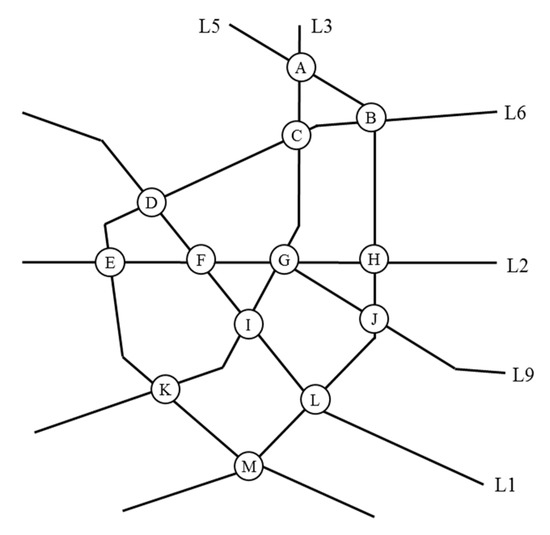
Figure 3.
A sketch of urban rail transit network.
4.1. Conversion of Network into Connected Graph
4.1.1. Cross Transfer at Single Station
For the common transfer structure shown in Figure 1a, station connecting and in Figure 3 is of this type. The directions of the lines are expressed as vertices of the connected graph. The up direction of is and the down direction of is . The up direction of is and the down direction of is . Then, the connected graph is shown in Figure 4. In this case, there is a two-way passenger flow in a connection pair, where the arrow direction indicates the direction of transfer passenger flow.
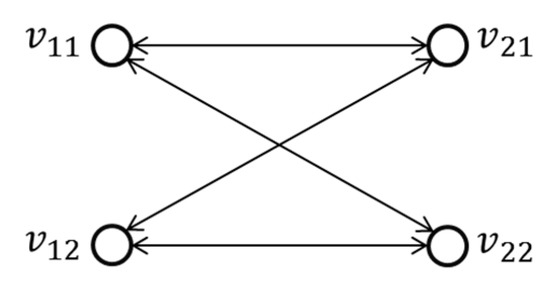
Figure 4.
Connected graph of cross transfer at single station.
4.1.2. Terminal Transfer at Single Station
For the two cases of Figure 1b,c, because the transfer station is the terminal station of one or two lines, the actual number of connection pairs is less. For example, station in Figure 3 is the terminal station of , and the connection between and is transformed into a connected graph, as shown in Figure 5. In this case, there is only one-way passenger flow in a connection pair.
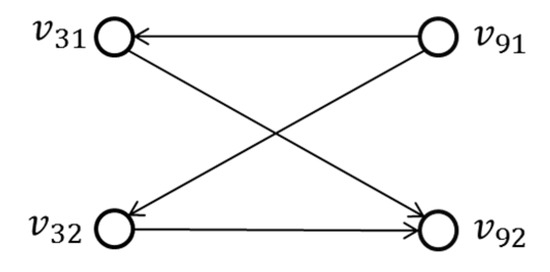
Figure 5.
Connected graph of terminal transfer at a single station.
4.1.3. Transfer at Multiple Stations
For the case shown in Figure 1d, when there are two or more transfer stations between two lines, there will be multiple edges between the corresponding vertices in the connected graph. In Figure 3, and are transfer stations between and , and the connected graph is shown in Figure 6.
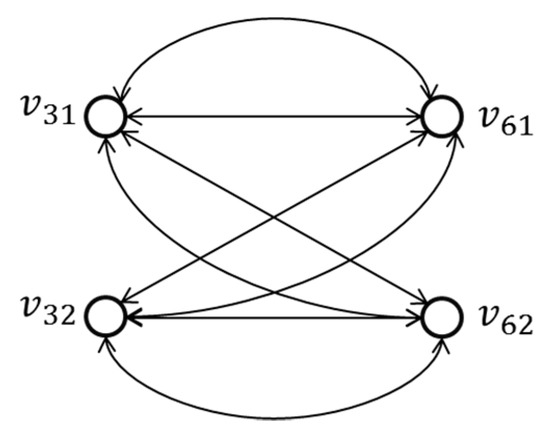
Figure 6.
Connected graph of transfer at multiple stations.
In this case, it is necessary to modify the connected graph. Only one edge should be reserved between two vertices. The modifying ideas are as follows—by comparing the weights of each edge in the same direction between two vertices, the edge with the highest weight is retained, and the other edges are discarded. The equation is as follows:
where subscript means the nth transfer station, and the other indexes share the same meaning as that in Equation (2).
4.1.4. Combination into Connected Graphs of Wire Network
The connected graph of various transfer structures can be combined to form the whole connected graph of the network. The urban mass transit network shown in Figure 6 is converted into a connected graph shown in Figure 7. Each edge is two-way or one-way. Its direction represents the direction of transfer passenger flow. It does not affect the solution of the minimum spanning tree and is not marked in the graph.
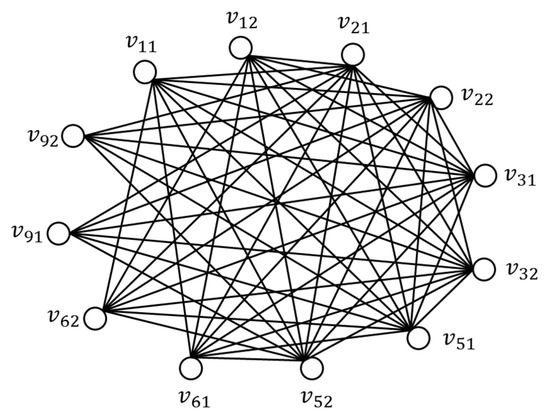
Figure 7.
Connected graph of urban mass transit network.
4.2. Matrix Representation of Connected Graphs
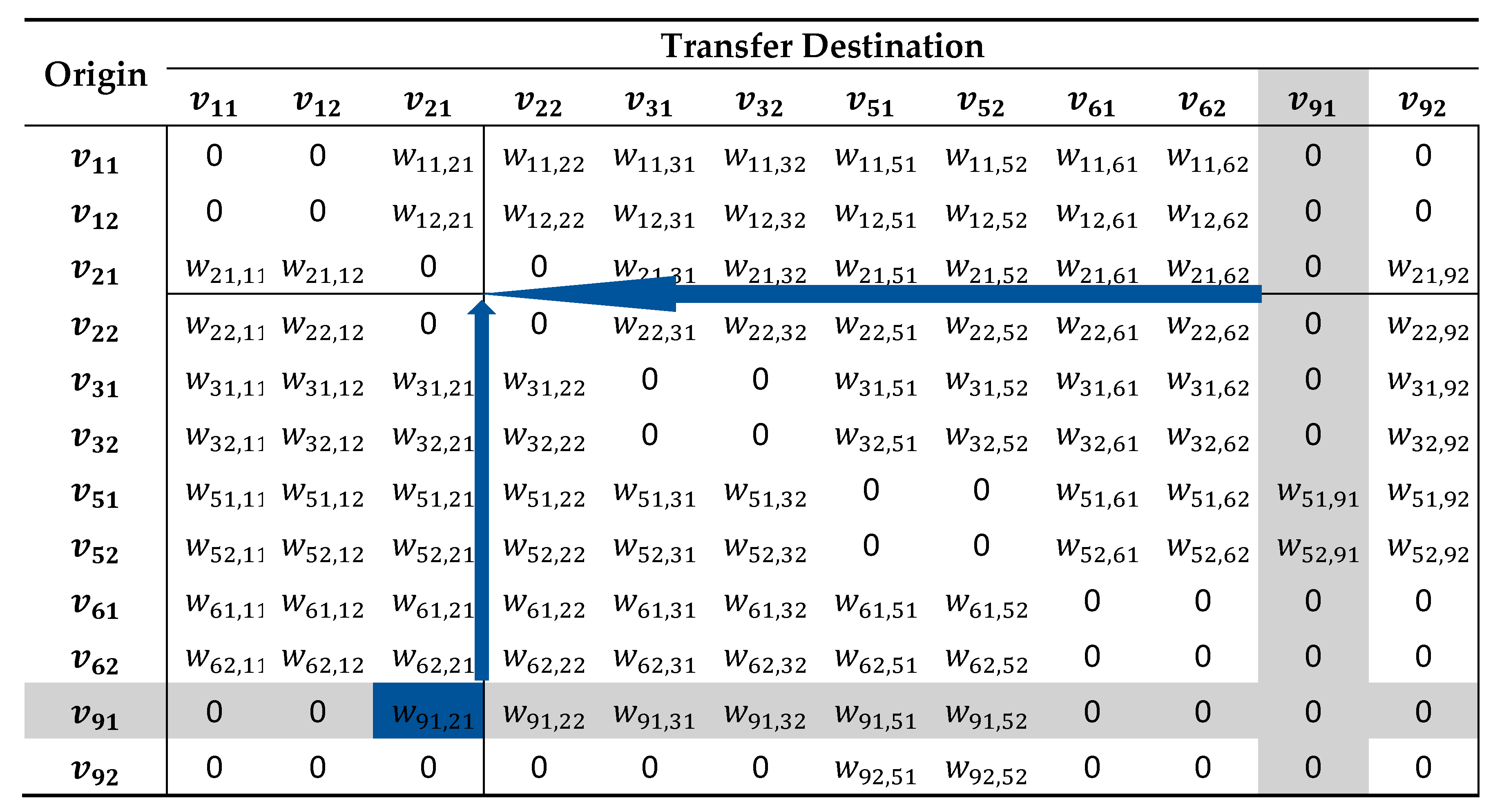
Algorithms are closely related to data structures. Algorithms affect the construction of data structures, and data structures are the basis of algorithms. Weight matrix is an important data structure; it can be used not only as the storage structure of a graph but also to solve the objective by artificial or software program. It is an important method to construct a spanning tree. We set each vertex of the connected graph as the row label and the column label of the weight matrix in turn. From the row label to the column label, a connection pair is formed. The weight of the matrix is the last train passenger volume. For the convenience of visual display, the weight matrix is recorded in the form of a table called a weight table. The first row and the first column of the weight table are labeled as vertices of connected graphs, respectively. Combining with the actual situations of Figure 3 and Figure 7, the weight table is formed, as shown in Table 1.

Table 1.
Weight table of last train connection.
According to the actual operation, there is no transfer between the up and the down directions of the same line except for wrong boarding, thus the weight is recorded as zero. There is no transfer between lines without connection, and the weight is recorded as zero. For the connection pair with two-way transfer passenger flow, its weight is listed in the table.
4.3. Solving Method
4.3.1. Weight Selection of Two-Way Edges
The weights of the edges are derived from the transfer passenger volume in the last train time domain. Therefore, in the cross transfer structure, each connection pair has two-way passenger flow—that is, the two-way edge described in Section 4.1.4. Therefore, there are two weights in the corresponding cells of the weight table. As described in Section 1.2, single connection is a normal situation of transfer connection. The last train transfer between two directions within a connection pair is mutually exclusive. Combining with the scheme objective of maximizing transfer passenger volume, the two weights of each edge is compared, and only the larger one is retained. The equation is as follows:
where the arrows indicate transfer direction, and the other indexes share the same meaning as that in Equation (2).
4.3.2. Maximum Spanning Tree Construction Method
Based on the weight table, the maximum spanning tree of the connected graph can be constructed by using a Prim algorithm. Set as the weight table, where is the set of row and column labels corresponding to the vertex of the connected graph, and is the set of weights corresponding to the transfer passenger volume of the last train.
Combined with the basic idea of the Prim algorithm, in order to optimize the solution process, we divide the weight table into zones, as shown in Table 2.

Table 2.
Zoning of weight table.
Zone I is the selected zone, and the corresponding set is , which is the set of the selected vertices in the process of solving. Zones II and III are zones to be selected and contain vertices in , which connect with the vertices in . Zone IV is the unselected zone and contains vertices in , which are not connected to the vertices in .
According to the property of the maximum spanning tree, in the process of solving, the newly selected vertex needs to be connected with the existing vertices, while the newly selected edge should not form a closed loop with the existing edges. If the new vertex and the edge are selected from Zone I, a closed loop will be formed with the existing parts. The vertices and edges in Zone IV are not connected to the existing parts. Therefore, the newly selected vertices and edges can only be generated from Zones II and III.
The process of solving the maximum spanning tree by a Prim algorithm is to select vertices one by one from Zones II or III according to the weight of each edge, and ensure the connection with the vertices in Zone I. The newly selected vertices are added to Zone I continuously until Zone I contains all vertices and areas II, III, and IV are empty.
For the weight table shown in Table 1, if taking as the initial vertex, the initial value of is {}, and the initial zone division of Table 1 is shown in Table 3. After solving the maximum spanning tree, .

Table 3.
Initial zone division of weight table.
Based on zone division of the weight table, the steps of constructing the maximum spanning tree using the Prim algorithm are as follows:
Step 1. Initialize , .
Step 2. Select the maximum weight in Zone II and Zone III, put the corresponding vertex in , the corresponding edge in , and move the rows and the columns corresponding to the weight to Zone I, thus updating the four zones.
Step 3. Determine whether equals ; if so, the maximum spanning tree construction is completed, and if not, continue Step 2 until .
For the update of zones in Step 2, an example is shown in Table 4.

Table 4.
Update of weight table.
Assuming that, in a solution step, , the maximum weight in Zones II and III are , thus the newly selected vertex is . The rows and columns corresponding to should be moved to the back of rows and columns corresponding to . Therefore, new rows and columns are added to Zone I, and Zones II, III, and IV are updated accordingly
5. Calculation Example
In this section, combined with the actual data of last train transfer passenger volume in the network (shown in Figure 3), the maximum spanning tree is solved by using a Prim algorithm, and the optimization scheme of the last train connection is sought. In the initial stage of modeling, we use the artificial modeling method. In the software development stage, we use Visual Studio tools and Visual C# language to program and model and to verify the feasibility of the model.
5.1. Statistics of Last Train Transfer Passenger Volume
In the actual operation of urban rail transit, the operation days are usually divided into different categories according to the characteristics of passenger volume, such as working days, holidays, pre-festival days, etc. This paper chooses the sample of working days during the stable period of operation, and get the big data of transfer passenger volume in last train time domain (22:00–23:30), and takes its statistical expectation as the value of transfer passenger volume. The calculation equation is as follows:
where index means the nth sample working day, the arrows indicate transfer direction, and the other indexes share the same meaning as that in Equation (2).
According to the calculation equation, the weight table is obtained, as shown in Table 5.

Table 5.
Two-way weight table for last train connection.
5.2. Maximum Spanning Tree Solution
Firstly, combined with Section 4.3.1, the mutually exclusive two-way transfer passenger flow is screened by comparison, and the one-way weight table is obtained, as shown in Table 6.

Table 6.
One-way weight table for last train connection.
Secondly, the maximum spanning tree is constructed according to the method described in Section 3.3. The process is shown in Table 7.

Table 7.
Maximum spanning tree construction process.
Based on the steps above, the maximum spanning tree can be obtained, and its set of edges is . The maximum spanning tree of the connection graph is shown in Figure 8.
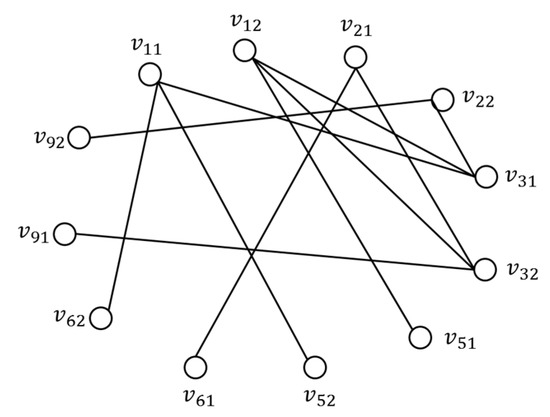
Figure 8.
The maximum spanning tree of the connection graph.
5.3. Connection Order of Last Train in the Network
Sorting the edges of the maximum spanning tree by weight in descending order, the connection priority and the sequence of the last train on each line can be determined, as shown in Table 8.

Table 8.
Connection order of the last train in the network.
5.4. Calculating the Timetable of the Last Train
According to the last train connection sequence listed in Table 8, the down direction of L1 should be taken as the benchmark, and its departure time of the last train should be the basis for calculating the departure time of the last train on other lines. The equation for calculating the last train departure time of each line is as follows.
where is the departure time of the last train in the origin line direction, and is the departure time of the last train in the transfer destination line direction. and are the times required for the last train to run from the departure station to the transfer station. is the transfer walking time of passengers between two directions. is the transfer time margin.
5.5. Initial Scheme Optimization and Adjustment
The initial scheme obtained by the Prim algorithm needs to be optimized and adjusted according to the actual operation constraints.
5.5.1. Constraint Test of Last Train Time Domain
Considering the limitation of the earliest closing time and the maintenance time, the departure time of the last train on each line should meet the constraints of the last train time domain.
where and are respectively the earliest and the latest time in the last train time domain.
When the last train departure time of a certain direction exceeds the time domain, it should be adjusted, and the connecting directions should be adjusted accordingly, so as to ensure that the last train time of each line is in the time domain. When the adjustment cannot meet the time domain constraints, the connection relation between the overrun direction and its connection directions should be broken from low to high priority and then adjusted again according to the principle of priority to meet the time domain constraints.
5.5.2. Adjustment of Transfer Time Margin for Secondary Connection Relations
The initial scheme defines the priority transfer connection relations in order to achieve the maximum transfer passenger volume; we define it as the primary connection relations. Other connection relations not determined in the initial scheme are defined as secondary connection relations. The ideal situation of secondary connection should be single connection, and the typical transfer failure of a “just miss” should be avoided. “Just miss” means that the last train just leaves when passengers arrive at the platform [37]. Therefore, for the initial scheme, it is necessary to check the transfer time margin of secondary connection relations. If the transfer time margin does not meet the requirements, it should be adjusted by changing the departure time, the station stop time, or the runtime without breaking the primary connection.
6. Results and Discussion
6.1. Results
The derivation from Figure 3 to Figure 7 shows the method of converting the network structure into the last train connected graph. The derivation from Figure 7 to Table 1 shows the method of converting the connected graph into the weight matrix. In the case of a fixed network, operators can implement the conversion according to this method, thus facilitating the solution of the objective.
Table 2, Table 3 and Table 4 show the basic method of using the improved Prim algorithm to solve the problem—that is, the table operation method. Equation (5) shows the method of calculating the matrix weight by using the big data of transfer volume in the last train time domain.
Table 5, Table 6 and Table 7 show the solving process by using the actual network and data. The result of the last step in Table 7 shows the connection sequence of each line direction—that is, the content shown in Table 8. According to the last train departure time of the reference line direction, the departure time of other line directions can be calculated according to Equation (6).
6.2. Discussion
The model construction method proposed in this paper has good applicability to different network structures. The solution based on the actual case shows that the improved Prim algorithm has good operability, and the table operation method can be easily implemented both by manual and computer solution.
The model constructed in this paper is single-objective. It takes the transfer volume as the basic data for decision-making. The main consideration is to achieve maximum transfer. In the theme of the last train connection scheme, the decision-making basis considered by relevant researchers is generally the generalized cost of passenger travel, such as travel time, distance, and economic costs. Compared with the existing research, the maximum transfer proposed in this paper can also be regarded as a kind of generalized cost from a macro perspective. Whether they can achieve transfer is an important factor that passengers consider in the last train stage, and it will directly affect their satisfaction.
In addition, there should be other considerations for the last connection scheme, such as the connection between urban and suburban areas and passenger transport of large traffic hubs. They are also the constraints of decision-making. This is one direction of the authors’ future research, which could transform the single-objective of the model into a multi-objective.
7. Conclusions
Whether the last train transfer is successful or not has a direct impact on passengers’ travel feelings. Rationally aquatinting the last train connection scheme is an important problem faced by operation enterprises in the stage of network operation. Aimed at solving this problem, this paper mainly completes the following research:
(1) Based on the analysis of the connection structure and the accessibility form, a scheme model is proposed. This model aims at maximizing the transfer passenger volume of the last train in the network and transforms the last train connection problem into the maximum spanning tree problem of the connected graph.
(2) Based on the big data of transfer passenger volume in the last train time domain, this paper proposes an improved Prim algorithm to solve the maximum spanning tree. This algorithm is a calculation method of the initial connection scheme and demonstrates an example based on the actual data in a certain urban mass transit network.
(3) The main considerations for optimizing and adjusting the initial scheme are put forward, and the adjusting methods are discussed.
The research results of this paper include the working methods of the following stages: model building, decision-making data selection, initial scheme calculation, scheme adjustment, and optimization. Through the practical application test, it is proved that the novelties of the paper—that is, the model built method, the basic data used, and the calculation method—can solve the target problem, which has strong operability. It has strong practical operability and reliability. It provides an assistant decision-making tool for operation enterprises in the scheme of network operation, which can effectively enhance the scientific level of operation management.
Author Contributions
Writing—original draft, X.Z.; writing—review and editing, X.Z., Q.L. and S.Y.
Funding
This research was funded by Science and Technology Project of Ministry of Housing and Urban-Rural Development, grant number 2016-S5-013.
Acknowledgments
The authors would like to thank the editors and the anonymous referees for their valuable comments and suggestions which improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salicrú, M.; Fleurent, C.; Armengol, J.M. Timetable-based operation in urban transport: Run-time optimization and improvements in the operating process. Transp. Res. Part A 2011, 8, 721–740. [Google Scholar] [CrossRef]
- Belenky, A.S. Operations Research in Transportation Systems; Springer: Berlin, Germany, 1998. [Google Scholar]
- Janani, M.; Muthu, C.; Arun, A.; Gururaj, P.; Thiyagaraj, S. Optimization of transportation system using OR (Operational Research) approaches. Int. J. Sci. Eng. Technol. 2014, 3, 651–654. [Google Scholar]
- Wirasinghe, S.C. Modeling and optimization of transportation systems. J. Adv. Transp. 2011, 45, 231–232. [Google Scholar] [CrossRef]
- Wong, R.C.W.; Yuen, T.W.Y.; Fung, K.W.; Leung, J.M.Y. Optimizing timetable synchronization for rail mass transit. Transp. Sci. 2008, 42, 57–69. [Google Scholar] [CrossRef]
- Yousef, S.; Alireza, K. A practical model for transfer optimization in a transit network: Model equationtions and solutions. Transp. Res. Part A 2010, 6, 377–389. [Google Scholar]
- Kang, L.J.; Meng, Q. Two-phase decomposition method for the last train departure time choice in subway networks. Transp. Res. Part B Methodol. 2017, 104, 568–582. [Google Scholar] [CrossRef]
- Ning, L.Q.; Zhao, P.; Xu, W.K.; Qiao, K.; Yao, X.M. Timetable synchronization optimization for urban rail transit in the last trains’ hour. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 108–114. [Google Scholar]
- Chen, Y.; Bai, Y.; Feng, X.J.; Li, Z.J. Last train timetable synchronization optimization on urban rail networks with dwell time extension. J. Transp. Syst. Eng. 2017, 17, 228–234. [Google Scholar]
- Alireza, K.; Yousef, S. Transfer optimization in transit networks: Headway and departure time coordination. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1531–1536. [Google Scholar]
- Bai, G.Z.; Guo, J.; Shi, H.G.; Yang, Y.; Zhang, T.H. Optimization of convergence based on the coordination of train departure time in the subway transfer station. J. Transp. Syst. Eng. Inf. Technol. 2013, 13, 134–139. [Google Scholar]
- Kang, L.J.; Wu, J.J.; Sun, H.J.; Zhu, X.N.; Gao, Z.Y. A case study on the coordination of last trains for the Beijing subway network. Transp. Res. Part B 2014, 72, 112–127. [Google Scholar] [CrossRef]
- Kang, L.J.; Zhu, X.N.; Wu, J.J.; Sun, H.J.; Siriya, S.; Kanokvate, T. Departure time optimization of last trains in subway networks: Mean-Variance model and GSA algorithm. J. Comput. Civ. Eng. 2015, 29, 1–12. [Google Scholar] [CrossRef]
- Xu, W.K.; Zhao, P.; Ning, L.Q. Last train delay management in urban rail transit network: Bi-objective MIP model and genetic algorithm. KSCE J. Civ. Eng. 2018, 22, 1436–1445. [Google Scholar] [CrossRef]
- Chen, X.F.; Wang, B.X. Coordination and optimization of connecting trains in a transfer station of urban mass transit. In Proceedings of the 16th COTA International Conference of Transportation Professionals, Shanghai, China, 6–9 July 2016; pp. 901–912. [Google Scholar]
- Zhou, Y.F.; Zhou, L.S.; Yue, Y.X. Synchronized and coordinated train connecting optimization for transfer stations of urban rail networks. J. China Railw. Soc. 2011, 3, 9–16. [Google Scholar]
- Zhou, W.L.; Deng, L.B.; Xie, M.Q.; Yang, X.; Wang, W.H. Coordination optimization of the first and last trains’ departure time on urban rail transit network. Adv. Mech. Eng. 2013, 5, 1–12. [Google Scholar] [CrossRef]
- Kou, C.G.; He, S.W.; He, B.S. Study on connection optimization of last train departure time on urban mass transit network. Adv. Mater. Res. 2014, 1030, 2211–2214. [Google Scholar] [CrossRef]
- Xiang, W.X.; Wang, Y.H. A multi-objective programming model for subway last train timetabling. In Proceedings of the 3rd International Conference on Electrical and Information Technologies for Rail Transportation (EITRT), Changsha, China, 20–22 October 2017; pp. 791–800. [Google Scholar]
- Chung, E.H. Transfer Coordination Model and Real-Time Strategy for Inter-Modal Transit Services; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- Shang, Y.F.; Zhou, L.S.; Tong, L.; Cai, C.J. The research of first and last trip optimization under the network of urban mass transit. Appl. Mech. Mater. 2013, 409–410, 1311–1314. [Google Scholar] [CrossRef]
- Bassel, J.Y. Improving Transit Service Connectivity: The Application of Operations Planning and Operations Control Strategies; MIT: Cambridge, MA, USA, 2004. [Google Scholar]
- Liang, Q.S.; Li, X.; Xu, R.H. Optimization of train connection time at urban mass transit transfer station. Urban Mass Transit. 2015, 4, 9–13. [Google Scholar]
- Cai, C.J.; Zhou, L.S.; Shang, Y.F. Research on the last train connection in the urban mass transit system. Adv. Mater. Res. 2015, 1065–1069, 3334–3338. [Google Scholar] [CrossRef]
- Kang, L.J.; Zhu, X.N. Strategic timetable scheduling for last trains in urban railway transit networks. Appl. Math. Model. 2017, 45, 209–225. [Google Scholar] [CrossRef]
- Zhang, M.; Du, S.M. Transfer coordination optimization for network operation of urban rail transit based on hierarchical preference. J. China Railw. Soc. 2009, 31, 9–14. [Google Scholar]
- Kang, L.J.; Wu, J.J.; Sun, H.J.; Zhu, X.N.; Wang, B. A practical model for last train rescheduling with train delay in urban railway transit networks. Omega 2015, 50, 29–42. [Google Scholar] [CrossRef]
- Jiang, Z.B.; Li, F.; Xu, R.H. A simulation model for estimating train and passenger delays in large-scale rail transit networks. J. Cent. South Univ. 2012, 12, 3603–3613. [Google Scholar] [CrossRef]
- Li, Y.P. Study on stability of last train connection under delays on urban rail transit. Appl. Mech. Mater. 2014, 641–642, 757–762. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Guo, J.Y.; Du, T.T. Research on passenger guidance system of urban rail transit network based on timetable of last train. China Railw. Sci. 2014, 2, 111–119. [Google Scholar]
- Guo, J.Y.; Jia, L.M.; Qin, Y.; Wang, B. Trip planning considering last trains running. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems—(ITSC 2013), The Hague, The Netherlands, 6–9 October 2013; pp. 2132–2137. [Google Scholar]
- Guo, J.Y.; Jia, L.M.; Xu, J.; Qin, Y. An algorithm for trip planning with constraint of transfer connection in urban mass transit network. In Proceedings of the 11th International Symposium on Distributed Computing and Applications to Business, Engineering & Science, Guilin, China, 19–22 October 2012; pp. 341–344. [Google Scholar]
- Jaroslav, N. A few remarks on the history of MST-problem. Arch. Math. 1997, 33, 15–22. [Google Scholar]
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Pettie, S.; Ramachandran, V. An optimal minimum spanning tree algorithm. J. ACM ICALP 2000, 1853, 49–60. [Google Scholar]
- Xu, R.H.; Li, X. Comprehensive optimization for connection scheme of last trains in urban mass transit network. J. Tongji Univ. (Nat. Sci.) 2012, 10, 1510–1516. [Google Scholar]
- Chung, M.K.; Chang, C.S. Timetable synchronization of mass rapid transit system using multiobjective evolutionary approach. IEEE Trans. Syst. Man Cybern. Part C 2008, 5, 636–648. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).