A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information
Abstract
:1. Introduction
- There is no proper structure for capturing the uncertainty in the preferences provided by the DMs.
- During the aggregation of preferences, the interrelationships between attributes are not properly captured.
- Relative importance (weights) of each DM is not systematically calculated, which causes inaccuracies in the aggregation of preferences.
- Attribute weights are not systematically calculated, which causes inaccuracies in prioritization of CVs, and moreover, the hesitation, during preference elicitation, is also not properly captured.
- Prioritization of CVs by considering the nature of attributes and from different angles is lacking.
- Probabilistic linguistic term set (PLTS) [21] is used as the data structure for preference elicitation, which manages uncertainty by associating occurring probability values for each linguistic term. This overcomes the limitation of hesitant fuzzy linguistic term set (HFLTS) [22], which ignores occurring probability values. The PLTS is a generalization of linguistic distribution assessment [23], which allows partial ignorance.
- The relative importance of each DM is calculated systematically by using the newly proposed programming model that utilizes the partial information about the reliability of each DM effectively.
- Attributes’ weights are calculated systematically by considering DMs’ hesitation during preference elicitation with the help of statistical variance (SV) method under the PLTS context.
- Preferences are aggregated sensibly by considering the interrelationship between attributes by using a hybrid operator. The linguistic terms are aggregated using a case-based method, and occurring probabilities are aggregated using Muirhead mean operator under the PLTS context. Moreover, the DMs’ relative importance values are calculated systematically, which provides much reasonable aggregation of preferences.
- COPRAS method is extended under PLTS for prioritizing CVs, which considers the nature of attributes and handles preferences from different angles.
2. Basic Concepts of LTS, HFLTS, and PLTS
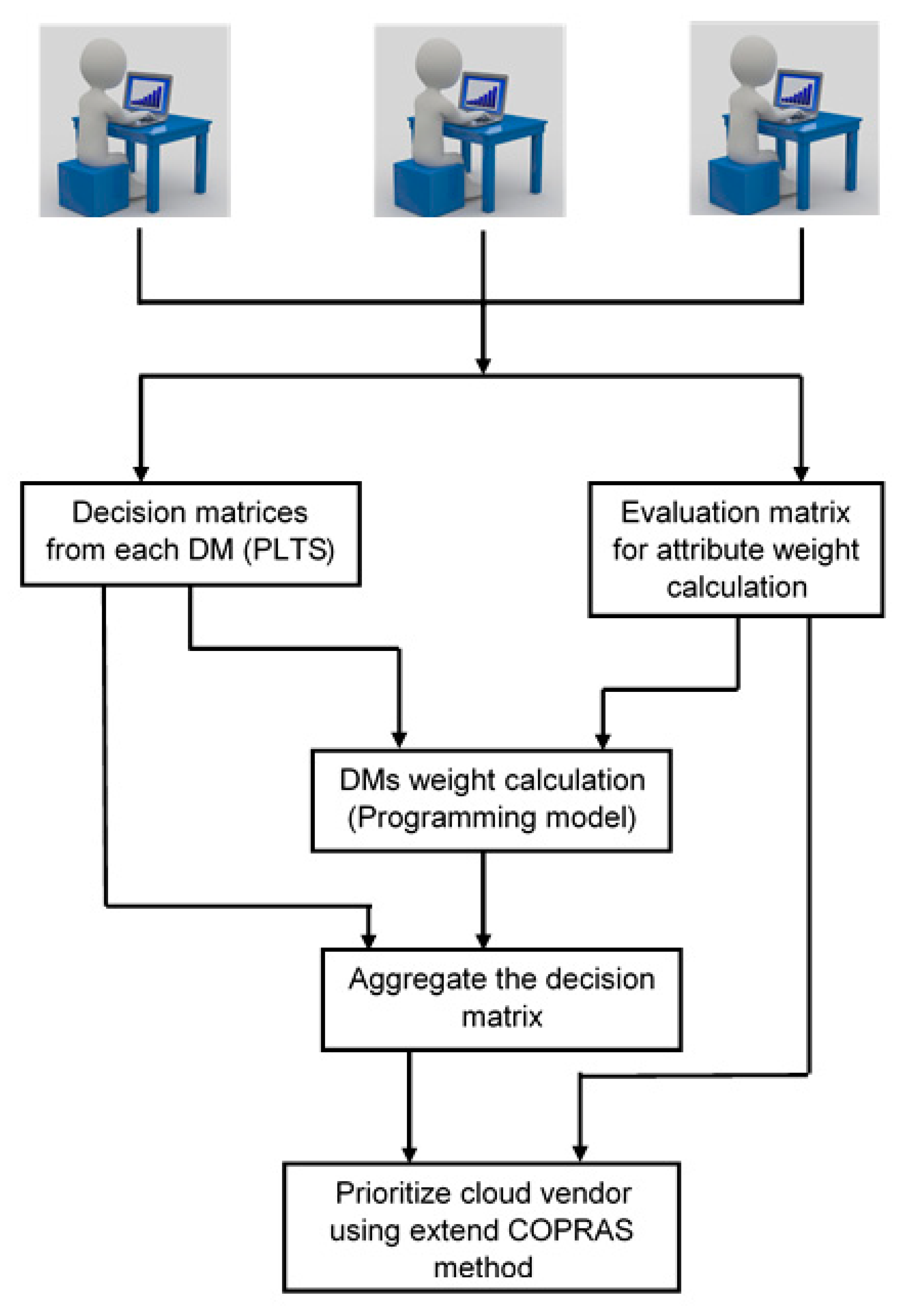
3. Proposed Decision Framework for CV Selection
3.1. Proposed Attributes’ Weight Calculation Method
- Step 1:
- Form a weight calculation matrix with PLTS information of order where denotes the number of DMs and denotes the number of attributes.
- Step 2:
- Transform the PLTS information into a single value matrix by using Equation (5).where is the subscript of the linguistic term, is the total number of instances, and is the occurring probability associated with that linguistic term.
- Step 3:
- Determine the SV for each attribute by using Equation (6). The SV is a vector of order .where is the mean value of the attribute, is the SV of the attribute, and is the total number of DMs.
- Step 4:
- Normalize the SV from step 3 to obtain weights of attributes. Use Equation (7) to obtain the weight vector of order .where is the weight of the attribute.
3.2. Proposed DMs’ Weight Calculation Method
- Step 1:
- Transform the decision matrix from each DM into weighted decision matrices by using Equation (8).where is the subscript of the linguistic term, is the probability associated with the linguistic term, and is the weight of the attribute.
- Step 2:
- Calculate positive ideal solution (PIS) and negative ideal solution (NIS) from the decision matrices obtained from step 1. The PIS and NIS values are calculated for each attribute, and it is given by Equations (9) and (10).where is the PIS and is the NIS.
- Step 3:
- A programming model is proposed for determining weights of DMs. This model is solved using MATLAB® optimization toolbox for calculating the weights of DMs.
3.3. Proposed Hybrid Aggregation Operator under PLTS Context
- Formation of a virtual set is avoided.
- The inter-relationships between attributes is properly captured.
- Risk appetite values are considered along with the relative importance of each DM.
- The relative importance of each DM is calculated systematically by properly capturing the uncertainty in the process.
3.4. Extended COPRAS Method Under PLTS Context
- Step 1:
- Identify the benefit and cost type attributes. The aggregated matrix from Section 3.3 (of order ) and the attributes’ weight vector (of order ) from Section 3.1 is considered as input for the prioritization process.
- Step 2:
- Calculate the COPRAS parameters by using Equations (14) and (15). These parameters are calculated for each alternative under both equal and unequal attributes’ weight conditions.
- Step 3:
- Determine the prioritization order by using Equation (16). This parameter is also calculated for each alternative.where is the strategy value in the range 0 to 1.
4. Numerical Example of Cloud Vendor Selection
- Step 1:
- Start.
- Step 2:
- Form three decision matrices of order where five CVs are rated by using six attributes. The DMs use PLTS information for preference elicitation.
- Step 3:
- Form an attribute weight calculation matrix of order where three DMs provide their preferences on each of the six attributes.
- Step 4:
- Aggregate the three decision matrices by using the proposed aggregation operator (refer Section 3.3). The operator uses DMs’ weights calculated from Section 3.2 for aggregation.
- Step 5:
- Results are compared with other methods, and the strengths and weaknesses are discussed in Section 5.
- Step 6: End.
5. Comparative Investigation of Proposed Framework vs. Others
- The data structure used for preference information considers both the linguistic evaluation and the occurring probability associated with each term. This allows the rational selection of CV, based on a set of attributes.
- The aggregation of preferences is done effectively by capturing the interrelationship among attributes. This allows effective aggregation of the preferences.
- The hesitation of DMs, during preference elicitation, is also effectively captured during the weight calculation of attributes.
- DMs’ weight values are calculated in a systematic manner by making better use of partial information.
- CVs are prioritized rationally by mitigating rank reversal issue when adequate changes are made to the CVs.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garg, S.K.; Versteeg, S.; Buyya, R. A framework for ranking of cloud computing services. Future Gener. Comput. Syst. 2013, 29, 1012–1023. [Google Scholar] [CrossRef]
- Buyya, R.; Yeo, C.S.; Venugopal, S.; Broberg, J.; Brandic, I. Cloud computing and emerging IT platforms: Vision, hype, and reality for delivering computing as the 5th utility. Future Gener. Comput. Syst. 2009, 25, 599–616. [Google Scholar] [CrossRef]
- Garrison, G.; Wakefield, R.L.; Kim, S. The effects of IT capabilities and delivery model on cloud computing success and firm performance for cloud supported processes and operations. Int. J. Inf. Manag. 2015, 35, 377–393. [Google Scholar] [CrossRef]
- Misra, S.C.; Mondal, A. Identification of a company’s suitability for the adoption of cloud computing and modelling its corresponding Return on Investment. Math. Comput. Model. 2011, 53, 504–521. [Google Scholar]
- Somu, N.; Kirthivasan, K.; Shankar, S.S. A computational model for ranking cloud service providers using hypergraph based techniques. Future Gener. Comput. Syst. 2017, 68, 14–30. [Google Scholar] [CrossRef]
- Kumar, R.R.; Mishra, S.; Kumar, C. A Novel Framework for Cloud Service Evaluation and Selection Using Hybrid MCDM Methods. Arab. J. Sci. Eng. 2018, 43, 7015–7030. [Google Scholar] [CrossRef]
- Kumar, R.R.; Kumar, C. A Multi Criteria Decision Making Method for Cloud Service Selection and Ranking. Int. J. Ambient Comput. Intell. 2018, 9, 1–14. [Google Scholar] [CrossRef]
- Rădulescu, C.Z.; Rădulescu, D.M.; Harţescu, F. A cloud service providers ranking approach, based on SAW and modified TOPSIS methods. In Proceedings of the 16th International Conference on Informatics in Economy (IE 2017), Bucharest, Romania, 4–5 May 2017. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar]
- Kumar, R.R.; Kumar, C. An evaluation system for cloud service selection using fuzzy AHP. In Proceedings of the 11th International Conference on Industrial and Information Systems (ICIIS 2016), Uttarkhand, India, 3–4 December 2016. [Google Scholar]
- Patiniotakis, I.; Verginadis, Y.; Mentzas, G. PuLSaR: Preference-based cloud service selection for cloud service brokers. J. Internet Serv. Appl. 2015, 6, 1–14. [Google Scholar] [CrossRef]
- Liu, S.; Chan, F.T.S.; Ran, W. Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst. Appl. 2016, 55, 37–47. [Google Scholar] [CrossRef]
- Wagle, S.S.; Guzek, M.; Bouvry, P. Cloud service providers ranking based on service delivery and consumer experience. In Proceedings of the 4th IEEE International Conference on Cloud Networking (CloudNet 2015), Niagara Falls, ON, Canada, 5–7 October 2015. [Google Scholar]
- Krishankumar, R.; Arvinda, S.R.; Amrutha, A.; Premaladha, J.; Ravichandran, K.S. A decision making framework under intuitionistic fuzzy environment for solving cloud vendor selection problem. In Proceedings of the 2017 International Conference on Networks and Advanced Computational Technologies (NetACT), Kerala, India, 20–22 July 2017. [Google Scholar]
- Krishankumar, R.; Ravichandran, K.S.; Tyagi, S.K. Solving cloud vendor selection problem using intuitionistic fuzzy decision framework. In Neural Computing and Applications; Springer: Berlin, Germany, 2018; pp. 1–14. [Google Scholar]
- Somu, N.; Gauthama, G.R.; Kirthivasan, K.; Shankar, S.S. A trust centric optimal service ranking approach for cloud service selection. Future Gener. Comput. Syst. 2018, 86, 234–252. [Google Scholar] [CrossRef]
- Ding, S.; Wang, Z.; Wu, D.; Olson, D.L. Utilizing customer satisfaction in ranking prediction for personalized cloud service selection. Decis. Support Syst. 2017, 93, 1–10. [Google Scholar] [CrossRef]
- Zheng, X.; Da Xu, L.; Chai, S. Ranking-Based Cloud Service Recommendation. In Proceedings of the 1st International Conference on Edge Computing IEEE 2017, Honolulu, HI, USA, 25–30 June 2017. [Google Scholar]
- Pan, Y.; Ding, S.; Fan, W.; Li, J.; Yang, S. Trust-enhanced cloud service selection model based on QoS analysis. PLoS ONE 2015, 10, e0143448. [Google Scholar] [CrossRef]
- Ghosh, N.; Ghosh, S.K.; Das, S.K. SelCSP: A framework to facilitate selection of cloud service providers. IEEE Trans. Cloud Comput. 2015, 3, 66–79. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic linguistic term sets in multi-attribute group decision making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Zhang, G.; Dong, Y.; Xu, Y. Consistency and consensus measures for linguistic preference relations based on distribution assessments. Inf. Fusion 2014, 17, 46–55. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A Sequential Selection Process in Group Decision Making with a Linguistic Assessment Approach. Inf. Sci. 1995, 239, 223–239. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A rational consensus model in group decision making using linguistic assessments. Fuzzy Sets Syst. 1997, 88, 31–49. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z. Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Inf. Sci. 2016, 372, 407–427. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Grover, N. Intuitionistic fuzzy multi-attribute group decision-making with an application to plant location selection based on a new extended VIKOR method. Inf. Sci. 2016, 370, 184–203. [Google Scholar] [CrossRef]
- Koksalmis, E.; Kabak, Ö. Deriving Decision Makers’ Weights in Group Decision Making: An Overview of Objective Methods. Inf. Fusion 2018, 49, 146–160. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Tamošaitiene, J. Selection of the effective dwelling house walls by applying attributes values determined at intervals. J. Civ. Eng. Manag. 2008, 14, 85–93. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Tamošaitiene, J.; Marina, V. Multicriteria selection of project managers by applying grey criteria. Technol. Econ. Dev. Econ. 2008, 14, 462–477. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Tamošaitien, J. Multi-Attribute Decision-Making Model by Applying Grey Numbers. Inst. Math. Inform. Vilnius. 2009, 20, 305–320. [Google Scholar]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R.; Ghodratnama, A.; Mohammadi, M. Robot selection by a multiple criteria complex proportional assessment method under an interval-valued fuzzy environment. Int. J. Adv. Manuf. Technol. 2014, 73, 687–697. [Google Scholar] [CrossRef]
- Gorabe, D.; Pawar, D.; Pawar, N. Selection Of Industrial Robots using Complex Proportional Assessment Method. Am. Int. J. Res. Sci. Technol. Eng. Math. Sci. Technol. Eng. Math. 2014, 5, 140–143. [Google Scholar]
- Chatterjee, P.; Chakraborty, S. Material selection using preferential ranking methods. Mater. Des. 2012, 35, 384–393. [Google Scholar] [CrossRef]
- Chatterjee, P.; Athawale, V.M.; Chakraborty, S. Materials selection using complex proportional assessment and evaluation of mixed data methods. Mater. Des. 2011, 32, 851–860. [Google Scholar] [CrossRef]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater. Des. 2017, 121, 237–253. [Google Scholar] [CrossRef]
- Chatterjee, K.; Kar, S. A multi-criteria decision making for renewable energy selection using Z-Numbers. Technol. Econ. Dev. Econ. 2018, 24, 739–764. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Hashemkhani Zolfani, S. Integrated QFD-MCDM framework for green supplier selection. J. Clean. Prod. 2017, 142, 3728–3740. [Google Scholar] [CrossRef]
- Costa, P.M.A.C. Evaluating Cloud Services Using Multicriteria Decision Analysis. Master’s Thesis, Tecnico Lisboa, Lisboa, Portugal, July 2013. [Google Scholar]
- Xie, W.; Xu, Z.; Ren, Z.; Wang, H. Probabilistic Linguistic Analytic Hierarchy Process and Its Application on the Performance Assessment of Xiongan New Area. Int. J. Inf. Technol. Decis. Mak. 2018, 16, 1–32. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, X. Probabilistic linguistic VIKOR method to evaluate green supply chain initiatives. Sustainability 2017, 9, 1231. [Google Scholar] [CrossRef]
- Cường, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Ma, S.; Wang, X. M-Polar fuzzy sets: An extension of bipolar fuzzy sets. Sci. World J. 2014, 2014, 416530. [Google Scholar] [CrossRef] [PubMed]
- Smarandache, F. Neutrosophic Set—A Generalization of the Intuitionistic Fuzzy Set. J. Def. Resour. Manag. 2010, 1, 107–116. [Google Scholar]


| Ref | Application | QoS Parameters | Preference Type | Aggregate Method | Weight of Attrib ute and DMs | Ranking |
|---|---|---|---|---|---|---|
| [6] | Cloud service evaluation and selection | CPU performance Disk I/O consistency Disk Performance Memory performance Cost | Numeric | No | Attribute: AHP DMs: No | TOPSIS |
| [7] | Cloud service selection | Accountability, Agility, Assurance, Cost, Performance, Security | Numeric | No | Attribute: Pairwise comparison DMs: No | TOPSIS |
| [8] | Cloud service provider ranking | Cost, Security, and privacy, and Performance | Numeric | No | Attributes: SAW DMs: No | Modified TOPSIS |
| [10] | Selection of cloud service providers | Cost, performance, and security | Both | No | Attribute: Pairwise comparison DMs: No | Fuzzy AHP |
| [11] | Cloud service recommendation based on preference | Service response time, support satisfaction | Both | No | Attribute: Pairwise comparison Decision makers: No | Fuzzy AHP |
| [12] | Cloud vendor selection | Technology, Organization, and Environment | Both | Weighted arithmetic operator | Attributes: SV DMs: TOPSIS | Aggregation-based ranking |
| [13] | Cloud service ranking | Availability, Reliability, Performance, Cost, Security | BothLinguistic | Intersection operator of IFN | No | Service-based ranking |
| [14] | Cloud vendor selection | Reimbursement, Uptime, Configurability, Data transfer, Block storage | Both | SIFWG | Attribute: Normalized rank summation operator DMs: No | IF-AHP |
| [15] | Cloud vendor selector | Economics, Technology, Organization, Environment, CV profile | Both | AIFWG operator | Attribute: IFSV DMs: No | IF-VIKOR |
| [16] | Identification of trustworthy cloud service providers | Trust | Numeric | No | Attribute: No DMs: No | HBFFOA |
| [17] | Cloud service candidate selection | Customers preferences and expectations of QoS | Both | No | No | Enhanced KRCC |
| [18] | QoS rating and ranking of service providers | Upload responsiveness of three storage clouds | Numeric | No | No | Spearman coefficient |
| [19] | Selection of trustworthy cloud services | Trust enhanced similarity | Numeric | No | No | Similarity measure by Jjaccard’s coefficient and distance computation by Pearson Correlation coefficient |
| [20] | Cloud service provider selection | Trust. Competence and Risk | Both | No | No | Ranking-based on trust and competence |
| Decision Maker-1 | ||||||
| CSPs | C1 | C2 | C3 | C4 | C5 | C6 |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| Decision Maker-2 | ||||||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| Decision Maker-3 | ||||||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| DMs | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| D1 | ||||||
| D2 | ||||||
| D3 |
| Decision Maker-1 | ||||||
| CSPs | C1 | C2 | C3 | C4 | C5 | C6 |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| Decision Maker-2 | ||||||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| Decision Maker-3 | ||||||
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| Decision Maker-1 | ||||||
| CSPs | C1 | C2 | C3 | C4 | C5 | C6 |
| PIS | ||||||
| NIS | ||||||
| Decision Maker-2 | ||||||
| PIS | ||||||
| NIS | ||||||
| Decision Maker-3 | ||||||
| PIS | ||||||
| NIS | ||||||
| CSPs | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 |
| CSPs | Equal Weights | Unequal Weights | ||||
|---|---|---|---|---|---|---|
| P | R | Q | P | R | Q | |
| A1 | 2.39 | 0.40 | 3.17 | 83.26 | 23.61 | 164.49 |
| A2 | 1.61 | 0.12 | 7.48 | 64.98 | 8.39 | 378.13 |
| A3 | 1.20 | 0.21 | 4.36 | 38.30 | 12.17 | 257.47 |
| A4 | 2.05 | 0.18 | 5.42 | 73.77 | 11.85 | 281.73 |
| A5 | 1.92 | 0.35 | 3.25 | 74.21 | 20.15 | 181.11 |
| Factors | Cloud Vendor Selection Methods | ||||
|---|---|---|---|---|---|
| Proposed | [1] | [6] | [8] | [18] | |
| Data for analysis | PLEs | Crisp | Fuzzy number | ||
| Rating style | Likert scale | SLA | Likert scale | ||
| Aggregation performed? | yes | no | |||
| DMs’ weight considered? | yes | no | yes | ||
| Attributes’ weights considered? | yes | no | yes | ||
| Prioritization of CVs? | yes | ||||
| Rank reversal issue | Mitigated from CVs’ perspective | Occurs | Mitigated from CVs’ perspectives | ||
| Interrelationship between attributes | Effectively considered | Not considered | |||
| Hesitation in preference information | Effectively considered | Not considered | Effectively considered | ||
| Partial information on each DM | Effectively considered | Not considered | Not needed | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivagami, R.; Ravichandran, K.S.; Krishankumar, R.; Sangeetha, V.; Kar, S.; Gao, X.-Z.; Pamucar, D. A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information. Symmetry 2019, 11, 682. https://doi.org/10.3390/sym11050682
Sivagami R, Ravichandran KS, Krishankumar R, Sangeetha V, Kar S, Gao X-Z, Pamucar D. A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information. Symmetry. 2019; 11(5):682. https://doi.org/10.3390/sym11050682
Chicago/Turabian StyleSivagami, R., K. S. Ravichandran, R. Krishankumar, V. Sangeetha, Samarjit Kar, Xiao-Zhi Gao, and Dragan Pamucar. 2019. "A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information" Symmetry 11, no. 5: 682. https://doi.org/10.3390/sym11050682
APA StyleSivagami, R., Ravichandran, K. S., Krishankumar, R., Sangeetha, V., Kar, S., Gao, X.-Z., & Pamucar, D. (2019). A Scientific Decision Framework for Cloud Vendor Prioritization under Probabilistic Linguistic Term Set Context with Unknown/Partial Weight Information. Symmetry, 11(5), 682. https://doi.org/10.3390/sym11050682







