Abstract
Diet has long been considered a risk factor related to an increased risk of cancer. This challenges us to understand the relationship between the immune system and diet when abnormal cells appear in a tissue. In this paper, we propose and analyze a model from the point of view of a person who follows a healthy diet, i.e., one correlated to the food pyramid, and a person who follows an unhealthy diet. Normal cells and immune cells are used in the design of the model, which aims to describe how the immune system functions when abnormal cells appear in a tissue. The results show that the immune system is able to inhibit and eliminate abnormal cells through the three following stages: the response stage, the interaction stage, and the recovery stage. Specifically, the failure of the immune system to accomplish the interaction stage occurs when a person follows an unhealthy diet. According to the analysis and simulation of our model, we can deduce that dietary pattern has a significant impact on the functioning of the immune system.
1. Introduction
Lifestyle has changed significantly in recent decades due to rapid development in every sphere of life. Consequently, the rate of noncommunicable diseases (NCDs), such as cardiovascular disease, cancer, chronic respiratory disease, and diabetes, has dramatically increased. In 2016, the World Health Organization (WHO) reported that 71% of all deaths worldwide occurred as a result of NCDs. According to the report, the highest mortality figures were those related to cardiovascular disease, representing 44% of deaths from the four main NCDs. The second most deadly disease was cancer, accounting for approximately 22% of deaths from the four main NCDs; while chronic respiratory disease and diabetes reached around 9% and 4%, respectively. In addition, gender variation in NCDs is another important factor. Research found that adult men are more likely to be affected than adult women, with 22% of men and 15% of women being affected [1]. According to a recent study, cancer is more common in certain countries; for example, Australia reported the highest percentage of cancer, with 4680 people per 100,000 having the disease. New Zealand registered 4381 people per 100,000. The number of cancer cases has been estimated as 3522 per 100,000 in the USA, compared with 3192 registered cases per 100,000 in the United Kingdom [2]. The tissues and organs of the human body are formed from tiny cells. There is a one-to-one correspondence between cells and human body growth. The more increased the number of cells, the more tissue grows. The cells between conception and adulthood divide and grow very quickly [3]. Yet, the functions of these cells vary, and as a result the division and growth of the cells depend on their functions. For example, blood and skin cells divide continuously, while some cells have particular functions in the body and do not usually multiply. Concerning the multiplication of cells, it is possible for them to multiply as many as 60 times before dying, as a result of the signals that control cellular growth and death [4,5]. On the other hand, they can become damaged during the process of division, which can lead to self-elimination. This process is known as apoptosis and it protects the human body from cancer. Conversely, cell division is sometimes abnormal when there is damage during cell division, with very unique characteristics [3,4,5]. In such cases, the immune system reacts to protect the human body by preventing these cells from growing into a tumor [3,4,5]. Assessing modern lifestyles is the key to understanding the causes of the increasing rates of cancer. One of the disadvantages of the development of society is that dietary habits have changed to encompass more fast and processed foods. These types of foods have a higher calorie count, contain more protein, and have lower amounts of fiber and carbohydrates than healthy foods, which are rich in natural sources of vitamins and minerals and high in fiber and carbohydrates [6]. Studies have shown the increase in death rate associated with a diet based on animal products and a high intake of carbohydrates, and contrarily, how a vegetable-based diet and a low carbohydrate intake reduces the mortality rate. Furthermore, malnutrition debilitates the immune system and increases the mortality rate as well as elevating the risk of contracting NDCs [7]. It has been shown that only 5–10% of cancers occur as a result of internal factors such as inherited mutations, hormones, and immune conditions, and that 90–95% of cancers are due to lifestyle and environmental factors [8]. Dietary habits are one of the main factors related to the weakening of the immune system and the risk of cancer [9,10,11,12]. From 1994, mathematical researchers started to formulate tumor–immune interaction models using the function of Michaelis–Menten [13,14]. In 1995, Mayer and others proposed a basic mathematical model of the immune response by using two ordinary differential equations to describe the interaction between the immune system and a pathogen, such as a tumor cell or virus. Their model succeeded in illustrating that the combination of a few proposed nonlinear interaction rules between the immune system and pathogens is able to generate a considerable variety of immune responses, with many of them being observed both experimentally and clinically. Hence, the process of the interaction of the immune system with pathogens can be described dynamically [15]. In 2003, Magda Galach used the simplified model of Kuznetsov–Taylor and changed the Michaelis–Menten function using the Lotka–Volterra form [16]. Many models have used ordinary differential equations, partial differential equations, and delay differential equations to illustrate the growth of tumors and their treatments [17,18,19]. In the last few years, mathematical researchers have dynamically examined cancer risk factors and yet still have a great deal to uncover. Estrogen has been studied as a breast cancer risk [20]; furthermore, Green and others studied the relationship between body mass index, menopausal status, estrogen replacement therapy and the risk of breast cancer [21]. In 2016, Roberto and others proposed an obesity–cancer model using ordinary differential equations to illustrate the association between obesity and cancer risk [22]. Additionally, they presented the effects of obesity on the optimal control program of chemotherapy. This model differs from that of De Pillis and Radunskaya [23] by adding a dynamic equation related to stored fat [24]. Other studies have presented models regarding drug therapy which contribute to decision making and early cancer treatment [25]. In 2018, Alharbi and Rambely suggested dynamically that switching back to a healthy lifestyle boosted the immune system in terms of inhibiting or eliminating a moderately abnormal cell [26]. Hence, the immune system has the ability to protect the human body from developing cancer.
In 1618, Thomas Adams stated that “Prevention is so much better than healing because it saves the labour of being sick” [27]. In this work, we propose and simulate the immune–healthy diet model (IHDM) based on the models of references [15,26] using ordinary differential equations to study the behavior of the immune system when responding to the appearance of abnormal cells which fail to eliminate themselves. Usually, these types of cells do not need to be treated clinically. However, the appearance of abnormal cells in the tissue is considered as an emergency situation, with any progression being able to trigger the formation of tumor cells and the development of cancer. Therefore, most cancers develop as a consequence of multiple abnormalities, which accumulate over many years [5]. For instance, colon cancer has increased more than tenfold between the ages of 30 and 50, and tenfold again between 50 and 70 [28].
We aim to enhance understanding of the symmetry and antisymmetry of the relationship between diet habits and the function of the immune system, raise awareness of healthy habits and promote healthy eating habits. In doing so, we hope that the results of this paper contribute to increasing awareness of cancer risk.
This paper is organized as follows. In Section 2, we present the IHDM and analyze the equilibrium points of the model and stability cases. In Section 3, we analyze the stability of the equilibrium points for the immune–unhealthy diet model (IUNHDM). The numerical simulation of the IHDM and IUNHDM are presented in Section 4. The conclusion is presented in Section 5.
2. The Immune—Healthy Diet Model (IHDM)
The immune system is very complex. One of its main functions is to recognize pathogens and to protect the body from developing diseases. However, the response of the immune system is affected by dietary habits, physical activity, stress, and sleep habits. A balanced diet and adequate intake of vitamins act to boost the immune system [29].
Our model is composed of ordinary differential equations, and it supposes that the individual follows a healthy diet as per the food pyramid, which is shown in Figure 1. This food pyramid follows recommendations from a report from the World Cancer Research Fund (WCRF) and the American Institute for Cancer Research (AICR), which recommends drinking water, eating a diet rich in wholegrains, vegetables, fruits, and beans, and having a lower intake of red and processed meats, as well as sugars and sweets [30,31]. The IHDM is formulated into two main populations: normal cells and immune cells activated as a result of the inability of the abnormal cells to eliminate themselves automatically. According to a cell’s life cycle, we formulated the first equation to describe the behavior of normal cells during the process of their dynamic division and growth and to consider that some cells might divide abnormally. In addition, the natural death of the normal cells where the elimination of these cells occurs by apoptosis was not considered. The dynamic process of the interaction between the immune cells with the abnormal cells is presented in the second equation. This considers abnormal cells in the primary stage, which is where most cancers develop as a consequence of multiple abnormalities accumulating over many years. At this stage, the immune system eliminates them from growing before they turn into tumor cells (by attacking and repairing processes).
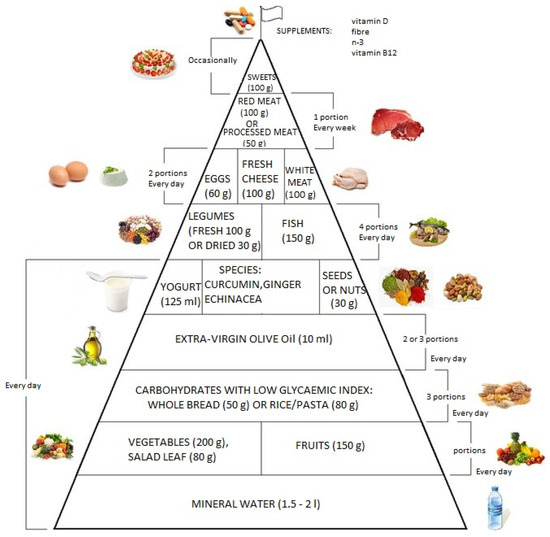
Figure 1.
The dietary management food pyramid according to the World Cancer Research Fund (WCRF) and American Institute for Cancer Research (AICR) where the amounts of food are estimated based on nutritional and practical considerations.
The IHDM is given as follows:
with initial values and where the dependent variables N and I represent the population of normal cells and immune cells, respectively. The parameters , and are real and positive. The rate of growth of normal cells is represented by the parameter r and the rate of appearance of abnormal cells during the cell life cycle of the normal cell is given by . Furthermore, the fixed source of immune cells is represented by and their rate of natural death is represented by . The ability of immune cells to eliminate abnormal cells determined by the Michaelis–Menten term [15]. The coexistence of abnormal cells stimulates the immune system to respond [20]. The rate of this response is represented by and the parameter m represents the threshold rate of the immune system. The parameters and display the interaction between the abnormal cells and immune cells. The ability of the immune cells to eliminate abnormal cells or inhibit them is given by parameter , whereas the parameter illustrates the decreasing number of immune cells as a result of their interaction with abnormal cells. In the IHDM, the rate of the parameter represents the case where the immune system is strong and succeeding in performing its function and the person is following a healthy diet [29].
2.1. Equilibrium Points
In this section, we use nullclines from system (1) to compute the equilibrium points as follows:
We classify the equilibrium points according to their biological terms as the following:
- 1
- Primary response stage: The immune system recognizes the appearance of abnormal cells in the tissue, immune cells start to grow, and ; this point is given by
- 2
- Interaction stage: The immune cells eliminate or inhibit the abnormal cells, this means at the end of the interaction. This point is given bywhere
- 3
- Recovery stage: Immune cells that are involved in the reaction tend to zero and all abnormal cells are substituted with normal cells. This point is represented by
2.2. Analysis Stability of Equilibrium Points
According to the concept of the Hartman–Grobman theorem, the hyperbolic equilibrium point in the neighborhood of a nonlinear dynamical system is topologically equivalent to its linearization. Therefore, the Jacobian of the nonlinear dynamic of (1) is computed as follows:
where The stability cases according to the above equilibrium points are as follows:
- 1.
- Stability of primary response stage- : Under the hypothesis of the IHDM, the immune system is able to protect the human body from developing diseases. This means that it responds directly in cases of emergency such as the appearance of abnormal cells in the tissue. The Jacobian (2) at equilibrium point is computed as:
Proposition 1.
Since the immune system is strong, the equilibrium point is a stable node.
- 2.
- Stability of interaction stage- : This stage describes the ability of the immune cells to inhibit and eliminate the abnormal cells to prevent them from progressing to cancer over many years. We consider the model as having a significant interaction if abnormal cells are dying or being inhibited by the immune cells. This means that parameter at . To examine the stability of equilibrium point we compute the Jacobian (2) at this point aswhere
Proposition 2.
There is an unstable saddle equilibrium point during the interaction stage.
- 3.
- Stability of recovery stage- : According to the physiological process, the number of immune cells which are involved in the interaction starts to reduce automatically after inhibiting and eliminating the abnormal cells. Furthermore, the normal cells divide and grow, taking the place of the removed abnormal cells. To examine the stability of this point, we compute the Jacobian at as follows:where
Proposition 3.
In the recovery stage, the system might to be stable.
With reference to propositions (1,2,3), we conclude this section with the following remark:
Remark 1.
The IHDM has the following properties:
- The system has three equilibrium points;
- The system has two equilibrium points which are stable nodes, which shows that the immune system plays a pivotal role in protecting the human body from diseases.
- The system has only one equilibrium point which is an unstable saddle, which shows the interaction between the immune system and abnormal cells.
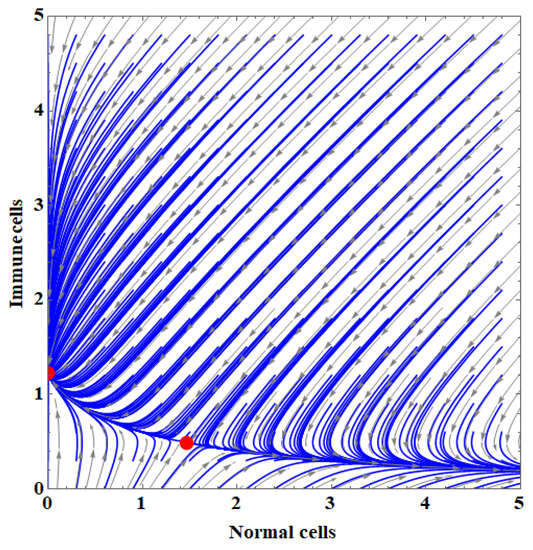
- The phase portrait of the IHDM and its solutions around the equilibrium points are shown in Figure 2 and Figure 3.
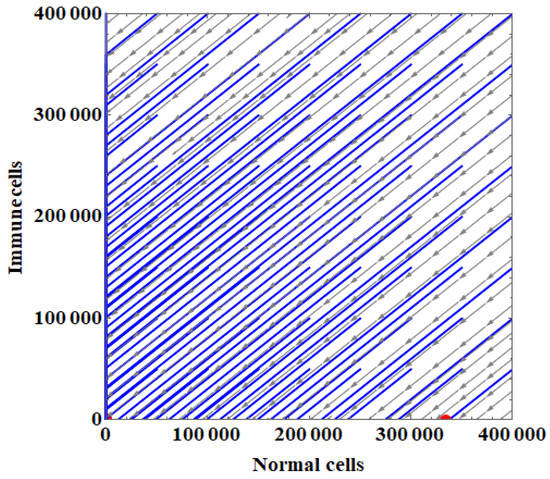 Figure 3. The phase portrait of the IHDM and its solutions around the recovery equilibrium points.
Figure 3. The phase portrait of the IHDM and its solutions around the recovery equilibrium points.
3. Immune-Unhealthy Diet Model (IUNHDM)
A Global Nutrition report (2016) stated that every third person in the world is inflicted with malnutrition [32]. On this basis, a pre-clinical experiment proved that high protein and fructose diets damage the immune system and cause cancer [33,34,35]. In this section, we highlight why a weak immune system fails to protect the human body from developing cancer; we do this using a similar system to that presented in (1) and under the assumption that the person follows an unhealthy diet. For instance, the western-style diet which is characterized by a high consumption of proteins (especially high in processed and red meats), sugar, salt, and fat when compared to a healthy diet comprising an intake of fruits and vegetables [36,37,38]. Several studies showed that a high sugar and protein diet damages the immune system and promotes cancer [33,34,39]. Hence, In the IUNHD, the effects of an unhealthy diet are presented dynamically according to the rate of two parameters: and . In this section, we analyze the model considering an example where the immune system is weak as a result of the person following an unhealthy diet.
3.1. Equilibrium Points:
The model has only two equilibrium points in the feasible region, when it is compared to the IHDM. These equilibrium points are represented as follows:
- Primary response stage: In this stage, the immune system recognizes abnormal cells as foreign; this point is represented by This is a similar equilibrium point to that of the IHDM.
- Coexistence stage: In this stage, the immune cells treat abnormal cells as normal cells; this point is represented by
Remark 2.
Mathematically, both the recovery and the coexistence stages are the same, but their meaning in terms of physiology is totally different. The stage of recovery follows the interaction stage, which means that point represents the total of the population after the substitution of abnormal cells with normal cells. However, the point of in the IUNHDM may mathematically indicate the coexisting population of both normal cells and abnormal cells, as suggested by [20]; this type of coexistence might trigger cancer [40].
Remark 3.
This model does not have an equilibrium point for the interaction stage; this means that one of the following is true:
- There was a response from the immune system but the immune cells did not become involved in the interaction because the immune system was weak, or;
- The immune cells became involved in the interaction but failed to inhibit or eliminate the abnormal cells. Hence, this type of interaction damages the immune cells. In other words, the population of before inhibiting or eliminating the abnormal cells.
3.2. Stability of Equilibrium Points
- 1.
- Stability of primary response stage: Since this point is identical to the primary response stage for the IHDM, we use (3) to examine the stability of this stage for the IUNHDM.
Proposition 4.
The point which represents the primary response stage is the unstable node for the IUNHDM.
Proof.
On the basis of the weakness of the immune system, we can hypothesize that I < r, where . That means that the parameter of failed to achieve its highest peak rate. Therefore, the eigenvalues of matrix (3) have a different sign. Accordingly, the equilibrium point is an unstable node. □
- 2.
- Stability of coexistence stage: This stage is considered to be a trigger for cancer because the immune cells die without inhibiting or eliminating the abnormal cells. This era of rapid development affecting our lifestyle, especially our dietary habits, is one of the main causes of abnormal cells progressing early into tumor cells. Since this is mathematically similar to the recovery point in the IHDM, the stability case is given by the following proposition:
Proposition 5.
The point which represents the coexistence stage is stable.
Remark 4.
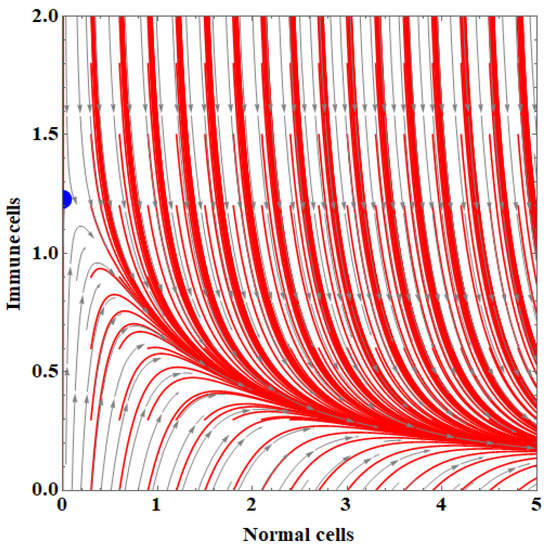
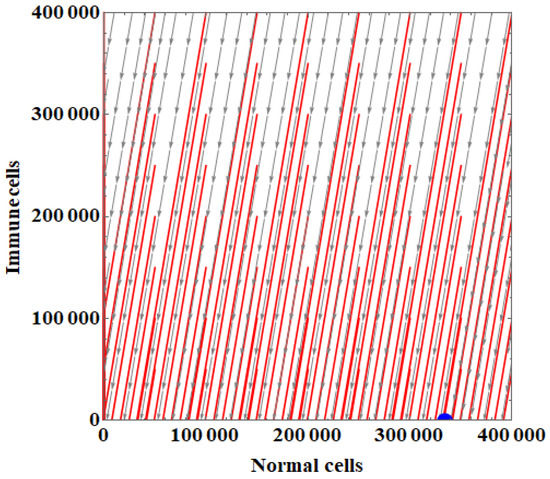
The phase portrait of the IUNHDM and its solutions around the equilibrium points is shown in Figure 4 and Figure 5.

Figure 4.
The phase portrait of the immune-unhealthy diet model (IUNHDM) and its solutions around the response equilibrium point.

Figure 5.
The phase portrait of the IUNHDM and its solutions around the coexistence equilibrium point.
4. Numerical Simulation
Both the IHDM and the IUNHDM were simulated using Mathematica software with the built-in functionality NDSolve. The proposed system of ordinary differential equations can be solved with any standard numerical method. For this, we used an explicit Runge–Kutta with a difference order of four and a step size of 1/10,000. The reliability and accuracy of the proposed numerical method can be seen from the residual error which is shown in Figure 6, Figure 7, Figure 8 and Figure 9.
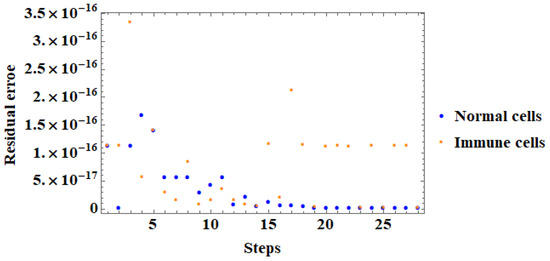
Figure 6.
The residual error at steps for the proposed numerical method for the IHDM.
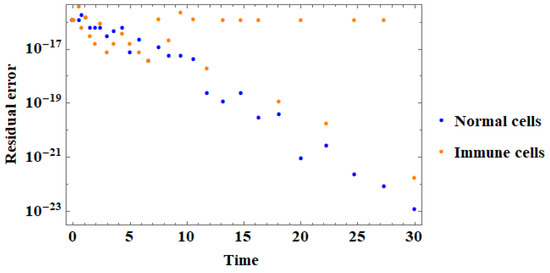
Figure 7.
The residual error at time t for the proposed numerical method for the IHDM.
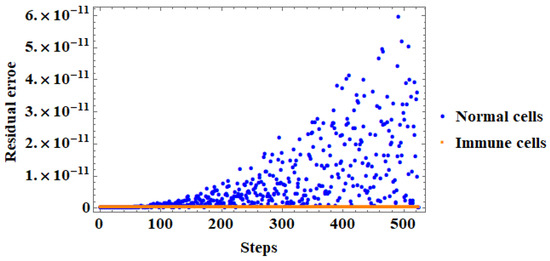
Figure 8.
The residual error at steps for the proposed numerical method for the IUNHDM.
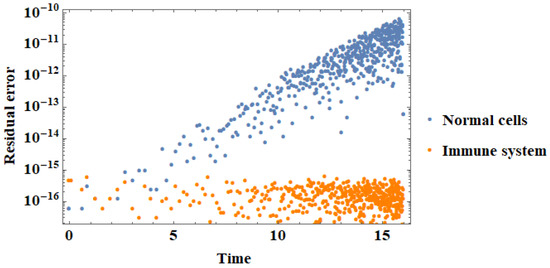
Figure 9.
The residual error at time t for the proposed numerical method for the IUNHDM.
The simulation of the IHDM and the IUNHDM indicated that the immune system response is affected by specific parameters, namely, , and These parameters are put as , and for the IHDM and , and for the IUNHMD. In addition, the immune system can respond to an emergency case if and only if the threshold rate achieves its peak, which is given by ; it is reduced to in the IUNHDM. This reveals a weakness in the immune system. Furthermore, the impact of the interaction between the immune system and abnormal cells depends on the rate of two parameters: and By comparing both models, we can deduce that the immune system succeeded in performing its function if and only if
The behavior of the cells in the IHDM and the IUNHDM are shown in Figure 10 and Figure 11, respectively. Furthermore, The numerical simulation revealed that in the IHDM, the immune system recognized abnormal cells as foreign bodies and started to inhibit or eliminate them within the first five days. In addition, the immune system put a copy of the abnormal cells in its memory, which helps it to eliminate them if they appear again or begin to progress. This is clearly seen as the population of immune cells returns to its initial value after the 10th day of interaction. Furthermore, the horizontal growth of normal cells indicates that normal cells divide and grow by following the signals of control cellular growth and death [5]. On the other hand, the response of the immune system and attitude of their cells were delayed in the IUNHDM. Hence, the immune cells failed to become involved in the interaction and reduced to zero, while the normal cells had a mutation which forced them to grow vertically, something which can lead to carcinoma [5,40].
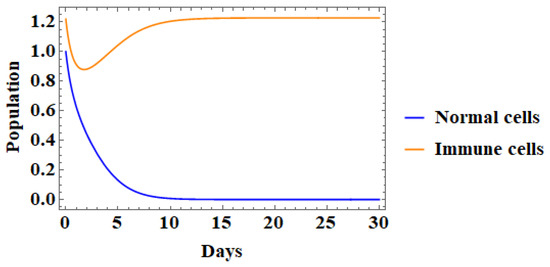
Figure 10.
The behavior of the IHDM where , , , , and
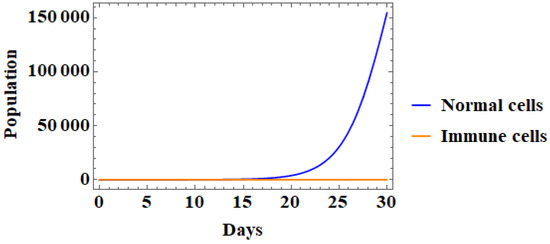
Figure 11.
The behavior of the IUNHDM where , , and
5. Conclusions
Alharbi and Rambely [26] formulated their model to examine the impact a modern lifestyle has on our health, as well as the impact of switching back from an unhealthy lifestyle to a healthy lifestyle. In this study, our model aims to understand the natural function of the immune system as regards protecting the human body from developing cancer where the progress of abnormal cells might trigger the appearance of tumor cells. Hence, the immune–healthy diet and immune–unhealthy diet models have been studied dynamically, analytically, and numerically. By comparing the results of the analysis and simulation of both the IHDM and IUNHDM, we suggested that there are three stages which act to stop abnormal cells from progressing into tumor cells. In the first stage, the immune system receives a signal which provokes it to recognize abnormal cells as foreign. Next, immune cells are activated to attack the abnormal cells. The results of this interaction lead to the inhibition or elimination of the abnormal cells. Finally, the immune cells typically die after the interaction stage, which indicates that the body is in the recovery stage. These processes were interrupted in the immune–unhealthy diet model, in which the interaction between the immune cells and abnormal cells failed to eliminate the abnormal cells and also led to a decrease in immune cells. Thereafter, the abnormal cells succeeded in coexisting with the normal cells; this type of coexistence might trigger cancer [5,20,22,24,26,40]. On the basis of the analysis and simulation of the IHDM and the IUNHDM, we can infer that the process of elimination or inhibition of abnormal cells by the immune system is affected by two main parameters, namely, and . When a person follows a healthy diet (correlating with the food pyramid), his/her immune system will be strong and able to recognize damaged cells, responding by repairing or eliminating them. By contrast, following an unhealthy diet leads to a weakened immune system, which harms its function. As a result, abnormal cells will stimulate a response from the immune system, encouraging it to increase the generation of immune cells. This stimulation increased when associated with the IUNHDM and decreased when associated with IHDM. In summary, symmetry and antisymmetry are basic characteristics in the understanding of the relationship between dietary patterns and the behavioral responses of the immune system when protecting the human body from developing diseases. The symmetry of the IHDM and IUNHDM can be seen when the immune system in both models responds to abnormal cells appearing in the tissue, as well as the responses in the recovery stage. The results also suggested some similarities in terms of the function of the immune system in both models, possibly affected by diet habits. Although the mathematical model that is proposed in this work contributes to understanding the general dynamics of pathogens, it is well-known that mathematical models cannot take all variables into account. For this reason, it is highly recommended to conduct clinical experiments to consider real cases in order to confirm the results of our mathematical model and to show more precise results. In the future, we will expand this work to study the dynamic effect of the growth of abnormal cells and their activity. In addition, we plan to apply our work to other pathogens.
Author Contributions
Conceptualization, S.A.A.; Funding Acquisition, A.S.R.; Methodology, S.A.A.; Project Administration, A.S.R.; Supervision, A.S.R.; Validation, A.S.R.; Writing—Original Draft, S.A.A.; Writing—Review and Editing, A.S.R.
Funding
This research is funded by a grant from Universiti Kebangsaan Malaysia.
Acknowledgments
We are indebted to Universiti Kebangsaan Malaysia for providing financial support and facilities for this research under the grant GUP-2017-112.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. World Health Statistics 2018: Monitoring Health for the SDGs Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef]
- Howard, P.; Whittaker, B. Placement Learning in Cancer & Palliative Care Nursing-E-Book: A Guide for Students in Practice; Elsevier Health Sciences: Philadelphia, PA, USA, 2012. [Google Scholar]
- Alberta, B.; Lewis, J.; Roberta, K.; Johnson, A.; Raff, M.; Walter, P. Molecular Biology of the Cell; Garland PUB: New York, NY, USA, 2008. [Google Scholar]
- Cooper, G.M.; Hausman, R.E. The Cell: A Molecular Approach; ASM Press: Washington, DC, USA, 2000; Volume 2. [Google Scholar]
- Boulet, L.P. Asthma and obesity. Clin. Exp. Allergy 2013, 43, 8–21. [Google Scholar] [CrossRef]
- Fung, T.T.; van Dam, R.M.; Hankinson, S.E.; Stampfer, M.; Willett, W.C.; Hu, F.B. Low-carbohydrate diets and all-cause and cause-specific mortality: Two cohort studies. Ann. Intern. Med. 2010, 153, 289–298. [Google Scholar] [CrossRef]
- Loeb, K.R.; Loeb, L.A. Significance of multiple mutations in cancer. Carcinogenesis 2000, 21, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Banerjee, S.; Ghosh, A.K. Dietary-induced cancer prevention: An expanding research arena of emerging diet related to healthcare system. J. Adv. Pharm. Technol. Res. 2012, 3, 16. [Google Scholar]
- Yusof, A.S.; Isa, Z.M.; Shah, S.A. Dietary patterns and risk of colorectal cancer: A systematic review of cohort studies (2000–2011). Asian Pac. J. Cancer Prev. 2012, 13, 4713–4717. [Google Scholar] [CrossRef] [PubMed]
- Yusof, A.S.; Isa, Z.M.; Shah, S.A. Perceptions of Malaysian colorectal cancer patients regarding dietary intake: A qualitative exploration. Asian Pac. J. Cancer Prev. 2013, 14, 1151–1154. [Google Scholar] [CrossRef]
- Shahar, S.; Shafurah, S.; Hasan Shaari, N.S.; Rajikan, R.; Rajab, N.F.; Golkhalkhali, B.; Zainuddin, Z.M.D. Roles of diet, lifetime physical activity and oxidative DNA damage in the occurrence of prostate cancer among men in Klang Valley, Malaysia. Asian Pac. J. Cancer Prev. 2011, 12, 605–611. [Google Scholar]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, D.; Panetta, J.C. Modeling immunotherapy of the tumor–immune interaction. J. Math. Biol. 1998, 37, 235–252. [Google Scholar] [CrossRef]
- Mayer, H.; Zaenker, K.; An Der Heiden, U. A basic mathematical model of the immune response. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 155–161. [Google Scholar] [CrossRef]
- Gałach, M. Dynamics of the Tumor—Immune System Competition—The Effect of Time Delay. Int. J. Appl. Math. Comput. Sci. 2003, 13, 395–406. [Google Scholar]
- Villasana, M.; Radunskaya, A. A delay differential equation model for tumor growth. J. Math. Biol. 2003, 47, 270–294. [Google Scholar] [CrossRef] [PubMed]
- Rihan, F.; Rihan, N. Dynamics of Cancer-Immune System with External Treatment and Optimal Control. J. Cancer Sci. Ther. 2016, 8, 257–261. [Google Scholar] [CrossRef]
- Bratus, A.; Samokhin, I.; Yegorov, I.; Yurchenko, D. Maximization of viability time in a mathematical model of cancer therapy. Math. Biosci. 2017, 294, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Mufudza, C.; Sorofa, W.; Chiyaka, E.T. Assessing the effects of estrogen on the dynamics of breast cancer. Comput. Math. Methods Med. 2012, 2012, 473572. [Google Scholar] [CrossRef]
- Green, L.E.; Dinh, T.A.; Smith, R.A. An estrogen model: The relationship between body mass index, menopausal status, estrogen replacement therapy, and breast cancer risk. Comput. Math. Methods Med. 2012, 2012, 792375. [Google Scholar] [CrossRef] [PubMed]
- Ku-Carrillo, R.A.; Delgadillo, S.E.; Chen-Charpentier, B. A mathematical model for the effect of obesity on cancer growth and on the immune system response. Appl. Math. Model. 2016, 40, 4908–4920. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Radunskaya, A. A mathematical tumor model with immune resistance and drug therapy: An optimal control approach. Comput. Math. Methods Med. 2001, 3, 79–100. [Google Scholar] [CrossRef]
- Ku-Carrillo, R.A.; Delgadillo-Aleman, S.E.; Chen-Charpentier, B.M. Effects of the obesity on optimal control schedules of chemotherapy on a cancerous tumor. J. Comput. Appl. Math. 2017, 309, 603–610. [Google Scholar] [CrossRef]
- Wu, J.; Tan, Y.; Chen, Z.; Zhao, M. Data Decision and Drug Therapy Based on Non-Small Cell Lung Cancer in a Big Data Medical System in Developing Countries. Symmetry 2018, 10, 152. [Google Scholar] [CrossRef]
- Alharbi, S.; Rambely, A.S. Stability Analysis of Mathematical Model on the Effect of Modern Lifestyles Towards the Immune System. J. Qual. Meas. Anal. 2018, 14, 99–114. [Google Scholar]
- Rosen, B.; Israeli, A.; Shortell, S. Accountability and Responsibility in Health Care: Issues in Addressing an Emerging Global Challenge; World Scientific: London, UK, 2012. [Google Scholar]
- Cairns, J. Cancer: Science and Society; WH Freeman: New York, NY, USA, 1978. [Google Scholar]
- Karacabey, K.; Ozdemir, N. The Effect of Nutritional Elements on the Immune System. J. Obes. Weight Loss Ther. 2012, 2, 152. [Google Scholar] [CrossRef]
- World Cancer Research Fund; American Institute for Cancer Research. Diet, Nutrition, Physical Activity and Cancer: A Global Perspective. 2018. Available online: https://www.wcrf.org/sites/default/files/Summary-third-expert-report.pdf (accessed on 1 August 2018).
- Rondanelli, M.; Faliva, M.A.; Miccono, A.; Naso, M.; Nichetti, M.; Riva, A.; Guerriero, F.; De Gregori, M.; Peroni, G.; Perna, S. Food pyramid for subjects with chronic pain: Foods and dietary constituents as anti-inflammatory and antioxidant agents. Nutr. Res. Rev. 2018, 31, 131–151. [Google Scholar] [CrossRef] [PubMed]
- Achadi, E.; Ahuja, A.; Bendech, M.A.; Bhutta, Z.A.; De-Regil, L.M.; Fanzo, J.; Fracassi, P.; Grummer-Strawn, L.M.; Haddad, L.J.; Hawkes, C.; et al. Global Nutrition Report: From Promise to Impact: Ending Malnutrition by 2030; International Food Policy Research Institute: Washington, DC, USA, 2016. [Google Scholar]
- Marwitz, S.E.; Woodie, L.N.; Blythe, S.N. Western-style diet induces insulin insensitivity and hyperactivity in adolescent male rats. Physiol. Behav. 2015, 151, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Sample, C.H.; Martin, A.A.; Jones, S.; Hargrave, S.L.; Davidson, T.L. Western-style diet impairs stimulus control by food deprivation state cues: Implications for obesogenic environments. Appetite 2015, 93, 13–23. [Google Scholar] [CrossRef]
- Shaharudin, S.H.; Sulaiman, S.; Shahril, M.R.; Emran, N.A.; Akmal, S.N. Dietary changes among breast cancer patients in Malaysia. Cancer Nurs. 2013, 36, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Subar, A.F.; Hollenbeck, A.; Schatzkin, A. Dietary fiber intake and mortality in the NIH-AARP diet and health study. Arch. Intern. Med. 2011, 171, 1061–1068. [Google Scholar] [CrossRef]
- Tilg, H.; Moschen, A.R. Food, immunity, and the microbiome. Gastroenterology 2015, 148, 1107–1119. [Google Scholar] [CrossRef]
- Uranga, J.A.; López-Miranda, V.; Lombo, F.; Abalo, R. Food, nutrients and nutraceuticals affecting the course of inflammatory bowel disease. Pharmacol. Rep. 2016, 68, 816–826. [Google Scholar] [CrossRef]
- Newmark, H.L.; Yang, K.; Kurihara, N.; Fan, K.; Augenlicht, L.H.; Lipkin, M. Western-style diet-induced colonic tumors and their modulation by calcium and vitamin D in C57Bl/6 mice: A preclinical model for human sporadic colon cancer. Carcinogenesis 2008, 30, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Hatami, M.; Esmaeil Akbari, M.; Abdollahi, M.; Ajami, M.; Jamshidinaeini, Y.; Davoodi, S.H. The relationship between intake of macronutrients and vitamins involved in one carbon metabolism with breast cancer risk. Tehran Univ. Med. J. TUMS Publ. 2017, 75, 56–64. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).