Abstract
Due to the fact that cascade control can improve the single-loop’s performance well and reduce the integral error from disturbance response, it has been one of the most important control strategies in industrial production, especially in thermal power plant and chemical engineering. However, most of the existing research is based on the Gaussian system and other few studies on the non-Gaussian cascade disturbance system also have obvious defects. In this paper, an effective control loop performance assessment (CPA) of cascade control system for many non-Gaussian distributions even the unknown mixture disturbance noise has been proposed. Compared to the minimum variance control (MVC) approach, the minimum entropy control (MEC) method can obtain a more accurate estimate. In this method, like MVC, the primary loop output and secondary loop output can be represented as invariant and dependent terms, then adopted estimated distribution algorithm (EDA) is used to achieve the system model and disturbances. In order to show the effectiveness of MEC, some simulation examples based on different perturbations are given.
1. Introduction
As the cascade control can improve the performance better than the single loop, and reduce the deviation from the disturbance response, cascade control loop has been widely used in chemical industrial, thermal power plant, and DC motor [1,2], especially in oil refinery and high pressure drum water control. However, although the initial cascade control loop can meet the designing performance specifications, over time, the control loop’s performance will deteriorate due to many factors, including the maintained controllers and the aging of the equipment, without or insufficient feed-forward compensation [3]. The study that is proposed by Honeywell illustrated that nearly half of the control system were working on the poor performance situation [4]. If the deterioration of the control loop still sustains without any identification, it will cause an economic loss of one hundred million dollars, even leading to the destruction of environment and threatening the safety of industrial workers.
Therefore, since the 1980s, many methods for system performance evaluation have appeared [5]. Since these algorithms use statistical knowledge to analyze system performance, they are also known as statistical process control, but they still fail to give the performance of the current loop. Hence Harris proposed one performance index by using the MVC [6]. It represents the starting of the research based on MVC among the CPA field. The performance of the control loop can be given only by system output whatever delay time is known or not. Then more research had been done in this field. In 1996, Harris proposed a performance evaluation method for a multiple-input multiple-output (MIMO) feedback control system [7]. Although the MVC controllers can meet the control performance requirement, the system robustness perform poorly. Hence, a generalized minimum variance (GMV) concept was raised by Grimble, he used this benchmark as single-loop CPA index and designed the corresponding controller based on GMV concepts. Unfortunately, it is necessary to add errors and control weighting factors to the control loop. Unless a fixed weight value is used, it is difficult to choose the appropriate weighting factor unless a constant weight is used. Huang and Shah presented a linear quadratic Gaussian (LQG) benchmark based on the MVC method [8]. Since the minimum variance of the output is only calculated compared to MVC, LQG also needs to calculate the minimum variance of the input, so for the same system, the LQG benchmark can better reflect the gap between the current actual performance and the ideal performance. However, compared to the traditional MVC benchmark, LQG is too complicated to implement in real industrial processes. In addition, many new CPA means has been put forward with further research. Such as the Hurst index is presented by Srinivasan, although it requires no prior knowledge [9,10], under the mixture noise environment this method may cause severe error. Sadasivarao tried to import the generic algorithm to cascade control loop to design optimal PID controller [11]. Yu uses CPA tools to get random sample jitter to show performance impact [12]. Ye presented a method about how to design the optimal cascade loop [13].
Although all these methods have been quite mature, all previous research on CPA was based on the assumption that interference interferes with Gaussian distribution. In fact, in real industrial processes, the disturbance of the control loop may be not only Gaussian noise, but also beta noise, or even a mixture of multiple unknown noises. In such a situation, for one system with non-Gaussian noise, those methods above maybe not a good benchmark for cascade control loop. In order to solve this problem, the MEC benchmark has been proposed. However, in the past publications [14,15,16], there is very little research in this area, especially for the cascade control loop. The research on cascade control loop based the MEC is presented by Jianhua Zhang [17], he proposed the Renyi Entropy to deal with systems in which disturbance is non-Gaussian. However, the method he used have been proved incorrectly [18,19], because he ignored the linear relationship when calculated the discrete entropy. In literature [19], the method is only used in single loop system. For cascade control system, the derivation of algorithm and the iteration of estimated distribution algorithm (EDA) need to be re-derived. In literature [20], Zhang proposed one improved Renyi Entropy method based on the mean value, it overcomes the mean shift of the output, but the efficiency of the algorithm reduced seriously.
Therefore, in this paper, one effective benchmark based on rational entropy is raised. It aims to establish an optimal MEC benchmark for cascade loop system with non-Gaussian disturbance. Also, the EDA is used to estimate the distribution of disturbance and identify the system ARMA model parameters, then the CPA benchmark is given. The efficiency can be improved greatly.
The structure of this paper is as follow: In Section 2, the conventional MVC is reviewed. In Section 3, the MEC will be introduced and the method of how to obtain estimated parameter vector and disturbance based on improved EDA algorithm is illustrated in detail. In Section 4, a simulation case is given. In Section 5, a conclusion is made.
2. Routinely MVC for Cascade Control System
2.1. Introduction of Cascade System
Consider the general cascade control system with unity feedback in Figure 1, where the is the set point, is the output error, is the controller output, is the system disturbance, is the disturbance filters, the effect of all unknown disturbances to the two loops are represented by them. is the primary and secondary loop controllers, for , it denotes the transfer function of feedback controller, is the sample time, and is the system output of outer loop and inner loop. The output control loop transfer function is and the inner loop transfer function is . The discrete shift is substituted by the backward shift . Obviously, the output is
where the primary loop transfer function is with the time delay equal to , and is the primary transfer model without any time delay. Similarly, the inner loop function can be written as and the inner loop time delay is . Both the two disturbance are assumed as a rational function with the backward shift . For simplify, is usually set to zero.
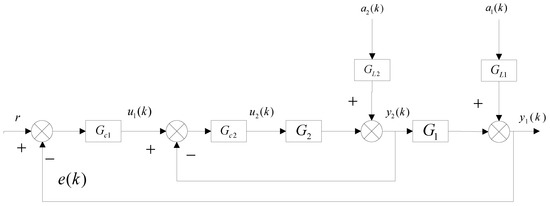
Figure 1.
Common cascade control system.
2.2. MVC Strategy of Cascade Control System
The MVC method based on cascade control system decomposes the system output into two parts by using the Diophantine equation. For simplify and universality, make the system input equal to zero, then the Equation (1) can be decomposed as
The disturbances transfer function can be replaced by following Diophantine equations,
where is the polynomial of with order of and are polynomials of with order of . , are residual polynomial coefficients of the Equations (4)–(6). Substituted Equations (4)–(6) into Equation (1), the outer loop output is given as,
Specifically, the polynomials are feedback invariant, they only depend on the unknown-disturbance and they can be decomposed as
Thus, the feedback-invariant term is represented as an AR model, the model is used as the performance benchmark of MVC. When , the optimal controller can be obtained and the MV of is,
where are the coefficient matrices of the polynomial .
Thus, MVC index for cascade control can be defined as:
where is the optimal MV of the system output, and the is the variance of actual output. In the literature [4], Harris had noted that the index under the MVC is only valid for the noise which is subject to Gaussian distribution [21,22,23,24,25,26]. However, most external disturbances in realistic industrial processes are non-Gaussian. Thus, the MVC based on CPA is not reliable. Consider the following system from literature [15],
where the disturbance is subject to distribution, the probability density function (PDF) of it is given by,
where make . For , the parameter , , similarly, , , . According to the MVC method, the PI controller and the P controller can be used as, and . The normal probability plots are shown in Figure 2. From the Figure 2, we can find that the actual and estimated Freq are shift on the x-axis. The MVC algorithm is not sensitive to the means shift. When the noise is subject to Gaussian distribution which means that the mean is zero, the actual and estimated frequency will not reflect the mean shift. However, when the noise is subject to non-Gaussian distribution, its mean is non-zero. Hence, the actual frequency and estimated frequency are shift on the x-axis. This is a serious defect for performance evaluation. The corresponding distribution plots are shown in Figure 3.
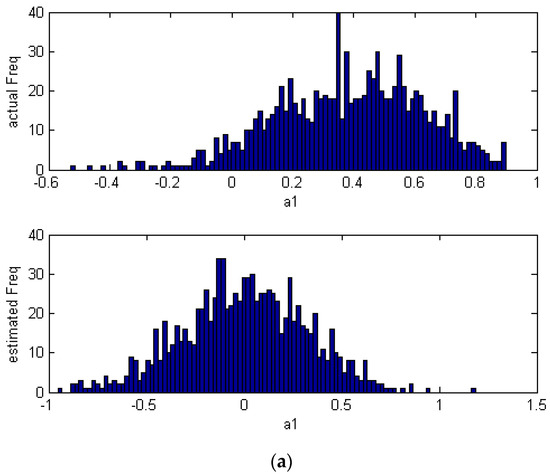
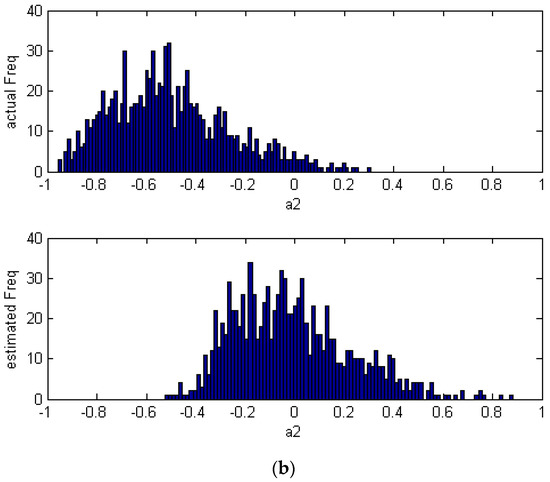
Figure 2.
The actual and estimated distribution of (a) and (b) which are non-Gaussian disturbances.
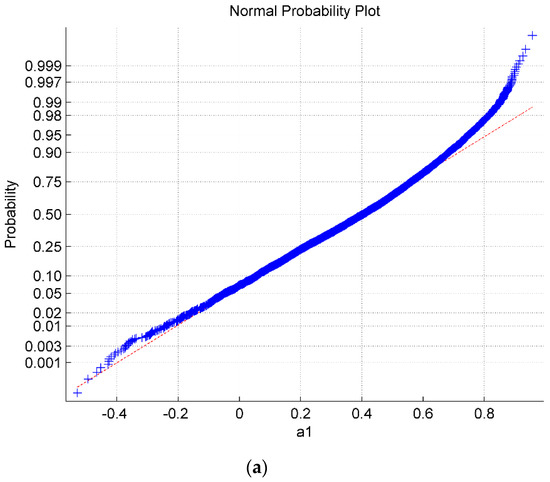
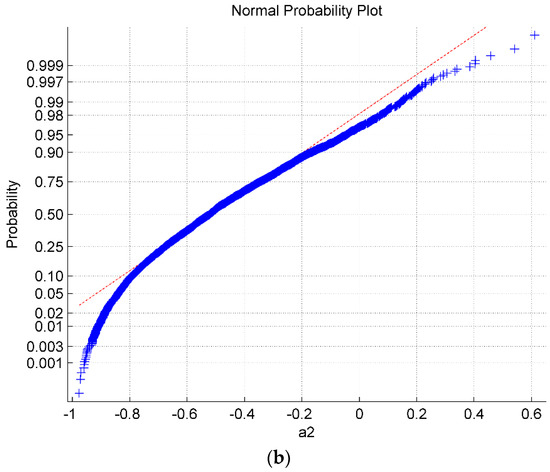
Figure 3.
Normal probability plots of the actual disturbance (a) and (b) which are non-Gaussian disturbance.
Figure 3 illustrates that the disturbance is subject to non-Gaussian distribution because the plots deviates the straight line. The response with different disturbance of cascade control are shown in Figure 4, and the inner and outer loop output distribution are shown in Figure 5. As can be seen from Figure 4 and Figure 5, the performance of the main output is significantly better than the performance of the secondary loop output , but the MVC indices of the two loops are diametrically opposed, they are and , respectively. According to this example, using the MVC method for a non-Gaussian system may result in erroneous results.
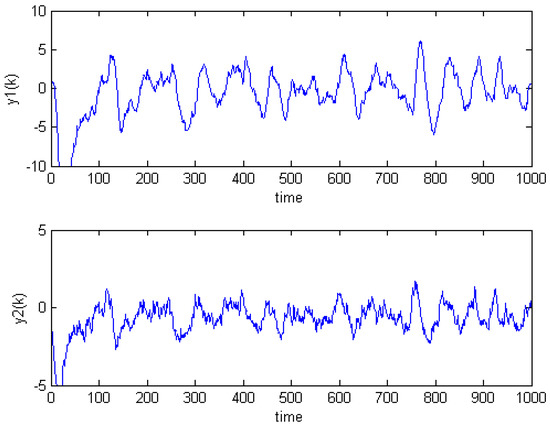
Figure 4.
Output of two disturbances.
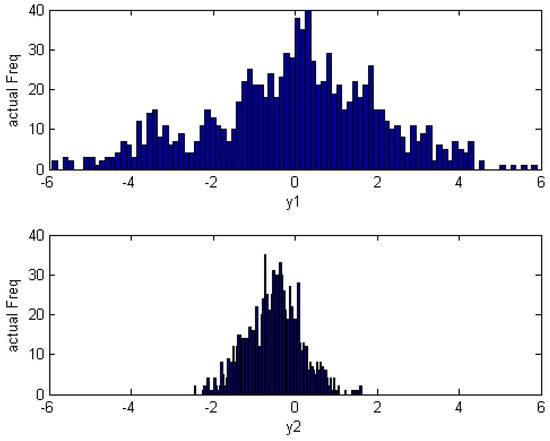
Figure 5.
Output distribution of two disturbances .
3. Minimum Entropy Control
3.1. Entropy Information Analysis
According to information theory, entropy is the probability of an uncertain variable [17], and entropy is determined by the probability distribution function of a random variable. Zhang [17] proposed a cascaded control CPA method based on minimum entropy. According to his method, the parameterization formula of Renyi entropy is,
where the is a continuous parameter and is the discrete random variable. The element has probability , hence, .
Thus, the author gave the entropy calculate of cascade control system,
Hence,
which based on the following lemma and means minimum entropy.
Lemma 1
[17]. , where x is a random variable and c is a constant.
Lemma 2
[17]. The entropy of joint distribution can be represented by conditional entropy which can be expressed as , where and are random variables.
Lemma 3
[17]. On a common probability space, while and are the random variables.
However the conclusion in Equation (15) is wrong because the above linear relationship cannot been ignored. For example, considering the following model,
where is the disturbance and is the discrete time. According to the above lemma, the entropy is
Then the density plot of output with different coefficients is shown in Figure 6.
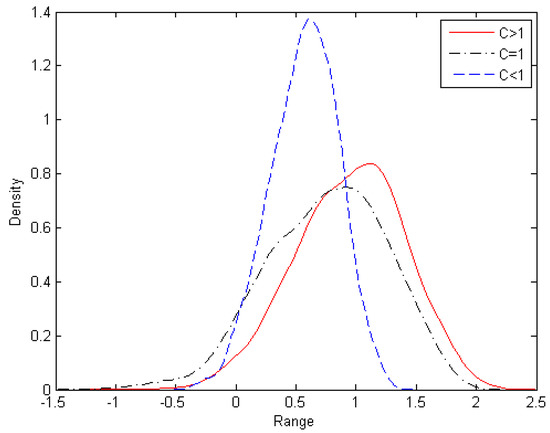
Figure 6.
The density plot of output with different coefficient.
It is obviously that different coefficient will lead to different density distributions, hence the theory in literature [17] is wrong. In fact, considering continuous case,
where the is the PDF of the continuous variables , and assume that the PDF . According to Lemma 2, there is the equation . However, this equation is not set up according to the Equation (18). It seems that entropy is not suitable as a benchmark. Fortunately, a Renyi entropy (RE) is proposed in literature [19] which is calculated as,
where the is a random variable whatever it is discrete or continuous and is its PDF. This type entropy can prevent the index becoming negative of Inf [19]. In addition, it still has most properties of Shannon entropy. In this paper, RE is used to calculate the performance index.
3.2. Minimum Entropy Based on EDA
The entropy in Equation (19) cannot be calculated easily because the delay time and disturbance of process model are unknown. Thus, we can use the estimation of distribution algorithms (EDA) to obtain the model parameters and extern disturbances. The EDA is a new statistical method to search the global optimal solution during several population evolutions [14,26,27,28,29,30,31,32].
In the above equations, are the parameter of polynomials, and is the order of each polynomial. There are many methods to estimate the order of model and its delay time [19,23,24]. In this paper, we use the AIC criterion to obtain the order and delay time. Thus, the Equation (21) can be represented as,
where
is the observational vector and
is the parameter vector. Thus, the estimated residual is given as,
Then we use the EDA to obtain the fitness parameter vector while the residual achieves minimum. The EDA algorithm is following,
- (1)
- Firstly, generate individuals as a seed by recursive extended least squares algorithm (RELS), where is the count of generation.
- (2)
- From the seed in generation, select R group individuals to calculate the mean value of residuals according to Equations (23)–(25). Remove those seeds which is less than the threshold value . Re-sampling to make the number of parameter space is not less than .
- (3)
- Add some seeds from the new parameter space and establish new probability model where the probability model can be expressed as,where the is the mean of lth generation parameter vector and is the variance of lth generation parameter vector .
- (4)
- Set and add N-R new parameter into space based on the probability model which is set upon step (3).
- (5)
- Repeat step (2) to step (5) until meeting the stopping criterion.
Through above process, are obtained. And we can obtain the actual entropy from the system output. Hence, the performance index based on MEC is given as,
4. Simulation Case
In this section, the MEC methods is adopted with the system in Section 2. Since the Renyi entropy method mentioned in Section 3.1 is not applicable to continuous time-delay systems, we cannot compare the Renyi entropy method with the RE entropy method and the traditional MVC algorithm for stochastic continuous systems.
4.1. Cascade Control System with Gaussian Disturbance
The system structure is shown in Figure 1, for Gaussian noise, make the variances of different disturbances are , respectively. According to the Equation (12), the time delay are . The normal probability of Gaussian disturbance with different variance is shown in Figure 7, and the estimated and actual disturbance distribution plots based on MVC are in Figure 8. Actually, the estimated disturbance variances which using the MVC benchmark are . Obviously, the variances are close to actual disturbance variance.
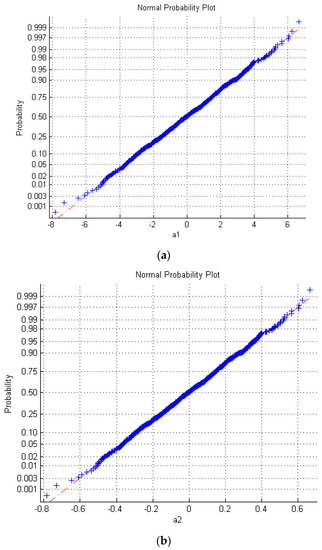
Figure 7.
The normal probability of two disturbances (a) and (b) .
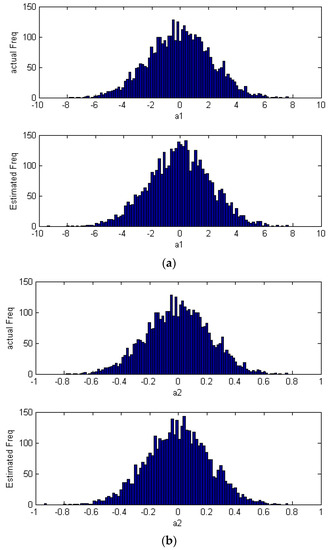
Figure 8.
The actual and estimated distribution plots from different disturbances (a) and (b) based on minimum variance control (MVC).
Assume that the disturbance is unknown, we can use the EDA to estimate the system model and disturbance distribution. Routinely, we set the seed selection criteria is and stopping criteria is which means achieving optimal residual and smallest entropy. Thus, the estimated disturbances are shown in Figure 9. The variance of estimated disturbance is .
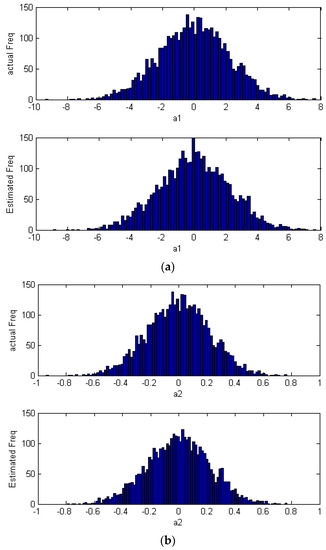
Figure 9.
The distribution plots of two different disturbances (a) and (b) based on minimum entropy control (MEC).
The performance assessment of this system based on MVC and MEC is as follows.
4.2. Cascade Control System with Non-Gaussian Disturbance
We use the same noise as the beta noise mentioned in the Section 2. The MVC performance assessment has been given in Section 2. For MEC, the estimated disturbances are given in Figure 10.
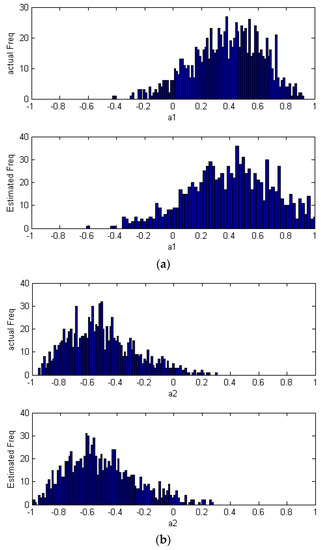
Figure 10.
The actual and estimated distribution plots of two disturbances (a) and (b) based on MEC.
According this new MEC method, the residual can be obtained based the identification model by using Diophantine equation. And according to simulation in the Section 2, the index based on different methods can be given.
From the Table 1 and Table 2, we can find the method which is proposed in this paper performs well on Gaussian and non-Gaussian disturbance.

Table 1.
The index by MVC and MEC benchmarks of primary loop (Gaussian).

Table 2.
The index by MVC and MEC benchmarks of primary loop (non-Gaussian).
5. Conclusions
To improve the cascade control loop performance, we need to identify its model. In the past, many CPA algorithms had been proposed, but most of these are based on second order statistics and the disturbance is assumed as Gaussian noise. However, in the actual industry, the disturbance of the cascade control system is usually a mixture of several unknown disturbances, and is generally subject to a non-Gaussian distribution. Since the minimum variance control is not suitable for non-Gaussian cascade systems, this paper proposes a reliable performance evaluation method based on minimum entropy, which can be used for cascade control loops with non-Gaussian disturbances. The MEC method is proposed based on rational entropy. In order to obtain a more accurate estimation of parameter vector and perturbation, an improved EDA algorithm is adopted. The effectiveness of this approach has been demonstrated in previous simulations. Thus, it can be concluded that these methods can be used for cascade control system whether the disturbance is in a Gaussian distribution or not. In addition, further research is needed to improve the efficiency of EDA.
Author Contributions
Funding acquisition, Y.-G.W.; methodology, Q.Z.; software, W.Z.; validation, Q.C. and F.-F.L.; writing—original draft preparation, Q.Z.; writing—review and editing, Q.Z.
Funding
This research was funded by National Natural Science Foundation, grant number is 61074087, 61703277, 11502145.
Acknowledgments
The simulation data used to support the findings of this study are included within the article. The simulation data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moreno-Valenzuela, J.; Guzman-Guemez, J. Experimental evaluations of voltage regulators for a saturated boost DC-to-DC power converter. Trans. Inst. Meas. Control. 2016, 38, 327–337. [Google Scholar] [CrossRef]
- Moreno-Valenzuela, J.; González-Hernández, L. Operational space trajectory tracking control of robot manipulators endowed with a primary controller of synthetic joint velocity. ISA Trans. 2011, 50, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Khamseh, S.A.; Sedigh, A.K.; Moshiri, B.; Fatehi, A. Control performance assessment based on sensor fusion techniques. Control Eng. Pract. 2016, 49, 14–28. [Google Scholar] [CrossRef]
- Ender, D.B. Process control performance: Not as good as you think. Control Eng. 1993, 40, 180–190. [Google Scholar]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis: Part III: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar] [CrossRef]
- Harris, T.J. Assessment of control loop performance. Can. J. Chem. Eng. 1989, 67, 856–861. [Google Scholar] [CrossRef]
- Harris, T.J.; Boudreau, F.; MacGregor, J.F. Performance assessment of multi-variable feedback controllers. Automatica 1996, 32, 1505–1518. [Google Scholar] [CrossRef]
- Huang, B.; Shah, S.L. Performance Assessment of Non-Minimum Phase Systems. In Performance Assessment of Control Loops; Springer: London, UK, 1999. [Google Scholar]
- Srinivasan, B.; Spinner, T.; Rengaswamy, R. Control loop performance assessment using detrended fluctuation analysis (DFA). Automatica 2012, 48, 1359–1363. [Google Scholar] [CrossRef]
- Pillay, N.; Govender, P. A Data Driven Approach to Performance Assessment of PID Controllers for Set point Tracking. Daaam Int. Symp. Intell. Manuf. Autom. 2013, 69, 1130–1137. [Google Scholar]
- Sadasivarao, M.V.; Chidambaram, M. PID controller tuning of cascade control systems using genetic algorithm. J. Indian Inst. Sci. 2006, 86, 343–354. [Google Scholar]
- Yu, W.; Wilson, D.I.; Young, B.R. Control performance assessment in the presence of sampling jitter. Chem. Eng. Res. Des. 2012, 90, 129–137. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, B.; Shao, M.; Zhang, Y. Polymerizer temperature cascade control system based on generalized predictive control. Phys. Procedia 2012, 24, 184–189. [Google Scholar]
- Yue, H.; Zhou, J.; Wang, H. Minimum entropy control of B-spline PDF systems with mean constraint. Automatica 2006, 42, 989–994. [Google Scholar] [CrossRef]
- Wang, H. Minimum entropy control of non-Gaussian dynamic stochastic systems. IEEE Trans. Autom. Control. 2002, 47, 398–403. [Google Scholar] [CrossRef]
- Wang, H. Bounded Dynamic Stochastic Systems: Modelling and Control; Springer: London, UK, 2000. [Google Scholar]
- Zhang, J.H.; Zhang, L.; Chen, J.; Xu, J.; Li, K. Performance assessment of cascade control loops with non-Gaussian disturbances using entropy information. Chem. Eng. Res. Des. 2015, 104, 68–80. [Google Scholar] [CrossRef]
- You, H.; Zhou, J.; Zhu, H.; Li, D. Performance assessment based on minimum entropy of feedback control loops. In Proceedings of the IEEE Data Driven Control and Learning Systems Conference, Chongqing, China, 26–27 May 2017. [Google Scholar]
- Zhou, J.L.; Jia, Y.Q.; Jiang, H.X.; Fan, S.Y. Non-Gaussian Systems Control Performance Assessment based on Rational Entropy. Entropy 2018, 20, 331. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Lee, F.; Chen, Q.; Sun, Z. Improved Renyi Entropy Benchmark for Performance Assessment of Common Cascade Control System. IEEE Access. 2019, 7, 6796–6803. [Google Scholar] [CrossRef]
- Zhang, P.; Qin, G.; Wang, Y. Optimal Maintenance Decision Method for Urban Gas Pipelines Based on as Low as Reasonably Practicable Principle. Sustainability 2019, 11, 153. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Jin, Y. RM-MEDA: A regularity model-based multi-objective estimation of distribution algorithm. IEEE Trans. Evol. Comput. 2008, 12, 41–63. [Google Scholar] [CrossRef]
- Shi, Y.; Fang, H. Kalman filter-based identification for systems with randomly missing measurements in a network environment. Int. J. Control. 2010, 83, 538–551. [Google Scholar] [CrossRef]
- Padhan, D.G.; Majhi, S. Modified smith predictor based cascade control of unstable time delay processes. ISA Trans. 2012, 51, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ding, F.; Shi, Y. An efficient hierarchical identification method for general dual-rate sampled-data systems. Automatica 2014, 50, 962–970. [Google Scholar] [CrossRef]
- Sagarna, R.; Arcuri, A.; Yao, X. Estimation of distribution algorithms for testing object oriented software. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 438–444. [Google Scholar]
- Hauschild, M.; Pelikan, M. An introduction and survey of estimation of distribution algorithms. Swarm Evol. Comput. 2011, 1, 111–128. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.M.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inform. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Klir, G.J.; Smith, R.M. On measuring uncertainty and uncertainty based information: Recent developments. Ann. Mathemat. Artific. Intell. 2001, 32, 5–33. [Google Scholar] [CrossRef]
- Guo, L.; Yin, L.P.; Wang, H.; Chai, T.Y. Entropy optimization filtering for fault isolation of nonlinear non-Gaussian stochastic systems. IEEE Trans. Autom. Control. 2009, 54, 804–810. [Google Scholar]
- Zhou, J.L.; L, G.T.; Wang, H. Robust tracking controller design for non-Gaussian singular uncertainty stochastic distribution systems. Automatica 2014, 50, 1296–1303. [Google Scholar] [CrossRef]
- Caticha, A. Relative Entropy and Inductive Inference. Am. Inst. Phys. 2004, 707, 75–96. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).