Abstract
This paper introduces a mathematical model of a convection flow of magnetohydrodynamic (MHD) nanofluid in a channel embedded in a porous medium. The flow along the walls, characterized by a non-uniform temperature, is under the effect of the uniform magnetic field acting transversely to the flow direction. The walls of the channel are permeable. The flow is due to convection combined with uniform suction/injection at the boundary. The model is formulated in terms of unsteady, one-dimensional partial differential equations (PDEs) with imposed physical conditions. The cluster effect of nanoparticles is demonstrated in the , and base fluids. The perturbation technique is used to obtain a closed-form solution for the velocity and temperature distributions. Based on numerical experiments, it is concluded that both the velocity and temperature profiles are significantly affected by . Moreover, the magnetic parameter retards the nanofluid motion whereas porosity accelerates it. Each -based and -based nanofluid in the suction case have a higher magnitude of velocity as compared to the injections case.
1. Introduction
Heat transport in unsteady laminar flows has numerous real-world applications, particularly flows in a porous channel with permeable walls, which include medical devices, aerodynamic heating, chemical industry, electrostatic precipitation, petroleum industry, nuclear energy, and polymer technology. Based on this motivation, many researchers have considered the porous channel problem with suction and injection under different physical conditions. In earlier studies, Torda [1] studied the boundary layer flow with the suction/injection effect. Berman [2] derived an exact solution for the channel flow taking into consideration the uniform suction/injection at the boundary wall of the channel. The suction and injection and the combined effect of heat and mass transfer on a moving continuous flat surface were analyzed by Erickson et al. [3]. Alamri et al. [4] studied the Poiseuille flow of nanofluid in a channel under Stefan blowing and the second-order slip effect. Zeeshan et al. [5] reported analytical solutions for the Poiseuille flow of nanofluid in a porous wavy channel. Hassan et al. [6] investigated the flow of based nanofluid on a wavy surface. Ellahi et al. [7] studied the boundary layer Poiseuille plan flow of kerosene oil based nanofluid fluid with variable thermal conductivity. Ijaz et al. [8] presented a comprehensive study on the interaction of nanoparticles in the flow of nanofluid in a finite symmetric channel. Some recent important and interesting studies can be found in [9,10,11,12].
Magnetohydrodynamic (MHD) is referred to as the magnetic properties of the fluids under the influence of an electromagnetic force. MHD flows have numerous applications in MHD bearings and MHD pumps. Many studies have been carried out on MHD flow in the literature. Abbas et al. [13] investigated the MHD flow of Maxwell fluid in a porous channel. The convective MHD flow of second-grade fluid was reported by Hayat and Abbas [14]. The effect of a transverse magnetic field on different flows in a semi-porous channel was presented by Sheikholeslami et al. [15]. Ravikumar et al. [16] studied three dimensional MHD due to the pressure gradient over the porous plate. Batti et al. [17] analyzed the heat transfer flow of nanofluid in a channel. They studied the effect of thermal radiation and the MHD effect by using Roseland’s approximation, Ohm’s law, and Maxwell equations. Ma et al. [18] study the MHD flow of nanofluid in a U-shaped enclosure using the Koo–Kleinstreuer–Li (KKL) correlation approximation for the effective thermal conductivity. Opreti [19] studied water-based silver nanofluid over a stretching sheet. They considered the effect of MHD, suction/injection, and heat generation/absorption in their study. Hosseinzadeh et al. [20] investigated the MHD squeezing flow of nonfluid in a channel. They presented analytical solutions by using similarity transformation and the perturbation technique. Narayana et al. [21] developed a mathematical model for the MHD stagnation point flow of Watler’s-B fluid nanofluid.
Nano-sized particles of () nanoparticles inside -based fluids are commonly known as silver-based nanofluids. The viscosity of the nanofluids containing metallic nanoparticles has a much higher thermal conductivity than the nanofluids containing metallic oxide and non-metallic nanoparticles. Because of this, the interest of researchers in investigating nanofluids containing metallic nanoparticles has increased recently. The first exact solutions for different types of nanofluid were developed by Loganathan et al. [22]. Qasim et al. [23] reported numerical solutions for MHD ferrofluid in a stretching cylinder. Amsa et al. [24] investigated nanofluid flow near a vertical plate containing five different nanoparticles. The radiative heat transfer in the natural convection flow of oxide nanofluid was studied by Das and Jana [25]. Dhanai et al. [26]. Numerically studied the MHD mixed convection flow of nanofluid in a cylindrical coordinate system. The MHD rotational flow of nanofluid taking into consideration the effect of a porous medium, thermal radiation, and the chemical reaction was presented by Reddy et al. [27]. For some other interesting studies, readers are referred to [28,29,30,31,32,33,34,35,36,37,38,39,40].
Motivated by the above-discussed literature, the present study focused on the MHD channel flow of nanofluid in a porous medium with the suction and injection effect. The flow of electrically conducting nanofluid is considered under the influence of a transverse magnetic field. The analytical solutions for the proposed model are developed by using the perturbation method. The solutions are numerically computed, and the influence of various flow parameters is studied graphically.
2. Problem Description
Consider a porous channel of a width, , filled with incompressible and based nanofluids with nanoparticles. The channel walls are stationary with isothermal temperature conditions. The flow in the x-direction due to the temperature gradient is shown in Figure 1. Under the assumption of [11], the governing equations are as follows:
together with the following physical conditions:
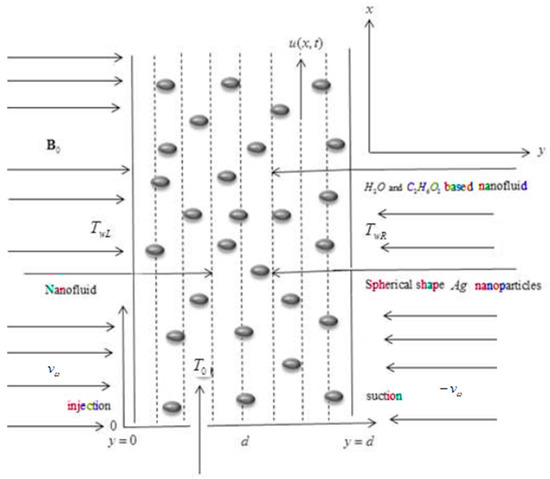
Figure 1.
Physical configuration and coordinate system.
By using Xuan et al.’s [28] model, the effective thermal conductive, , and dynamic viscosity, , of nanofluids are defined as:
where and are used, is the nanoparticles’ volume fraction, and is the radius of gyration for a number of particles. The static part in the effective thermal conductivity is derived from Maxwell’s [29] model and the effective viscosity is derived from Brinkman’s [30] model. Xuan et al.’s [28] model:
where the numerical values of the thermo-physical of base fluid and nanoparticles are given in Table 1 [11,31]. The radiative heat flux is given by:

Table 1.
Thermo-physical properties of base fluid and nanoparticles.
Substituting Equation (8) into Equation (2), gives:
The dimensionless variables:
Are introduced into Equations (1) and (9), we get:
where:
The following general perturbed solutions are considered for Equations (11)—(14), the following type of solutions are assumed:
Which lead to the following solutions:
where:
The solutions of Equations (21) and (23) under the boundary conditions, (22) and (24), are obtained as:
where:
Using Equations (25) and (26), Equation (16) becomes:
The solutions of Equations (17) and (19) after substituting Equation (25) under the boundary conditions, (18) and (20), are obtained as:
With:
Finally, substituting Equations (28) to (30) into Equation (16), we get:
3. Nusselt Number
The dimensionless expression for the Nusselt number is given by:
4. Skin-Friction
From Equation (31), the skin friction is calculated as:
5. Results and Discussion
In this section, the graphs of the velocity and temperature for and based nanofluids containing nanoparticles were plotted for different values of volume fraction, , and buoyancy parameter, permeability parameter, magnetic parameter, and radiation parameter, for both cases of suction and injection. The thermophysical properties of the base fluids and nanoparticles are mentioned in Table 1. For this purpose, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 were plotted. Figure 2, Figure 3, Figure 4 and Figure 5 were prepared to study the effects of the velocity for the cases of suction and injection of in and based nanofluids, respectively. It was found that the velocity increases with increasing for both cases of suction and injection. However, no variation is observed in the velocity of in based nanofluids in the case of injection. This behavior of velocity is found to be similar qualitatively to the results of Hajmohammadi et al. [32], however, they used in water-based nanofluids.
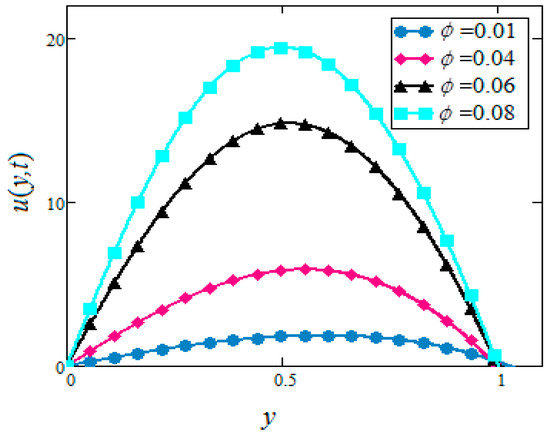
Figure 2.
Velocity profiles for different values of of in water based nanofluids when
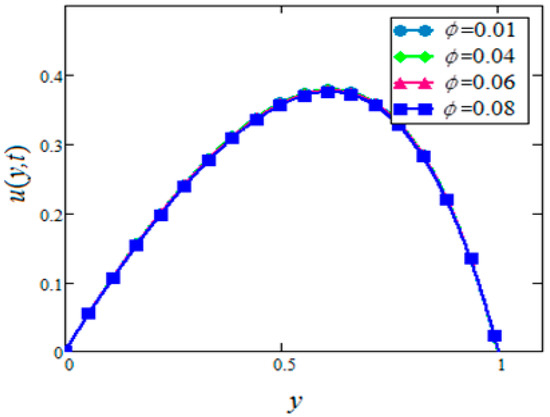
Figure 3.
Velocity profiles for different values of of in water based nanofluids when
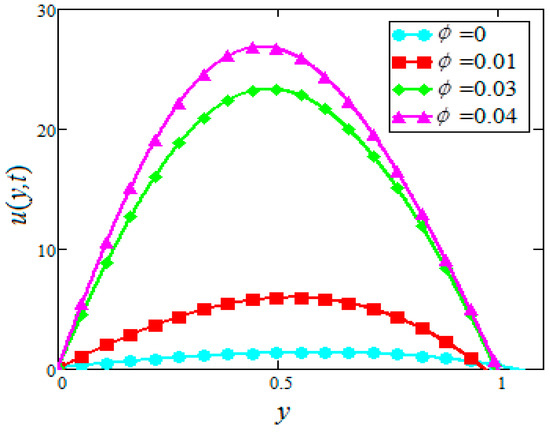
Figure 4.
Velocity profiles for different values of of in EG based nanofluids when
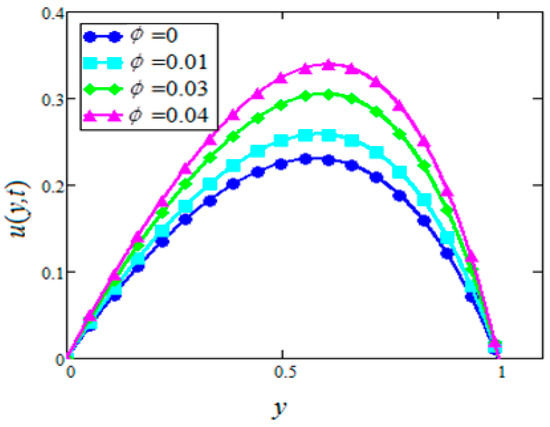
Figure 5.
Velocity profiles for different values of of in EG based nanofluids when
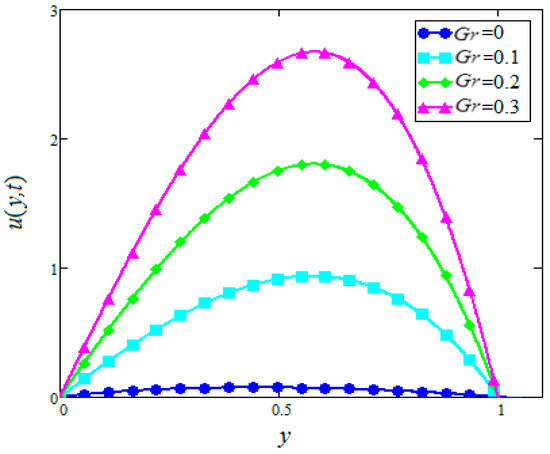
Figure 6.
Velocity profiles for different values of of in water based nanofluids when
Figure 7.
Velocity profiles for different values of of in water based nanofluids when
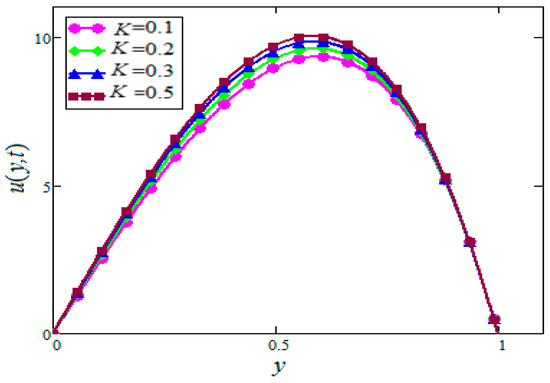
Figure 8.
Velocity profiles for different values of of in water based nanofluids when
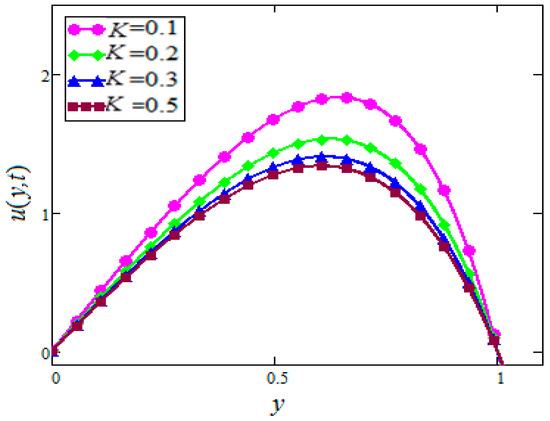
Figure 9.
Velocity profiles for different values of of in water based nanofluids when
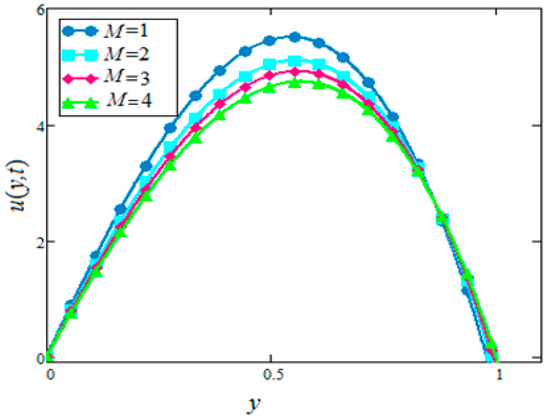
Figure 10.
Velocity profiles for different values of of in water based nanofluids when
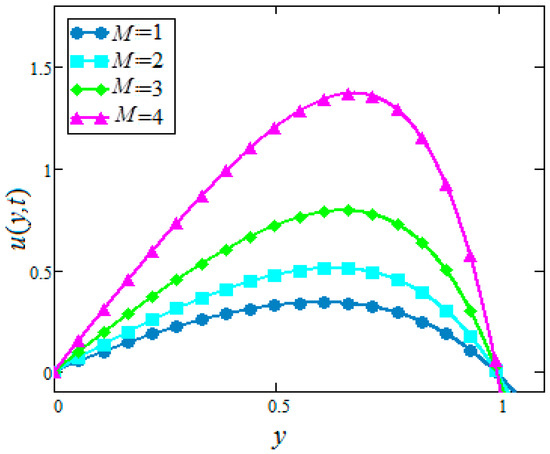
Figure 11.
Velocity profiles for different values of of in water based nanofluids when
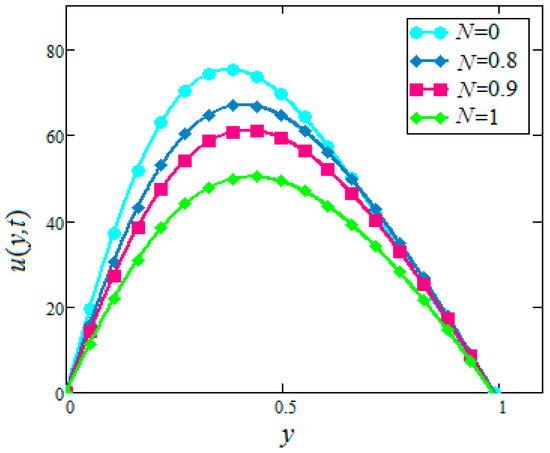
Figure 12.
Velocity profiles for different values of of in water based nanofluids when
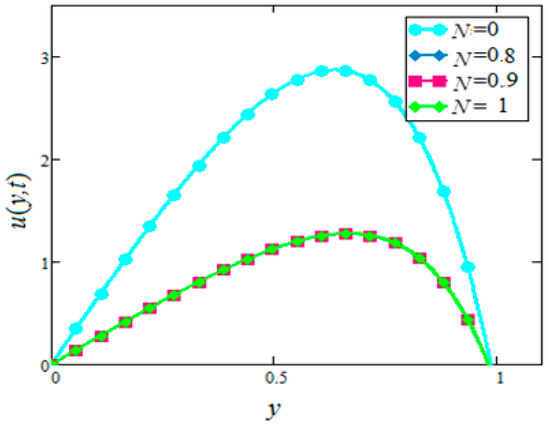
Figure 13.
Velocity profiles for different values of of in water based nanofluids when
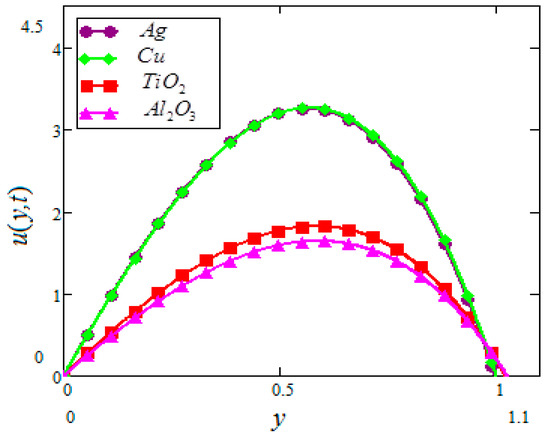
Figure 14.
Velocity profiles for different types of nanoparticles in water based nanofluids when
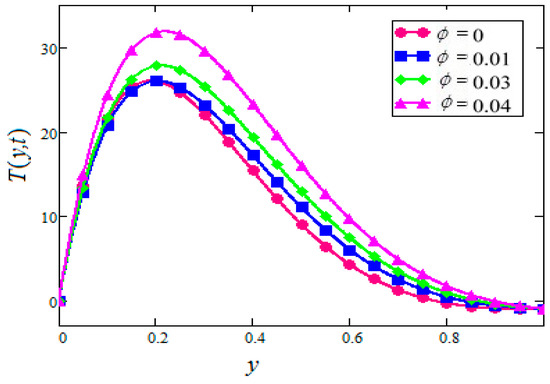
Figure 15.
Temperature profiles for different values of of in water based nanofluids when
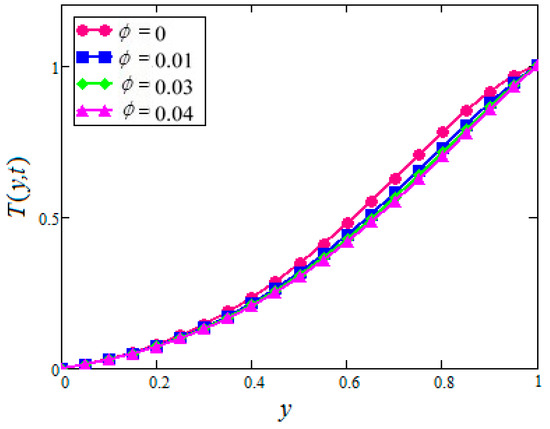
Figure 16.
Temperature profiles for different values of of in water based nanofluids when
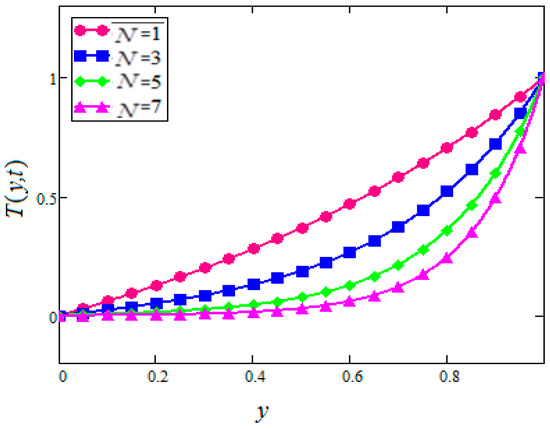
Figure 17.
Temperature profiles for different values of of in water based nanofluids when
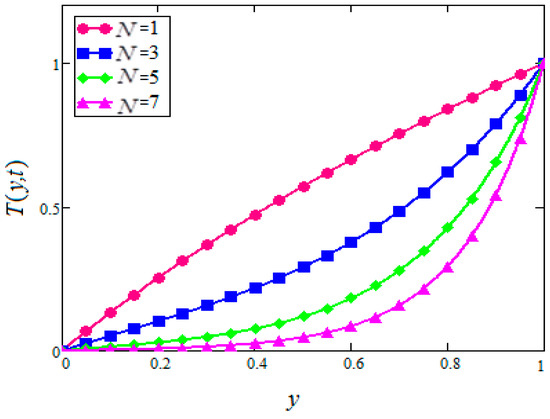
Figure 18.
Temperature profiles for different values of of in water based nanofluids when
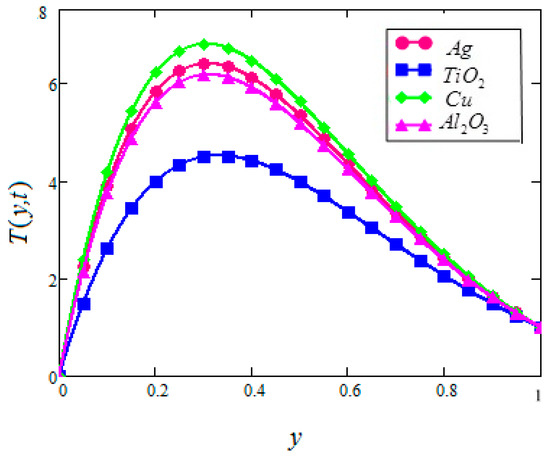
Figure 19.
Temperature profiles for different types of nanoparticles in water based nanofluids when
Figure 6 and Figure 7 are plotted for different values of for both cases of suction and injection. It is noted from Figure 6 that the velocity of in water-based nanofluids increases with the increase of in the case of suction for in water-based nanofluids while the velocity is decreased in the case of injection. The velocity in Figure 6, where , is not linear. However, the increasing values of make it look like linear.
Figure 8 and Figure 9 were plotted to check the effect of , the velocity of in water-based nanofluids, for both cases of suction and injection. One can see from Figure 8 and Figure 9 that the effect of suction, , on the velocity of nanofluids is opposite to the case of injection.
The effect of the magnetic parameter, , on the velocity profile is studied in Figure 10 and Figure 11. For the case of suction, the nanofluid’s velocity profile decreases with increasing values of . This effect is due to the Lorentz forces. Greater values of correspond to stronger Lorentz forces, which reduces the nanofluid velocity. However, this trend reverses for the injection case.
Figure 12 and Figure 13 shows that the velocity profiles of in nanofluids increase with the decrease of in the case of suction. This physically means that an increase in increases the conduction, which in turn decreases the viscosity of nanofluids. Decreasing the viscosity of nanofluids increases the velocity of nanofluids. However, the effect is the opposite due to the suction, whereas no variation is observed for injection. However, the velocity of zero radiation is greater than the velocity of nanofluids with radiation.
The velocity profiles for different types of nanoparticles in water-based nanofluids are represented in Figure 14. It is clear that the velocity of and in water-based nanofluids is greater than and in water-based nanofluids. As mentioned in previous problems, different types of nanoparticles have different thermal conductivities and viscosities. It was concluded in our previous problems [31,32] that metallic nanoparticles, like and , had smaller velocities as compared to metallic oxide nanoparticles, like and , due to high thermal conductivities and viscosities. However, the effect is the opposite to this problem because of the condition of permeable walls or suction. Due to these situations, different velocities have been observed.
The effect of in nanofluids on the temperature profiles is shown in Figure 15 and Figure 16 for the cases of suction and injection. It was found that the temperature of nanofluids increases with the increase of for the suction velocity whereas no significant variation is observed for the injection case.
Figure 17 and Figure 18 are sketched to show the effect of on the temperature profiles of in based nanofluids for both cases of suction and injection. The effects of different types of nanoparticles on the temperature of based nanofluids are plotted in Figure 19 for injection. It is observed that in water-based nanofluid has the highest temperature followed by , and in based nanofluids. This is due to the higher thermal conductivities of copper followed by , and in water-based nanofluids. Due to these situations, different velocities were observed.
6. Conclusions
The channel flow of nanofluids in a porous medium with permeable walls was studied. The focal point of this research was to study the influence of permeable walls on momentum and heat transfer. The permeable parameter, which physically corresponds to suction and injection, was incorporated in both the momentum and energy equations. Expressions for the velocity and temperature were obtained. The effects of various parameters, such as thermal Grashof number, volume fraction, different types of nanoparticles, radiation, permeability, magnetic, suction, and injection, were studied in different plots. The concluding remarks are as follows:
- It was found that the velocity of nanofluids increases with an increase of the volume fraction, radiation, and permeability parameter in the case of suction whereas an opposite behavior was noted in the case of injection.
- The velocity of nanofluids decreases with an increase of the magnetic parameter while the opposite behavior was noted in the case of injection.
- The temperature of nanofluids was found to decrease with an increase of for the extraction of fluid from the walls whereas a very small change was observed in the case of injection.
- Finally, it was noticed that different types of nanoparticles have different effects on the velocity and temperature due to suction and injection.
Author Contributions
All the authors contributed equally to the conception of the idea, implementing and analyzing the experimental results, and writing the manuscript.
Funding
This research was funded by Deanship of Scientific Research at Princess Nourah bint Abdulrahman University. (Grant No# ٢٦٩/ص/٣٩).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Water | |
| Ethelyn glycol | |
| Velocity component in the direction | |
| Temperature | |
| Suction | |
| Injection | |
| Density of nanofluid | |
| Magnetic parameter | |
| Peclet number | |
| Dynamic viscosity of nanofluid | |
| thermal expansion coefficient | |
| Acceleration due to gravity | |
| Heat capacitance of nanofluids | |
| The thermal conductivity of nanofluid | |
| Mean radiation absorption coefficient | |
| Reynolds’ number | |
| Grashof number | |
| Radiation parameter |
References
- Torda, T.P. Boundary Layer Control by Distributed Surface Suction or Injection. Bi-Parametric General Solution. J. Math. Phys. 1953, 32, 312–314. [Google Scholar] [CrossRef]
- Berman, A.S. Laminar flow in channels with porous walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Erickson, L.E.; Fan, L.T.; Fox, V.G. Heat and mass transfer on moving continuous flat plate with suction or injection. Ind. Eng. Chem. Fundam. 1966, 5, 19–25. [Google Scholar] [CrossRef]
- Alamri, S.Z.; Ellahi, R.; Shehzad, N.; Zeeshan, A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: An application of Stefan blowing. J. Mol. Liq. 2019, 273, 292–304. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Ellahi, R.; Alamri, S.Z. Convective Poiseuille flow of Al 2 O 3-EG nanofluid in a porous wavy channel with thermal radiation. Neural Comput. Appl. 2018, 30, 3371–3382. [Google Scholar] [CrossRef]
- Hassan, M.; Marinb, M.; Alsharifc, A.; Ellahide, R. Convective heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Shehzad, N.; Alamri, S.Z. Structural impact of kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: Application of cooling process. J. Mol. Liq. 2018, 264, 607–615. [Google Scholar] [CrossRef]
- Ijaz, N.; Zeeshan, A.; Bhatti, M.M.; Ellahi, R. Analytical study on liquid-solid particles interaction in the presence of heat and mass transfer through a wavy channel. J. Mol. Liq. 2018, 250, 80–87. [Google Scholar] [CrossRef]
- Ali, F.; Aamina, A.; Khan, I.; Sheikh, N.A.; Saqib, M. Magnetohydrodynamic flow of brinkman-type engine oil based MoS 2-nanofluid in a rotating disk with Hall Effect. Int. J. Heat Technol. 2017, 4, 893–902. [Google Scholar]
- Jan, S.A.A.; Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M.; Gohar, M. Engine oil based generalized brinkman-type nano-liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana-Baleanu fractional model. Numer. Methods Partial Differ. Equ. 2018, 34, 1472–1488. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Khan, A. Entropy Generation in Different Types of Fractionalized Nanofluids. Arab. J. Sci. Eng. 2019, 44, 1–10. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Shafie, S.B. Convection in ethylene glycol-based molybdenum disulfide nanofluid. J. Therm. Anal. Calorim. 2019, 135, 523–532. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Natural convection channel flow of CMC-based CNTs nanofluid. Eur. Phys. J. Plus 2018, 133, 549. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC-based-CNT’s nanofluid through a porous medium. Chaos Solitons Fractals 2018, 116, 79–85. [Google Scholar] [CrossRef]
- Abbas, Z.; Sajid, M.; Hayat, T. MHD boundary-layer flow of an upper-convected Maxwell fluid in a porous channel. Theor. Comput. Fluid Dyn. 2006, 20, 229–238. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z. Heat transfer analysis on the MHD flow of a second grade fluid in a channel with porous medium. Chaos Solitons Fractals 2008, 38, 556–567. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ashorynejad, H.R.; Domairry, D.; Hashim, I. Investigation of the laminar viscous flow in a semi-porous channel in the presence of uniform magnetic field using optimal homotopy asymptotic method. Sains Malays. 2012, 41, 1177–1229. [Google Scholar]
- Ravikumar, V.; Raju, M.C.; Raju, G.S.S. MHD three dimensional Couette flow past a porous plate with heat transfer. IOSR J. Math. 2012, 1, 3–9. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Heat transfer with thermal radiation on MHD particle–fluid suspension induced by metachronal wave. Pramana 2017, 89, 48. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z.; Sheremet, M.A. Numerical study of MHD nanofluid natural convection in a baffled U-shaped enclosure. Int. J. Heat Mass Transf. 2019, 130, 123–134. [Google Scholar] [CrossRef]
- Upreti, H.; Pandey, A.K.; Kumar, M. MHD flow of Ag-water nanofluid over a flat porous plate with viscous-Ohmic dissipation, suction/injection and heat generation/absorption. Alex. Eng. J. 2018, 57, 1839–1847. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Alizadeh, M.; Ganji, D.D. Hydrothermal analysis on MHD squeezing nanofluid flow in parallel plates by analytical method. Int. J. Mech. Mater. Eng. 2018, 13, 4. [Google Scholar] [CrossRef]
- Narayana, P.V.; Tarakaramu, N.; Makinde, O.D.; Venkateswarlu, B.; Sarojamma, G. MHD Stagnation Point Flow of Viscoelastic Nanofluid Past a Convectively Heated Stretching Surface. Defect Diffus. Forum 2018, 387, 106–120. [Google Scholar] [CrossRef]
- Loganathan, P.; Chand, P.N.; Ganesan, P. Radiation effects on an unsteady natural convective flow of a nanofluid past an infinite vertical plate. Nano 2013, 8, 1350001. [Google Scholar] [CrossRef]
- Qasim, M.; Khan, Z.H.; Khan, W.A.; Shah, I.A. MHD boundary layer slip flow and heat transfer of ferrofluid along a stretching cylinder with prescribed heat flux. PLoS ONE 2014, 9, e83930. [Google Scholar] [CrossRef] [PubMed]
- Khalid, A.; Khan, I.; Shafie, S. Exact solutions for free convection flow of nanofluids with ramped wall temperature. Eur. Phys. J. Plus 2015, 130, 57. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N. Natural convective magneto-nanofluid flow and radiative heat transfer past a moving vertical plate. Alex. Eng. J. 2015, 54, 55–64. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects: Buongiorno’s model. Powder Technol. 2016, 288, 140–150. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N.; Sulochana, C. Influence of chemical reaction, radiation and rotation on MHD nanofluid flow past a permeable flat plate in porous medium. J. Niger. Math. Soc. 2016, 35, 48–65. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q.; Hu, W. Aggregation structure and thermal conductivity of nanofluids. AIChE J. 2003, 49, 1038–1043. [Google Scholar] [CrossRef]
- Maxwell, J.C.; Thompson, J.J. A Treatise on Electricity and Magnetism; Oxford University Press: Oxford, UK, 1904. [Google Scholar]
- Brinkman, H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Ali, F.; Saqib, M.; Khan, I.; Sheikh, N.A. Heat Transfer Analysis in Ethylene Glycol Based Molybdenum Disulfide Generalized Nanofluid via Atangana–Baleanu Fractional Derivative Approach. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 217–233. [Google Scholar]
- Hajmohammadi, M.R.; Maleki, H.; Lorenzini, G.; Nourazar, S.S. Effects of Cu and Ag nano-particles on flow and heat transfer from permeable surfaces. Adv. Powder Technol. 2015, 26, 193–199. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. New Direction of Atangana–Baleanu Fractional Derivative with Mittag-Leffler Kernel for Non-Newtonian Channel Flow. In Fractional Derivatives with Mittag-Leffler Kernel; Springer: Cham, Switzerland, 2019; pp. 253–268. [Google Scholar]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476–482. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of fractional differential equations to heat transfer in hybrid nanofluid: Modeling and solution via integral transforms. Adv. Differ. Equ. 2019, 52. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hassan, M.; Vafai, K. On boundary layer magnetic flow of nano-Ferroliquid under the influence of low oscillating over stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Akbar, N.S. Study of peristaltic flow of nanofluid with entropy generation in a porous medium. J. Porous Med. 2017, 20, 461–478. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).