Abstract
Structural designers that design buildings use different criteria to select the frames’ materiality and structural solutions. Very often, the primary test is the cost of construction. Sometimes, solutions are determined by the terms of structure, architectural preferences, technological needs, fire safety requirements, environmental conditions, exploitation costs over the life of the building, ecological aspects, and experience, etc. This paper proposes an approach for analyzing the structural elements of buildings taking into account the impact on the environment using jointly incorporating subjective and objective aspects. The objective to combine the most important criteria into a single unit and carry out the overall assessment could be done by giving each variable a weighted value and perform a so-called multi-criteria analysis. This article shows the efficiency of the structural solution of the one-story building. The case study presents an investigation and comparison of five possible symmetrical structural solutions by multi-criteria assessment methods: The analysis of three steel frameworks differs majorly due to the beam-column characteristics, as well as precast RC frame structures case and combined steel beams and RC columns frame option. Possible solutions must meet all the essential requirements of the building, including mechanical resistance and stability. The obtained results show a broad assessment of the structural solutions of the building.
1. Introduction
Environmental restoration, revival and recovery are vital principles for sustainable development. There is a symmetrical balance when all the parts of the objects are well balanced [1]. Correct, logical and rational construction projects are reliable and sound products that for a long time have met the critical architectural, quality and design requirements; safety; price; and influence, and are expected to have a lower long-term impact on the environment [2]. Designers make their final decisions according to several requirements. Scientists have proposed many strategies to improve the profitability of the construction industry and apply sustainable construction methods [3]. The evolution of architecture has highlighted the advantages of the principle of symmetry [4]. It has emerged as artifacts, buildings and artificial environments [5]. It affects such building conditions as structural efficiency, attractive structures, economic production, and functional or aesthetic requirements. Geometric symmetry means symmetry in the plane, and structural symmetry says that the centers of mass and resistance are at the same point. The ideal shape is the most straightforward: round. Besides, large L-shaped, zigzag-shaped or large wing structures are undesirable in hazardous areas. It includes compliance with standardization requirements, production of repeat elements and mass production that reduces production costs [6]. Some architecture and basic principles (targeted planning and symmetric arrangement, vertical support elements and symmetrical structural elements) enhance the load on structural elements [7]. Symmetry is an essential element of architecture that reflects the balance between building construction and loading. Symmetric simple geometry structures are safer, more efficient and more predictable than asymmetric structures. The asymmetric building is the weakest when there is a dynamic cross-force due to involved displacement associated with the base shear. Therefore, symmetrical shapes are preferred but not asymmetric. Proper design efficiency contributed to the appropriate arrangement of vertical bearing elements, as well as uniform and balanced openings distribution. Therefore, symmetry and regularity are generally reliable [8].
The selection process of the fundamental building system process shows the trade-off among different options. Decision-makers could use multi-criteria decision-making (MCDM) methods such as AHP, TOPSIS, and COPRAS [9], as well as PROMETHEE families [10] and others to determine the best choice. Decisions made in complex contexts need these methods for practical solutions. The fact that construction materials contribute to sustainable building management has been proven by many studies [11,12]. Energy consumption and (CO2) emissions are the two critical indicators of sustainability in the construction industry. The primary source of adverse environmental impact on the life cycle of buildings is energy consumption at the stage of long-term building use [13]. The building sector accounts for about 40% of global primary energy consumption. When the service-life regarding the structural safety or serviceability of a deteriorating building does not meet the original target, the options for life cycle maintenance strategies need to be changed. The selection typically depends on costs and execution time [14] being redefined and developed throughout the early design stages. The structure produced by using only environmentally friendly materials is not necessary for a sustainable building. It is required to optimize the selection of materials for greater sustainability [15]. However, adequately selected materials and technologies, suppliers and contractors significantly improve the performance of the building [16,17,18].
Steel industry and research have been struggling to improve its environmental performance [15] and enable satisfying clients’ needs, providing high structural quality and performance while pursuing sustainability [19]. Cold-formed structures have one of the top load capacity-to-weight ratios among the common structural components and bring economic, social and environmental benefits by decreasing raw materials consumption, with lighter foundations preserving the soil and its movements, the economy in handling and transportations and reduces labor fatigue. Furthermore, such structures present a rival structural behavior under seismic loads [20]. Bitarafan specified the suitability of cold-formed steel structures for naturally damaged regions, studying the more suitable construction techniques [21]. Steel is the world’s most used and recycled metal. The iron and steel industry is known to be the most significant energy consuming manufacturing sector, consuming 5% of the world’s total energy consumption and emitting about 6% of the entire anthropogenic CO2 [22]. While different materials can only be down-cycled, steel can be recycled countless times keeping its properties and quality (multi-cycling) [23]. Using scrap, the production of steel through EAF (electric arc furnace) instead of through BOF (basic oxygen furnace) can reduce about 32.14% up to 40.32% of the CO2 emissions per ton of steel. According to Junichiro [24], the energy consumption through EAF is about 10.2 GJ per steel ton whereas through BOF it is 32.9 GJ/t. These values are in the range presented by Flues et al. [25]. Also, recent data from World Steel Association [26] shows that to recycling 1 ton of steel spares more than 1.4 t of iron ore, 1.4 t of CO2 emissions, 120 of limestone, 740 kg of coal, and two-thirds of the amount of energy spent in the steel production process.
The production of cement and cement-based composites is not an environmentally friendly process. Therefore, evaluating the environmental stress produced by concrete structures during the different phases of life is a fundamental design requirement [27]. Stakeholders estimate it either by the global energy consumed or, equivalently, by the CO2 released during the entire cycle of life. Concrete is predominantly utilized in buildings and infrastructure worldwide by using ordinary Portland cement (OPC) as a binder. In recent years, the annual world cement production has grown from 1.0 billion tons to approximately 1.7 billion tons, which is enough to produce 1 m3 of concrete per person.
As a result, the cement industry is commonly regarded as being in a period of high growth. However, the sector has been confronted since the late 1990s by the need to reduce its environmental load, including carbon dioxide (CO2) emissions. Some estimates suggest that the amount of CO2 emitted from the global output of OPC may be as high as 7% of the total global CO2 emissions. Furthermore, the production of OPC involves severe collateral environmental impacts, such as environmental pollution caused by dust and the enormous energy consumption required from having a plasticity temperature over 1300 °C. For these reasons, the cement industry has been challenged in the past 10 years to effectively reduce and control CO2 emissions effectively.
Nevertheless, progress and innovation in materials and construction processes felt towards these goals. As stated by Burgan and Sansom [28], the path towards sustainability reflects acting in the three main impact areas—environment, society and economy. The sustainability of development is in line with the needs of the current generation in designing, managing and navigating change, ensuring that future generations can meet their needs [29]. A sustainable society considers two critical issues: environment and safety [30]. Development of a sustainable product includes dematerialization, recycling, and compelling design considerations. Ecological design, reduced use of energy, and focus on utility instead of ownership are also important issues in this concept. Adopting sustainable construction practices involves integrating all of the principles of sustainable construction (SC) into the construction project’s life cycle plan, with every stakeholder having responsibility for carrying out sustainability practices. Every stakeholder specifically contributes when improving sustainability, while owners play an essential role in requiring other stakeholders to adopt SC practices [31,32]. Stakeholders need to shape the products and the building’s life cycle [33]. The owners’ subsequent decision-making and practices are more likely to promote the start of projects, and the real driving force for SC can come from the owners [33]. From the economic perspective, steel solutions enable less construction and operational costs, reducing the life cycle costs, being also a cost- and time-efficient solution [14]. On the environmental front, lightweight structures represent a decrease in raw materials’ consumption, allow lighter foundations, preserve the soil, and reduce its movement; also, steel is entirely recyclable. The steel structures can be easily re-used or adapted to new functionalities. Structural designers use different criteria to select structural solutions [34]. Designers significantly impact the sustainable performance of a building by selecting the proper materials [35].
The common practice in design processes is an economic assessment or classic approach using the reliability theory and risk management of several of the most possible structural solutions [36]. As a result, stakeholders select the option with the lowest price, while omitting non-economic factors (ecological, social, metaphysical (feelings), and cultural aspects) [37,38,39]. The selection of suitable materials for building design is essential [40]. Designers rarely use multi-criteria analysis to solve complicated problems. Besides, unresolved issues regarding the subjective qualitative measurements and criteria weights are present in problem solution models [41].
2. Multi-Criteria Decision-Making
An integral part of contemporary human activities is choosing the most efficient solutions and justifying the selected alternatives and judgments of selected justifying procedures. Muckler and Seven [42] pointed out that all objective measurement involves subjective judgments. Firstly, developers of plans select which problems must be solved and which ones not. Humans implement almost all decisions of civil engineers in practice. Humans necessarily filled all measurement in science and technology is filled with subjective elements, whether in selecting measures or in collecting, analyzing or interpreting data. In Kant’s view, all knowledge begins with human experience and is concurrent with the experience. The need for qualitative multi-criteria evaluation caused it—information contents by the inexact scale of measurement. It is consecutive. The main problem, however, is dealing with qualitative information. Many methods, qualitative data consider as pseudo-metric data, but officially forbid it as a way to consider qualitative details. Qualitative multi-criteria methods, in general, have to be survivable from the classification of the actual data. The lack of information in a multi-criteria analysis may emerge from two sources: (1) an imprecise definition of alternatives, evaluation criteria and preferences (or preference scenarios); and (2) an inaccurate measurement of the effects of other options on evaluation criteria (the 80s called impact matrix) and preference weights. One symmetry description is to say that it is the result of a balanced proportion harmony.
It is worth noting that besides the methodological developments, there are a large number of successful applications of MCDM methods to real-world problems that have made MCDM a domain of great interest, both for academics and for industry practitioners [43]. The increasing complexity of the rapidly evolving business, engineering, science, and technology environments entails making the right decisions when considering environmental, market and economic considerations. The stages of a typical MCDM procedure in civil engineering are shown in Figure 1. Often, different MCDM techniques do not lead to the same results. Multi-criteria utility models are models designed to obtain the utility of items or alternatives that can be evaluated on more than one criterion.
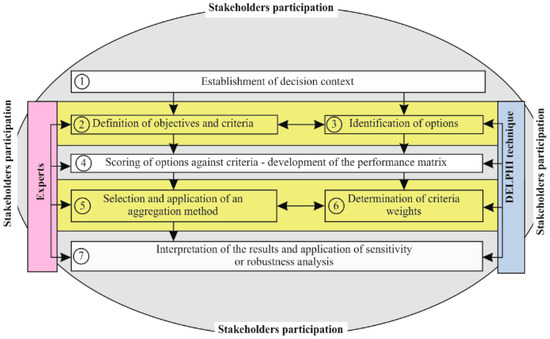
Figure 1.
A procedure of MCDM (multi-criteria decision-making) in civil engineering.
2.1. Available MCDM Methods for Problem-Solving
In the last three decades, scientists have developed dozens of MCDM methods [44] that have been applied to address various issues in civil engineering [45,46,47] and used for sustainability problems [48]. A large variety of different problems emerging in civil engineering projects can adequately be addressed using the MCDM methodology and its related techniques [49]. They differ concerning how they combine the data. MCDM methods are broadly classified into two classes: discrete MCDM or MADM and continuous MODM (Multi-Objective Decision Making) optimization methods [50]. They all require the definition of options and criteria, and most of them demand a measure (e.g., weights) for assessing the relative significance of the criteria.
2.2. A Hybrid MCDM Model for Problem Solution
This work uses a hybrid method, i.e., a combination of fuzzy ARAS, fuzzy form of the multiplicative utility function, and DHP (Figure 2). Belton and Stewart [51] point to the need for such an integrated approach; applying hybrid methods or multiple different techniques simultaneously to the same decision problem might well serve the purpose from the behavioral and educational point of view. Researchers and practitioners had and lately increasingly supported the use of hybrid methods. Such approaches most frequently use two or more MCDM methods or a combination of the MCDM methods and other decision support approaches.
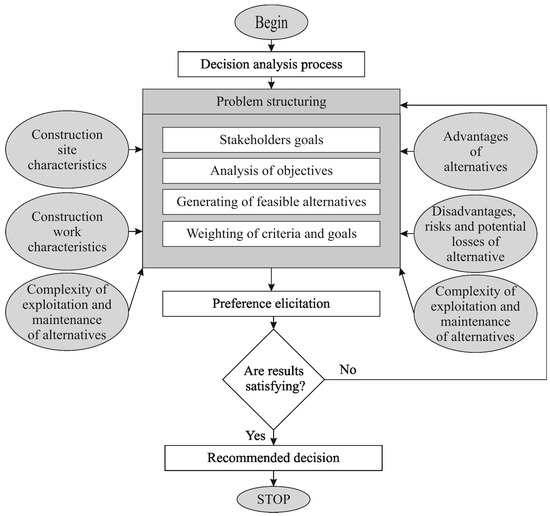
Figure 2.
Structure of the hybrid decision support system, based on the ARAS-F, fuzzy multiplicative utility method and Delphi Hierarchy Process.
The integrated approach consists of three phases. In phase 1, a teamwork approach is taken to formulate the ideas for decision-making. In this stage, decision-makers define the alternatives. In the first step, a team of five selected experts selects the methods to evaluate and score options, determine communication procedures for the evaluation process and create an evaluation timeline. The most popular methods are rated according to Saaty’s and Ergu’s [52] 16 criteria. Later, three different MCDM methods are selected to solve the problem: The Analytic Hierarchy Process (AHP) method to determine criteria weights, the ARAS-F, and the fuzzy product model (modified by the paper’s authors) for multi-criteria assessment of feasible alternatives.
In the second step, a set of evaluation criteria using the nominal group technique Delphi are established.
In the third step, a set of cardinal criteria weights to determine the relative importance of evaluation categories (based on the AHP) is provided.
Finally, the overall multi-attribute utility performance score for each feasible alternative is determined.
2.2.1. Fuzzy Number
Various types of membership functions are used. In this study, fuzzy triangular numbers (TFN) are used. A fuzzy set is a class of objects with a continuum of membership grades. A membership function, which assigns to each object a degree of membership ranging between zero and one, characterizes the set. A fuzzy set A defined in space X is a set of pairs:
where fuzzy set A is characterized by its membership function , which associates with each element , a real number . The value at x represents the grade of membership of x in A and is interpreted as the membership degree to which x belongs to A. So the closer the value is to one, the more x belongs to A, .
A crisp or ordinary subset A of X can also be seen as a fuzzy set in X with a membership function as its characteristic function, i.e.,
The set X, specifically as a universe of discourse, can be written as . Sometimes a fuzzy set A in x is denoted by listing the ordered pairs , where the elements with zero degrees are usually not listed. Thus, fuzzy set A in X can be represented as , where and .
When the universe of discourse is discrete and finite with cardinality n, that is X = x1, x2, …, xn, the fuzzy set A can be represented as
When the universe of discourse X is an interval of real numbers, fuzzy set A is expressed as
A fuzzy number is a triangular fuzzy number (α, β, γ) if three parameters (α < β < γ) fully describes its membership function.
2.2.2. Defuzzification
A defuzzification process is applied to obtain a crisp output. Defuzzification is the production of a quantifiable result in fuzzy logic, given fuzzy sets and corresponding membership grades. Scientists proposed different defuzzification techniques. The triangular membership function is the most typical (Figure 3). Laarhoven and Pedrycz [53] defined the basic operations of fuzzy triangular numbers and as follows:
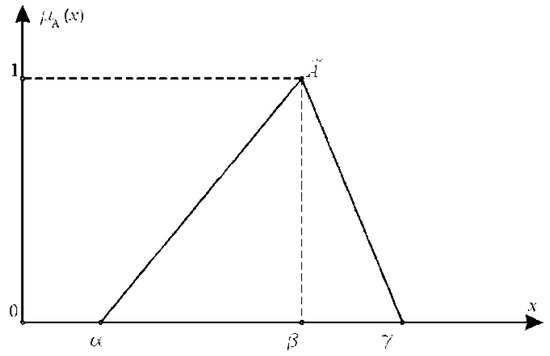
Figure 3.
Triangular membership function.
2.3. The DHP (Delphi Hierarchy Process)
To strengthen the AHP method, Khorramshahgol and Moustakis [54] suggested a new DHP (Delphi Hierarchy Process) technique, which incorporates the Delphi method to collect expert judgments (Figure 4). It makes use of the advantages of AHP in determining the weights of criteria and the simplicity of fuzzy ARAS or fuzzy form of the multiplicative utility function for ranking alternatives.
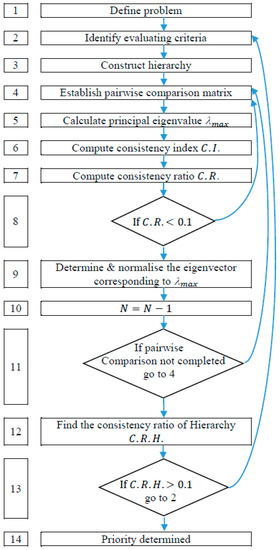
Figure 4.
The process of the AHP.
Most human solutions are compromises between competing goals. They refer to the assessment of multiple alternatives [55]. A fundamental problem of decision theory is to choose the proper approach to derive weights for a set of criteria according to significance. Relative importance is usually judged according to several criteria [56]. A variety of methods are proposed for eliciting weights. There is no best way to set criteria weights. The ratio method, swing method and tradeoff method (called pricing out) [57] are general weight elicitation procedures applied in engineering researches. Schoemaker and Waid [55] compared five fundamentally different approaches for determining such weights.
The review of past works shows that AHP is the most common MCDM method used to solve civil engineering multi-attribute decision-making problems. The oldest reference dates from 1972 [58]). Later, Saaty [56] described the technique. An analysis process using the AHP is shown in Figure 4. The AHP modeling process is based on four principles: structuring the decision problem, measurement technique (the impact of the elements of the hierarchy is assessed through paired comparisons done separately in reference to each of the aspects of the level immediately above), data collection, determination of normalized weights, and synthesizing to find a solution to the problem [59].
For the establishment of a pair-wise comparison matrix A; Let C1, C2, …, Cn denote the set of elements, while aij represents a quantified judgment on a pair of elements Ci and Cj. The relative importance of the two aspects is rated using a scale (Table 1). These scales yield an n × n matrix A as C1, C2, …, Cn where aij = 1 and aij = 1/aij, i, j = 1, 2, …, n. In matrix A, the problem becomes one of assigning to the n elements C1, C2, …, Cn a set of numerical weights w1, w2, …, wn that reflect the recorded judgments.

Table 1.
Saaty’s original nine-point scale of relative importance for pairwise comparison.
Saaty recommends a nine-level dominance scale, which Saaty describes by appealing to Miller’s [60] magical number seven plus two (Table 1) [56]. There are n(n − 1)/2 judgments required to develop an n × n judgment matrix since reciprocals are automatically assigned in each pair-wise comparison.
According to Saaty, the largest eigenvalue would be
Saaty proposed utilizing the consistency index (CI) and consistency ratio (CR) to verify the consistency of the comparison matrix. CI and CR are defined as follows:
Here, the RI (Table 2) represents the average consistency index over numerous random elements of the same order reciprocal matrices.

Table 2.
Random consistency indices for the different number of criteria (n).
2.3.1. Fuzzy Group Criterion Weight is Determined as Follows:
After the criteria weights from the AHP are established, the synthesizing of the ratio judgments is performed.
Suppose that are fuzzy group weights for n criteria and is the fuzzy triangular number
where , , is the minimum possible value, , , is the most probable value and , , is the maximal possible value of j criterion.
The CR ≤ 0.1 indicates that the matrix reached consistency.
2.3.2. Additive Ratio Assessment Method (ARAS) with Fuzzy Criteria Values (ARAS-F)
The MCDM ARAS method [61,62] with a fuzzy criteria values method [63] was selected to solve the problem. At the first stage, a problem is represented by the fuzzy decision-making matrix of preferences for m reasonable alternatives rated on n criteria:
where —fuzzy value represents the performance value of the i alternative regarding the j criterion, —the optimal value of j criterion. A tilde “~” is placed above a symbol if the symbol represents a fuzzy set.
If the optimal value of j criterion is unknown, then
At the next stage, dimensionless criteria values from the matching criteria are calculated and expressed in the normalized decision-making matrix :
The criteria, whose preferred values are maximal, are standardized as follows:
The cost type criteria (preferred values are minimal) are normalized as follows:
The third stage, normalized-weighted matrix is defined. The sum of the weights is limited as follows:
Normalized-weighted values of all the criteria are calculated as follows:
where is the weight (importance) of the j criterion and is the normalized rating of the j criterion.
The following task determines the values of the optimality function:
where is the value of the optimality function of the i selection.
The most significant value is the best, and the last value is the worst.
The result of fuzzy decision making for each alternative is a fuzzy number . There are several methods for defuzzification. The center-of-area is the most practical and easy to apply for this reason:
The equation used for the calculation of the utility degree of an alternative is given below:
where Si and S0 are the optimal criterion values, obtained from Equation (24).
2.3.3. The fuzzy Multiplicative Utility Function
The transitive decomposable model was introduced by Krantz et al. [64] as a natural generalization of the model. It amounts to replacing the addition operation by a general function that is increasing in each of its arguments.
The criteria values with favorable minimal values are transformed as follows:
The optimality function values are calculated as follows:
The equation used for the calculation of the utility degree of an alternative is given below:
where Ui and U0 are the optimal criterion values, obtained from Equation (27).
2.3.4. Integrated Utility Function
An integrated utility value of a considered alternative is calculated as given below:
where KAi are Ki values obtained from Equations (25) and (27) respectively.
3. Description of the Problem
The authors investigated a real case study as an object for multi-criteria assessment. The dimensions of the building are 78 × 9 × 3.5 (h) m. A structure consists of 14 transverse frames 9 × 3.5 (h) m (see Figure 5) set in step 6 meters. There are three identical buildings at the site. Therefore, 42 frames are needed.
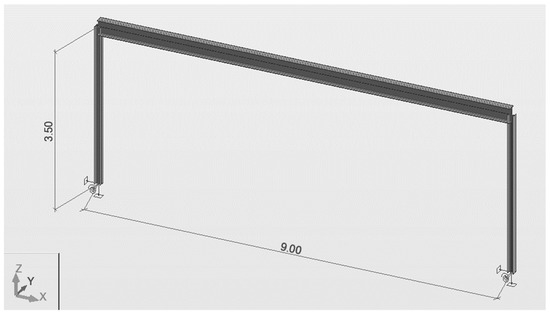
Figure 5.
Analyzed symmetric frame.
Only structural elements of the frames are included in the analysis. Bracings and other secondary elements are disregarded in the investigation. The objective of the research is a selection and multi-criteria assessment of structural solutions. The building design must satisfy the essential requirements of the building. Five possible structural solutions are investigated. There are three cases of steel frames (Case 1, Case 2 and Case 3); those significant differences are due to the initial rotational stiffness of the beam-to-column joints [65,66,67], one frame from the precast RC columns and beam (Case 4), and one frame from the precast RC columns and steel beam (Case 5).
As the span of the frame is only 9 meters, the beams are used as the main roof load-bearing structural elements in all cases. Steel grade S355 in all cases is used for the steel elements. All the structural calculations are performed according to the rules of design codes. Fulfillment of the ultimate limit state and serviceability limit state checked. The lists of the materials were compounded for all cases.
Case 1. Beam cross-section of the IPE300 and columns cross-sections of the HEA160 profiles. For beam-to-column, connection six M20 bolts of 10.9 grade and 20-mm thickness end-plate were used. Horizontal stiffeners 8 mm of thickness were used as well. For column-to-foundation, joint four M20 bolts of 10.9 grade and 25-mm thickness were base plate used. The joints of the frame are shown in Figure 6. The initial rotational stiffness of beam-to-column joints was 14270 kNm/rad. For column-to-foundation joints, the initial rotational stiffness was 15500 kNm/rad. The element and fittings fulfill the requirements of limit states.
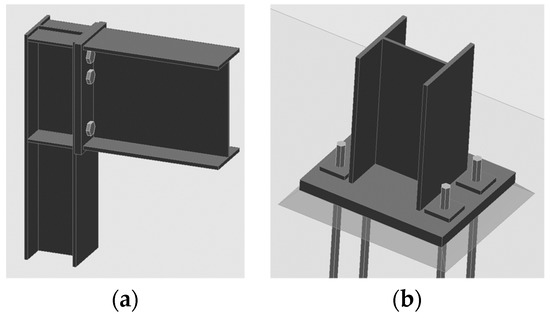
Figure 6.
Bolted beam-to-column with (a) transverse stiffeners and column-to-foundation (b) joints.
Case 2. Beam cross-section of the IPE330 and columns cross-sections of the HEA140 profiles. For beam-to-column, connection six M20 bolts of 10.9 grade and 16-mm thickness end-plate used. No additional stiffeners were used. For column-to-foundation, joint four M20 bolts of 10.9 grade and 25-mm thickness base plate were used. The joints of the frame are shown in Figure 7. The initial rotational stiffness of beam-to-column joints was 9730 kNm/rad. For column-to-foundation joints, the initial rotational stiffness was 9300 kNm/rad. In comparison to Case 1, these joints are more flexible, because they have no stiffeners in the column for the beam-to-column joint and the column has a smaller cross-section. The element and fittings fulfill the requirements of limit states.
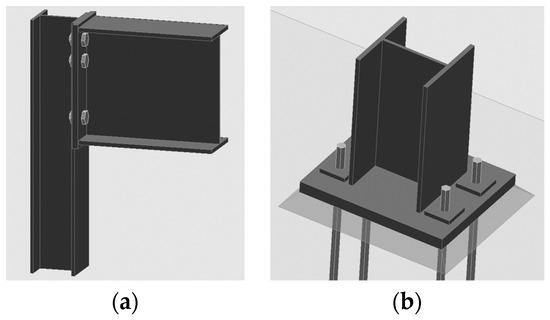
Figure 7.
Unstiffened bolted beam-to-column (a) and column-to-foundation (b) joints.
Case 3. Beam cross-section of the IPE360 and columns cross-sections of the HEA140 profiles. The beam of the column joints is pinned. No bending moments in beam-to-column connections exist. For column-to-foundation, joint four M20 bolts of 10.9 grade and 25-mm thickness base plate were used. The joints of the frame are shown in Figure 8. The initial column-to-foundation joints was 10,800 kNm/rad. The beam on the columns was supported, that means no bending moments in the ends of the beam and the top of the columns appeared. The element and joints fulfill the requirements of limit states.
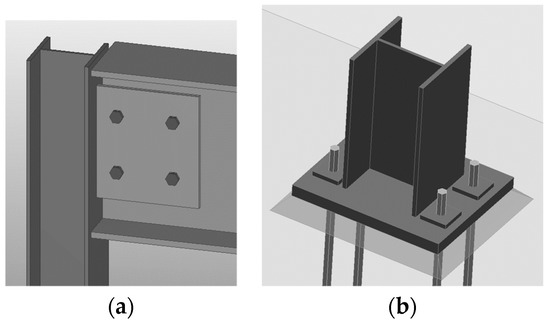
Figure 8.
Pinned beam-to-column (a) and column-to-foundation (b) joints.
Case 4. In this case, the frame was made from precast concrete beam and columns. The columns on the foundations had fixed rigidity. The beam to the columns was connected as pinned. The columns were designed from 250 × 250 mm squares and beams from 250 × 400 (h) rectangular cross-sections. The joints of the frame are shown in Figure 9.
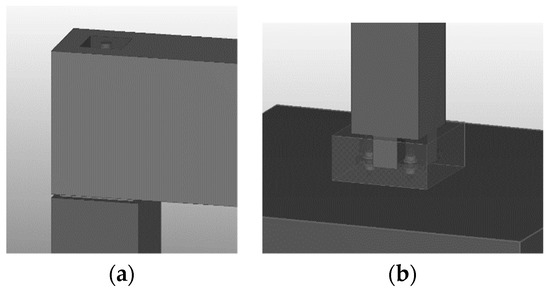
Figure 9.
Pinned beam-to-column (a) and column-to-foundation (b) joints.
The column-to-foundation joints are rigid. This joint was designed using the system of anchor bolts and column shoes for fixing columns to the support rigidly (Peikko certificate). The beam on the columns was supported directly. Columns were reinforced using regular unstrained reinforcement, and beams were reinforced using unstrained and pre-stressed reinforcement as well. The structures of the frame fulfill the requirements of limit states.
Case 5. In this case, the elements of the frame were made from different materials. The columns were designed as precast RC elements. The beams are made of steel. The columns on the foundations had fixed rigidity. The beam on the columns was connected as pinned. The columns were designed by a 250 × 250 mm square cross-section. Beam cross-section of the IPE360 profile. The joints of the frame are shown in Figure 10.
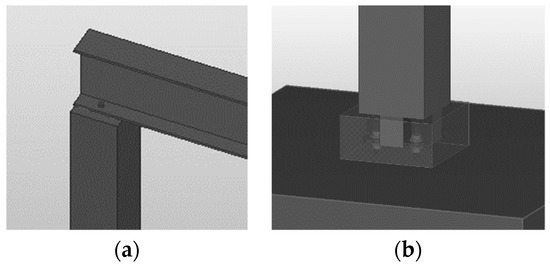
Figure 10.
Pinned beam-to-column (a) and column-to-foundation (b) joints.
The column-to-foundation joints are as rigid as in Case 4. The columns are reinforced using regular unstrained reinforcement. The steel beam on the columns was supported directly. The structures of the frame fulfill the requirements of limit states.
4. Problem Solution
Criteria set and weights of criteria were determined by applying DHP. A group of experts was formed, consisting of three civil engineers, one architect and one economist. It aimed to determine feasible alternatives, criteria set for assessment and criteria weights (Table 3).

Table 3.
Criteria set determined for the case study, based on the DHP.
Five experts (E1, …, E5) assessed the importance of the criteria according to the original Saaty’s nine-point scale as shown in Table 4. The fuzzy criteria weights are determined by using the AHP method according to all experts’ opinions (Table 5).

Table 4.
The opinion of experts regarding criteria importance according to Saaty’s nine-point scale.

Table 5.
Criteria values for frame alternatives.
Table 6 and Table 7 present the considered alternatives representing the frames. A multi-criteria evaluation was performed using the ARAS-F and fuzzy multiplicative utility function (MULT-F) values. The ranks (R) assigned in the assessment for the case study are shown in Table 8. Beside this, in Table 8, the integrated assessment of alternatives is presented.

Table 6.
Criteria values for frame alternatives: initial DMM.

Table 7.
Criteria values for frame alternatives: normalized-weighted DMM.

Table 8.
The integrated solution results: ranks of alternatives.
The calculations made with the ARAS-F and the MULT-F gave different results. According to the ARAS-F method, the alternative A4 representing frame, which was made from precast concrete beam and columns, was best suited, while the alternative A1, representing the beam cross-section of the IPE300 and columns cross-sections of the HEA160 profiles was ranked second. According to the MULT-F method, the alternative A1, representing the beam cross-section of the IPE300 and columns cross-sections of the HEA160 profiles, was best suited; while the alternative A4, representing the frame, was made from precast concrete beam and columns representing the beam cross-section of the IPE300 and columns cross-sections of the HEA160 profiles was ranked fourth. The alternative A1 was the best suited according to the integrated assessment of alternative performances.
5. Results and Conclusions
In today’s business environment, decision-making is a difficult and time-consuming process involving many criteria. In most cases, these criteria have imprecise and vague values and are challenging. In this study, the integration of the DHP, Fuzzy ARAS, and fuzzy multiplicative multi-criteria utility function shows the significant advantage in data mining for processing uncertain information in effective alternative evaluations.
Five possible solutions to the framed structure were analyzed. Three cases were designed using structural steel elements. One example with precast RC elements and one case mixed RC columns and steel beam. For all cases, lists of materials were combined and multi-criteria analysis performed.
Evaluating construction solutions for the implementation is a complex task which requires proper consideration of the technique and engineering management.
To overcome this problem, the model developed was based on the DHP, fuzzy ARAS, and fuzzy multiplicative utility function value to collect and analyze the judgments of experts for the selected criteria and potential alternatives.
In this study, the MCDM model considered six criteria for evaluating as follows: x1—Costs, x2—Impact on the environment, x3—Installment time, x4—Weight (tons), x5—Consumption of steel, x6—Consumption of concrete. The criteria set listed from the most important in decreasing importance order. The problem solution using the ARAS-F method result shows that the best method is to use alternative A4 and after that A1 alternative. The worst alternative is A5 and the second worst is A3. The difference among scores of the best and worst alternatives is 44%. The MULT-F method shows that the best alternative is A1 alternative, the A2 alternative ranks as the second best, while A5 is the worst alternative, and A4 is the second worst alternative. The alternatives rank is as follows: The MULT-F method is not sensitive to the criteria weights values, and the ratio of the best and worst scores is 3.25. The alternatives rank as follows We offer to rank alternatives according to integrated utility values of investigated alternatives. In this case, the best alternative is the first, and the worst one is the fifth alternative. The ratio of the best alternative score to the worst alternative score equals 89 percent. The final ranking of alternatives is as follows: .
The proposed hybrid assessment approach has significantly reduced the required number of experts’ judgments.
Multi-criteria assessment has shown that the alternative A1 is the best suited according to the integrated evaluation of alternative performances and constructors should implement it in practice.
The fuzzy ANP (Analytic Network Process) could be developed and implemented for future research work, based on fuzzy linguistic preference relations or its hybrid approaches with many different methods such as fuzzy the PROMETHEE, fuzzy ELECTRE, fuzzy VIKOR, fuzzy SAW, fuzzy ARAS, and fuzzy TOPSIS.
This paper shows that the hybrid approach presented here is useful in the evaluation of alternatives in a significant number of decision-making problems.
Author Contributions
Conceptualization, A.D., Z.T. and K.U.; methodology, Z.T., A.D.; software, Z.T.; validation, Z.T., A.D. and K.U.; formal analysis, Z.T.; investigation, A.D. and K.U.; resources, A.D.; data curation, K.U.; original draft preparation, A.D. and Z.T.; writing—review and editing, Z.T., and K.U.; supervision, A.D.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hashemkhani Zolfani, S.; Zavadskas, E.K.; Turskis, Z. Design of products with both International and Local perspectives based on Yin-Yang balance theory and SWARA method. Econ. Res. -Ekon. Istraživanja 2013, 26, 153–166. [Google Scholar] [CrossRef]
- Yepes, V.; García-Segura, T.; Moreno-Jiménez, J.M. A cognitive approach for the multi-objective optimization of RC structural problems. Arch. Civ. Mech. Eng. 2015, 15, 1024–1036. [Google Scholar] [CrossRef]
- Peldschus, F.; Zavadskas, E.K.; Turskis, Z.; Tamošaitienė, J. Sustainable assessment of construction site by applying game theory. Inz. Ekon. -Eng. Econ. 2010, 21, 223–237. [Google Scholar]
- Sousa, J.P.; Xavier, J.P. Symmetry-based generative design and fabrication: A teaching experiment. Autom. Constr. 2015, 51, 113–123. [Google Scholar] [CrossRef]
- Salunkhe, A.U. Behavior of RCC In-Filled Buildings with Different Configurations of Plan under Seismic Force. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Jaganathan, S.; Nesan, L.J.; Ibrahim, R.; Mohammad, A.H. Integrated design approach for improving architectural forms in industrialized building systems. Front. Archit. Res. 2013, 2, 377–386. [Google Scholar] [CrossRef]
- Pachta, V.; Papayianni, I. The study of the historic buildings of Eclecticism in Thessaloniki under the prism of sustainability. Procedia Environ. Sci. 2017, 38, 283–289. [Google Scholar] [CrossRef]
- Banginwar, R.S.; Vyawahare, M.R.; Modani, P.O. Effect of plans configurations on the seismic behaviour of the structure by response spectrum method. Int. J. Eng. Res. Appl. (IJERA) 2012, 2, 1439–1443. [Google Scholar]
- Yin, H.; Xiao, Y.; Wen, G.; Qing, Qi.; Deng, Y. Multiobjective optimization for foam-filled multi-cell thin-walled structures under lateral impact. Thin-Walled Struct. 2015, 94, 1–12. [Google Scholar] [CrossRef]
- Balali, V.; Zahraie, B.; Roozbahani, A. A Comparison of AHP and PROMETHEE Family Decision Making Methods for Selection of Building Structural System. Am. J. Civ. Eng. Archit. 2014, 2, 149–159. [Google Scholar] [CrossRef]
- Bakens, W. Sustainable Building and Construction: Contributions by International Organisations. In Smart and Sustainable Built Environments; Blackwell Publication: Hoboken, NJ, USA, 2005; pp. 275–288. [Google Scholar]
- Giama, E.; Papadopoulos, A.M. Assessment tools for the environmental evaluation of concrete, plaster and brick elements production. J. Clean. Prod. 2015, 99, 75–85. [Google Scholar] [CrossRef]
- Pajchrowski, G.; Noskowiak, A.; Lewandowska, A.; Strykowski, W. Materials composition or energy characteristic—What is more important in environmental life cycle of buildings? Build. Environ. 2014, 72, 15–27. [Google Scholar] [CrossRef]
- Fiorino, L.; Iuorio, O.; Macillo, V.; Landolfo, R. Performance-based design of sheathed CFS buildings in seismic area. Thin-Walled Struct. 2012, 61, 248–257. [Google Scholar] [CrossRef]
- Weisenberger, G. Sustainability and the structural engineers. Pract. Period. Struct. Des. Constr. 2011, 16, 146–150. [Google Scholar] [CrossRef]
- Aretoulis, G.; Kalfakakou, G.; Striagka, F. Construction material supplier selection under multiple criteria. Oper. Res. 2010, 10, 209–230. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Kalibatas, D. An approach to multi-attribute assessment of indoor environment before and after refurbishment of dwellings. J. Environ. Eng. Landsc. Manag. 2009, 17, 5–11. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Selecting a contractor by using a novel method for multiple attribute analysis: Weighted Aggregated Sum Product Assessment with grey values (WASPAS-G). Stud. Inform. Control 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Vilutienė, T.; Turskis, Z.; Šaparauskas, J. Multi-criteria analysis of Projects’ performance in construction. Arch. Civ. Mech. Eng. 2014, 14, 114–121. [Google Scholar] [CrossRef]
- Dubina, D. Behavior and performance of cold-formed steel-framed houses under seismic action. J. Constr. Steel Res. 2008, 64, 896–913. [Google Scholar] [CrossRef]
- Bitarafan, M.; Zolfani, H.S.; Arefi, S.L.; Zavadskas, E.K. Evaluating the construction methods of cold-formed steel structures in reconstructing the areas damaged in natural crises, using the methods AHP and COPRAS-G. Arch. Civ. Mech. Eng. 2012, 12, 360–367. [Google Scholar] [CrossRef]
- Quader, M.A.; Ahmed, S.; Ghazilla, R.A.R.; Ahmed, S.; Dahari, M. Evaluation of criteria for CO2 capture and storage in the iron and steel industry using the 2-tuple DEMATEL technique. J. Clean. Prod. 2015, 120, 1–14. [Google Scholar] [CrossRef]
- Gervásio, H. A Sustentabilidade do Aço e das Estruturas Metálicas, Construmetal 2008; Congresso Latino-Americano da Construção Metálica: São Paulo, Brazil, 2008. [Google Scholar]
- Junichiro, O.; Keigo, A.; Toshimasa, T.; Miyuki, N.; Kenichi, W.; Fuminori, S. International comparisons of energy efficiency in power, steel, and cement industries. Energy Policy 2012, 44, 118–129. [Google Scholar]
- Flues, F.; Rübbelke, D.; Vögele, S. Energy Efficiency and Industrial Output: The Case of the Iron and Steel Industry. FEEM Working Paper No. 96. 2013. Available online: https://www.feem.it/m/publications_pages/201311261233104NDL2013-096.pdf (accessed on 18 February 2019).
- World Steel Association. Fact Sheet—Raw Materials; World Steel Association: Brussels, Belgium, 2014. [Google Scholar]
- Fantilli, A.P.; Chiaia, B. Eco-mechanical performances of cement-based materials: An application to self-consolidating concrete. Constr. Build. Mater. 2013, 40, 189–196. [Google Scholar] [CrossRef]
- Burgan, B.A.; Sansom, M.R. Sustainable steel construction. J. Constr. Steel Res. 2006, 62, 1178–1183. [Google Scholar] [CrossRef]
- World Commission on Environment and Development (WCED). Our Common Future (The Brundtland Report); Oxford University Press: New York, NY, USA, 1987; p. 43. [Google Scholar]
- Yagi, K.; Halada, K. Materials development for a sustainable society. Mater. Des. 2001, 22, 143–146. [Google Scholar] [CrossRef]
- Shen, L.Y.; Song, S.C.; Hao, J.L.; Tam, V.W.Y. Collaboration among project participants towards sustainable construction e a Hong Kong study. Open Constr. Build. Technol. J. 2008, 2, 59–68. [Google Scholar] [CrossRef]
- Abidin, N.Z.; Pasquire, C.L. Revolutionize value management: A mode towards sustainability. Int. J. Proj. Manag. 2007, 25, 275–282. [Google Scholar] [CrossRef]
- Shen, L.; Tam, V.W.Y.; Tam, L.; Ji, Y. Project feasibility study: The key to successful implementation of sustainable and socially responsible construction management practice. J. Clean. Prod. 2010, 18, 254–259. [Google Scholar] [CrossRef]
- Šaparauskas, J.; Zavadskas, E.K.; Turskis, Z. Selection of façade’s alternatives of commercial and public buildings based on multiple criteria. Int. J. Strateg. Prop. Manag. 2011, 15, 189–203. [Google Scholar] [CrossRef]
- Florez, L.; Castro-Lacouture, D. Optimization model for sustainable materials selection using objective and subjective factors. Mater. Des. 2013, 46, 310–321. [Google Scholar] [CrossRef]
- Turskis, Z.; Gajzler, M.; Dziadosz, A. Reliability, risk management, and contingency of construction processes and projects. J. Civ. Eng. Manag. 2012, 18, 290–298. [Google Scholar] [CrossRef]
- Van Kesteren, I.E.H. Product designers’ information needs in materials selection. Mater. Des. 2008, 29, 133–145. [Google Scholar] [CrossRef]
- Medineckiene, M.; Zavadskas, E.K.; Björk, F.; Turskis, Z. Multi-criteria decision-making system for sustainable building assessment/certification. Arch. Civ. Mech. Eng. 2015, 15, 11–18. [Google Scholar] [CrossRef]
- Štreimikienė, D.; Šliogerienė, J.; Turskis, Z. Multi-criteria analysis of electricity generation technologies in Lithuania. Renew. Energy 2016, 85, 148–156. [Google Scholar] [CrossRef]
- Takano, A.; Hughes, M.; Winter, S. A multidisciplinary approach to sustainable building material selection: A case study in a Finnish context. Build. Environ. 2014, 82, 526–535. [Google Scholar] [CrossRef]
- Iwaro, J.; Mwasha, A.; Williams, R.G.; Zico, R. An Integrated Criteria Weighting Framework for the sustainable performance assessment and design of building envelope. Renew. Sustain. Energy Rev. 2014, 29, 417–434. [Google Scholar] [CrossRef]
- Muckler, F.A.; Seven, S.A. Selecting performance measures: “Objective” versus “subjective” measurement. Hum. Factors 1992, 34, 441–455. [Google Scholar] [CrossRef]
- Stefanoiu, D.; Borne, P.; Popescu, D.; Filip, F.G.; El Kamel, A. Optimization in Engineering Sciences. Approximate and Metaheuristic Methods; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z. Multiple criteria decision making (MCDM) methods in economics: An overview. Technol. Econ. Dev. Econ. 2011, 17, 397–427. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Turskis, Z.; Adeli, H. Hybrid multiple-criteria decision-making methods: A review of applications in engineering. Sci. Iran. Trans. Civ. Eng. 2016, 23, 1–20. [Google Scholar]
- Turskis, Z.; Zavadskas, E.K.; Antucheviciene, J.; Kosareva, N. A hybrid model based on fuzzy AHP and fuzzy WASPAS for construction site selection. Int. J. Comput. Commun. Control 2015, 10, 113–128. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Bagočius, V. Multi-criteria selection of a deep-water port in the Eastern Baltic Sea. Appl. Soft Comput. 2015, 26, 180–192. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Govindan, K.; Antucheviciene, J.; Turskis, Z. Hybrid multiple criteria decision-making methods: A review of applications for sustainability issues. Econ. Res. -Ekon. Istraživanja 2016, 29, 857–887. [Google Scholar] [CrossRef]
- Keršulienė, V.; Turskis, Z. A hybrid linguistic fuzzy multiple criteria group selection of a chief accounting officer. J. Bus. Econ. Manag. 2014, 15, 232–252. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Belton, V.; Stewart, T.J. Multiple Criteria Decision Analysis: An Integrated Approach; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Saaty, T.L.; Ergu, D. When is a Decision-Making Method Trustworthy? Criteria for Evaluating Multi-Criteria Decision-Making Methods. Int. J. Inf. Technol. Decis. Mak. 2015, 14, 1171–1187. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Khorramshahgnol, R.; Moustakis, V.S. Delphic hierarchy process (DHP): A methodology for priority setting derived from the Delphi method and Analytical Hierarchy Process. Eur. J. Oper. Res. 1988, 37, 347–354. [Google Scholar] [CrossRef]
- Schoemaker, P.J.H.; Waid, C.C. An experimental comparison of different approaches to determining weights in Additive Utility Models. Manag. Sci. 1982, 28, 182–196. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Saaty, T.L. An Eigenvalue Allocation Model for Prioritization and Planning; Working Paper; University of Pennsylvania, Energy Management and Policy Center: Philadelphia, PA, USA, 1972. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Miller, G.A. The magical number seven, plus or minus two: Some limits in our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K. A novel method for multiple criteria analysis: Grey additive ratio assessment (ARAS-G) method. Informatica 2010, 21, 597–610. [Google Scholar]
- Turskis, Z.; Zavadskas, E.K. A new fuzzy additive ratio assessment method (ARAS-F). Case study: The analysis of fuzzy multiple criteria in order to select the logistic centers location. Transport 2010, 25, 423–432. [Google Scholar] [CrossRef]
- Krantz, D.H.; Luce, R.D.; Suppes, P.; Tversky, A. Foundations of Measurement: Additive and Polynomial Representations; Academic Press: New York, NY, USA, 1971; Volume 1. [Google Scholar]
- Daniūnas, A.; Urbonas, K. Analysis of the steel frames with semirigid beam-to-beam and beam-to-column knee joints under bending and axial forces. Eng. Struct. 2008, 30, 3114–3118. [Google Scholar] [CrossRef]
- Daniūnas, A.; Urbonas, K. Influence of the semi-rigid bolted joints on the frame behavior. J. Civ. Eng. Manag. 2010, 16, 237–241. [Google Scholar] [CrossRef]
- Gečys, T.; Daniūnas, A.; Bader, T.K.; Wagner, L.; Eberhardsteiner, J. 3D finite element analysis and experimental investigations of a new type of timber beam-to-beam connection. Eng. Struct. 2015, 86, 134–145. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).