Abstract
With the rapid development and widespread applications of Internet of Things (IoT) systems, the corresponding security issues are getting more and more serious. This paper proposes a multistage asymmetric information attack and defense model (MAIAD) for IoT systems. Under the premise of asymmetric information, MAIAD extends the single-stage game model with dynamic and evolutionary game theory. By quantifying the benefits for both the attack and defense, MAIAD can determine the optimal defense strategy for IoT systems. Simulation results show that the model can select the optimal security defense strategy for various IoT systems.
1. Introduction
As another revolutionary development of the information industry after computers, the Internet, and mobile communication, Internet of Things (IoT) systems are widely used in smart cities, smart healthcare, smart homes, and smart transportation. Although the IoT has brought convenience to people’s work and life, it also has brought many security problems. In recent years, various types of cyberattacks have gradually shifted from the traditional Internet and mobile Internet to the IoT [1]. The number of attacks against IoT vulnerability has been increasing. The scope and scale of these attacks have also gradually expanded.
In order to improve the overall defense capability of the IoT, plenty of researchers have actively explored and achieved rich results in the related research of active defense systems. Because of the attack–defense process, the IoT is consistent with the basic characteristics and application scenarios of game theory, a new method is provided by applying game theory to the construction of the IoT attack and defense system [2]. For example, Ryutov [3] proposed a security game model, based on an attacker, defender, and user, using extended game theory to describe the interaction behavior between the attacker and defender, attacker and user, and user and defender. Solan [4] introduced the concept of the relative importance degree of nodes and proposed a network risk assessment method based on the two-person zero-sum game model.
The selection of a defense strategy is an important part of the dynamic attack and defense system of the IoT. In order to select the optimal defense strategy, the defender needs to comprehensively consider the effectiveness of the defense strategy, the defense operation cost and negative impact and other factors, and balance the risk of attack reduction and the cost of defense. Most of the traditional studies on attack–defense games are based on rational assumptions and complete information hypotheses. However, in practical applications, due to the opposition between offense and defense, it is difficult to fully grasp each other’s game information, so the complete information hypothesis is difficult to meet. In addition, since the players in the game are all bounded rational individuals, the decision-makers of both offense and defense have great rational limitations when the problems are complicated and there are many influencing factors. Under this circumstance, the completely rational assumptions are difficult to satisfy in reality. Therefore, researchers have proposed a new round of research on the dynamic evolutionary game model of incomplete information. For example, Fudenberg et al [5]. proposed a dynamic game model, innovatively transforming the network attack and defense map into a network game tree by establishing a "virtual node" to study the strategy choice in active defense. Jiang [6] summarizes and analyzes the network attack and defense security, and proposes use of the refined Bayesian method to calculate the equilibrium state. Cheng et al. [7] proposed a strategy selection method based on evolutionary game theory, which changes its behavior according to the analysis of offensive and defensive strategy information and strategic income dynamics. Huang et al. [8] demonstrated the existence and uniqueness of the Nash equilibrium point in the offensive and defensive process of noncooperative evolutionary game.
In addition, most of the current research focuses on the attacker and defender’s behavior in a single stage, but multistage offensive and defensive games are more common in the actual situation. By analyzing the attacker’s and defender’s activities and the influencing factors of previous stages, it can be more accurate to obtain the other player’s situation and select optimal strategies. Zhuang [9] analyzed the behavior of both sides of the offensive and defensive, and gave a simplified method of selecting the optimal strategy. Jose [10] analyzed the multistage continuous attack and defense process and applied the idea of the game to target valuations and allocation. Huang [11] built a network attack and defense model by combining evolutionary game theory and the Markov decision process, and proposed a method for selecting the optimal defense strategy. Hu [12] expanded the static analysis of the attack and defense process into dynamic analysis under the condition of incomplete information, using the Bayesian method to obtain the optimal defense strategy. Olsder [13] formulated a Stackelberg game in the case of a nonzero-sum game and concluded that if each player’s cost function is either nonquadratic or nonconvex, both pure and mixed Stackelberg strategies can achieve equilibrium. If the cost function is quadratic and strictly convex, then only pure Stackelberg strategies can exist.
Therefore, according to the previous deficiencies, this paper proposes MAIAD, a multistage IoT dynamic attack–defense model based on evolutionary game theory under the premise of asymmetric information. MAIAD analyzes the confrontation and evolution trend of offensive and defensive behaviors. By calculating the cost/benefit of the offensive and defensive strategy, the optimal defense strategy for the IoT system is proposed, which provides a good reference for defense decision-makers to develop IoT security defense strategies.
Aiming at the above problems, this paper proposes a multistage IoT dynamic attack–defense model based on evolutionary game theory under the premise of information asymmetry, MAIAD. MAIAD can be used to analyze the trend of the confrontation and evolution of offensive and defensive activities. By calculating the cost/benefit of the offensive and defensive strategy, the optimal defense strategy of the IoT system is obtained, which provides a good reference for decision makers.
2. The Multistage Asymmetric Information Attack and Defense Model
The IoT is an extension and expansion of the Internet. Many theoretical frameworks for Internet systems can be migrated and applied to IoT systems [14]. Evolutionary game theory is a theory combining game theory analysis and dynamic evolution analysis. In this theory, the game process goes through multiple iterations and finally reaches the dynamic equilibrium state [15]. In each round, offensive and defensive players with limited information adjust their strategies to improve their own interests according to the newly acquired information and vested interests.
2.1. Analysis of Attack and Defense Game Processes
The defense signal is the key factor for the attacker to analyze and determine the type of defender and select the action decision. In order to deter attackers, induce attack activities, and increase defense revenue, defenders often deploy false defense signals related to defense measures and strength in advance. Therefore, this paper also takes into account the role of defense signals when selecting security policies.
In the single-stage game of the IoT model, both offensive and defensive players use the Bayesian rule to select the optimal decision based on the environmental information and the collected information to achieve the refined Bayesian equilibrium state. However, under the premise of asymmetric information, since the players have different levels of security knowledge and skills, the resulting decision-making mechanism and benefits will be different. As the number of game stages increases, low-yield game participants will continue to learn the strategies of higher-yielding participants, thereby improving their decision-making mechanisms. With the learning mechanism, the activities of both offensive and defensive sides continue to be in a multistage state, showing a trend of dynamic evolution.
Based on the bounded rationality and asymmetric information premise, this paper constructs a multistage attack and defense signal evolution game model of the IoT. By establishing the replicator dynamics equation of the evolutionary game, this paper analyzes the evolution of the decision-making mechanism of the game participants, calculates the quantitative benefits, and solves the evolutionary equilibrium which is helpful to select the optimal defense strategy.
For the overall multistage evolutionary game process, the specific analysis is as follows:
(1) The first stage
The defender terrorizes, deceives, and induces the attacker by releasing the defense signal. The attacker makes a judgment on the type of the defender based on the information in the intelligence gathering phase and the defense signal released by the defender. Afterwards, both offensive and defensive sides can obtain quantitative benefits with various strategies and select the appropriate offensive and defensive strategies at this stage. The defense signal is strongest in the first phase, denoted as δT = 1.
(2) The second stage
Both offensive and defensive sides make a judgment on the type of defender based on the defense strategy at the previous stage and the defense signal at current stage. At the same time, the probability of strategy selection in the strategy set will also change under the influence of the learning mechanism over time. At this stage, the deterrent, deception, and induction of the defense signal begin to decay, denoted as 0 < δT < 1.
(3) After multiple stages
The offensive and defensive sides repeat the above process at each stage of the game. At this time, the attacker can completely determine the type of the defender, that is, the role of the defense signal disappears, denoted as δT = 0. As a result, the incomplete information state transitions to a complete information state, and the offensive and defensive games reach a dynamic balance.
2.2. Definition of the MAIAD
MAIAD means multistage IoT attack and defense model. The MAIAD is constructed on the following three basic assumptions.
Assumption 1.
Asymmetric information. The defender can observe the attacker performing the action, but cannot realize when the attacker takes action.
Assumption 2.
Bounded rationality. Game participants have a bounded rationality between perfect rationality and irrationality, which means that the players have limited ability when making decision.
Assumption 3.
Interest assumption. Both offensive and defensive sides select game strategies in accordance with the principle of maximizing their own interests.
Definition 1.
The MAIAD uses an eight-tuple representation (N, θ, S, M, P, T, δT, U).
- 1.
- N represents the set of participants in the game, and the participants in the offensive and defensive game are the subject of the strategy choice and the strategist. Na stands for the attacker set of the IoT system and is a follower. Nd is the leader of the defenders.
- 2.
- θ represents the type space of the defender and the attacker. Depending on the defensive capabilities, the type of defender can be divided into a high level defender θh, medium level defender θm, and low level defender θl, θd = (θh,θm,θl). The type information of the defender is private information. The attacker has only one type θa= (η).
- 3.
- S represents the set of policies of the attacker and defender, where DS represents the defender’s policy set, DS = {ai | i = 1,2,…}, AS represents the attacker’s policy set, AS = { dj | j = 1,2,…}.
- 4.
- M represents the defense signal space. The defender selects and releases the false defense signal according to the preset signal release mechanism. For the convenience of representation, the signal name is consistent with the name of the defender type. M ≠ ∅, M = (mh, mm, ml). For the purpose of deterrence, deception, and inducement of an attacker, the true type of defense signal and defender is not necessarily consistent.
- 5.
- T represents the number of stages in a multistage game, i.e., T = {1,2,…,n}.
- 6.
- P represents a set of game beliefs. In stage T, pi represents the probability of selecting the attack strategy ASi, qi represents the probability of selecting the defense strategy DSi, , .
- 7.
- δT is a discount factor, which indicates that as the game progresses, the proportion of the defender’s return is smaller than the initial stage’s discount ratio in the process of increasing T, 0 ≤ δT ≤ 1. When T = 1, δ1 = 1, it means that in the initial game stage, the released false defense signal has no attenuation. At this time, the defense signal has the strongest ability to deter, deceive, and induce the attacker, and the defense party gains. When 1 < T < n, 1 < δT < n, δT has a monotonously decreasing characteristic, that is, as the game evolves, the false defense signal will decay and the attenuation will increase, and the defense party will decrease; when T = n, δn = 0, which means that after the game between the two parties reaches a certain level, the influence of the false defense signal on the game result completely disappears, and the multistage dynamic attack and defense game degenerates into the static game problem under the condition of incomplete information.
- 8.
- U = {Ua, Ud} is a collection of utility functions for attackers and defenders. It indicates the gain or loss obtained by the offensive and defensive sides from the game. Ua is the utility function of the attacker. Ud is the utility function of the defender. When the offensive and defensive sides use different attack and defense strategies to play the game, they will get different income values.
2.3. Quantification of Attack and Defense Strategy Cost/Benefit
Definition 2.
The Attack Cost (AC)indicates the economic, time, hardware and software, and labor resources that an attacker spends due to the selection of an attack strategy.
Definition 3.
The Defense Cost (DC)indicates resources such as the economy, time, hardware and software equipment, labor, and the impact of the degradation of service quality caused by the defender’s selection of a certain defense strategy.
Definition 4.
Defense Effectiveness εindicates the effectiveness of the defensive strategy d for an attack a. When the attack can be completely blocked, ε(a, d) = 1; when the defense strategy is invalid, ε(ai, dj) = 0; in other cases, 0 < ε(ai, dj) < 1.
Definition 5.
System Damage Cost (SDC)indicates the damage caused to the system by an attacker after launching an attack.
Definition 6.
Signal Deception Explore (SDE)indicates that the defender is obsessed with real defense information, releasing false signal spoofing, and inducing the cost of the attacker. If the signal matches the true type of the defender, the SDE is zero. According to the gap between the real defense information and the false defense information, the SDE is relatively quantized and expressed by the integer value in the interval [0, 100].
In general, the greater the gap between defenders and defense signals, the greater the difficulty and cost of camouflage. The classification and quantification of SDE are shown in Table 1.

Table 1.
Signal deception explore (SDE) level quantization example.
Using different strategies to conduct offensive and defensive confrontation will result in different offensive and defensive returns. In each phase, the attacker’s return expectation is:
The defender’s income expectation is:
3. Optimal Strategy Selection
3.1. Evolutionary Game Equilibrium
There are two important concepts in the evolutionary game equilibrium:
(1) Replicator Dynamics Equation
If the individual who chooses the strategy s gets less than the average return of the group, the growth rate of the number of individuals of that selection strategy s will be less than 0 [16], and vice versa. The replicator dynamics equation is a dynamic differential equation of the frequency at which a strategy is adopted in a population, and is generally expressed by:
where is the proportion or probability of adopting the strategy s in a population, indicates the fitness when using the strategy s, indicates the average fitness.
(2) Evolutionary equilibrium
Evolutionary game is a process of constantly replacing a less satisfactory strategy with a “satisfactory strategy” until the state of dynamic equilibrium is reached, in which either side is no longer willing to unilaterally change its strategy [17,18]. This dynamic equilibrium is called evolutionary equilibrium.
Given the type of participants and a limited set of attack and defense strategies, each participant wants to maximize their expected benefits in the evolutionary game process. Under the guidance of this principle, participants who choose strategies that are not good enough will tend to choose the best strategy based on the results of the previous round of games, until all individuals in this group choose the best strategy. At this time, for each game participant i, there is a strategy which is the best countermeasure against another game participant. For
3.2. Optimal Strategy Selection
In this paper, the MAIAD is established by analog evolution game theory model. When the optimal defense strategy is selected, the equilibrium state of the evolutionary game is analyzed, and the evolutionary equilibrium is solved by the replicator dynamics equation.
The type of the defender is = (high level defender, medium level defender, low level defender), defense signal is , defense strategy set is , attacker type is , the attack strategy set is , and the gains of both offense and defense are .
Bring both offensive and defensive players into the game participants. For the multistage evolutionary game equilibrium, , , , the following evolutionary game equilibrium solution steps can be obtained:
(1) Set strategy selection probabilities
According to the defense signal released by the defender, the attacker establishes a probability inference on the optional policy set.
(2) Obtain the attack equation
The attacker’s replicator dynamics equation is:
With , , where aij is the income function when the attacker selects the attack strategy ASi.
(3) Obtain the defense equation
The defender’s replicator dynamics equation is:
With , , where dij is the income function when the defender chooses the defense strategy DSj.
(4) Calculate the cost/benefit
In the multistage game, as the attacker gradually determines the type of defender, the future income will gradually decrease on the basis of the initial return. Therefore, this paper introduces the discount factor δT into the original return function U to calculate the future income. The value is calculated as follows:
(5) Solve the equilibrium
According to the evolutionary game equilibrium state, the replicator dynamics equations of both offense and defense should be equal to 0, and the game equilibrium solution should satisfy the following equations:
with ,
By solving the above equations comprehensively, we can obtain the strategy selection set in the evolution equilibrium state {, }. According to the evolutionary game theory, the attack and defense strategy at this time is the best choice for both offense and defense, which means is the optimal defense strategy.
4. Experimental Verification
Since the network structure of most IoT systems is huge and complex, including many subsystems and network domains, such as device terminals, mobile phones, and clouds, this paper simplifies and decomposes them into several Security Risk Domains (SRDs) [19], which are subsystems that contain typical security vulnerabilities of the system. The following experiments apply the MAIAD model proposed in three different IoT systems, including smart home, smart camera, and smart transportation, to select the optimal defense strategy and verify the feasibility and effectiveness of the proposed solution.
4.1. Attack and Defense Strategy Set
4.1.1. Smart Home Network
The structure of the SRD of a smart home network is shown in Figure 1. It controls the working state of the IoT device through the router and transmits information through the wireless communication network. By identifying the vulnerabilities of the smart home system, an attack strategy set can be obtained as shown in Table 2. The attack cost quantization value corresponding to each attack strategy is also given in the table. In order to cope with the mentioned system vulnerabilities, the defender can adopt the defense strategy set as shown in Table 3. The table also gives the quantitative value of the defense cost corresponding to each defense behavior.
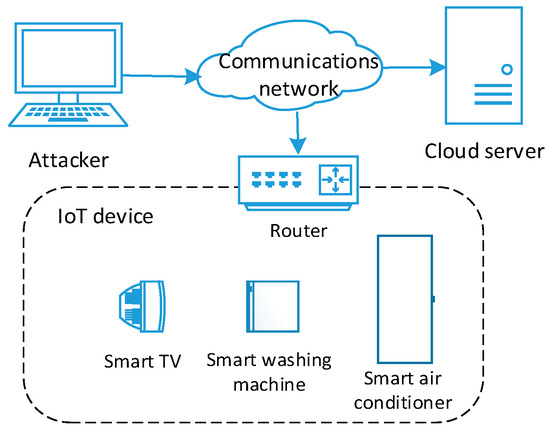
Figure 1.
Structure of a smart home network.

Table 2.
Description of attack actions.

Table 3.
The description of defense actions.
4.1.2. Smart Camera Network
The structure of the SRD of a smart camera network is shown in Figure 2. Its attack strategy set and defense strategy set are shown as Table 4 and Table 5.
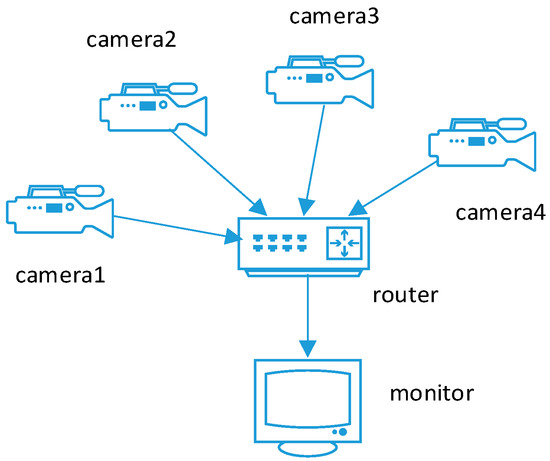
Figure 2.
Structure of a smart camera network.

Table 4.
Description of attack actions.

Table 5.
Description of defense actions.
4.1.3. Smart Transportation System
Similarly, the structure of the SRD of a smart transportation system is shown in Figure 3. Its attack strategy set and defense strategy set are shown as Table 6 and Table 7.
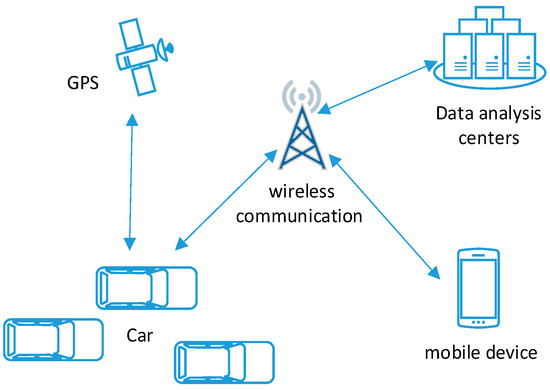
Figure 3.
Structure of a smart transportation system.

Table 6.
Description of attack actions.

Table 7.
Description of defense actions.
4.2. Optimal Strategy Calulation
In order to simplify the calculation, there are only high-level defenders and low-level defenders in three SRDs. In all three applications, we set the real defender level as a low-level defender and the fake defense signal as a high-level defender, i.e., SDE = 70. The attack strategy set in this system includes a1 and a2, and the defense strategy set includes d1 and d2.
The schematic diagram of the attack and defense game process is shown as Figure 4.
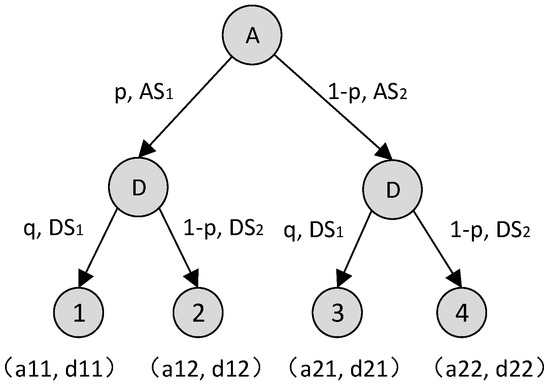
Figure 4.
Attack and Defense Game Diagram.
4.2.1. Smart Home Network
According to the calculation formula given in Section 2.3, the expected cost/benefit of the attack and defense strategies in this experiment are:
The expected benefits of the defender using different strategies are:
The average revenue of the defender is:
For defense strategy DS1, the probability that the defender chooses this strategy is a function of time, and its dynamic rate of change can be xpressed as:
In the same way, the expected benefits of using different strategies by the attacker can be obtained:
The average revenue of the attacker is:
The dynamic rate of change of choosing strategy AS1 is:
Since the optimal defense strategy is always generated in the equilibrium state, this case analyzes and solves the evolutionary game equilibrium in the last stage. At this time, δT = 0, and the objective function R is equal to the income function U, i.e., . Then, we obtain the evolutionary stability strategy through the phase diagram.
The following is an analysis of the evolutionary stability strategy of the defender in the case where the probability of the attacker’s selection strategy is different. According to the replicator dynamics equation of the defender, the defender’s evolutionary stability strategy selection has three cases (Figure 5):
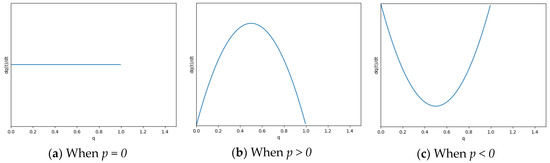
Figure 5.
Phase diagram.
According to Figure 5a, when p = 0, for any defense strategy selection probability, there is D(q) = 0. However, if p ≠ 0, D(q) will change drastically, so the state represented by Figure 5 is not stable. The evolutionary stability strategy of the defender should be obtained when the tangent slope of the curve is negative. According to the Figure 5b, when p > 0, d1 (q = 1) is the defender evolutionary stability strategy. According to the Figure 5c, when p < 0, d2 (q = 0) is the defender evolutionary stability strategy. Since p cannot be less than 0, d2 is the optimal defense strategy for this IoT system.
4.2.2. Smart Camera Network
Similarly, according to the formula given in Section 2.3, for defense strategy DS1, the dynamic rate of change can be expressed as:
The dynamic rate of change of choosing strategy AS1 is:
By solving and anylazing the equations, we can obtain that d1 is the optimal defense strategy for this IoT system.
4.2.3. Smart Transportation System
For defense strategy DS1, the probability that the defender chooses this strategy is a function of time, and its dynamic rate of change can be expressed as:
The dynamic rate of change of choosing strategy AS1 is:
By solving and anylazing the equations, we find that d2 is the optimal defense strategy for this IoT system.
4.3. Simulation Results
4.3.1. Smart Home Network
In order to prove that the analysis results are consistent with the results in the actual scene, we use Matlab to simulate and obtain the evolutionary game equilibrium. The result is presented as Figure 6. The horizontal axis represents time and the vertical axis represents the initial values of q. From the figure, we can see that no matter what the initial probability p is, the system finally reaches stability at q = 1, which proves that d1 is the optimal defense strategy solution and the proposed MAIAD model is feasible and effective.
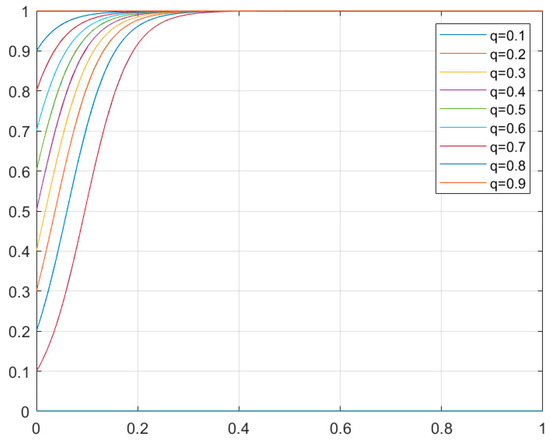
Figure 6.
D(q) curve simulation diagram.
4.3.2. Smart Camera Network
The result of the evolutionary game equilibrium is presented as Figure 7. From the figure, we can see that the system will eventually reach stability at q = 1 regardless of the initial probability p, which means d1 is the optimal strategy solution.
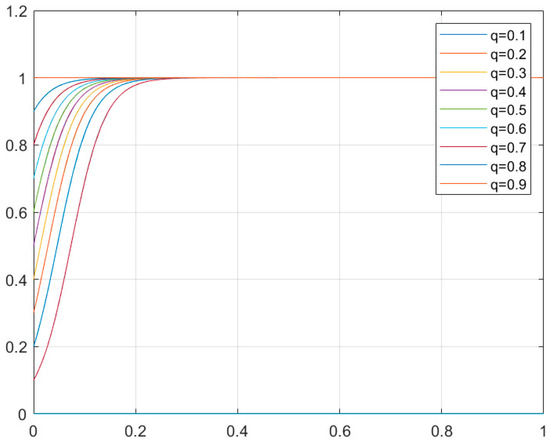
Figure 7.
D(q) curve simulation diagram.
4.3.3. Smart Transportation System
Similarily, the result is presented as Figure 8. From the figure, we can see that the system will eventually reach stability at q = 0 regardless of the initial probability p, which means d2 is the optimal strategy solution.
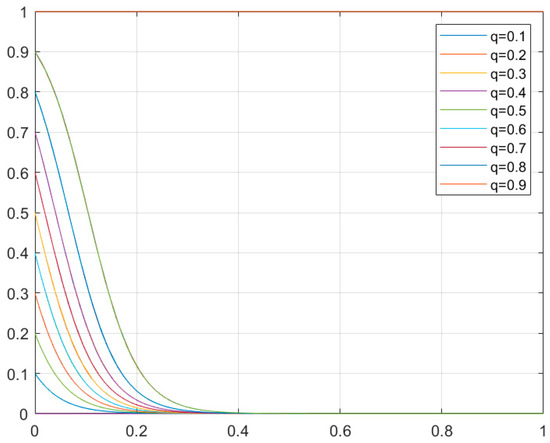
Figure 8.
D(q) curve simulation diagram.
5. Conclusions and Future Research Directions
Based on evolutionary game theory, this paper analyzed the dynamic attack and defense process of the IoT systems in different stages, and built a multistage IoT security defense model. The model proposes a method to quantify the benefit/cost of the attacking and defending strategies, and uses the replication dynamics equation to calculate the probability of attack and defense strategy selection. Finally, the evolutionary balance is solved to obtain the optimal defense strategy by simulating the offensive and defensive behaviors in different IoT systems. The feasibility of selecting the optimal defense strategy is verified by Matlab simulation, which can provide guidance for decision-makers to choose an appropriate IoT security defense strategy.
One interesting future research direction is to consider optimizing the income function. The current factors affecting the income function are the monetary cost of launching an attack (or implementing defensive actions) and the success rate of implementing the strategy. However, sometimes, money may not be the main influencing factor of the IoT system. Some hidden costs should also be taken into consideration. For example, the adverse effects of IoT attacks on users can destroy a company’s reputation. Occasionally, the money cost of implementing the defensive measures is small, but it takes a long time for defenders to observe and monitor, which means the time cost is too high. Therefore, in future research, we will optimize the income function by considering more influencing factors to make it better suited to actual situations.
Another possible future research direction is to consider the existence and evolution of mutants. In general, there are two possible cases after a rare mutant emerges. In one case, the mutant cannot invade the group, and gradually disappears in the process of evolution. In the other case, the mutant can invade the group if its reproductive fitness in the population is greater than the original fitness. In this paper, we carried out our research in the former, relatively simple case. In future research, the evolution of mutants can be studied in depth by introducing random regression matrices or equations.
Author Contributions
Conceptualization, Y.Y. and B.C.; Methodology, Y.Y.; Software, Y.Z.; Validation, Y.C. and C.L.; Formal Analysis, Y.Z.; Investigation, C.L.; Resources, Y.C.; Data Curation, B.C.; Writing—Original Draft Preparation, B.C.; Writing—Review & Editing, Y.Y.; Project Administration, Y.Y.
Funding
This research was funded by [the National Key R&D Program of China] grant number [2017YFB0802703], [Major Scientific and Technological Special Project of Guizhou Province] grant number [20183001], [Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data] grant number [2018BDKFJJ014], [Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data] grant number [2018BDKFJJ019] and [Open Foundation of Guizhou Provincial Key Laboratory of Public Big Data] grant number [2018BDKFJJ022].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Hong, X.; Li, F.; Zhan, B.H. Information Security Assessment and Risk Assessment; Electronic Industry Press: Beijing, China, 2012. [Google Scholar]
- Lye, K.W.; Wing, J.M. Game strategies in network security. Int. J. Inf. Secur. 2005, 4, 71–86. [Google Scholar] [CrossRef]
- Ryutov, T.; Orosz, M.; Blythe, J.; von Winterfeldt, D. A Game Theoretic Framework for Modeling Adversarial Cyber Security Game among Attackers, Defenders, and Users; Security and Trust Management; Springer International Publishing: New York, NY, USA, 2015; pp. 274–282. [Google Scholar]
- Solan, E.; Vieille, N. Correlated equilibrium in stochastic games. Game Econ. Behav. 2002, 38, 362–399. [Google Scholar] [CrossRef]
- Fudenberg, D.; Tirole, J. Game Theory; Massachusettes Institute of Technology Press: Boston, MA, USA, 2012. [Google Scholar]
- Jiang, Y.; Zhang, H.; Song, X.; Jiao, X.; Hung, W.N.; Gu, M.; Sun, J. Bayesian-Network-Based Reliability Analysis of PLC Systems. IEEE Trans. Ind. Electron. 2013, 60, 5325–5336. [Google Scholar] [CrossRef]
- Cheng, D.; He, F.; Qi, H.; Xu, T. Modeling, analysis and control of networked evolutionary games. IEEE Trans. Autom. Control 2015, 60, 2402–2415. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, H.; Wang, J. Defense strategies selection based on attack–defense evolutionary game model. J. Commun. 2017, 38, 168–176. [Google Scholar]
- Shan, X.; Zhuang, J. Modeling Cumulative Defensive Resource Allocation against a Strategic Attacker in a Multiperiod Multitarget Game. Reliab. Eng. Syst. Saf. 2018, 179, 12–26. [Google Scholar] [CrossRef]
- Jose, V.R.; Zhuang, J. Technology Adoption, Accumulation, and Competition in Multiperiod Attacker-Defender Games. Adv. Mater. Res. 2013, 18, 1178–1181. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, H.; Wang, J. Markov Evolutionary Games for Network Defense Strategy Selection. IEEE Access 2017, 5, 19505–19516. [Google Scholar] [CrossRef]
- Hu, H.; Liu, Y.; Zhang, H.; Pan, R. Optimal Network Defense Strategy Selection Based on Incomplete Information Evolutionary Game. IEEE Access 2018, 6, 29806–29821. [Google Scholar] [CrossRef]
- Basar, T.; Olsder, G. Mixed Stackelberg strategies in continuous-kernel games. In Proceedings of the IEEE Conference on Decision & Control Including the Symposium on Adaptive Processes, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Jiang, W.; Fang, B.X.; Tian, Z.H.; Zhang, H.L. Evaluating Network Security and Optimal Active Defense Based on Attack–defense Game Model. Chin. J. Comput. 2009, 32, 817–827. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, H.; Wang, R.; Gu, M.; Sun, J.; Sha, L. Data-centered runtime verification of wireless medical cyber-physical system. IEEE Trans. Ind. Inform. 2017, 13, 1900–1909. [Google Scholar] [CrossRef]
- Wang, B.; Cai, J.; Zhang, S.; Li, J. A network security assessment model based on attack–defense game theory. In Proceedings of the International Conference on Computer Application & System Modeling, Taiyuan, China, 22–24 October 2010. [Google Scholar]
- Jin-Dong, W.A.; Ding-Kun, Y.; Hengwei, Z.H. Active defense strategy selection based on the static Bayesian game. In Proceedings of the IET International Conference on Cyberspace Technology, Beijing, China, 7 April 2016. [Google Scholar]
- Jiang, Y.; Zhang, H.; Zhang, H.; Liu, H.; Song, X.; Gu, M.; Sun, J. Design of Mixed Synchronous/Asynchronous Systems with Multiple Clocks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2220–2232. [Google Scholar] [CrossRef]
- Zhuang, J.; Bier, V.M. Secrecy and Deception at Equilibrium, with Applications to Anti-Terrorism Resource Allocation. Def. Peace Econ. 2011, 22, 43–61. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).