Abstract
Hypergraph theory is the most developed tool for demonstrating various practical problems in different domains of science and technology. Sometimes, information in a network model is uncertain and vague in nature. In this paper, our main focus is to apply the powerful methodology of fuzziness to generalize the notion of competition hypergraphs and fuzzy competition graphs. We introduce various new concepts, including fuzzy column hypergraphs, fuzzy row hypergraphs, fuzzy competition hypergraphs, fuzzy k-competition hypergraphs and fuzzy neighbourhood hypergraphs, strong hyperedges, kth strength of competition and symmetric properties. We design certain algorithms for constructing different types of fuzzy competition hypergraphs. We also present applications of fuzzy competition hypergraphs in decision support systems, including predator–prey relations in ecological niche, social networks and business marketing.
Keywords:
fuzzy competition hypergraph; fuzzy k-competition hypergraph; fuzzy open neighbourhood; fuzzy closed neighbourhood; ecological niches MSC:
05C65; 05C85; 68R10; 03E72
1. Introduction
In mathematical modeling, competition graphs are sufficient to specify well defined behaviors of objects and specifically predator–prey relations. In 1968, while studying applications of graph theory in ecology, Cohen introduced the notion of a competition graph. Competition graphs have been applied to various fields of biological sciences and technology. After the strong motivation of energy and food competition in food webs between species, competition graphs were a part of active research in recent years. In 2004, Sonntag and Teichert [1] introduced the notion of competition hypergraphs. These representations are crisp hypergraphs that do not describe all the competitions of real-world problems. These models contain uncertainty and fuzzy in nature for problems that are more relevant to everyday life, including critical writing style of a writer, predator–prey relationship, trading relationship among different communities, honesty leadership quality of a politician and, signal strength of wireless devices. Motivating from this idea, we have applied the notion of fuzzy sets to competition hypergraphs to study the problems having nonlinear uncertainties.
In 1965, Zadeh [2] introduced the strong mathematical notion of fuzzy set in order to discuss the phenomena of vagueness and uncertainty in various real-life problems. Using the concept of fuzzy relations introduced by Zadeh [3], the idea of fuzzy graph was given by Kaufmann [4]. The fuzzy relations in fuzzy sets were studied by Rosenfeld [5] and he introduced the structure of fuzzy graphs, obtaining analysis of various graph theoretical concepts. Lee-kwang and Lee [6] redefined and extended the notion of fuzzy hypergraphs whose idea was first discussed by Kaufmann [4]. Later, the idea of fuzzy hypergraph was studied by Goetschel in [7,8]. The concept of interval-valued fuzzy hypergraphs was initiated by Chen [9] and Parvathi et al. [10] generalized the idea of hypergraphs to intuitionistic fuzzy hypergraphs. Moreover, Akram and Dudek [11], Akram and Luqman [12,13,14], and Akram and Shahzadi [15] have discussed certain extensions of fuzzy hypergraphs with applications.
Samanta and Pal [16] studied fuzzy k-competition graphs and p-competition graphs. Later, Samanta et al. [17] introduced the concept of m-step fuzzy competition graphs. Applying the idea of bipolar fuzzy sets to competition graphs, Alshehri and Akram [18] introduced the notion of bipolar fuzzy competition graphs and applied this idea to economic systems. Furthermore, the study of bipolar fuzzy competition graphs was discussed by Sarwar and Akram in [19]. Certain competition graphs based on neutrosophic environment were described in [20,21]. In this research paper, we introduce the concept of fuzzy competition hypergraphs as a generalized case of fuzzy competition graphs. We study various new concepts, including fuzzy column hypergraphs, fuzzy row hypergraphs, fuzzy competition hypergraphs, fuzzy k-competition hypergraphs and fuzzy neighbourhood hypergraphs and investigate some of their interesting properties. We design certain algorithms for the construction of different types of fuzzy competition hypergraphs. We also present applications of fuzzy competition hypergraphs in decision support systems, including food webs, social networks and business marketing.
We have used basic notions and terminologies in this research paper. For other terminologies, notations and definitions not given in the paper, the readers are referred to [2,3,5,9,10,17,19,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
Definition 1.
A fuzzy hypergraph on a non-empty set X is a pair where , are fuzzy subsets on X such that , for all . ρ is a fuzzy relation on the fuzzy subsets such that
2. Fuzzy Competition Hypergraphs
In this section, we discuss various types of fuzzy competition hypergraphs with certain properties and algorithms.
Definition 2.
Let be the adjacency matrix of a fuzzy digraph on a non-empty set X. The fuzzy row hypergraph of , denoted by , having the same set of vertices as and the set of hyperedges is defined as
The degree of membership of hyperedges is defined as
Definition 3.
The fuzzy column hypergraph of , denoted by , having the same set of vertices as and the set of hyperedges is defined as
The degree of membership of hyperedges is defined as
The methods for computing fuzzy row hypergraph and fuzzy column hypergraph are given in Algorithms A1 and A2, respectively.
Example 1.


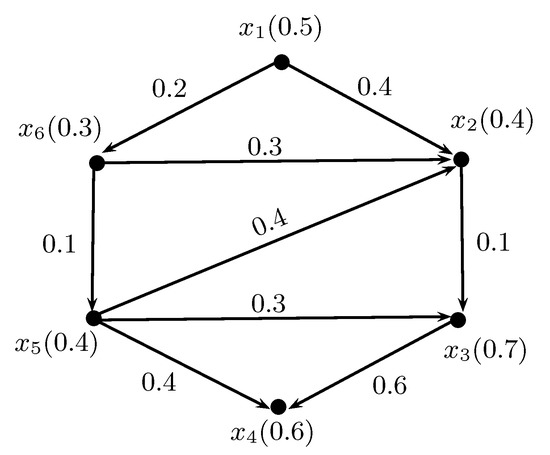

Consider the universe , μ a fuzzy set on X and a fuzzy relation in X as defined in Table 1 and Table 2, respectively. The fuzzy digraph is shown in Figure 1. The adjacency matrix of G is given in Table 3.

Table 1.
Fuzzy vertex set .

Table 2.
Fuzzy relation .

Figure 1.
Fuzzy digraph .

Table 3.
Adjacency matrix.
Using Algorithm A1 and Table 3, there are three hyperedges , and , corresponding to the columns and of adjacency matrix, in fuzzy row hypergraph of . The membership degree of the hyperedges is calculated as
,
,
.
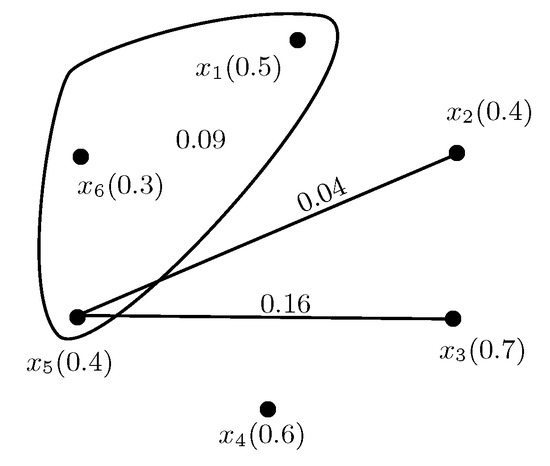
The fuzzy row hypergraph is shown in Figure 2. Using Algorithm A2 and Table 3, the hyperedges in fuzzy column hypergraph of G are , and , corresponding to the rows and of the adjacency matrix. The membership degree of the hyperedges is calculated as

Figure 2.
.
,
,
.
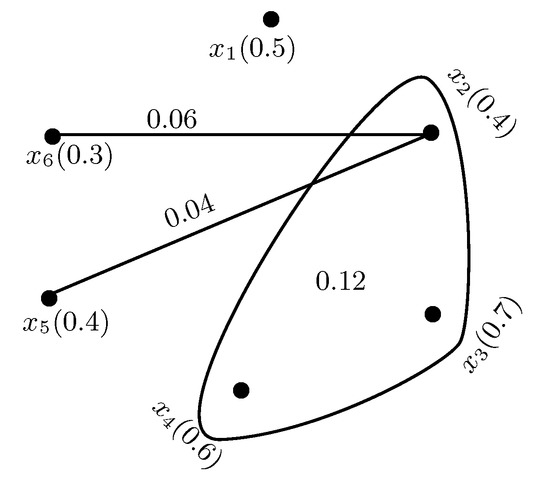
The fuzzy column hypergraph is given in Figure 3.

Figure 3.
.
Definition 4.
[25] A fuzzy digraph on a non-empty set X is a pair of functions and , such that for all , .
Definition 5.
[16] A fuzzy out neighbourhood of a vertex x of a fuzzy digraph is a fuzzy set where and is defined by .
Definition 6.
[16] The fuzzy in neighbourhood of vertex x of a fuzzy digraph is a fuzzy set where and is defined by .
Definition 7.
Let be a fuzzy digraph on a non-empty set X. The fuzzy competition hypergraph on X having the same vertex set as and there is a hyperedge consisting of vertices if . The degree of membership of hyperedge is defined as
where denotes the height of fuzzy set .
The method for constructing fuzzy competition hypergraph of a fuzzy digraph is given in Algorithm A3.
Lemma 1.
The fuzzy competition hypergraph of a fuzzy digraph is a fuzzy row hypergraph of .
Proof.
Let be a fuzzy digraph; then, for any hyperedge of ,
It follows that E is a hyperedge of fuzzy row hypergraph. □
Example 2.

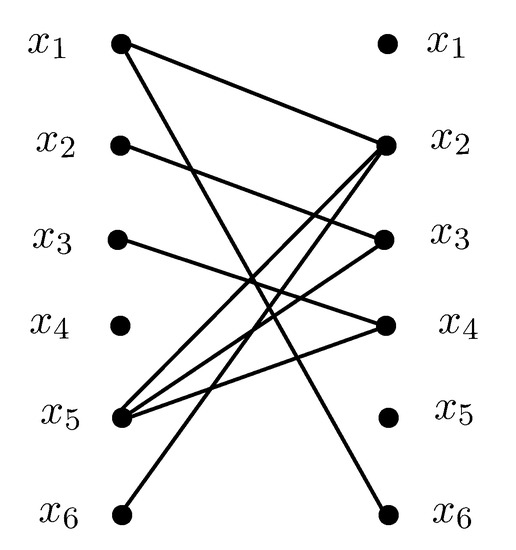
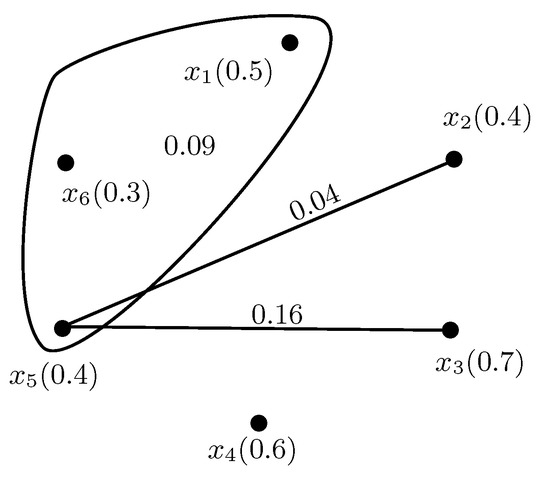
Consider the fuzzy digraph given in Figure 1. The fuzzy out neighbourhood and fuzzy in neighbourhood of all the vertices are given in Table 4.

Table 4.
Fuzzy out neighbourhood and fuzzy in neighbouhood of vertices in .
Using Algorithm A3, the relation of is given in Figure 4. The construction of fuzzy competition hypergraph from is given as follows:

Figure 4.
Representation of fuzzy relation in
- Since , and , and are hyperedges in .
- For hyperedge : , .
- Similarly, and .
The fuzzy competition hypergraph is given in Figure 5. From Figure 2 and Figure 5, it is clear that fuzzy competition hypergraph is a fuzzy row hypergraph.

Figure 5.
Fuzzy competition hypergraph .
Definition 8.
The fuzzy double competition hypergraph having same vertex set as and there is a hyperedge consisting of vertices if and . The degree of membership of hyperedge is defined as
The method for the construction of fuzzy double competition hypergraph is given in Algorithm A4.
Lemma 2.
The fuzzy double competition hypergraph is the intersection of fuzzy row hypergraph and fuzzy column hypergraph.
Proof.
Let be a fuzzy digraph; then, for any hyperedge of ,
It follows that the fuzzy double competition hypergraph is the intersection of a fuzzy row hypergraph and fuzzy column hypergraph. □
Example 3.
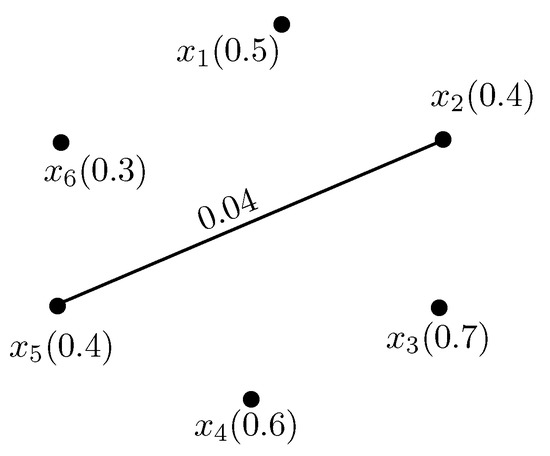
Consider the example of fuzzy digraph shown in Figure 1. From Example 2, the fuzzy double competition hypergraph of Figure 1 is given in Figure 6. In addition, Figure 2, Figure 3 and Figure 6 show that the fuzzy double competition hypergraph is the intersection of fuzzy row hypergraph and fuzzy column hypergraph.

Figure 6.
Definition 9.
Let be a fuzzy digraph on a non-empty set X. The fuzzy niche hypergraph has the same vertex set as G and there is hyperedge consisting of vertices if either or . The degree of membership of hyperedge is defined as
Lemma 3.
The fuzzy niche hypergraph is the union of fuzzy row hypergraph and fuzzy column hypergraph.
Example 4.
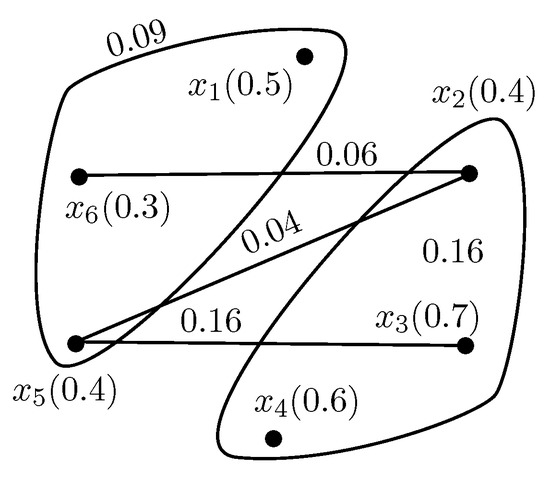
The fuzzy niche hypergraph of Figure 1 is shown in Figure 7, which is the union of Figure 2 and Figure 3.

Figure 7.
Definition 10.
Let H be a fuzzy hypergraph and t be the smallest non-negative number such that is a fuzzy niche hypergraph of some fuzzy digraph where is a fuzzy set on t isolated vertices ; then, t is called fuzzy niche number of H denoted by .
Lemma 4.
Let H be a fuzzy hypergraph on a non-empty set X with and is a fuzzy niche hypergraph of an acyclic digraph G then for all, ,
Proof.
On the contrary, assume that, for some , either or , where . Then, by definition of a fuzzy niche hypergraph, z is adjacent to all vertices in —a contradiction to the fact that . □
Lemma 5.
Let H be a fuzzy hypergraph with and is a fuzzy niche hypergraph of an acyclic fuzzy digraph then for all , and .
Proof.
On the contrary, assume that and . Clearly, because is acyclic. According to Lemma 4, .
Consider another fuzzy digraph such that and , where
Clearly, and . Thus, which contradicts the fact that . Hence, for all , and . □
Definition 11.
Let be a fuzzy hypegraph on a non-empty set X. A hyperedge is called strong if .
Theorem 1.
Let be a fuzzy digraph. If contains exactly one vertex, then the hyperedge of is strong if and only if .
Proof.
Assume that where l is degree of membership of u. As therefore, . Thus, the hyperedge in would be strong if by Definition 11. □
Definition 12.
Let k be a non-negative real number number; then, the fuzzy k-competition hypergraph of a fuzzy digraph is fuzzy hypergraph which has the same fuzzy vertex set as in and there is a hyperedge in if . The membership degree of the hyperedge E is defined as
where .
Example 5.
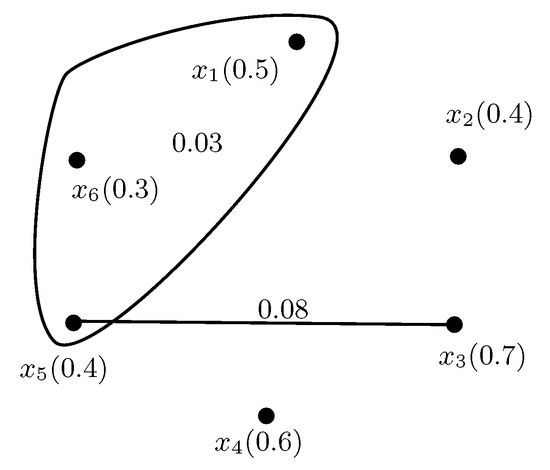

Figure 8.
Fuzzy competition hypergraph.
Remark 1.
For , a fuzzy k-competition hypergraph is simply a fuzzy competition hypergraph.
Theorem 2.
Let be a fuzzy digraph. If and for some , then the hyperedge is strong in .
Proof.
Let be a fuzzy k-competition hypergraph of fuzzy digraph . Suppose for , . Now,
Thus, the hyperedge E is strong in . □
Fuzzy Neighbourhood Hypergraphs
The concepts of fuzzy open neighbourhood and fuzzy closed neighbourhood are given in Definition 13.
Definition 13.
[16] The fuzzy open neighbourhood of a vertex y in a fuzzy graph is a fuzzy set where and a membership function defined by .
Definition 14.
[16] The fuzzy closed neighbourhood of a vertex y in a fuzzy graph is defined as .
Definition 15.
The fuzzy open neighbourhood hypergraph of a fuzzy graph is a fuzzy hypergraph whose fuzzy vertex set is the same as G and there is a hyperedge in if . The membership function is defined as
The fuzzy closed neighbourhood hypergraph is defined on the same lines in the following definition.
Definition 16.
The fuzzy closed neighbourhood hypergraph of is a fuzzy hypergraph whose fuzzy set of vertices is same as G and there is a hyperedge in if . The membership function is defined as
Example 6.
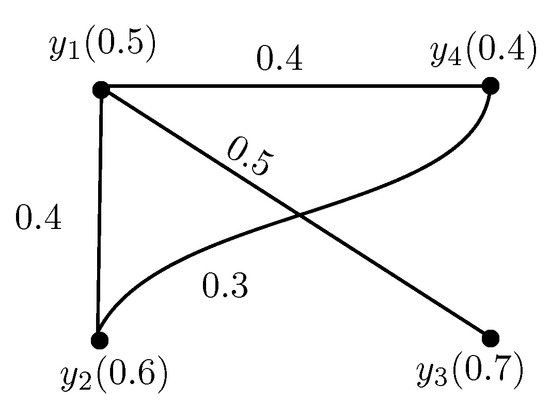

Consider the fuzzy graph on set as shown in Figure 9. The fuzzy open neighbourhoods are given in Table 5.

Figure 9.
Fuzzy graph .

Table 5.
Fuzzy open neighbourhood of vertices.
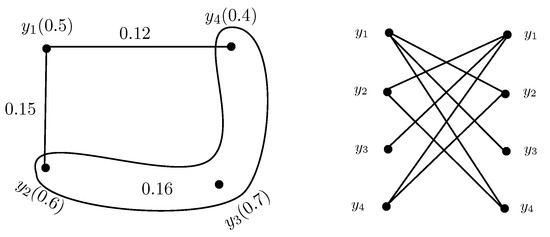
Define a relation by if as shown in Figure 10. If, for , then is a hyperedge of . Since, from Figure 10, , and , therefore, are hyperedges of . The degree of membership of each hyperedge can be computed using Definition 15 as follows.

Figure 10.
Fuzzy open neighbourhood hypergraph of G.
For , . Similarly, and . The fuzzy open neighbourhood hypergraph constructed using Definition 13 from is given in Figure 10.
The fuzzy closed neighbourhoods of all the vertices in G are given in Table 6. Since therefore, is a hyperedge of and . The fuzzy closed neighbourhood hypergraph is given in Figure 11.

Table 6.
Fuzzy closed neighbourhood of vertices.
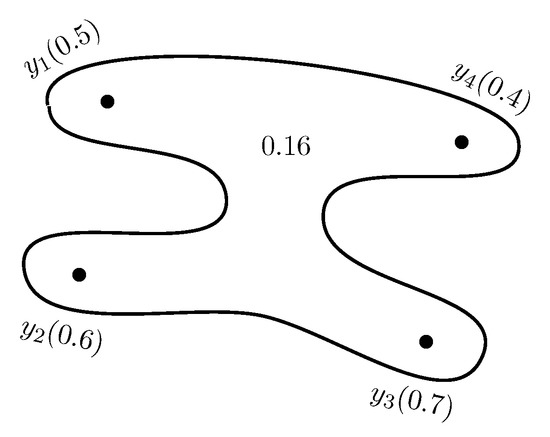
Figure 11.
Fuzzy closed neighbourhood hypergraph.
Using different types of fuzzy neighbourhood of the vertices, some other types of fuzzy hypergraphs are defined here.
Definition 17.
Let k be a non-negative real number; then, the fuzzy -competition hypergraph of a fuzzy graph is a fuzzy hypergraph having the same fuzzy set of vertices as G and there is a hyperedge in if . The membership value of E is defined as
where .
Definition 18.
The fuzzy -competition hypegraph of G is denoted by and there is a hyperedge E in if . The membership value of E is defined as
where .
Definition 19.
[16] Let be a fuzzy digraph. The underlying fuzzy graph of
is a fuzzy graph such that
where . The relations between fuzzy neighbourhood hypergraphs and fuzzy competition hypergraphs are given in the following theorems.
Theorem 3.
Let be a symmetric fuzzy digraph without any loops; then, where is the underlying fuzzy graph of .
Proof.
Let correspond to the fuzzy graph . In addition, let and . Clearly, the fuzzy k-competition hypergraph and the underlying fuzzy graph have the same fuzzy set of vertices as . Hence, has the same vertex set as G. It remains only to show that for every . Thus, there are two cases.
Case 1: If, for each , in then . Since G is symmetric, in . Thus, and for all .
Case 2: If, for some , in then . Thus,
where . Since is a symmetric fuzzy digraph, . Hence, . Since were taken to be arbitrary, the result holds for all hyperedges E of . □
Theorem 4.
Let be a symmetric fuzzy digraph having loops at every vertex; then, where is the underlying fuzzy graph of .
Proof.
Let be an underlying fuzzy graph corresponding to fuzzy digraph . Let and . The fuzzy k-competition graph as well as the underlying fuzzy graph have the same vertex set as . It follows that has the same fuzzy vertex set as G. It remains only to show that for every . As the fuzzy digraph has a loop at every vertex, the fuzzy out neighbourhood contains the vertex itself. There are two cases.
Case 1: If, for all , in then, . As is symmetric therefore, in . Hence, and so for all .
Case 2: If for some , in then . As is symmetric fuzzy digraph and has loops at every vertex; therefore, . Hence, . As were taken to be arbitrary, the result holds for all hyperedges of . □
3. Applications of Fuzzy Competition Hypergraphs
In this section, we present several applications of fuzzy competition hypergraphs in food webs, business marketing and social networks.
3.1. Identifying Predator–Prey Relations in Ecosystems
We now present application of fuzzy competition hypergraphs in order to describe the interconnection of food chains between species, flow of energy and predator–prey relationship in ecosystems. The strength of competition between species represents the competition for food and common preys of species. We will discuss a method to give a description of species relationship, danger to the population growth rate of certain species, powerful animals in ecological niches and lack of food for weak animals.
Competition graphs arose in connection with an application in food webs. However, in some cases, competition hypergraphs provide a detailed description of predator–prey relations than competition graphs. In a competition hypergraph, it is assumed that vertices are defined clearly but in real-world problems, vertices are not defined precisely. As an example, species may be of different type like vegetarian, non-vegetarian, weak or strong.
Fuzzy food webs can be used to describe the combination of food chains that are interconnected by a fuzzy network of food relationship. There are many interesting variations of the notion of fuzzy competition hypergraph in ecological interpretation. For instance, two species may have a common prey (fuzzy competition hypergraph), a common enemy (fuzzy common enemy hypergraph), both common prey and common enemy (fuzzy competition common enemy hypergraph), and either a common prey or a common enemy (fuzzy niche hypergraph). We now discuss a type of fuzzy competition hypergraph in which species have common enemies known as fuzzy common enemy hypergraph.
Let be a fuzzy food web. The fuzzy common enemy hypergraph has the same vertex set as G and there is a hyperedge consisting of vertices if . The degree of membership of hyperedge is defined as
The strength of common enemies between species can be calculated using Algorithm A3. Consider the example of a fuzzy food web of 13 species giraffe, lion, vulture, rhinoceros, African skunk, fiscal shrike, grasshopper, baboon, leopard, snake, caracal, mouse and impala. The degree of membership of each species represents the species’ ability of resource defence. The degree of membership of each directed edge represents the strength to which the prey is harmful for the predator. The fuzzy food web is shown in Figure 12. The directed edge between the giraffe and the lion shows that the giraffe is eaten by the lion and similarly.
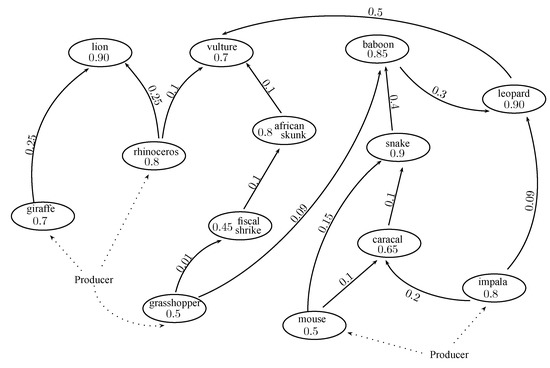
Figure 12.
Fuzzy food web.
The degree of membership of the lion is , which shows that the lion has ability of resource defence, i.e., it can defend itself against other animals as well as survive many days if the lion does not find any food. The directed edge between giraffe and lion has degree of membership , which represents that the giraffe is harmful for the lion because a giraffe can kill a lion with its long legs. This is an acyclic fuzzy digraph. The fuzzy out neighbourhoods are given in Table 7.

Table 7.
Fuzzy out neighbourhoods of vertices.
The fuzzy common-enemy hypergraph is shown in Figure 13. The hyperedges in Figure 13 show that there are common enemies between giraffe and rhinoceros, rhinoceros, African skunk and leopard, grasshopper and snake, mouse and impala, and baboon and impala. The membership value of each hyperedge represents the degree of common enemies among the species.
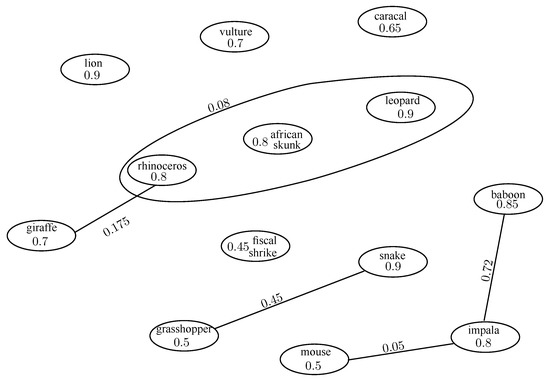
Figure 13.
Fuzzy common enemy hypergraph.
The hyperedge has a maximum degree of membership, which shows that the impala and the baboon have the largest number of common enemies, whereas the mouse and the impala have the least number of common enemies.
3.2. Identifying Competitors in the Business Market
Fuzzy competition hypergraphs are a key approach to studying the competition, profit and loss, market power and rivalry among buyers and sellers using fuzziness in hypergraphical structures. We now discuss a method to study the business competition for power and profit, success and business failure, and demanding products in market.
In the business market, there are competitive rivalries among companies that are endeavoring to increase the demand and profit of their product. More than one company in the market sells identical products. Since various companies regularly market identical products, every company wants to attract a consumer’s attention to its product. There is always a competitive situation in the business market. Hypergraph theory is a key approach to studying the competitive behavior of buyers and sellers using structures of hypergraphs. In some cases, these structures do not study the level of competition, profit and loss between the companies. As an example, companies may have different reputations in the market according to market power and rivalry. These are fuzzy concepts and motivates the necessity of fuzzy competition hypergraphs. The competition among companies can be studied using a fuzzy competition hypergraph known as fuzzy enmity hypergraph.
We present a method for calculating the strength of competition of companies in the following Algorithm 1.
| Algorithm 1: Business competition hypegraph. |
|
Consider the example of a marketing competition between seven companies DEL, CB, HW, AK, LR, RP, SONY, RA, LR, three retailers, one retailer outlet and one multinational brand as shown in Figure 14.
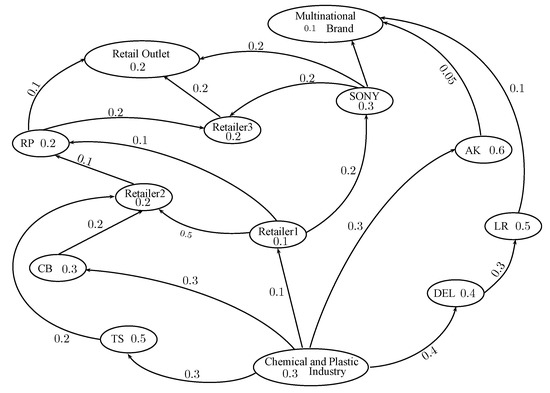
Figure 14.
Fuzzy marketing digraph.
The vertices represent companies, retailers, outlets and brands. The degree of membership of each vertex represents the strength of rivalry (aggression) of each company in the market. The degree of membership of each directed edge represents the degree of rejectability of company’s x product by company y. The strength of competition of each company can be discussed using fuzzy competition hypergraph known as fuzzy enmity hypergraph. The fuzzy out neighbouhoods are calculated in Table 8.

Table 8.
Fuzzy out neighbourhoods of companies.
The fuzzy enmity hypergraph of Figure 14 is shown in Figure 15. The degree of membership of each hyperedge shows the strength of rivalry between the companies.
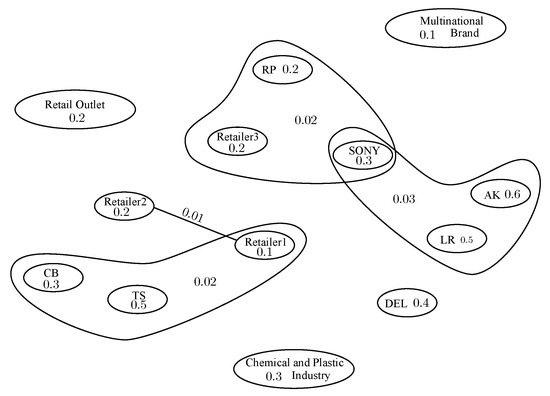
Figure 15.
Fuzzy competition hypergraph.
The strength of rivalry of each company is calculated in Table 9, which shows its enmity value within the business market. Table 9 shows that SONY is the biggest rival company among other companies.

Table 9.
Strength of rivalry between companies.
3.3. Finding Influential Communities in a Social Network
Fuzzy competition hypergraphs have a wide range of applications in decision-making problems and decision support systems based on social networking. To elaborate on the necessity of the idea discussed in this paper, we apply the notion of fuzzy competition hypergraphs to study the influence, centrality, socialism and proactiveness of human beings in any social network.
Social competition is a widespread mechanism to figure out a best-suited group economically, politically or educationally. Social competition occurs when individual’s opinions, decisions and behaviors are influenced by others. Graph theory is a conceptual framework to study and analyze the units that are intensely or frequently connected in a network. Fuzzy hypergraphs can be used to study the influence and competition between objects more precisely. The social influence and conflict between different communities can be studied using a fuzzy competition hypergraph known as fuzzy influence hypergraph.
The fuzzy influence hypergraph has the same set of vertices as and there is a hyperedge consisting of vertices if . The degree of membership of hyperedge is defined as
The strength of influence between different objects in a fuzzy influence hypergraph can be calculated by the method presented in Algorithm 2. The complexity of algorithm is .
| Algorithm 2: Fuzzy influence hypergraph. |
|
Consider a fuzzy social digraph of Florientine trading families Peruzzi, Lambertes, Bischeri, Strozzi, Guadagni, Tornabuon, Castellan, Ridolfi, Albizzi, Barbadori, Medici, Acciaiuol, Salviati, Ginori and Pazzi. The vertices in a fuzzy network represent the name of trading families. The degree of membership of each family represents the strength of centrality in that network. The directed edge indicates that the family x is influenced by y. The degree of membership of each directed edge indicates to what extent the opinions and suggestions of one family influence the other. The degree of membership of Medici is , which shows that Medici has a central position in a trading network. The degree of membership between Redolfi and Medici is , which indicates that Redolfi follows of the suggestions of Medici. The fuzzy social digraph is shown in Figure 16.
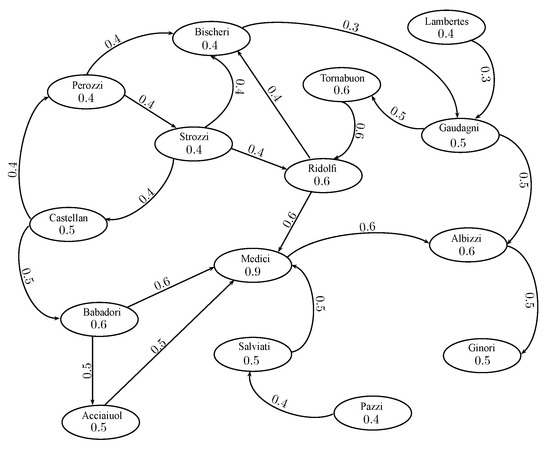
Figure 16.
Fuzzy social digraph.
To find the most influential family in this fuzzy network, we construct its fuzzy influence hypergraph. The fuzzy in neighbourhoods are given in Table 10.

Table 10.
Fuzzy in neighbourhoods of all vertices in social networks.
The fuzzy influence hypergraph is shown in Figure 17. The degree of membership of each hyperedge shows the strength of social competition between families to influence the other trading families. The strength of competition of vertices using Algorithm 2 is calculated in Table 11, where represents the strength to which each trading family influences the other families. Table 11 shows that Acciaiuol and Medici are most influential families in the network.
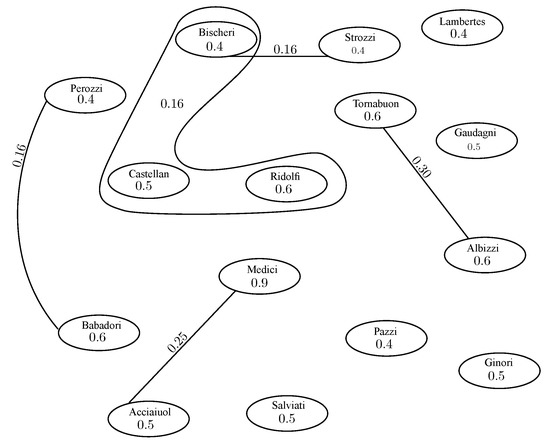
Figure 17.
Fuzzy influence hypergraph.

Table 11.
Degree of influence of vertices.
A View of Fuzzy Competition Hypergraphs in Comparison with Fuzzy Competition Graphs
The concept of fuzzy competition graphs presented in [16,17] can be utilized successfully in different domains of applications. In the existing methods, we usually consider fuzziness in pairwise competition and conflicts between objects. However, in these representations, we miss some information about whether there is a conflict or a relation among three or more objects. For example, Figure 15 shows the strong competition for profit among SONY, LR and AK. However, if we draw the fuzzy competition graph of Figure 14, we cannot discuss the group-wise conflict among companies. Sometimes, we are not only interested in pair-wise relations but also in group-wise conflicts, influence and relations. The novel notion of fuzzy competition hypergraphs are a mathematical tool to overcome this difficulty. We have presented different methods for solving decision-making problems. These methods not only generalize the existing ones but also give better results regarding uncertainty.
4. Conclusions
In this research paper, we have applied the powerful technique of fuzziness to generalize the notion of competition hypergraphs and fuzzy competition graphs. Fuzzy models give more precision, flexibility and compatibility to the system as compared to the crisp models. We have mainly discussed the construction methods of various types of fuzzy hypergraphs using open and closed neighbourhoods, strong hyperedges, kth strength of competition and symmetric properties. We have also established strong relations among fuzzy k-competition hypergraphs and underlying fuzzy graphs along with fuzzy digraphs having loops at vertices. We have applied fuzzy competition hypergraphs to real-world problems for representation of fuzziness in different domains including identification of predator–prey relations, competitions in the business market and social networks which motivate the idea introduced in this research paper. We have designed certain algorithms to solve these decision-making problems.
Author Contributions
M.S., M.A. and N.O.A. conceived and designed the experiments; M.S. and N.O.A. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Algorithm A1: Method for construction of fuzzy row hypergraph |
|

Table A1.
Adjacency matrix.
Table A1.
Adjacency matrix.
| A | … | |||
|---|---|---|---|---|
| … | ||||
| … | ||||
| ⋮ | ⋮ | ⋮ | … | ⋮ |
| ... |
| Algorithm A2: Method for construction of fuzzy column hypergraph |
|
| Algorithm A3: Construction of fuzzy competition hypergraph |
|
| Algorithm A4: Construction of fuzzy double competition hypergraph |
|
References
- Sonntag, M.; Teichert, H.M. Competition hypergraphs of digraphs with certain properties. II. Hamiltonicity. Discuss. Math. Graph Theory 2008, 28, 23–34. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Similarity relations and fuzzy orderings. Inf. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Kaufmann, A. Introduction la Thorie des Sous-Ensembles Flous Lusage des Ingnieurs (Fuzzy Sets Theory); Masson: Paris, France, 1975. [Google Scholar]
- Rosenfeld, A. Fuzzy Graphs; Fuzzy Sets and Their Applications; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Lee-kwang, H.; Lee, K.-M. Fuzzy hypergraph and fuzzy partition. IEEE Trans. Syst. Man Cybern. 1995, 25, 96–102. [Google Scholar] [CrossRef]
- Goetschel, R.H.; Craine, W.L.; Voxman, W. Fuzzy transversals of fuzzy hypergraphs. Fuzzy Sets Syst. 1996, 84, 235–254. [Google Scholar] [CrossRef]
- Goetschel, R.H. Fuzzy colorings of fuzzy hypergraphs. Fuzzy Sets Syst. 1998, 94, 185–204. [Google Scholar] [CrossRef]
- Chen, S.M. Interval-valued fuzzy hypergraph and fuzzy partition. IEEE Trans. Syst. Man Cybern. 1997, 27, 725–733. [Google Scholar] [CrossRef] [PubMed]
- Parvathi, R.; Thilagavathi, S.; Karunambigai, M.G. Intuitionistic fuzzy hypergraphs. Cybern. Inf. Technol. 2009, 9, 46–48. [Google Scholar]
- Akram, M.; Dudek, W.A. Intuitionistic fuzzy hypergraphs with applications. Inf. Sci. 2013, 218, 182–193. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A. Certain concepts of bipolar fuzzy directed hypergraphs. Mathematics 2017, 5, 17. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A. Intuitionistic single-valued neutrosophic hypergraphs. OPSEARCH 2017, 54, 799–815. [Google Scholar] [CrossRef]
- Akram, M.; Luqman, A. Bipolar neutrosophic hypergraphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 1699–1713. [Google Scholar] [CrossRef]
- Akram, M.; Shahzadi, G. Hypergraphs in m-polar fuzzy environment. Mathematics 2018, 6, 28. [Google Scholar] [CrossRef]
- Samanta, S.; Pal, M. Fuzzy k-competition and p-competition graphs. Fuzzy Inf. Eng. 2013, 2, 191–204. [Google Scholar] [CrossRef]
- Samanta, S.; Akram, M.; Pal, M. m-step fuzzy competition graphs. J. Appl. Math. Comput. 2015, 47, 461–472. [Google Scholar]
- Al-shehri, N.O.; Akram, M. Bipolar fuzzy competition graphs. Ars Comb. 2015, 121, 385–402. [Google Scholar]
- Sarwar, M.; Akram, M. Novel concepts of bipolar fuzzy competition graphs. J. Appl. Math. Comput. 2017, 54, 511–547. [Google Scholar] [CrossRef]
- Akram, M.; Nasir, M. Certain competition graphs based on intuitionistic neutrosophic environment. Information 2017, 8, 132. [Google Scholar] [CrossRef]
- Akram, M.; Siddique, S. Neutrosophic competition graphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 921–935. [Google Scholar] [CrossRef]
- Akram, M.; Sarwar, M. New applications of m-polar fuzzy competition graphs. New Math. Nat. Comput. 2018, 14, 249–276. [Google Scholar] [CrossRef]
- Berge, C. Graphs and Hypergraphs; North-Holland Publishing Company: Amsterdam, The Nertherland, 1973; Volume 7. [Google Scholar]
- Harary, F. Graph Theory; Addison-Wesley: Reading, MA, USA, 1972. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Successor and source of (fuzzy)finite state machines and (fuzzy)directed graphs. Inf. Sci. 1996, 95, 113–124. [Google Scholar] [CrossRef]
- Samanta, S.; Pal, M. Bipolar fuzzy hypergraphs. Int. J. Fuzzy Log. Syst. 2012, 2, 17–28. [Google Scholar] [CrossRef]
- Sarwar, M.; Akram, M. New applications of m-polar fuzzy matroids. Symmetry 2018, 9, 319. [Google Scholar] [CrossRef]
- Zhan, J.; Malik, H.M.; Akram, M. Novel decision-making algorithms based on intuitionistic fuzzy rough environment. Int. J. Mach. Learn. Cybern. 2018. [Google Scholar] [CrossRef]
- Radhamani, C.; Radhika, C. Isomorphism on fuzzy hypergraphs. IOSR J. Math. 2012, 2, 24–31. [Google Scholar]
- Akram, M.; Sarwar, M. Novel applications of m-polar fuzzy competition graphs in decision support system. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Bhattacharya, P. Some remarks on fuzzy graphs. Pattern Recognit. Lett. 1987, 6, 297–302. [Google Scholar] [CrossRef]
- Chen, S.M. A new approach to handling fuzzy decision-making problems. IEEE Trans. Syst. Man Cybern. 1988, 18, 1012–1016. [Google Scholar] [CrossRef]
- Cohen, J.E. Interval Graphs and Food Webs: A Finding and a Problem, Document 17696-PR; RAND Coporation: Santa Monica, CA, USA, 1968. [Google Scholar]
- Klir, G.; Yuan, B. Fuzzy Sets and Fuzzy Logic; Prentice Hall: Upper Saddle River, NJ, USA, 1995; Volume 4. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Fuzzy Graphs and Fuzzy Hypergraphs, 2nd ed.; Springer: Heidelberg/Berlin, Germany, 2001. [Google Scholar]
- Sonntag, M.; Teichert, H.M. Competition hypergraphs. Discret. Appl. Math. 2004, 143, 324–329. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).