Abstract
A new type of discrete soliton, which we call zigzag solitons, is founded in two-component discrete Rabi lattices with long-range hopping. The spontaneous symmetry breaking (SSB) of zigzag solitons is also studied. Through numerical simulation, we found that by enhancing the intensity of the long-range linearly-coupled effect or increasing the total input power, the SSB process from the symmetric soliton to the asymmetric soliton will switch from the supercritical to subcritical type. These results can help us better understand both the discrete solitons and the Rabi coupled effect.
1. Introduction
Spontaneous symmetry breaking (SSB) is a spontaneous process of symmetry breaking, by which a physical system in an asymmetric state ends up in an asymmetric state. In solid state and energy physics, SSB is a fundamental phenomenon [1,2,3,4,5]. In addition, much attention has been paid to SSB in nonlinear optics and Bose–Einstein condensates (BECs) [6,7,8,9,10,11,12,13,14,15,16,17,18,19]. SSB can occur in various optical systems, such as double-well systems [20,21,22], dual-core fibers [23] and waveguide arrays [24,25,26]. In BECs, the usual candidates can achieve SSB, such as double-well [27,28] and dual-core [29] systems. Generally, two types of SSB exist, i.e., the subcritical and supercritical types, and they are tantamount to the first and second phase transitions in thermodynamics, respectively. Phase transition is very important in physics, so how to control both SSB and the phase transition in these two types of systems has become a hot research topic in optics and BEC over the last twenty years [30,31,32,33,34,35,36,37,38,39]. In particular, the SSB of discrete solitons were studied precisely in relation to the same effect in the continuous counterpart of a discrete system [40].
In [41], we first designed single-component waveguide arrays with a long-range linearly-coupled effect and created digital solitons. On the basis of this work, we extend two-component waveguide arrays with the Rabi coupled effect, which can be emulated in various optical systems, such as dual-core waveguides [42,43,44], dual-core Bragg gratings [45] and period twisted waveguides [46]. Through numerical simulation, we found that by inducing the Rabi coupled effect in a two-component discrete system with the long-range linearly-coupled effect, a new type of discrete soliton, which we call zigzag solitons, can stably exist. The features of SSB, including the switch point from the supercritical type to the subcritical type in this system, are also studied.
The remainder of the paper is arranged as follows: in the second part, we briefly introduce the models and methods used for the stability analysis. In the third part, we study zigzag solitons and their mobility. In the fourth part, the SSB of zigzag solitons are presented in detail. Finally, the fifth part summarizes this paper.
2. Model and Methods
The model is shown in Figure 1. It consists of two rows of waveguide arrays. The long-range linearly-coupled effect, by employing the non-zero off-diagonal elements in the coupled matrix [41], exists in each row of the waveguide arrays, as shown as yellow dashed lines in Figure 1. Rabi coupled effects exist between the upper and lower rows of the waveguide arrays, as shown as red and green dashed lines in Figure 1. The red dashed lines represent the positive Rabi coupled effect, and the green dashed lines represent the negative Rabi coupled effect.
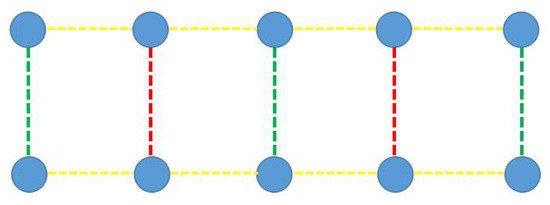
Figure 1.
Model for two-component parallel waveguide arrays. The yellow dashed lines represent the long-range linearly-coupled effect. The red and green dashed lines represent the positive and negative coupling effects, respectively. They create the Rabi coupled effect.
The model is described as follows:
where are the two-component fields, and the total power is defined as follows:
The coupled matrix elements in Equation (1) are given by:
where is the coupling strength between waveguides in the same row. In soliton dynamics, linear coupling will broaden the energy distribution, so it must be balanced by the nonlinear effect to form solitons. For simulation convenience, we set to one, where , to ensure that the system returns to the nearest-neighbor-coupled model when . d is the normalized decay length. It represents the strength of the long-range linearly-coupled effect in the waveguide arrays. If the separation between waveguides is extremely narrow, such a higher order cross-coupled effect can be induced [47].
In Equation (1), and represent the complex coupling between two-component waveguide arrays. is the strength of Rabi coupling. is the synthetic gauge phase, which is easy to implement in BEC [48,49,50,51]. In an optical system, it is difficult to realize the synthetic gauge phase. However, in [52], by introducing complex coupling, the synthetic gauge phase between the waveguides was realized in a certain sense. Inspired by this work, we introduce similar complex couplings between the upper and lower rows of waveguide arrays. For the convenience of simulation, the coupling strength value is simplified to one, and the synthetic gauge phase takes specific values of . In this way, the coupling is switched between positive and negative to create Rabi coupling. When n in Equation (1) is even, , as shown in the red dashed lines of Figure 1; in contrast, when nis odd, , as shown in the green dashed line of Figure 1.
The soliton solutions of Equation (1) can be assumed as:
where represents the stationary solution of solitons and represents the propagation constant. A vector composed of and is defined as follows:
Substituting Equation (5) into Equation (1), a matrix equation can be obtained as follows:
where . Here, C represents the long-range linearly-coupled effect between the waveguides in each component, and I is the diagonal matrix, in which the diagonal element , and I represents the Rabi coupled effect between two components of waveguide arrays. The stability of the stationary mode for Equation (6) can be numerically identified by computing the eigenvalues for small perturbations and by direct simulations. The perturbed solution is given as . Substituting this solution into Equation (6) with linearization leads to the eigenvalue problem:
The solution is stable if all the eigenvalues of perturbation are real.
3. Discrete Zigzag Solitons and Their Mobility
In this part, the imaginary time propagation (ITP) method [53] is used to study the fundamental solution of . It is also worth noting that we fix and set as two controllable parameters of Equation (1) for convenience in the numerical simulations.
Through numerical simulation, a new type of soliton is found that we call zigzag solitons. Figure 2a shows typical zigzag solitons in this system, which looks like sawteeth. This means that the optical energy appears to hop up and down in the waveguide arrays, which has never been observed in other optical soliton systems. This occurs because the Rabi coupled effect between two components of waveguide arrays, and in Equation (1), changes the distributions of the optical energy and forms sawteeth-type zigzag solitons.
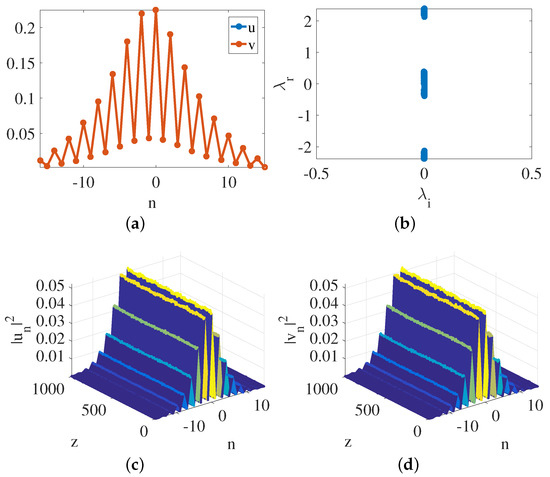
Figure 2.
. (a) Symmetric sawteeth-type zigzag solitons. (b) Eigenvalues of of the solitons, showing that the solitons are stable. (c,d) Real-time evolution of the soliton solutions with and , respectively, showing that the solitons are stable. In the model, the total number of waveguides in each component is fixed at 32.
The numerical simulation also shows that these sawteeth-type zigzag solitons are symmetric and stable, as shown by the eigenvalues of the system in Figure 2b and the real-time evolution of the soliton solution with and in Figure 2c,d.
Stable asymmetric fundamental zigzag solitons can also exist in the system. Typical examples are shown in Figure 3, and unstable zigzag solitons are shown in Figure 4. These new zigzag solitons are caused by the Rabi coupled effect and have not previously been reported.
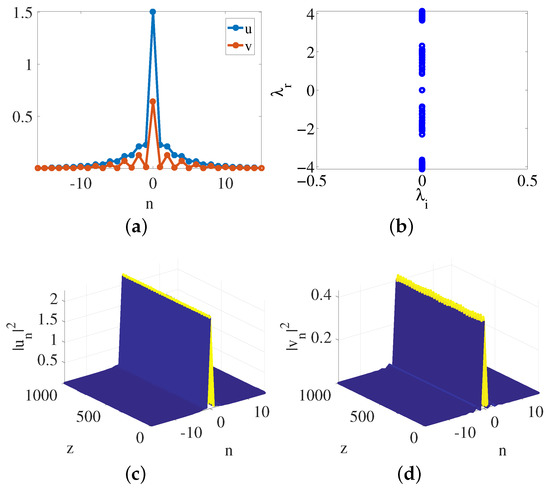
Figure 3.
. (a) Asymmetric zigzag solitons. (b) Eigenvalues of of the solitons, showing that the solitons are stable. (c,d) Real-time evolution of the soliton solutions with and , respectively, showing that the solitons are stable. In the model, the total number of waveguides in each component is fixed at 32.
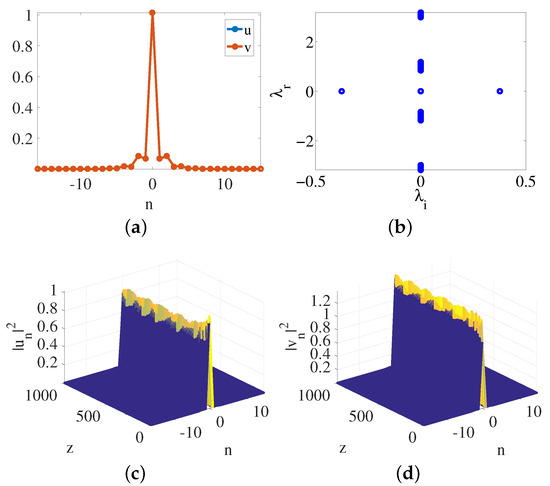
Figure 4.
. (a) Unstable symmetric zigzag solitons. (b) Eigenvalues of of the solitons, showing that the solitons are unstable. (c,d) Real-time evolution of the soliton solutions of and , respectively, showing that the solitons are unstable. The total number of waveguides in each component is 32.
At the end of this section, the mobility of the zigzag solitons is shown. After introducing kicking into the solution, , direct evolution is conducted to test the mobility. The kicking strength is . Figure 5 shows the mobility of sawteeth-type zigzag solitons, which implies that the zigzag solitons have potential use in all-optical network routers.
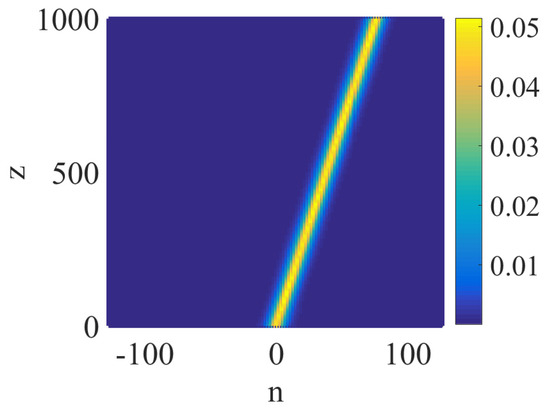
Figure 5.
Mobility of the symmetric sawteeth-type zigzag solitons. , and the kicking strength is . The total number of waveguides in each component is 256.
4. SSB of Zigzag Solitons
In this section, we study the SSB of zigzag solitons. A characteristic parameter, the asymmetry parameter (ASP), is defined to study the transition from symmetric to asymmetric solitons, as follows:
In Equation (8), represents and means that the two-component solutions are the same; we define them as symmetric solitons. On the contrary, represents , which means that the two-component solutions are different; we define them as asymmetric solitons. In statistical physics, parameter Equation (8) is called the order parameter. Through numerical simulations, we found that increasing the total power P or decreasing the decay length d can modulate SSB. Figure 6 shows typical examples of two types of SSB versus P and d.
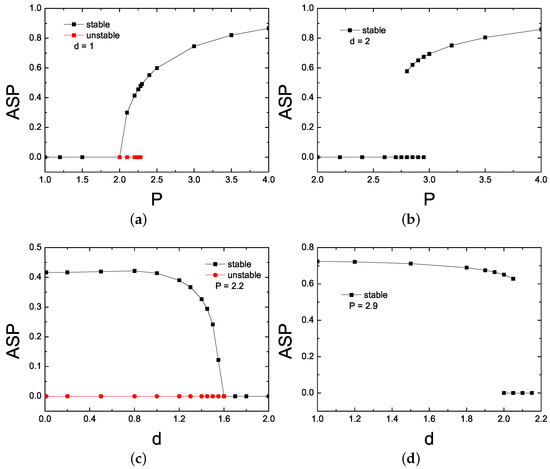
Figure 6.
Two types of spontaneous symmetry breaking (SSB), showing by asymmetry parameter (ASP). (a) Supercritical type, ASP vs. P, with d set at one. (b) Subcritical type, ASP vs. P, with d set at two. (c) Supercritical type, ASP vs. d, with P set at 2.2. (d) Subcritical type, ASP vs. d, with P set at 2.9. The solid black curves indicate the stable soliton solutions, and the red lines indicate the unstable soliton solutions.
In Figure 7, we show the stable regions of symmetric and asymmetric solitons and bistable regions on the plane. Generally, there exist two types of SSB, subcritical type and supercritical type, which are tantamount to the first and second kinds of phase transition in thermodynamics, respectively. The former one, i.e., subcritical type (discontinuity and existence mixed phase), features branches of the asymmetric states first going backward after the bifurcation point and then turning forward; the latter one, the supercritical type (continuous), features asymmetric branches going immediately forward after the bifurcation point.
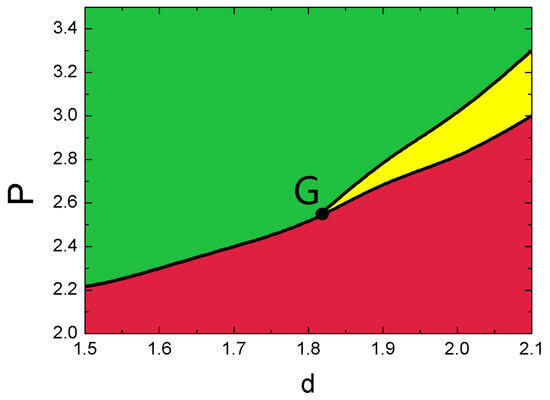
Figure 7.
Stable regions of symmetric solitons (red) and asymmetric solitons (green) and their bistable regions (yellow).
In this model, SSB switches from supercritical type to the subcritical type in the region or . is called the G point and is where the transition between the two types of SSBs occurs. In fact, the SSBs that occur in our system are always for solitons with finite widths, and the SSBs disappear as the total power of the soliton trends to zero. Our numerical simulations show that the symmetry transition becomes sharper when the control parameter is close to the G point. Figure 7 clearly shows that the long-range linearly-coupled effect can switch the SSB transition from supercritical type to the subcritical type by increasing the strength of long-range linearly-coupled effect d or increasing the total power P. In fact, the oscillatory nature (zigzag) does play a role in SSB. The G point indicates when the SSB switches from the supercritical type to the subcritical type in the () plane, which occurs at a large value of d. Without this oscillatory nature, the G point occurs at a small value of d [54]. This occurs because the subcritical type of SSB tends to be produced with wider solitons. The waveguides that induce SSB rely mainly on the value of in the Rabi coupling lattices in Equation (1). This Rabi coupling creates the oscillatory nature of zigzag solitons, which are much wider than non-oscillatory solitons. On the other hand, the larger d is, the stronger the long-range linearly-coupled effect between waveguides is, which contributes to wider solitons. Under the combination of these two effects (vertical Rabi coupling and the horizontal long-range linearly-coupled effect), the G point is changed in the () plane.
At the end of this part, we show a typical example of the relationship with supercritical and subcritical SSBs in Figure 8. The relationship satisfies the Vakhitov–Kolokolov (VK) criterion [55]. In 1973, Vakhitov and Kolokolov used a linear approximation with perturbation to find the stability criterion for the principal mode of the nonlinear wave equation. This criterion is called the Vakhitov–Kolokolov (VK) criterion, and it is a necessary stability condition of solitons. In the system of self-focusing nonlinearity, as in the proposed model, the VK criterion is expressed as [56].
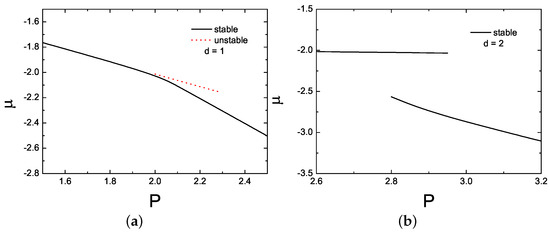
Figure 8.
relationship of two types of SSB. (a) Supercritical type with d set at one. (b) Subcritical types with d set at two. The solid black curves indicate stable soliton solutions, and the red dotted lines indicate unstable soliton solutions.
5. Conclusions
In this work, we studied the Rabi coupled effect in two-component optical waveguide arrays with the long-range linearly-coupled effect. In addition, the stability of solitons and their SSB was studied. Based on numerical simulation, we found that a new type of stable zigzag solitons can exist in this system. By increasing the strength of the long-range linearly-coupled effect d or increasing the total power P, SSB can switch from the supercritical type to the subcritical type. These results help fill the blanks in the general picture of SSBs with the Rabi coupled effect and the long-range coupled effect. Finally, the new type of zigzag solitons may provide the abilities of signal data processing and could be used in fabricating new types of digital optical devices.
Author Contributions
The authors contributed equally to this work.
Funding
This research was funded by the PhD Start-up Fund of the Natural Science Foundation of Guangdong Province of China grant number 2017A030310354, the Natural Science Foundation of Guangdong Province grant number 2017A030313025 and the National Natural Science Foundation of China grant numbers 61571197, 11575063, 61172011 and 11705155.
Acknowledgments
Zhijie Mai acknowledges Yongyao Li for the useful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Susskind, L. Dynamics of spontaneous symmetry breaking in the weinberg-salam theory. Phys. Rev. D 1979, 20, 2619–2625. [Google Scholar] [CrossRef]
- Weinberg, E.J. Radiative corrections as the origin of spontaneous symmetry breaking. Phys. Rev. D 1973, 7, 1888–1910. [Google Scholar]
- Cornwall, J.M.; Norton, R.E. Spontaneous symmetry breaking without scalar mesons. Phys. Rev. D 1974, 8, 3338–3346. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B.; Scherk, J.; Ferrara, S.; Girardello, L.; Nieuwenhuizen, P.V. Spontaneous symmetry breaking and higgs effect in supergravity without cosmological constant. Nucl. Phys. 1979, 147, 105–131. [Google Scholar] [CrossRef]
- O’Raifeartaigh, L. Spontaneous symmetry breaking for chirals scalar superfields. Nucl. Phys. 1975, 96, 331–352. [Google Scholar] [CrossRef]
- Paré, C.; Florjanczyk, M. Approximate model of soliton dynamics in all-optical couplers. Phys. Rev. A 1990, 41, 6287–6295. [Google Scholar] [CrossRef] [PubMed]
- Snyder, A.W.; Mitchell, D.J.; Poladian, L.; Rowland, D.R.; Chen, Y. Physics of nonlinear fiber couplers. J. Opt. Soc. Am. B 1991, 8, 2102–2118. [Google Scholar] [CrossRef]
- Chu, P.L.; Malomed, B.A.; Peng, G.D. Soliton switching and propagation in nonlinear fiber couplers: Analytical results. J. Opt. Soc. Am. B 1993, 10, 1379–1385. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A. Novel soliton states and bifurcation phenomena in nonlinear fiber couplers. Phys. Rev. Lett. 1993, 70, 2395–2398. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A.; Skinner, I.M.; Chu, P.L.; Peng, G.D. Symmetric and asymmetric solitons in twin-core nonlinear optical fibers. Phys. Rev. E 1996, 53, 4084–4091. [Google Scholar] [CrossRef]
- Kevrekidis, P.G.; Chen, Z.; Malomed, B.A.; Frantzeskakis, D.J.; Weinstein, M.I. Spontaneous symmetry breaking in photonic lattices: Theory and experiment. Phys. Lett. A 2005, 340, 275–280. [Google Scholar] [CrossRef]
- Ng, H.T.; Leung, P.T. Two-mode entanglement in two-component Bose-Einstein condensates. Phys. Rev. A 2005, 71, 351–367. [Google Scholar] [CrossRef]
- Matuszewski, M.; Malomed, B.A.; Trippenbach, M. Spontaneous symmetry breaking of solitons trapped in a double-channel potential. Phys. Rev. A 2007, 75, 063621. [Google Scholar] [CrossRef]
- Dounas-Frazer, D.R.; Hermundstad, A.M.; Carr, L.D. Ultracold bosons in a tilted multilevel double-well potential. Phys. Rev. Lett. 2007, 99, 200402. [Google Scholar] [CrossRef] [PubMed]
- Trippenbach, M.; Infeld, E.; Gocaek, J.; Matuszewski, M.; Oberthaler, M.; Malomed, B.A. Spontaneous symmetry breaking of gap solitons and phase transitions in double-well traps. Phys. Rev. A 2008, 78, 013603. [Google Scholar] [CrossRef]
- Satija, I.I.; Balakrishnan, R.; Naudus, P.; Heward, J.; Edwards, M.; Clark, C.W. Symmetry-breaking and symmetry-restoring dynamics of a mixture of Bose-Einstein condensates in a double well. Phys. Rev. A 2009, 79, 033616. [Google Scholar] [CrossRef]
- Qi, R.; Yu, X.-L.; Li, Z.B.; Liu, W.M. Non-Abelian Josephson effect between two F = 2 spinor Bose-Einstein condensates in double optical traps. Phys. Rev. Lett. 2009, 102, 185301. [Google Scholar] [CrossRef] [PubMed]
- Salasnich, L.; Malomed, B.A.; Toigo, F. Competition between symmetry breaking and onset of collapse in weakly coupled atomic condensates. Phys. Rev. A 2010, 81, 045603. [Google Scholar] [CrossRef]
- Mazzarella, G.; Malomed, B.A.; Salasnich, L.; Salerno, M.; Toigo, F. Rabi-Josephson oscillations and self-trapped dynamics in atomic junctions with two bosonic species. J. Phys. B 2011, 44, 035301. [Google Scholar] [CrossRef]
- Wang, C.; Kevrekidis, P.G.; Whitaker, N.; Malomed, B.A. Two-component nonlinear Schrödinger models with a double-well potential. Phys. D 2008, 237, 2922–2932. [Google Scholar] [CrossRef]
- Li, Y.; Pang, W.; Fu, S.; Malomed, B.A. Nonlinear modes and symmetry breaking in rotating double-well potentials. Phys. Rev. A 2012, 85, 053821. [Google Scholar] [CrossRef]
- Chen, G.; Luo, Z.; Wu, J.; Wu, M. Switch between the types of the symmetry breaking bifurcation in optically induced photorefractive rotational double-well potential. J. Phys. Soc. Jpn. 2013, 82, 034401. [Google Scholar] [CrossRef]
- Albuch, L.; Malomed, B.A. Transitions between symmetric and asymmetric solitons in dual-core systems with cubic-quintic nonlinearity. Math. Comput. Simul. 2007, 74, 312–322. [Google Scholar] [CrossRef]
- Mak, W.C.K.; Malomed, B.A.; Chu, P.L. Solitons in coupled waveguides with quadratic nonlinearity. Phys. Rev. E 1997, 55, 6134. [Google Scholar] [CrossRef]
- Mak, W.C.K.; Malomed, B.A.; Chu, P.L. Asymmetric solitons in coupled second-harmonic-generating waveguides. Phys. Rev. E 1998, 57, 1092. [Google Scholar] [CrossRef]
- Driben, R.; Malomed, B.A.; Chu, P.L. All-optical switching in a two-channel waveguide with cubic-quintic nonlinearity. J. Phys. B 2006, 39, 2455. [Google Scholar] [CrossRef]
- Gubeskys, A.; Malomed, B.A. Symmetric and asymmetric solitons in linearly coupled Bose-Einstein condensates trapped in optical lattices. Phys. Rev. A 2007, 75, 063602. [Google Scholar] [CrossRef]
- Gubeskys, A.; Malomed, B.A. Spontaneous soliton symmetry breaking in two-dimensional coupled Bose-Einstein condensates supported by optical lattices. Phys. Rev. A 2007, 76, 043623. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Pang, W.; Malomed, B.A. Symmetry breaking in dipolar matter-wave solitons in dual-core couplers. Phys. Rev. A 2013, 87, 013604. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, R. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Raghavan, S.; Smerzi, A.; Fantoni, S.; Shenoy, S.R. Coherent oscillations between two weakly coupled Bose-Einstein condensates: Josephson effects, π oscillations, and macroscopic quantum self-trapping. Phys. Rev. A 1999, 59, 69–82. [Google Scholar] [CrossRef]
- Mazzarella, G.; Moratti, M.; Salasnich, L.; Salerno, M.; Toigo, F. Atomic Josephson junction with two bosonic species. J. Phys. B 2009, 42, 125301. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Malomed, B.A. Spontaneous symmetry breaking in Schrödinger lattices with two nonlinear sites. Phys. Rev. A 2011, 83, 053844. [Google Scholar] [CrossRef]
- Pang, W.; Guo, H.; Chen, G.; Mai, Z. Symmetry breaking bifurcation of two-component soliton modes in an inverted nonlinear random lattice. J. Phys. Soc. Jpn. 2014, 83, 034402. [Google Scholar] [CrossRef]
- Luo, Z.; Li, Y.; Pang, W.; Liu, Y.; Wang, X. Dipolar matter-wave soliton in one-dimensional optical lattice with tunable local and nonlocal nonlinearities. J. Phys. Soc. Jpn. 2013, 82, 124401. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Z.; Liu, J.; Li, Y. Fundamental modes in a waveguide pipe twisted by inverted nonlinear double-well potential. Laser Phys. 2014, 24, 045403. [Google Scholar] [CrossRef]
- Fan, Z.; Shi, Y.; Liu, Y.; Pang, W.; Li, Y.; Malomed, B.A. Cross-symmetric dipolar-matter-wave solitons in double-well chains. Phys. Rev. E 2017, 95, 032226. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Guan, Y.; Li, H.; Luo, Z.; Mai, Z. Nonlinear defect localized modes and composite gray and anti-gray solitons in one-dimensional waveguide arrays with dual-flip defects. Opt. Commum. 2017, 397, 105–111. [Google Scholar] [CrossRef]
- Brazhnyi, V.A.; Malomed, B.A. Localized modes in two-dimensional schrödinger lattices with a pair of nonlinear sites. Opt. Commum. 2014, 324, 277–285. [Google Scholar] [CrossRef]
- Herring, G.; Kevrekidis, P.G.; Malomed, B.A.; Carreterogonzalez, R.; Frantzeskakis, D.J. Symmetry breaking in linearly coupled dynamical lattices. Phys. Rev. E 2007, 76, 066606. [Google Scholar] [CrossRef] [PubMed]
- Mai, Z.; Fu, S.; Wu, J.; Li, Y. Discrete solitons in waveguide arrays with long-range linearly coupled effect. J. Phys. Soc. Jpn. 2014, 83, 034404. [Google Scholar] [CrossRef]
- Snyder, A.W.; Mitchell, D.J.; Poladian, L.; Rowland, D.R.; Chen, Y. Linear approach for approximating spatial solitons and nonlinear guided modes. J. Opt. Soc. Am. B 1991, 8, 1618–1620. [Google Scholar] [CrossRef]
- Romangoli, M.; Trillo, S.; Wabnitz, S. Soliton switching in nonlinear couplers. Opt. Quantum. Electron. 1992, 24, S1237–S1267. [Google Scholar]
- Huang, W.-P. Coupled-mode theory for optical waveguides: An overview. J. Opt. Soc. Am. A 1994, 11, 963–983. [Google Scholar] [CrossRef]
- Mak, W.C.K.; Malomed, B.A.; Chu, P.L. Solitary waves in coupled nonlinear waveguides with Bragg gratings. J. Opt. Soc. Am. B 1998, 15, 1685–1692. [Google Scholar] [CrossRef]
- Chen, Z.; Malomed, B.A. Gap solitons in Rabi lattices. Phys. Rev. E 2017, 95, 032217. [Google Scholar] [CrossRef] [PubMed]
- Gordon, R. Harmonic oscillation in a spatially finite array waveguide. Opt. Lett. 2004, 29, 2752–2754. [Google Scholar] [CrossRef] [PubMed]
- Mancini, M.; Pagano, G.; Cappellini, G.; Livi, L.; Rider, M.; Catani, J.; Sias, C.; Zoller, P.; Inguscio, M.; Dalmonte, M.; Fallani, L. Observation of chiral edge states with neutral fermions in synthetic hall ribbons. Science 2015, 349, 1510–1513. [Google Scholar] [CrossRef] [PubMed]
- Stuhl, B.K.; Lu, H.I.; Aycock, L.M.; Genkina, D.; Spielman, I.B. Visualizing edge states with an atomic bose gas in the quantum hall regime. Science 2015, 349, 1514–1518. [Google Scholar] [CrossRef] [PubMed]
- Celi, A.; Tarruell, L. Physics probing the edge with cold atoms. Science 2015, 349, 1450–1451. [Google Scholar] [CrossRef] [PubMed]
- Cheon, S.; Kim, T.H.; Lee, S.H.; Yeom, H.W. Chiral solitons in a coupled double peierls chain. Science 2015, 350, 182–185. [Google Scholar] [CrossRef] [PubMed]
- Golshani, M.; Weimann, S.; Jafari, K.; Nezhad, M.K.; Langari, A.; Bahrampour, A.; Eichelkraut, T.; Mahdavi, S.M.; Szameit, A. Impact of loss on the wave dynamics in photonic waveguide lattices. Phys. Rev. Lett. 2014, 113, 123903. [Google Scholar] [CrossRef] [PubMed]
- Chiofalo, M.L.; Succi, S.; Tosi, M.P. Ground state of trapped interacting bose-einstein condensates by an explicit imaginary-time algorithm. Phys. Rev. E 2000, 62, 7438. [Google Scholar] [CrossRef]
- Mai, Z.; Pang, W.; Wu, J.; Li, Y. Symmetry breaking of discrete solitons in two-component waveguide arrays with long-range linearly coupled effect. J. Phys. Soc. Jpn. 2015, 84, 014401. [Google Scholar] [CrossRef]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potentials. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).