Schützenberger Symmetries in Network Structures

Abstract

It is known that the set of all networks of fixed order form a semigroup. This fact provides for the Green’s $\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ and $\mathit{𝓓}$ equivalence classifications of all such networks. These classifications reveal certain structural invariants common to all networks within a Green’s equivalence class and enables the computation of the associated invariant preserving symmetries that transform a network into another network within a Green’s equivalence class. Here, the notion of Schützenberger symmetries in network structures is introduced. These are computable symmetries which transform any network within an $\mathit{𝓗}$-equivalence class into another network within that class in a manner that preserves the associated structural invariants. Useful applications of Schützenberger symmetries include enabling the classification and analysis of biological network data, identifying important relationships in social networks, and understanding the consequences of link reconfiguration in communication and sensor networks.

1. Introduction

Symmetry is a principle which has served as a guide for the spectacular advances that have been made in modern science. In general, a symmetry associated with a “situation” is defined as an “immunity to change” for some aspect of the “situation” [1]. As discussed in [1], in order for a “situation” to have a symmetry: (a) the aspect of the “situation” remains unchanged (i.e., invariant) when a change (e.g., a transformation) is performed; and (b) it must be possible to perform the change, although the change does not actually have to be performed. For example—in physics—any mathematical expression describing a physical system, whether subatomic or macroscopic, must be invariant under space and time translations.

Group theory is the traditional mathematical language used to describe symmetry and its associated invariant properties (recall that an abstract group is a set $S$ of elements together with a law of composition “$\circ$” such that for $x,y,z\in S$: (i) $x\circ y\in S$; (ii) $x\circ \left(y\circ z\right)=\left(x\circ y\right)\circ z$; (iii) there is an identity element $e\in S$ such that $x\circ e=e\circ x=x$; and (iv) for $x\in S$ there is an inverse $x^{-1}\in S$ such that $x\circ x^{-1}=x^{-1}\circ x=e$). As a simple example, the set $S$ of 0°, 90°, 180° and 270° rotations in the plane of a square about its fixed center under “composition of rotations” forms a symmetry group for the square (0° is the identity element and the inverse of an $X^{\circ }\in S$ rotation is a ${360}^{\circ }-X^{\circ }$ rotation). Each of these rotations is a symmetry which brings the square into coincidence with itself, i.e., they preserve the invariant shape of the square.

In recent years the concepts of generalized symmetry and Green’s symmetry have been introduced in the context of symmetries of graphs and digraphs [2,3,4] and have been used to discuss properties that remain invariant during the evolution of networks [5]. These symmetries of an object are based upon a semigroup description of the object and require the application of Green’s $\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ and $\mathit{𝓓}$ equivalence relations to the object’s semigroup description. In the case of (abstract) networks, the application of Green’s symmetry principles identifies structural invariants common to all networks within a Green’s equivalence class. These are necessarily invariants for network evolutions occurring within a Green’s equivalence class—i.e., Green’s evolutions. Green’s symmetry principles also provide a method for computing the transformations—or symmetries—that produce network evolutions which preserve these invariants (as discussed in [5], analysis of these transformations can provide insight into aspects of the internal structural dynamics of the network’s evolution).

The purpose of this paper is to extend the notions of Green’s $\mathit{𝓛}$ and $\mathit{𝓡}$ symmetries and evolutions in network structures [5] to include Schützenberger symmetries and evolutions. In this context, Schützenberger symmetries are network symmetries associated with fixed order networks contained within a Green’s $\mathit{𝓗}$-equivalence class that preserve certain structural properties common to all networks in that equivalence class. As will be discussed and shown below, there are computable sets of right and sets of left Schützenberger symmetries associated with each Green’s $\mathit{𝓗}$-equivalence class such that: (a) each right (left) symmetry transforms by right (left) multiplication any network within an $\mathit{𝓗}$-class into another network within that class; (b) the $\mathit{𝓗}$-class evolutions defined by these symmetries preserve the associated structural invariants; (c) these symmetries contain information about how the invariant preserving changes in network structure occur during the evolution [5]; and (d) these sets of right and left Schützenberger symmetries are monoids (semigroups with an identity element) which have permutation group representations—i.e., the right and left Schützenberger symmetry groups—which permute the networks within an $\mathit{𝓗}$-class and preserve the associated invariants. These groups and symmetries have the properties that for any two $\mathit{𝓗}$-equivalence classes in the same: (i) Green’s $\mathit{𝓓}$-equivalence class, the associated right Schützenberger symmetry groups are isomorphic to one another; and (ii) Green’s $\mathit{𝓛}$-equivalence class, the sets of right and left Schützenberger symmetries are the same.

In order to make this paper reasonably self-contained, the relevant definitions and terminology from semigroup theory are summarized in the next section (for additional depth and clarification the reader is invited to consult such standard references as [6,7]). The semigroup of networks $N_V$ on a fixed set $V$ of nodes is defined in Section 3. Green’s equivalence classifications of $N_V$ and the associated invariant properties are reviewed in Section 4 (for the sake of brevity, the proofs of lemmas and theorems in Section 3 and Section 4 are omitted, but can be found in [4,5]). Schützenberger network symmetries and symmetry groups are introduced in Section 5 and aspects of the theory are illustrated using simple examples in Section 6 and Section 7. Concluding remarks comprise the final section of this paper.

2. Semigroups

A semigroup $S\equiv \left(S,\circ \right)$ is a set S and an associative binary operation “$\circ$” called multiplication defined upon the set (contrast this with the above definition of a group and note that a group is a semigroup endowed with the additional special properties given by items (iii) and (iv)). The right (left) multiplication of $x\in S$ by $y\in S$ is the product $x\circ y\in S\left(y\circ x\in S\right)$. An element $e\in S$ is an identity if $x\circ e=e\circ x=x$ for $x\in S$. An identity can be adjoined to S by setting $S^1=S{\displaystyle \cup }\left\{e\right\}$ and defining $x\circ e=e\circ x=x$ for $x\in S^1$. A semigroup which has an identity is a monoid. If $x\circ x=x$ for $x\in S^1$, then x is an idempotent. Semigroups $S\equiv \left(S,\circ \right)$ and $T\equiv \left(T,*\right)$ are isomorphic (denoted $S\approx T$) when there is a bijective map $\theta :S\to T$ such that $\theta \left(x\circ y\right)=\theta \left(x\right)*\theta \left(y\right)$ for all $x,y\in S$. They are anti-isomorphic if $\theta \left(x\circ y\right)=\theta \left(y\right)*\theta \left(x\right)$ for all $x,y\in S$. Hereafter, the juxtaposition $xy$ will also be used for the multiplication $x\circ y$.

The well-known $\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ and $\mathit{𝓓}$ Green’s equivalence relations on a semigroup $S$ partition $S$ into a highly organized “egg box” structure using relatively simple algebraic properties. In particular, the equivalence relation $\mathit{𝓛}\left(\mathit{𝓡}\right)$ on $S$ is defined by the rule that $x\mathit{𝓛}y\left(x\mathit{𝓡}y\right)$ if and only if $S^{1}x=S^{1}y\left(x{S}^1=y{S}^1\right)$ for $x,y\in S$ and the equivalence relation $\mathit{𝓗}=\mathit{𝓛}{\displaystyle \cap }\mathit{𝓡}$ is similarly defined so that $x\mathit{𝓗}y$ if and only if $x\mathit{𝓛}y$ and $x\mathit{𝓡}y$. The relations $\mathit{𝓛}$ and $\mathit{𝓡}$ commute under the composition “$•$” of binary relations and $\mathit{𝓓}\equiv \mathit{𝓛}•\mathit{𝓡}=\mathit{𝓡}•\mathit{𝓛}$ is the smallest equivalence relation containing $\mathit{𝓛}$ and $\mathit{𝓡}$.

For $x\in S$ and $X\in \left\{\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},\mathit{𝓓}\right\}$ denote the $X$ class containing $x$ by $\mathrm{X}\left(x\right)$, where $\mathrm{X}=\mathrm{L},\mathrm{R},\mathrm{H},$ or $\mathrm{D}$ when $X=\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ or $\mathit{𝓓}$, respectively. Thus, $x\mathrm{X}y$ if and only if $\mathrm{X}\left(x\right)=\mathrm{X}\left(y\right)$. If $x,y\in S$ and $\mathrm{R}\left(x\right)=\mathrm{R}\left(y\right)\left(\mathrm{L}\left(x\right)=\mathrm{L}\left(y\right)\right)$, then there exist elements $s\left(t\right)$ in $S^1$ such that $xs=y\left(tx=y\right)$. Since $\mathit{𝓗}=\mathit{𝓛}{\displaystyle \cap }\mathit{𝓡}$, then it is necessarily the case that when $\mathrm{H}\left(x\right)=\mathrm{H}\left(y\right)$ there exist elements $s$ and $t$ in $S^1$ such that $xs=y$ and $tx=y$, respectively.

3. The Semigroup ${\mathit{N}}_{\mathit{V}}$

The semigroup $B_n$ of Boolean matrices is the set of all $n\times n$ matrices over $\left\{0,1\right\}$ with Boolean composition $\gamma =\alpha \circ \beta$ defined by:

$${\gamma }_{ij}={\vee }_{k\in J}\left({\alpha }_{ik}\wedge {\beta }_{kj}\right)$$

as the semigroup multiplication operation. Here $J=\left\{1,2,\cdots ,n\right\}$, $\wedge$ denotes Boolean multiplication (i.e., $0\wedge 0=0\wedge 1=1\wedge 0=0$, $1\wedge 1=1$), and $\vee$ denotes Boolean addition (i.e., $0\vee 0=0$, $0\vee 1=1\vee 0=1\vee 1=1$). Note that because there exists an $e\in B_n$ such that $e{B}_n=B_n=B_{n}e$, then $B_n$ is a monoid.

The rows (columns) of any $\alpha \in B_n$ are Boolean row (column) $n$—vectors, i.e., row (column) $n$—tuples over $\left\{0,1\right\}$, and come from the set $V_n\left(W_n\right)$ of all Boolean row (column) $n$—vectors. These vectors can be added coordinate-wise using Boolean addition. If $u,v\in V_n\left(W_n\right)$, then $u⊑v$ when the ith coordinate $u_i=1$ implies the ith coordinate $v_i=1$, $1\le i\le n$ (⊑ is a partial order).

Let $\mathbf{0}\left(\mathbf{1}\right)$ be either the zero (unit) row or zero (unit) column vector (the context in which $\mathbf{0}\left(\mathbf{1}\right)$ is used defines whether it is a row or column vector). The matrix with $\mathbf{0}$ in every row—i.e., the zero matrix—is denoted by “□” and the matrix with $\mathbf{1}$ in every row is denoted by “ω”. For $\alpha \in B_n$, the row space $\Gamma \left(\alpha \right)$ of $\alpha$ is the subset of $V_n$ consisting of $\mathbf{0}$ and all possible Boolean sums of (one or more) nonzero rows of α. $\Gamma \left(\alpha \right)$ is a lattice $(\Gamma \left(\alpha \right),⊑)$ under the partial order ⊑. The row (column) basis $r\left(\alpha \right)$ $\left(c\left(\alpha \right)\right)$ of α is the set of all row (column) vectors in $\alpha$ that are not Boolean sums of other row (column) vectors in α. Note that each vector in $r\left(\alpha \right)$ $\left(c\left(\alpha \right)\right)$ must be a row (column) vector of α. The vector $\mathbf{0}$ is never a basis vector and the empty set $\varnothing$ is the basis for the □ matrix [8,9].

The semigroup $B_X$ of binary relations on a set $X$ of cardinality $n$ (denoted $\left|X\right|=n$) is the power set of $X\times X$ with multiplication $a=bc$ being the “composition of binary relations” defined by:

$$a=\left\{\left(x,y\right)\in X\times X:\left(x,z\right)\in b,\left(z,y\right)\in c,\mathrm{when}z\in X\right\}.$$

It is easy to see that a bijective index map $f:X\to J$ induces an isomorphism $\lambda :B_X\to B_n$ defined by $\lambda \left(a\right)=\alpha$, where $a_{ij}=1$ if $\left(f^{-1}\left(i\right),f^{-1}\left(j\right)\right)\in a$ and is $0$ if $\left(f^{-1}\left(i\right),f^{-1}\left(j\right)\right)\notin a$. $B_n$ is therefore the Boolean matrix representation of $B_X$ [10].

A network $E$ of order $n$ is the pair $E=\left(V,C\right)$, where $V$ is a nonempty set of nodes with $\left|V\right|=n$, and the binary relation $C\subseteq V\times V$ is the set of directed links connecting the nodes of the network. Thus, $E$ is both a digraph and a binary relation. If $\left(x,y\right)\in C$, then node $x\left(y\right)$ is an in(out)-neighbor of node $y\left(x\right)$. The in-neighborhood of $x\in V$ is the set $I\left(E;x\right)$ of all in-neighbors of $x$ and the out-neighborhood of $x\in V$ is the set $O\left(E;x\right)$ of all out-neighbors of $x$.

Let $N_V$ be the set of networks on $V$ and define “multiplication of networks” $E,F\in N_V$ by $EF=G\equiv \left(V,C^{\#}\right)$, where $E=\left(V,C\right)$, $F=\left(V,C^{\prime }\right)$, and:

$$C^{\#}=\left\{\left(x,y\right)\in V\times V:\left(x,z\right)\in C,\left(z,y\right)\in C^{\prime },\mathrm{when}z\in V\right\}.$$

Lemma 1.

$N_V$is a semigroup that is isomorphic to$B_V$.

Lemma 2.

If$\left|V\right|=n$, then$N_V\approx B_n$.

Thus, $N_V$ is a monoid and $B_n$ is a Boolean matrix representation of $N_V$.

4. Green’s Equivalence Classifications of ${\mathit{N}}_{\mathit{V}}$ and Associated Invariants

Let $\theta :N_V\to B_n$ be the isomorphism of Lemma 2 and $f:V\to J$ be an associated index bijection. If ${\alpha }_{i*}$ is the ith Boolean row vector and ${\alpha }_{*j}$ is the jth Boolean column vector in the matrix $\alpha =\theta \left(E\right)$ corresponding to network $E$, then ${\alpha }_{i*}$ encodes the out-neighbors of node $f^{-1}\left(i\right)$ in $E$ as the set:

$$O\left(E;f^{-1}\left(i\right)\right)=\left\{f^{-1}\left(k\right):{\alpha }_{ik}=1,k\in J\right\}$$

and ${\alpha }_{*j}$ encodes the in-neighbors of node $f^{-1}\left(j\right)$ in $E$ as the set:

$$I\left(E;f^{-1}\left(j\right)\right)=\left\{f^{-1}\left(j\right):{\alpha }_{kj}=1,k\in J\right\}$$

when ${\alpha }_{i*}\in r\left(\alpha \right)$ and ${\alpha }_{*j}\in c\left(\alpha \right)$, then $O_r\left(E;f^{-1}\left(i\right)\right)=O\left(E;f^{-1}\left(i\right)\right)$ is a basis out-neighborhood and $I_c\left(E;f^{-1}\left(j\right)\right)=I\left(E;f^{-1}\left(j\right)\right)$ is a basis in-neighborhood for network $E$. Thus, a basis neighborhood in $E$ is a non-empty neighborhood in $E$ which is not the set union of other neighborhoods in $E$.

Let $O_r\left(E\right)$ be the set of basis out-neighborhoods and $I_c\left(E\right)$ be the set of basis in-neighborhoods in network $E$. Additionally, define $P\left(E\right)$ as the set whose elements are $\varnothing$ and the sets generated by the closure under set union of the out-neighborhoods in $E$ and let $\left(P\left(E\right),\subseteq \right)$ be the poset ordered by the set inclusion relation “$\subseteq$”. Thus, when $\theta \left(E\right)=\alpha$, it may be formally stated that:

Lemma 3.

$\left(P\left(E\right),\subseteq \right)$is a lattice that is isomorphic to$\left(\Gamma \left(\alpha \right),\subseteq \right)$.

In what follows, $\left(P\left(E\right),\subseteq \right)$ will be referred to as the $\Pi$ lattice for $E$.

The following theorem provides complete $\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ and $\mathit{𝓓}$ equivalence classifications of all networks of a fixed order:

Theorem 1.

Let$E,F\in N_V$. Then:

i. 

$\mathrm{L}\left(E\right)=\mathrm{L}\left(F\right)$if and only if$O_r\left(E\right)=O_r\left(F\right);$

ii. 

$\mathrm{R}\left(E\right)=\mathrm{R}\left(F\right)$if and only if$I_c\left(E\right)=I_c\left(F\right);$

iii. 

$\mathrm{H}\left(\mathrm{E}\right)=\mathrm{H}\left(\mathrm{F}\right)$if and only if$O_r\left(E\right)=O_r\left(F\right)$and$I_c\left(E\right)=I_c\left(F\right)$;

iv. 

$\mathrm{D}\left(\mathrm{E}\right)=\mathrm{D}\left(\mathrm{F}\right)$if and only if$\left(P\left(E\right),\subseteq \right)$and$\left(P\left(F\right),\subseteq \right)$are lattice isomorphic.

Thus, the Green’s $\mathit{𝓛},\mathit{𝓡},$ and $\mathit{𝓗}$ equivalence classifications of the networks in $N_V$ partition the networks into $\mathit{𝓛},\mathit{𝓡},$ and $\mathit{𝓗}$ classes which have (generally distinct) nodes with identical out-neighborhoods, identical in-neighborhoods, and both identical out-neighborhoods and in-neighborhoods, respectively, whereas the $\mathit{𝓓}$ equivalence classification partitions the networks in $N_V$ into classes having isomorphic $\Pi$ lattices which are generated by their out-neighborhoods. These out-neighborhoods, in-neighborhoods, and $\Pi$ lattices are the invariants for each equivalence class. Transformations applied to a network that keeps the network in the same equivalence class are Green’s symmetries since they necessarily preserve these invariants.

5. The Schützenberger Symmetries and Groups for an $\mathit{𝓗}$-Equivalence Class of Networks

Of interest here are the $\mathit{𝓗}$-equivalence classes of networks in $N_V$, their invariants as specified by Theorem 1(iii), and the associated Schützenberger symmetries and groups. To this end, consider an arbitrary $\mathit{𝓗}$-equivalence class $H$ of networks in the monoid $N_V$ and let $M_H\equiv \left\{E\in N_V:hE\in H,h\in H\right\}$. This clearly defines $M_H$ as a sub-monoid of $N_V$ that acts upon $H$ from the right according to $H\times M_H\stackrel{\rho }{\to }H$, where ρ is the monoid action defined by $\rho \left(h,E\right)=hE$ (in the Boolean matrix representation, $\rho \left(h,E\right)=h\circ E$). Since ρ preserves the $H$ membership, then $M_H$ is the special set of Green’s symmetries called the set of right Schützenberger symmetries for the networks in $H$ which preserve the associated network invariants. The right Schützenberger problem for $H$ is to find $M_H$ (note from the last sentence in Section 2 that the right Schützenberger problem is satisfiable because semigroup theory guarantees the existence of at least one symmetry $E$ such that $hE\in H,h\in H$).

Although the following facts are well known [6,11], they are stated here for the reader’s convenience without proof as the next theorem:

Theorem 2.

(i) The action ρ is equivalent to a monoid homomorphism$\phi :M_H\to {\mathcal{T}}_H$to the full transformation monoid${\mathcal{T}}_H$on$H$such that${\Gamma }_H^R\equiv im \phi$is a simply transitive group of permutations of$H$under right multiplication with$\left|{\Gamma }_H^R\right|=\left|H\right|$; (ii) if$H$contains an idempotent, then$H$is a group and${\Gamma }_H^R\approx H$; (iii) if$H$and$H^{\prime }$are in the same$\mathit{𝓓}$-equivalence class, then${\Gamma }_H^R\approx {\Gamma }_{H^{\prime }}^R$; and (iv) if$H$and$H^{\prime }$are in the same$\mathit{𝓛}$-equivalence class, then$M_H=M_{H^{\prime }}$.

The group ${\Gamma }_H^R$ is the right Schützenberger symmetry group for the networks in $H$. It acts upon $H$ from the right according to $H\times {\Gamma }_H^R\stackrel{r}{\to }H$, where $r$ is the right group action $r\left(h,g\right)=hg$, i.e., $H$ is a right ${\Gamma }_H^R$-set.

Now let $T_H\equiv \left\{F\in N_V:Fh\in H,h\in H\right\}$ be the sub-monoid of $N_V$ that acts on $H$ from the left according to $T_H\times H\stackrel{\lambda }{\to }H$, where $\lambda \left(F,h\right)=Fh$. The set $T_H$ is the set of left Schützenberger symmetries for the networks in $H$ which preserve the associated network invariants. The left Schützenberger problem for $H$ is to find $T_H$ (the left Schützenberger problem is also satisfiable since semigroup theory guarantees the existence of at least one such symmetry).

The following results are also well known [6] and are stated here without proof for the reader’s convenience as the next theorem:

Theorem 3.

(i) The action$\lambda$is equivalent to a monoid anti-homomorphism$\psi :T_H\to {\mathcal{T}}_H$into the full transformation monoid${\mathcal{T}}_H$on$H$such that${\Gamma }_H^L\equiv im \psi$is a simply transitive group of permutations of$H$under left multiplication with$\left|{\Gamma }_H^R\right|=\left|H\right|$; (ii) every element of${\Gamma }_H^L$commutes with every element of${\Gamma }_H^R$; and (iii)${\Gamma }_H^L$is anti-isomorphic to${\Gamma }_H^R$.

The group ${\Gamma }_H^L$ is the left Schützenberger symmetry group for the networks in $H$. It acts upon $H$ from the left according to ${\Gamma }_H^L\times H\stackrel{\ell }{\to }H$, where $\ell$ is the left group action $\ell \left(g,h\right)=gh$, i.e., $H$ is a left ${\Gamma }_H^L$-set.

6. Example: Solving the Right Schützenberger Problem for Simple Two Node Networks

In order to illustrate aspects of the results developed in the last section, refer to Table 1 and Figure 1 in [4] and first consider the right Schützenberger problem for the singleton $\mathit{𝓗}$-equivalence class containing the simple network designated by η with node and directed link sets $V=\left\{a,b\right\}$ and $A=\left\{\left(a,b\right),\left(b,a\right),\left(b,b\right)\right\}$, respectively, and neighborhood basis sets $O_r\left(\eta \right)=\left\{\left\{a,b\right\},\left\{b\right\}\right\}=I_c\left(\eta \right)$. In general, solutions to the right Schützenberger problem for $H$ are found by solving the equation $hE=h^{\prime }$ for $E$ for every $h,h^{\prime }\in H$ when $h,h^{\prime },$ and $E$ are the associated Boolean matrices and multiplication is Boolean composition of matrices. This case is quite trivial since $H=\left\{\eta \right\}$ and the associated Boolean equation is $\eta \circ E=\eta$, or:

$$\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)\circ \left(\begin{array}{cc}{E}_{11}& E_{12}\\ E_{21}& E_{22}\end{array}\right)=\left(\begin{array}{cc}\left(0\wedge E_{11}\right)\vee \left(1\wedge E_{21}\right)& \left(0\wedge E_{12}\right)\vee \left(1\wedge E_{22}\right)\\ \left(1\wedge E_{11}\right)\vee \left(1\wedge E_{21}\right)& \left(1\wedge E_{12}\right)\vee \left(1\wedge E_{22}\right)\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right).$$

By inspection it is easily seen that this equation is satisfied when $E_{11}=1$, $E_{12}=0 \mathrm{or} 1$, $E_{21}=0$, and $E_{22}=1$ so that:

$$M_H=\left\{\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)\right\}.$$

It is obvious that, since $\eta \circ E=\eta$, the monoid action ρ preserves the neighborhood basis sets $O_r\left(\eta \right)$ and $I_c\left(\eta \right)$.

Since $\left|H\right|=1$, it is a trivial observation that ${\mathcal{T}}_H$ is the identity permutation $id$ of η with itself and ${\Gamma }_H^R\equiv im \phi =id$ in which case $\left|{\Gamma }_H^R\right|=1=\left|H\right|$ (Theorem 2(i)). Clearly, because the permutation is the identity, the right group action $r$ necessarily preserves the neighborhood basis sets $O_r\left(\eta \right)$ and $I_c\left(\eta \right)$.

Now consider the network $\beta$ with $V=\left\{a,b\right\}$ and $A=\left\{\left(a,a\right),\left(a,b\right),\left(b,b\right)\right\}$ and note that (Theorem 1): (i) L(β) = L(η) so that $O_r\left(\beta \right)=\left\{\left\{a,b\right\},\left\{b\right\}\right\}=O_r\left(\eta \right)$; and (ii) D(β) = D(η) so that $\left(P\left(\beta \right),\subseteq \right)$ and $\left(P\left(\eta \right),\subseteq \right)$ are each lattice isomorphic to an undirected path of length 2. The procedure for solving the right Schützenberger problem for $H^{\prime }=\left\{\beta \right\}$ is identical to that for η and yields (Theorem 2(iv)):

$$M_{H^{\prime }}=\left\{\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)\right\}=M_H.$$

Additionally, ${\mathcal{T}}_{H^{\prime }}$ is the identity permutation $id$ of $\beta$ with itself in which case ${\Gamma }_{H^{\prime }}^R\equiv im \psi =id$. Since $\beta$ is an idempotent, then $H^{\prime }$ is isomorphic to the trivial group and ${\Gamma }_{H^{\prime }}^R\approx H^{\prime }$ (Theorem 2(ii)). It is also obvious that ${\Gamma }_{H^{\prime }}^R\approx {\Gamma }_H^R$ (as is required by Theorem 2(iii) because D(β) = D(η)). The right monoid and group actions on $H^{\prime }$ also clearly preserve the basis neighborhoods of $\beta$.

7. Example: Solving the Schützenberger Problems for an $\mathit{𝓗}$-Class of Map Networks

A map network is a special network in which every node is connected by a directed link to exactly one node, i.e., its topology is effectively that of a map on its node set. Consequently, the monoid of all map networks ${ℳ}_V\subset N_V$ on a fixed node set $V$ is isomorphic to the full transformation semigroup ${\mathcal{T}}_V$ and its Green’s equivalence classification, i.e., “egg box” structure, is identical to that of ${\mathcal{T}}_V$ [6].

Let $V=\left\{1,2,3\right\}$ and denote a map network on $V$ by $\left(xyz\right),x,y,z\in V,$ where $x$ represents the link $\left(1,x\right)$, $y$ represents the link $\left(2,y\right)$, and $z$ represents the link $\left(3,z\right)$. For example, the network $\left(332\right)$ has $\left\{\left(1,3\right),\left(2,3\right),\left(3,2\right)\right\}$ as it set of links. The “egg box” for ${ℳ}_{\left\{1,2,3\right\}}$ is shown in Figure 1. There, each separate large “egg box” is a distinct $\mathit{𝓓}$-class, each small “box” is an $\mathit{𝓗}$-class, rows of $\mathit{𝓗}$-classes within $\mathit{𝓓}$-classes are $\mathit{𝓡}$-classes, and columns of $\mathit{𝓗}$-classes within $\mathit{𝓓}$-classes are $\mathit{𝓛}$-classes. Although more complicated, solving the right Schützenberger problem for any $\mathit{𝓗}$-class in ${ℳ}_{\left\{1,2,3\right\}}$ follows the same procedure as that used in Section 6. For example, choose $H=\left\{\left(313\right),\left(131\right)\right\}$ and observe that—as required by Theorem 1(iii)—each of these networks have the same out-neighborhood basis set $O_r\left(\left(313\right)\right)=\left\{\left\{1,3\right\}\right\}=O_r\left(\left(131\right)\right)$ and in-neighborhood basis set $I_c\left(\left(313\right)\right)=\left\{\left\{1,3\right\},\left\{2\right\}\right\}=I_c\left(\left(131\right)\right)$. Using the Boolean matrix representations of the networks and solving the equations:

$$\left(i\right)\left(313\right)\circ \left(xyz\right)=\left(313\right);\left(ii\right)\left(131\right)\circ \left(xyz\right)=\left(131\right);\left(iii\right)\left(313\right)\circ \left(xyz\right)=\left(131\right);\mathrm{and}\left(iv\right)\left(131\right)\circ \left(xyz\right)=\left(313\right)$$

yields:

$$M_H=\left\{\left(123\right),\left(113\right),\left(133\right),\left(321\right),\left(311\right),\left(331\right)\right\},$$

where $\left(123\right)$ is the monoid identity. The first three symmetries in $M_H$ are solutions to equations (i) and (ii) and the last three are solutions to (iii) and (iv). Since $\left|{\Gamma }_H^R\right|=\left|H\right|=2$ and ${\mathbb{Z}}_2=\left\{id,z\right\}$, where $zz=id,$ is the only group of order $2$ (up to isomorphism), then ${\Gamma }_H^R\approx {\mathbb{Z}}_2\approx {\mathcal{T}}_H$ and it must be the case that the surmorphism $\phi :M_H\to {\mathbb{Z}}_2$ maps according to $\left(123\right)\mapsto id,\left(113\right)\mapsto id,\left(133\right)\mapsto id,\left(321\right)\mapsto z,\left(311\right)\mapsto z,$ and $\left(331\right)\mapsto z$.

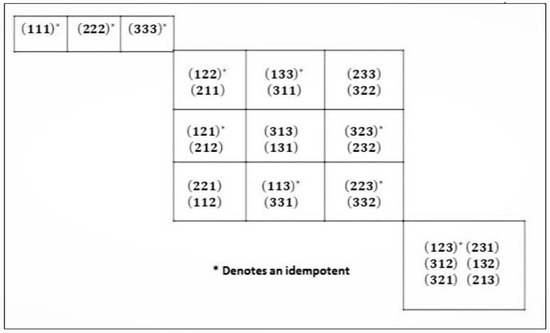
Figure 1. The “egg box” for ${ℳ}_{\left\{1,2,3\right\}}$ (classification from [12]).

Solving the left Schützenberger problem for $H$ requires solving the equations:

$$\left(i\right)\left(xyz\right)\circ \left(313\right)=\left(313\right);\left(ii\right)\left(xyz\right)\circ \left(131\right)=\left(131\right);\left(iii\right)\left(xyz\right)\circ \left(313\right)=\left(131\right);\mathrm{and}\left(iv\right)\left(xyz\right)\circ \left(131\right)=\left(313\right)$$

to find:

$$T_H=\left\{\left(123\right),\left(321\right),\left(121\right),\left(323\right),\left(212\right),\left(232\right)\right\}.$$

The first four symmetries in $T_H$ are solutions to $\left(i\right)$ and $\left(ii\right)$ and the last two are solutions to $\left(iii\right)$ and $\left(iv\right)$. Since ${\Gamma }_H^L\approx {\mathcal{T}}_H\approx {\mathbb{Z}}_2=\left\{i{d}^{\prime },z^{\prime }\right\}$ then $\psi :T_H\to {\mathcal{T}}_H$ maps as $\left(123\right)\mapsto i{d}^{\prime },\left(321\right)\mapsto i{d}^{\prime },\left(121\right)\mapsto i{d}^{\prime },\left(323\right)\mapsto i{d}^{\prime },\left(212\right)\mapsto z^{\prime },$ and $\left(232\right)\mapsto z^{\prime }$. That $\psi$ is an anti-homomorphism is a consequence of the fact that ${\mathcal{T}}_H\approx {\mathbb{Z}}_2$ (i.e., if $\psi \left(xy\right)=i{d}^{\prime }$, then $\psi \left(x\right)=i{d}^{\prime }=\psi \left(y\right)$ or $\psi \left(x\right)=z^{\prime }=\psi \left(y\right)$ in which case $\psi \left(y\right)\psi \left(x\right)=i{d}^{\prime }i{d}^{\prime }=i{d}^{\prime }$ or $\psi \left(y\right)\psi \left(x\right)=z^{\prime }{z}^{\prime }=i{d}^{\prime }$; and if $\psi \left(xy\right)=z^{\prime }$, then $\psi \left(x\right)=i{d}^{\prime }$ and $\psi \left(y\right)=z^{\prime }$ or $\psi \left(x\right)=z^{\prime }$ and $\psi \left(y\right)=i{d}^{\prime }$ in which case $\psi \left(y\right)\psi \left(x\right)=z^{\prime }i{d}^{\prime }=z^{\prime }$ or $\psi \left(y\right)\psi \left(x\right)=i{d}^{\prime }{z}^{\prime }=z^{\prime }$). Similar reasoning shows that ${\Gamma }_H^R$ and ${\Gamma }_H^L$ are anti-isomorphic.

8. Concluding Remarks

In general, any system which has a semigroup description can be partitioned into equivalence classes using Green’s equivalence relations. As shown in previous research [4,5], Green’s $\mathit{𝓛},\mathit{𝓡},\mathit{𝓗},$ and $\mathit{𝓓}$ classifications of the semigroup of all networks of fixed order yield network invariants and symmetries that provide new insights into the fundamental nature of network structure and evolution. This paper has introduced an additional type of network symmetry—the Schützenberger symmetry—which is also a natural consequence of Green’s classifications of networks. In particular, Schützenberger symmetries and their group representations (Schützenberger symmetry groups) transform networks in an $\mathit{𝓗}$-class amongst themselves in a manner that preserves the associated invariant neighborhood sets. Like Green’s $\mathit{𝓛}$ and $\mathit{𝓡}$ symmetries [5], Schützenberger symmetries can be computed from first principles.

Useful applications of these symmetries and invariants include understanding the consequences of link reconfiguration in communication and sensor networks, e.g., [13], identifying important relationships in social networks, e.g., [14], and providing classification and analysis of biological network data, e.g., [15]. In conclusion, it is noted that research associated with understanding the “internal dynamics” of $\mathit{𝓛}$ and $\mathit{𝓡}$ class evolutions and quantifying their complexities is reported in [5]. Since an $\mathit{𝓗}$-class evolution is both an $\mathit{𝓛}$ and an $\mathit{𝓡}$ class evolution, it would be interesting to investigate how these results apply to $\mathit{𝓗}$-class evolutions.