k-Space Magnetism as the Origin of Superconductivity

Abstract

The nonadiabatic Heisenberg model presents a nonadiabatic mechanism generating Cooper pairs in narrow, roughly half-filled “superconducting bands” of special symmetry. Here, I show that this mechanism may be understood as the outcome of a special spin structure in the reciprocal space, hereinafter referred to as “k-space magnetism”. The presented picture permits a vivid depiction of this new mechanism highlighting the height similarity as well as the essential difference between the new nonadiabatic and the familiar Bardeen–Cooper–Schrieffer mechanism.

1. Introduction

The nonadiabatic Heisenberg model (NHM) [1] is an extension of the Heisenberg model [2] going beyond the adiabatic approximation. It is based on three postulates related to the atomic-like motion [2,3,4] of the electrons in narrow, roughly half-filled energy bands. An atomic-like motion is characterized by electrons occupying localized states which for their part move as Bloch waves through the crystal. The NHM does not represents the localized states by (hybrid) atomic functions but solely by symmetry-adapted and optimally-localized Wannier functions forming an exact unitary transformation of the Bloch functions of a narrow, roughly half-filled energy band.

The energy bands in the band structures of the metals are degenerate at several points and lines (of symmetry) of the Brillouin zone. Hence, it is generally not possible to find narrow, roughly half-filled closed energy bands in the band structures of the metals as they are required for the construction of optimally localized Wannier functions. However, in the band structures of those metals that experimentally prove to be superconductors, the construction of such Wannier functions becomes possible if we allow the Wannier functions to be spin dependent [5]. This observation leads to the definition of “superconducting bands” [5]: The Bloch functions of a superconducting band can be unitarily transformed into optimally localized spin-dependent Wannier functions that are symmetry-adapted to the full space group of the metal.

Within the NHM, the atomic-like motion in a superconducting band produces Cooper pairs below a transition temperature [6]. The aim of the paper is to show that this nonadiabatic mechanism can be understood as the outcome of a special spin structure in the reciprocal space referred to as “$\mathit{k}$-space magnetism”. In Section 2, we declare what we mean by $\mathit{k}$-space magnetism. In Section 3, we show that $\mathit{k}$-space magnetism leads directly to the formation of Cooper pairs at low temperatures. In Section 4, we finally show that the NHM provides an interaction producing $\mathit{k}$-space magnetism in narrow, roughly half-filled superconducting bands when we leave the adiabatic approximation.

2. k-Space Magnetism

Within the NHM, strongly correlated electrons in a narrow, roughly half-filled superconducting band produce a special spin structure at the Fermi level that we call “$\mathit{k}$-space magnetism”: the electron spins of the Bloch electrons are no longer parallel or anti-parallel to a fixed symmetry axis (usually the z axis), but are parallel or anti-parallel to an axis $z_{\mathit{k}}$ determined by the $\mathit{k}$ vector of the electron, as is visualized in Figure 1. The direction of $z_{\mathit{k}}$ changes continuously in the $\mathit{k}$ space and is not independent of $\mathit{k}$ in a narrow, roughly half-filled superconducting band. The spin $s=\pm \frac{1}{2}$ of the Bloch electron at wave vector $\mathit{k}$ still may lie parallel (for $s=+\frac{1}{2}$) or anti-parallel (for $s=-\frac{1}{2}$) to the predefined $z_{\mathit{k}}$ axis. Thus, $\mathit{k}$-space magnetism does not create a magnetic field and is invariant under time inversion.

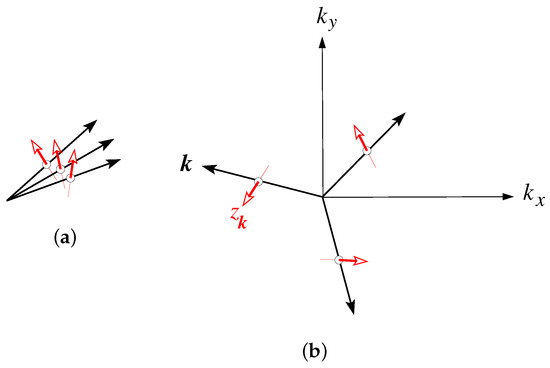
Figure 1. Visualization of the $\mathit{k}$ space magnetism in a narrow, roughly half-filled superconducting band: the black arrows show the $\mathit{k}$ vectors of Bloch electrons moving in general positions at the Fermi level, and the red arrows indicate the symmetry axis $z_{\mathit{k}}$ of the spin of the Bloch electron with wave vector $\mathit{k}$. The $z_{\mathit{k}}$ axes generally intersect the drawing plane. Panel (a) demonstrates that the $z_{\mathit{k}}$ axes change continuously in $\mathit{k}$ space; and Panel (b) shows the $\mathit{k}$ vectors of three Bloch electrons connected by symmetry (in a crystal with the hexagonal space group P3) and demonstrates that also the $z_{\mathit{k}}$ axes are connected by symmetry.

Two questions emerge at this point: (1) Why does $\mathit{k}$-space magnetism produces Cooper pairs? (2) Which interaction produces $\mathit{k}$-space magnetism? These questions are answered in Section 3 and Section 4, respectively.

3. k-Space Magnetism Producing Cooper Pairs

Consider an electron system ${\epsilon }^{km}$ exhibiting $\mathit{k}$-space magnetism at the Fermi level. The interaction producing the $\mathit{k}$-space magnetism is defined in Section 4; here, we assume it to exist.

At any scattering process in the electron system ${\epsilon }^{km}$, the total electron spin of the scattered electrons is not conserved since the spin direction is $\mathit{k}$ dependent. Hence, the electrons must interchange spin angular momenta with the lattice of the atomic cores. Consequently (Section 3.1 of Ref. [6]), at any electronic scattering process, two crystal-spin-1 bosons are excited or absorbed.

At zero (or very low) temperature, the crystal-spin-1 bosons will be only virtually excited. That means that each boson pair is reabsorbed instantaneously after its generation. Hence, whenever a boson pair is excited during a certain scattering process

$${\mathit{k}}_1,{\mathit{k}}_2\to {\mathit{k}}_1^{\prime },{\mathit{k}}_2^{\prime }$$

(1)

of the two electrons ${\mathit{k}}_1$ and ${\mathit{k}}_2$, this boson pair is reabsorbed instantaneously during a second scattering process

$${\mathit{k}}_3,{\mathit{k}}_4\to {\mathit{k}}_3^{\prime },{\mathit{k}}_4^{\prime }$$

(2)

of two other electrons ${\mathit{k}}_3$ and ${\mathit{k}}_4$. Consequently, the resulting total scattering process

$${\mathit{k}}_1,{\mathit{k}}_2,{\mathit{k}}_3,{\mathit{k}}_4\to {\mathit{k}}_1^{\prime },{\mathit{k}}_2^{\prime },{\mathit{k}}_3^{\prime },{\mathit{k}}_4^{\prime }$$

(3)

must conserve the total electron spin. Only in this case, the boson pair created during the first process in Equation (1) is completely reabsorbed during the second process in Equation (2). However, also at the scattering processes in Equation (3) of four electrons, the total spin is generally not conserved since the spin direction still is $\mathit{k}$ dependent.

The only scattering processes within ${\epsilon }^{km}$ conserving the total electron spin are scattering processes between Cooper pairs: since the system is invariant under time-inversion, the spins of the Bloch states labeled by $\mathit{k}$ and by $-\mathit{k}$ lie exactly opposite. When both states are occupied at the same time, they form a Cooper pair with exactly zero total spin. Hence, any scattering process between Cooper pairs

$${\mathit{k}}_1,-{\mathit{k}}_1;{\mathit{k}}_2,-{\mathit{k}}_2\to {\mathit{k}}_1^{\prime },-{\mathit{k}}_1^{\prime };{\mathit{k}}_2^{\prime },-{\mathit{k}}_2^{\prime }$$

(4)

conserves the total spin angular momentum within ${\epsilon }^{km}$, see the detailed group-theoretical discussion in Section 3.2 of Ref. [6]. This scattering process (Equation (4)) comprises the two processes

$${\mathit{k}}_1,{\mathit{k}}_2\to {\mathit{k}}_1^{\prime },{\mathit{k}}_2^{\prime }$$

(5)

destroying a Cooper pair and creating a boson pair, and the subsequent process

$$-{\mathit{k}}_1,-{\mathit{k}}_2\to -{\mathit{k}}_1^{\prime },-{\mathit{k}}_2^{\prime }$$

(6)

recomposing the Cooper pair and reabsorbing the boson pair. This only possible combined scattering process within ${\epsilon }^{km}$ represents the well-known Bardeen–Cooper–Schrieffer (BCS) mechanism [7] in ${\epsilon }^{km}$, see Section 3.2 of Ref. [6]. However, the mechanism in ${\epsilon }^{km}$ differs from the BCS mechanism because it is effective solely between Cooper pairs. It necessarily produces Cooper pairs possessing only one half of the degrees of freedom of free electrons. This necessary reduction of the degrees of freedom may be compared with the effect of constraining forces in classical systems. Thus, we speak of quantum mechanical constraining forces stabilizing the Cooper pairs in ${\epsilon }^{km}$ [6], or, more illustratively, by “spring mounted Cooper pairs” [8].

4. Strongly Correlated Electrons Producing k-Space Magnetism

In the framework of the NHM, the electrons of a narrow, roughly half-filled superconducting band lower their total Coulomb energy by producing $\mathit{k}$-space magnetism. This far-reaching assertion follows from the three postulates of the NHM [1] and from the special properties of the spin-dependent Wannier functions representing the atomic-like states in a superconducting band. In Section 4.1, we first repeat the definition of spin-dependent Wannier functions in the special case of a metal with one atom in the unit cell (the general definition is given in Ref. [5]), and in Section 4.2 we show that the postulates of the NHM define an interaction producing $\mathit{k}$-space magnetism.

4.1. Spin-Dependent Wannier Functions

For the sake of simplicity, we consider a metal with only one atom in the unit cell. In this case, superconducting bands are single bands [5]. Furthermore, we assume that this metal possesses a narrow, half-filled superconducting band in its band structure. By definition we can unitarily transform the Bloch functions of this band into optimally localized and symmetry-adapted spin-dependent Wannier functions [5]. We do this by replacing the Bloch functions ${\phi }_{\mathit{k}}\left(\mathit{r}\right)$ of the superconducting band by Bloch spinors

$${\phi }_{\mathit{k},m}(\mathit{r},t)=\sum _{s=-\frac{1}{2}}^{+\frac{1}{2}}{f}_{ms}\left(\mathit{k}\right)u_s\left(t\right){\phi }_{\mathit{k}}\left(\mathit{r}\right)$$

(7)

with $\mathit{k}$ dependent spin directions. The functions $u_s\left(t\right)$ denote Pauli’s spin functions:

$$u_s\left(t\right)={\delta }_{st},$$

(8)

where $s=\pm \frac{1}{2}$ and $t=\pm \frac{1}{2}$ are the spin quantum number and the spin coordinate, respectively. (To simplify, we ignore that in some points of symmetry the Bloch spinors may not be written in the form of Equation (7) [5].) The coefficients $f_{ms}\left(\mathit{k}\right)$ in Equation (7) form a $\mathit{k}$ dependent two-dimensional matrix

$$\mathbf{f}\left(\mathit{k}\right)=\left[f_{ms}\left(\mathit{k}\right)\right]$$

(9)

which is unitary,

$${\mathbf{f}}^{-1}\left(\mathit{k}\right)={\mathbf{f}}^{†}\left(\mathit{k}\right),$$

(10)

in order that the spin-dependent Wannier functions in Equation (11) form a complete orthonormal basis in the superconducting band. The Bloch spinors ${\phi }_{\mathit{k},m}(\mathit{r},t)$ are usual Bloch functions with anti-parallel spins possessing, however, a $\mathit{k}$ dependent symmetry axis $z_{\mathit{k}}$ defined by the matrix $\mathbf{f}\left(\mathit{k}\right)$.

Since still we consider a superconducting band, the coefficients $f_{ms}\left(\mathit{k}\right)$ can be chosen in such a way that the spin-dependent Wannier functions

$$w_m(\mathit{r}-\mathit{R},t)=\frac{1}{\sqrt{N}}\sum _{\mathit{k}}^{BZ}{e}^{-i\mathit{k}\mathit{R}}{\phi }_{\mathit{k},m}(\mathit{r},t)$$

(11)

are optimally localized and symmetry-adapted to the full space group of the considered metal [5]. The sum in Equation (11) is over the N vectors $\mathit{k}$ of the first Brillouin zone (BZ), and $\mathit{R}$ denotes a lattice vector. However, the coefficients $f_{ms}\left(\mathit{k}\right)$ cannot be chosen independent of $\mathit{k}$ since, as mentioned in Section 1, we cannot unitarily transform the Bloch functions of the superconducting band into usual (i.e., spin-independent) Wannier functions that are also optimally localized and symmetry-adapted. Hence, the spin-dependent Wannier functions differ substantially from usual spin-independent Wannier functions even if we neglect spin-orbit effects.

The Bloch spinors may be calculated from the spin-dependent Wannier functions by the equation

$${\phi }_{\mathit{k},m}(\mathit{r},t)=\frac{1}{\sqrt{N}}\sum _{\mathit{R}}^{BvK}{e}^{i\mathit{k}\mathit{R}}{w}_m(\mathit{r}-\mathit{R},t),$$

(12)

where the sum now is over the N lattice vectors $\mathit{R}$ of the Born-von Kàrmàn volume (BvK).

4.2. Nonadiabatic Interaction Producing k-Space Magnetism

Let be the operator

$$H=H_{HF}+H_{Cb}$$

(13)

the Hamiltonian in the superconducting band with $H_{HF}$ and

$$H_{Cb}=\sum _{\mathit{R},m}⟨{\mathit{R}}_1,m_1;{\mathit{R}}_2,m_2|H_{Cb}|{\mathit{R}}_1^{\prime },m_1^{\prime };{\mathit{R}}_2^{\prime },m_2^{\prime }⟩c_{{\mathit{R}}_1{m}_1}^{†}{c}_{{\mathit{R}}_2{m}_2}^{†}{c}_{{\mathit{R}}_2^{\prime }{m}_2^{\prime }}{c}_{{\mathit{R}}_1^{\prime }{m}_1^{\prime }}$$

(14)

representing the Hartree–Fock and Coulomb energy, respectively. The fermion operators $c_{\mathit{R}m}^{†}$ and $c_{\mathit{R}m}$ create and annihilate electrons in the localized states $|\mathit{R},m⟩$ represented by the spin-dependent Wannier functions $w_m(\mathit{r}-\mathit{R},t)$ in Equation (11). We write $H_{Cb}$ as

$$H_{Cb}=H_c+H_{ex}+H_z,$$

(15)

where $H_c$ and $H_{ex}$ contain the matrix elements of $H_{Cb}$ with

$${\mathit{R}}_1={\mathit{R}}_1^{\prime }\mathrm{and}{\mathit{R}}_2={\mathit{R}}_2^{\prime },$$

(16)

and

$${\mathit{R}}_1={\mathit{R}}_2^{\prime }\mathrm{and}{\mathit{R}}_2={\mathit{R}}_1^{\prime },$$

(17)

respectively, and $H_z$ comprises the remaining (non-diagonal) matrix elements with

$$\{{\mathit{R}}_1,{\mathit{R}}_2\}\ne \{{\mathit{R}}_1^{\prime },{\mathit{R}}_2^{\prime }\}.$$

(18)

The operators $H_c$ and $H_{ex}$ represent the Coulomb repulsion and the exchange interaction, respectively, between atomic-like electrons and, hence, do not contradict the picture of localized electron states moving as Bloch waves through the crystal. $H_z$, on the other hand, represents an interaction destroying the atomic-like motion [1].

Now, consider the operator

$$H^{\prime }=H_{HF}+H_c+H_{ex}=H-H_z$$

(19)

being gained from H in Equation (13) by putting $H_z$ equal to zero, and assume the exact ground states $|G⟩$ and $|G{}^{\prime }⟩$ of H and $H^{\prime }$, respectively, to be determined. The first postulate of the NHM states that a pure atomic-like motion is energetic more favorable than an atomic-like motion disturbed by $H_z$,

$$⟨G\left|H\right|G⟩>⟨G{}^{\prime }|H^{\prime }|G{}^{\prime }⟩,$$

(20)

if the superconducting band is one of the narrowest bands in the considered metal, see the detailed substantiation in Ref. [1].

The second postulate of the NHM states that the electronic transitions represented by $H_z$ are attributed to the adiabatic approximation and do not occur in the true nonadiabatic system,

$$⟨{\mathit{R}}_1,m_1,n;{\mathit{R}}_2,m_2,n\left|H_{Cb}\right|{\mathit{R}}_1^{\prime },m_1^{\prime },n;{\mathit{R}}_2^{\prime },m_2^{\prime },n⟩=0,$$

(21)

for

$$\{{\mathit{R}}_1,{\mathit{R}}_2\}\ne \{{\mathit{R}}_1^{\prime },{\mathit{R}}_2^{\prime }\}$$

(22)

if Inequality (20) is true. At the transition to the nonadiabatic system, the electron system lowers its total Coulomb energy by the “nonadiabatic condensation energy”

$$\Delta E=⟨G\left|H\right|G⟩-⟨G{}^{\prime }|H^{\prime }|G{}^{\prime }⟩.$$

(23)

Equation (21) is suggested by the fact that the non-diagonal matrix elements of $H_{Cb}$ depend very sensitively on the exact form of the localizes orbitals and, hence, only small modifications should be required to suppress the transitions represented by $H_z$. The modified localized orbitals cannot be described within the adiabatic approximation (since here Inequality (20) is true) but require the introduction of nonadiabatic localized states

$$|\mathit{R},m,\nu ⟩,$$

(24)

possessing the same symmetry as the spin-dependent Wannier functions, see the detailed discussion in Ref. [1]. The new quantum number $\nu$ labels the nonadiabatic motion of the atomic core following the motion of the localized electron, and $\nu =n$ labels the special states satisfying Equation (21).

The nonadiabatic symmetry operators (as defined in Equation (B9) of Ref. [1]) no longer act on the electronic coordinates alone, but additionally on the coordinate describing that part of the motion of the atomic core that follows the motion of the electron. Thus, the electronic motion in the nonadiabatic localized states $|\mathit{R},m,\nu ⟩$ is not so confined by symmetry as in the adiabatic states $|\mathit{R},m⟩$. The electrons now move in a potential depending on which of the adjacent localized states are occupied and on the present positions of these electrons. Hence, the nonadiabatic localized states represent a strongly correlated atomic-like motion.

It is essential that the NHM does not only neglect $H_z$ but postulates a nonadiabatic mechanism suppressing the transitions generated by $H_z$. This has the important consequences that, first, the nonadiabatic Hamiltonian commutes with the operators of the space group if and only if the nonadiabatic localized states are adapted to the symmetry of the space group [1], and, second, the naked electrons no longer have exact Fermi character. Now, the Fermi excitations are represented by electrons occupying the nonadiabatic states $|\mathit{R},m,n⟩$ traveling as Bloch states through the crystal.

The nonadiabatic states are postulated to interpret Inequality (20) and to understand Equation (21). I believe that it would be physically needless to try to determine explicitly the highly complex localized functions representing the nonadiabatic states. We may assume that the modifications of the adiabatic electronic orbitals required in Equation (21) are so small that any calculation of expectation values (i.e., of diagonal matrix elements) still can be performed within the adiabatic approximation. That means that any expectation value in the superconducting band can be determined in close approximation by replacing the nonadiabatic localized functions by the adiabatic spin-dependent Wannier functions [1].

This has the consequences that, first, the spin-dependent Wannier functions must be adapted to the symmetry of the space group such that the nonadiabatic Hamiltonian correctly commutes with the operators of the space group, and, second, the expectation values of the electronic spin directions are determined by the Bloch spinors in Equation (12) because they represent the nonadiabatic Bloch states within the adiabatic approximation. Thus, the adiabatic Bloch spinors in Equation (12) define the spin direction of the electrons in the nonadiabatic system, and, consequently, produce $\mathit{k}$-space magnetism.

In summary, the electrons in a narrow, roughly half-filled superconducting band may lower their Coulomb energy by the nonadiabatic condensation energy $\Delta E$ in Equation (23) by producing $\mathit{k}$-space magnetism, as described in Section 2. The $\mathit{k}$ dependent spin directions are defined by the coefficients $f_{ms}\left(\mathit{k}\right)$ in Equation (7), which in turn are determined by the demand that the spin-dependent Wannier functions must be optimally localized and symmetry-adapted to the space group of the considered metal.

5. Discussion

The aim of this paper is to give a graphic description of the nonadiabatic mechanism of Cooper pair formation defined within the NHM. The presented picture clearly shows the peculiar features of the Cooper pair formation within a superconducting band: first, the postulates of the NHM suggest that the strongly correlated atomic-like motion in a narrow, roughly half-filled superconducting band produces $\mathit{k}$-space magnetism in the nonadiabatic system (as described in Section 2), and, secondly, at sufficiently low temperatures the $\mathit{k}$-space magnetism produces Cooper pairs in turn. This picture clearly demonstrates that the formation of Cooper pairs produced by $\mathit{k}$-space magnetism shows a great resemblance, but also a striking difference as compared with the familiar BCS mechanism [7]. On the one hand, the formation of Cooper pairs is still mediated by bosons but, on the other hand, the electrons necessarily form Cooper pairs below a transition temperature. This necessity of the Cooper pair formation we compare with the effect of constraining forces in classical systems and, consequently, we speak of constraining forces stabilizing the Cooper pairs [6]. There is evidence that these constraining forces are essential for the formation of Cooper pairs, see, e.g., the Introduction of Ref. [9]. In this context, the question of whether there exists an attractive interaction between the electrons is of secondary importance.