Abstract
This study aimed to determine the reliability of the damage criteria that was adopted by the peak particle velocity (PPV) method and the single degree of freedom (SDOF) approach to assess the damage level of a box-shaped underground tunnel. An advanced arbitrary Lagrangian Eulerian (ALE) technique available in LS-DYNA software was used to simulate a symmetrical underground tunnel that was subjected to a surface detonation. The validation results of peak pressure into the soil revealed a good consistency with the TM5-855-1 manual within differences that were much less than previous numerical studies. The pressure contours revealed that the blast waves travelled into the soil in a hemispherical shape and the peak reflected the pressure of the tunnel that occurred immediately before the incident pressure reached its highest value. The assessment results proved that the criteria of the above methods could efficiently predict the damage level of a box-shaped tunnel under different circumstances of explosive charge weight and lining thickness at a depth of 4 m within slight differences that were observed during van and small delivery truck (SDT) explosions. However, the efficiency of both the methods was varied with the increase of burial depth. Whereas, using the PPV method significantly underestimated or overestimated the damage level of the tunnel, especially during SDT and container explosions with a lining thickness of 250 mm at burial depths of 6 and 8 m, respectively, the damage level that was obtained by the SDOF method greatly matched with the observed failure modes of the tunnel. Furthermore, new boundary conditions and equations were proposed for the damage criteria of the PVV method.
1. Introduction
In the last decades, the increase of terrorist attacks on underground tunnels, such as the bombings of Moscow, London, and Belarus, has highlighted the horrible effects of these events. According to the previous records, explosion attacks via a vehicle was the most used method by terrorists to achieve these assaults due to their massive charge power, high success rate, and severe destruction [1,2]. The collapse of tunnels could cause a lot of losses in lives and considerable financial implications, as well as a complete interruption of its transportation line. Hence, great measures are demanded to protect these structures from terrorist attacks.
Tunnel structures could be subjected to internal or external blasts. The new control and security systems have been successfully used to monitor the internal blast inside a tunnel [3,4]. However, external explosions, unfortunately, are the most likely to achieve their purpose due to the absence of proper technology to detect these events before occurring [3,5,6]. In this research area, there are no records available for a field trial due to the difficulties to acquire such a study in terms of cost and safety. Nevertheless, a number of researchers [7,8,9,10,11,12] successfully implemented the centrifuge methods in order to model the blast behaviour of underground structures with the circular cross-section. De et al. [9,10] conducted several centrifuge trails to study the influence of surface detonation on the behaviour of a cylindrical structure buried in dry sand. The centrifuge methods are limited to smaller models due to the variation of the gravity field within the trail bucket, which could cause an inaccurate prediction of the tunnel’s response [8].
Recently, the advanced numerical techniques were broadly used to analyse the behaviour of underground tunnels that were exposed to internal or external explosions owing to its vital ability to provide valuable data within a short time, lower cost, and secure environment. Several scholars investigated the dynamic behaviour of underground tunnels exposed to an internal detonation, such as [13,14,15,16,17,18]. Tiwari et al. [19,20] evaluated the behaviour of an underground tunnel with a circular shape under the impact of an internal blast by using a coupled Eulerian-Lagrangian (CEL) solver that was available in ABAQUS software [21]. The results proved that the tunnel safety significantly improved at the thicker tunnel lining, whereas the displacement was decreased by 90% when the lining thickness of 550 mm is used as compared with the thickness of 350 mm. Furthermore, the displacement of the tunnel lining appeared to be in a close relationship with the explosive charge weight, whereas the displacements during explosions of 25 and 50 kg TNT charge weight were less than 100 kg TNT by 58.4% and 3.3%, respectively.
On the other hand, several studies aimed to evaluate the dynamic behaviour of underground tunnels exposed to a surface detonation. Most of these studies were concerned about the dynamic response of underground tunnels with circular shapes. Luo et al. [22] subjected a surface TNT charge weight ranging between 100 and 300 kg on a circular underground tunnel that was placed in a sandy soil. The outcomes revealed that the tunnel was safe during the explosion of 100 kg TNT charge weight at a burial depth of 1.5 m. Yang et al. [23] used an arbitrary Lagrangian-Eulerian (ALE) technique available in LS-Dyna software [24] to assess the behaviour of a quarter symmetrical circularly-shaped underground tunnel located inside a sandy loam soil. The damage evaluation results via the values of effective stress showed that the tunnel with 350 mm lining thickness was safe at depths of more than 7 m within explosion magnitudes that were less than 500 kg of TNT. Koneshwaran [3,4] proved that the ALE technique is more suitable to determine the dynamic behaviour of a quarter symmetrical circularly-shaped underground tunnel within a higher accuracy as compared with the smooth particle hydrodynamics (SPH) approach. The tunnel was located in a sandy soil and modelled by using Material 84 (Winifith Concrete) available in LS-Dyna software [24]. The tunnel safety was evaluated via the crack width property that was provided by the Winifith material model. The results proved that the tunnel was safe when it was placed at depths of 6.35 and 9.52 m under exploded charge weights less than 625 and 1125 kg, respectively.
In the literature review, limited numerical studies were performed to assess the behaviour of box-shaped underground tunnels that were exposed to a surface explosion. Mobaraki and Vaghefi [25] analysed the effects of buried depth on the safety of a symmetrical box-shaped tunnel exposed to a detonation of a 1000 kg TNT charge weight via using the ALE method available in LS-Dyna software [24]. The tunnel was placed into a sandy soil and its behaviour was assessed according to the tunnel peak particle velocity (PPV) criterion. The results revealed that the underground tunnel with roof and wall thicknesses of 700 and 800 mm, respectively, was damaged at distances ranging between 0 and 2 m from the explosion centre, whereas it was safe at depths of between 2 and 25 m. Mussa et al. [26] used the ALE method to simulate the symmetrical underground box-shaped tunnel under the effects of lining thickness, burial depth, and explosive charge weight. The liner of the tunnel was modelled using Material 3 (MAT_Plastic_Kinematic) without considering the strain rate sensitivity of the concrete and the reinforcement under blast loads. The damage assessment was performed via the single degree of freedom approach (SDOF) that was proposed by Fallah and Louca [27], which mainly depends on the lateral displacement of structural members, and the results proved that the tunnel with 500 mm lining thickness was collapsed at a burial depth of 4 m during the surface explosion of a container truck.
According to the previous studies, the behaviour of the box-shaped underground tunnel is still not well understood. Thus, the present study was conducted in order to determine the behaviour of this tunnel’s type under the effect of a surface explosion by using an advanced ALE method available in LS-Dyna. The main objective of the study is to compare between the prior methods that were used to assess the damage levels of a box-shaped underground tunnel.
1.1. Blast Damage Assessment Methods of a Box-Shaped Tunnel
In general, it is difficult to obtain acceptable damage criteria of underground tunnels due to the effects of several factors, such as the blast intensity, tunnel stiffness, and soil properties. The previous studies adopted two methods to assess the damage level of box-shaped underground tunnels by using the peak particle velocity (PPV) [25] and single degree of freedom (SDOF) approaches [26]. During 1948 to 1952, massive scale detonation tests were performed by US Army Corps of Engineers close to unlined tunnels in a sandy soil [28]. According to these tests, the damage criteria of the underground tunnel were categorized into four levels according to the peak particle velocity (PPV) values, as shown in Table 1. Kendorski et al. [29] reported that the cracks in the shotcrete lining of underground tunnels occurred when the PPV exceeds approximately 1.22 m/s. Nevertheless, Nakano et al. [30] stated that the shotcrete cracking produced by an adjacent tunnel explosion occurred when the PPV reached 0.7 m/s.

Table 1.
Damage criteria of the peak particle velocity (PVV) method.
On the other hand, Fallan and Louca [27] simplified the structure to an equivalent elastic-perfect plastic SDOF model. This model defined the damage levels according to the maximum deflection of structure (yc). Thus, various damage levels were suggested corresponding to the value of yc, which is set to be the mid-height lateral displacement of the structural member to reduce uncertainties in predicting the critical deflections, as shown in Table 2. This damage criterion was used by Mussa et al. [26] in order to assess the damage level of a box-shaped tunnel.

Table 2.
Damage criteria of the single degree of freedom approach (SDOF) method.
2. Numerical Modelling
2.1. Geometry Details and Meshing
A box-shaped railway underground tunnel with 500 mm lining thickness for the roof and wall constructed in Spain at a depth of 4 m with a height of 7.5 m and width of 10 m was modelled [31]. A quarter of the field with dimensions of (25 × 25 × 30) m was modelled, according to the Alekseenko test, owing to the symmetry of the YZ and YX planes [32]. However, at dimensions of (10 × 10 × 22.5) m, a comparable behaviour as the Alekseenko test field appeared, and, consequently, these dimensions were used in the current research to decrease the computational cost and time, as described in Figure 1. The tunnel was placed into sandy soil that was directly beneath the explosion centre, which is considered as the most critical position according to [23,26]. The soil, air, and tunnel parts were modelled by using a solid (164) element, which is considered as the most widely used element in explicit analyses, and which could be only defined by using eight nodes [33]. The blast load was defined by using the (Initial_Volume_Fraction_Geometry) available in LS-Dyna as a spherical shape by specifying its radius and detonation point [24]. The surface detonation occurred by using a container truck carrying a 4536 kg TNT charge weight, which is considered as the most critical condition, as stated by [26].
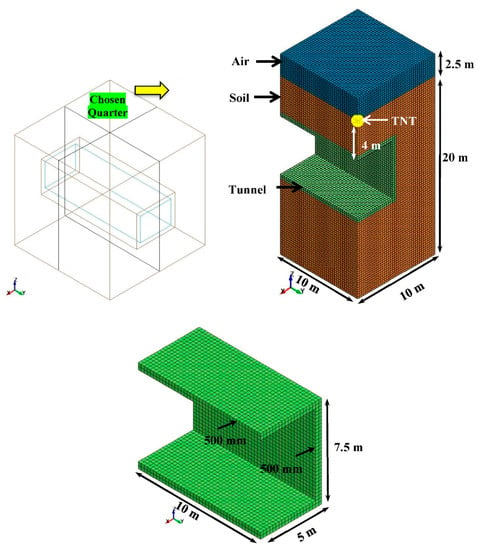
Figure 1.
Geometry details of the numerical model.
2.2. Material Model
2.2.1. Air
The air was modelled by using material 9 (MAT_Null), which required defining the linear polynomial equation of state (EOS) [24]. The pressure was calculated by using the following equation [34,35]:
where is the ratio of current mass density, C0, C1, C2, C3, C4, C5, and C6 are constants, and E0 is represented the initial internal energy per unit volume. The adopted EOS symbolizes an ideal gas that was dominated by a gamma law, whereas the constants (C0, C1, C2, C3, and C6) are equal to 0 and (C4, and C5) are equal to γ − 1. Accordingly, the equation of pressure can be rewritten, as follows:
where is an adiabatic constant, which usually taken as 1.4 for the ideal gas. Table 3 shows the main parameters of the air utilized in the current research [23].

Table 3.
Parameters of the air.
2.2.2. Tunnel
Material 16 (MAT_Pseudo_Tensor) was utilized to model the tunnel structure. It is suited to simulate the underground reinforced concrete structures that were subjected to blast loadings [24]. An automatic internal generation of a simple “generic” model for concrete can be achieved by inserting a negative value for A0 equal to −145, so that a trilinear equation of state (EOS) Type 8 will be automatically created from the unconfined compressive strength () and the Poisson ratio (Pr). The maximum principal stress for failure (SIGF) [24] is assumed to be the fc and is equal to 61.18 MPa. A smeared modelling option available in Material 16 was used to simulate the rebar due to a large number of model elements, as well as its ability to deliver reasonable results within lower cost and time than that needed by discrete models [36]. Strain rate sensitivity was defined for the concrete and rebar by using dynamic increase factor (DIF) curves, as shown in Figure 2. The DIF curve was obtained during a laboratory test conducted in UKM University on concrete with a compressive strength of 61.18 MPa via the split Hopkinson pressure bar (SHPB) impact test within a strain rate range of up to 103.87 s–1 [37]. For steel, the DIF of grade 60 rebar was determined by using Malvar‘s equation [38]. Table 4 shows the tunnel parameters, where SIGF is the unconfined concrete compressive strength (fc), Pr is the Poisson ratio of concrete, Er is the elastic modulus of steel, PEr is the reinforcement percentage, PRr is the Poisson ratio of steel, and SIGY is the steel yield stress ().
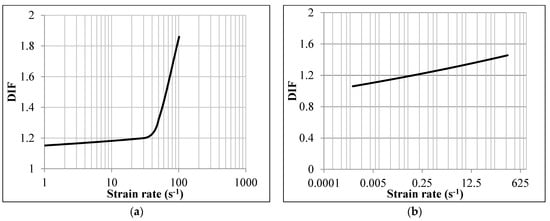
Figure 2.
Full range of dynamic increase factor (DIF) at different strain rates for (a) concrete, and (b) steel.

Table 4.
Parameters of the tunnel.
2.2.3. Soil
Material 5 (MAT_Soil_and_Foam) was used to model the sandy loam soil [39]. It is a simple model that works as a fluid and had been verified to be appropriate in the modelling of the soil [32]. Foster et al. [40] described the soil properties, and these properties were assessed by the National Soil Dynamics and Auburn University (NSDL-AU) from the soil compaction model components [41,42]. Table 5 and Table 6 show the adopted soil parameters of the present study [43], where G represented the shear modulus of the soil, Ku is the bulk modulus at the unloading path, a0, a1, and a2 are the constants of the yield function, and Pcut is the pressure cut-off of the tensile fracture [24,44].

Table 5.
Parameters of the soil.

Table 6.
Triaxial hydrostatic compression records of the sandy soil.
2.2.4. TNT
Material 8 (MAT_High_Explosive_Burn) was used to model the TNT charge weight that was carried by a container truck [45]. This model has been broadly utilized in the engineering calculations due to its flexibility in calibration. The equation of state (EOS) proposed by Jones–Wilkens–Lee (JWL) was used to define the pressure released by the chemical energy throughout the blast, as follows [46,47]:
where A, B, R1, R2, ω are constants, and V is indicated to the relative volume of the explosive material [24]. Table 7 shows the adopted parameters of the TNT charge [33].

Table 7.
Parameters of the TNT charge.
2.3. Boundary Condition
A non-reflection boundary condition was used to the infinity domain to reduce the stress wave reflection. On the other hand, the motion of the nodes normal to the symmetry planes XZ and YZ were fixed. The upper surface was free, while the base was assumed as a rock bed and was fixed in all directions, as shown in Figure 3 [3].
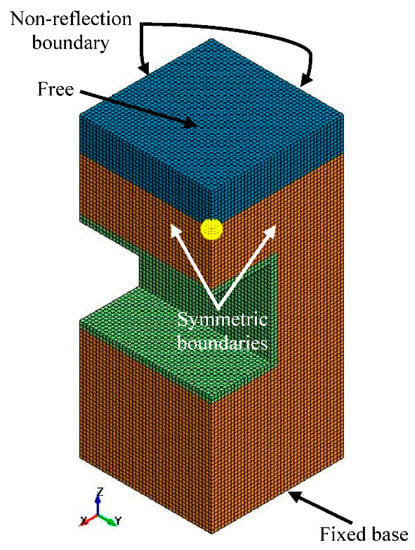
Figure 3.
Boundary condition.
2.4. Arbitrary Lagrangian Eulerian (ALE) Solver
The ALE solver is a technique which capable to gather the main advantages of Eulerian and pure Lagrangian solvers. Its nodes are characterised by a unique movement during the analysis, whereas the nodes are able to travel in a pattern combined between Lagrangian and Euler formulations in order to provide the capability of continuous rezoning [25]. This solver can efficiently handle problems with great mesh deformations with superior resolution than other methods. Fluid-structure interfaces (FSI) are broadly used in the ALE solver in order to provide a coupling algorithm between a fluid and structure, which fulfils with the conservation equations of mass, energy, and momentum [48]. Therefore, this feature was used to simulate the present numerical model by considering the air, soil, and TNT as Eulerian meshes, which act as a fluid and remain fixed in space, while the tunnel structure acts as a pure Lagrangian mesh that can move with the material. An ALE multi-material group was used to simulate the mixture of various materials in each adopted mesh [49]. Constrained_Lagrange_In_Solid was used to achieve the coupling algorithm between Lagrangian and Eulerian meshes [24].
3. Results and Discussions
3.1. Validation of Numerical Models
3.1.1. Peak Pressure of Blast Waves into the Soil
Initially, the numerical model was created without the tunnel structure in order to monitor the transmission of blast shock waves into the soil during the explosion of a container truck. A convergence study was conducted via using meshes with element sizes of 125, 250, 375, and 500 mm. The outcomes of this study were compared with the results of the empirical equation that was provided by technical manual (TM5-855-1) to estimate the peak pressure values inside soil during a blast surface explosion, as follows [50]:
where Pp is the peak pressure of blast wave into the soil (MPa); f is the coupling factor, which equals to 0.14 for the surface blast in air; n and are the attenuation and acoustic impedance coefficients of the sandy loam soil, which are equal 2.75 and 4.972, respectively, as described in TM5-855-1 [50]; R is the distance to the explosion centre in m; and, W is the weight of the explosive charge in kg. A similar approach was used by several scholars to validate the propagation of explosion waves into the soil [3,23,25,26,51].
The results of convergence study demonstrated that the element sizes of 125 and 250 mm are the most suitable to predict the blast waves pressure inside soil, as shown in Figure 4. The total number of the numerical model elements with mesh sizes of 125 and 250 mm was 144,000 and 1,152,000, respectively. Consequently, a very high computational time of up to 49.25 h was needed to analyse the numerical model with a mesh size of 125 mm, as compared with a mesh size of 250 mm, which needed 6.32 h. Therefore, the element size of 250 mm is considered the most favoured size to simulate the numerical models of the current study.
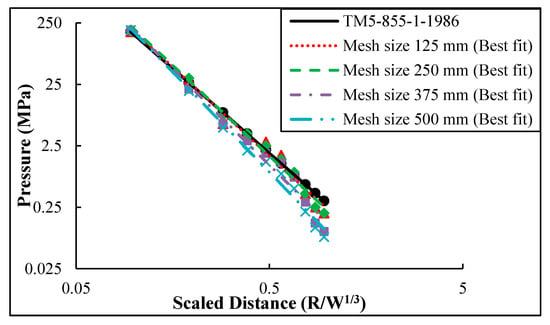
Figure 4.
Convergence test results of blast wave propagation into sandy loam soil.
Table 8 proves that the numerical model was efficiently able to estimate the values of peak pressure at depths of 1 to 7 m within a difference range of 1.01 to 18.70%. Nevertheless, the differences had significantly increased at depths 8 to 10 m, and recorded a difference range of 40.48 to 60%, since the location of the charge weight at the same ground level resulted in a greater dissipation of explosive energy into the air [32]. This model is considered as an improved version of the previous model proposed in our prior study [26], whereas the differences in peak pressures were significantly reduced from 14.93, 70.11, and 90.11% to 1.01, 16.92, and 40.48% at depths of 4, 6, and 8 m, respectively. This reduction is attributed to include the radial velocity factor in the (Initial _Volume_Fraction_Geometry) option which considerably affects the prorogation of blast waves into the soil [24]. Additionally, the initial mesh remapping factor must equal 0.2 when the ALE reference system type is chosen as the mesh smoothing option for shock waves, whereas the element grid can be contracted in the vicinity of the blast shock front [52].

Table 8.
Comparison of TM5 and numerical peak pressures at different depths into soil during a container truck explosion.
A similar trend of differences was observed by other scholars with the increase of soil depth during the numerical analysis for the quarter symmetrical models of soil, air, and TNT, as shown in Table 9 [23,25]. Yang et al. [23] reported high differences in the pressure as compared with TM5 even at a depth of 4 m during the explosion of 250 kg TNT charge. On the other hand, Mobaraki and Vaghefi [25] observed a good consistency with the TM5 at depths of 4 and 6 m during a detonation of a similar amount of explosive charge weight, however, the variances were highly increased at a burial depth of 8 m.

Table 9.
Differences percentage between TM5 and numerical results of previous studies.
Figure 5 appears the behaviour of the blast waves into the soil in term of pressure at different depths under the explosion centre of a container truck. It is proved that the distance and time from the blast centre could considerably decrease the pressure of blast waves by 853.83% at a burial depth of 8 m as compared to 4 m due to the dissipation of the blast waves into the sandy loam soil [53].
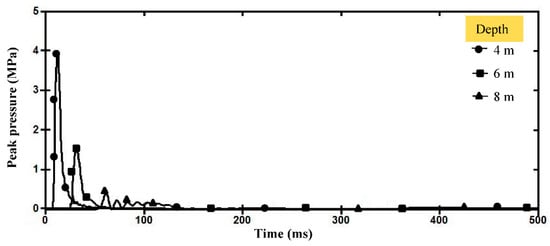
Figure 5.
Behaviour of shock waves into soil at different times during a container truck explosion.
3.1.2. Validation of Tunnel Dynamic Response
As mentioned previously, there are no available databases on full-scale field experiments to determine the behaviour of underground tunnels under the effect of a surface blast. Therefore, a convergence study was conducted to ensure the accuracy of tunnel behaviour. The study mainly depends on the results of the verification and the convergence test of the blast wave’s propagation inside soil, as described in Section 3.1.1, above in order to avoid the contact and node-to-node problems. The results of the convergence study conducted during the validation of the blast wave’s propagation into sandy soil revealed that the element size of 250 mm could give an accurate solution to the problem in a shorter time as compared with a mesh of 125 mm. However, the element size of 250 mm may cause overestimation for the dynamic response of the underground tunnel in some cases, like the tunnel of 250 mm lining thickness. Therefore, the convergence study was performed to validate the tunnel behaviour by using element meshes with 125 and 250 mm, as shown in Figure 6.
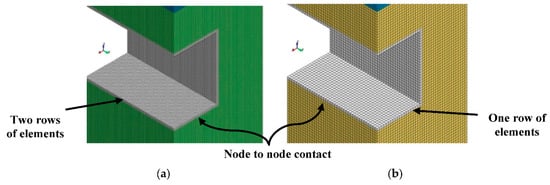
Figure 6.
Convergence study of tunnel response with a lining thickness of 250 mm by using mesh sizes of (a) 125 mm, and (b) 250 mm.
The outcomes revealed that the mesh size of 250 mm could efficiently estimate the dynamic response of the tunnel as in cases of lining thicknesses of 250 and 500 mm within differences less than 2.17 and 2.96% in terms of displacement, as well as, 8.22 and 7.32% in terms of velocity, respectively, as compared with a mesh size of 125 mm, as shown in Figure 7. Therefore, the mesh size of 250 mm was used to simulate the models of the present study to reduce the computational time, except the tunnel with 250 mm lining thickness, which was modelled by a mesh size of 125 mm to accurately represent the response of the tunnel, particularly in terms of failure. The prior studies proved that element sizes of 250 and 500 mm were capable of precise analysis of the three-dimensional model of the tunnel under a surface blast loading [23,25].
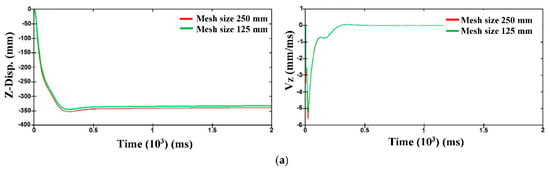
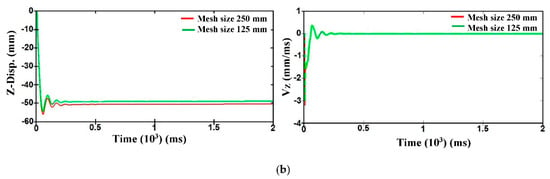
Figure 7.
Convergence test results of tunnel with lining thickness of (a) 250 mm, and (b) 500 mm.
3.2. Propagation of Blast Wave
3.2.1. Soil
The values of peak pressure into the soil were almost identical and its contours determined at different interval times of 12, 32, 62, and 124 ms before and after inserting the tunnel structure. The chosen time intervals corresponded to the values of peak incident pressure into the soil at depths of 4, 6, 8, and 10 m, respectively. The pressure response at a depth of 4 m was started at 7 ms and its maximum value was 3.98 MPa, which was recorded after 12 ms. Obviously, the main difference between the two cases is the affected region in the soil. The existence of the tunnel structure in the soil prevents the blast-induced waves from migrating to a deeper soil layer by reflecting the incident pressure. In addition, the results of pressure contours revealed that the explosion waves were travelled into the sandy soil in a hemispherical shape before and after inserting the tunnel structure, as shown in Figure 8. Its area was considerably increased with the wave propagation and results in a crater, which obviously matches the remarked phenomenon during the blast of the Ryongchon railway station in North Korea [23].
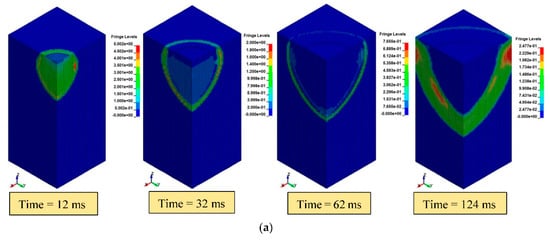
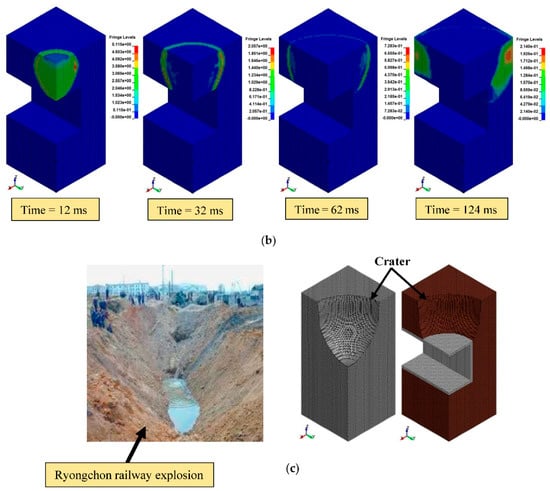
Figure 8.
Propagation and pressure contours of blast waves inside the soil: (a) before tunnel insertion; (b) after tunnel insertion; and, (c) the formation of a crater.
3.2.2. Tunnel
Figure 9 shows the reflected pressure contours of the underground tunnel at different time intervals, ranging from 9 to 500 ms. This revealed that the maximum pressure at a depth of 4 m was 4.87 MPa recorded after 9 ms, which means that the reflected pressure occurred immediately before the incident pressure reached its highest value. In other words, the total energy of the blast wave was transferred from the soil to the tunnel lining. A gradual decrease in the reflected pressure value was observed with the increase of the time interval until it became almost constant after 500 ms.
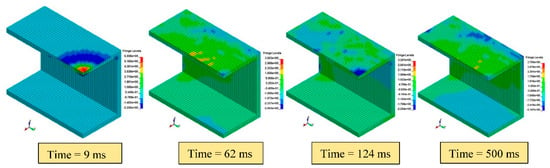
Figure 9.
Pressure contours of the underground tunnel.
3.3. Damage Assessment Results
The damage assessment was carried out for the tunnel roof centre due to this area being the most critical and destroyed, and which recorded the highest values of velocity and lateral displacement. A similar observation was determined by other researchers [23,25,26].
3.3.1. PPV Method
The damage levels that were proposed by Hendron [28] in Table 1 of Section 1.1, based on the PPV of the roof centre, were used to assess the behaviour of a box-shaped tunnel, as shown in Figure 10. Two tunnel cases were examined with a thickness of 250 mm and 500 mm at depths of 4 m and 6 m. The results indicated that the tunnels were greatly damaged at a depth of 4 m. A general failure level occurred at 250 mm lining thickness, while a local failure was noted at 500 mm lining thickness under the container truck detonation. On the other hand, an intermittent failure was observed for both thicknesses at a burial depth of 8 m. This assessment method was utilized by Mobaraki and Vaghefi [25], and reported that the tunnel with a roof thickness of 700 mm was safe at burial depths of more than 2 m. The results clearly revealed that the tunnel roof centre had faced intense blast waves at a burial depth of 4 m, which has a higher vertical velocity by 244.15% as compared with the shock wave velocity at a depth of 6 m. This behaviour may clearly reflect the great effect of soil depth on the tunnel safety, which works as a protective layer to dissipate the energy of blast waves. In addition, significant attention should be paid regarding choosing the soil that has the highest damping ratio in order to increase the resistance of the tunnel against an incredible surface explosion, such as a container.
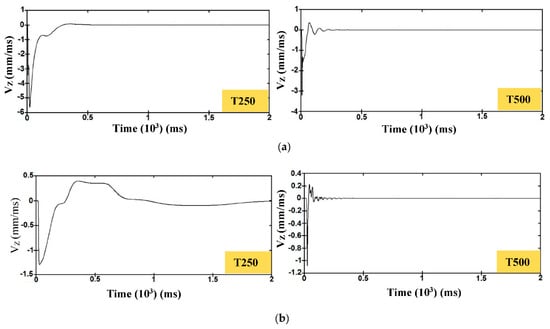
Figure 10.
Time histories of vertical velocity and reflected pressure for the tunnel roof centre at a burial depth of (a) 4 m, and (b) 6 m.
3.3.2. SDOF Method
In this study, the tunnel was simplified to an equivalent elastic-perfect SDOF model, according to Fallan and Louca [27]. This model defined the damage criterion based on the maximum displacement (yc) of the mid-height structural member, as shown in Table 2 above. Accordingly, yc was set to be the maximum numerical displacement of the tunnel, which occurred at the roof centre. The results revealed that the tunnel roof centre with 250 mm lining thickness collapsed at burial depths of 4 and 6 m. On the other hand, the lining thickness of 500 mm showed a considerable decrease in the lateral displacement. Nevertheless, the roof centre has recorded a high damage level at the burial depth of 4 m due to the high intensity of blast waves.
With the increase of burial depth, the lining thickness of 500 mm was able to resist a container explosion at burial depth of 6 m within a low damage level boundary condition. Once again, the burial depth of the tunnel was capable of reducing the lateral displacement of roof centre from 352.18 and 56.02 mm to 122.29 and 10.32 mm for lining thicknesses of 250 and 500 mm, respectively, as shown in Figure 11. Similar effect of burial depth on the tunnel safety was observed by several scholars [23,26]. Mussa et al. [26] revealed that the box-shaped tunnels with lining thicknesses of 250 and 500 mm collapsed at burial depths of 4 and 6 m, respectively. This observation may be attributed to the material model that was used in the study that neglected the strain rate sensitivity of concrete and rebar.
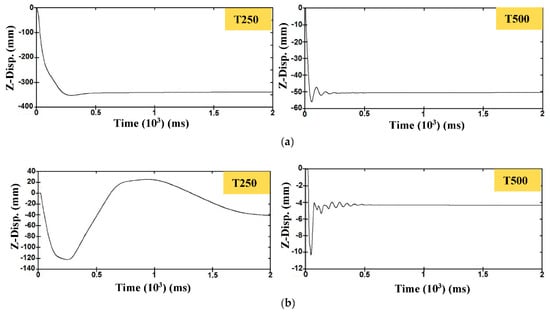
Figure 11.
Time history of lateral displacement for tunnel roof centre at burial depth of (a) 4 m, and (b) 6 m.
4. Comparison between Damage Assessment Methods
Based on the above results, it can be observed that the two assessment methods were efficiently capable to evaluate the behaviour of a box-shaped underground tunnel with some differences, which was particularly observed with the increase of burial depth. Therefore, a wide comparison was conducted to ensure the reliability of these methods. The effects of lining thickness, explosive charge weight, and burial depth on the tunnel velocity and displacement values were included in this comparison, as described in Table 10. The selected charge weights were a sedan, van, small delivery truck (SDT), and container, which were able to carry 227, 454, 1814, and 4536 kg of TNT charge weight, respectively. A lining thickness of 750 mm and burial depth of 8 m were also examined to provide an extensive reference to the feasibility of these assessment methods.

Table 10.
Velocity and displacement values of a tunnel roof centre at different explosive charge weights, lining thicknesses, and burial depths.
The results proved that the velocity and the lateral displacement values of the tunnel roof centre gradually increased by boosting the explosive charge weight magnitude due to the high intensity of the shock waves. On the other hand, a gradual reduction in the velocity and displacement was observed with the increase of the burial depth and lining thickness, owing to the high reflection ability of the thick tunnel lining and the dissipation of blast waves at large depths. The specifications that are mentioned in Section 1.1 were used to assess the damage behaviour of the tunnel under different circumstances, as shown in Table 11. The results indicated that the PPV and SDOF methods could be used efficiently to estimate the damage behaviour of a box-shaped tunnel at a shallow depth of 4 m, particularly during a container explosion. However, some differences were observed during van and SDT explosions, whereas the SDOF method recorded a medium failure level for the tunnel with lining thickness of 250 mm under a van explosion, while it was safe according to the PPV method. On the other hand, the SDOF stated that the tunnel with lining thicknesses of 500 and 750 mm were safe during a SDT, while it intermittently failed according to the PPV method.

Table 11.
Damage level of the tunnel based on the criteria of the PPV and SDOF methods.
The clear differences between the two methods were observed with the increase of the burial depth. Using the PPV method significantly underestimated or overestimated the damage level of the tunnel, especially during a SDT and container explosion. It recorded intermittent failure and safe levels for the tunnel with 250 mm lining thickness throughout a container explosion at burial depths of 6 m and 8 m, respectively. However, the observed failure mode of the tunnel clearly indicated that the tunnel was incredibly damaged at these depths during a container explosion, as shown in Figure 12. Moreover, no damage remarks were observed for the tunnel with lining thicknesses of 500 and 750 mm at depths of 6 and 8 m, while it intermittently failed, according to the PPV assessment. In contrast, the failure levels of the tunnel with a lining thickness of 250 mm clearly agreed with the damage levels recorded by the SDOF method, which stated that the tunnel had collapsed and was severely damaged at burial depths of 6 and 8 m, respectively, during a container explosion. Additionally, the tunnel was safe when the lining thicknesses of 500 and 750 mm were utilized at these depths. Therefore, the SDOF method could be considered to be more reliable to assess the damage level of a box-shaped tunnel and can be broadly used to ensure the safe design of these structures against a massive surface explosion.
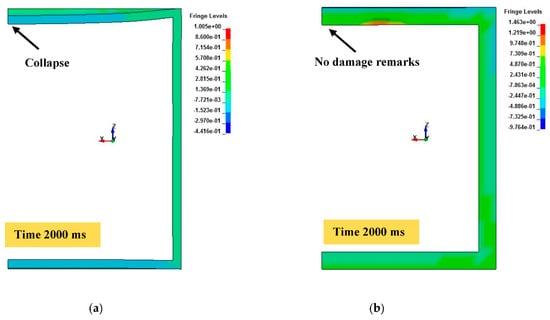
Figure 12.
Failure modes of the tunnel roof centre at a depth of 6 m during a container explosion with lining thickness of (a) 250 mm, (b) 500 mm.
Proposed Damage Criteria and Equation of the PVV Method
New boundary conditions were proposed for the damage levels of the PVV method based on the values of peak particle velocity corresponding to the lateral displacement of the tunnel, as shown in Table 10 above. The boundary conditions were suggested for each studied lining thickness of 250, 500, and 750 mm, as described in Table 12.

Table 12.
Proposed damage criteria of the PVV method at different lining thickness.
It can be noted that the lining thickness played an effective role in defining the damage levels of a box-shaped tunnel under a blast load by using the PPV method. The proposed boundary conditions indicated that the tunnel with a lining thicknesses of 500 and 750 mm capable to resist a peak particle velocity reach up to 1.105 mm/ms, while it was less than 0.058 mm/ms in the case of a lining thickness of 250 mm, which might clearly reflect the weakness of this liner. Additionally, the general failure (GF) of the tunnel was only observed in the case of a lining thickness of 250 mm, whereas, it did not appear at higher lining thicknesses because of the high ability to reflect and dissipate the blast waves. The assessment of tunnel damage behaviour, according to the proposed damage criteria, agreed considerably with the results of the SDOF method, as mentioned in Section 3.3.2 above, and as shown in Table 13. Therefore, the new criteria could significantly enhance the design accuracy of underground box-shaped tunnel structures under a massive surface explosion.

Table 13.
Damage level of tunnel based on the proposed criteria of the PPV method.
Based on the new boundary condition an equation was proposed to determine the relationship between PPV and burial depth, lining thickness, and charge weight by using the response surface methodology (RSM), which is available in the Design Expert software (version 11) [54]. The quadratic model was the most appropriate to analyse the data and to determine the relationship as follows:
where D is the burial depth between 4 and 8 m, T is the lining thickness between 250 and 750 mm, and W is the charge weight between 227 and 4536 kg.
PPV = 0.877890 − 0.377653 D + 0.000487 T + 0.001727 W + 0.000440 × D × T − 0.000156 × D × W − 1.66866 × 10–6 × T × W + 0.019156 D2 − 6.48000 × 10−7 × T2 + 1.00580 × 10−7 × W2
The variance analysis (ANOVA) was utilized to assess the precision of the adopted model, as shown in Table 14. It is indicated that the model can be successfully used to estimate the values of PPV at different burial depths, lining thicknesses, and charge weights. The quality of the model was determined according to the value of the correlation coefficient (R2), which is recommended to be close to 1, with a minimum value of 0.8 [55,56]. Furthermore, the variances between the Predicted and Adjusted (R2) have to be less than 0.2 and the adequate precision (AP) greater than 4 to achieve a clear signal of the model [57].

Table 14.
The results of the variance analysis (ANOVA) analysis for the PPV model.
5. Conclusions
The results can be summarized, as follows:
- The numerical validation results revealed a good consistency with technical manual (TM5-855-1) at depths between 1 and 7 m within differences ranging from 1.01–18.70%. However, the results diverged at large depths of more than 8 m with differences ranging between 40.48 and 60%.
- The pressure contours proved that the blast waves travelled inside the soil in a hemispherical shape before and after inserting the tunnel structure, which considerably reduced the values of incident pressure by obstructing the propagation of blast waves to large depths.
- The pressure contours of the tunnel revealed that the peak reflected pressure that occurred immediately before the incident pressure reached its highest value, which means that the total energy of the blast waves transferred from the soil to the tunnel lining.
- Using of SDOF method to assess the damage levels of a box-shaped tunnel was more reliable and harmonic with the tunnel failure modes as compared with the PPV method at the studied cases of lining thickness, burial depth, and explosive charge weight.
- The assessment of tunnel damage based on the proposed damage criteria and the equation of the PVV method matched considerably with the results of the SDOF method. Hence, these criteria might be broadly adopted by engineers to ensure an accurate design of underground box-shaped tunnel structures exposed to massive surface explosions.
Author Contributions
Conceptualization, M.H.M. and A.A.M.; Methodology, M.H.M., and A.A.M.; Software, M.H.M.; Validation, M.H.M., and A.A.M.; Formal Analysis, M.H.M.; Investigation, M.H.M.; Resources, A.A.M., R.H., and S.N.R.; Data Curation, M.H.M., and A.A.M.; Writing-Original Draft Preparation, M.H.M.; Writing-Review & Editing, M.H.M., A.A.M., and R.H.; Visualization, M.H.M., and A.A.M.; Supervision, A.A.M., R.H., and S.N.R.; Project Administration, A.A.M., R.H., and S.N.R.; Funding Acquisition, A.A.M., and R.H.
Acknowledgments
A special thanks to the Fundamental Research Grant Scheme (FRGS/1/2015/TK01/UKM/02/4) and Arus Perdana Grant (AP-2015-011) for their financial support in order to accomplish the current research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kong, L.; Jin, F.; Jiang, M. Analysis of the way and scale of terroristic raid. Blasting 2007, 24, 29–88. [Google Scholar]
- Verma, H.K.; Samadhiya, N.K.; Singh, M.; Goel, R.K.; Singh, P.K. Blast induced rock mass damage around tunnels. Tunn. Underg. Space Technol. 2018, 71, 149–158. [Google Scholar] [CrossRef]
- Koneshwaran, S. Blast Response and Sensitivity Analysis of Segmental Tunnel; Queensland University of Technology: Brisbane, Australia, 2014. [Google Scholar]
- Koneshwaran, S.; Thambiratnam, D.P.; Gallage, C. Blast Response of Segmented Bored Tunnel Using Coupled SPH–FE Method in Structures; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Buonsanti, M.; Leonardi, G. 3-D simulation of tunnel structures under blast loading. Arch. Civ. Mech. Eng. 2013, 13, 128–134. [Google Scholar] [CrossRef]
- Koneshwaran, S.; Thambiratnam, D.P.; Gallage, C. Response of segmented bored transit tunnels to surface blast. Adv. Eng. Softw. 2015, 89, 77–89. [Google Scholar] [CrossRef]
- Davies, M. Dynamic soil structure interaction resulting from blast loading. Centrifuge 1994, 94, 319–324. [Google Scholar]
- Davies, M.; Williams, A. Centrifuge modelling the protection of buried structures subjected to blast loading. In Structures under Shock and Impact II, Proceedings of the Second International Conference, Portsmouth, UK, 16–18 June 1992; Thomas Telford Publishing: London, UK, 1992. [Google Scholar]
- De, A. Numerical simulation of surface explosions over dry, cohesionless soil. Comput. Geotech. 2012, 43, 72–79. [Google Scholar] [CrossRef]
- De, A.; Morgante, A.N.; Zimmie, T.F. Mitigation of blast effects on underground structure using compressible porous foam barriers. In Poromechanics V, Proceedings of the Fifth Biot Conference on Poromechanics, Vienna, Austria, 10–12 July 2013; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- Kutter, B.L.; O’Leary, L.M.; Thompson, P.Y.; Lather, R. Gravity-scaled tests on blast-induced soil-structure interaction. J. Geotech. Eng. 1988, 114, 431–447. [Google Scholar] [CrossRef]
- Whittaker, J. Centrifugal and Numerical Modeling of Buried Structures. A Centrifuge Study of the Behavior of Buried Conduits under Airblast Loads; Department of Civil Environmental and Architectural Engineering, University of Colorado Boulder: Boulder, CO, USA, 1987; Volume 3. [Google Scholar]
- Liu, H. Damage of cast-iron subway tunnels under internal explosions. In Geo-Frontiers 2011: Advances in Geotechnical Engineering; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 1524–1533. [Google Scholar]
- Liu, H. Soil-structure interaction and failure of cast-iron subway tunnels subjected to medium internal blast loading. J. Perform. Constr. Facil. 2011, 26, 691–701. [Google Scholar] [CrossRef]
- Choi, S.; Wang, J.; Munfakh, G.; Dwyre, E. 3D nonlinear blast model analysis for underground structures. In GeoCongress 2006: Geotechnical Engineering in the Information Technology Age; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 1–6. [Google Scholar]
- Hu, Q.; Yuan, Y. Numerical Simulation of Internal Blast Effects on a Subway Station, in Computational Structural Engineering; Springer: Berlin/Heidelberg, Germany, 2009; pp. 699–706. [Google Scholar]
- Yu, H.; Wang, Z.; Yuan, Y.; Li, W. Numerical analysis of internal blast effects on underground tunnel in soils. Struct. Infrastruct. Eng. 2016, 12, 1090–1105. [Google Scholar] [CrossRef]
- Tiwari, R.; Chakraborty, T.; Matsagar, V. Dynamic analysis of a twin tunnel in soil subjected to internal blast loading. Indian Geotech. J. 2016, 46, 369–380. [Google Scholar] [CrossRef]
- Tiwari, R.; Chakraborty, T.; Matsagar, V. Dynamic analysis of underground tunnels subjected to internal blast loading. In Proceedings of the World Congress of Computational Mechanics (WCCM XI), Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Tiwari, R.; Chakraborty, T.; Matsagar, V. Dynamic Analysis of Tunnel in Soil Subjected to Internal Blast Loading. Geotech. Geol. Eng. 2017, 35, 1491–1512. [Google Scholar] [CrossRef]
- Hibbitt, Karlsson, and Sorensen. ABAQUS/Explicit: User’s Manual; Hibbitt, Karlsson and Sorenson Incorporated: Rhode Island, NY, USA, 2001; Volume 1. [Google Scholar]
- Luo, K.-S.; Wang, Y.; Zhao, Y.-T.; Hunag, L.-K. Numerical simulation of section subway tunnel under surface explosion. J. PLA Univ. Sci. Technol. 2007, 6, 022. [Google Scholar]
- Yang, Y.; Xie, X.; Wang, R. Numerical simulation of dynamic response of operating metro tunnel induced by ground explosion. J. Rock Mech. Geotech. Eng. 2010, 2, 373–384. [Google Scholar]
- Ls-Dyna, L. Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007. [Google Scholar]
- Mobaraki, B.; Vaghefi, M. Numerical study of the depth and cross-sectional shape of tunnel under surface explosion. Tunn. Undergr. Space Technol. 2015, 47, 114–122. [Google Scholar] [CrossRef]
- Mussa, M.H.; Mutalib, A.A.; Hamid, R.; Naidu, S.R.; Radzi, N.A.M.; Abedini, M. Assessment of damage to an underground box tunnel by a surface explosion. Tunn. Undergr. Space Technol. 2017, 66, 64–76. [Google Scholar] [CrossRef]
- Fallah, A.S.; Louca, L. Pressure–impulse diagrams for elastic-plastic-hardening and softening single-degree-of-freedom models subjected to blast loading. Int. J. Impact Eng. 2007, 34, 823–842. [Google Scholar] [CrossRef]
- Hendron, A. Engineering of Rock Blasting on Civil Projects; Hall, W.J., Ed.; Structural and Geotechnical Mechanics, a Volume Honoring NM Newmark; Prentice-Hall: Englewood Cliffs, NJ, USA, 1977; pp. 242–277. [Google Scholar]
- Kendorski, F.; Jude, C.; Duncan, W. Effect of blasting on shotcrete drift linings. Min. Eng. 1973, 25, 38–41. [Google Scholar]
- Nakano, K.-I.; Okada, S.; Furukawa, K.; Nakagawa, K. Vibration and cracking of tunnel lining due to adjacent blasting. Doboku Gakkai Ronbunshu 1993, 462, 53–62. [Google Scholar] [CrossRef][Green Version]
- Perea, C.; Alcala, J.; Yepes, V.; Gonzalez-Vidosa, F.; Hospitaler, A. Design of reinforced concrete bridge frames by heuristic optimization. Adv. Eng. Softw. 2008, 39, 676–688. [Google Scholar] [CrossRef]
- Henrych, J.; Major, R. The Dynamics of Explosion and Its Use; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Autodyn, A. Interactive Non-Linear Dynamic Analysis Software, Version 12, User’s Manual; SAS IP Inc.: Cary, NC, USA, 2009. [Google Scholar]
- Wang, Y.; Lee, S. Experimental study of water tank under impulsive loading. Arch. Civ. Mech. Eng. 2015, 15, 986–996. [Google Scholar] [CrossRef]
- Jiang, N.; Zhou, C. Blasting vibration safety criterion for a tunnel liner structure. Tunn. Undergr. Space Technol. 2012, 32, 52–57. [Google Scholar] [CrossRef]
- Jendele, L.; Cervenka, J.; Saouma, V.; Pukl, R. On the choice between discrete or smeared approach in practical structural FE analyses of concrete structures. In Proceedings of the Fourth International Conference on Analysis of Discontinuous Deformation Glasgow, Scotland, UK, 6–8 June 2001. [Google Scholar]
- Mohamed, H.; Mussa, A.A.M. Roszilah Hamid, and Sudharshan N. Raman, Dynamic Properties of High Volume Fly Ash Nanosilica (HVFANS) Concrete Subjected to Combined Effect of High Strain Rate and Temperature. Latin Am. J. Solids Struct. 2018, 15. [Google Scholar] [CrossRef]
- Malvar, L.J.; Crawford, J.E. Dynamic increase factors for steel reinforcing bar. In Proceedings of the 28th DDESB Seminar, Orlando, FL, USA, August 1998. [Google Scholar]
- Krieg, R.D. A Simple Constitutive Description for Cellular Concrete; Sandia National Laboratories: Albuquerque, NM, USA, 1972. [Google Scholar]
- Foster, W.A., Jr.; Johnson, C.E.; Chiroux, R.C.; Way, T.R. Finite element simulation of cone penetration. Appl. Math. Comput. 2005, 162, 735–749. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, Y.; Yu, G.; Liu, X. Evaluation of influence of vibrations generated by blasting construction on an existing tunnel in soft soils. Tunn. Undergr. Space Technol. 2014, 43, 59–66. [Google Scholar] [CrossRef]
- Bailey, A.C.; Johnson, C.E. A soil compaction model for cylindrical stress states. Trans. ASAE 1989, 32, 822–825. [Google Scholar] [CrossRef]
- Kulak, R.F.; Bojanowski, C. Modeling of cone penetration test using SPH and MM-ALE approaches. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Shin, J.-H.; Moon, H.-G.; Chae, S.-E. Effect of blast-induced vibration on existing tunnels in soft rocks. Tunn. Undergr. Space Technol. 2011, 26, 51–61. [Google Scholar] [CrossRef]
- Cheng, D.; Hung, C.; Pi, S. Numerical simulation of near-field explosion. J. Appl. Sci. Eng. 2013, 16, 61–67. [Google Scholar]
- Xie, L.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Wang, G.H.; Zhao, J. Damage evolution mechanisms of rock in deep tunnels induced by cut blasting. Tunn. Undergr. Space Technol. 2016, 58, 257–270. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.L.; Liu, C.Y.; Zhang, G.-X.; Lian, Y.; Tian, Y.; Xiao, Y.; Xie, X. Dynamic response of rectangular prestressed membrane subjected to uniform impact load. Arch. Civ. Mech. Eng. 2017, 17, 586–598. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA theory manual. Livermore Softw. Technol. Corp. 2006, 3, 25–31. [Google Scholar]
- Alia, A.; Souli, M. High explosive simulation using multi-material formulations. Appl. Ther. Eng. 2006, 26, 1032–1042. [Google Scholar] [CrossRef]
- US Army Engineers Waterways Experimental Station. Fundamentals of Protective Design for Conventional Weapons; TM5-855-1; US Army Engineers Waterways Experimental Station: Vicksburg, MS, USA, 1986. [Google Scholar]
- Mussa, M.H.; Mutalib, A.A. Numerical analysis of underground tunnels induced by ground truck explosion. In Proceedings of the CAASR International Conference on Innovative Engineering and Technologies & Advanced Theoretical Computer Applications, Bangkok, Thailand, 27–28 November 2015. [Google Scholar]
- Tabatabaei, Z.S.; Volz, J.S. A comparison between three different blast methods in LS-DYNA: LBE, MM-ALE, Coupling of LBE and MM-ALE. In Proceedings of the 12th International LS-DYNA Users Conference, Dearborn, MI, USA, 5–7 June 2012. [Google Scholar]
- Mutalib, A.A.; Bakhary, N. Empirical Formulae to Predict Pressure and Impulsive Asymptotes for P–I Diagrams of RC Columns Strengthened with FRP. J. Teknol. 2011, 55, 27–38. [Google Scholar] [CrossRef]
- Vaughn, N.; Polnaszek, C. Design-Expert® Software; Stat-Ease, Inc.: Minneapolis, MN, USA, 2007. [Google Scholar]
- Joglekar, A.; May, A. Product excellence through design of experiments. Cereal Foods World 1987, 32, 857–868. [Google Scholar]
- Noordin, M.Y.; Venkatesh, V.C.; Sharif, S.; Elting, S.; Abdullah, A. Application of response surface methodology in describing the performance of coated carbide tools when turning AISI 1045 steel. J. Mater. Process. Technol. 2004, 145, 46–58. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments 6th Edition with Design Expert Software; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).