Abstract
The main goal of the local theory for crystals developed in the last quarter of the 20th Century by a geometry group of Delone (Delaunay) at the Steklov Mathematical Institute is to find and prove the correct statements rigorously explaining why the crystalline structure follows from the pair-wise identity of local arrangements around each atom. Originally, the local theory for regular and multiregular systems was developed with the assumption that all point sets under consideration are -systems or, in other words, Delone sets of type in d-dimensional Euclidean space. In this paper, we will review the recent results of the local theory for a wider class of point sets compared with the Delone sets. We call them t-bonded sets. This theory, in particular, might provide new insight into the case for which the atomic structure of matter is a Delone set of a “microporous” character, i.e., a set that contains relatively large cavities free from points of the set.
1. Introduction
Crystallization is naturally perceived as a process resulting from a mutual interaction of only nearby atoms. It is believed that the long-range order of atomic structures of crystals is determined by local rules restricting the arrangement of nearby atoms. Feynmann wrote “When the atoms of matter are not moving around very much, they get stuck together and arrange themselves in a configuration with as low an energy as possible. If the atoms in a certain place have found a pattern which seems to be of low energy, then the atoms somewhere else will probably make the same arrangement. For these reasons, we have in a solid material a repetitive pattern of atoms. In other words, the conditions in a crystal are this way. The environment of a particular atom in a crystal has a certain arrangement, and if you look at the same kind of an atom at another place farther along, you will find one whose surroundings are exactly the same. If you pick an atom farther a long by the same distance, you will find the conditions exactly the same once more. The pattern is repeated over and over again and, of course, in three dimensions” ([1], Ch. 30). As we see, Feynmann emphasizes that the “surroundings are exactly the same”, and the identity condition for the surroundings (clusters) in a point set implies that the symmetry group of the set is point-transitive. It is obvious that if a Delone set possesses a transitive symmetry group, then the clusters of an equal radius around each point of the set are the same. However, the question about what kind of “local identity” for a Delone set should be required to guarantee a “global order” remained unanswered until the 1970s.
Actually, in this field, before the 1970s, there were no rigorously-proved mathematical statements until B. Delone and R. Galiulin (probably to some extent influenced by N. Belov) formulated the problem and Delone’s students N. Dolbilin and M. Stogrin developed a mathematically-sound local theory of crystals (see, for instance, [2,3,4,5,6]).
In this paper, we review the history and development of the local theory for regular systems and crystals. This review was sparked by recent developments in local theory, as well as the generalization of the results of the theory for regular sets (Definition 2) and crystals to the wider class of sets that we call t-bonded sets (Definition 7) that contains the class of Delone sets (Definition 1) as a proper subclass.
In the local theory for Delone sets of type , the parameter R (the radius of the largest ‘empty ball’) plays a new role: any two points from the Delone set can be linked by a sequence of points from the Delone set in which the inter-point distance for any two consecutive points does not exceed . On the other hand, among Delone sets, there are “microporous” sets for which the doubled emptiness radius significantly exceeds the ‘bond parameter’ t. Moreover, a set may not be a Delone set at all, but each of two points of the set can be boundedby a point sequence in which the distance between any consecutive points is bounded above by some positive value t.
In 1976, the second author introduced the concept of t-bonded sets under the name of d-connected sets [3], which is a generalization of the concept of Delone sets. In light of the developments in the local theory for Delone sets since 1976, as well as in chemistry and crystallography, we believe that the local theory for t-bonded sets needs to be developed to describe atomic structures that are represented by “microporous” Delone sets, as well as by non-Delone sets. We also hope that using the parameter t will spur progress in solving the regularity radius problem for Delone sets in .
At the end of the Introduction, one should mention that the discovery of quasicrystals (1984, Nobel Prize 2011) triggered a new wave of research for about three decades. The best model for quasicrystals is a Meyer set, i.e., a Delone set X such that its Minkowski difference is also a Delone set. It should be noted that the lattices, regular and multiregular sets we describe in our paper are a particular case of Meyer sets. Focusing on the local theory for regular systems, we do not discuss this area, though Meyer sets are of great interest from the viewpoint of local theory. What are the properties of clusters that compose a Meyer set? How does the cluster counting function grow depending on the cluster’s radius? These challenging questions still need to be answered. The reader interested in the theory of Meyer sets can be referred to J. Lagarias [7].
2. Delone Sets, Crystals and -Bonded Sets
In this section, we present the basic definitions and theorems related to the local theory for crystals and t-bonded sets. According to the concept of a crystal, which goes back to E.S. Fedorov [8], a crystal, or a multiregular system, is defined as the finite union of several point orbits with respect to a crystallographic group.
The concept of a crystal is based on the notion of an -system, which models the atomic structure of any solid matter, including those that have an amorphous structure. The elegant theory of -systems was constructed by Delone [9,10]. The key point of the theory by Delone is the idea of the so-called “empty ball”. Nowadays, the -systems are called Delone (Delaunay) sets.
Definition 1.
(Delone set) Let be the Euclidean space and r and R some positive numbers. A set is called a Delone set of type if:
- (i)
- (r-condition) any open ball of radius r has at most one point from X;
- (ii)
- (R-condition) any closed ball of radius R has at least one point from X.
Remark 1.
The Definition 1 of a Delone set requires the existence of numbers r and R with specified properties. However, for the sake of shortening the theorems’ statements and proofs, we included these two parameters into the definition of a Delone set as a characteristic of the set. Even more, we chose r as the supremum of all numbers such that set X satisfies r-condition and R as the infimum of the set of all numbers that satisfy the R-condition. In this paper, we will use the term -systems whenever we need to make a reference to the parameters R or r, and we will use Delone set otherwise.
Hilbert and Cohn-Vossen [11] suggested considering a regular point set as a point set that looks from each of its points the same up to infinity. However, any attempt to introduce rigor into the explanation of what “looks the same from each point up to infinity” or “in set X the view is the same from each point up to infinity” means would inevitably involve the concepts of symmetries of X, the symmetry group , which should act transitively on X.
Definition 2.
(Regular system) A Delone set X is called a regular system if for any two points x and y from X, there is a symmetry s of X such that , i.e., if the symmetry group acts transitively on X.
Remark 2.
It follows immediately from Definition 2 that a regular system X is an orbit , where x is a point from X, and G is, generally speaking, a subgroup of . We remind that the G-orbit of x is the set .
Definition 3.
(Discrete group) A group , where is the group of all isometries of , is called a discrete subgroup, if the orbit of any point is a discrete subset of .
Definition 4.
Let G be a discrete subgroup of . We call a closed domain in a fundamental domain of group G if:
- (i)
- for any point , the intersection of and the orbit is not empty;
- (ii)
- for any point , the interior of contains at most one point from .
Definition 5.
(Crystallographic group) A discrete subgroup is called crystallographic if a fundamental domain of G is compact.
Statement 1.
(For the proof, see [6,12]). A set is a regular system if and only if X is an orbit of a point with respect to a crystallographic group G.
Definition 6.
(Crystal [8]) We say that a set is a crystal if X is the G-orbit of a finite set , i.e., , where is a crystallographic group.
Thus, a crystal can be regarded as a union of orbits of several points with respect to the same crystallographic group G. Figure 1 below is an example of crystal X, which is the G-orbit of a three-element set , where G is the complete group of orientation preserving isometries of the square lattice. The G-orbit of one (blue) point of is a lattice. The G-orbit of another (red) point of set is a regular system consisting of four lattices. The G-orbit of the third (green) point of is a regular set consisting of four lattices. Thus, the crystal X in Figure 1 is a union of three regular sets, or the union of nine congruent and parallel lattices.
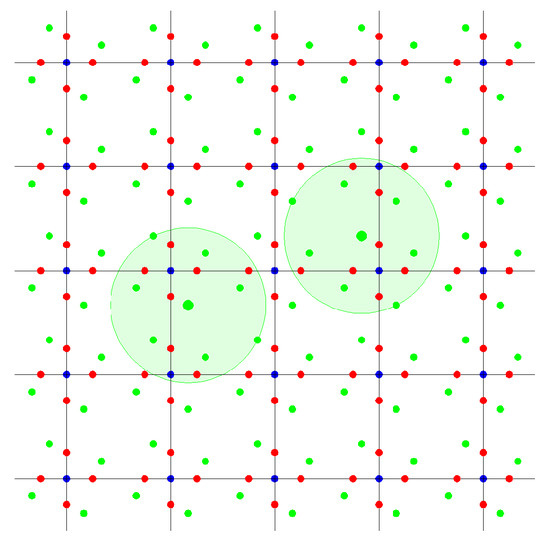
Figure 1.
Crystal (the union of three regular systems).
The concept of crystal as a crystallographic orbit of a certain finite point set was described by Fedorov. Though the definition does not contain explicitly the idea of periodicity, Fedorov was convinced that any crystallographic group acting in 3D space contains a subgroup of finite index consisting of pure translations. Moreover, he presented arguments that, in his opinion, constituted a proof of this fact. Though his arguments contained a serious gap, the fact itself turned out to be true. It is relatively easy to prove that a crystallographic group acting in the Euclidean plane contains a translational subgroup of finite index. The proof for is due to A. Schoenflies [13] and based on new profound ideas. In 1900, D. Hilbert in the XVIIIth problem posed a question about the finiteness of the number of non-isomorphic crystallographic groups for a given dimension d [14]. The affirmative answer to this question followed from the availability of a translational subgroup of finite index in the crystallographic group for any d [15].
Theorem 1.
(Schoenflies–Bieberbach) A crystallographic subgroup G of contains a translational subgroup T with a finite index h, where index .
It is known that (the order of the full group of a d-cube) for all d except . Thus, for example, is the order of the group of the regular hexagon, and is the order of the group of the 24-cell.
By the Schoenflies–Bieberbach theorem, the crystallographic group G is partitioned into h cosets . Therefore, any crystal is the union of a finite number of congruent and parallel lattices of rank d, i.e., , where points belong to . It is easy to see that for given , any subset is a point lattice, and lattices for all i and j are pairwise congruent and parallel. The number of lattices here does not exceed . Sometimes, the number of lattices is strongly less than , because some points of can be either equivalent to each other or fixed with respect to some isometries from G. The following theorem establishes the equivalence of different definitions of a crystallographic group (see, e.g., [6]).
Theorem 2.
(Equivalent definitions of a crystallographic group) The following properties of a subgroup G of the group are equivalent.
- (i)
- G is a crystallographic group by Definition 5 above.
- (ii)
- G is a space group. That is, the subgroup of all pure translations T in G is a d-dimensional lattice, which is necessary for the maximal abelian subgroup of G.
- (iii)
- There exists such that is a Delone set of .
- (iv)
- For any , the G-orbit is a Delone set in .
We would like to point out that Delone sets have the following property that plays a significant role in most proofs of the local theory of crystals.
Statement 2.
(See, e.g., [2]) For any two points x and of a Delone set X of type , there is a finite sequence of points from X, such that , .
From now on throughout the paper, we will not necessarily consider Delone sets, but uniformly-discrete sets, which are defined as sets that fulfil the r-condition: for some positive r, any open ball of radius r has at most one point from X.
Definition 7.
(t-bonded set) We call a uniformly-discrete set a t-bonded set, where t is a positive number, if for any two points x and , there is a finite sequence of points from X such that , .
The sequence , for which , is called a t-chain and denoted by .
Statement 2 implies that any Delone set of type is a -bonded set.
Definition 8.
(Regular t-bonded system) A t-bonded set X is called a regular t-bonded system if for any two points x and y from X, there is a symmetry s of X such that , i.e., if the symmetry group acts transitively on X.
Theorem 3 slightly improves the bound for t in Statement 2.
Theorem 3.
Any Delone set of type , , is a t-bonded set with , where .
Since the value of is close to one for , there are Delone sets of type , which are t-bonded sets with the value of t arbitrarily close to . However, there are crystalline structures, (e.g., zeolites) that are presented as Delone sets of type for which the bond parameter t is significantly shorter than .
The proof of the local criterion for regular systems ([2]) uses the fact of -linking of a Delone set of type . However, in fact, it is not the parameter R of a Delone set X that is essential, but the ‘bond’ parameter t. The upper bound for the regularity radius of the X, i.e., for the size of the local region that determines the regularity of X, also depends on the value of t. In this respect, the value of in many structures seems to be unnecessarily large, though for some Delone sets, the value of t can be very close to .
3. Clusters in -Bonded and Delone Sets
Throughout the paper, unless stated differently, we consider t-bonded sets X in Euclidean d-space that are of rank d, i.e., . Thus, X only fulfills the r-condition and, generally speaking, is not a Delone set. As for a Delone set, it is reasonable to choose r as the supremum of all numbers r such that the set X satisfies the r-condition.
It is clear that . For some Delone sets, the value of t can be chosen significantly less than . For instance, if is the cubic lattice, then t can be chosen as the edge length of the cube and .
In the local theory, the concept of a cluster plays a central role. We note that the concepts of the cluster , as well as the concepts of the clusters’ equivalence and of the clusters’ group of symmetries we adopt in this paper are the same for both Delone sets and t-bonded sets.
Definition 9.
(Cluster) For , a ρ-cluster centered at point is defined as a set of all points such that , i.e., where is the closed ball of radius ρ centered at x.
Since in a Delone set of type , any two points can be connected by a -chain, the bond parameter t for a t-bonded set has a role similar to the value in a Delone set. Therefore, it is important to compare the difference between -clusters in the case of Delone sets and t-clusters in the case of t-bonded sets. For instance, the following statement is true for Delone sets.
Statement 3.
In a Delone set , the dimension of the affine hull of a -cluster is equal to the dimension d of space.
As for a t-cluster in a t-bonded set , an analogous statement on its rank, i.e., on the dimension of the affine hull of the t-cluster, generally speaking, is wrong.
Example 1.
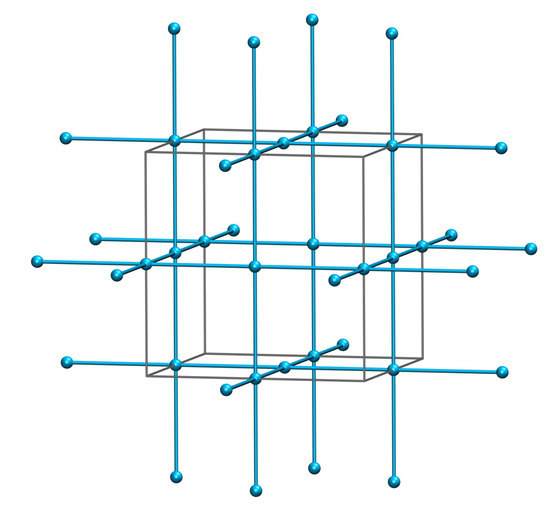
A Delone set X in for which the parameter t is significantly smaller than , all t-clusters have rank 2, although the whole set X has rank 3, is depicted in Figure 2.

Figure 2.
Structure of NbO.
This set X can be described as follows. Let be an integer point lattice of rank 3 constructed on the orthonormal basis, and . Then X is a Delone set with parameters and . It is easy to see that X is a t-bonded set with . Though each t-cluster is a ‘cross’ of rank 2, the set X is of rank 3. Moreover, since all -clusters in X are centrally symmetrical and mutually equivalent (see Definition 10 below), X is a regular system [16,17,18].
This example shows that even for regular systems, the rank of a cluster can start with low values and grow with the cluster’s radius. The behavior of clusters’ rank for a t-bonded set is described by the following statements (Theorems 4 and 5). We will use a shorter notation for the rank of the cluster .
Theorem 4.
Assume that for a t-bonded set and some , the following condition holds for any ,
Then, for all and for all , one has and .
From now on, we assume the rank of X to be equal to d.
Theorem 5.
Let be a t-bonded set, such that for every given , the ranks of ρ-clusters are equal for all . Then, for any and any , the rank .
Theorem 5 follows from Theorem 4 because under the conditions of Theorem 5, the stabilization of the rank of a growing cluster at any point definitely occurs before the radius of the cluster reaches the value .
Definition 10.
(Cluster equivalence) Given a set X in , , and two points x and , we say that the ρ-clusters and are equivalent, if there is an isometry g of , such that and .
For this equivalence relation, the set of all -clusters in X is presented as a disjoint union of equivalence classes. For a t-bonded set X, the set of equivalence classes for is, generally speaking, infinite. However, we will focus on t-bonded sets of finite type.
Definition 11.
(Set of finite type) A set X is said to be of finite type if the set of classes of ρ-clusters is finite for any .
Definition 12.
(Cluster counting function) For a t-bonded set X of finite type, the number of equivalence classes of ρ-clusters in X is a function of ρ, which is called the cluster counting function and denoted by .
It is obvious that the cluster counting function is a positive, piecewise constant, integer-valued, monotonically non-decreasing and continuous from the left function.
For Definitions 2 and 6, if a t-bonded set X is a Delone set, then X is a regular system or a crystal if and only if its cluster counting function for all is equal to one, or bounded from above , respectively. In the latter case, is the number of orbits in crystal X.
Let us denote by a group of all isometries of , which leave fixed.
Definition 13.
(Symmetry of a cluster) Assume , then an isometry is called a symmetry of the cluster if .
We should emphasize that in the definition, we require that a symmetry of a cluster leaves its center x fixed. We denote by a group of all symmetries of the cluster .
Let , , be an n-dimensional plane where . Then, any symmetry leaves the plane invariant. Let and be the restriction of to the . Then, the group of all restrictions , where , can be considered as the symmetry group of X in the group of isometries of .
If , then . Let , we denote the orthogonal complement to passing through the point x by . This complement is a -plane. It is easy to see that any symmetry is an orthogonal mapping of d-space that leaves the subspace and the orthogonal complement invariant. Therefore, an isometry g from is a symmetry of the cluster if and only if it fulfills the following two conditions: (1) the isometry g, restricted to the , is an isometry of that leaves invariant; (2) the restriction to the orthogonal complement is an isometry of that leaves point x fixed.
One should emphasize that since and is a finite set, the group is finite. It follows from the fact that any isometry of the n-dimensional space is determined uniquely by the -image of an affinely independent -point set in the -cluster .
The following lemma [19] summarizes some facts about the cluster group. Unlike Delone sets, where the affine hull of a -cluster is , it is not the case for clusters in t-bonded sets. Therefore, in proofs of the local theory for t-bonded sets, we have to monitor the rank of the affine hulls of extending clusters until its stabilization occurs, as in Theorem 5.
Lemma 1.
The following statements hold true for any given .
- (1)
- If aff and , then , where , and is the group of isometries of the orthogonal complement that leave point x fixed.
- (2)
- The group is a finite subgroup of . Particularly, if aff, then group is a finite subgroup of .
- (3)
- The group is finite if and only if the rank of is equal to d or .
All proofs are straightforward.
4. Local Criterion for Regular -Bonded Systems
In this section, we will discuss the local criterion for regular t-bonded systems [19]. The criterion is a generalization of the local criterion for Delone sets [2].
Here, we note that if for x and and , the -clusters and are equivalent, then their groups and are conjugate in , since for any g such that and , we have .
Now, we prove a theorem that plays an important role in proving the local criteria for regular systems. The following theorem is a generalization of a result from the pioneering work [2] in the local theory. We would like to emphasize that in Theorem 6, the parameter has no specific meaning, unlike in the local theory for Delone sets where it is equal to . In the future, whenever we apply this theorem to the local theory of t-bonded sets, we assign to the parameter the value of the parameter t.
Theorem 6.
(δ-extension) Assume that for points x and and for some positive ρ and δ, the clusters and are equivalent, and the groups and coincide:
Then, any isometry such that and also maps the -cluster onto , i.e., .
Proof.
Since for a given , the clusters and are equivalent, there is at least one isometry such that and .
Let f be an arbitrary isometry that maps -cluster onto -cluster . Let us take the composition , then we have:
It follows from (3) that . Hence, by condition (2) of Theorem 6, . Let us put , . Thus, . Since g maps onto and maps onto , we conclude that f maps onto . ☐
One of the central goals of the local theory for t-bonded, as well as for Delone sets is to determine the ‘regularity radius’ in terms of t and d or in terms of r, R, and d, respectively. The regularity radius for t-bonded sets is defined analogously to the definition for Delone sets.
Definition 14.
(Regularity radius)
Given and , the regularity radius is a number such that:
- (1)
- if for a t-bonded set X in , then X is a regular system;
- (2)
- for any , there is a t-bonded set Y in with , which is not a regular system.
As is well known, the upper bound for the regularity radius for Delone sets is derived from the local criterion for Delone sets (Theorem 8 [2]). In [19], the local criterion has been established for t-bonded sets.
Theorem 7.
(Local criterion for a regular t-bonded system) Given a t-bonded set X in , assume that there is such that the following two conditions hold:
- (1)
- ;
- (2)
- for some point .
Then, Sym acts on X transitively.
The proof of this criterion based on Theorem 6 is rather elegant. Since the proofs of all the local criteria for regular, as well as for multiregular systems are very similar, we will not give a proof of Theorem 7. However, we will prove Theorem 15, from which the local criteria for regular and multiregular sets follow. The proof of Theorem 15 uses the same idea only under more general conditions.
A well-known local criterion for regular Delone sets [2] is a particular case of the local criterion for regular t-bonded sets.
Theorem 8.
(Local criterion for a regular Delone system) A Delone set Xis a regular set if and only if there is a positive number such that two conditions hold:
- (1)
- ;
- (2)
- .
The following corollaries follow immediately from the local criteria.
Corollary 1.
Assume that X is a t-bonded set in . If in X and is a trivial group, then for any , i.e., X is a regular t-bonded system.
Corollary 2.
Assume that X is a -system in . If in X and is a trivial group, then for any , i.e., X is a regular Delone set.
Atomic structures of many crystals are centrally symmetric, and the next two theorems demonstrate that for Delone sets with centrally symmetric clusters, the local conditions that guarantee the regularity of the whole set are much simpler than in the general case.
New important results related to this case of centrally symmetric structures have been recently proven for any dimension d by N. Dolbilin [16] (Theorems 9 and 10) and N.Dolbilin, A. Magazinov [17,18] (Theorem 11). So far, no similar results are proven for t-bonded sets.
Definition 15.
(Locally antipodal set) A Delone set in which each -cluster is centrally symmetric about its center x is called locally antipodal (i.e., locally centrally symmetric).
Theorem 9.
A Delone set is centrally symmetric about each of its points if and only if it is locally antipodal.
Theorem 10.
For any dimension d, if a Delone set is locally antipodal, the condition implies that X is a regular set.
Theorem 11.
Any locally antipodal Delone set is a crystal.
It looks surprising that in Theorem 11 there are no conditions on . Nevertheless, just from the local antipodality of X, it follows that X is a crystal.
As we have already mentioned, one of the major problems in the local theory is estimating the regularity radius for Delone sets of type from above and from below. In fact, it has been known that for all (see, e.g., [19,20]). Significant progress in this direction was made by the Working Group on Delone Sets (consisting of seven authors [21]) at the Workshop on Soft Packings, Nested Clusters and Condensed Matter, held at the American Institute of Mathematics (AIM) in San Jose, California, USA, 19–23 September 2016. Working together, the group established a new lower bound for the regularity radius for any dimension d (Theorem 12).
Theorem 12.
(Lower bound for the radius of regularity) Suppose R is a fixed positive number. For any , there exists a non-regular d-dimensional -system such that and X is not a regular set.
In our opinion, it is very interesting that the regularity radius grows at least linearly depending on dimension d.
5. -Bonded and Delone Sets in and
We will start the section with the discussion of an example of a very special type of Delone sets in . Namely, this structure has led the Working Group at the AIM’s Workshop to the d-dimensional construction (named by the group Engel sets) and to Theorem 12.
Statement 4.
For any dimension and any positive , there is a system X that is not a regular system, though for this system.
Proof.
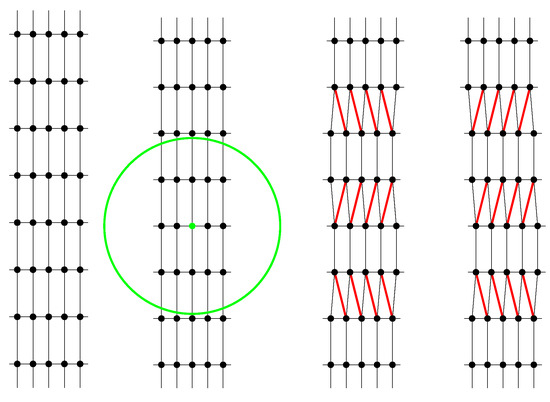
We will explicitly construct an example of such a system in .
Let us start with a rectangular lattice of rank 2 constructed on the orthogonal basis with a ‘small’ base b and a ‘large’ height h such that (left picture in Figure 3). We can choose parameter R for lattice as half of the diagonal of the -rectangle. In the second picture from the left (Figure 3), the circle has radius , where the positive number can be chosen arbitrarily small if is sufficiently large.

Figure 3.
Construction of Engel sets in plane.
Let us modify the lattice into a different Delone set in the following way. Let us enumerate the horizontal rows of (see the left picture) by a bi-infinite sequence (the order goes upwards). Let us select from them all odd rows of rectangles and fix positive number c, where . Now, let every odd row be shifted with respect to the the even row adjacent from below by c either to the left (the shift is denoted by L), or to the right (denoted by R). The points of two adjacent rows and form vertices of the rectangles. The points of the next pair of rows and form the next row of rectangles shifted either to the left or to the right side. The vertices of the rectangles from the shifted rows form a new Delone set . However, by means of different sequences of shifts, one can construct infinitely, even uncountably, many different, non-congruent other sets. It is easy to see that for each set, the parameter R remains the same as in . Moreover, for such a set, . Among these sets, there are regular systems. A set is a regular system if and only if a corresponding bi-infinite sequence of shifts is one of three forms: , , and . In all other (uncountably many!) cases, is not a regular set, although . In Figure 3, the last two pictures on the right are examples of this process ( and ). The Delone set depicted in the very right picture is not a regular system. ☐
Further on in this section, we will discuss local criteria for following [20,22]. Since the local theory for t-bonded sets is a generalization of the theory for Delone sets, the statements will be formulated for t-bonded sets whenever possible, whereas corresponding results for Delone sets will be presented as a particular case for .
Lemma 3 [22] below is a generalization for t-bonded sets of a very valuable Lemma 2 for Delone sets [5].
We would like to note that in the Lemmas 2 and 3, below the conditions and , respectively, imply that groups or , respectively, are conjugate for all .
Lemma 2.
(Stogrin) Let be a Delone set with condition and q the order of a rotation in for some point . Then, .
Stogrin’s lemma is generalized for t-bonded sets as follows.
Lemma 3.
Let be a t-bonded set such that and . Let also q stand for the order of a rotation axis in for some .
- Then, X is either a non-collinear set for which or a collinear set.
- If X is collinear, it is a regular system of three types:
- X is a two-point set;
- X is a lattice on a line;
- X is a bi-lattice, i.e., the union of two congruent and parallel lattices on a line.
Now, we are going to formulate some results on the upper bound for .
Definition 16.
For a finite group G, a sequence of consecutively embedded subgroups,
starting with G and ending with the trivial group , is called a tower of G; the number m is called the height of the tower.
We denote by the maximum height of a tower of G.
The following upper bound for is trivial: The remark below easily follows from Theorem 7.
Remark 3.
Assume for a t-bonded set X, for and , the cluster group is finite. Let , where , then X is a regular t-bonded system.
The next remark immediately follows from Remark 3 and reproduces the analogous important property for Delone sets.
Remark 4.
In a t-bonded set X in , if the cluster group for some and is trivial and , then X is a regular t-bonded system.
We note that the local criterion, Lemma 2, and these simple remarks regarding Delone sets were the starting point for proving the following theorem obtained long ago independently by M. Shtogrin and independently by N. Dolbilin [20]. Besides the above-mentioned observations, the proof of Theorem 13 requires many additional arguments.
Theorem 13.
(-theorem) For a Delone set X in , if , then X is a regular system.
As far as t-bonded sets are concerned, the following theorem is proved in [22].
Theorem 14.
(-theorem) For a t-bonded set X in , if , then X is a regular t-bonded system.
The last two theorems are relatively similar and comparable. The -theorem is valid for a wider class of sets, but on the other hand, it does not directly imply the -theorem (because the condition is more akin to the condition than to the condition ).
6. Local Criteria for Multiregular -Bonded Systems and Crystals
In this section, following [19,23], we will extend the results of the local criteria from the class of Delone sets to the class of multiregular t-bonded systems [4,6,23].
Definition 17.
(Multiregular t-bonded systems) A t-bonded set is a multiregular t-bonded system if there is a finite set such that:
This definition is analogous to that of a crystal (Definition 6). However, in some respects, the situation is quite different. For instance, in the case of crystals, we deal with Delone sets, which are always infinite sets. As far as t-bonded sets are concerned, any finite set X is a t-bonded set for some value t and can be considered a multiregular system: where each element of
is a representative of an orbit from In particular, if a finite set X is totally asymmetric, i.e., Sym(X) is trivial, then the set X can be considered as the union of one-point orbits
Nevertheless, the following question is correct in any case, finite or infinite, for t-bonded sets and Delone sets.
Let us call a t-bonded set an m-regular t-bonded system if the number of classes in X/Sym(X) is m. Are there conditions that guarantee that a t-bonded (Delone) set X is an m-regular t-bonded system respectively crystal)? The criteria of regularity for multiregular t-bonded sets (Theorem 16 [19]) and crystals (Theorem 17 [4,6,23]) answer these questions.
The idea of proof of the criterion for multiregular t-bonded sets is similar to that of the analogous criterion for a crystal (see, e.g., [4,6,23]). In the case of a t-bonded set, in order to prove this criterion, we do not need to prove that the group is a crystallographic group, though it needs to be proved for the crystals. Local criterion for regular systems (Theorem 7) is a particular case of Theorem 16. Theorem 15 is a core of local criteria and, from our point of view, not only technical, but also of interest in its own right.
For any given , the set X is partitioned into subsets , such that for any two points , their -clusters and are equivalent, and both belong to the i-th equivalence class of -clusters: . For example, if X is a regular system, then for any , all -clusters are equivalent, and the partition is trivial, i.e., the only class of the partition is the entire set X.
Theorem 15.
Let a t-bonded set X fulfill Conditions (1) and (2) below:
- (1)
- (2)
Let also be a subset of X as defined above before the theorem statement; and for given points x and from , let fulfill the following conditions: and . Then:
- (i)
- g is a symmetry of the entire set X;
- (ii)
- For any , the group generated by all symmetries g of X with the conditions above acts transitively on every set ,
- (iii)
- does not depend on i, i.e., .
Proof.
Let us take and g such that and , then we prove that g is a symmetry of X.
First, we will prove that for any point . Let us connect an arbitrary point to x by a t-chain . We will show that g-images of all points in the chain starting with and ending with belong to X.
Since , it follows that and where . Since and , by Theorem 6, it follows that .
Since in the t-chain, the distance , applying the same argument to the points and as we applied to the and , we prove that for any positive integer , and .
Hence, and .
To show that g is a surjection, we note that the inverse isometry maps onto x and onto . Applying the same argument to as we applied to g, we show that maps X onto X. Therefore, for any , . Hence, g is a surjection.
Now, let us consider the group containing all such isometries g taken for any pair of points from . We have just proved that the group , as well as any other subset , , leaves invariant. Moreover, by the assumption, is the Sym and acts on transitively.
Next, we have , and . Inversely, any symmetry leaves invariant. Therefore, for any , and (iii) is proved. ☐
Theorem 15 immediately implies the local criterion for m-regular t-bonded systems.
Theorem 16.
(Local criterion for m-regular t-bonded systems) A t-bonded set is an m-regular t-bonded system if and only if there is some such that two conditions hold:
- (1)
- (2)
In order to obtain a similar criterion for crystals (Theorem 17) from Theorem 16, we will need to augment the proof of Theorem 16 by proving that the group Sym is crystallographic. Though the X is a Delone set, this does not imply that the group Sym is crystallographic, because in this case, the group Sym does not act transitively on the X. To establish the crystallography of the group Sym, it should be proved that at least one subset is a Delone set. The existence of a crystallographic group follows from two facts. First, the X is the union of the finite number of Delone sets , and second, Sym acts transitively on each .
Theorem 17.
(Local criterion for crystals) A Delone set is a crystal if and only if for some , the two conditions hold:
- (1)
- (2)
7. On Delone Sets of Finite Type and -Bonded Sets of Infinite Type
In this section, we discuss Delone and t-bonded sets of finite type (Definition 11). We will show how different Delone sets and t-bonded sets are, as far as the property “to be a set of finite type” is concerned. For Delone sets, there exists a local condition of a Delone set X to be a set of finite type (Statement 5). Therefore, for a Delone set X, if the counting function is finite for , then the set X is of finite type. For t-bonded sets that are not Delone sets, the situation is quite different. For a given arbitrarily large , there are t-bonded sets for which , but the entire set is not of finite type (Theorem 18). Statement 5 below is well known, and its proof can be found in [7] or [20]; the proof of Theorem 18 is presented in this paper for the first time.
Statement 5.
If X is a Delone set with , then for all , the cluster counting function , i.e., X is a set of the finite type.
Now, we return to a more general case when X is a t-bonded set. The following theorem shows that the case of t-bonded sets differs from the case of Delone sets.
Theorem 18.
Given , for an arbitrarily large , there is a t-bonded set such that , but for any , .
Proof.
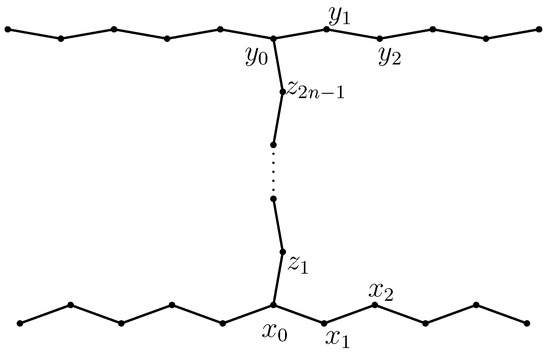
We will construct an example of such a t-bonded set X of infinite type in plane with orthogonal coordinates .
We take two positive numbers a and b, where is irrational and . Given an arbitrarily large , we draw two horizontal lines and , given by:
Along each of the lines and , we construct ‘horizontal’ broken lines whose vertices constitute subsets and .
The vertex set of the infinite broken line along is determined as follows:
- , for all (i.e., i is even) and
- , for all (i.e., i is odd) and .
The altitude in an equilateral triangle is chosen so that segment-lengths , , ∆ of the broken line are equal to t.
The vertex set of the infinite broken line along is determined as follows:
- , for all and
- for all , , .
The altitude in the equilateral triangle is chosen so that segment-lengths , , ∆ of the second broken line are also equal to t.
Note that all the points of with even indices are on the line , and all the points of with odd indices are below this line.
Similarly all points of with even indices are on the line , and all points of with odd indices are above this line.
The distance between and is equal to . Since is irrational, it is easy to see that if we take any other pair and of vertices from and , respectively, the distance .
Let the third point set be the vertex set of a finite broken line along the interval with the endpoints and . The broken line is constructed as follows.
Let a number be such that and is integer. Now, we construct a broken line with vertices and segment-lengths all equal to t, where:
- if i is even, where, we note, and ;
- if i is odd.
Here, the altitude in the equilateral triangle is chosen so that the lateral sides and of the triangle are both equal to t.
Now, we define a t-bonded set (Figure 4).

Figure 4.
Point set .
The role of is to make the entire set Xt-bonded. We emphasize that by construction of X, any t-cluster in X has rank 2, i.e., the dimension of the affine hull of the is equal to two for any point .
It is easy to see that . In fact, clusters , are equivalent for all i with that holds if .
Analogously, for , clusters are equivalent if .
Besides these two classes of -clusters in X, there is a finite amount of non-equivalent -clusters centered at points and with and , respectively, and there is a finite amount of also non-equivalent -clusters centered at points of . Therefore, .
Throughout the rest of the proof, we will consider clusters centered at points and only with even indices i and j. To be consistent with all the notations, let us redesignate the points with even indices i with new natural indices p, where , . A similar change is done for the points where j is even, , where . Then, and , where p and q are positive integer numbers.
Take a circle centered at with radius , . Let be so small that and the line intersect over a chord with the the length where . Let also be taken less than the distance between two rows of the vertex set . Since , for any .
Let us consider a set Q of all pairs such that , i.e., the point belongs to the cluster centered at the point . Any such pair satisfies the inequality , or, in other words, satisfies the inequality:
By the Dirichlet theorem, the inequality:
has infinitely many solutions in positive integers .
Let be the continued fraction of and the n-th convergent. The sequence of convergents determines the following two sequences of positive integer numbers:
such that:
Now, for each integer positive n, we take the n-th convergent and the corresponding pair of points where and . Due to (8) for all sufficiently large n (), the following inequality holds:
By the choice of , it follows from (9) that belongs to the cluster . Moreover, for all .
Let and be two pairs from Q, i.e., and . It is easy to see that for the clusters and , there are at most two potentially possible isometries of the plane that establish the equivalence of these clusters. In fact, since , points and also belong to the cluster . We can even say that if , these two points are the only two points that belong to the cluster at the distance a from the center of . The same observation is true regarding the cluster , centered in the point . This means that any isometry g of plane that would establish the equivalence of the clusters and should map the center onto the and points and onto points and (though we do not claim that the order of these two points should be preserved). Since the isometry g has to map onto , which are both on line , there can be at most two isometries of this type. The first option is for g to be a parallel shift when maps onto and maps onto . The other option, when g is the same translation followed by the reflection around the vertical line, .
Let us prove now that and are not equivalent provided and . Note that and . We will prove that neither a translation, nor a translation, followed by the reflection around line , can establish the equivalence of the clusters and .
Assume that g is a translation of one cluster into another, then . It follows that , i.e., . The latter contradicts the fact that is irrational. If g is assumed to be the superposition of the translation along the axis and the reflection about the vertical line , then we have , and consequently, we get the contradiction again: is rational.
Therefore, -clusters and are not equivalent for two different pairs and from the infinite set Q. Hence, we have that for X, and for any . ☐
8. Summary
In the paper, we reviewed the local theory of regular and multiregular Delone and t-bonded sets. The most significant progress in this area since our presentation on a similar subject at the 4th Annual International Conference on Computational Mathematics, Computational Geometry and Statistics in Singapore in 2015 [23], is the development of the local theory for t-bonded sets; publishing of a proof of the -theorem; and establishing the lower bound of the radius of regularity for Delone sets (Theorem 12 [17,24]). The concept of t-bonded sets seems to be more appropriate to describe the chemical bonds existing between atoms in real structures. In many respects, this theory follows the tracks of the local theory of regular Delone systems. However, the concept of t-bonded sets extends the class of Delone sets, and therefore, it is no surprise that in spite of the similarity of the theories, there are new features in those t-bonded sets that are not Delone sets.
From our point of view, the highest priorities in the studies of the local theory for Delone sets and t-bonded sets are establishing the values of the regularity radius (Definition 14) for Delone sets and t-bonded sets as a function of d and R, and t, respectively, improving the existing upper bounds for the regularity radius in 3D space ( for t-bonded sets and for Delone sets) and establishing some additional conditions for t-bonded sets (like locally-symmetric Delone sets) that would allow one to establish the regularity radius for these sets. The second direction that from our point of view is worth pursuing is to extend the theory of regular sets for clusters defined by other metrics.
Author Contributions
The Review part of the paper was written by Mikhail Bouniaev and Nikolay Dolbilin jointly. Nikolay Dolbilin has written Section 7 describing conditions for t-bonded sets to be of finite type.
Acknowledgments
The authors would like to express their deep appreciation to the reviewers who thoroughly read the paper and made many very valuable remarks and suggestions that helped to improve the paper. The work of N. Dolbilin was supported by the Russian Science Foundation Grant 14-50-00005.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Feynmann, R.; Leighton, R.; Sands, M. The Feynmann Lectures on Physics; Addison-Wesley: London, UK, 1963; Volume 2. [Google Scholar]
- Delone, B.N.; Dolbilin, N.P.; Stogrin, M.I.; Galiuilin, R.V. A local criterion for regularity of a system of points. Soviet Math. Dokl. 1976, 17, 319–322. [Google Scholar]
- Dolbilin, N.P. On Local Properties for Discrete Regular Systems. Sov. Math. Dokl. 1976, 230, 516–519. [Google Scholar]
- Dolbilin, N.P.; Stogrin, M.I. A local criterion for a crystal structure. In Proceedings of the IXth All-Union Geometrical Conference, Chisinau, Moldova, 20–22 September 1988; p. 99. (In Russian). [Google Scholar]
- Stogrin, M.I. On the upper bound for the order of axis of a star in a locally regular Delone set, Geometry, Topology, Algebra and Number Theory, Applications. In Proceedings of the International Conference Dedicated to the 120th Anniversary of Boris Nikolaevich Delone (1890–1980), Moscow, Russia, 16–20 August 2010; Abstracts. Steklov Mathematical Institute: Moscow, Russia, 2010; pp. 168–169. (In Russian). [Google Scholar]
- Dolbilin, N.P.; Lagarias, J.C.; Senechal, M. Multiregular point systems. Discret Comput. Geometry 1998, 20, 477–498. [Google Scholar] [CrossRef]
- Lagarias, J. Geometric Models for Quasicrystals I. Delone Sets of Finite Type. Discret Comput. Geometry 1999, 21, 161–191. [Google Scholar] [CrossRef]
- Fedorov, E.S. Elements of the Study of Figures. Zap. Mineralog. Obsc. 1985, 21, 1–279. [Google Scholar]
- Delaunay, B. Sur la sphère vide. A la mémoire de Georges Voronoï. Bull. Acad. Sci. l’URSS 1934, 6, 793–800. [Google Scholar]
- Delone, B.N. Geometry of positive quadratic forms. Uspekhi Matematicheskikh Nauk 1937, 3, 16–62. (In Russian) [Google Scholar]
- Hilbert, D.; Cohn-Vossen, S. Geometry and Imagination; AMS Chelsea Pub.: Providence, RI, USA, 1999; p. 367. [Google Scholar]
- Charlap, L. Bieberbach Groups and Flat Manifolds; Springer: New York, NY, USA, 1986. [Google Scholar]
- Schoenflies, A. Kristallsysteme und Kristallstruktur; Druck und verlag von BG Teubner: Leipzig, Germany, 1891. [Google Scholar]
- Milnor, J. Hilbert’s problem 18: On crystallographic groups, fundamental domains, and on sphere packing, in: Mathematical Developments Arising From Hilbert Problems. In Proceedings of the Symposia in Pure Mathematics; American Math. Soc.: Providence, Rhode Island, 1976; Volume 28, pp. 491–506. [Google Scholar]
- Bieberbach, L. Ueber die Bewegungsgruppen des n-dimensionalen Euklidischen Raumes I. Math. Ann. 1911, 70, 207–336. [Google Scholar] [CrossRef]
- Dolbilin, N.P. A Criterion for crystal and locally antipodal Delone sets. Vestnik Chelyabinskogo Gos Universiteta 2015, 3, 6–17. (In Russian) [Google Scholar]
- Dolbilin, N.P.; Magazinov, A.N. Locally antipodal Delauney Sets. Russ. Math. Surv. 2015, 70, 958–960. [Google Scholar] [CrossRef]
- Dolbilin, N.P.; Magazinov, A.N. The Uniqueness Theorem for Locally Antipodal Delone Sets. Proc. Steklov Inst. Math. 2016, 294, 215–221. [Google Scholar] [CrossRef]
- Bouniaev, M.; Dolbilin, N. Regular and Multiregular t-bonded Systems. J. Inf. Process. Jpn. 2017, 25, 735–740. [Google Scholar]
- Dolbilin, N. Delone Sets in : The Regularity Conditions. Fundam. Prikl. Mat. 2016, 21. An English translation will appear in the English version of ‘Journal of Mathematical Sciences’ in 2018. (In Russian) [Google Scholar]
- Baburin, I.; Bouniaev, M.; Dolbilin, N.; Erochovets, N.; Garber, A.; Krivovichev, S.; Schulte, E. A Lower Bound for the Regularity Radius of Delone Sets. Acta Cryst. 2017. submitted. [Google Scholar]
- Bouniaev, M.M.; Dolbilin, N.P. Regular t-bonded Systems in . Eur. J. Comb. (Mem. Michele Deza) 2018, in press. [Google Scholar]
- Mikhail, M.; Bouniaev, N.P. PDolbilin, Local Theory of Crystals: Development and Current Status. In Proceedings of the 4-th Annual International Conference on Computational Mathematics, Computational Geometry and Statistics, Singapore, 26–27 January 2015; pp. 39–45. [Google Scholar]
- Dolbilin, N. Delone Sets: Local Identity and Global Symmetry. In Discrete Geometry and Symmetry; Memory Karoly Bezdek’s and Egon Schulte’s 60th Birthdays; Proceedings in Mathematics and Statistics, (to Appear); Conder, M.D.E., Deza, A., Ivich, A., Eds.; Springer: Weiss, UK, 2018. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).