Abstract
Although combinatorial testing has been widely studied and used, there are still some situations and requirements that combinatorial testing does not apply to well, such as a system under test whose test cases need to be performed contiguously. For thorough testing, the testing requirements are not only to cover all the interactions among factors but also to cover all the value sequences of every factor. Generally, systems under test always involve constraints and dependencies in or among test cases. The constraints among test cases have not been effectively specified. First, we introduce extended covering arrays that can achieve both t-way combinatorial coverage and t-wise sequence coverage, and propose a clocked computation tree logic-based formal specification method for specifying constraints. Then, Particle Swarm Optimization (PSO) based Extended covering array Generator (PEG) is elaborated. To evaluate the constructed test suites, a method for verifying the constraints’ validity is presented, and kernel functions for measuring the coverage are also introduced. Finally, the performance of the proposed PEG is evaluated using several sets of benchmark experiments for some common constraints, and the feasibility and usefulness of PEG is validated.
1. Introduction
With the development of computer technology and the increase in custom requirements, software systems are becoming more powerful and complex. In fact, the emergence of unexpected faults in such systems is inevitable. Once the system encounters a certain fault, it is likely to fail. Failure means that the system operates with unexpected behaviors. Testing is a very necessary and significant means of system quality assurance during the product development life cycle [1]. A report released by NIST (National Institute of Standards and Technology) in 2002 stated that software system bugs cost the U.S. economy 59.5 billion dollars annually [2]. However, more than one third of this cost could be saved if better testing is performed [2]. A contributing test method that can exactly find more faults with fewer test cases is urgently needed.
Combinatorial testing (CT) [3,4,5,6] is an efficient testing method through which an optimal or near optimal test suite with fewer test cases can be designed or generated. CT has proven to be an effective technique for detecting faults caused by interactions among configurations or factors in a given input space [7]. The empirical studies of system bugs suggest that CT is equivalent to exhaustive testing in a certain sense [8,9]. Although CT has been widely studied and used, there are still some situations and requirements that combinatorial testing does not apply to well, such as a system under test (SUT) whose test cases need to be performed contiguously. For thorough testing, the testing requirements of this SUT are not only to cover all the interactions among factors, but also to cover all the value sequences of every factor. When CT is used to design a test suite for this SUT, only the interactions among factor values can be effectively covered to a certain level according to the t-way combinatorial criterion; there is no effective criterion for the value sequences of every factor [10]. For example, the “text effect” application of “Microsoft Word” has seven options for users to modify some highlighted text. These options are “subscript”, “superscript”, “strikethrough”, “double strikethrough”, “all caps”, “small caps”, and “shadow” [9]. The font-processing function within the application correctly modifies the highlighted text on the screen according to the settings consisting of these options. When using CT, a test suite with several test cases can be generated to cover interactions among every t options. When the test suite is executing, the font-processing function modifies the text according to the test cases in sequence. However, the sequence of settings in every factor from contiguous test cases cannot be guaranteed to be tested at a certain level, such as a sequence from text with subscript to text without subscript for the “subscript” option with binary settings.
To solve the mentioned sequence coverage requirement, a t-way sequence coverage criterion for the requirement was proposed [11] based on the t-way combinatorial coverage criterion. The t-way sequence coverage criterion was first introduced to apply to event sequence testing. In terms of an SUT with n input events, each event can only be input once during a test. Each test case in the test suite covers subsequences with length t , and the covered t events in a subsequence do not have to be neighboring. A t-way sequence coverage test suite can cover all subsequences that have t different events. The size of a t-way sequence coverage test suite is considerably less than that of the exhaustive test suite. Thus, a t-way sequence coverage test suite can replace the exhaustive test suite, which cannot be executed in practice. Another similar form of t-way sequence coverage is t-wise sequence coverage, which was presented by Kruse [12]. t-wise sequence coverage applies to SUTs with n inputs each of which can appear more than once in a test. Additionally, the t inputs covered in a subsequence must be contiguous. The two types of sequence coverage criteria generally meet the sequence coverage requirement. Then, for SUTs whose test cases need to be performed contiguously, test suites can cover both the interactions among factor values and the value sequences of every factor by combining t-way combinatorial coverage and t-wise sequence coverage. The simplest way to combine them is to generate test suites separately and then integrate them into a large test suite. Although some coverage redundancies exist in the integrated large test suite, it successfully enables testing of SUTs with test cases performed contiguously.
In practice, SUTs always involve constraints or dependencies in or among test cases [1], such as interaction must not appear in a test case or value must not be input after . If a test does not meet the constraints, the test is invalid. To automatically generate a valid test suite, the constraints should first be formally specified. Then, the formal specification of constraints can be used to direct the test suite generation. Although some formal specification methods have been used, such as linear temporal logic (LTL) and computation tree logic (CTL), the constraints among test cases or test steps have not been effectively specified, such as when the third input is , the fifth input must be . Because of the existence of constraints, when a t-way combinatorial coverage test suite is used alone, it may potentially violate the constraints among test cases. When a t-wise sequence coverage test suite is used alone, it may potentially violate the constraints in a test case. Hence, simply combining these two test suites into a large test suite is infeasible.
In this paper, we present a research work on extending covering arrays for sequence coverage, and we introduce extended covering arrays that can achieve both t-way combinatorial coverage and t-wise sequence coverage. Then, we propose a formal specification method for specifying constraints based on clocked computation tree logic (CCTL), which is an extension of CTL. The main contribution of this paper is to propose extended covering arrays with combinatorial coverage and sequence coverage for SUTs with test cases to be performed contiguously. This research has practical application value and will improve the efficiency of software testing. To evaluate the constructed test suites, a method for verifying constraints’ validity among test cases is presented corresponding to the specification method, and kernel functions are also introduced to measure the coverage for constructed test suites.
As Particle Swarm Optimization (PSO) is competitive in uniform and variable strength covering array generation [13], we propose Particle swarm optimization based Extended covering array Generator (PEG) for constructing extended covering arrays in this paper. The performance of our proposed PEG is evaluated using several sets of benchmark experiments for some common constraints and the feasibility and usefulness of PEG is validated.
The remainder of this paper is organized as follows. First, Section 2 reviews the theoretical background and methods for sequence coverage testing. Some relative definitions are given in Section 3. Section 4 introduces extended covering arrays. Section 5 outlines the design and implementation of PEG, including its corresponding algorithms. Section 6 presents evaluation methods for verifying constraints’ validity and measuring coverage. The results of 12 benchmark systems under test generated by PEG are presented in Section 7. Finally, the paper is concluded with a brief summary and provides a discussion of future research in Section 8.
2. Related Work
Here, we review previous work toward efficient solutions about sequence coverage requirements using combinatorial testing.
In terms of SUTs with n input events, where each event occurs exactly once in a test, the CT-based testing is sequence-based t-way testing. Kuhn is perhaps the first person to apply sequence-based t-way testing. He proposed a “quick and dirty” (QnD) algorithm, which is based on a greedy algorithm and likely has room for improvement [14], and he then presented Sequence Covering Arrays (SCAs) according to covering arrays [15]. Subsequently, he proposed a modified greedy algorithm that can handle the constraints between event pairs [16], and he used to test labeled transition systems [17]. He reported several algorithms for generating with the proposed t-way sequence coverage criterion. These algorithms represent the first effort to systematically explore possible strategies for solving the problem of t-way test sequence generation in a general context. Zamli discussed the sequence-based fixed and variable strength testing as an extension of existing t-way strategies and noted that there is clearly room for improvement, particularly for the t-way sequence coverage testing [11]. Then, a sequence-based t-way interaction testing strategy using the bees algorithm was presented by Zamli [18]. The proposed algorithm shows a promising result when compared to QnD through an experiment. A method for a t-way event-driven test suite generation based on simulated annealing called t-way Event-Driven Input Sequence Test Case (EDISTC-SA) generator was presented by Rahman [19]. Farchi defined a test as an ordered tuple of input parameter values and introduced the ordered constraints and the ordered interaction coverage criteria [10]. Then, an efficient algorithm for generating test suites with minimum sizes that satisfies the ordered interaction coverage criteria was proposed and evaluated on several real-life systems. are of practical value in testing. As exhaustive testing always consists of an incredible magnitude of tests, can reduce the cost of testing by decreasing the number of tests.
An innovative approach that combines model-based testing and combinatorial testing to design executable and feasible test sequences was described by Nguyen [20]. The approach starts from a finite state model, and based on the model, it generates executable paths that represent sequences of events to be executed against the SUT. Then, these paths are transformed to the equivalence classes of a classification tree [21]. The first children classifications of the root node of the tree represent the events, and the classes of a classification are the optional values of the corresponding event. Finally, the executable test cases corresponding to an executable path are generated from the classification tree using t-way testing. The classification tree method [21], which is a model-based black-box test design technique [22], was proposed based on equivalence partitioning, and it is always used for systematic test design and description of test cases. Mature products based on the classification tree method to design test sequences are TESTONA [23] and TESSY [24,25]. Using the classification tree method, the input domain of an SUT is regarded under various aspects assessed as equivalent by the tester. For every aspect, disjoint and complete classifications are partitioned. The subsequent partition of every aspect through classifications is a graphical representation based on the form of a tree [21]. Classes, which are disjointed abstractions of individual input levels for test purposes [26], derived from these classifications may be further classified even recursively [21]. The tree is the head of the combination table corresponding to a test suite, and test cases are the body of the combination table. Test cases are constituted by combining classes from different classifications and correspond to test steps of the testing task. During the test run, test cases are generally executed in sequential order. The testing design of the classification tree method has been widely used for embedded systems [12], embedded automotive systems [12,22,26,27,28] and web applications [29] in terms of functional requirements. In addition, “Modbat” and Microsoft’s ”Spec Explorer” are also model-based test case generating tools. “Modbat” can generate state transitions coverage test cases [30]. Microsoft’s “Spec Explorer” can generate automated test cases by running traversal techniques to achieve a form of transition coverage and enable testers to find violations of the requirements with a minimum of manual effort [31].
Generally, there are constraints among test steps in real systems [12,32,33]. Once test steps in a test suite that violate the constraints exist, the test suite is invalid for testing. Thus, it is very important to specify constraints and generate valid test suites based on the specifications [12]. Schooljan described the linear temporal logic (LTL)-based formal specification method for dependency rules [34]. In his work, temporal logic expressions are used to validate each test step of a test sequence. The specification of dependency rules cannot describe the constraints within test steps subjected to LTL. A similar work was conducted by Fraser, in which constraints were presented by computation tree logic (CTL) [33]. Using LTL and CTL, the constraints among test cases were specified, whereas the test cases involving constraints are restricted to neighboring test cases. Krupp and Müller proposed an innovative application of clocked CTL (CCTL) logic to describe the constraints in real-time systems [35]. The corresponding proposed model checker can verify the validity of test sequences by combining I/O interval specifications and CCTL expressions. Some similar coverage requirements with t-way testing criteria were proposed by Kruse [1,12], such as state coverage, transition coverage and state pair coverage. The state coverage is similar to the 1-wise sequence coverage, which needs all the states to be covered at least once, and constraints among test cases involving the order of states in every factor need to be avoided. The transition coverage is 2-wise sequence coverage, which needs all the transitions of states of every factor to be covered at least once. The state pair coverage is similar to the 2-way combinatorial coverage, which requires all the interactions between two factors to be covered at least once, and the constraints among test cases involving the order of states in every factor need to be avoided. Then, three algorithms to generate state coverage and transition coverage test cases were proposed [10].
3. Background
Before we introduce extended covering arrays, we present the existing covering arrays. When using CT, the first step is to develop the input space model of the SUT [36]. The term “input” is used here in a general sense; any factor that can have an influence on the behavior of the SUT and that can be kept under control is considered to be an “input” [36]. The input space model implicitly defines the SUT’s valid input space [37]. Given that an SUT has k input factors , and factor has values or levels, the input space model of the SUT can be represented as . P is the set of factors , and V is the set of numbers of values . For each factor , we use to denote the set of values, abbreviated as .
CT approaches systematically extract and produce a set of configurations that will be run in the testing phase from the input space model [36]. A set of configurations is called a test suite and a t-way covering array, in which each valid combination among factor values corresponding to t different factors appears at least once.
Definition 1.
Given a set with , if belongs to the set of factors P with and belongs to , the set I is defined as a t-way interaction to be covered [38].
We use the set to denote all the t-way interactions to be covered.
Definition 2.
A test case is a k-dimensional vector with [38,39].
Given a test case and an interaction , if meets, then we say that T covers I, denoted as . We use to denote all the interactions covered by T.
Definition 3.
Consider that A is an mixed-level covering array, denoted by [38,40], such that every column i only has elements from the set and every possible t-way interaction is at least covered in one row of A. t is the strength of .
If the smallest n for exists, we also denote it by . Another alternative form of is , which indicates that there are parameters with values, parameters with values, and so forth. It is clear that . When the sizes of all the value sets are the same, , we use covering array to replace mixed covering array. If the smallest n for exists, we also denote it by or .
A single set of configurations consists of one value from every factor. However, not all combinations of factor values may be valid, as some constraints related to some certain factor values exist. Once a single set of configurations contains these values, the single set is invalid. Such existing constraints are often caused by logical relationships among factors. For a calendar example, if factor "month" takes February, then factor "date" must take no more than 29. To guarantee that a test suite avoids all the invalid combinations successfully, the constraints must be modeled and specified.
Definition 4.
is a constraint covering array, where a new variable forbidden interaction F is introduced to present the set of constraints [40]. For each constraint interaction in F, there is , where x denotes the "do not care" values. The constraints are often called forbidden tuples [41,42] and forbidden edges [43].
When the k factors have different number of values, constraint mixed-level covering arrays are used.
For example, an SUT has three factors A, B and C with , and a constraint . The constraint mixed covering array is shown in Table 1. covers all the value pairs between each two factors, except .

Table 1.
.
4. Extended Covering Arrays
In this section, we introduce extended covering arrays.
4.1.
When shown in Table 1 is used to test an SUT contiguously, 2-way combinations are covered. If the SUT has a sequence coverage requirement, then the two-value sequences of each factor are not completely covered. As in the test sequence of factor A, only three two-value sequences , , and are covered. If we use a 2-wise sequence coverage test suite as shown in Table 2, although all the sequences of two values of each factor are covered, some value combinations are not covered, such as and . If both the sequence coverage and combinatorial coverage are required, then the only way to satisfy this requirement is to combine them into a test suite. However, combining them into a test suite may lead to some redundancies and a larger size. To design test suites that can meet both sequence coverage and combinatorial coverage with smaller sizes, extended covering arrays are defined.

Table 2.
A 2-wise sequence coverage test suite.
Definition 5.
Consider that a array A is an extended mixed-level covering array, denoted by , where is combinatorial coverage strength and is sequence coverage strength, such that every column i only has elements from the set and the following two conditions are met:
- ①
- for each interaction with length (), there is at least one row r (), ;
- ②
- in each column i , for every possible value sequence with length such as , there are contiguous rows with .
If the smallest n for exists, we also denote it by . Another alternative form of is . When the sizes of all the value sets are the same, , we denote the extended covering array as or .
For the example presented above, an is shown in Table 3. The extended covering array covers all combinatorial pairs and two value sequences only with size 10.

Table 3.
.
4.2.
In real systems, in addition to the constraints among factor values, there are constraints that involve sequences of factor values. Such a sequence of factor values is also often identified by logically specifying constraints. These two types of constraints must be avoided in final test suites; otherwise, test suites may be invalid. Thus, the specification and model of the constraints are the preconditions to design and generate test suites. On the one hand, the specification of constraints can help to avoid constraints in the process of constructing test suites. On the other hand, the specification of constraints can help to verify whether the designed test suites are valid. We also define the extended constraint covering array as . As there exist constraints that involve value sequences of each factor, some interactions of factor values may not appear in one test case in practice. See Section 5 for details. This produces a conceptual differences between and . In other words, may violate the first condition in Definition 5. Then, we modify the first condition of to fit . The modified condition is that could cover as many t-way interactions as possible. The t-way interactions covered in can be measured in the method described in SubSection 6.2. When the k factors have different number of values, extended constraint mixed-level covering arrays are used. have the same expression forms with .
The set C is the set of constraint statements specified by CCTL. CCTL is a variant of timed CTL based on I/O-interval structures introduced by Ruf [44,45] in the context of the real-time system model checker. The I/O-interval structures are used in state transition systems to express time annotations. A time annotation is a constraint that assigns a -time interval for a state transition [44]. -time intervals can help CCTL to precisely model time in which state transitions occur compared to LTL and CTL [44]. For this reason, -time intervals can also support describing the temporal relationship among inputs based on time steps precisely. This is the maximum benefit of CCTL. Thus, we use CCTL to model the constraint relationship.
The CCTL syntax is defined as follows [46]:
where is an atomic proposition and are time bounds with . ¬, ∧, →, ⊕, ∨ and ⊗ are the classical logic operators included in CCTL syntax. is the CCTL formula. X, F, U and G are the temporal operators, where X is the “next” operator, F is the “final“ operator, G is the “always” operator, and U is the “until” operator. A and E are path quantifiers. A “path” is an infinite sequence of states, denoted as . If a CCTL formula is true in path , then we write . Because there are potentially many paths in a system, E means that “at least one path exists that satisfies the temporal operator”, and A means “for all paths that satisfy the temporal operator”. In testing, the generated is equivalent to the path because it should satisfy the constraints presented by CCTL formulas, denoted as . As there exists at least a test suite which is used to test, we use the path quantifier E in this paper to specify constraints. Based on a constraint which belongs to a test case or involves test cases, the specification of constraints are divided into the following two parts.
4.2.1. The Specification of Constraints in a Test Case
The constraints in a test case indicate the restrictions among factor values. These types of constraints correspond to the traditional covering array. The constraints forbid the appearance of some certain value combinations that are composed of different factors. Because generating a test case that avoids all the constraints is a boolean satisfiability problem [47], a formal specification is needed in the process of automatically generating test cases. Generally, the constraints are often represented in conjunctive normal form (CNF) [47].
For a forbidden tuple , the formal specification is . In addition, there are always two types of internal constraints for an SUT to limit each test case to having one and only one value from every factor. They are the at-least and at-most constraints [47]. The at-least constraints are needed to ensure that there is no less than one value of each factor in a test case, and the at-most constraints are needed to ensure that no more than one value is assigned to a factor in a test case.
- at-most constraints: for each factor with its value set and a test case , there exists that and , and the at-most constraints can be denoted as . The at-most constraints mean that each two values of one factor must not appear in a same test case.
- at-least constraints: for each factor with its value set and a test case , the at-least constraints can be denoted as . The at-least constraints mean that there must be at least one value of a factor appearing in a test case.
4.2.2. The Specification of Constraints among Test Cases
The constraints involving value sequences of factors are constraints among test cases or test steps. The constraints are generally divided into absolute constraints and relative constraints according to whether constraints have the logical operator “→”. Absolute constraints do not contain the logical operator “→”, whereas relative constraints have the logical operator “→”. The relative constraints in front and behind of “→” are composed of the absolute constraints presented by , , and . Relative constraints means that when the condition in front of “→” is tenable, the condition behind of “→” must be tenable.
Each temporal operator can represent a type of absolute constraint. A formal description of the temporal operators is presented below. Given and with :
- : There exists an in which the uth test case satisfies . It is the same as ;
- : , and for all : ;
- : , and ;
- : There exists at least one i with : .
We always omit “” in the specification of constraints. The constraints specified above are the absolute constraints. Then, we introduce the relative constraints. We classify the relative constraints according to the symbol in front of “→”. We define that when the constraint has the form of in front of other temporal operators, then the th test case is regarded as the first test case for the following representations. Given , with and :
- (1)
- : When the uth test case satisfies , , the th test case holds , ;
- : When the uth test case satisfies , , the th test case is regarded as the first test case for as the . Then, , and for all : ;
- : When the uth test case satisfies , , the th test case is regarded as the first test case for as the . Then, , and ;
- : When the uth test case satisfies , : At least one i exists with : with .
- (2)
- : and for all , exists: with ;
- : and for all , exists: At least one l exists with : with .
- (3)
- : , and exists: with ;
- : , and exists: At least one l exists with : with .
- (4)
- : At least one i exists with : : with ;
- : At least one i exists with : : At least one l exists with : with .
- (5)
- : For each test case in , if there is a test case i that holds , the th test case is regarded as the first test case for as : for all : ;
- : For each test case in , if there is a test case i that holds , the th test case is regarded as the first test case for as . Then, : and ;
4.3. A Case Study
Two real SUTs are analyzed in this subsection.
The first real system under test is the “VideoGame”, which is described in Ref [1]. “VideoGame” has two factors: one is “startingGame” and the other is “Pause”. Factor “startingGame” has four levels and they are “startingGame”, “startup”, “controlling” and “gameOver”, and factor “Pause” has two levels and they are “running” and “paused”. In terms of factor “startingGame”, “startingGame” level can transit to itself and “startup”, “startup” level can transit to itself and “controlling”, “controlling” level can transit to itself and “gameOver”, and “gameOver” level can transit to itself and “startingGame”. In terms of factor “Pause”, “running” level can only transit to “paused” and “paused” level can only transit to “running”. The limitations that restrict levels not to transit to others are constraints. Combined with the at-most constraints and at-least constraints, the constraints of “VideoGame” are obtained. Thus, the of the “VideoGame” can be constructed as shown in Table 4 and its constraint set C is as follows. The has covered all the eight possible level combinations and ten level transitions:

Table 4.
An of the “VideoGame”.
The second real system under test is the “text effect” application of “Microsoft Word”, which has seven options for users to modify some highlighted text. These options are “subscript”, “superscript”, “strikethrough”, “double strikethrough”, “all caps”, “small caps”, and “shadow” [9]. Each option has optional values: one is “true” and the other is “false”. Three value combination constraints exist, and they are , and . The font-processing function within the application correctly modifies the highlighted text on the screen according to the settings consisting of these options. When tests are executing, the font-processing function modifies the text according to the test cases in sequence. Thus, the of the “text effect” application can be constructed as shown in Table 5 and its constraint set C is as follows. The has covered all the 81 possible value combinations and 28 value transitions:

Table 5.
An of the “text effect” application.
5. The Construction of Extended Covering Arrays
5.1. Particle Swarm Optimization
The Particle Swarm Optimization (PSO) was originally put forward by Kennedy [48] as an optimization technique inspired by the swarm behavior of birds in 1995. The swarm of particles always moves towards the optimal position in the process of optimization. The position of a particle indicates the solution under optimization. The speed of a particle indicates the tendency of evolution and the degree of variation. The fitness factor value of a particle indicates the degree of optimization. Each particle remembers its coordinates in the solution space where it has found its best solution so far, which is called . In addition to , particles track the overall best value obtained by any particle in the population, called . The process of evolution will continue untill the iteration time is reached. As a result of the discrete values in parameters, we adopt the discrete version of PSO (DPSO), which has been used in covering array generation [13]. The particle updates its coordinate according to Equations (2) and (3):
where t is the current iteration number, j is the component of the dimension k, i is the particle index, are the acceleration coefficients to adjust the weight between components, is the inertia weight in the range of , and are two random factors ranged in . According to the equations above, each particle updates its velocity by following its and in order to produce a movement towards a better region in the search space.
5.2. The PEG Strategy
5.2.1. The Interaction and Constraint Maps Generation Algorithm
In PEG, fitness factor values that indicate the degree of optimization are used to choose best particles. Hence, in order to compute the fitness factor values of particles conveniently, effective data structures are necessary. We propose Combinatorial Interaction Maps () and Sequence Interaction Maps () as the structures that are used to choose best particles. Similarly, to verify the constraint validity of each particle, effective data structures are also necessary. We propose Combinatorial Constraint Maps () and Sequence Constraint Maps () as the structures that are used to validate constraint validity. The “Map” here is an associative container in C++ that stores elements formed by a combination of a key value and a mapped value, following a specific order. Algorithm 1 shows the corresponding generation algorithm of them. The algorithm receives and C as inputs, and generates , , and one by one.
| Algorithm 1 The interaction and constraint maps generation algorithm. |
| Input: Output:, , and
|
Figure 1 shows an example of generating , , and from , , and . Here, the at-most and at-least constraints are omitted, as they are only used for constraint validity verification. The keys of the four maps are factors or factor combinations, and the values mapped to the keys are a set of values of factors. The values in combinatorial maps represent factor value combinations, whereas the values in sequence maps represent factor value sequences. In the algorithm, the is generated first. Then all the value combinations of each factors are generated in . When is generated, each factor value combination that appears in must be removed from it. For example, the value combination is a constraint in . Thus, it must not appear in . The generation process of and is similar with the generation of and . The is generated first. Then, all the value sequences with length of each factor are generated in . When is generated, each value sequence that appears in must be removed from it.
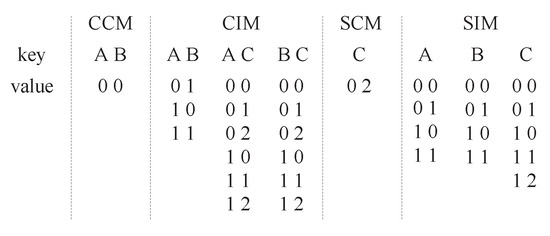
Figure 1.
The generation of , , and .
5.2.2. The Generation Algorithm
The generation algorithm is performed immediately after the generation of , , and . The use of and is essential for computing fitness factor values. The use of and is essential for validating the constraint validity of test cases. The main idea of the algorithm is that the algorithm makes fully use of the ability of seeking excellent solutions to generate good results. As usually constraints that are related to sequences are very complex, this algorithm supports three kinds of most common constraints. The three kinds of common constraints are: ① initial value constraints of factors that are presented by ; ② combinatorial value constraints among factors; and ③ value transition constraints of any factor. The algorithm is shown as Algorithm 2.
| Algorithm 2 The generation algorithm. |
| Input:; , , , R, P; , , and Output:
|
The algorithm is explained in the following aspects.
- (1)
- Processing of the initial value constraintWhen an SUT has an initial value constraint that is presented by , then an initial test case in which each factor is assigned its initial value is generated. Then, the factor value combinations and value sequences of factors covered in the test case are removed from and in line 3. As the generated test case is the first test case in , only if , it covers value sequences in . Otherwise, it does not cover value sequences in .
- (2)
- Population initializationThe generation algorithm is initialized by generating a random population position space and a random population velocity space for each particle in line 6. The position of each particle takes the form of a k-dimensional vector, , where each dimension represents a random integer number from the value set . The velocity of each particle also takes the form of a k-dimensional vector, , where each dimension is also simultaneously initialized with a random integer number between and .
- (3)
- Population updateDuring the iteration of the algorithm, velocities and positions of the population particles are updated in line 8 according to Equations 2 and 3. After each iteration, if is out of the range , then is updated with the previous value . If is out of the range , then is updated with a random value in the range. Each particle updates its with the solution space where it has its largest fitness factor value thus far. The global best solution is updated with the particle that has the larger fitness factor value and satisfies the constraint validity. We use the SAT solver zChaff to verify the combinatorial constraint validity. The SAT solver is initialized in line 1 and the at-most and at-least constraints are generated as the initialization parameters of the SAT solver. The value transition constraints of factors are verified by comparing with .
- (4)
- Fitness factor valueFitness factor values are used with PSO in a greedy fashion to identify better particles. A fitness factor value of a test case is the sum of the number of factor value combinations with size covered in and the number of value sequences of each factor covered in composed with generated test cases.
- (5)
- Population disturbanceTo guarantee the avoidance of the local optimum, after each iteration, one random position in is updated by a random value in line 9. We denote the new particle as . If the fitness factor value of is larger than that of , replace with .
- (6)
- Searching strategyAfter the iteration progresses, if the fitness factor value of is , a searching strategy is applied in line 23. At this time, almost a large proportion of factor value combinations are covered and some value sequences of factors may be left. To find the remaining value sequences of factors as early as possible, we present a searching strategy. In the searching strategy, a new test case is constructed one by one factor value to guarantee that it has the potential to cover as many as value sequences of factors or to help the subsequent test case to cover value sequences of factors. The searching strategy is divided into two situations. The first situation is to judge each value of the last generated test case whether belongs to a value sequence uncovered in . If there exists a value sequence in , the value must be guaranteed that it is not the last value in the value sequence. Then, the subsequent value is inserted into a new test case, such that the value a in the last generated test case belongs to a uncovered value sequence and the value b is inserted into the new test case. If the first situation does not exist, a second situation is performed. A schematic shown in Figure 2 is used to illustrate it. The precondition of the second condition is that each value can reach other values for each factor. Given a generated value in a last generated test case, a traversal hierarchy is constructed based on the values that can be reached. Suppose that is the uncovered value sequence. A path can reach , and then the value 0 is inserted into the new test case. This process guarantees that, if the fitness factor value of is still less than 0 after the next iteration progress, then the first situation of the searching strategy works. It should be noted that when a new value is inserted into the new test case, the new test case’s constraint validity must be satisfied, otherwise a random value that can satisfy the constraint validity is inserted. The searching strategy can guarantee that at least one factor can be updated towards the direction, where the fitness factor value of is greater than 0.
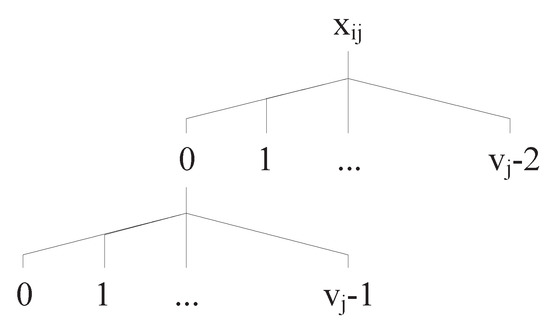 Figure 2. A schematic of the second situation of the searching strategy.
Figure 2. A schematic of the second situation of the searching strategy. - (7)
- End conditionWhether is empty, the algorithm has two end conditions. If is empty, the algorithm is terminated when all the value sequences of factors and factor value combinations are covered in lines from 15 to 17. If is not empty, the algorithm is terminated only when all the value sequences of factors are covered in lines from 19 to 21. The reason is that, owning to the existence of the constraints of value sequences, some factor value combinations can perhaps not appear in one test case. For example, an SUT has factors A and B, and each factor has values 0, 1 and 2. The input value sequence of each factor is restricted in circles from 0 to 2. Thus, there are only three value combinations , and that exist. When , has value combinations and six of them can never be covered. Therefore, to avoid an infinite loop, the end condition is only .
6. Evaluation Methods of Extended Covering Arrays
6.1. Verification of Constraints
An important problem is the verification of constraints for constructed extended covering arrays. The extended covering arrays that are verified to be valid can be used. According to the two types of constraints, the verification is also divided into two types. One is the verification of constraints in a test case and the other is the verification of constraints among test cases.
6.1.1. Verification of Constraints in a Test Case
The constraints in a test case can be presented in conjunctive normal form and CCTL, such as and . The constraint verification is essentially the boolean satisfiability problem, irrespective of which presentation is used. There are two types of tools according to the presentations. For the conjunctive normal form, the verification tools are zChaff [49], Simple Theorem Prover (STP) [50], and MiniSAT [51]. For the CCTL form, the verification tools are Spin [52] and NuSMV [53]. The constraints of factor value combinations, the at-least and at-most constraints are all the inputs of the tools. The tools provide a “true” or “false” result for each test case at the end of the verification process.
6.1.2. Verification of Constraints among Test Cases
Although there is not an effective tool that can be used for CCTL, some formulas can be used for directing the verification of constraints among test cases. For different absolute constraints, different verification measures should be taken. Given and ,
- ①
- Verify whether the nth test case satisfies directly.
- ②
- We can use the recursion formula to verify . First, verify whether the first test case is . Second, regard the next test case as the first test case as the . Then, execute the verification process to verify by repeating the process above.
- ③
- First, use the recursion formula to transform to by repeating the process. Then, verify with the recursion formula .
- ④
- Verify whether there exists a positive integer i with that makes that the ith test case holds .
To verify the relative constraints, the constraints need to be split into two parts according to the logical operator “→”. Then, verify the condition on the left of “→” first. If the condition holds, verify the constraint on the right of the operator “→”. Once there is one step in the verification process where the violates the constraints, the is invalid.
6.2. Coverage Measurement
Given a test suite, we expect that the test suite covers all the value combinations among factors and value sequences of each factor with a size that is as small as possible. We can use Formula (4) to calculate the coverage, where the symbol "Covered" indicates the number of targets that have already been covered and "Total" indicates the total targets to be covered in theory:
Consider the . It has factor value combinations to be covered and value sequences with size . Thus, there are targets to be covered. When considering the constraints, the number of targets to be covered should be less than the targets without considering constraints.
Because coverage measurement is essentially pattern analysis, which has been widely used in many domains [54], we define the coverage measurement with combinatorial coverage and sequence coverage.
6.2.1. Measurement of Combinatorial Coverage
Given a test suite and an interaction with , , indicates the number of -way combinations:
indicates the number of interactions covered in , and is the set of all interactions with . is a characteristic function used for comparing with :
Another form of is the following:
The kernel function based on is as follows:
There is for the kernel function. If there are no constraints, then . Thus, the formula to calculate combinatorial coverage is as follows:
6.2.2. Measurement of Sequence Coverage
Given a test suite and for each sequence , of factor , the mapping indicates the number of sequences from column i in :
The sequence is viewed as a series of three subsequences , and . is the value set of factor , and is the set of all the sequences with length . is a characteristic function used for comparing with :
Another form of is as follows:
The kernel function based on is as follows:
There is for the kernel function. If there are no constraints, then . Thus, the formula to calculate sequence coverage is the following:
7. Experiments
This section describes the experimental results of PEG performed on a benchmark of SUTs. Then, more complex constraints that PEG can not support are discussed.
7.1. Experimental Results of PEG
PEG is developed in the environment that consists of a desktop computer with Windows 7 (Dell, Xiamen, China), 2.6 GHz Core 2 Duo CPU, 2 GB of RAM. It is coded and implemented in Qt Creator 4.8.1 (C++) (Digia, Helsinki, Finland).
For the experiments, we use a benchmark with 12 different SUTs. Six of them are from Ref. [12]. They are the “Keyboard”, the “Microwave”, the “Autoradio”, the “Coffee Machine”, the “Elevator” and the “Transmission”. The reason why we choose them is that they have more than one factor and for each factor of them each value can reach to others. The “text effect“ application of “Microsoft Word” is also chosen as an SUT. Besides the seven real world SUTs, we supplement five SUTs to increase the configuration diversity of SUTs. The details of the SUTs are given in Table 6. The configurations of factors and factor values are listed in the third column. Three kind of constraints are listed from the fourth column to the sixth column.

Table 6.
General characteristics of systems under test.
As PEG depends on some degree of randomness, it is non-deterministic. Thus, we performed 30 independent runs per SUT/coverage criterion for a statistical analysis. We use PEG to generate coverage and , coverage, respectively. The results are shown in Table 7 and Table 8. As SUT2 and SUT7 have the configuration of two factors, they can not have test suites with coverage. Thus we use the asterisks “*” to mark the results which are performed with coverage in Table 8. To demonstrate the performance of PEG, best generated sizes, average generated sizes, best generated time and average generated time are presented for each SUT. The average coverage of targets are also reported corresponding to factor value combinations with coverage and value sequences of each factor with coverage.

Table 7.
Results of PEG with and .

Table 8.
Results of PEG with and .
Generally, the generated time increases as the number of factors and factor values grows. However, the generated time of SUT1 seems longer than other SUTs. This is mainly because much time is wasted in the calls of the SAT solver under combination constraints. Based on the results obtained, PEG can generate satisfactory results with total coverage when SUTs have no constraints related to value sequences of factors. When SUTs have the constraints related to value sequences of factors, PEG can cover all the target value sequences with covering as many factor value combinations as possible. Overall, the results show that PEG is feasible and useful to generate .
7.2. Discussion
As everyone knows, a fundamental problem with software testing is that testing under all combinations of inputs and preconditions is not feasible, even with a simple product. The SUTs with test cases to be performed contiguously still face this problem. attempt to use as few test cases as possible to cover as many factor value combinations and value sequences of factors as possible. The purpose of is to find more system defects. Compared with the manual test suite generation, can design more comprehensive test suites. fill the blank of the test case generation method for SUTs with test case to be performed contiguously and are of great significance to ensure the reliability and quality of SUTs. will be widely applied to many fields with high reliability requirement, such as aviation, spaceflight and weapon industry. In these industries, most of the input instructions of components are messages that consist of some relevant elements and are needed to be performed contiguously. are very suitable for the element value combinations and value sequences of elements in the messages.
Take an input instruction of a radar as an example. A high coverage test is needed to ensure the radar works normally under various working conditions. Table 9 shows the instruction of the radar under test. The instruction needs to be input contiguously to control its working mode. When scanning mode is “fixed point”, the scanning speed and the sector scan scope needs to be assigned invalid values, and the scan center needs to be assigned a degree in the range of . When scanning mode is “sector scan”, the scanning speed needs to be assigned a valid speed, the sector scan scope needs to be assigned a valid scan scope, and the scan center needs to be assigned a degree in the range of . When scanning mode is “circular scan”, the scanning speed needs to be assigned a valid speed, the sector scan scope and the scan center needs to be assigned an invalid value. are feasible to be used as the test suites, and can improve the test coverage dramatically compared to design test suites manually. There is a large amount of input messages in the industry like the previous instruction and high coverage test suites are needed for those messages. Therefore, we believe that have a broad application prospect.

Table 9.
An instruction of a radar under test.
However, PEG still needs to be improved in practice for more complex contraints. The SUTs whose test cases need to be performed contiguously usually have the three kinds of constraints that are the prerequisites of PEG. More complex constraints may be exist though they have hardly been seen in real world systems, such as the constraints between factors values from one test step to another [32]. Refs. [12,32] have put forward the requirement of generating test suites under complex constraints and described some complex constraints as follows:
- If value from factor C is selected in test case , then value from factor C must be selected in the succeeding test step .
- If in , then in a later .
- If in , then in all to .
- If in , then in all to .
- If or in , then in a later .
These complex constraints can all be presented in CCTL as follows. As they do not give the configurations of factors and factor values, we could not construct their test suites:
Ref. [33] has presented a simplified real world system with complex constraints that is a simplified controller of a car. It has two boolean inputs that represent the user’s decision to accelerate or brake. Upon acceleration, the car starts moving, with either a slow or fast velocity. Upon braking, the car immediately stops. The velocity is also a factor of the example. Figure 3 depicts the values of the three factors that impact the car controller.
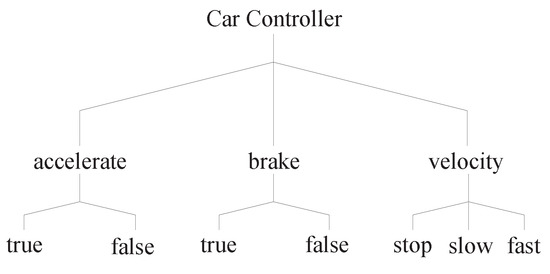
Figure 3.
The factor values of the simplified car controller presented as a classification tree.
As to pedal the brake and accelerator at the same time should be avoided when driving, the value combination of “accelerate = true” and “brake = true” is a constraint for the car controller. This value combination constraint can be denoted as . For each factor, there are also at-least and at-most constraints. Figure 4 shows the states and the transitions of states [33]. A constraint that can be denoted as restricts the first state of the car controller. Figure 5 shows the value transitions of each factor. When “velocity = stop” holds in a test case, “velocity=fast” cannot occur in the next test case. The constraint is . When “velocity = slow” holds in a test case, “velocity=slow” cannot occur in the next test case. The constraint is . Integrated with seven other complex constraints that are given in [33], all the constraints consist of the constraint set C in as follows:
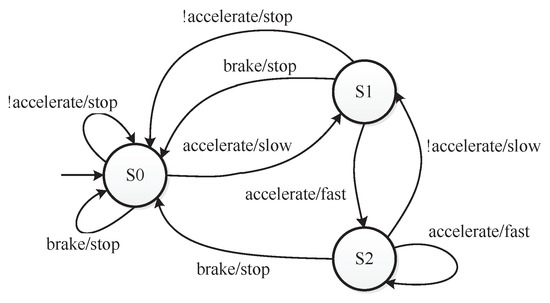
Figure 4.
The state transitions of the car controller.
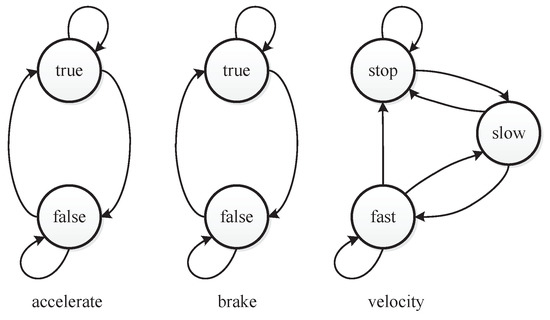
Figure 5.
The value transitions of each factor.
The of the car controller presented in Table 10 is generated by PEG without considering complex constraints. The combinatorial coverage of this is , as the combination {accelerate=true, brake=true} is a constraint that is forbidden to appear. The sequence coverage of this is , as "velocity=stop" → "velocity=fast" and "velocity=slow" → "velocity=slow" are value sequence constraints. As PEG cannot handle complex constraints, the in Table 10 violates complex constraints. The first and second test cases violate the constraint , as when the first test is (accelerate=false, brake=false, velocity=stop), the second test case violates the . In the same way, the second and third test cases violate . The third and fourth test cases violate . The fourth and fifth test cases violate . The seventh and eighth test cases violate . The ninth and tenth test cases violate . The tenth and eleventh test cases violate . The eleventh and twelfth test case violate . To illustrate an that satisfies the complex constraints, an is constructed manually as shown in Table 11. As the configuration is simple, we can construct it manually. The shown in Table 11 satisfies all the constraints and covers all the value combinations and value sequences of each factors.

Table 10.
An generated by PEG without complex constraints.

Table 11.
An generated manually.
Through the analysis above, though PEG can produce satisfactory , PEG still has some limitations to generate for SUTs with complex constraints. The emerging complex constraints can be specified by CCTL actually. It is certain that more real world SUTs with complex constraints are needed and analyzed, so that complex constraints can be classified and handled reasonably.
8. Conclusions
In this paper, we have proposed extended covering arrays with t-way combinatorial coverage and t-wise sequence coverage for SUTs whose test cases need to be performed contiguously. In extended covering arrays, we have introduced the clocked computation tree logic based formal specification method for specifying constraints. A Particle swarm optimization based Extended covering array Generator (PEG) that can produce feasible and useful with common constraints has also been presented. The performance of PEG is assessed considering benchmark experiments. For generated test suites, the method for verifying constraints’ validity has been presented corresponding to the constraint specification method. Moreover, kernel functions that can measure the coverage of generated test suites have be given. Compared with the manual test suite generation, can design more comprehensive test suites, which improves the possibility of finding system defects. In a word, fill the blank of the test case generation method for SUTs with test case to be performed contiguously and are of great significance to ensure the reliability and quality of SUTs. Though some deficiencies exists, we still believe that can have a broad application prospect through continuous progress in practice.
As part of our future work, we will first optimise PEG to cover more possible value combinations under the constraints of value sequences, then try to find real world SUTs with complex constraints and extend PEG to support them. Compared to the fixed strength combinatorial testing, the variable strength combinatorial testing usually considers the actual interaction relationship in software sufficiently. Therefore, with variable strength are also worthy of study.
Author Contributions
The authors contributed equally to this work and wrote this paper together.
Acknowledgments
The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ferrer, J.; Kruse, P.M.; Chicano, F.; Alba, E. Search based algorithms for test sequence generation in functional testing. Inf. Softw. Technol. 2014, 58, 419–432. [Google Scholar] [CrossRef]
- Tassey, G. The economic impacts of inadequate infrastructure for software testing. Natl. Inst. Stand. Technol. 2002, 15, 125. [Google Scholar]
- Kacker, R.N.; Kuhn, D.R.; Lei, Y.; Lawrence, J.F. Combinatorial testing for software: An adaptation of design of experiments. Measurement 2013, 46, 3745–3752. [Google Scholar] [CrossRef]
- Nie, C.; Leung, H. A survey of combinatorial testing. ACM Comput. Surv. 2011, 43, 33–63. [Google Scholar] [CrossRef]
- Kuhn, D.R.; Kacker, R.N.; Lei, Y. Practical combinatorial testing. Nist Spec. Publ. 2010, 10, 19–23. [Google Scholar]
- Kuhn, D.R.; Bryce, R.; Duan, F.; Ghandehari, L.S.; Lei, Y.; Kacker, R.N. Combinatorial testing: Theory and practice. Adv. Comput. 2015, 99, 1–66. [Google Scholar]
- Cohen, D.M.; Dalal, S.R.; Fredman, M.L.; Patton, G.C. The aetg system: An approach to testing based on combinatorial design. IEEE Trans. Softw. Eng. 1997, 23, 437–444. [Google Scholar] [CrossRef]
- Kuhn, D.R.; Wallace, D.R.; Gallo, A.M. Software fault interactions and implications for software testing. IEEE Trans. Softw. Eng. 2004, 30, 418–421. [Google Scholar] [CrossRef]
- Kuhn, D.R.; Kacker, R.N.; Lei, Y. Introduction to Combinatorial Testing; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Farchi, E.; Segall, I.; Tzorefbrill, R.; Zlotnick, A. Combinatorial testing with order requirements. In Proceedings of the IEEE Seventh International Conference on Software Testing, Verification and Validation Workshops, Cleveland, OH, USA, 31 March–4 April 2014; pp. 118–127. [Google Scholar]
- Zamli, K.Z.; Othman, R.R.; Zabil, M.H.M. On sequence based interaction testing. In Computers and Informatics; Universiti Tenaga Nasional: Selangor, Malaysia, 2011; pp. 662–667. [Google Scholar]
- Kruse, P.M. Enhanced Test Case Generation With the Classification Tree Method; Freie Universität Berlin: Berlin, Germany, 2014. [Google Scholar]
- Ahmed, B.S.; Zamli, K.Z.; Lim, C.P. Application of particle swarm optimization to uniform and variable strength covering array construction. Appl. Soft Comput. 2012, 12, 1330–1347. [Google Scholar] [CrossRef]
- Qnd. Available online: http://csrc.nist.gov/groups/SNS/acts/sequencecovarrays.html (accessed on 5 February 2018).
- Kuhn, D.R.; Higdon, J.M.; Lawrence, J.F.; Kacker, R.N.; Lei, Y. Efficient methods for interoperability testing using event sequences. Crosstalk J. Def. Softw. Eng. 2012, 25, 15–18. [Google Scholar]
- Kuhn, D.R.; Higdon, J.M.; Lawrence, J.F.; Kacker, R.N.; Lei, Y. Combinatorial methods for event sequence testing. In Proceedings of the IEEE Fifth International Conference on Software Testing, Verification and Validation, Montreal, QC, Canada, 17–21 April 2012; pp. 601–609. [Google Scholar]
- Yu, L.; Lei, Y.; Kacker, R.N.; Kuhn, D.R.; Lawrence, J. Efficient algorithms for t-way test sequence generation. In Proceedings of the International Conference on Engineering of Complex Computer Systems, Paris, France, 18–20 July 2012; pp. 220–229. [Google Scholar]
- Hazli, M.Z.M.; Zamli, K.Z.; Othman, R.R. Sequence-based interaction testing implementation using bees algorithm. In Proceedings of the 2012 IEEE Symposium on Computers & Informatics (ISCI), Penang, Malaysia, 18–20 March 2012; pp. 81–85. [Google Scholar]
- Rahman, M.M.; Othman, R.R.; Ahmad, R.B.; Rahman, M.M. A meta heuristic search based t-way event driven input sequence test case generator. Int. J. Simul. Syst. Sci. Technol. 2014, 15, 65–71. [Google Scholar]
- Nguyen, C.D.; Marchetto, A.; Tonella, P. Combining model-based and combinatorial testing for effective test case generation. In Proceedings of the International Symposium on Software Testing and Analysis, Minneapolis, MN, USA, 15–20 July 2012; pp. 100–110. [Google Scholar]
- Grochtmann, M.; Grimm, K. Classification trees for partition testing. Softw. Test.Verif. Reliab. 1993, 3, 63–82. [Google Scholar] [CrossRef]
- Conrad, M.; Fey, I.; Sadeghipour, S. Systematic model-based testing of embedded automotive software. Electron. Notes Theor. Comput. Sci. 2005, 111, 13–26. [Google Scholar] [CrossRef]
- Mattner, B. Testona. Available online: http://www.testona.net/ (accessed on 1 March 2018).
- Razorcat, Tessy. Available online: http://www.razorcat.com/downloads-tessy.html (accessed on 1 March 2018).
- Büchner, F. Test case design using the classification tree method. ATZelektronik Worldw. 2007, 2, 15–17. [Google Scholar]
- Lamberg, K.; Beine, M.; Eschmann, M.; Otterbach, R.; Conrad, M.; Fey, I. Model-based testing of embedded automotive software using mtest. J. Passeng. Carselectron. Electr. Syst. 2004, 7, 132–140. [Google Scholar]
- Mjeda, A.; Mcelligott, P.; Ryan, K.; Thiel, S. Reactive Model-Based Testing Design for Embedded Automotive Software; Sae International: Hongkong, China, 2008. [Google Scholar]
- Conrad, M.; Krupp, A. An extension of the classification-tree method for embedded systems for the description of events. Electron. Notes Theor. Comput. Sci. 2006, 164, 3–11. [Google Scholar] [CrossRef]
- Kruse, P.M.; Nasarek, J.; Fernandez, N.C. Systematic testing of web applications with the classification tree method. In Proceedings of the XVII Iberoamerican Conference on Software Engineering, Pucón, Chile, 23–25 April 2014; pp. 219–232. [Google Scholar]
- Artho, C.V.; Biere, A.; Hagiya, M.; Platon, E.; Seidl, M.; Tanabe, Y.; Yamamoto, M. Modbat: A Model-based API tester for event-driven systems, verification and testing. In Proc. 9th Haifa Verification Conference; Springer: Cham, Switzerland, 2013; pp. 112–128. [Google Scholar]
- Anand, S.; Burke, E.K.; Chen, T.Y.; Clark, J.; Cohen, M.B.; Grieskamp, W.; Harman, M.; Harrold, M.J.; Mcminn, P. An orchestrated survey on automated software test case generation. J. Syst. Softw. 2013, 86, 1978–2001. [Google Scholar] [CrossRef]
- Kruse, P.M.; Wegener, J. Test sequence generation from classification trees. In Proceedings of the IEEE Fifth International Conference on Software Testing, Verification and Validation, Montreal, QC, Canada, 17–21 April 2012; pp. 539–548. [Google Scholar]
- Fraser, G.; Wotawa, F.; Ammann, P.E. Testing with model checkers: A survey. Softw. Test. Verif. Reliab. 2009, 19, 215–261. [Google Scholar] [CrossRef]
- Schooljan, H. Test Sequence Validation and Generation Using Classification Trees; Delft University of Technology: Delft, The Netherlands, 2013. [Google Scholar]
- Krupp, A.; Mueller, W. Modelchecking von klassifikationsbaum-testsequenzen. In Proceedings of the GI/ITG/GMM Workshop “Methoden und Beschreibungssprachen zur Modellierung und Verifikation von Schaltungen und Systemen”, Munich, Germany, 5–7 April 2005. [Google Scholar]
- Yilmaz, C.; Fouche, S.; Cohen, M.B.; Porter, A.; Demiroz, G.; Koc, U. Moving forward with combinatorial interaction testing. Computer 2014, 47, 37–45. [Google Scholar] [CrossRef]
- Yilmaz, C. Test case-aware combinatorial interaction testing. IEEE Trans. Softw. Eng. 2013, 39, 684–706. [Google Scholar] [CrossRef]
- Martínez, C.; Moura, L.; Panario, D.; Stevens, B. Locating errors using eLAs, covering arrays, and adaptive testing algorithms. Siam J. Discret. Math. 2010, 23, 1776–1799. [Google Scholar] [CrossRef]
- Sheng, Y.; Wei, C.; Jiang, S. Constraint test cases generation based on particle swarm optimization. Int. J. Reliab. Qual. Saf. Eng. 2017, 24, 1750021-1–1750021-21. [Google Scholar] [CrossRef]
- Alsewari, A.R.A.; Zamli, K.Z. Design and implementation of a harmony-search-based variable-strength t-way testing strategy with constraints support. Inf. Softw. Technol. 2012, 54, 553–568. [Google Scholar] [CrossRef]
- Yu, L.; Lei, Y.; Nourozborazjany, M.; Kacker, R.N.; Kuhn, D.R. An efficient algorithm for constraint handling in combinatorial test generation. In Proceedings of the 2013 IEEE Sixth International Conference on Software Testing, Verification and Validation, Luxembourg, Luxembourg, 18–22 March 2013; pp. 242–251. [Google Scholar]
- Yu, L.; Duan, F.; Lei, Y.; Kacker, R.N. Constraint handling in combinatorial test generation using forbidden tuples. In Proceedings of the IEEE Eighth International Conference on Software Testing, Verification and Validation Workshops, Graz, Austria, 13–17 April 2015; pp. 1–9. [Google Scholar]
- Danziger, P.; Mendelsohn, E.; Moura, L.; Stevens, B. Covering arrays avoiding forbidden edges. Theor. Comput. Sci. 2008, 410, 5403–5414. [Google Scholar] [CrossRef]
- Ruf, J.; Kropf, T. Symbolic model checking for a discrete clocked temporal logic with intervals. In Advances in Hardware Design and Verification; Springer: Boston, MA, USA, 1997; pp. 146–163. [Google Scholar]
- Ruf, J.; Kropf, T. Modeling and Checking Networks of Communicating Real-Time Processes. In Correct Hardware Design and Verification Methods; Springer: Berlin/Heidelberg, Germany, 2008; pp. 267–279. [Google Scholar]
- Flake, S.; Müller, W.; Ruf, J. Mapping of Structured English Sentences To Cctl Formulae; University of Paderborn: Paderborn, Germany, 2000. [Google Scholar]
- Cohen, M.B.; Dwyer, M.B.; Shi, J. Constructing interaction test suites for highly-configurable systems in the presence of constraints: A greedy approach. IEEE Trans. Softw. Eng. 2008, 34, 633–650. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- S. R. Group, Zchaff. Available online: https://www.princeton.edu/~chaff/zchaff.html (accessed on 20 February 2018).
- Cadar, C.; Ganesh, V.; Pawlowski, P.M.; Dill, D.L.; Engler, D.R. Exe: Automatically generating inputs of death. In ACM Transactions on Information and System Security (TISSEC); ACM: New York, NY, USA, 2008; Volume 12, pp. 1–38. [Google Scholar]
- Niklas, E.; Niklas, S. Minisat. Available online: http://minisat.se/ (accessed on 20 February 2018).
- Spin. Available online: http://spinroot.com/spin/whatispin.html (accessed on 20 February 2018).
- Nusmv. Available online: http://nusmv.fbk.eu/ (accessed on 20 February 2018).
- Last, M. Kernel Methods for Pattern Analysis; China Machine Press: Beijing, China, 2005. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).