Another Approach to Roughness of Soft Graphs with Applications in Decision Making

Abstract

Fuzzy sets, rough sets and soft sets are different tools for modeling problems involving uncertainty. Graph theory is another powerful tool for representing the information by means of diagrams, matrices or relations. A possible amalgamation of three different concepts rough sets, soft sets and graphs, known as soft rough graphs, is proposed by Noor et al. They introduced the notion of vertex, edge induced soft rough graphs and soft rough trees depending upon the parameterized subsets of vertex set and edge set. In this article, a new framework for studying the roughness of soft graphs in more general way is introduced. This new model is known as the modified soft rough graphs or $\mathcal{MSR}$-graphs. The concept of the roughness membership function of vertex sets, edge sets and of a graph is also introduced. Further, it has been shown that $\mathcal{MSR}$-graphs are more robust than soft rough graphs. Some results, which are not handled by soft rough graphs, can be handled by modified soft rough graphs. The notion of uncertainty measurement associated with $\mathcal{MSR}$-graphs is introduced. All applications related to decision makings are only restricted to the information of individuals only, not their interactions, using this technique we are able to involve the interactions (edges) of individuals with each other that enhanced the accuracy in decisions.

1. Introduction

For solving many problems involving uncertainty and vagueness in engineering, social sciences, economics, computers sciences and in several other areas, our traditional classical methods are not always absolutely effective. These traditional and conventional mechanism of reasoning, modeling and computing are usually crisp and deterministic. Zadeh introduced a successful tool known as fuzzy sets [1], based on the membership function. The situations concerning with the vagueness and uncertainty were also been tackled by the effective tool of probability. However, this tool is valuable only when the occurrence of event is totally determined by the chance. In contrast with fuzzy set theory and probability theory, some other theories like rough set theory, soft set theory, neutrosophic set theory and an amalgamation of these theories have been studied ([1,2,3,4,5,6,7], and the references therein) to deal with uncertainty.

In 1982, Pawlak [3] introduced the concept of rough sets as a mathematical tool for imprecise and uncertain data. The basic advantage of this theory is that it does not involve any additional information about the data like the membership in fuzzy sets. The rough sets theory defined by Pawlak is based on partition or an equivalence relation. Many applications of rough set theory, probability theory, and rough set theory can be seen in the followings [4,5,8,9,10,11,12,13], these include applications in data mining, machine learning, pattern recognition and knowledge discovery. The blending of rough sets with fuzzy sets and referring them to graphs with concepts of fuzzy sets or rough sets can be seen in [14,15,16,17]. The above said theories have different approaches to tackle vagueness, imprecision and uncertainty. Each said theory has its own limitations and restrictions. While dealing with such theories, a question arises, how to handle multi-attributes? Molodtsov [18] introduced a novel concept of soft sets as a powerful mathematical tool for dealing multi-attribute uncertainty. This newer concept has enough parameters, which make it free from those difficulties which the contemporary theories have and that makes it popular among the experts and researchers working in different fields of research like operation research, probability theory, smoothness of functions and many more. Later on the theory has been modified in some aspects to handle many problems [19,20,21]. A number of applications were established and used regarding decision making problems and multi-attributes modeling using soft sets, [22,23,24,25,26,27].

Feng et al. [28] introduced the concept of soft rough sets which is a blend of soft and rough sets. Clearly, in a rough set model, an equivalence relation is used to form the granulation structure of the universe while a soft set can be used to form the granulation structure of the universe in soft rough model. Huge number of applications, presented by many researchers in data labeling problems, data mining, attributes reduction problems, knowledge based systems, some can be seen in [23,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

A graph can be used to represent many real life problems in computer science especially, which are otherwise abstract. Euler, known as father of graph theory, was universally credited when he settled a famous Kōnigsberg Bridge problem [43] in 1736. After that, many mathematicians applied graph theory in finite fields, for details readers are referred to ([44], and the references therein).

The concept of soft graphs and their basic operations are defined in [45], which were required to handle multi-attributes problems related with graph theory. A number of generalizations of soft graphs are available in [46,47,48]. Soft sets and rough sets are different approaches that provide efficient tools for modeling the problems involving uncertainty and granularity in information system. Graphs are another powerful tool for representing the information by means of diagrams, matrices or relations. Particularly soft graphs serve this purpose fruitfully. Apparently no direct link exists between above said theories. However an effort is made by [49] to establish some kind of linkage and to discuss the uncertainty in soft graphs. He introduced the concept of soft rough graphs, where instead of equivalence classes, parameterized subsets of vertices and edges serve the aim of finding the lower and upper approximations. In such process, some unusual situations may occur like the upper approximation of a non-empty vertex/edge set may be empty. Upper approximation of a subset K of vertices or edges may not contain K. In our present article we endeavour to search a positive answer to above unusual situations and shortcomings. To strengthen the concept of soft rough graphs, a tgeneralized approach is presented, called modified soft rough graphs ($\mathcal{MSR}$-graphs), whose lower and upper vertex and edge approximations are different from those of Noor [49] but the elemental concepts are closely akin. It is shown that the $\mathcal{MSR}$-graphs are more precise and finer than soft rough graphs. Uncertainty measurement is an important issue in the field of rough set theory. There are many approaches available in literature for reasoning with uncertainty. We have discussed uncertainty measures associated with $\mathcal{MSR}$-graphs such as information entropy and rough entropy. The notion of information granules is an important topic in rough set theory, which gives an idea about the objects which are indistinguishable from each other. Here the concept of granularity measures for $\mathcal{MSR}$-graphs has been introduced. The layout of this paper is as follows.

In Section 2, some basic concepts are revised. Section 3, is devoted to present the concept of modified soft rough graphs ($\mathcal{MSR}$-graphs, lower, upper $\mathcal{MSR}$-vertex approximations, lower, upper $\mathcal{MSR}$-edge approximations and the roughness membership function for modified soft rough graphs. Moreover, the notion of $\mathcal{MSR}$-equal relations is proposed and the related properties are explored. Section 4 is about uncertainty measurements associated with modified soft rough graphs and it is shown how these are linked. Section 5 is concerned about the application of $\mathcal{MSR}$-graphs. An algorithm is developed in a realistic way to compute the effectiveness of some diseases among colleagues working in same office. Vertices are denoted by the 20 colleagues and the interaction of these colleagues are presented by the edges. Measure of optimality ${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right),$ and possibly measure of optimality ${\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)$ are defined with the help of lower and upper $\mathcal{MSR}$-vertex approximations of the given graph and using marginal fuzzy sets as weights corresponding to each person, the persons at high risk for having given diseases are found. Computations are made using MATLAB program. Results are shown in tables. Conclusion of the paper is presented in Section 6.

2. Preliminaries

In this section, we will review some relevant definitions and concepts which will helpful for rest of the paper.

Definition 1 

([44]). A graph $G^{\ast }$ is a triple consisting of a vertex set $V\left(G^{\ast }\right)$, an edge set $E\left(G^{\ast }\right),$ and a relation that associates with each edge two vertices called its endpoints.

Definition 2 

([44]). An edge whose endpoints are equal, is called a loop and multiple edges are edges having the same pair of endpoints.

Definition 3 

([44]). A graph $G^{\ast }$ is called simple if it has no loops or multiple edges. A simple graph is specified by its vertex set and edge set, treating the edge set as a set of unordered pairs of vertices and writing $e=xy$ or $e=yx$ for an edge e having end points x and y.

Definition 4 

([44]). A directed graph or digraph $G^{\ast }$ is a triple containing a vertex set $V\left(G^{\ast }\right)$, an edge set $E\left(G^{\ast }\right),$ and a function assigning each edge an ordered pair of vertices. The first vertex of the ordered pair is called the tail of the edge and the second is called the head ; together, they are the endpoints.

Definition 5 

([20]). Let A be the set of parameters. A pair $\left(\xi ,A\right)$ is called a soft set over the set U of universe, where $\xi :A\to P\left(U\right)$ is a set valued mapping and $P\left(U\right)$ is the power set of U.

Definition 6 

([28]). Let $S=\left(\xi ,A\right)$ be a soft set over $U.$ Then, the pair $\mathcal{A}=\left(U,S\right)$ is called soft approximation space. Based on the soft approximation space $\mathcal{A}$, we define

$${{\displaystyle \underline{aprx}}}_{\mathcal{A}}\left(X\right)=\left\{u\in U:\exists \alpha \in A,\left[u\in \xi \left(\alpha \right)\subseteq X\right]\right\},$$

$${\overline{aprx}}_{\mathcal{A}}\left(X\right)=\left\{u\in U:\exists \alpha \in A,\left[u\in \xi \left(\alpha \right),\xi \left(\alpha \right)\cap X\ne \varnothing \right]\right\}$$

assigning to any set $X\subseteq U$, the sets ${{\displaystyle \underline{aprx}}}_{\mathcal{A}}\left(X\right)$ and ${\overline{aprx}}_{\mathcal{A}}\left(X\right),$ are called soft $\mathcal{A}$-lower approximation and soft $\mathcal{A}$-upper approximation of X, respectively.

The sets

$$Pos\left(X\right)={{\displaystyle \underline{aprx}}}_{\mathcal{A}}\left(X\right),$$

$$Neg\left(X\right)=-{\overline{aprx}}_{\mathcal{A}}\left(X\right),$$

$$andBnd\left(X\right)={\overline{aprx}}_{\mathcal{A}}\left(X\right)-{{\displaystyle \underline{aprx}}}_{\mathcal{A}}\left(X\right)$$

are called the soft $\mathcal{A}$-positive region, the soft $\mathcal{A}$-negative region, and the soft $\mathcal{A}$-boundary region of X, respectively. If ${\overline{aprx}}_{\mathcal{A}}\left(X\right)={{\displaystyle \underline{aprx}}}_{\mathcal{A}}\left(X\right),$ X is said to be soft $\mathcal{A}$-definable; otherwise X is called a soft $\mathcal{A}$-rough set.

Definition 7 

([45]). Let $G^{\ast }=\left(V,E\right)$ be a simple graph and A be the set of parameters. A quadruple $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is called a soft graph, where

(1) 

$\left(\xi ,A\right)$ is a soft set over V,

(2) 

$\left(\psi ,A\right)$ is a soft set over E, and

(3) 

$\left(\xi \left(\alpha \right),\psi \left(\alpha \right)\right)$ is a subgraph of $G^{\ast },$ for all $\alpha \in A.$

Definition 8 

([49]). A graph $\mathfrak{G}=(G^{\ast },F_{\ast },K_{\ast },F^{\ast },K^{\ast },A,X)$ is called soft rough graph if it satisfies the following conditions:

(1) 

$G^{\ast }=\left(V,E\right)$ is a simple graph.

(2) 

A be a non-empty set of parameters.

(3) 

X be any non-empty subset of V.

(4) 

($F^{\ast }(X)$, $F_{\ast }(X)$, A) be a soft rough set over V .

(5) 

$(K^{\ast }(X),K_{\ast }(X),A)$ be a soft rough set over E.

(6) 

$H^{\ast }(X)=(F^{\ast }(X),K^{\ast }(X))$ and $H_{\ast }(X)=(F_{\ast }(X),K_{\ast }(X))$ are subgraphs of $G^{\ast }$. A soft rough graph can be represented by $\mathfrak{G}=\langle F_{\ast },K_{\ast },F^{\ast },K^{\ast },A,X\rangle =\{H^{\ast }(X),H_{\ast }(X)\}$.

3. Modified Soft Rough Graphs

In this section, based on the properties and usefulness of both rough sets and soft sets, we introduce the notion of Modified Soft Rough Graphs ($\mathcal{MSR}$-graphs). Basic properties and results of such graphs are investigated and discussed which enable us to put these graphs to more effective practical use.

Definition 9.

Let $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ be a soft graph. Let $\mu :V\to P\left(A\right)$ be a map such that $\mu \left(x\right)=\{\alpha \in A:x\in \xi \left(\alpha \right)\}.$ Denote by ${\mathfrak{Q}}_m=\left(V,\mu \right)$ and call it Modified soft rough vertex ($\mathcal{MSR}$-vertex)approximation space. Based on ${\mathfrak{Q}}_m=\left(V,\mu \right)$, we define two sets, called the lower $\mathcal{MSR}$-vertex approximation and the upper $\mathcal{MSR}$-vertex approximation respectively as follows:

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)=\{x\in X:\mu \left(x\right)\ne \mu \left(y\right)\mathit{for}\mathit{all}y\in X^c\},X^c=V-X$$

and

$${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)=\{x\in V:\mu \left(x\right)=\mu \left(y\right)\mathit{for}\mathit{some}y\in X\}$$

If ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)={\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right),$ then X is called $\mathcal{MS}$-vertex definable set and the graph

$G_{{\mathfrak{Q}}_m}:=\left(\mathcal{V},E\right)$ is called $\mathcal{MS}$-vertex definable graph otherwise X is called $\mathcal{MSR}$-vertex set and $G_{{\mathfrak{Q}}_m}$ is called $\mathcal{MSR}$-vertex graph. Define and denote the lower and upper $\mathcal{MSR}$-vertex approximations of $G_{{\mathfrak{Q}}_m}$ by

$${\displaystyle \underline{G_{{\mathfrak{Q}}_m}}}=\left({{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right),E\right)$$

and

$$\overline{G_{{\mathfrak{Q}}_m}}=\left({\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right),E\right)$$

for any $X\subseteq V.$

Definition 10.

Let $G_{{\mathfrak{Q}}_m}:=\left(\mathcal{V},E\right)$ be a $\mathcal{MSR}$-vertex graph. Then the vertex roughness membership function of $X\subseteq V$ is denoted and defined as

$${\eta }_{{}_{G_{{\mathfrak{Q}}_m}}}\left(X\right)=1-\frac{1}{2}\left[1+\frac{\left|{{\displaystyle \underline{aprx}}}_{{}_{{\mathfrak{Q}}_m}}\left(X\right)\right|}{\left|{\overline{aprx}}_{{}_{{\mathfrak{Q}}_m}}\left(X\right)\right|}\right].$$

It can be seen that if ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)\ne {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)$ then ${\eta }_{{}_{G_{{\mathfrak{Q}}_m}}}\left(X\right)=0.$ So the graph $G_{{\mathfrak{Q}}_m}$ is $\mathcal{MSR}$-vertex definable graph. i.e., there is no roughness.

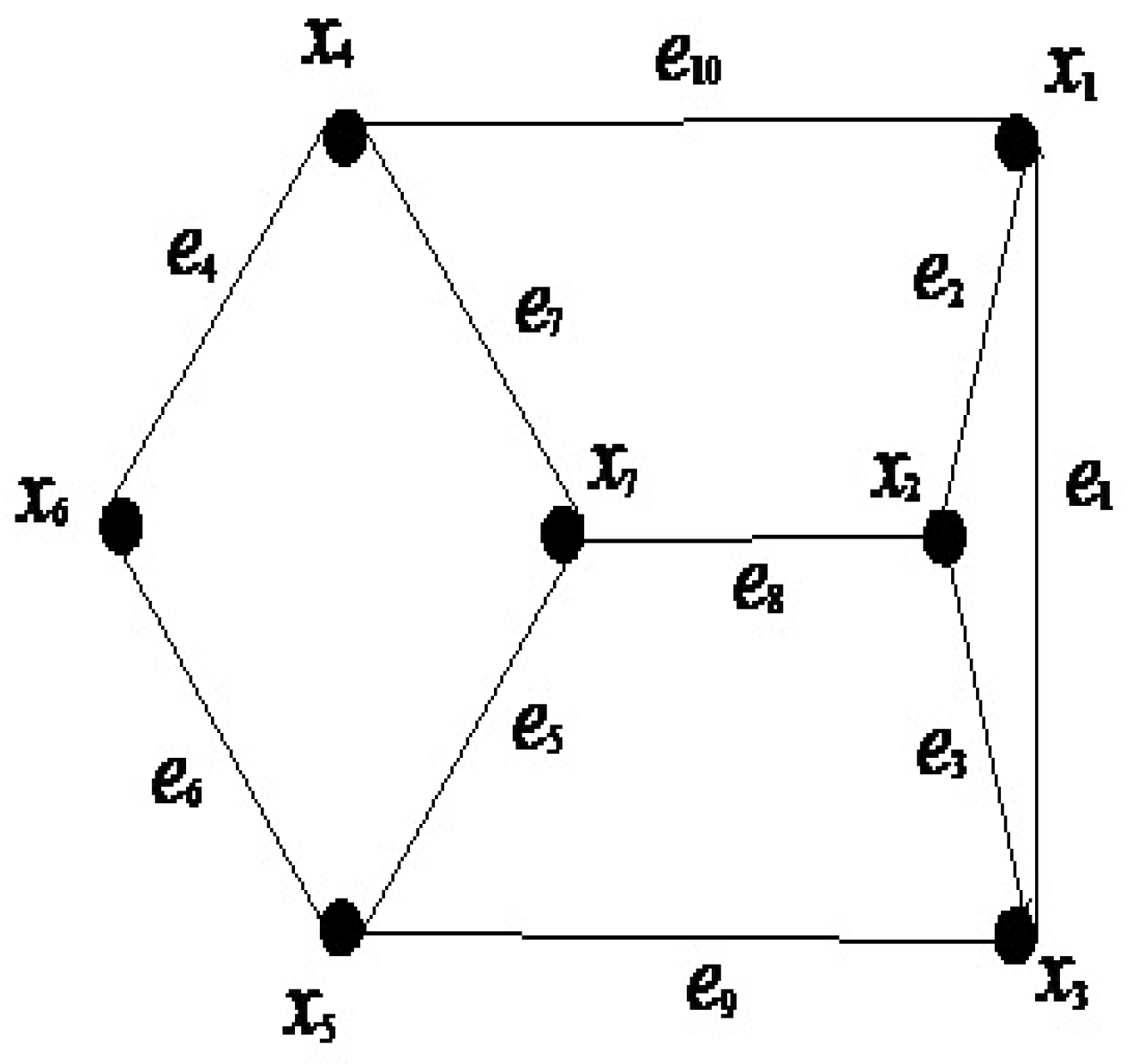
Example 1.

Let $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ be a soft graph over a simple graph $G^{\ast }=(V,E),$ where $V=\left\{x_1,x_2,x_3,x_4,x_5,x_6,x_7\right\}$ and $E=\left\{e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9,e_{10}\right\}$ as shown in Figure 1. Let $\left(\xi ,A\right)$ be a soft set over V with $A=\left\{{\alpha }_{{}_1},{\alpha }_{{}_2},{\alpha }_{{}_3},{\alpha }_4\right\}$ as the set of parameters such that $\xi \left({\alpha }_{{}_1}\right)=\left\{x_1,x_3,x_5,x_7\right\},$ $\xi \left({\alpha }_{{}_2}\right)=\left\{x_1,x_4,x_7\right\},\xi \left({\alpha }_{{}_3}\right)=\left\{x_2,x_6\right\},$ $\xi \left({\alpha }_4\right)=\left\{x_2,x_3,x_5\right\}$, as shown in

Table 1. Tabular representation of soft set $\left(\xi ,A\right)$.

	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$	${\mathit{x}}_7$
${\alpha }_{{}_1}$	1	0	1	0	1	0	1
${\alpha }_2$	1	0	0	1	0	0	1
${\alpha }_{{}_3}$	0	1	0	0	0	1	0
${\alpha }_4$	0	1	1	0	1	0	0

.

Let $X=\{x_1,x_2,x_5,x_6\},$ $X^c=\{x_3,x_4,x_7\}.$ Let $\mu :V\to P\left(A\right)$ be a map such that $\mu \left(x\right)=\{\alpha :x\in \xi \left(\alpha \right)\}.$ So $\mu \left(x_1\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_2}\},$ $\mu \left(x_2\right)=\{{\alpha }_{{}_3},{\alpha }_{{}_4}\},$ $\mu \left(x_3\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_4}\},\mu \left(x_4\right)=\{{\alpha }_{{}_2}\},$ $\mu \left(x_5\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_4}\},$ $\mu \left(x_6\right)=\{{\alpha }_{{}_3}\}$ and $\mu \left(x_7\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_2}\}.$ Here $\mu \left(x_1\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_2}\}=\mu \left(x_7\right)$ and $\mu \left(x_3\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_4}\}=\mu \left(x_5\right).$

Therefore

$$\begin{array}{ccc}\hfill {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)& =& \{x_2,x_6\}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)& =& \{x_1,x_2,x_3,x_5,x_6,x_7\}\hfill \end{array}$$

showing that ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)\ne {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)$, so $G_{{\mathfrak{Q}}_m}:=\left(\mathcal{V},E\right)$ is $\mathcal{MSR}$-vertex graph, where

$${\displaystyle \underline{G_{{\mathfrak{Q}}_m}}}=\left({{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right),E\right)=\left(\left\{x_2,x_6\right\},\left\{e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9,e_{10}\right\}\right)$$

and

$$\overline{G_{{\mathfrak{Q}}_m}}=\left({\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right),E\right)=\left(\left\{x_1,x_2,x_3,x_5,x_6,x_7\right\},\left\{e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9,e_{10}\right\}\right).$$

Furthermore, ${\eta }_{{}_{G_{{\mathfrak{Q}}_m}}}\left(X\right)=1-\frac{1}{2}\left[1+\frac{\left|{{\displaystyle \underline{aprx}}}_{{}_{{\mathfrak{Q}}_m}}\left(X\right)\right|}{\left|{\overline{aprx}}_{{}_{{\mathfrak{Q}}_m}}\left(X\right)\right|}\right]=1-\frac{1}{2}\left[1+\frac{2}{6}\right]=0.333.$

Definition 11.

Let $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ be a soft graph. Let $\lambda :E\to P\left(A\right)$ be a map such that $\lambda \left(e\right)=\{\alpha \in A:e\in \psi \left(\alpha \right)\}.$ Denote by ${\mathfrak{R}}_m=\left(E,\lambda \right)$ and call it Modified soft rough edge approximation space. Based on ${\mathfrak{R}}_m=\left(E,\lambda \right)$, we define two sets, called the lower $\mathcal{MSR}$-edge approximation and the upper $\mathcal{MSR}$-edge approximation respectively as follows:

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)=\{e\in Y:\lambda \left(e\right)\ne \lambda \left(f\right)\mathit{for}\mathit{all}f\in Y^c\},Y^c=E-Y$$

and

$${\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)=\{e\in Y:\lambda \left(e\right)=\lambda \left(f\right)\mathit{for}\mathit{some}f\in Y\}$$

If ${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)={\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right),$ then Y is called $\mathcal{MS}$-edge definable set and the graph $G_{{}_{{\mathfrak{R}}_m}}:=\left(V,\mathcal{E}\right)$ is called $\mathcal{MS}$-edge definable graph otherwise Y is called $\mathcal{MSR}$-edge set and $G_{{}_{{\mathfrak{R}}_m}}$ is called $\mathcal{MSR}$-edge graph. Define and denote the lower and upper $\mathcal{MSR}$-edge approximations of $G_{{}_{{\mathfrak{R}}_m}}$ by

$${\displaystyle \underline{G_{{\mathfrak{R}}_m}}}=\left(V,{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\right)$$

and

$$\overline{G_{{\mathfrak{R}}_m}}=\left(V,{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)\right)$$

for any $Y\subseteq E.$

Definition 12.

Let $G_{{}_{{\mathfrak{R}}_m}}:=\left(V,\mathcal{E}\right)$ be a $\mathcal{MSR}$-edge graph. Then the edge roughness membership function of $Y\subseteq E$ is denoted and defined as

$${\eta }_{{}_{G_{{}_{{\mathfrak{R}}_m}}}}\left(Y\right)=1-\frac{1}{2}\left[1+\frac{\left|{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}{\left|{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}\right].$$

It can be seen that if ${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\ne {\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)$ then ${\eta }_{{}_{G_{{\mathfrak{R}}_m}}}\left(Y\right)=0.$ So the graph $G_{{}_{{\mathfrak{R}}_m}}$ is $\mathcal{MSR}$-edge definable graph. i.e., there is no roughness.

Example 2.

From Example 1, let $\left(\psi ,A\right)$ be a soft sets over E as shown in

Table 2. Tabular representation of soft set $\left(\psi ,A\right)$.

	${\mathit{e}}_1$	${\mathit{e}}_2$	${\mathit{e}}_3$	${\mathit{e}}_4$	${\mathit{e}}_5$	${\mathit{e}}_6$	${\mathit{e}}_7$	${\mathit{e}}_8$	${\mathit{e}}_9$	${\mathit{e}}_{10}$
${\alpha }_{{}_1}$	0	0	1	1	0	1	0	0	1	0
${\alpha }_{{}_2}$	0	1	0	1	0	0	1	0	0	1
${\alpha }_{{}_3}$	1	0	1	0	1	0	1	1	0	0
${\alpha }_{{}_4}$	0	0	1	0	0	1	1	0	1	1

.

Let $Y=\left\{e_2,e_3,e_4,e_6,e_9,e_{10}\right\}\subseteq E$ then

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)=\left\{e_2,e_3,e_4,e_6,e_9,e_{10}\right\}$$

and

$${\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)=\left\{e_2,e_3,e_4,e_6,e_9,e_{10}\right\}$$

Clearly ${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)={\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right),$ for $Y\subseteq E,$ So Y is $\mathcal{MS}$-edge definable set and the graph

$G_{{}_{{\mathfrak{R}}_m}}:=\left(V,\mathcal{E}\right)$ is $\mathcal{MS}$-edge definable graph. Also

$${\eta }_{{}_{G_{{}_{{\mathfrak{R}}_m}}}}\left(Y\right)=1-\frac{1}{2}\left[1+\frac{\left|{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}{\left|{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}\right]=0.$$

That is, there is no roughness.

Definition 13.

The roughness membership function ${\eta }_{{}_{G_m^{\ast }}}\left(G^{\ast \ast }\right)$ of any subgraph graph $G^{\ast \ast }=\left(X,Y\right)$ can be found by

$${\eta }_{{}_{G_m^{\ast }}}\left(G^{\ast \ast }\right)=1-\frac{1}{2}\left[\frac{\left|{{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)\right|}{\left|{\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)\right|}+\frac{\left|{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}{\left|{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)\right|}\right].$$

Definition 14.

A soft graph $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is called $\mathcal{MS}$-definable if

(1) 

X is $\mathcal{MS}$-vertex definable i.e., ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)={\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)$ and

(2) 

Y is $\mathcal{MS}$-edge definable i.e., ${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)={\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right).$

Definition 15.

A soft graph $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is called $\mathcal{MSR}$-graph if

(1) 

X is $\mathcal{MSR}$-vertex set i.e., ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right)\ne {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right)$

(2) 

Y is $\mathcal{MSR}$-edge set i.e., ${{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\ne {\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right).$

A $\mathcal{MSR}$-graph is denoted by $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right).$

Definition 16.

By a lower and upper approximations of the $\mathcal{MSR}$-graph $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$, we mean ${\displaystyle \underline{aprx}}\left(G_m\right)=\left({{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X\right),{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y\right)\right)$ and $\overline{aprx}\left(G_m\right)=\left({\overline{aprx}}_{{\mathfrak{Q}}_m}\left(X\right),{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y\right)\right)$ respectively, for any $X\subseteq V$ and $Y\subseteq E.$

Proposition 1.

Let $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ be a soft graph such that $Q_m=\left(V,\xi \right)$ and $R_m=\left(E,\psi \right)$ represents respectively, the $\mathcal{MSR}$-vertex approximation space and $\mathcal{MSR}$-edge approximation space, then

(i)

${\displaystyle \underline{aprx}}\left(G^{\ast }\right)=G^{\ast }=\overline{aprx}\left(G^{\ast }\right)$

(ii)

${\displaystyle \underline{aprx}}\left(\varnothing \right)=\overline{aprx}\left(\varnothing \right)=\varnothing$

(iii)

If $G_1\subseteq G_2$ then ${\displaystyle \underline{aprx}}\left(G_1\right)\subseteq {\displaystyle \underline{aprx}}(G_2)$ and $\overline{aprx}\left(G_1\right)\subseteq \overline{aprx}(G_2)$

(iv)

$\overline{aprx}\left(G_1\cap G_2\right)\subseteq \overline{aprx}\left(G_1\right)\cap \overline{aprx}\left(G_2\right)$

(v)

${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)={\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right)$

(vi)

${\displaystyle \underline{aprx}}\left(G_1\cup G_2\right)\supseteq {\displaystyle \underline{aprx}}\left(G_1\right)\cup {\displaystyle \underline{aprx}}\left(G_2\right)$

(vii)

$\overline{aprx}\left(G_1\cup G_2\right)=\overline{aprx}\left(G_1\right)\cup \overline{aprx}\left(G_2\right),$ where $G_1$ and $G_2$ are subgraphs of $G^{\ast }$.

Proof. 

$\left(i\right)$ and $\left(ii\right)$ directly follows from the definitions of $\mathcal{MSR}$-vertex/edge approximations.

$\left(iii\right)$ Let $G_1\subseteq G_2$ so $\left(X_1,Y_1\right)\subseteq \left(X_2,Y_2\right)$ or $X_1\subseteq X_2$ and $Y_1\subseteq Y_2.$ Let $\left(x,e\right)\in {\displaystyle \underline{aprx}}\left(G_1\right)=\left({{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_1,{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_1\right)$ such that $x\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_1$ and $e\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_1.$ That is, $x\in X_1$ with $\mu \left(x\right)\ne \mu \left(z\right)$ for all $z\in X_1^c$ and $e\in Y_1$ with $\lambda \left(e\right)\ne \lambda \left(h\right)$ for all $h\in Y_1^c.$ Since $X_1\subseteq X_2$ and $Y_1\subseteq Y_2$, so $x\in X_2$ with $\mu \left(x\right)\ne \mu \left(z\right)$ for all $z\in X_2^c$ and $e\in Y_2$ with $\lambda \left(e\right)\ne \lambda \left(h\right)$ for all $h\in Y_2^c.$ Thus $x\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_2$ and $e\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_2$ showing that $\left(x,e\right)\in \left({{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_2,{{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_2\right)={\displaystyle \underline{aprx}}(G_2).$ Hence $G_1\subseteq G_2$ implies ${\displaystyle \underline{aprx}}\left(G_1\right)\subseteq {\displaystyle \underline{aprx}}(G_2).$ Similarly one can show if $G_1\subseteq G_2$ then $\overline{aprx}\left(G_1\right)\subseteq \overline{aprx}(G_2).$

$\left(iv\right)$ Since $\left(G_1\cap G_2\right)$ is contained in both $G_1$ and $G_2,$ so by $\left(iii\right)$ $\overline{aprx}\left(G_1\cap G_2\right)\subseteq \overline{aprx}\left(G_1\right)$ and $\overline{aprx}\left(G_1\cap G_2\right)\subseteq \overline{aprx}\left(G_2\right).$ Therefore $\overline{aprx}\left(G_1\cap G_2\right)\subseteq \overline{aprx}\left(G_1\right)\cap \overline{aprx}\left(G_2\right).$

$\left(v\right)$ Since $G_1\cap G_2\subseteq G_1$ and $G_1\cap G_2\subseteq G_2$ so by $\left(iii\right)$ ${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)\subseteq {\displaystyle \underline{aprx}}\left(G_1\right)$ and ${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)\subseteq {\displaystyle \underline{aprx}}\left(G_2\right)$. Hence ${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)\subseteq {\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right).$ Now for reverse inclusion, we suppose $\left(x,e\right)\in {\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right).$ Which implies $\left(x,e\right)\in {\displaystyle \underline{aprx}}\left(G_1\right)$ and $\left(x,e\right)\in {\displaystyle \underline{aprx}}\left(G_2\right)$ such that $x\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_1,$ $e\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_1$ and $x\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}{X}_2,$ $e\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}{Y}_2.$ So $x\in X_1$ with $\mu \left(x\right)\ne \mu \left(y\right)$ for all $y\in X_1^C$ and $x\in X_2$ with $\mu \left(x\right)\ne \mu \left(z\right)$ for all $z\in X_2^C$ implies $x\in \left(X_1\cap X_2\right)$ with $\mu \left(x\right)\ne \mu \left(y\right)$ for all $y\in X_1^C\cup X_2^C$. Which shows $x\in \left(X_1\cap X_2\right)$ with $\mu \left(x\right)\ne \mu \left(y\right)$ for all $y\in {\left(X_1\cap X_2\right)}^c$, so $x\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(X_1\cap X_2\right)$. Similarly we can show $e\in {{\displaystyle \underline{aprx}}}_{{\mathfrak{R}}_m}\left(Y_1\cap Y_2\right)$. So $\left(x,e\right)\in {\displaystyle \underline{aprx}}\left(G_1\cap G_2\right).$ Thus ${\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right)\subseteq {\displaystyle \underline{aprx}}\left(G_1\cap G_2\right).$ Hence ${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)={\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right).$

$\left(vi\right)$ Since $G_1\subseteq G_1\cup G_2$ and $G_2\subseteq G_1\cup G_2$ so by $\left(iii\right),$ ${\displaystyle \underline{aprx}}\left(G_1\right)\subseteq {\displaystyle \underline{aprx}}\left(G_1\cup G_2\right)$ and ${\displaystyle \underline{aprx}}\left(G_2\right)\subseteq {\displaystyle \underline{aprx}}\left(G_1\cup G_2\right).$ Hence ${\displaystyle \underline{aprx}}\left(G_1\cup G_2\right)\supseteq {\displaystyle \underline{aprx}}\left(G_1\right)\cup {\displaystyle \underline{aprx}}\left(G_2\right).$

$\left(vii\right)$ It is easy to show, by using $\left(iii\right),$ that $\overline{aprx}\left(G_1\right)\cup \overline{aprx}\left(G_2\right)\subseteq \overline{aprx}\left(G_1\cup G_2\right).$ Conversely suppose that $\left(x,e\right)\in \overline{aprx}\left(G_1\cup G_2\right)=\left({\overline{aprx}}_{{\mathfrak{Q}}_m}(X_1\cup X_2),{\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y_1\cup Y_2\right)\right)$ then $x\in {\overline{aprx}}_{{\mathfrak{Q}}_m}(X_1\cup X_2)$ and $e\in {\overline{aprx}}_{{\mathfrak{R}}_m}\left(Y_1\cup Y_2\right).$ Which implies $x\in \left(X_1\cup X_2\right)$ with $\mu \left(x\right)=\mu \left(y\right)$ for some $y\in {\left(X_1\cup X_2\right)}^{}$ and $e\in \left(Y_1\cup Y_2\right)$ with $\lambda \left(e\right)=\lambda \left(f\right)$ for some $f\in \left(Y_1\cup Y_2\right).$ So $x\in X_1$ with $\mu \left(x\right)=\mu \left(y\right)$ for some $y\in X_1$ or $x\in X_2$ with $\mu \left(x\right)=\mu \left(y\right)$ for some $y\in X_2.$ Both these conditions shows $x\in {\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_1$ or $x\in {\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_2$. So $x\in \left({\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_1\cup {\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_2\right)$. Similarly, it can be shown that $e\in \left({\overline{aprx}}_{{\mathfrak{R}}_m}{Y}_1\cup {\overline{aprx}}_{{\mathfrak{R}}_m}{Y}_2\right).$ Thus $\left(x,e\right)\in \left({\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_1,{\overline{aprx}}_{{\mathfrak{R}}_m}{Y}_1\right)$ or $\left(x,e\right)\in \left({\overline{aprx}}_{{\mathfrak{Q}}_m}{X}_2,{\overline{aprx}}_{{\mathfrak{R}}_m}{Y}_2\right).$ Which means $\left(x,e\right)\in \overline{aprx}\left(G_1\right)$ or $\left(x,e\right)\in \overline{aprx}\left(G_2\right).$ That is, $\left(x,e\right)\in \overline{aprx}\left(G_1\right)\cup \overline{aprx}\left(G_2\right).$ Thus $\overline{aprx}\left(G_1\cup G_2\right)\subseteq \overline{aprx}\left(G_1\right)\cup \overline{aprx}\left(G_2\right).$ □

Remark 1.

In the proof $(v)$ of Proposition 1, we have proved ${\displaystyle \underline{aprx}}\left(G_1\cap G_2\right)={\displaystyle \underline{aprx}}\left(G_1\right)\cap {\displaystyle \underline{aprx}}\left(G_2\right)$. If we want to prove this result by the approach used by [49], we have to employ a strong condition on soft sets $\left(\xi ,A\right)$ and $\left(\psi ,A\right)$ to be intersection complete. However in our approach, no such condition is required.

Now in the following, we define some relations associated with modified soft rough graphs.

Definition 17.

Let a soft graph be $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right).$ Then for two $\mathcal{MSR}$-graphs $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$, we define

(i)

$G_m\simeq G_m^{\ast }$ if and only if ${\displaystyle \underline{aprx}}\left(G_m\right)={\displaystyle \underline{aprx}}\left(G_m^{\ast }\right)$

(ii)

$G_m\eqsim G_m^{\ast }$ if and only if $\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m^{\ast }\right)$

(iii)

$G_m\approx G_m^{\ast }$ if and only if ${\displaystyle \underline{aprx}}\left(G_m\right)={\displaystyle \underline{aprx}}\left(G_m^{\ast }\right)$ and $\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m^{\ast }\right).$

The above relations $\left(i\right)$ to $\left(iii\right)$ are respectively called, the lower $\mathcal{MSR}$-equal relation, the upper $\mathcal{MSR}$-equal relation and the $\mathcal{MSR}$-equal relation.

Proposition 2.

The relations $\simeq ,$≂ and ≈ defined on $\mathcal{MSR}$-graphs are equivalence relations.

Proposition 3.

Suppose $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is soft graph defined on simple graph $G^{\ast }=\left(V,E\right)$. Then for two $\mathcal{MSR}$-graphs $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$, the following hold:

(i)

$G_m\eqsim G_m^{\ast }$ if and only if $G_m\eqsim G_m\cup G_m^{\ast }\eqsim G_m^{\ast }.$

(ii)

If $G_{{}_{1}m}\eqsim G_{{}_{1}m}^{\ast }$ and $G_{{}_{2}m}\eqsim G_{{}_{2}m}^{\ast }$ then $G_{{}_{1}m}\cup G_{{}_{2}m}\eqsim G_{{}_{1}m}^{\ast }\cup G_{{}_{2}m}^{\ast }.$

(iii)

If $G_m\subseteq G_m^{\ast }$ then $\left(G_m\cup {\left(G_m^{\ast }\right)}^c\right)\eqsim G^{\ast }$,

(iv)

If $G_m\subseteq G_m^{\ast }$ and $G_m\eqsim G^{\ast }$, then $G_m^{\ast }\eqsim G^{\ast }$.

Proof. 

$\left(i\right)$ Let $G_m\eqsim G_m^{\ast }$ then $\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m^{\ast }\right).$ However, from Proposition 1$\left(vii\right)$, $\overline{aprx}\left(G_m\cup G_m^{\ast }\right)=\overline{aprx}\left(G_m\right)\cup \overline{aprx}\left(G_m^{\ast }\right)$ which implies that $\overline{aprx}\left(G_m\cup G_m^{\ast }\right)=\overline{aprx}\left(G_m\right)\cup \overline{aprx}\left(G_m^{\ast }\right)=\overline{aprx}\left(G_m\right)\cup \overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m^{\ast }\right)$, so $G_m\eqsim G_m\cup G_m^{\ast }$ and $G_m\cup G_m^{\ast }\eqsim$ $G_m^{\ast }$ showing that $G_m\eqsim G_m\cup G_m^{\ast }\eqsim G_m^{\ast }$. Conversely suppose that $G_m\eqsim G_m\cup G_m^{\ast }\eqsim G_m^{\ast }$. Since ≂ is an equivalence relation, so it is transitive. Thus, $G_m\eqsim G_m^{\ast }.$

$\left(ii\right)$ The proof is similar to the proof of (i).

$\left(iii\right)$ Suppose $G_m\eqsim G_m^{\ast }$ then $\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G_m^{\ast }\right).$ Then by Proposition 1$\left(vii\right),$ $\overline{aprx}\left(\left(G_m\right)\cup {\left(G_m^{\ast }\right)}^c\right)=\overline{aprx}\left(G_m\right)\cup \overline{aprx}{\left(G_m^{\ast }\right)}^c=\overline{aprx}\left(G_m^{\ast }\right)\cup \overline{aprx}{\left(G_m^{\ast }\right)}^c=\overline{aprx}\left(G_m^{\ast }\cup {\left(G_m^{\ast }\right)}^c\right)=\overline{aprx}\left(V,E\right)=\overline{aprx}\left(G^{\ast }\right).$ Therefore $\left(G_m\cup {\left(G_m^{\ast }\right)}^c\right)\eqsim G^{\ast }.$

$\left(iv\right)$ Suppose $G_m\subseteq G_m^{\ast }$ and $G_m\eqsim G^{\ast }$, then by definition $\overline{aprx}\left(G_m\right)=\overline{aprx}\left(G^{\ast }\right).$ which implies $\overline{aprx}\left(G^{\ast }\right)=\overline{aprx}\left(G_m\right)\subseteq \overline{aprx}\left(G_m^{\ast }\right)$. So $\overline{aprx}\left(G^{\ast }\right)\subseteq \overline{aprx}\left(G_m^{\ast }\right).$ However, $G_m^{\ast }\subseteq G^{\ast }$ shows $\overline{aprx}\left(G_m^{\ast }\right)\subseteq \overline{aprx}\left(G^{\ast }\right).$ Hence $\overline{aprx}\left(G_m^{\ast }\right)=\overline{aprx}\left(G^{\ast }\right)$ or equivalently $G_m^{\ast }\eqsim G^{\ast }.$ □

Proposition 4.

Suppose $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is soft graph. Then for two $\mathcal{MSR}$-graphs $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$, the following hold:

(i)

$G_m\simeq G_m^{\ast }$ if and only if $G_m\simeq G_m\cap G_m^{\ast }\eqsim G_m^{\ast }.$

(ii)

$G_{{}_{1}m}\simeq G_{{}_{1}m}^{\ast }$ and $G_{{}_{2}m}\simeq G_{{}_{2}m}^{\ast }$ then $G_{{}_{1}m}\cap G_{{}_{2}m}\simeq G_{{}_{1}m}^{\ast }\cap G_{{}_{2}m}^{\ast }.$

(iii)

If $G_m\subseteq G_m^{\ast }$ then $\left(G_m\cap {\left(G_m^{\ast }\right)}^c\right)\simeq \varnothing$, where $G^{\ast }=\left(V,E\right)$ is a simple graph.

(iv)

If $G_m\subseteq G_m^{\ast }$ and $G_m\simeq G^{\ast }$, then $G_m^{\ast }\simeq G^{\ast }$.

Proof. 

Proof follows from Proposition 1 and 3. □

Remark 2.

In order to show the similar results in Propositions 2 and 3, in case of soft rough graphs of proposed in [49], the soft sets $\left(\xi ,A\right)$ and $\left(\psi ,A\right)$ must be intersection complete but in case of our proposed model of modified soft rough graphs, no such condition is required on $\left(\xi ,A\right)$ and $\left(\psi ,A\right)$.

Proposition 5.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph and $G=\left(G_{{}_{\mathfrak{Q}}},G_{\mathfrak{R}}\right)$ be a soft rough graph then ${\displaystyle \underline{aprx}}\left(G\right)\subseteq {\displaystyle \underline{aprx}}\left(G_m\right).$

Proof. 

To prove ${\displaystyle \underline{aprx}}\left(G\right)\subseteq {\displaystyle \underline{aprx}}\left(G_m\right),$ we have to prove only ${\displaystyle \underline{aprx}}\left(X\right)\subseteq {\displaystyle \underline{aprx}}\left(X_m\right)$ and ${\displaystyle \underline{aprx}}\left(Y\right)\subseteq {\displaystyle \underline{aprx}}\left(Y_m\right)$, where $X\subseteq V$ and $Y\subseteq E.$

Let $x\in {\displaystyle \underline{aprx}}(X)$ then $x\in \xi \left(\alpha \right)\subseteq X$ for $\alpha \in A,$ which shows $x\in X$ and $\alpha \in \mu \left(x\right).$ Suppose on contrary, $x\notin {\displaystyle \underline{aprx}}\left(X_m\right).$ Then $\mu \left(x\right)=\mu \left(y\right)$ for some $y\in X^C=V-X.$ Since $\alpha \in \mu \left(x\right)$ so $\alpha \in \mu \left(y\right)$ which implies $y\in \xi \left(\alpha \right).$ However, $\xi \left(\alpha \right)\subseteq X$ so $y\in X.$ Which is a contradiction because $y\in X^C.$ So $x\in {\displaystyle \underline{aprx}}\left(X_m\right).$ Hence ${\displaystyle \underline{aprx}}\left(X\right)\subseteq {\displaystyle \underline{aprx}}\left(X_m\right).$ Similarly if $e\in {\displaystyle \underline{aprx}}(Y)$ then we can show ${\displaystyle \underline{aprx}}\left(Y\right)\subseteq {\displaystyle \underline{aprx}}\left(Y_m\right).$ Hence we conclude that ${\displaystyle \underline{aprx}}\left(G\right)\subseteq {\displaystyle \underline{aprx}}\left(G_m\right).$ □

Remark 3.

From above Proposition ${\displaystyle \underline{aprx}}\left(G\right)\subseteq {\displaystyle \underline{aprx}}\left(G_m\right)$, it is clear that granules of information in $\mathcal{MSR}$-graph $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ are finer than soft rough graph $G=\left(G_{{}_{\mathfrak{Q}}},G_{\mathfrak{R}}\right).$ Thus $\mathcal{MSR}$-graph are more robust than soft rough graph.

4. Uncertainty Measurement in Modified Soft Rough Graphs

Different membership functions for reasoning with uncertainty has been proposed in literature [50,51,52,53]. In this section, some uncertainty measurements such as information entropy, naive granularity measure, elementary entropy and rough entropy of modified soft rough graphs are proposed. Further, some theoretical properties are obtained and investigated.

Definition 18.

Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ be $\mathcal{MSR}$-vertex approximation space and $\alpha \in A$, then the set $C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)=\left\{\mu \left(x\right):x\in \xi \left(\alpha \right)\right\}$ is called the soft association of parameter $\alpha \in A.$

Definition 19.

Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ be $\mathcal{MSR}$-vertex approximation space and $\alpha \in A.$ Then the soft neighborhood of α is denoted $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right),$ and is defined as $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)=\cap \left\{\mu \left(x\right):x\in \xi \left(\alpha \right)\right\}=\cap C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)$.

Definition 20.

Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ and ${\mathfrak{Q}}_m^{\ast }=\left(V,{\mu }^{\ast }\right)$ be two $\mathcal{MSR}$-vertex approximation spaces with

(i)

For all $\mu \left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right),$ there exists ${\mu }^{\ast }\left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}^{\ast }\left(\alpha \right)$ such that $\mu \left(x\right)\subseteq {\mu }^{\ast }\left(x\right)$ and

(ii)

For all ${\mu }^{\ast }\left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}^{\ast }\left(\alpha \right),$ there exists $\mu \left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)$ such that $\mu \left(x\right)\subseteq {\mu }^{\ast }\left(x\right).$ Then we say ${\mathfrak{Q}}_m^{\ast }$ is finer than ${\mathfrak{Q}}_m$ and denote it by ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$.

Note that a similar definition can be made for $\mathcal{MSR}$-edge approximation spaces.

Proposition 6.

Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ and ${\mathfrak{Q}}_m^{\ast }=\left(V,{\mu }^{\ast }\right)$ be two $\mathcal{MSR}$-vertex approximation spaces such that ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$. Then $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)$.

Proof. 

$\left(i\right)$ Suppose $z\in N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)=\cap \left\{\mu \left(x\right):x\in \xi \left(\alpha \right)\right\}=\cap C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)$. Then $z\in \mu \left(x\right)$ for any $\mu \left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right).$ By Definition $4.3,$ for any ${\mu }^{\ast }\left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}^{\ast }\left(\alpha \right),$ there exists $\mu \left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)$ such that $z\in \mu \left(x\right)\subseteq {\mu }^{\ast }\left(x\right).$ Hence $z\in {\mu }^{\ast }\left(x\right),$ for any ${\mu }^{\ast }\left(x\right)\in C_{{}_{{\mathfrak{Q}}_m}}^{\ast }\left(\alpha \right).$ Thus, $z\in \cap C_{{}_{{\mathfrak{Q}}_m}}^{\ast }\left(\alpha \right)=N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right).$ Consequently, $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right).$ □

Proposition 7.

Let ${\mathfrak{R}}_m=\left(E,\lambda \right)$ and ${\mathfrak{R}}_m^{\ast }=\left(E,{\lambda }^{\ast }\right)$ be two $\mathcal{MSR}$-edge approximation spaces such that ${\mathfrak{R}}_m⪯{\mathfrak{R}}_m^{\ast }$. Then $N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)$.

Proof. 

The proof is similar to the proof of Proposition 6. □

Note: From now onwards, $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ will represent a $\mathcal{MSR}$-graph with ${\mathfrak{Q}}_m=\left(V,\mu \right)$ and ${\mathfrak{R}}_m=\left(E,\lambda \right)$ as $\mathcal{MSR}$-vertex approximation space and $\mathcal{MSR}$-edge approximation space, respectively unless stated otherwise.

Definition 21.

Let $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then the neighborhood information entropy of $G_m$ is defined

$${\eta }_{{}_{Ent}}\left(G_m\right)={\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}\right]+{\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]$$

Proposition 8.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$ are two $\mathcal{MSR}$-graphs such that ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$ and ${\mathfrak{R}}_m⪯{\mathfrak{R}}_m^{\ast }.$ Then ${\eta }_{{}_{Ent}}\left(G_m\right)\ge {\eta }_{{}_{Ent}}\left(G_m^{\ast }\right).$

Proof. 

From Propositions 6 and 7, we have $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)$ and $N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right).$ Which implies

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}\right]& \ge & {\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|V\right|}\right]\mathrm{and}\hfill \\ \hfill {\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]& \ge & {\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|E\right|}\right].\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}\right]+{\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]& \ge & {\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|V\right|}\right]+\hfill \\ & & {\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|E\right|}\right].\hfill \\ \hfill \mathrm{Which}\mathrm{shows}\mathrm{that}{\eta }_{{}_{Ent}}\left(G_m\right)& \ge & {\eta }_{{}_{Ent}}\left(G_m^{\ast }\right).\hfill \end{array}$$

 □

Remark 4.

The neighborhood information entropy ${\eta }_{{}_{Ent}}\left(G_m\right)$ attains the maximum value $2-\frac{1}{\left|V\right|}-\frac{1}{\left|E\right|}$ when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=1=\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|$ and achieves the minimum values 0 when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=\left|V\right|$ and $\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|=\left|E\right|,$ for $\alpha \in A.$

Definition 22.

Let $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then the naive granularity measure of $G_m$ is defined

$${\eta }_{{}_{Gran}}\left(G_m\right)=\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}+\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}.$$

Proposition 9.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$ are two $\mathcal{MSR}$-graphs such that ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$ and ${\mathfrak{R}}_m⪯{\mathfrak{R}}_m^{\ast }.$ Then ${\eta }_{{}_{Gran}}\left(G_m\right)\le {\eta }_{{}_{Gran}}\left(G_m^{\ast }\right).$

Proof. 

The proof is similar to the proof of Proposition 8. □

Remark 5.

The granularity measure ${\eta }_{{}_{Gran}}\left(G_m\right)$ achieves the maximum value 2 when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=\left|V\right|$ and $\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|=\left|E\right|$ and attains the minimum values $\frac{1}{\left|V\right|}+\frac{1}{\left|E\right|}$ when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=1=\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|,$ for $\alpha \in A$.

Proposition 10.

Let $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then ${\eta }_{{}_{Ent}}\left(G_m\right)+{\eta }_{{}_{Gran}}\left(G_m\right)=2.$

Proof. 

$$\begin{array}{ccc}\hfill {\eta }_{{}_{Ent}}\left(G_m\right)+{\eta }_{{}_{Gran}}\left(G_m\right)& =& \left[{\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}\right]+{\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}\left[1-\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]\right]+\hfill \\ & & \left[\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}+\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]\hfill \\ & =& \frac{1}{\left|V\right|}\left|V\right|+\frac{1}{\left|E\right|}\left|E\right|=2\hfill \end{array}$$

 □

Definition 23.

Let $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then the neighborhood elementary entropy of $G_m$ is defined

$${\eta }_{{}_{N-Ent}}\left(G_m\right)=-\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}-\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}.$$

Proposition 11.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$ are two $\mathcal{MSR}$-graphs such that ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$ and ${\mathfrak{R}}_m⪯{\mathfrak{R}}_m^{\ast }.$ Then ${\eta }_{{}_{N-Ent}}\left(G_m^{\ast }\right)\le {\eta }_{{}_{{}_{N-Ent}}}\left(G_m\right).$

Proof. 

From Propositions 6 and 7, we have $N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)$ and $N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\subseteq N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)$ for $\alpha \in A.$ Which shows

$$\begin{array}{ccc}\hfill -\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}& \ge & -\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|V\right|}\mathrm{and}\hfill \\ \hfill -\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}& \ge & -\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|E\right|}\hfill \\ \hfill -\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}-\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}& \ge & -\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|V\right|}-\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m^{\ast }}}\left(\alpha \right)\right|}{\left|E\right|}\hfill \\ \hfill \mathrm{Consequently},{\eta }_{{}_{N-Ent}}\left(G_m^{\ast }\right)& \le & {\eta }_{{}_{{}_{N-Ent}}}\left(G_m\right).\hfill \end{array}$$

 □

Remark 6.

The neighborhood granularity measure ${\eta }_{{}_{{}_{N-Ent}}}\left(G_m\right)$ achieves the maximum value ${log}_2\left|V\right|+{log}_2\left|E\right|,$ when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=1=\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|$ and attains the minimum values 0 when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=\left|V\right|$ and $\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|=\left|E\right|,$ for $\alpha \in A$.

Definition 24.

$G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then the neighborhood rough entropy of $G_m$ is defined

$${\eta }_{{}_{NR-Ent}}\left(G_m\right)=-{\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}{log}_2\frac{\left|1\right|}{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}-{\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}{log}_2\frac{\left|1\right|}{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}.$$

Proposition 12.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ and $G_m^{\ast }=\left(G_{{}_{{\mathfrak{Q}}_m}}^{\ast },G_{{}_{{\mathfrak{R}}_m}}^{\ast }\right)$ are two $\mathcal{MSR}$-graphs such that ${\mathfrak{Q}}_m⪯{\mathfrak{Q}}_m^{\ast }$ and ${\mathfrak{R}}_m⪯{\mathfrak{R}}_m^{\ast }.$ Then ${\eta }_{{}_{NR-Ent}}\left(G_m\right)\le {\eta }_{{}_{NR-Ent}}\left(G_m^{\ast }\right).$

Proof. 

The proof is similar to the proof of Proposition 11 by using Proposition 6, Proposition 7 and Definition 24 □

Remark 7.

The neighborhood rough entropy ${\eta }_{{}_{NR-Ent}}\left(G_m\right)$ achieves the maximum value ${log}_2\left|V\right|+{log}_2\left|E\right|,$ when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=\left|V\right|$ and $\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|=\left|E\right|.$ Also ${\eta }_{{}_{NR-Ent}}\left(G\right)$ attains the minimum values 0 when $\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|=1=\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|,$ for any $\alpha \in A.$

Proposition 13.

Suppose $G_m=\left(G_{{}_{{\mathfrak{Q}}_m}},G_{{}_{{\mathfrak{R}}_m}}\right)$ be a $\mathcal{MSR}$-graph. Then ${\eta }_{{}_{N-Ent}}\left(G_m\right)+{\eta }_{{}_{NR-Ent}}\left(G_m\right)={log}_2\left|V\right|+{log}_2\left|E\right|.$

Proof. 

$$\begin{array}{ccc}\hfill {\eta }_{{}_{N-Ent}}\left(G_m\right)+{\eta }_{{}_{NR-Ent}}\left(G_m\right)& =& \left[-\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|}-\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|}\right]+\hfill \\ & & \left[-{\displaystyle \sum _{x\in V}}\frac{1}{\left|V\right|}{log}_2\frac{\left|1\right|}{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}-{\displaystyle \sum _{e\in E}}\frac{1}{\left|E\right|}{log}_2\frac{\left|1\right|}{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}\right]\hfill \\ & =& -\left[\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\left[\frac{\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}{\left|V\right|\left|N_{{}_{{\mathfrak{Q}}_m}}\left(\alpha \right)\right|}\right]\right]-\left[\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\left[\frac{\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}{\left|E\right|\left|N_{{}_{{\mathfrak{R}}_m}}\left(\alpha \right)\right|}\right]\right]\hfill \\ & =& -\left[\frac{1}{\left|V\right|}{\displaystyle \sum _{x\in V}}{log}_2\left[\frac{1}{\left|V\right|}\right]\right]-\left[\frac{1}{\left|E\right|}{\displaystyle \sum _{e\in E}}{log}_2\left[\frac{1}{\left|E\right|}\right]\right]\hfill \\ & =& {log}_2\left|V\right|+{log}_2\left|E\right|.\hfill \end{array}$$

 □

5. Application of Modified Soft Rough Graphs

In this section, an algorithm is formulated for decision making problems based on modified soft rough graphs. To show the application of modified soft rough graphs in decision making, an example is constructed. Suppose $V=\left\{x_1,x_2,\dots ,x_n\right\}$ be the set of n objects$\left(\mathrm{persons}\right)$ and $A=\left\{{\alpha }_{{}_1},{\alpha }_{{}_2},\dots ,{\alpha }_m\right\}$ be the set of m parameters$\left(\mathrm{diseases}\right)$. Let $G^{\ast }=\left(V,E\right)$ be a simple graph whose vertex set is V and edge set is $E.$ Let $\left(\xi ,A\right)$ and $\left(\psi ,A\right)$ be two soft sets over V and E respectively such that for each i, $G_i=\left(\xi \left({\alpha }_i\right),\psi \left({\alpha }_i\right)\right)$ is a subgraph of $G^{\ast }$ showing that $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is a soft graph. Where

$$\begin{array}{ccc}\hfill \xi \left({\alpha }_i\right)& =& \left\{x_j\in V:x_j\mathrm{may}\mathrm{have}\mathrm{viral}\mathrm{disease}{\alpha }_i\right\},\mathrm{and}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \psi \left({\alpha }_i\right)& =& \left\{x_i{x}_j\in E:x_i\mathrm{with}\mathrm{disease}{\alpha }_i\mathrm{has}\mathrm{interaction}\mathrm{with}{x}_j\right\}\hfill \end{array}$$

(2)

For basic evaluation, let $S=\{S_1,S_2,\dots ,S_r\}$ be the set of r experts and let $\left(\rho ,S\right)$ be a soft set over V. Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ be $\mathcal{MSR}$-vertex approximation space then ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)$ and ${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)$ can be calculated by

$$\begin{array}{ccc}\hfill {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)& =& \{x\in S_i:\mu \left(x\right)\ne \mu \left(y\right)\mathrm{for}\mathrm{all}y\in S_i^c\},S_i^c=V-S_i\mathrm{and}\hfill \\ \hfill {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)& =& \{x\in V:\mu \left(x\right)=\mu \left(y\right)\mathrm{for}\mathrm{some}y\in S_i\}.\hfill \end{array}$$

Now we compute the fuzzy functions ${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)$ and ${\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)$ given by

$${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{{\displaystyle \underline{\rho \left(S_k\right)}}}}\left(x_p\right)\mathrm{and}{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{\overline{\rho \left(S_k\right)}}}\left(x_p\right).$$

where ${\chi }_{{}_{{\displaystyle \underline{\rho \left(S_k\right)}}}}$ and ${\chi }_{{}_{\overline{\rho \left(S_k\right)}}}$ are a kind of indicator functions, defined by

$$\begin{array}{ccc}\hfill {\chi }_{{}_{{\displaystyle \underline{\rho \left(S_k\right)}}}}\left(x_p\right)& =& \left\{\begin{array}{c}1\mathrm{if}{x}_p\mathrm{is}\mathrm{in}{{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_k\right)\right)\\ 0,\mathrm{otherwise}\end{array}\right.\mathrm{and}\hfill \\ \hfill {\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)& =& \left\{\begin{array}{c}1\mathrm{if}{x}_p\mathrm{is}\mathrm{in}{\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_k\right)\right)\\ 0,\mathrm{otherwise}\end{array}\right.\hfill \end{array}$$

Now the marginal weights for each $x_p$, can be computed by;

$$\begin{array}{ccc}\hfill \delta \left(x_p\right)& =& \frac{1}{n}\left[{\delta }_r\left(x_p\right)+{\delta }_c\left(x_p\right)\right]\mathrm{for}p=1,2,3,\dots ,n,\mathrm{where}\hfill \\ \hfill {\delta }_r\left(x_p\right)& =& {\displaystyle \underset{i=1}{\sum ^k}}{\chi }_{{}_E}\left(x_p{x}_i\right),\mathrm{is}\mathrm{the}\mathrm{measures}\mathrm{of}\mathrm{interaction}\mathrm{of}{x}_p\mathrm{with}{x}_k,\mathrm{and}\hfill \\ \hfill {\delta }_c\left(x_p\right)& =& {\displaystyle \underset{i=1}{\sum ^k}}{\chi }_{{}_E}\left(x_i{x}_p\right)\mathrm{is}\mathrm{the}\mathrm{measures}\mathrm{of}\mathrm{interaction}\mathrm{of}{x}_k\mathrm{with}{x}_p.\hfill \end{array}$$

where ${\chi }_{{}_E}$ is an indicator function on $E,$ defined by

$${\chi }_{{}_E}\left(x_k{x}_p\right)=\left\{\begin{array}{c}1\mathrm{if}{x}_k{x}_p\mathrm{form}\mathrm{an}\mathrm{edge}\\ 0,\mathrm{otherwise}\end{array}\right..$$

Finally, we calculate the evaluation function given by $\Theta (x_p)=\frac{1}{2}\left[{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)+{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)\right]\delta \left(x_p\right).$

The person $x_k$ is at high risk if $x_k=\stackrel{}{{\displaystyle \underset{i}{max}}}\left\{\Theta (x_i)\right\},$ $i=1,2,3,\dots ,n.$ One can apply this algorithms in other related problems.

5.1. Pseudo Code

Step 1: Input is the soft graph $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$.

Step 2: Find $\mathcal{MSR}$-vertex approximation space ${\mathfrak{Q}}_m=\left(V,\mu \right)$.

Step 3: Find lower $\mathcal{MSR}$-vertex approximation ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)\backslash \backslash$ according to Definition 9.

Step 4: Find upper $\mathcal{MSR}$-vertex approximation ${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)\backslash \backslash$ according to Definition 9.

Step 5: Compute the fuzzy functions ${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)$ and ${\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)$ given by

$${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{{\displaystyle \underline{\rho \left(S_k\right)}}}}\left(x_p\right)\mathrm{and}{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{\overline{\rho \left(S_k\right)}}}\left(x_p\right).$$

Step 6: Apply the marginal function $\delta$ for all vertices $x_p,$ given by

$$\delta \left(x_p\right)=\frac{1}{n}\left[{\delta }_r\left(x_p\right)+{\delta }_c\left(x_p\right)\right]$$

Step 7: Apply the evaluation function $\Theta$ for all vertices $x_p,$ given by

$$\Theta (x_p)=\frac{1}{2}\left[{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)+{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)\right]\delta \left(x_p\right).$$

The vertex $x_k$ is optimal if $x_k=\stackrel{}{{\displaystyle \underset{i}{max}}}\left\{\Theta (x_i)\right\},$ $i=1,2,3,\dots ,n.$

5.2. Example

Suppose during the annual medical checkup of persons working in an office, five viral diseases found in a group of 20 people $V=\left\{x_1,x_2,x_3,\dots ,x_{20}\right\}$, through different sources such as body fluids contaminated with a virus, having sex with an infected person, eating contaminated food, breathing air polluted by a virus and insect bite. The above process of infection results in a diversity of symptoms that vary in severity and character, depending upon the individual factor and the kind of viral infection. Suppose $A=\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5\right\}$ be the set of parameters such that ${\alpha }_1$ represents “ body fluids contaminated with a virus”, ${\alpha }_2$ represents “entering of virus in human body through having sex with an infected person”, ${\alpha }_3$ represents “entering of virus in human body through eating contaminated food”, ${\alpha }_4$ represents “entering of virus in human body through breathing air polluted by a virus” and ${\alpha }_5$ represents “entering of virus in human body through insect bite”. It is also assumed that a person $x_j$ may have more than one viral disease. Suppose $G^{\ast }$ be a simple digraph having vertex set V of 20 persons and edge set E.

Let $\left(\xi ,A\right)$ be a soft set over V as shown in

Table 3. Tabular representation of soft set $\left(\xi ,A\right)$.

	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$	${\mathit{x}}_7$	${\mathit{x}}_8$	${\mathit{x}}_9$	${\mathit{x}}_{10}$	${\mathit{x}}_{11}$	${\mathit{x}}_{12}$	${\mathit{x}}_{13}$	${\mathit{x}}_{14}$	${\mathit{x}}_{15}$	${\mathit{x}}_{16}$	${\mathit{x}}_{17}$	${\mathit{x}}_{18}$	${\mathit{x}}_{19}$	${\mathit{x}}_{20}$
${\alpha }_1$	0	0	0	1	1	1	1	1	1	0	0	0	0	0	0	1	0	1	1	1
${\alpha }_2$	1	1	0	1	0	0	0	0	0	1	0	1	1	1	1	0	0	0	1	0
${\alpha }_3$	0	1	1	0	1	0	0	1	1	0	1	0	0	0	0	0	1	0	0	1
${\alpha }_4$	1	0	0	0	0	1	1	1	0	0	0	0	1	0	1	0	1	1	1	0
${\alpha }_5$	0	1	1	0	1	0	0	0	1	1	1	0	1	0	0	0	0	1	1	0

such that

$$\xi \left({\alpha }_i\right)=\left\{x_j\in V:x_j\mathrm{may}\mathrm{have}\mathrm{viral}\mathrm{disease}{\alpha }_i\right\},$$

$$\xi \left({\alpha }_1\right)=\{x_4,x_5,x_6,x_7,x_8,x_9,x_{16},x_{18},x_{19},x_{20}\},$$

$$\xi \left({\alpha }_2\right)=\{x_1,x_2,x_4,x_{10},x_{12},x_{13,}{x}_{14},x_{15},x_{19}\}$$

$$\xi \left({\alpha }_3\right)=\{x_2,x_3,x_5,x_8,x_9,x_{11},x_{17},x_{20}\}$$

$$\xi \left({\alpha }_4\right)=\{x_1,x_6,x_7,x_8,x_{13},x_{15},x_{17},x_{18},x_{19}\},$$

$$\xi \left({\alpha }_5\right)=\{x_2,x_3,x_5,x_9,x_{10},x_{11},x_{13},x_{18},x_{19}\}.$$

Let $\left(\psi ,A\right)$ be a soft set over E such that

$$\psi \left({\alpha }_i\right)=\left\{x_i{x}_j\in E:x_i\mathrm{with}\mathrm{disease}{\alpha }_i\mathrm{has}\mathrm{interaction}\mathrm{with}{x}_j\right\},$$

$$\psi \left({\alpha }_1\right)=\left\{\begin{array}{c}{x}_8{x}_{19},x_8{x}_{20},x_8{x}_7,x_8{x}_4,x_8{x}_6,x_4{x}_5,x_4{x}_8,x_4{x}_{18},x_4{x}_{20},x_{16}{x}_4,x_{16}{x}_5,x_{16}{x}_6,x_{16}{x}_7,x_{16}{x}_{19},x_{16}{x}_{20}\\ x_{16}{x}_4,x_7{x}_5,x_7{x}_{16},x_5{x}_8,x_5{x}_9,x_6{x}_7,x_6{x}_{16},x_6{x}_{18},x_6{x}_{19},x_6{x}_{20},x_6{x}_5,x_6{x}_4,x_7{x}_9,x_7{x}_{20}\end{array}\right\}$$

(3)

$$\psi \left({\alpha }_2\right)=\left\{\begin{array}{c}{x}_4{x}_2,x_4{x}_{13},x_2{x}_4,x_1{x}_{15},x_1{x}_{19},x_1{x}_{14},x_{10}{x}_{12},x_{10}{x}_{13},x_{10}{x}_{15},x_{10}{x}_{19},x_{10}{x}_1,x_{10}{x}_2,x_{12}{x}_1\\ x_{14}{x}_4,x_{14}{x}_{10},x_{14}{x}_{12},x_{12}{x}_{10},x_{12}{x}_{15},x_{14}{x}_1,x_{14}{x}_2,x_{12}{x}_2,x_{12}{x}_4,x_{12}{x}_{19},\\ x_{14}{x}_{13},x_{14}{x}_{15},x_{14}{x}_{19},x_{15}{x}_{10},x_{15}{x}_{14}\end{array}\right\},$$

(4)

$$\psi \left({\alpha }_3\right)=\left\{\begin{array}{c}{x}_2{x}_{17},x_3{x}_8,x_3{x}_9,x_3{x}_{20},x_3{x}_{11},x_5{x}_{11},x_5{x}_3,x_8{x}_{17},x_{11}{x}_{17},x_{15}{x}_{17},x_{15}{x}_{18},x_{15}{x}_{19},x_{15}{x}_8,x_{17}{x}_2,\\ x_8{x}_9,x_9{x}_2,x_9{x}_3,x_9{x}_{11},x_9{x}_{20},x_9{x}_5,x_{11}{x}_2,x_{11}{x}_3,x_{11}{x}_{20},x_{11}{x}_5,x_{17}{x}_{11},x_{17}{x}_{20},\\ x_{20}{x}_2,x_{20}{x}_5,x_{20}{x}_{11},x_{20}{x}_9,x_{17}{x}_3\end{array}\right\},$$

(5)

$$\psi \left({\alpha }_4\right)=\left\{\begin{array}{c}{x}_1{x}_7,x_1{x}_8,x_1{x}_{17},x_6{x}_1,x_6{x}_{13},x_6{x}_{17},x_7{x}_8,x_7{x}_1,x_{13}{x}_1,x_{13}{x}_6,x_{13}{x}_8,x_{17}{x}_{18},x_{17}{x}_{19},\\ x_{18}{x}_{19},x_{18}{x}_1,x_{18}{x}_{13},x_{18}{x}_{15},x_{18}{x}_{17}\end{array}\right\}$$

$$\psi \left({\alpha }_5\right)=\left\{x_2{x}_{11},x_2{x}_{13},x_2{x}_{19},x_3{x}_{18},x_3{x}_{19},x_3{x}_{10},x_5{x}_{19},x_9{x}_{10},x_{10}{x}_{18},x_{10}{x}_3,x_{19}{x}_{13},x_{19}{x}_9\right\}$$

Let $\mu :V\to P\left(A\right)$ be a map such that $\mu \left(x\right)=\{\alpha :x\in \xi \left(\alpha \right)\}.$ Then $\mu \left(x_1\right)=\{{\alpha }_{{}_2},{\alpha }_4\}=\mu \left(x_{15}\right),$ $\mu \left(x_2\right)=\{{\alpha }_{{}_2},{\alpha }_{{}_3},{\alpha }_{{}_5}\},$ $\mu \left(x_3\right)=\{{\alpha }_{{}_3},{\alpha }_{{}_5}\}=\mu \left(x_{11}\right),\mu \left(x_4\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_2},{\alpha }_{{}_4}\},$ $\mu \left(x_5\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_3},{\alpha }_{{}_5}\}=\mu \left(x_9\right)=\mu \left(x_{20}\right),$ $\mu \left(x_6\right)=\mu \left(x_7\right)=\{{\alpha }_{{}_1},{\alpha }_4\},$ $\mu \left(x_8\right)=\{{\alpha }_{{}_1},{\alpha }_{{}_3},{\alpha }_{{}_4}\}\},\mu \left(x_{10}\right)=\{{\alpha }_{{}_2},{\alpha }_{{}_5}\},$ $\mu \left(x_{12}\right)=\mu \left(x_{14}\right)=\{{\alpha }_{{}_2}\}$ and $\mu \left(x_{13}\right)=\{{\alpha }_{{}_2},{\alpha }_{{}_4},{\alpha }_{{}_5}\}.$ Let $\left(\rho ,S\right)$ be the soft set (can be seen in

Table 4. Tabular representation of $\left(\rho ,S\right)$.

	Doctors	${\mathit{S}}_1$	${\mathit{S}}_2$	${\mathit{S}}_3$
Patients
$x_1$		1	0	1
$x_2$		1	0	0
$x_3$		1	0	0
$x_4$		1	0	0
$x_5$		0	1	0
$x_6$		0	1	0
$x_7$		0	0	0
$x_8$		1	0	0
$x_9$		0	1	1
$x_{10}$		1	0	1
$x_{11}$		0	0	0
$x_{12}$		0	0	0
$x_{13}$		0	0	1
$x_{14}$		0	0	0
$x_{15}$		0	0	0
$x_{16}$		0	0	1
$x_{17}$		0	1	0
$x_{18}$		1	1	0
$x_{19}$		0	1	1
$x_{20}$		1	0	1

) which shows whether a staff member is at high risk or not, giving the values 1 or 0 respectively. Where S is the set of 3 expert doctors .i.e., $S=\{S_1,S_2,S_3\}.$

A MATLAB code is developed to perform all the calculations. Let ${\mathfrak{Q}}_m=\left(V,\mu \right)$ be $\mathcal{MSR}$-vertex approximation space. If we consider the technique proposed in [49] then we have the following lower and upper approximations as

$$\begin{array}{ccc}\hfill {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(S_i\right)& =& \left\{x\in V:\exists \alpha \in A,\left[x\in \xi \left(\alpha \right)\subseteq S_i\right]\right\},\hfill \\ \hfill {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(S_i\right)& =& \left\{x\in V:\exists \alpha \in A,\left[x\in \xi \left(\alpha \right),\xi \left(\alpha \right)\cap S_i\ne \varnothing \right]\right\}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{That}\mathrm{is},{{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_1\right)\right)& =& {{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_2\right)\right)={{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_3\right)\right)=\{\}\mathrm{and}\hfill \\ \hfill {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_1\right)\right)& =& {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_2\right)\right)={\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_3\right)\right)=V.\hfill \end{array}$$

From these lower and upper approximations, we get no information with uncertainty about the patients from experts. Now we apply lower and upper approximations of our proposed model.

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)=\{x\in S_i:\mu \left(x\right)\ne \mu \left(y\right)\mathrm{for}\mathrm{all}y\in S_i^c\},S_i^c=V-S_i$$

That is,

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_1\right)\right)=\{x_2,x_4,x_8\}$$

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_2\right)\right)=\{x_{17},x_{18},x_{19}\}$$

$${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_3\right)\right)=\{x_{10},x_{13},x_{16},x_{19}\}$$

and

$${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)=\{x\in V:\mu \left(x\right)=\mu \left(y\right)\mathrm{for}\mathrm{some}y\in S_i\}.$$

gives

$${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_1\right)\right)=\{x_1,x_2,x_3,x_4,x_5,x_8,x_9,x_{10},x_{11},x_{15},x_{18},x_{20}\}$$

$${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_2\right)\right)=\{x_5,x_6,x_7,x_9,x_{15},x_{17},x_{18},x_{19},x_{20}\}$$

$${\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_3\right)\right)=\{x_1,x_5,x_9,x_{10},x_{13},x_{15},x_{16},x_{19},x_{20}\}.$$

It can be seen that ${{\displaystyle \underline{aprx}}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)\subseteq {\overline{aprx}}_{{\mathfrak{Q}}_m}\left(\rho \left(S_i\right)\right)$ for $i=1,2,3.$ That is, the properties of Pawlak [3] rough sets have been translated into the proposed model whereas it cease to happen in model proposed in [49]. Now we compute the fuzzy functions ${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)$ and ${\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)$ given by

$${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{{\displaystyle \underline{\rho \left(S_k\right)}}}}\left(x_p\right)\mathrm{and}{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)=\frac{1}{r}{\displaystyle \underset{k=1}{\sum ^r}}{\chi }_{{}_{\overline{\rho \left(S_k\right)}}}\left(x_p\right).$$

Which implies

$$\begin{array}{ccc}\hfill {\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_1\right)& =& 0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_2\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_3\right)=0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_4\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_5\right)=0\hfill \\ \hfill {\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_6\right)& =& 0={\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_7\right),{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_8\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_9\right)=0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{10}\right)=\frac{1}{3},\hfill \\ \hfill {\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{11}\right)& =& 0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{12}\right)=0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{13}\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{14}\right)=0,{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{15}\right)=0,\hfill \\ \hfill {\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{16}\right)& =& \frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{17}\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{18}\right)=\frac{1}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{19}\right)=\frac{2}{3},{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_{20}\right)=0.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\eta }_{\overline{\rho \left(S\right)}}\left(x_1\right)& =& \frac{2}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_2\right)=\frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_3\right)=\frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_4\right)=\frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_5\right)=1\hfill \\ \hfill {\eta }_{\overline{\rho \left(S\right)}}\left(x_6\right)& =& \frac{1}{3}={\eta }_{\overline{\rho \left(S\right)}}\left(x_7\right)={\eta }_{\overline{\rho \left(S\right)}}\left(x_8\right),{\eta }_{\overline{\rho \left(S\right)}}\left(x_9\right)=1,{\eta }_{\overline{\rho \left(S\right)}}\left(x_{10}\right)=\frac{2}{3},\hfill \\ \hfill {\eta }_{\overline{\rho \left(S\right)}}\left(x_{11}\right)& =& \frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{12}\right)=0,{\eta }_{\overline{\rho \left(S\right)}}\left(x_{13}\right)=\frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{14}\right)=0,{\eta }_{\overline{\rho \left(S\right)}}\left(x_{15}\right)=1,\hfill \\ \hfill {\eta }_{\overline{\rho \left(S\right)}}\left(x_{16}\right)& =& \frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{17}\right)=\frac{1}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{18}\right)=\frac{2}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{19}\right)=\frac{2}{3},{\eta }_{\overline{\rho \left(S\right)}}\left(x_{20}\right)=1.\hfill \end{array}$$

Clearly $\mathcal{G}=\left(G^{\ast },\xi ,\psi ,A\right)$ is a soft graph. The interaction of all persons with each other and the marginal fuzzy sets for rows and columns are given in

Table 5. Tabular representation of interaction of all persons.

Persons	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$	${\mathit{x}}_7$	${\mathit{x}}_8$	${\mathit{x}}_9$	${\mathit{x}}_{10}$	${\mathit{x}}_{11}$	${\mathit{x}}_{12}$	${\mathit{x}}_{13}$	${\mathit{x}}_{14}$	${\mathit{x}}_{15}$	${\mathit{x}}_{16}$	${\mathit{x}}_{17}$	${\mathit{x}}_{18}$	${\mathit{x}}_{19}$	${\mathit{x}}_{20}$	${\mathit{\delta }}_{\mathit{r}}$
$x_1$	0	0	0	0	0	0	1	1	0	0	0	0	0	1	1	0	1	0	1	0	6
$x_2$	1	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	1	0	1	0	5
$x_3$	0	0	0	0	0	0	0	1	1	1	1	0	0	0	0	0	0	1	1	1	7
$x_4$	1	0	1	0	1	0	0	1	0	0	0	0	0	0	0	0	0	1	0	1	6
$x_5$	0	0	1	0	0	0	0	1	1	0	1	0	0	0	0	0	0	0	1	0	5
$x_6$	1	0	0	1	1	0	1	0	0	0	0	0	1	0	0	1	1	1	1	1	10
$x_7$	1	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	0	0	0	1	6
$x_8$	0	0	0	1	0	1	1	0	1	0	0	0	0	0	0	0	1	0	1	1	7
$x_9$	0	1	1	0	1	0	0	0	0	1	1	0	0	0	0	0	0	0	0	1	6
$x_{10}$	1	1	1	0	0	0	0	0	0	0	0	1	1	0	1	0	0	1	1	0	8
$x_{11}$	0	1	1	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	5
$x_{12}$	1	1	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	0	1	0	6
$x_{13}$	1	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	0	3
$x_{14}$	1	1	0	1	0	0	0	0	0	1	0	1	1	0	1	0	0	0	1	0	8
$x_{15}$	0	0	0	0	0	0	0	1	0	1	0	0	0	1	0	0	1	1	1	0	6
$x_{16}$	0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	1	1	6
$x_{17}$	0	1	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	1	1	6
$x_{18}$	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	1	0	5
$x_{19}$	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	2
$x_{20}$	0	1	0	0	1	0	0	0	1	0	1	0	0	0	0	0	0	0	0	0	4
${\delta }_c$	9	8	6	7	11	4	6	5	4	5	6	2	7	10	5	2	7	6	13	9

.

Now we calculate the evaluation function given by

$$\Theta (x_p)=\frac{1}{2}\left[{\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}\left(x_p\right)+{\eta }_{\overline{\rho \left(S\right)}}\left(x_p\right)\right]\delta \left(x_p\right).$$

By simple calculations, it is found that

$$\begin{array}{ccc}\hfill \Theta \left(x_1\right)& =& 0.250,\Theta \left(x_2\right)=0.200,\Theta \left(x_3\right)=0.108,\Theta \left(x_4\right)=0.117,\Theta \left(x_5\right)=0.275,\hfill \\ \hfill \Theta \left(x_6\right)& =& 0.175,\Theta \left(x_7\right)=0.083,\Theta \left(x_8\right)=0.217,\Theta \left(x_9\right)=0.275,\Theta \left(x_{10}\right)=0.375,\hfill \\ \hfill \Theta \left(x_{11}\right)& =& 0.067,\Theta \left(x_{12}\right)=0.000,\Theta \left(x_{13}\right)=0.167,\Theta \left(x_{14}\right)=0,\Theta \left(x_{15}\right)=0.275,\hfill \\ \hfill \Theta \left(x_{16}\right)& =& 0.150,\Theta \left(x_{17}\right)=0.183,\Theta \left(x_{18}\right)=0.225,\Theta \left(x_{19}\right)=0.467,\Theta \left(x_{20}\right)=0.175\hfill \end{array}$$

For a threshold $\beta \in \left[0,1\right],$ it can be seen that the all person $x_i$ are at optimum for all $i,$ in which $\Theta \left(x_i\right)\ge \beta .$ The person $x_k$ is at high risk if $x_k=\stackrel{}{{\displaystyle \underset{i}{max}}}\left\{\Theta (x_i)\right\},$ $i=1,2,3,\dots ,n.$ So by calculations, the person $x_{19}$ is best optimal.

6. Conclusions

A possible fusion of three concepts rough sets, soft sets and graphs, known as soft rough graphs, is introduced by [49]. During this attempt, some shortcomings become the part of the theory. In order to remove these shortcomings, a new approach is being introduced to study the roughness of soft graphs and the resulting graphs are called modified soft rough graphs. The theory of approximation of a soft graph is also investigated to obtain $\mathcal{MSR}$-vertex graph and $\mathcal{MSR}$-edge graph. The related properties of both soft rough graphs and modified soft rough graphs are surveyed. It is shown that the $\mathcal{MSR}$-graphs are more precise and finer than soft rough graphs. Different uncertainty measures like information entropy and granularity measures are discussed for $\mathcal{MSR}$-graphs. A real life example of decision making problem is formulated to optimized the diagnosis process of some diseases in an office where we have compared the robustness of the proposed model with soft rough graphs proposed by Noor in [49]. An algorithm is developed in a realistic way to compute the effectiveness of diseases among colleagues working in same office. The set of edges has been used to describe the interaction between the persons. This interaction may cause the spreadness of diseases among the staff members. Using the concepts of lower/upper $\mathcal{MSR}$-vertex approximations, the fuzzy sets ${\eta }_{{\displaystyle \underline{\rho \left(S\right)}}}$ and ${\eta }_{\overline{\rho \left(S\right)}}$ are introduced, while the marginal fuzzy sets ${\delta }_r\left(x_p\right)$ and ${\delta }_c\left(x_p\right)$ are used to find the measure of interaction of any staff member $x_i$ with $x_j$ and vice versa. Finally, the evaluation function has pointed out the optimal carriers of diseases. All the calculations are made on MATLAB program.

We hope that our results in this article would constitute a base for DM problems of real life based on soft rough graphs. In future work it is also under consideration, how the upper and lower $\mathcal{MSR}$-edge approximations can be used to optimized the algorithm.

References and Notes