Abstract
Pythagorean fuzzy sets are highly appealing in dealing with uncertainty as they allow for greater flexibility in regards to the membership and non-membership degrees by extending the set of possible values. In this paper, we propose a multi-criteria group decision-making approach based on the Pythagorean normal cloud. Some cloud aggregation operators are presented in this paper to facilitate the appraisal of the underlying utilities of the alternatives under consideration. The concept and properties of the Pythagorean normal cloud and its backward generation algorithm, aggregation operators and distance measurement are outlined. The proposed approach resembles the TOPSIS technique, which, indeed, considers the symmetry of the distances to the positive and negative ideal solutions. Furthermore, an example from e-commerce is presented to demonstrate and validate the proposed decision-making approach. Finally, the comparative analysis is implemented to check the robustness of the results when the aggregation rules are changed.
1. Introduction
Decision-making is an important issue in the domain of economics and society in general [1,2], ass human input and interaction are often the decisive elements of the decision-making. Accordingly, expressing and handling cognitive information has been a focal topic related to the decision-making literature. What is more, it has been established that the use of exact ratings (e.g., exact numerical values) might not allow defining the preferences of the decision-makers to a substantial degree [3,4,5], which might reduce the effectiveness of the decision-making in general [6]. What is more, a decision-maker can fathom the limitations of his/her competences or possibilities to provide ratings in regards to certain alternatives and criteria in general. Realizing this, they might attach the corresponding information to their ratings [7,8], thus providing an additional dimension in the decision-making process. All in all, the information rendered by the decision-makers might be imprecise (in the case that no exact values are provided), incomplete (in the case that certain values are missing) and uncertain (in the case that the likelihood of observing different values can be specified). Under these circumstances, the theory of the fuzzy sets can be regarded as a possible means for handling the decision-making process and overcoming the limitations, which would have existed if conventional tools (e.g., crisp sets) had been applied. In order to account for different structures of uncertainty, the literature has proposed different strands of the fuzzy set theory since its initial definition by Zadeh [9,10]. In particular, the intuitionistic fuzzy set (IFS) theory [11] and interval-valued IFS theory [12] were put forward by Atanassov et al. Indeed, the application of such concepts allows one to account for the incompleteness and inconsistencies existing in information provided by the decision-makers. In principle, this implies that the underlying cognitive peculiarities of decision-makers can be accounted for. Yet, another example of the concepts for handling imprecise information is the hesitant fuzzy set proposed by Torra [13], which allows considering the hesitancy to provide certain ratings of the alternatives. The establishment of multiple theoretical concepts for imprecise information provides opportunities for more realistically handling multi-criteria decision-making problems (MCDM) in general.
However, the very existence of the multitude of the fuzzy set-based concepts does not warranty successful implementation of these in the area of MCDM. The practical implementation of the fuzzy sets requires certain restrictions to be satisfied. Turning to IFS, which is one of the most flexible tools for handling imprecise information, the decision-makers need to ensure that the sum of the degrees of membership and non-membership is not greater than unity. However, in some fuzzy MCDM problems, the decision-makers may fail to deliver their ratings in line with the requirements on the sum of the degrees of membership and non-membership as required by the theory of the IFS. In such instances, the application of the IFSs becomes rather complicated (e.g., decision-maker might be asked to reiterate the procedure of rating) and even impossible. Therefore, there have been certain attempts to rectify this shortcoming by modifying the underlying assumptions. The Pythagorean fuzzy sets (PFSs) proposed by Yager [14] can be identified as an option for modeling situations that cannot be defined in terms of IFSs due to difficulties associated with the restrictions on the degrees of membership and non-membership.
In order to ensure that the PFSs can be successfully applied in MCDM, dedicated techniques have been proposed. The aggregation operators for the PFSs can be considered as an important tool for the application of the PFSs in the MCDM problematique. The correspondence among membership degrees to the Pythagorean fuzzy numbers (PFNs) and the complex numbers was established by Yager [15]. More specifically, it was shown that the degrees of membership to PFS can be treated as a special subclass of complex numbers. The mathematical representations of the PFSs were further reviewed by Liang et al. [16]. They also defined the PFNs. The TOPSIS technique was then extended with the PFNs, providing the mathematical expressions of PFSs and presenting the concept of the PFN. Furthermore, the latter study put forward the Pythagorean fuzzy TOPSIS (technique for order preference by similarity to an ideal solution) for handling the MCDM problems with PFNs. The averaging functions for the PFSs were discussed by Beliakov and James [17]. In particular, they sought to ensure that the aggregation of the membership degrees of the PFSs led to consistent results. The goal of operationalizing the collaboration-based recommender system by using the PFSs was addressed by Reformat and Yager [18]. Zeng [19,20] developed a Pythagorean fuzzy multi-attribute group decision-making (MAGDM) method based on probabilistic information and the ordered weighted averaging (OWA) approach.
Even though the fuzzy sets can describe the degree of membership to a certain concept with regards to the attitude of the decision-maker, as well as their confidence, the spread of such ratings might not be fully represented. Accordingly, the need for a more flexible representation of the uncertain data triggered the development of the normal cloud (NC) concept. Li et al. [21] acknowledged the random nature of the membership functions and unified the probability theory and fuzzy set theory, thus devising the NC. Taking the normal distribution as a reference, one can employ the NC to model deviations from the theoretical distribution. By doing so, one is able to describe the random phenomena and use this information in MCDM [22]. There are three numerical characteristics that characterize the random phenomenon in terms of an NC: (expectation), (entropy) and (hyper entropy). is the expected value of the sample data; is the spread of the sample values defining the uncertainty of the sample; is the uncertainty of the degree of membership. The NC theory has been revised by introducing the additional types of NCs. Numerous extensions of the NC have been developed. For example, the integral cloud was put forward by Li et al. [23]. In addition, a multidimensional cloud was proposed [24]. Jiang et al. [25] developed a trapezoidal cloud (TC) model. The combination of intuitionistic fuzzy set theory and conventional NC theory was offered by Wang and Yang [26] and yielded the intuitionistic normal cloud (INC) model.
As NCs represent uncertain information, they can be applied to handle MCDM problems [26]. The distance measure, the similarity measure, the entropy and the inclusion measure for PFSs have been discussed by Peng et al. [27,28]. The cloud generator algorithm was applied by Yang et al. [29] in a linguistic hesitant fuzzy decision-making framework. Distance measures play an important role in constructing the NC-based procedures for MCDM [30]. The aggregation of NCs is yet another research avenue that deserves much attention. When proposing the linguistic MCDM technique, such aggregation operators as the cloud weighted arithmetic averaging operator, cloud weighted geometric averaging operator, cloud-ordered weighted arithmetic averaging operator and cloud hybrid aggregation operator were developed by Wang et al. [31]. Given the existing different types of the clouds, the aggregation operators have been revised accordingly. Therefore, the operators for TC and INC have been proposed. Wang et al. [32] presented a number of arithmetic aggregation operators for the TCs (including weighted arithmetic averaging operator, ordered weighted arithmetic averaging operator and hybrid arithmetic operator). Turning to the PFNs, there have also been advancements in the sense of the development of the aggregation operators and rules of comparison. The Pythagorean fuzzy uncertain linguistic Maclaurin symmetric mean aggregation (PFULMSMA) operator and the weighted PFULMSMA (WPFULMSMA) operator have been put forward by Liu et al. [33]. Furthermore, Garg presented an improved accuracy function for the ranking order of interval-valued Pythagorean fuzzy sets (IVPFSs) [34].
This paper combines the notion of the NC with the PFS and develops the Pythagorean normal cloud (PNC). Thereafter, the group decision-making procedure based on the PNCs is proposed. the proposed approach relies on the backward cloud generator, aggregation operators and distance measures to deal with the proposed PNCs. These concepts are presented in the paper. In the proposed framework, the ratings provided by the experts are treated as could drops of PNCs. The proposed approach is based on the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) [35]. Application of the backward cloud generators allows considering the spread of the ratings provided by the experts rather than the average values only. The use of the aggregation operators allows constructing the aggregate indicators, which can further be used for decision-making. The paper concludes with an illustrative example where the proposed approach is tested by considering the case study of e-commerce.
2. Preliminaries
This section presents the focal concepts underpinning the proposed approach for cloud-based MCDM. More specifically, we describe the IFSs and a generalization thereof, namely the PFSs. The, we discuss the normal clouds and the generator algorithm, which allows transforming drops into a cloud. The concepts presented in this section will be further revised by incorporating the PFSs.
2.1. Intuitionistic Fuzzy Sets and Pythagorean Fuzzy Sets
The conventional fuzzy set has been generalized by Atanassov [11]. The resulting concept was termed intuitionistic fuzzy set. The IFS allows for a more detailed representation of vagueness and uncertainty, which makes it a promising tool for MCDM problems. The key feature of the IFS that makes it different from the conventional fuzzy sets is the different set of parameters describing membership to a certain fuzzy set. Therefore, an IFS can be defined as follows:
Definition 1.
Assuming there exists a certain fixed set , one can define an instance of IFS I in the following terms:
Values and are the degrees of membership and non-membership, respectively, and they define the extent to which a certain element x belongs to set I, under condition , for all . Given the presence of inequality in the condition for the degrees of membership and non-membership to an IFS, their sum might be lower than unity, which would imply the presence of indeterminacy in the decision-making process. Formally, the degree of indeterminacy for x with regards to X is defined as . Indeed, the MCDM requires assessments of multiple alternatives against different criteria, which is associated with assessing the membership of the elements to sets multiple times. In order to define this process in a more concise manner, the notion of the intuitionistic fuzzy number (IFN) has been introduced [33,34]. Specifically, a certain IFN can be defined in terms of the two-tuple containing the degrees of membership and non-membership, i.e., pair . Furthermore, one can introduce notation for IFN α, where
For any three IFNs , and , some operational laws of IFNs are introduced as follows [36]:
1. ;
2. ;
3. ;
4. .
The experts’ preferences might not be defined in terms of IFSs in case the experts cannot ensure that the constraint on the membership and non-membership degrees is maintained (i.e., their sum is not less than unity). Indeed, this might happen whenever the experts are not familiar with the IFS theory. In order to reduce the likelihood of such situations and improve the possibilities for the application of the fuzzy sets in the MCDM, a generalization of the IFS has been offered by Yager [14,15]. The resulting concept was termed PFS. The PFS can be defined as follows:
Definition 2.
Let us consider a fixed set , then a PFS P is defined in the following terms:
Similarly to the case of IFS, values and are the degrees of membership and non-membership, which define the extent to which a certain element x belongs to set P. However, the constraints on these two values are altered in the case of the PFS so that , for all . These changes imply that the calculation of the degree of indeterminacy is changed, as well: for any PFS P and , the degree of indeterminacy is calculated as . For the ease of notation, let the pair be called the Pythagorean fuzzy number (PFN) [14]. Further on, a shorthand notation can be used to refer to a certain PFN, namely , where the usual conditions hold and
According to Definitions 1 and 2, one can note that the key delineation between PFN and IFN is the way degrees of membership and non-membership are restricted. More specifically, the case of IFN involves , whereas the corresponding constraint in the case of PFN is . The relationships among IFNs and PFNs can be established by considering simple mathematical facts. Note that for any given set of values , if , then ; thus, if a certain number is an IFN, then it is definitely a PFN, yet the opposite does not hold.
Given three PFNs , and , Zhang et al. [37] presented the main operations for them, shown as:
1. ;
2. ;
3. ;
4. .
Definition 3.
Given any two PFNs, , there can be a natural quasi-ordering on the PFNs established in the following manner: if and only if and .
In order to facilitate the comparison of PFNs, Zhang and Xu [38] defined the following principles:
Definition 4.
For a PFN , is referred to as the score function of β. The score function can then be exploited when comparing these PFNs. For two PFNs and , if , then ; if , then .
Definition 5.
Let and be two PFNs, then:
is referred to as the Pythagorean fuzzy distance (PFD) between and .
2.2. NC and the Backward Cloud Generator
The observed sample data can be used to recover the underlying data generation process (DGP). In the case of multi-criteria decision-making, this procedure can be used to describe uncertain phenomena. In this sub-section, we discuss the procedure for establishing an NC, which represents the underlying DGP.
Definition 6.
Let us assume there exists a universe of discourse denoted by U. Furthermore, let there be a qualitative concept in U that is denoted as T. Then, let be a random realization of concept T, such that x follows , where . Given the conditions on the distribution of x, one can model the degree of certainty that x belongs to the concept T in the following way:
Thus, an NC defines the distribution of x in the universe U. In particular, a certain value of x is attached with a corresponding degree of certainty y, thus forming a cloud drop. The backward cloud generator of an NC allows aggregating separate drops into a cloud that defines the concept under analysis in a general manner. The backward generator proceeds as follows:
Step 1. Calculate the sample average along with first-order sample absolute central moment , and sample variance ;
Step 2. Obtain the estimates of , , : ;
Output: The estimate of .
3. Pythagorean Normal Cloud
The NC only defines the uncertainty surrounding the membership to a concept. However, the assessments might be associated with different degrees of confidence. This situation is present in IFSs and PFSs. Therefore, we update the concept of the NC with the PFSs in order to derive a more comprehensive means of the representations of uncertain information.
Definition 7.
For a given universe of discourse, U, one can characterize a PNC C in U in terms of and . Furthermore, can be represented by a Pythagorean fuzzy number (PFN) . Then, the is defined as:
Definition 8.
Let there be a set of PNCs with associated weighting vector of , such that and . The PNCWAA operator is:
In the earlier literature, Wang et al. discussed the main operations for NC [32], whereas other studies further developed those for INC [26]; besides, arithmetic operations for handling the TCs were outlined [25]. Based on the earlier literature, we present the following operational laws for the PNCs:
Definition 9.
Let and be two PNCs. Then, the following operational rules apply for and :
1. ;
2. ;
3. ;
4. ;
Theorem 1.
Let there be any three PNCs , and . For these PNCs, the following observations hold:
1. ;
2. ;
3. ;
4. ;
5. .
Proof.
According to Definition 9, we can obtain
According to Definition 9, we can also obtain
According to Definition 9, we can obtain
The proof for the fourth result of Theorem 1 is similar to that for the third result.
According to Definition 9, we can also note
3.1. Backward Cloud Generator and Aggregation Operators for PNCs
The extensive form of the data describing a certain concept (i.e., cloud drops) can be aggregated into an intensive form describing the same concept (i.e., cloud) by means of the backward cloud generator [39]. In general, the sample data are used in the backward cloud generator algorithm of a PNC to recover the estimates , which describe a PFN. In the context of group decision-making, the backward cloud generator can be used to aggregate the ratings provided by different experts into a single cloud (e.g., PNC), which considers not only the tendency, but also the spread of the assessments. Li et al. [21] proposed a backward cloud generator algorithm, which can be applied to generate the NCs. The backward cloud generator algorithm can be implemented by following these steps:
Step 1. Calculate the sample mean , where , The first-order sample absolute central moment can be expressed as , and sample variance can be expressed as ;
Step 2. Estimate the value of ;
Step 3. Estimate the value of , ;
Output: The estimated value of .
The clouds need to be aggregated in order to facilitate the decision-making process. To this end, the aggregation operators can be used. The cloud weighted arithmetic averaging operator and cloud weighted geometric averaging operator were brought forward by Wang et al. [30]. Further on, Wang and Yang [26] extended the weighted arithmetic averaging operator and presented an instance of aggregation operators for the intuitionistic normal clouds. In order to derive the utility of the alternatives considered in the MCDM problem when the PNCs are applied, one also needs the appropriate aggregation operators. Below, we present some aggregation operators for the PNCs, as well as discuss the properties thereof.
Definition 10.
Let be a set of PNCs. The PNC weighted arithmetic averaging operator (PNCWAA) is defined as:
where is the weight associated with , such that and . If , the PNCWAA boils down to the PNC arithmetic average (PNCAA) operator, defined as:
Theorem 2.
Let be a set of PNCs. Then, the result of the aggregation based on the PNCWAA operator is also a PNC, and:
Proof.
According to Theorem1 and Definitions 9 and 10, we can obtain
Definition 11.
Let be a set of PNCs. The PNC weighted geometric averaging operator (PNCWGA) is defined as:
where is the weight attached to , such that and . If , the PNCWGA is reduced to an PNC geometric average (PNCGA) operator, defined as:
Theorem 3.
Let be a set of PNCs. Then, the result of the aggregation based on the PNCWGA operator is also a PNC, and:
Proof.
According to Theorem 1 and Definitions 9 and 11, we can obtain
3.2. Distance Measures for PNCs
The distance measures are an important concept in MCDM. Indeed, they can be used to compare the alternatives considered against a reference point. In this subsection, the distance measures for PNCs alongside the properties of these measures are discussed. There have been distance measures for the integrated clouds developed by Wang and Liu [33]. Wang et al. [40] further considered the distance measures for interval integrated clouds. Following the principles outlined in the aforementioned papers, the distance measures for PNCs can be established as follows.
Definition 12.
Let there be any two PNCs and . The distance measure for the PNCs can be defined as:
where , , , . In addition, when , then ; the distance measure between two PNCs can be expressed as . Furthermore, when and , the distance between the two PNCs is the distance between two real numbers, and .
Property 1.
Let and be three PNCs, . Then, the distance measure given in Definition 12 satisfies the following properties:
1. ;
2. ;
3. , iff ;
4. .
4. PNC-Based MCGDM Method
An MCGDM approach for handling the problems with Pythagorean information is outlined in this section. The proposed approach is based on the TOPSIS [35]. We chose the TOPSIS approach due to the effectiveness and low computational burden associated with the computations underlying this approach. However, the MCDM framework based on the PNCs could be revised by applying such techniques as VIKOR (VIsekriterijumsko KOmpromisno Rangiranje) or Grey relational analysis, for instance.
Say we consider s alternatives , t decision-makers and n criteria . The criteria may have different importance as defined by the weight vector , where and . The ratings are provided by each decision-maker for each alternative against criterion in terms of the PFN .
The group MCDM proceeds by applying the backward cloud generator for the PNCs. The resulting data are then processed by applying the aggregation operators (PNCWAA or PNCWGA). The detailed procedure can be described in the following manner:
Step 1. The ratings provided by the experts are aggregated for each alternative and each criterion. The backward cloud generator algorithm described in Section 3.1 is applied to populate the PNC, which represents the aggregate rating for alternative against .
Step 2. The ratings for each alternative are aggregated across the criteria. The resulting overall utility of the alternative can be obtained by using the PNCWAA (or PNCWGA):
Step 3. Calculate the coordinates of the positive and negative ideal solutions. The following equation defines the way the coordinates of the positive ideal solution can be obtained:
The coordinates of the negative ideal solution can be obtained by considering the following equation:
Step 4. Each alternative is positioned in between the positive and negative ideal solutions. The distances to the ideal solutions are obtained by considering the distance measure given by Equation (12). For the i-th alternative, its distance to the positive ideal solution defined by Equation (14) is obtained as:
where , .
Step 5. Similarly, Equation (14) is exploited to measure the distance between the i-th alternative and the negative ideal solution defined by Equation (15):
where , .
Step 6. Rank the alternatives. The alternatives can be ordered on the basis of the normalized distance:
where smaller values of are associated with better alternatives . Therefore, the asymmetry between the two ideal solutions and an alternative is used to rank the alternatives.
5. Results
We follow the application presented by [41] to show the possibilities for the application of the proposed approach for decision-making in e-commerce. More specifically, the case of an Internet shop is considered. The data from a business-to-consumer (B2C) website based in China, Tmall.com, are used to implement the proposed approach and rank the goods sold online against several criteria.
The website allows the customers to express their opinions (ratings) regarding the products they have already bought. These ratings can be used for new costumers when making decisions to buy. As several aspects of the goods purchased can be evaluated, the MCDM problem emerges. Indeed, the opinions of the existing customers might be aggregated for different articles (alternatives) and criteria, thus defining a decision matrix.
Let us consider the case of four cameras , which are compared against each other in order to identify the most appealing one. Therefore, we set . The cameras are compared in terms of the three criteria (). The criteria considered are: the quality of the logistics service provider (), the level of service provided by the vendor () and the quality of each item (). The ratings are expressed on a five-point scale. The criteria are assumed to have different importance as manifested by the associated weight vector . The ratings provided by the previous consumers (experts) are aggregated into the PNCs (we omit the detailed description of this step for the sake of brevity).
5.1. Empirical Application
The MCDM procedure based on the resulting PNCs proceeds as follows:
Step 1. Aggregate the evaluations of each alternative under a certain criterion provided by all of the decision-makers by applying the backward generator. The criteria values of cameras and under the three criteria can be expressed as the following PNCs:
, ,
, ,
, ,
, ,
, ,
, .
Step 2. Obtain the overall utility scores for each camera. Based on Equation (13), the PNC utility scores of each camera can be expressed as:
, ,
, .
Step 3. Identify the coordinates describing the positive and negative ideal solutions. Following Equation (14), the positive ideal solution can be expressed as:
According to , the negative ideal solution can be expressed as:
Step 4. Measure the distance between the vector defining a certain camera and the positive ideal solution. Following Equation (16), we obtain the following distances:
Step 5. Measure the distance between the vector defining a certain camera and the negative ideal solution. Following Equation (17), we obtain the following distances:
.
Step 6. Rank the cameras. According to , the normalized distance can be used to rank the alternatives:
.
Clearly, ; thus, the cameras can be ranked as . Then, the best camera is .
The robustness of the MCDM approach needs to be checked by means of the sensitivity analysis. Specifically, we look at the changes in the criterion weights and the resulting changes in the ranking of the alternatives. First, we define the design of variations in the weighting vector. The vector for positive weights of criteria is such that the weights are normalized, that is . Then, if the weight of one criterion changes, the weight of other criteria must change accordingly in order to ensure they add up to unity. The resulting vector is then denoted as . Let us change the weight of criterion , , by a margin of . Then, the weights of the other criteria change by . Indeed, the following identity holds: . Observing that w and are related as and , we can get . Since , it is obvious that .
In order to proceed with the sensitivity analysis, we manipulate and set . The resulting weighting vectors and the corresponding orders of ranking are then summarized in Table 1. The key message is that the rating is stable in terms of the best- and worst-performing alternatives for . Figure 1 presents the differences in the normalized distances due to changes in the weighting vector induced by different values of .

Table 1.
Sensitivity of the ranking to the weights of criteria.
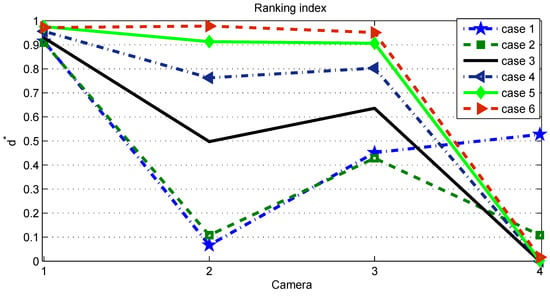
Figure 1.
Changes in the normalized distances due to changes in the weighting vector. Note: the cases represent those given in Table 2.
5.2. Comparative Analysis
The proposed PFNs approach is also compared to those based on the INC and neutrosophic normal cloud (NNC) approach developed by Wang and Yang [26] and Zhang et al. [41], respectively. Since the approach [26] was based on IFNs, the expert assessments used in the MCDM need to be transformed from the PFNs into IFNs. This step involves alterations in the membership and non-membership degrees: as the sum of these values and the degree of indeterminacy needs to be equal to unity, we normalize these values for each PFN. The resulting IFNs and the three-sigma principle are then applied when constructing the INCs for each alternative and criterion. The clouds are aggregated by considering the scores (ratings) and membership degrees of each drop within a corresponding cloud. The cloud drops are then generated from the aggregate clouds by Monte Carlo simulations. Then, the items are ranked by considering the average INC drop values for each alternative.
Aiming to increase the robustness of the analysis, we implement the Monte Carlo simulations so as to achieve 10,000 cloud drops. As we can see above, the proposed approach and the frameworks outlined by [26,41] all identify as the worst item. Anyways, the results regarding the most preferable item diverge. Specifically, the framework by [41] suggests as the best item, while the proposed approach and the method in [26] both identify as the best item. The results based on the methodology developed by Zhang et al. [41] are, therefore, the most divergent from the other two.
We further employ the uncertain pure linguistic information cloud (UPLC) model based on [42]. Utilizing UPLC to convert the uncertain linguistic values into an integrated cloud renders the following ranking of all alternatives: ; and the best camera is . Then, the generalized interval aggregation operator [43] is applied to aggregate the uncertain linguistic variables in the initial decision matrices to derive the individual utilities for the alternatives in the first stage and the uncertain pure linguistic hybrid harmonic averaging (UPLHAA) operator to aggregate the individual utilities in the second stage. The resulting ranking order of the alternatives is , and the best camera is .
Therefore, we apply different aggregation principles, which differ in terms of the order of aggregations (across decision-makers, across criteria) and the underlying aggregation operators. The results of the comparative analysis are summarized in Table 2. The proposed method appears to be valid in identifying the best- and worst-performing alternatives.

Table 2.
The ranking orders rendered by different methods. UPLC, pure linguistic information cloud; UPLHAA, pure linguistic hybrid harmonic averaging.
6. Conclusions
The concept of the Pythagorean normal cloud was proposed in this study. It allows expressing the expected value of the normal cloud as a Pythagorean fuzzy number (note that the Pythagorean fuzzy numbers offer more possibilities for constructing fuzzy ratings if opposed to the conventional fuzzy numbers). The proposed approach, therefore, allows for a greater flexibility in accounting for the confidence of the decision-makers and the distribution of their ratings.
The group MCDM procedure based on the Pythagorean normal clouds was developed. The backward cloud generator was applied to aggregate the expert assessments into the Pythagorean normal clouds. The concept of the PNC was then incorporated into aggregation operators. As a result, the Pythagorean normal cloud weighted arithmetic averaging operator and the Pythagorean normal cloud weighted geometric averaging operator were developed. Application of these operators allowed calculating the Pythagorean fuzzy utility of the alternatives considered. Based on the symmetry among the alternatives and the ideal solutions, the alternatives were ranked according to the values of the normalized distances.
An empirical application to e-commerce was presented in order to demonstrate the operationality of the proposed approach. The existing customers expressed opinions on the goods purchased, as well as their confidence in the form of the Pythagorean fuzzy numbers. These were further aggregated into Pythagorean normal clouds and processed in line with the suggested approach. The comparative analysis was carried out in order to demonstrate the validity of the proposed approach. Future research could aim to improve the weighting schemes used in the aggregation approach. For instance, the deviation of experts from the sample mean (i.e., their competence) could be taken into account when constructing the clouds.
Author Contributions
Conceptualization, J.Z. and T.B. Methodology, J.Z. and W.S. Software, J.Z. Writing, original draft preparation, J.Z. Writing, review and editing, T.B. and D.S. Supervision, W.S.
Funding
This research was funded by the National Natural Science Foundation of China (Nos. 71671165, 2017yyrw07), Natural Science in Universities of the General Project of Anhui Province (No. TSKJ2017B22) and the Financial engineering research and development center of Anhui Polytechnic University (No. JRGCKF201506).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rostamzadeh, R.; Esmaeili, A.; Nia, A.S.; Saparauskas, J.; Ghorabaee, M.K. A fuzzy ARAS method for supply chain management performance measurement in SMEs under uncertainty. Transform. Bus. Econ. 2017, 16, 319–348. [Google Scholar]
- Hu, K.H.; Jianguo, W.; Tzeng, G.H. Improving China’s regional financial center modernization development using a new hybrid MADM model. Technol. Econ. Dev. Econ. 2018, 24, 429–466. [Google Scholar] [CrossRef]
- Czubenko, M.; Kowalczuk, Z.; Ordys, A. Autonomous driver based on an intelligent system of decision-making. Cogn. Comput. 2015, 7, 1–13. [Google Scholar]
- Akusok, A.; Miche, Y.; Hegedus, J.; Nian, R.; Lendasse, A. A two stage methodology using K-NN and false-positive minimizing ELM for nominal data classification. Cogn. Comput. 2014, 6, 432–445. [Google Scholar]
- Mak, D.K. A fuzzy probabilistic method for medical diagnosis. J. Med. Syst. 2015, 39, 26–35. [Google Scholar]
- Meng, F.Y.; Chen, X.H. Correlation coefficients of hesitant fuzzy sets and their application based on fuzzy measures. Cogn. Comput. 2015, 7, 445–463. [Google Scholar]
- Zenebe, A.; Zhou, L.N.; Norcio, A.F. User preferences discovery using fuzzy models. Fuzzy Sets Syst. 2010, 161, 3044–3063. [Google Scholar]
- Vahidov, R.; Ji, F. A diversity-based method for infrequent purchase decision support in e-commerce. Electron. Commer. Res. Appl. 2015, 4, 143–158. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar]
- Zadeh, L.A. Probability measures of fuzzy events. J. Math. Anal. Appl. 1968, 23, 421–427. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar]
- Atanassov, K.T.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1998, 31, 343–349. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multi-criteria decision-making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar]
- Yager, R.R. Properties and applications of Pythagorean fuzzy sets. In Imprecision and Uncertainty in Information Representation and Processing; Angelov, P., Sotirov, S., Eds.; Springer: Cham, Switzerland, 2016; pp. 119–136. ISBN 978-3-319-26301-4. [Google Scholar]
- Liang, D.C.; Xu, Z.S.; Darko, A.P. Projection model for fusing the information of Pythagorean fuzzy multicriteria group decision-making based on geometric Bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Beliakov, G.; James, S. Averaging aggregation functions for preferences expressed as Pythagorean membership grades and fuzzy orthopairs. In Proceedings of the IEEE International Conference on Fuzzy Systems, Beijing, China, 6–11 July 2014; pp. 298–305. [Google Scholar]
- Reformat, M.Z.; Yager, R.R. Suggesting recommendations using Pythagorean fuzzy sets illustrated using Netflix movie data. In Information Processing and Management of Uncertainty in Knowledge-Based Systems; Laurent, A., Ed.; Springer: Berlin, Germany, 2014; pp. 546–556. ISBN 978-3-319-08794-8. [Google Scholar]
- Zeng, S.Z. Pythagorean fuzzy multiattribute group decision-making with probabilistic information and OWA approach. Int. J. Intell. Syst. 2017, 32, 1136–1150. [Google Scholar] [CrossRef]
- Zeng, S.Z.; Chen, J.P.; Li, X.S. A hybrid method for Pythagorean fuzzy multiple-criteria decision-making. Int. J. Inf. Technol. Decis. 2016, 15, 403–422. [Google Scholar]
- Li, D.Y.; Liu, C.Y.; Du, Y.; Han, X. Artificial intelligence with uncertainty. J. Softw. 2004, 15, 1583–1594. [Google Scholar]
- Wang, G.Y.; Xu, C.L.; Li, D.Y. Generic normal cloud model. Inf. Sci. 2014, 280, 1–15. [Google Scholar]
- Li, D.Y.; Han, J.W.; Shi, X.M.; Chan, M.C. Knowledge representation and discovery based on linguistic atoms. Knowl.-Based Syst. 1998, 10, 431–440. [Google Scholar]
- Wang, D.; Zeng, D.B.; Singh, V.P.; Xu, P.C.; Liu, D.F.; Wang, Y.K.; Zeng, X.K.; Wu, J.C.; Wang, L.C. A multidimension cloud model-based approach for water quality assessment. Environ. Res. 2016, 149, 113–121. [Google Scholar]
- Jiang, J.B.; Liang, J.R.; Jiang, W.; Gu, Z.P. Application of trapezium cloud model in conception division and conception exaltation. Comput. Eng. Des. 2008, 29, 1235–1240. [Google Scholar]
- Wang, J.Q.; Yang, W.E. Multiple criteria group decision-making method based on intuitionistic normal cloud by Monte Carlo simulation. Syst. Eng. Theory Pract. 2013, 33, 2859–2865. [Google Scholar]
- Peng, X.D.; Yuan, H.Y.; Yang, Y. Pythagorean fuzzy measures and their applications. Int. J. Intell. Syst. 2017, 32, 991–1029. [Google Scholar] [CrossRef]
- Peng, X.D.; Yang, Y. Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 2016, 31, 444–487. [Google Scholar]
- Yang, W.E.; Wang, J.Q.; Ma, C.Q.; Wang, X.F. Hesitant linguistic multiple criteria decision-making method based on cloud generating algorithm. Control Decis. 2015, 30, 371–374. [Google Scholar]
- Wang, J.Q.; Liu, T. Uncertain linguistic multi-criteria group decision-making approach based on integrated cloud. Control Decis. 2012, 27, 1185–1190. [Google Scholar]
- Wang, J.Q.; Peng, L.; Zhang, H.Y.; Chen, X.H. Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information. Inf. Sci. 2014, 274, 177–191. [Google Scholar]
- Wang, J.Q.; Wang, P.; Wang, J.; Zhang, H.Y.; Chen, X.H. Atanassov’s interval-valued intuitionistic linguistic multi-criteria group decision-making method based on trapezium cloud model. IEEE Trans. Fuzzy Syst. 2014, 23, 542–554. [Google Scholar]
- Liu, C.; Tang, G.L.; Liu, P.D. An approach to multicriteria group decision-making with unknown weight information based on Pythagorean fuzzy uncertain linguistic aggregation operators. Math. Probl. Eng. 2017. [Google Scholar] [CrossRef]
- Garg, H. A novel improved accuracy function for interval valued Pythagorean fuzzy sets and its applications in the decision-making process. Int. J. Intell. Syst. 2017, 32, 1247–1260. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer-Verlag: New York, NY, USA, 1981; ISBN 978-3-540-10558-9. [Google Scholar]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2008, 14, 1179–1187. [Google Scholar]
- Zhang, X.L.; Zhao, L.; Zang, J.Y.; Fan, H.M.; Cheng, L. Flatness intelligent control based on T-S cloud inference neural network. Trans. ISIJ 2014, 54, 2608–2617. [Google Scholar]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar]
- Luo, Z.Q.; Zhang, G.W. A new algorithm of backward normal onevariate cloud. J. Front. Comput. Sci. Technol. 2007, 1, 234–240. [Google Scholar]
- Wang, J.Q.; Peng, J.J.; Zhang, H.Y.; Liu, T.; Chen, X.H. An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar]
- Zhang, H.Y.; Ji, P.; Wang, J.Q.; Chen, X.H. A Neutrosophic normal cloud and its application in decision-making. Cogn. Comput. 2016, 8, 649–669. [Google Scholar]
- Peng, B.; Zhou, J.M.; Peng, D.H. Cloud model based approach to group decision-making with uncertain pure linguistic information. J. Intell. Fuzzy Syst. 2017, 32, 1959–1968. [Google Scholar]
- Peng, B.; Ye, C.M.; Zeng, S.Z. Uncertain pure linguistic hybrid harmonic averaging operator and generalized interval aggregation operator based approach to group decision-making. Knowl.-Based Syst. 2012, 36, 175–181. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).