Abstract
The thermoelastic dynamic response of a clamped Bernoulli beam was studied when it was irradiated by a movable, temporally non-Gaussian, laser pulse. Both the energy absorption depth and the time decaying effects were considered. The temperature distribution, deflection, vibration acceleration, and stress of the beam were derived analytically, and the variations of them with time and space were illustrated. It was shown that the vibration frequency is independent of the scanning speed of the laser pulse. It is important to notice that, although the deflection of the beam is small, high vibration acceleration can be induced in microbeams, which is important for failure and fracture of the beam. Moreover, compressive stress is induced in the beam, but the importance of temperature-induced stress and deformation-induced stress may be different according to the duration time and moving speed of the laser pulse.
1. Introduction
The thermoelastic process with a movable heat source is commonly employed in modern manufacturing processes and tribological applications, such as cutting, welding, and surface laser treatment [1]. During this process, the local surface of the substrate material, including biological tissues, metallic and nonmetallic materials, is suddenly irradiated by the laser beam; as a consequence, the temperature of the inner region nearby the heated surface sharply rises. Due to the thermo-mechanical coupling effect, high stress will occur in regions with a high-temperature gradient. Therefore, it is of great significance to delve into the effect of moving sources in the thermoelastic process. Regarding conduction-limited heating, the surface of the substrate material is heated beneath its melting temperature and the high rate of cooling on the surface modifies the microhardness and stress levels in the heated surface vicinity [2].
Many research works have been performed to evaluate the process of laser heating on metal or diode surfaces [3]. Among them, considerable numerical simulations have been carried out by utilizing finite element software. For example, Guan et al. [4] carried out numerical simulations of laser bonding of preloaded sheet metals. They pointed out that sheet deformation depends on the integration of the thermal and the pre-stresses when the sheet metal surface is irradiated by laser beams. Abbas [5] analyzed the nonlinear transient thermal stress distribution of a thick-walled FGM cylinder by considering the heat conduction model with one relaxation time. The influences of several parameters on the behaviors of physical quantities were evaluated, such as the thermal relaxation time, the temperature-dependent parameters, and the volume fraction parameter.
Though it is easy to carry out the numerical simulation of the heating process, the analytical solution provides a functional relationship between the material responses and the parameters of the pulse [6]. This can help people to deeply understand the physical mechanism of laser irradiation. Cui et al. [3] presented a 3D analytic model to study the thermal response of rectangular μ-ILEDs in a pulsed operation. Zhou et al. [7] proposed a thermal wave model of bioheat conduction to investigate thermal damage in biological tissues. Zhang et al. [8] established a coupled thermomechanical model with the C-V heat conduction law employed to delve into the thermoelastic behavior of a metal substrate with oxide layer and ceramic coating.
Most of the available literature considers the laser pulse as a uniform heat source. As far as we know, few works are related to time-decaying laser pulses. For example, Yilbas et al. [6] presented an analytic solution for thermal stresses in the short-pulse heating of a metallic surface subjected to an exponentially time-decaying laser. Zenkour and Abbas [9] conducted an analysis of transient thermal stress for a temperature-dependent hollow cylinder, which was exposed to a time-decaying temperature field.
Thermoelastic responses of the elastic medium subjected to moving heat sources have attracted much attention [10]. Yevtushenko and Ukhanska [11] studied displacements and thermal stresses in a 2D half-space induced by a movable heating source. Sarbani and Amitava [12] incorporated movable heating sources into generalized thermoelasticity theory. Abbas [13] investigated the thermoelastic behavior of a micro-scale beam irradiated by a movable heating source using Green and Naghdi theory Type III. Lotfy [14] studied the generalized thermoelastic behavior of an isotropic material by introducing an internal heat source that moves at a uniform speed. The magnetic-thermal-elastic behavior of a rod, whose properties were dependent on temperature, was investigated by Xiong and Guo [15]. In their work, the rod was assumed to be clamped on two ends and suffered from an initial magnetic field and a heat source moving along the axial direction. Distributions of non-dimensional temperature, displacement, and stress were obtained, and the effects of the material properties and the heat source velocity were discussed.
In summary, the existing literature has mainly focused on the temperature, displacement, and stress wave behavior of the medium during laser irradiation. However, when a substrate is irradiated by a laser pulse, vibration takes place because of the lack of damping. This phenomenon has been found in pulsed laser applications, such as laser forming, laser micro welding, and laser trimming of micro devices [16]. Consequently, the deformations and dynamic behaviors of microstructures under modern manufacturing techniques are increasingly becoming important.
Unfortunately, vibration behavior in laser-assisted manufacturing processes has hardly been discussed. Philip et al. [17] studied the vibration behavior in the elastic medium irradiated by a single laser pulse. Widlaszewski [18] reported related experimental work. Chen et al. [19] investigated the bending angle of laser forming under a line-shaped heating source both numerically and experimentally. Castellini et al. [20] calculated the laser-induced elastic vibration with an implicit algorithm of FEM.
This paper focuses on the thermoelastic response of a clamped beam subjected to a movable time-decaying laser pulse. The temperature is derived using Green’s function approach, and the deflection is derived using Duhamel’s method. The vibration acceleration is also obtained, which is important in inducing the stress. In addition, the importance of the two components of stress, i.e., the stress induced by deformation and the stress induced by temperature increment, is discussed.
2. Basic Formulations for This Problem
Consider a Bernoulli beam with Cartesian coordinates (), , and (), where the coordinate plane coincides with the neutral surface of the beam. The length, width, and thickness of the beam are , , and , respectively. A laser pulse is moving along the top surface of the beam towards right from the left edge at uniform speed .
The two-dimensional heat conduction equation based on Fourier’s law is [21]
where denotes the heat energy absorbed by the beam, which is expressed as [22,23]
where is the temperature increment, the thermal conductivity, the thermal diffusivity, the time, the energy absorption coefficient, the energy absorption depth, the power intensity of the laser pulse, the time duration of the laser pulse, and the Dirac delta function.
The vibration equation of the beam is [24]
where is the Young’s modulus, the moment of inertial, the displacement, the density, the cross section, and the linear thermal expansion coefficient. is the thermal moment.
The boundary conditions for heat conduction are
The beam is fixed at the left and right edges, namely, the deflection and the slope are both 0 at the two ends, which are given as
The initial conditions are set to be
3. Solutions to the Governing Equations
3.1. Solution to the Heat Conduction Equation
The Green’s function approach is applied in solving the heat conduction equation. First, the auxiliary problem for the same beam can be considered [21]:
and subjected to the condition
Considering the thermal boundary conditions Equation (4), the eigenfunctions of the problem are
where , .
It is important to notice that is an eigenfunction as well.
Green’s function of the heat conduction problem of Equations (1), (2), (4), and (6) is derived as
where .
Since the initial condition and boundary conditions of heat conduction problem are all 0, based on the method of Green’s function, the temperature is obtained as [21]
By substituting Equations (2) and (12) into Equation (13), one can obtain the temperature as
where
3.2. Solution of the Vibration Equation
By substituting the expression of temperature into the thermal moment , one can obtain
Vibration Equation (3) can be rewritten as
where .
By using the technique of separating variables, the deflection may be written as [25]
The vibration mode should satisfy the equation
For the beam with both ends fixed, the expression of is
where , and . are the roots of the equation .
Using the boundary conditions and the orthogonality relationships of the eigenfunctions, one obtains the following differential equation for [25]
where is the modal mass, and is the modal forcing function defined as
For the problem under consideration, the beam is static and at free status, namely, the initial deflection and velocity are 0, so Equation (20) is solved to yield
Therefore, the deflection of the beam with both ends fixed is
It is obtained from Equations (14), (15), (21), and (23) that the expression of deflection is
where
4. Calculation Results and Discussions
A beam made of gold is used in the following analysis. The parameters of the material are [26] , , , , and . The other parameters are , , ,, , and .
4.1. Temperature Variation
Figure 1 illustrates the variations in temperature increments on the surface of at three axial locations at the laser pulse velocity of 20 m s−1. It is shown that the temperature increment vibrates around 0 at the beginning. After some time, it increases in peak value and then drops to near zero very fast. Moreover, because of the motion of the laser pulse, it takes more time to reach the peak value of at the locations farther away from the left edge. It is clear that the peak arrives at the maximum value at the location of 0.002 m, which is equal to .
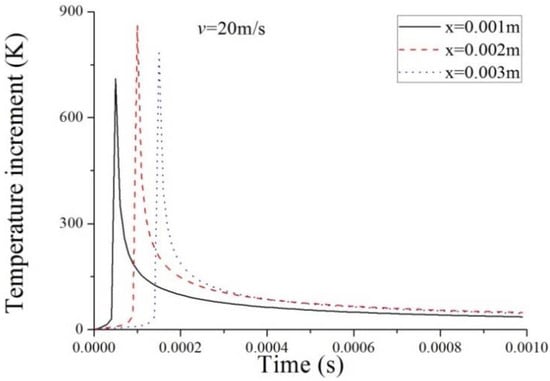
Figure 1.
Temporal variations of at different axial locations on the surface of ().
Figure 2 compares the time histories of temperature increments for three different moving velocity of laser pulse on the surface of at the location of . It is obvious that the maximum temperature drops with the rise in laser speed. In the case of higher speed of the laser pulse, less energy is absorbed at a specified location. Therefore, increases to a lower value. On the contrary, the heat energy is absorbed by a smaller region in the case of lower speed motion and the heat source intensity becomes stronger. Consequently, the temperature is higher.
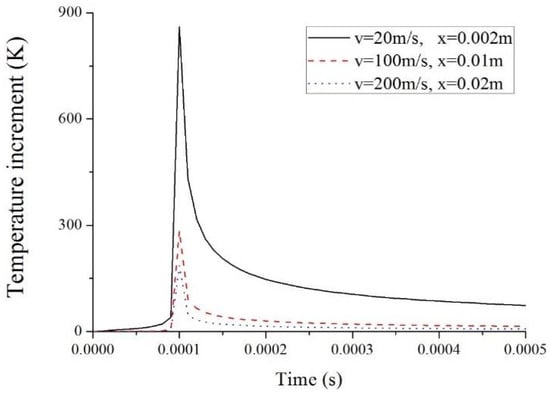
Figure 2.
Temperatures with maximum peak value for different laser velocities.
4.2. Deflection Variation
Figure 3, Figure 4, Figure 5 and Figure 6 illustrate the deflection of the beam as the motion speeds of laser pulse are 20, 100, and 200, respectively. Figure 3 shows the deflections at the midspan of the beam () for the three speeds of laser pulse. It is shown that the beam is vibrating and that the vibration behaviors are quite different for the three moving speeds of laser pulse.
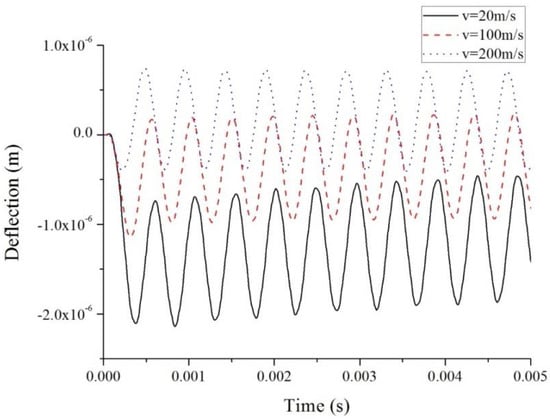
Figure 3.
Deflections at the midspan point for three velocities of laser pulse.
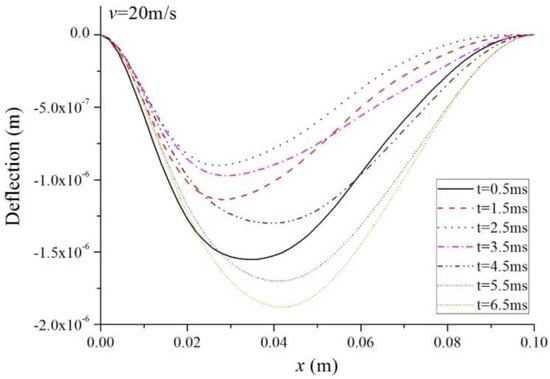
Figure 4.
Deflection along the beam span ().
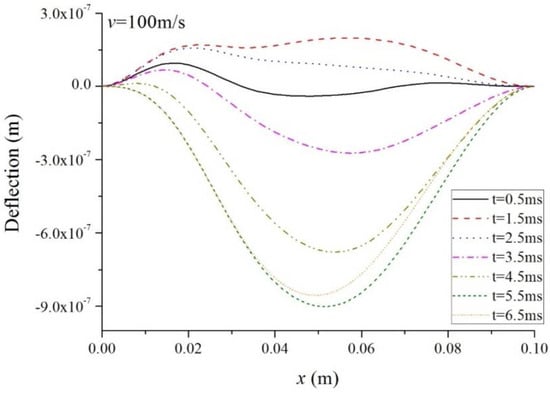
Figure 5.
Deflection along the beam span ().
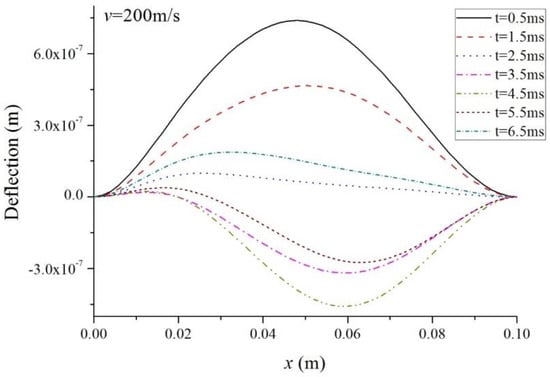
Figure 6.
Deflection along the beam span ().
Figure 4, Figure 5 and Figure 6 show the variations of deflections along the beam span. The influence of the laser speed on the beam vibration is obvious. The vibration amplitude differs along the axis, first rising to a peak value and then dropping to 0. Moreover, the vibration mode is not symmetrical around the midspan. The zero deflection at the two edges is due to the fact that the beam is clamped. The laser pulse leads to temperatures that are higher on the left part than on the right, which indicates a non-symmetric thermal load on the beam. Consequently, the unsymmetry behavior of deflection occurs, and the peak amplitude is higher on the left part. Furthermore, when the laser pulse moves faster, both the deflection and the vibration amplitude increase.
4.3. Frequency Spectra of Deflection
The fast Fourier transformation technique was adopted to obtain the vibration frequency. The frequency spectra for the beam at different velocities of the laser pulse are given in Figure 7. There are two frequencies: The first frequency is 0, which means the deflection takes the value of the equilibrium position of the vibration. The second one is the dynamic vibration frequency. The vibration frequencies for the three scanning velocities of the laser pulse are identical, the value being 2197.8 Hz.
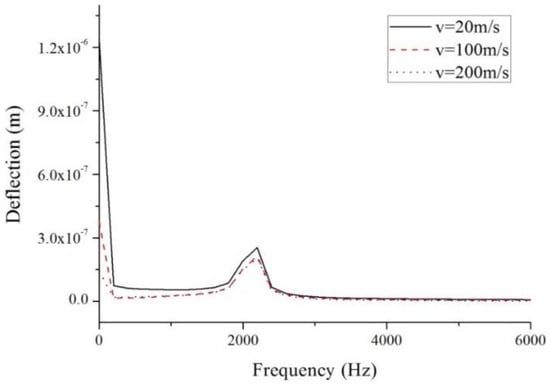
Figure 7.
Frequency spectra of deflection for different velocities of the laser pulse.
For the free-vibration of the beam, the natural frequency of is given by
The value of for the beam under consideration is 2118.8 Hz. The frequency increases a little when the beam is irradiated by a laser pulse. However, the frequency is independent with the scanning speed of the laser pulse.
According to vibration theory, it is high-frequency vibration when the frequency is over 1000 Hz, and the acceleration is taken as the vibration criterion [6]. Therefore, in the following, we will study the variation in the acceleration of the beam.
4.4. Vibration Behaviors and Properties of the Beam
Figure 8 shows the deflection, velocity, and acceleration of the beam at the mispan point at a laser speed of 20 . To make the values of comparative magnitude, the units of the deflection, velocity and acceleration are changed into , , and , respectively, where is the gravity acceleration. It is shown that the phases of deflection, velocity, and acceleration are different. It is important to notice that the vibration acceleration of the beam can reach a value of nearly 20 g at a laser speed of 20 m/s, which is quite high. It is known that the peak value of acceleration represents the impact force exerted on the beam, which can lead to failure and fracture of the beam. This implies that the probability of failure of the beam is highest under laser pulses at low moving speeds.
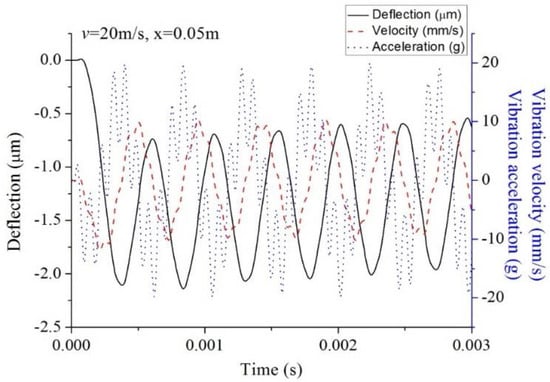
Figure 8.
Deflection, velocity, and acceleration of the beam at the midspan point ().
Figure 9, Figure 10 and Figure 11 show the vibration accelerations along the beam span under laser pulses at different motion velocities. It is clear that the peak value of acceleration decreases as moving velocity rises. It is shown that the vibration acceleration is not symmetric about the midpoint of the beam, due to the unsymmetric heat source. However, there is something different among the three cases. When the velocity of laser pulses is low, say, , the peak value of vibration acceleration occurs near the midpoint. However, when , the peak value occurs at the right part of the beam and the value of is lower at the left part than that at the right part. In the case of , this tendency is more obvious.
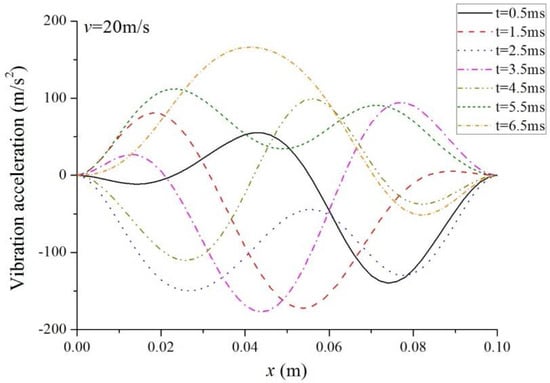
Figure 9.
Acceleration along the beam span ().
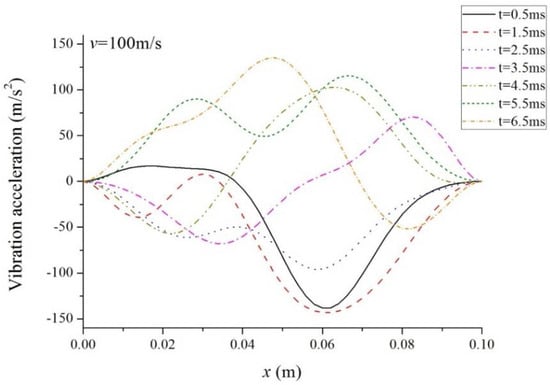
Figure 10.
Acceleration along the beam span ().
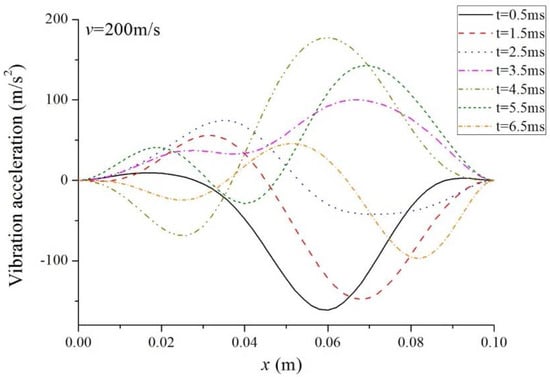
Figure 11.
Acceleration along the beam span ().
4.5. Behaviors of Stress
The temporal distributions of stress on the top surface of the beam when the laser speeds are 20 and , respectively, are shown in Figure 12 and Figure 13. Two locations along the beam span are considered: (1) the location that has the maximum temperature, namely, ; (2) the midspan of the beam, namely, . It can be found that the stress shows quite different behaviors at these two laser speeds.
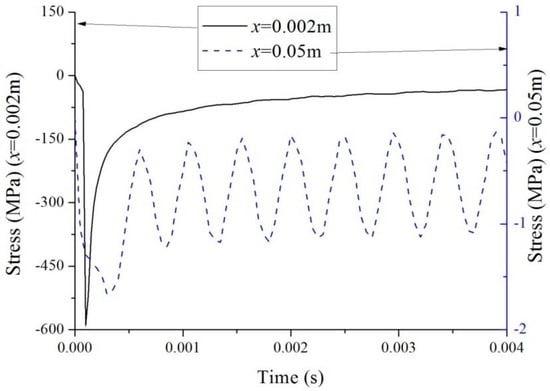
Figure 12.
Stress at two locations ().
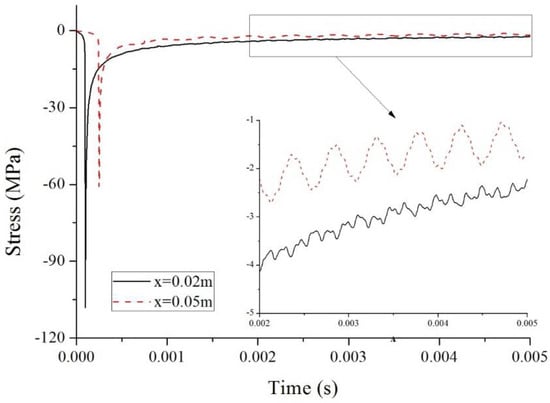
Figure 13.
Stress at two locations ().
At a low laser speed (), great compression stress occurs at the location , and it drops quickly as time passes. This tendency is similar to that of temperature. However, at the midspan of the beam, the stress is much lower and it vibrates with time. In other words, the stress is determined by temperature at the beginning but depends on the deflection after a while. However, in the case of a high speed (), the temperature increment is low, so the peak value of compression stress is low. At both locations, the stresses are determined by temperature at the beginning but vibrate with small magnitudes after a while. It is interesting that the vibration amplitude of stress is higher at the midspan than at the location of . This is because the vibration acceleration at the location of is much lower than that at the midspan, which leads to a smaller impact force on the beam. Generally, the peak compression stress is higher at lower speeds. That is to say, at a low laser pulse speed, the temperature increment is dominant in the stress field; however, stress is mainly determined by the deflection of the beam at high speeds.
Finally, the effect of the duration time of the laser pulse, , on stress and vibration acceleration is discussed. Suppose that a laser pulse moves at a speed of . The stresses at the midspan on the top surface when takes the values of 0.1, 0.5, and 1 ms are shown in Figure 14, Figure 15 and Figure 16. Total stress and its two components, the stress induced by deformation and the stress induced by temperature increment, are also shown in these figures. The vibration accelerations in the three cases are shown in Figure 17. As increases, the magnitude of the compression stress increases, and vibration acceleration decreases. When , stress is mainly determined by temperature increment. However, in the case of , the influence of temperature increment is obvious only at the beginning of irradiation.
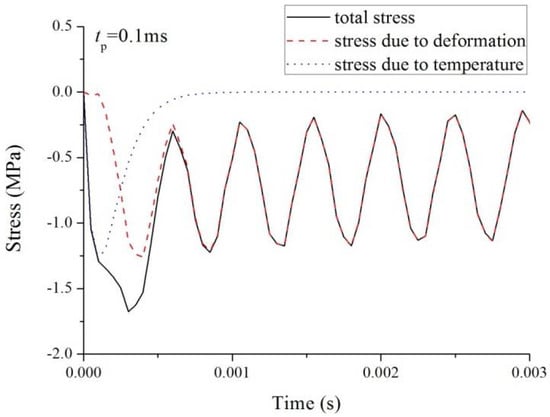
Figure 14.
Time histories of the total stress and its two components at the midspan on the top surface of the beam ().
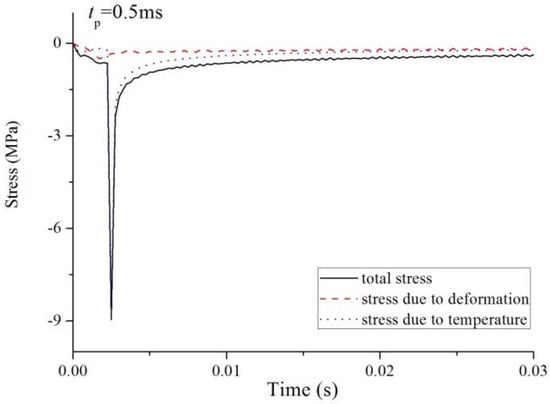
Figure 15.
Time histories of the total stress and its two components at the midspan on the top surface of the beam ().
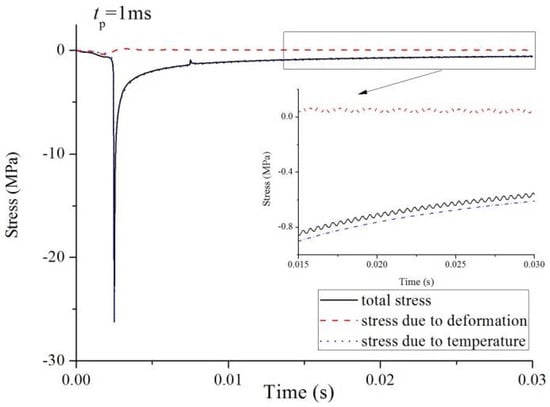
Figure 16.
Time histories of the total stress and its two components at the midspan on the top surface of the beam ().
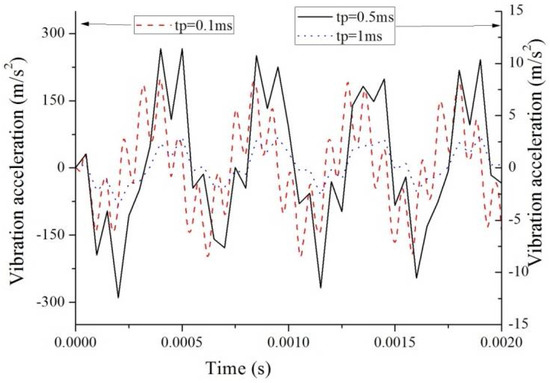
Figure 17.
Vibration acceleration vs at the midspan of the beam.
5. Conclusions
The thermoelastic behaviors and properties of a clamped beam that was applied to a time-decaying laser pulse were investigated. Considering both the energy absorption depth and the time-decaying profile of the laser pulse, the governing equations of this problem were established, and the analytical expressions of the temperature, deflection, vibration acceleration, and stress of the beam were derived. The following findings were obtained.
The heat propagation along the axis was obvious. The temperature increment reached a peak value at . When the laser speed decreased, the peak temperature increment increased.
The vibration frequency was independent of the scanning velocity of the laser pulse.
Although the deflection of the beam was small, high vibration acceleration was induced in the microbeams.
Compressive stress was induced in the beam, and the peak compression stress was higher at lower laser speeds. However, the importance of temperature-induced stress and deformation-induced stress may be different according to the scanning velocity and duration time of the laser pulses.
Author Contributions
Solution: X.Y. and J.M.; calculation: S.L.; investigation: Y.X.; manuscript review and editing: J.Y.; original draft preparation: Y.S.
Acknowledgments
This work was financially supported by the National Natural Science Foundation of China under grant number 11002017.
Conflicts of Interest
The authors declare they have no conflict of interest.
References
- Levin, P. A general solution of 3-D quasi-steady-state problem of a moving heat source on a semi-infinite solid. Mech. Res. Commun. 2008, 35, 151–157. [Google Scholar] [CrossRef]
- Shuja, S.Z.; Yilbas, B.S. Laser multi-beam heating of moving steel sheet: Thermal stress analysis. Opt. Laser Eng. 2013, 51, 446–452. [Google Scholar] [CrossRef]
- Cui, Y.; Bian, Z.G.; Li, Y.H.; Xing, Y.F.; Song, J.Z. 3D thermal analysis of rectangular microscale inorganic light-emitting diodes in a pulsed operation. J. Phys. D Appl. Phys. 2016, 49, 405101. [Google Scholar] [CrossRef]
- Guan, Y.J.; Sun, S.; Zhao, G.Q.; Luan, Y.G. Finite element modeling of laser bending of pre-loaded sheet metal. J. Mater. Proc. Technol. 2003, 142, 400–407. [Google Scholar]
- Abbas, I.A. Nonlinear transient thermal stress analysis of thick-walled FGM cylinder with temperature-dependent material properties. Meccanica 2014, 49, 1697–1708. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Ali, H.; Yousef, A. Thermal stress analysis and entropy generation rate due to laser short pulse heating of a metallic surface. Can. J. Phys. 2014, 92, 1681–1687. [Google Scholar] [CrossRef]
- Zhou, J.H.; Zhang, Y.W.; Chen, J.K. Non-Fourier heat conduction effect on laser-induced thermal damage in biological tissues. Numer. Heat Transf. Part A Appl. 2008, 54, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.M.; Zhang, L.; Chu, Z.X. Thermomechanical Coupling of Non-Fourier Heat Conduction with the C-V Model: Thermal Propagation in Coating Systems. J. Therm. Stress. 2015, 38, 1104–1117. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Nonlinear Transient Thermal Stress Analysis of Temperature-Dependent Hollow Cylinders Using a Finite Element Model. Int. J. Struct. Stab. Dyn. 2014, 14, 1450025. [Google Scholar] [CrossRef]
- Lykotrafitis, G.; Georgiadis, H.G. The three-dimensional steady-state thermo- elastodynamic problem of moving source over a half space. Int. J. Solids Struct. 2003, 40, 899–940. [Google Scholar] [CrossRef]
- Yevtushenko, A.A.; Ukhanska, O.M. The thermal stresses and displacements in a two-dimensional convective half-space for a moving heat source. Int. J. Heat Mass Transf. 1994, 37, 2737–2743. [Google Scholar] [CrossRef]
- Sarbani, C.; Amitava, C. Transient disturbances in a relaxing thermoelastic half space due to moving internal heat source. Int. J. Math. Math. Sci. 1998, 21, 595–602. [Google Scholar]
- Abbas, I.A. A GN model for thermoelastic interaction in a microscale beam subjected to a moving heat source. Acta Mech. 2015, 226, 2527–2536. [Google Scholar] [CrossRef]
- Lotfy, K. The elastic wave motions for a photothermal medium of a dual-phase- lag model with an internal heat source and gravitational field. Can. J. Phys. 2016, 94, 400–409. [Google Scholar] [CrossRef]
- Xiong, C.B.; Guo, Y. Effect of variable properties and moving heat source on magnetothermoelastic problem under fractional order thermoelasticity. Adv. Mater. Sci. Eng. 2016, 5341569. [Google Scholar] [CrossRef]
- Hsieh, H.S.; Lin, J.M. Laser-induced vibration during pulsed laser forming. Opt. Laser Technol. 2004, 36, 431–439. [Google Scholar] [CrossRef]
- Philp, W.R.; Booth, D.J.; Peery, N.D. Single pulse laser excitation of structure vibration using power density below the surface ablation threshold. J. Sound Vib. 1995, 185, 643–654. [Google Scholar] [CrossRef]
- Widlaszewski, J. Precise laser bending. In Proceedings of the Laser Assisted Net shape Engineering 2 (LANE’97), Erlangen, Germany, 23–26 September 1997; pp. 393–398. [Google Scholar]
- Chen, G.; Xu, X.; Poon, C.C.; Tam, A.C. Experimental and numerical studies on micro-scale bending of stainless steel with pulsed laser. Trans. ASME 1999, 66, 772–779. [Google Scholar] [CrossRef]
- Castellini, P.; Revel, G.M.; Scalise, L.; De Andrade, R.M. Experimental and numerical investigation on structural effects of laser pulses for modal parameter measurement. Opt. Laser Eng. 2000, 32, 565–581. [Google Scholar] [CrossRef]
- Ozisik, M.N. Heat Conduction; John Wiley & Sons, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Yang, C.Y. The determination of two moving heat sources in two-dimensional inverse heat problem. Appl. Math. Model. 2006, 20, 278–292. [Google Scholar] [CrossRef]
- Youssef, H.M. A two-temperature generalized thermoelastic medium subjected to a moving heat source and ramp-type heating: A state-space approach. J. Mech. Mater. Struct. 2009, 4, 1637–1648. [Google Scholar] [CrossRef]
- Kidwa-Kukla, J. Vibration of a beam induced by harmonic motion of a heat source. J. Sound Vib. 1997, 205, 213–222. [Google Scholar] [CrossRef]
- Shabana, A.A. Theory of Vibration, Volume II: Discrete and Continuous Systems; Springer: Berlin, Germany, 1992. [Google Scholar]
- Sun, Y.X.; Jiang, Y.; Yang, J.L. Thermoelastic damping of the axisymmetric vibration of laminated trilayered circular plate resonators. Can. J. Phys. 2014, 92, 1026–1032. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).