Abstract
In this paper, an improved set-membership proportionate normalized least mean square (SM-PNLMS) algorithm is proposed for block-sparse systems. The proposed algorithm, which is named the block-sparse SM-PNLMS (BS-SMPNLMS), is implemented by inserting a penalty of a mixed norm of weight-taps into the cost function of the SM-PNLMS. Furthermore, an improved BS-SMPNLMS algorithm (the (BS-SMIPNLMS algorithm) is also derived and analyzed. The proposed algorithms are well investigated in the framework of network echo cancellation. The results of simulations indicate that the devised BS-SMPNLMS and BS-SMIPNLMS algorithms converge faster and have smaller estimation errors compared with related algorithms.
1. Introduction
Echo cancellation is one of the most typical applications in adaptive filtering scenarios [1,2]. Among the many adaptive algorithms, the normalized least mean square (NLMS) is a classical algorithm due to its good performance and easy implementation [3,4]. The current research on echo cancellation focuses on network echo cancellation (NEC) and acoustic echo cancellation (AEC). Both of these applications have long and sparse impulse responses, which means that the filter needs many more taps and there are mostly zero or close to zero responses [5]. Additionally, the input signal of these two systems is usually a speech signal rather than white noise. Therefore, the performance of the traditional NLMS algorithm may reduce, and the convergence speed will slow down when it is used for dealing with acoustic and network echo cancellation. To further exploit the sparse characteristic of the echo path, the proportionate NLMS (PNLMS) and zero-attracting algorithms were proposed [6,7,8,9,10,11,12,13,14,15,16]. The proportionate adaptive filtering algorithms assign corresponding step sizes to each coefficient according to its magnitude, in contrast to the NLMS algorithm whose step sizes are unified. The result of the proportionate assignment is that the large coefficients obtain large step sizes while the small coefficients obtain small step sizes. Thus, proportionate adaptive filtering algorithms are more suitable for sparse systems. However, the convergent performance of the PNLMS algorithm decreases sharply following the initial fast convergence, and the PNLMS may even behave more poorly than the NLMS. We can draw the conclusion that we can benefit from the PNLMS algorithm only in the case when the system is quite sparse. To address this problem, many related improved algorithms have been proposed [17,18,19,20,21]. The improved PNLMS (IPNLMS) algorithm is the most classical of the variation algorithms [17]. The IPNLMS algorithm fully exploits the "proportionate" characteristic and has better performance than the NLMS and PNLMS when the channel response is neither sparse nor extremely dispersive.
The sparse system responses can usually be divided into three types based on their sparse features: generalized sparse response; single-clustering block-sparse response; and two-cluster or multi-cluster block-sparse response, as shown in Figure 1 [22].
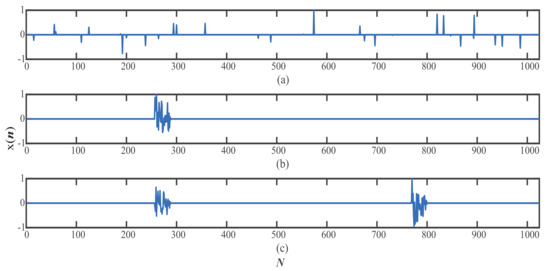
Figure 1.
Sparse system response type: (a) generalized sparse response; (b) single-clustering block-sparse response; (c) two-clustering block-sparse response.
In the generalized sparse system, the nonzero coefficients distribute randomly. In the clustering block-sparse systems, the nonzero coefficients distribute in clumps of 1–2 or even more. If there is more than one cluster, we generally consider the system as a multi-clustering block-sparse system. The echo response is a kind of single-clustering block-sparse system, and the satellite communication is a kind of multi-clustering block-sparse system. To take further advantage of the prior knowledge of the block-sparse feature, many corresponding algorithms were proposed in [22,23,24,25]. The algorithm proposed in [22] is named the BS-LMS, in which the main idea is to insert a mixed norm as a penalty to the cost function of the conventional LMS with same group partition sizes. The PB-IPNLMS algorithm proposed in [23] divides the channel response into two parts, the sparse part and the dispersive part. The proportionate algorithm is used for the sparse part while the non-proportionate algorithm is used for the dispersive part. However, the PB-IPNLMS has a notable unpleasant property in that the assumption of just one cluster exists, and its location must be known ahead of time. The IAF-PNLMS algorithm devised in [24] uses individual factors for each coefficient rather than a overall one. As a result, the IAF-PNLMS algorithm can get outstanding performance only when the impulse response exhibits high sparseness. The IIPNLMS algorithm proposed in [25] divides the echo path response into an active region and inactive region. The NLMS algorithm is used for the former, while the PNLMS is used for the latter. Some of the algorithms mentioned above cannot fully exploit the system block-sparsity and others do not deal well with multi-clustering block-sparsity. The BS-PNLMS algorithm proposed in [26] inserts a penalty of a mixed norm to the cost function of the PNLMS algorithm. This algorithm further exploits the block-sparsity of the estimated system as compared to the BS-LMS, and it can serve for the multi-clustering case in addition to the single-clustering case. In spite of this, the performance in terms of convergence rate, estimation error, and computational complexity still needs to be improved.
In recent decades, the set-membership (SM) filtering technique has gained extensive attention because of its good estimation performance and computational burden reduction [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. The SM filtering technique sets a model space in which there are input and output vector pairs. The updating of filter taps only occurs when the error of estimation is larger than the preset upper limit [33].
In this paper, we use the SM principle and the mixed norm to devise the block-sparse proportionate adaptive filtering algorithm to improve the estimation performances of the previous block-sparse algorithms. We replace the elements of the step size assignment matrix with the norm of the blocks instead of the absolute value. Therefore, the step size distribution of the new algorithm is based on the whole block value rather than the single coefficient value, which speeds up the convergence. In addition, the introduction of the SM principle also can help to improve the estimation accuracy and computation burden reduction. The proposed block-sparse SM-PNLMS (BS-SMPNLMS) algorithm, and its variant the improved BS-SMPNLMS (BS-SMIPNLMS) algorithm are well deduced and analyzed in detail. The performances of the devised BS-SMPNLMS and BS-SMIPNLMS algorithms are discussed in terms of the estimation error and tracking. The obtained results show that the two new block-sparse algorithms converge faster and provide smaller estimation errors compared with related algorithms .
The structure of this paper can be summarized as follows. In Section 2, we review the SM principle and the PNLMS algorithm. In Section 3, the BS-SMPNLMS and BS-SMIPNLMS algorithms are proposed within the framework of the block-sparse and set-membership theories. Section 4 presents the evaluation performances of both the BS-SMPNLMS and BS-SMIPNLMS algorithms in block-sparse signal processing. Section 5 summarizes the full text.
2. Review of Corresponding Algorithms
2.1. The PNLMS Algorithm
We assume the system input signal is , and the impulse response of estimated system is , whose length is N. The observed output signal can be described as
where denotes the noise signal which is assumed to be uncorrelated with . The estimation error is
where denotes the estimation signal. The updating equation of the PNLMS algorithm can be described as
where is an overall step size, and is a small regularization parameter. is the step size assignment matrix, which is diagonal and can be described as
The elements in are calculated by
where
Herein, is a positive constant of which range is usually , and its purpose is to avoid stalling in the case of it being much smaller than the largest element. is a regularization parameter, and it is used to avoid the updating stopping when all of the taps are zeros at beginning
The IPNLMS has the same update equation as the PNLMS, which is shown in Equation (3). The IPNLMS improves the elements in by introducing an adjusting parameter c into Equation (5)
where . When , the IPNLMS behaves as the NLMS, while when , the IPNLMS works like the PNLMS. We usually choose the value of c as 0 or –0.5.
2.2. Review of the SM Principle and Corresponding Algorithm
The model space in which includes input–output vector pairs is defined as . A upper bound of estimated error is . The criterion of set-membership is to seek the optimization subject to
When does not belong to , the problem of solving optimization of the SM-PNLMS can be described as
The updating equation of the SM-PNLMS is
where
3. The New BS-SMPNLMS and BS-SMIPNLMS Algorithms
Although the SM-PNLMS algorithm can both utilize the sparsity and simplify the computational complexity, its performance still needs to be improved when the response is block-sparse, which is common in real-world echo cancellation systems. Time-domain segmentation is an effective approach for block-sparse processing, and is adopted by some existing algorithms mentioned in Section 1. In addition, using a mixed norm such as the norm, norm, or norm is also an effective method of block-sparse system identification [43,44,45,46,47]. To further take advantage of the block-sparsity, we propose the block-sparse set-membership PNLMS (BS-SMPNLMS) algorithm to obtain better convergence behavior and a lower level of misadjustment. We introduce the norm into the cost function, and then the optimization problem turns to
Using the Lagrange multiplier, we can get the cost function of the devised BS-SMPNLMS algorithm
where
Herein, B is the number of blocks which can be described as , and L denotes the size of each block. Take derivative of Equation (14) , we can get
For the k th coefficient which belongs to the t th block, there is
Let
and
Then, we will get
and
Left multiply in Equation (19), and we can get
Then left multiply in the Equation (21),
Equation (20) can also described as
Therefore, we can get
The updating function is
where is a positive constant whose value is very small, and it is used to avoid the denominator being zero. The in (28) is the same as that in (11). Herein, the step size assignment matrix is described as
where
and
The parameter in Equation (29) denotes the row vector with L length and all of its elements are ones. In order to expand the BS-SMPNLMS to make it more useful for the dispersive application field, we propose an improved BS-SMPNLMS (BS-SMIPNLMS) algorithm. The relationship between the BS-SMPNLMS and the BS-SMIPNLMS is similar to that between the PNLMS and the IPNLMS. Hence, the updating equation of the BS-SMIPNLMS is the same as that of the BS-SMPNLMS. Equation (30) in the BS-SMIPNLMS is replaced by
From the updating function, we can conclude the computations in the two proposed algorithms. Because of inserting the SM principle, the total numbers of additions of the BS-SMPNLMS and BS-SMIPNLMS are less than and . The total numbers of multiplications are less than and . The total numbers of divisions of the two algorithms are less than 2. The number of comparison of the BS-SMPNLMS is . Besides, both of the algorithms need a B square root.
4. Simulation and Result Analysis
In this section, four experiments are constructed to verify the performances of the devised BS-SMPNLMS and BS-SMIPNLMS algorithms. All of the experiments are created with white Gaussian noise (WGN), colored noise, and a speech signal as input signals, respectively. Herein, we assume that the signal-to-noise ratio (SNR) is 30 dB. The colored noise is generated from the WGN with a pole at 0.8. The sampling frequency of the speech signal is 8 KHz. In the first and second experiments, the influences of the block size on the BS-SMPNLMS and BS-SMIPNLMS are investigated. In the third experiment, the performances of the BS-SMPNLMS and the BS-SMIPNLMS are compared with other related algorithms. In the fourth experiment, the upper bound of estimation error is investigated in detail, which is the key parameter of the BS-SMPNLMS and BS-SMIPNLMS algorithms.
Experiment 1. In this experiment, the estimation behaviors of the BS-SMPNLMS with different block sizes are studied. The response length of the block-sparse channel is assumed to be 1024. The single-clustering response as shown in Figure 1b is located at [257,288] which has 32 taps, while the two-clustering response as shown in Figure 1c is located at [257,272] and [769,800] which has 16 and 32 taps [26]. The performances of the BS-SMPNLMS for WGN, colored noise, and the speech signal with different block sizes of 4, 16, 32, and 64 are shown in Figure 2, Figure 3 and Figure 4, respectively. Each figure is divided into two parts. The first half of the 80,000 sample shows the performance of single-clustering, while the second half of the 80,000 sample shows the performance of two-clustering.
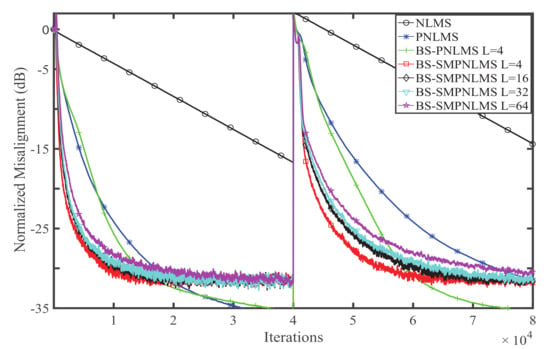
Figure 2.
Influence of block size on the BS-SMPNLMS for WGN. NLMS: normalized least mean square; PNLMS: proportionate NLMS; BS-PNLMS: block-sparse PNLMS; BS-SMPLMS: block-sparse set-membership PLMS; WGN: white Gaussian noise.
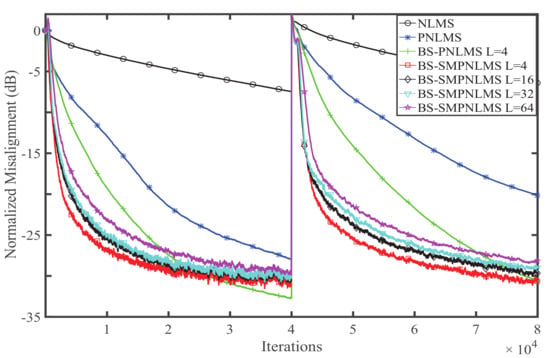
Figure 3.
Influence of block size on the BS-SMPNLMS for colored noise.
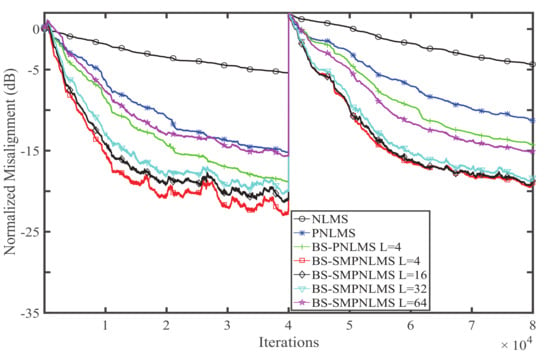
Figure 4.
Influence of block size on the BS-SMPNLMS for the speech signal.
The normalized misalignment is used to evaluate the estimating performance, and each simulation is repeated 10 times to get an average value. The simulation parameters are set as follows: when the input is the speech signal, the step sizes of the NLMS, PNLMS, and BS-PNLMS are . When the input is colored noise, all of the step sizes of the algorithms above are 0.1. When the input is WGN, all the step sizes of the algorithms are . The small positive constants of the NLMS, PNLMS, BS-PNLMS, and BS-SMPNLMS are . The parameters of the PNLMS, BS-PNLMS, and BS-SMPNLMS are , . The bound of the BS-SMPNLMS is .
From the simulation results we can see that independent of single-clustering or two-clustering, the BS-SMPNLMS with behaves best, with the smallest block size among the four cases. On the contrary, the BS-SMPNLMS with behaves the worst. The PNLMS and NLMS can be considered as the BS-PNLMS with and . Therefore, to obtain good estimation performance, the block size should be selected appropriately. Overall, the proposed BS-SMPNLMS algorithm with single-clustering performs better than that with two-clustering. The normalized misalignment of the colored noise input signal is smaller than that of the speech signal but larger than that of WGN. The convergence speed of the colored noise is faster than that of speech signal but slower than that of WGN.
Experiment 2. The estimation behaviors of the BS-SMIPNLMS with different block sizes are studied in this experiment. The simulation environment is almost the same as Experiment 1. The adjusted parameter of the IPNLMS, BS-IPNLMS, and BS-SMIPNLMS algorithms is . The performances of the BS-SMIPNLMS for WGN, colored noise, and the speech signal with the block sizes 4, 16, 32, and 64 are shown in Figure 5, Figure 6 and Figure 7, respectively.
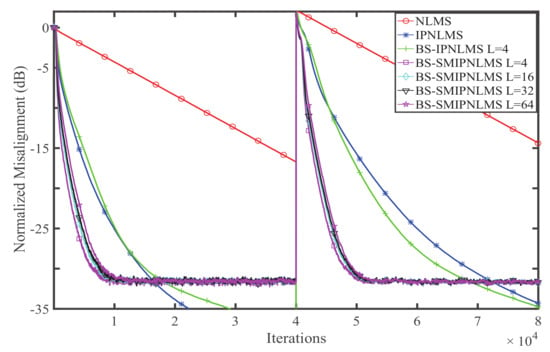
Figure 5.
Influence of block size on the BS-SMIPNLMS for WGN. IPNLMS: improved PNLMS; BS-SMIPNLMS: improved BS-SMPNLMS.
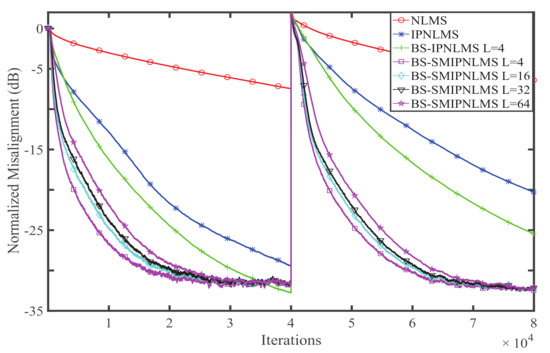
Figure 6.
Influence of block size on the BS-SMIPNLMS for colored noise.
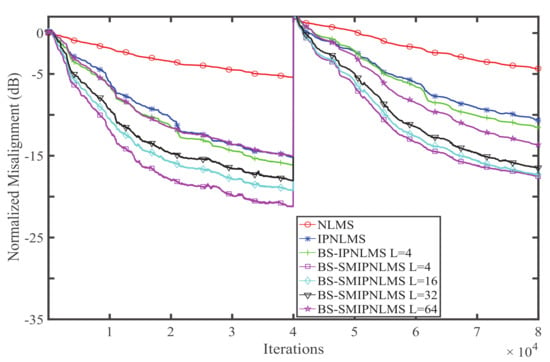
Figure 7.
Influence of block size on the BS-SMIPNLMS for the speech signal.
It is found that among the four situations of the block sizes 4, 16, 32, 64, the performance of the BS-SMIPNLMS with a block size of 4 is the best. The larger the block size is, the worse the algorithm behaves, with a trend is consistent with that of the BS-SMPNLMS.
Experiment 3. In this experiment, the performances of the BS-SMPNLMS and BS-SMIPNLMS algorithms are studied by comparison with the NLMS, PNLMS, IPNLMS, BS-PNLMS, and BS-IPNLMS algorithms. Herein, the block sizes are set to and . All the step sizes of the NLMS, PNLMS, IPNLMS, BS-PNLMS, and BS-IPNLMS algorithms are the same. The values are 0.05, 0.1, and 0.2 for WGN, colored noise, and the speech signal, respectively. The small positive constants of the NLMS, PNLMS, BS-PNLMS, and BS-SMPNLMS algorithms are , the parameters of the PNLMS, BS-PNLMS, and BS-SMPNLMS algorithms are , , and the bound of the BS-SMPNLMS algorithm is . The adjusted parameter of the IPNLMS, BS-IPNLMS, and BS-SMIPNLMS is . The results of the comparison with different input signals are shown in Figure 8, Figure 9 and Figure 10.
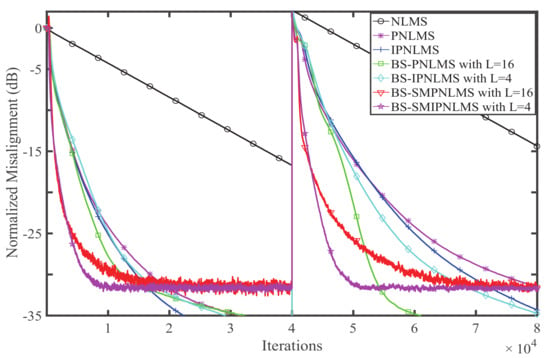
Figure 8.
Performance comparison of relevant algorithms for WGN.
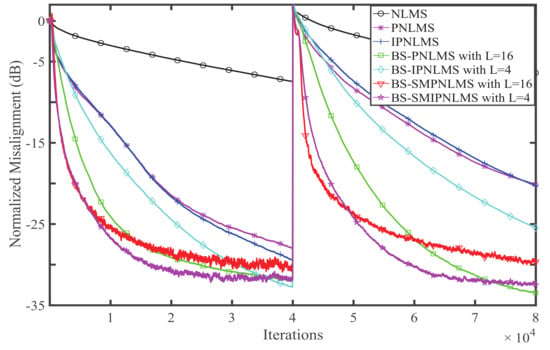
Figure 9.
Performance comparison of relevant algorithms for colored noise.
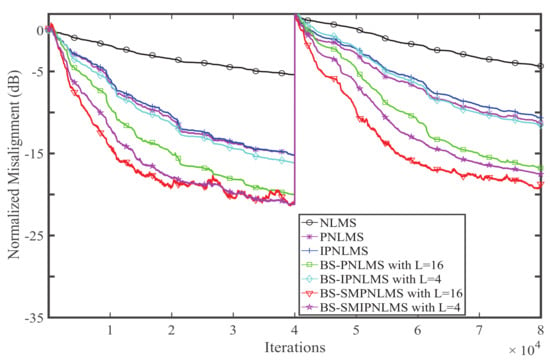
Figure 10.
Performance comparison of relevant algorithms for the speech signal.
It is observed that the devised BS-SMPNLMS and BS-SMIPNLMS algorithms behave better than the related algorithms. For the WGN input signal, the devised algorithms have a faster convergence rate. For the colored noise and the speech signal, the devised algorithms have both faster convergence and smaller misalignment.
Experiment 4. The parameter of the BS-SMPNLMS and BS-SMIPNLMS is a key parameter which can affect the convergence rate and the normalized misalignment. In this experiment, we study the performances of the BS-SMPNLMS and BS-SMIPNLMS algorithms, with . The effects of on the BS-SMPNLMS and BS-SMIPNLMS algorithms are presented in Figure 11 and Figure 12, respectively. Herein, we assume the input is the speech signal, and the . Other parameters are set as follows: block size , , , , .
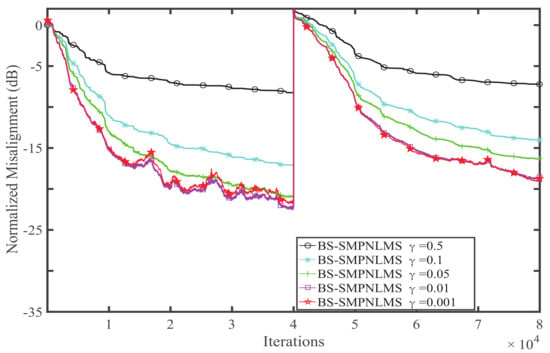
Figure 11.
Effects of on the BS-SMPNLMS algorithm.
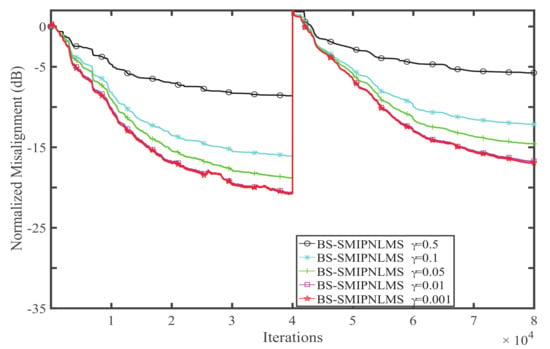
Figure 12.
Effects of on the BS-SMIPNLMS algorithm.
We find that when decreases from to , the normalized misalignment is reduced. However, the normalized misalignment stops decreasing when because the performances of and are almost the same. In previous experiments, we choose as the value of .
5. Conclusions
In this paper, two improved block-sparse SM-PNLMS algorithms for a block-sparse system have been proposed. The BS-SMPNLMS and BS-SMIPNLMS algorithms have been derived and their performances investigated and analyzed in detail with various inputs such as WGN, colored noise, and a speech signal . The simulation results showed that the BS-SMPNLMS behaves better than the traditional algorithms for both the single-clustering and two-clustering block-sparse systems. Besides, the influence of the key parameter of the BS-SMPNLMS algorithm was also studied.
Acknowledgments
This research is partly supported by the National Key Research and Development Program of China (2016YFE0111100), the National Science Foundation of China (61571149), the Science and Technology Innovative Talents Foundation of Harbin (2016RAXXJ044), the Opening Fund of Acoustics Science and Technology Laboratory (SSKF2016001), the Thirteenth Five-Year Plan (3020905030102), the Key Research and Development Program of Heilongjiang Province (GX17A016), the China Postdoctoral Science Foundation (2017M620918), the Natural Science Foundation of Beijing (4182077), the Natural Science Foundation of Heilongjiang Province (F2015026, JJ2018QN0420), the Science Research Project of Heilongjiang Provincial Education Department (12541877), and the Science and Technology Project of Qiqihar (GYGG-201301).
Author Contributions
Zhan Jin did the simulations and wrote the draft. Yingsong Li provided the idea of the BS-SMPNLMS and BS-SMIPNLMS algorithms. Jianming Liu checked the code and simulations. This paper was finished by all the authors together.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Benesty, J.; Gaensler, T.; Morgan, D.R.; Sondhi, M.M.; Gay, S.L. Advances in Network and Acoustic Echo Cancellation; Springer: Berlin, Germany, 2001. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 4th ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Diniz, P.S.R. Adaptive Filtering: Algorithms and Practical Implementation, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley-IEEE: New York, NY, USA, 2003. [Google Scholar]
- Digital Network Echo Cancellers; ITU-T Recommendation G.168; International Telecommunication Union: Geneva, Switzerland, 2009.
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptition in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Gu, Y.; Jin, J.; Mei, S. l0 norm constraint LMS algorithms for sparse system identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar]
- Deng, H.; Doroslova, M. Improved convergence of the PNLMS algorithm for sparse impluse response identification. IEEE Signal Process. Lett. 2005, 12, 181–184. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z.; Wang, Y. Adaptive channel estimation based on an improved norm constrained set-membership normalized least mean square algorithm. Wirel. Commun. Mobile Comput. 2017, 2017, 8056126. [Google Scholar] [CrossRef]
- Gui, G.; Mehbodniya, A.; Adachi, F. Least mean square/fourth algorithm for adaptive sparse channel estimation. In Proceedings of the 24th IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 296–300. [Google Scholar]
- Gui, G.; Peng, W.; Adachi, F. Sparse least mean fourth algorithm for adaptive channel estimation in low signal-to-noise ratio region. Int. J. Commun. Syst. 2014, 27, 3147–3157. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse channel estimation based on a p-norm-like constrained least mean fourth algorithm. In Proceedings of the 7th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–4. [Google Scholar]
- Li, Y.; Hamamura, M. Zero-attracting variable-step-size least mean square algorithms for adaptive sparse channel estimation. Int. J. Adapt. Control Signal Process. 2015, 29, 1189–1206. [Google Scholar] [CrossRef]
- Li, Y.; Hamamura, M. An improved proportionate normalized least-mean-square algorithm for broadband multipath channel estimation. Sci. World J. 2014, 2014, 572969. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Yang, R. Sparse adaptive channel estimation based on mixed controlled l2 and lp-norm error criterion. J. Frankl. Inst. 2017, 354, 1–25. [Google Scholar] [CrossRef]
- Gay, S.L. An efficient, fast converging adaptive filter for network echo cancellation. In Proceedings of the Conference Record of the Thirty-Second Asilomar Conference on Signals, Systems Computers, Pacific Grove, CA, USA, 1–4 November 1998. [Google Scholar]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. An improved proportionate NLMS algorithm based on the l0 norm. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010. [Google Scholar]
- Dong, Y.; Zhao, H. A new proportionate normalized least mean square algorithm for high measurement noise. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015. [Google Scholar]
- Liu, J.; Grant, S.L. A generalized proportionate adaptive algorithm based on convex optimization. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014. [Google Scholar]
- Jiang, S.; Gu, Y. Block-Sparsity-Induced Adaptive Filter for Multi-Clustering System Identification. IEEE Trans. Signal Process. 2014, 63, 5318–5330. [Google Scholar] [CrossRef]
- Loganathan, P.; Habets, E.A.P.; Naylor, P.A. A partitioned block proportionate adaptive algorithm for acoustic echo cancellation. In Proceedings of the Asia-Pacific Signal and Information Processing Association, Singapore, 14–17 December 2010. [Google Scholar]
- De Souza, F.D.C.; Tobias, O.J.; Seara, R. A PNLMS algorithm with individual activation factors. IEEE Trans. Signal Process. 2010, 58, 2036–2047. [Google Scholar] [CrossRef]
- Cui, J.; Naylor, P.; Brown, D. An improved IPNLMS algorithm for echo cancellation in packet-switched networks. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004. [Google Scholar]
- Liu, J.; Grant, S.L. Proportionate Adaptive Filtering for Block-Sparse System Identification. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 24, 623–630. [Google Scholar] [CrossRef]
- Liu, J.; Grant, S.L. Proportionate affine projection algorithms for block-sparse system identification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Liu, J.; Grant, S.L. Block sparse memory improved proportionate affine projection sign algorithm. Electron. Lett. 2015, 51, 2001–2003. [Google Scholar] [CrossRef]
- Combettes, P.L. The foundations of set theoretic estimation. Proc. IEEE 1993, 81, 182–208. [Google Scholar] [CrossRef]
- Nagaraj, S.; Gollamudi, S.; Kapoor, S.; Huang, Y.F. An adaptive set-membership filtering technique with sparse updates. IEEE Trans. Signal Process. 1999, 47, 2928–2941. [Google Scholar] [CrossRef]
- Werner, S.; Diniz, P.S.R. Set-membership affine projection algorithm. IEEE Signal Process. Lett. 2001, 8, 231–235. [Google Scholar] [CrossRef]
- Gollamudi, S.; Nagaraj, S.; Huang, Y.F. Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size. IEEE Signal Process. Lett. 1998, 5, 111–114. [Google Scholar] [CrossRef]
- Lin, T.M.; Nayeri, M.; Deller, J.R., Jr. Consistently convergent OBE algorithm with automatic selection of error bounds. Int. J. Adapt. Control Signal Process. 1998, 12, 302–324. [Google Scholar] [CrossRef]
- Gollamudi, S.; Nagaraj, S.; Huang, Y.F. Blind equalization with a deterministic constant modulus cost-a set-membership filtering approach. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000. [Google Scholar]
- Diniz, P.S.R. Adaptive Filtering: Algorithms and Practical Implementations, 2nd ed.; Kluwer: Boston, MA, USA, 2002. [Google Scholar]
- De Lamare, R.C.; Sampaio-Neto, R. Adaptive reduced-rank MMSE filtering with interpolated FIR filters and adaptive interpolators. IEEE Signal Process. Lett. 2005, 12, 177–180. [Google Scholar] [CrossRef]
- De Lamare, R.C.; Diniz, P.S.R. Set-membership adaptive algorithms based on time-vary error bounds for CDMA interference suppression. IEEE Trans. Veh. Technol. 2009, 58, 644–654. [Google Scholar] [CrossRef]
- Bhotto, M.Z.A.; Antoniou, A. Robust set-membership affine projection adaptive-filtering algorithm. IEEE Trans. Signal Process. 2012, 60, 73–81. [Google Scholar] [CrossRef]
- Clarke, P.; de Lamare, R.C. Low-complexity reduced-rank linear interference suppression based on set-membership joint iterative optimization for DS-CDMA systems. IEEE Trans. Veh. Technol. 2011, 60, 4324–4337. [Google Scholar] [CrossRef]
- Cai, Y.; de Lamare, R.C. Set-membership adaptive constant modulus beamforming based on generalized sidelobe cancellation with dynamic bounds. In Proceedings of the 10th International Symposium on Wireless Communication Systems, Berlin, German, 9–13 December 2013. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Sparse SM-NLMS algorithm based on correntropy criterion. IET Electron. Lett. 2016, 52, 1461–1463. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Mishali, M. Robust Recovery of Signals From a Structured Union of Subspaces. IEEE Trans. Inf. Theory 2009, 55, 5302–5316. [Google Scholar] [CrossRef]
- Stojnic, M.; Parvaresh, F.; Hassibi, B. On the Reconstruction of Block-Sparse Signals With an Optimal Number of Measurements. IEEE Trans. Signal Process. 2009, 57, 3075–3085. [Google Scholar] [CrossRef]
- Stojnic, M. l2/l1-Optimization in Block-Sparse Compressed Sensing and Its Strong Thresholds. IEEE J. Sel. Top. Signal Process. 2010, 4, 3025–3028. [Google Scholar]
- Liu, J.; Jin, J.; Gu, Y. Efficient Recovery of Block Sparse Signals via Zero-point Attracting Projection. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012. [Google Scholar]
- Elhamifar, E.; Vidal, R. Block-Sparse Recovery via Convex Optimization. IEEE Trans. Signal Process. 2012, 60, 4094–4107. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).