Abstract
This review deals with ideas and approaches to nonlinear phenomena, based on different branches of physics and related to biological systems, that focus on how small impacts can significantly change the state of the system at large spatial scales. This problem is very extensive, and it cannot be fully resolved in this paper. Instead, some selected physical effects are briefly reviewed. We consider sine-Gordon solitons and nonlinear Schrodinger solitons in some models of DNA as examples of self-organization at the molecular level, as well as examine features of their formation and dynamics under the influence of external influences. In addition, the formation of patterns in the generalized Fisher–KPP model is viewed as a simple example of self-organization in a system with nonlocal interaction at the cellular level. Symmetries of model equations are employed to analyze the considered nonlinear phenomena. In this context the possible relations between phenomena considered and released activity effect, which is assessed differently in the literature, are discussed.
1. Introduction
Interdisciplinary analysis of known phenomena and patterns in light of the emergence of new facts and challenges requires a deeper understanding of the basics of the studied field of science and its relationship with other fields. The introduction of new view points on known facts and new concepts sets new tasks that expand our understanding of the nature of phenomena, which, in turn, opens up new prospects for the development of technologies.
The intellectual component of any technology is a controlled process in which external controlled impacts are assumed to be small in comparison with the main (target) process. Generally speaking, in relatively simple linear systems, the relationship between its various components is proportional, in particular, in controlled systems, such is the connection between controlled process and the target process.
In nonlinear systems, the situation is fundamentally different. Possible relationships between the interacting parts of such systems can be extremely diverse and, of course, far from proportional.
Such variety is particularly inherent in complex nonlinear systems, consisting of a large number of interacting subsystems. Such systems can have a hierarchy of organization complexity, which in turn causes a hierarchy of inherent regularities, in particular considering the response of the system to external control.
The term “self-organization” is applicable to such systems, i.e., the ordering of the elements of one level in the system through internal interactions without external specific impact, which causes the formation of the units of the next qualitative level in the system. In other words, the formation of internal structures (spatially stable or space-time (dynamic)) occurs due to nonlinear interactions between the elements of a complex system, or its subsystems of the same level of complexity. This problem is extremely extensive and complex, and we do not set out the task of highlighting it in any finished form.
Instead, we give a brief overview of some selected physical effects/situations that are presented below. The issues were selected rather according to the preferences of authors than on the grounds of a systematic viewpoint. The main attention was drawn to phenomena of spatial and spatio-temporal self-organization in systems of different complexity levels in order to demonstrate certain key mechanisms responsible for the emergence and existence of such structures or phenomena and some of their specific properties. The lifespan of the structures or phenomena may differ substantially, but no matter what, it is sufficient for research purposes and allows one to observe interactions as a whole among themselves or with other elements of the system.
Structure types and mechanisms for their formation depend on the physical nature of the nonlinear system and on the nature of interactions in it, as well as on the level of complexity of its organization. Nonlinear mechanisms of self-organization of a complex system can play a crucial role at lower complexity levels, creating substructures in the system, the interaction of which generates the further organization of the system at the next level.
From the physical point of view, self-organization phenomena in biological systems can be considered at three basic levels: the quantum level (based on quantum concepts and regularities), the molecular level (concepts and patterns of classical physics) and the population level that includes the pattern formation phenomena of interacting cellular populations. Nonlinear systems can be divided into local and nonlocal ones by types of interaction that define the structural properties of the systems. Among them are classical and quantum systems, deterministic and stochastic ones.
The laws of quantum physics and electromagnetism regulate the structure formation and functions of molecules [1] in living matter. Quantum mechanics is taking into account the stability of living systems and cellular processes within these systems by means of quantum properties of the stability of molecules and by the fact that quantum collective effects can have a significant impact on the state of the system [2].
In general, collective effects in nonlinear complex systems cause a weak distribution of random or regular effects on the entire system, for example the Casimir effect in quantum systems (e.g., [3,4,5]) and the quantum Hall effect. Soliton phenomena in relatively simple nonlinear systems serve as an example of self-organization in a simple nonlinear system with local nonlinear interaction at the molecular level. The formation of structures (patterns) in reaction-diffusion systems provides similar results at the cellular level.
Here, we focus on sine-Gordon solitons and nonlinear Schrodinger solitons in some models of DNA as examples of self-organization at the molecular level, as well as features of their formation and dynamics under the influence of external influences. Besides, we discuss pattern formation in the well-known generalized Fisher–Kolmogorov–Petrovskii–Piskunov (Fisher–KPP) model as a simple example of self-organization in a system with nonlocal interaction at the cellular and population levels. Note that the mathematical background in the study of these models involves the ideas and approaches of the symmetry analysis of the equations from physics and biophysics. In this context, solitons are important examples of solutions endowed with symmetry properties, and to explore the generalized Fisher–KPP model equation, we apply the semiclassical approximation approach, which also incorporates the methods of symmetry analysis of model equations.
2. Soliton Excitations in Molecular Chains
2.1. The Concept of Solitons in Molecules
We discuss some characteristic features inherent in nonlinearities that can be associated with complexity and self-organization in biosystems at the biomolecular level in the context of systems biology [6].
Many biological functions are performed by a complex of biological macromolecules or clusters of molecules that are regarded as biological machines that consist of basic molecular units [7], which include proteins, nucleic acids, carbohydrates, lipids and several complexes of them. The macromolecular structure and its functions are characterized by a dynamic nature over wide time scales, and they depend on the signals detected by these bio-machines or on the output from these machines.
Small impacts on a single macromolecule can cause specific localized excitations that can propagate over the molecule and facilitate the information transfer through the macromolecule.
From a physical standpoint, we would like to pay attention to solitons and pattern formation as some of the most prospective and interesting approaches to the problems under consideration. In many publications on soliton topics in biology, solitons are regarded as one of the possible signal transduction pathways in bio-macromolecules according to the acknowledged works [8,9,10] and a great number of articles.
The concept of solitons in molecules had been initially suggested by an outstanding Soviet scientist, Alexander Davydov, in the 1980s [8,11] and has been developed by him and his school in cooperation with researches from different countries in numerous publications (e.g., [12,13,14] and the references therein).
Since then, soliton excitations in molecular chains have become the subject of intensive study and numerous applications in numerous articles (e.g., [9,15,16]).
Rotation soliton excitations in DNA have been investigated since the 1980s [17,18,19]. Yakushevich has given systematical and careful analysis of solitary conformational waves in DNA (see [10,20,21]).
Solitons in biological macromolecules could provide a possible mechanism for charge and energy transport during metabolism [22]. In recent papers, soliton models of charge transport in redox processes were suggested in order to facilitate our understanding of the origin of endogenous electromagnetic fields (EMF) and coherence and activation of the natural immune system [23,24,25].
In the next subsections, we will look in detail at how the dynamics of solitons can depend on external deterministic or random factors by examples of sine-Gordon (SG) and nonlinear Shcrodinger equation (NLSE) models [26,27,28,29] related to biomolecules, particularly models of DNA.
A great advantage of analytical methods is that they can provide a good insight into the relationship of solutions obtained and various parameters; we mainly use here analytical methods to consider the nonlinear models.
2.2. Kink Dynamics asExternal Factors for the Sine-Gordon DNA Model
Since the 1980s, many authors have discussed the question of whether the occurrence of conformational waves of the soliton type takes place in the DNA molecule (e.g., details can be found in [10,20,21]). We pay attention only to some of the points necessary to proceed to a survey of specific problems following [10,20].
The first was a paper by Englander et al. [17] in which a mechanical model of soliton excitations emerging in a double helix was proposed. Such excitations were recognized as a mechanism for conformational changes in condensed matter systems and in DNA in particular. For the first time, a nonlinear Hamiltonian of DNA dynamics that stimulated further research of soliton excitations in DNA was suggested. In a large number of subsequent articles, a significant contribution was made to the development of DNA study by promotion and analysis of new nonlinear equations of models and their soliton-like solutions; see, e.g., [18,19]. A detailed and careful survey of this period of the nonlinear DNA dynamics and a general description of different structural models of the internal nonlinear dynamics of the DNA molecule can be found in [10,20].
We are not going to compare these models in order to find the most efficient one; rather, we focus on the sine-Gordon (SG) model that describes the rotational motions of DNA bases following [26,27,28,29]. Such a type of model originally was suggested by Englander et al. [17], where an analogy between the dynamics of the DNA rotational degrees of freedom and the dynamics of a simple mechanical model of a chain of pendulums was used. Later on, the SG model applied to DNA was developed and improved in a number of papers. Yomosa [30,31] proposed a dynamic model where the conformation of DNA was determined by the energy of hydrogen bonds between interstrand complementary base pairs and the stacking energy between intrastrand adjacent bases. The Hamiltonian model includes these energy terms and the kinetic energy of the bases’ rotations. In the continuum limit, the discrete dynamic system of equations leads to a coupled SG-type model that describes the dynamics of the rotations of the DNA bases. Takeno and Homma [18,19] improved the plane base rotator model of Yomosa and obtained a nonlinear system of two coupled differential-difference equations, which, in a particular case, result in a discrete double SG equation. The discreetness allows one to consider base rotations in the plane orthogonal to the helical axis of the backbone structure. In particular cases, when the continuum limit can be used, this model admits kink-solitons propagating along the helical axis.
Peyrard and Bishop [15] studied the process of DNA denaturation in which only the transverse motion of bases along the hydrogen bond was taken into account.
Then, in [32,33,34,35,36] and in many later works, the improved nonlinear models were used to explain various properties of DNA dynamics, such as transcription regulation, DNA denaturation, protein synthesis and carcinogenesis.
To obtain the SG model equation for DNA, we consider an equation that describes rotational motions of a single isolated DNA base. The last one can be described as vibrations of a certain n-th pendulum (below, we follow the notations and the results of [26]):
where is the angle of deviation of the n-th pendulum from the equilibrium position, is the pendulum mass, is the pendulum length and g is the gravitational constant, . An equation of vibrations of a pendulum within a chain of interacting pendulums can be obtained by introducing two forces in Equation (1): affecting the pendulum from right and affecting the pendulum from left. Here, K is a parameter that characterizes the interaction between neighboring pendulums.
Now, we can rearrange Equation (1) by substituting and into (1) and multiplying each side of (1) by , then we obtain the following equation:
that is called the discrete sine-Gordon equation. To proceed to a continuous analog of this equation, we will assume that solutions vary noticeably only over distances that are much longer than the distance a between the nearest pendulums. We also introduce the z axis along which the pendulums are suspended, and the coordinates of the pendulums are written as , . As , the discrete variable is replaced by the continuous variable z. Passing to the limit in Equation (2), we come to the continuous analog of (2):
where R and m are taken to be constant. In more compact notations, Equation (3) takes the form of the SG equation:
where I is the moment of inertia of a pendulum, is the potential energy necessary to rotate a pendulum to a height of R and characterizes the rigidity of the horizontal force f. By analogy with the chain model of the pendulums and the DNA molecule, following [17], we can assume that Equation (4) describes the rotational dynamics of DNA bases where the parameters I, and V should be interpreted as follows. The parameter I is a moment of inertia of a base; V is the energy required to break the hydrogen bond within the pair; is a constant that characterizes the rigidity of the sugar-phosphate backbone; and Å is the distance between the nearest bases in DNA. The detailed analysis and estimate of the parameters I, and V for DNA can be found, for example, in [10,26].
The sine-Gordon Equation (4) can be integrated in the framework of the inverse scattering transform (IST) method in the class of functions with spatial derivatives decreasing at infinity as (see [37,38]). The SG Equation (4) possesses exact N-soliton solutions in this class of functions. Among them, the single-soliton solution (kink) is of particular interest, since such a solution is usually interpreted as a nonlinear conformation wave propagating along the DNA molecule [10]. A kink solution of Equation (4) has the following form:
Here, is the relative kink velocity, is the kink velocity and is interpreted as sound velocity corresponding to linear wave Equation (4) for , is the initial kink coordinate.
To explore the impact of external factors on the kink dynamics, we introduce a modified Equation (4) using perturbation terms following [27,28]:
Here, is a coefficient of dissipation, and the moment of an external force (below, we use the term force) is described by a function , time-dependent in the general case. The function is assumed to be bounded in time,
where is an amplitude of the external force.
From a physical point of view, the main effects of these perturbation terms on soliton dynamics are the emergence of a temporal dependence in the soliton parameters and the excitation of small amplitude-extended oscillations called phonons [39].
When the interaction between solitons and phonons is negligible, it can be assumed that the impact of small perturbations can be taken into account in the form of temporal dependence in the soliton parameters, while the soliton shape remains unchanged. This assumption is the foundation of the collective coordinates (CCs) method (see [29,40] and the references therein).
Note that the CCs method to some extent uses the concept of similarity solutions, known in symmetry analysis (see the well-known guides on symmetry analysis [41,42,43,44]) in the sense that the soliton solution taken as the CCs ansatz for perturbed SG equation or NLSE is a group invariant solution of the unperturbed equation. In addition, from a wider view on the use of symmetries in the study of DNA, the concept of chirality also could be of interest [45].
The idea of the CCs method was also used in earlier works. Thus, in the perturbative methods of McLaughlin and Scott and Fogel et al. [46,47,48], collective variables or coordinates, allowing the position and/or other soliton parameters to evolve in time, were used.
The energy analysis [46,47,48] for the sine-Gordon equation is used to study the evolution of kink velocity that is modeling the propagation of a local conformational perturbation along the DNA molecule under the simultaneous action of dissipation effects and special nonstationary external fields (we follow [27] and the references therein).
The Hamiltonian of the SG Equation (4) is a functional depending on a function :
Here and below, we use the notation . Substituting soliton (5) in (8), we get (for example, see [46]):
Here, is the variational derivative of with respect to . Substitution of kink Expression (5) into Equation (10) gives:
Assuming now that in the presence of external nonstationary force and the dissipation effect, the kink velocity v depends on time , we differentiate Equation (9) with respect to time . As a result, with the use of (11), the required equation for the kink velocity is:
Let us rewrite Equation (12) in a dimensionless form. Considering condition (7), we represent the function as:
where the dimensionless time-dependent function is normalized by the condition .
Let us introduce the dimensionless time , where the constant for DNA has an order of [27], and the dimensionless parameter is of the order of in this case. In these notations Equation (12) and (13) in the dimensionless form is:
The general solution of Equation (14) was obtained in [27] in an explicit analytical form. This allows one to explore quite simply and comprehensively the influence of external forces of various forms on the kink dynamics under the assumption that the kink conserves its shape in the course of motion, but its velocity changes under the influence of external factors. According to [27], the solution of Equation (14) with an arbitrary initial velocity reads as follows:
where .
To illustrate the potentialities of the above approach, we will consider the evolution of relative kink velocity under the simultaneous effect of dissipation () and harmonic external force of the form:
Here, is the dimensionless cyclic frequency. From (16) and (15), we can directly obtain the relative kink velocity as follows:
Equation (17) shows that oscillates in a range about the trend curve determined by the following expression:
It can be seen that exponentially decreases and asymptotically tends to zero as , whereas given by Equation (18) transforms into the asymptotic expression:
A graphical illustration of (17) and (18) is shown in Figure 1a,b for . For and , the kink motion is characterized by oscillations of about the mean position (the solid curve in Figure 1), which tends monotonically to a constant with an increase in , whereas the trend velocity tends to zero (the dashed curve in Figure 1). The periodic acceleration and deceleration of kink motion against the background of the general deceleration tendency corresponds qualitatively to the periodic action of the external force and dissipation.
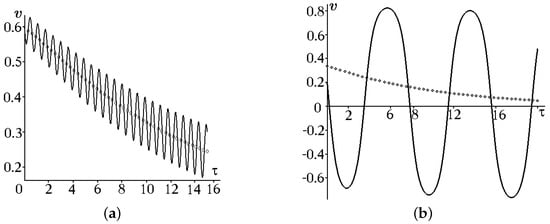
Figure 1.
Relative kink velocity (the solid curve) and the trend velocity (the open diamonds curve) for : (a) , and ; (b) , .
The evolution of the average relative kink velocity over the period on the time interval can be determined by the expression:
A time dependence of the average relative velocity obtained numerically with the use of Equations (17) and (20) is depicted in Figure 2. The graph in this figure shows that the trend velocity and the relative kink velocity averaged over the examined period coincide for different time intervals. Thus, Formula (20) can serve as an analytical expression for the relative kink velocity averaged over the examined period.
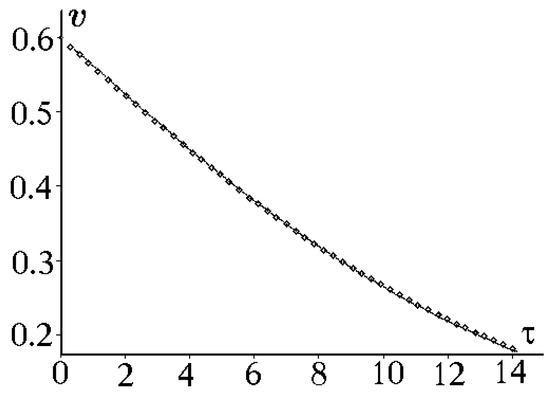
Figure 2.
Trend velocity (the dotted curve) and the average relative velocity (the open diamonds curve) for , and .
Further and above-mentioned analysis of the relative kink velocity evolution under simultaneous influence of the dissipation and external forces of different types can be found in [27].
Summing up, we can state that Expression (15) for the kink velocity essentially simplifies the investigation of the kink dynamics under the simultaneous effect of dissipation and time-dependent external force with different forms of time dependences of interest in physics.
For example, for a harmonic time-dependent external force, the kink velocity is characterized by oscillations about a rather monotonically-decreasing trend given by Equation (18). In addition, the use of Expression (15) allows us to set the task of controlling the kink dynamics by means of a suitable choice of the parameters of external forces.
The above approach, based on the collective variables [40,46,47,48] with the McLaughlin and Scott energetic method [46] and the evolution of the relative kink speed (15) also allows one to investigate the joint effect of dissipation, the external deterministic forces and a random force on the kink dynamics. We briefly review basic ideas and results following [28]. To do this, we write SG Equation (6) with additional terms in the dimensionless form as:
where , is the dissipation coefficient, is the nonstationary regular external force, is the diffusion coefficient and the random force is assumed to be the Gaussian white noise with mean value and correlation .
Here, v is the kink velocity, and characterizes the initial position of the kink. The Hamiltonian (8) is:
From Equations (22) and (23), we obtain the kink energy (9) as . Then, by analogy with (9)–(12), we derive the equation for the kink velocity :
where:
In what follows, we redesignate as t for simplicity and replace the variable according to the formula . Then, Equation (24) takes the form:
The variable is related to the kink momentum P as follows: , .
We consider Equation (26) with a random force to be the stochastic differential equation of the Langevin type for motion of the Brownian particle in accordance with the Stratonovich formalism [49,50].
The Fokker–Planck equation for a probability density function in designations of [49] for Equation (26) is written in the form:
An exact solution of Equation (27) has been found in [28] as:
where , and a function satisfies the equation:
For the kink momentum , Equation (28) takes the form:
The average value of the kink momentum for distribution function (29) is found as:
The variance is given by the expression:
where . Equation (30) shows that has the meaning of the average kink momentum for . The average value becomes the solution of Equation (26) when the random force is zero, . This is in agreement with the above results obtained for Equation (14) of [27] where the kink dynamics under the action of external regular force was considered. It should also be noted that the variance given by Equation (31) depends on the diffusion coefficient and is independent of the regular external force .
Figure 3 illustrates the dependence of the kink momentum variance on time. The graph in Figure 4 is given for the case when the moment has a definite value at , i.e., .
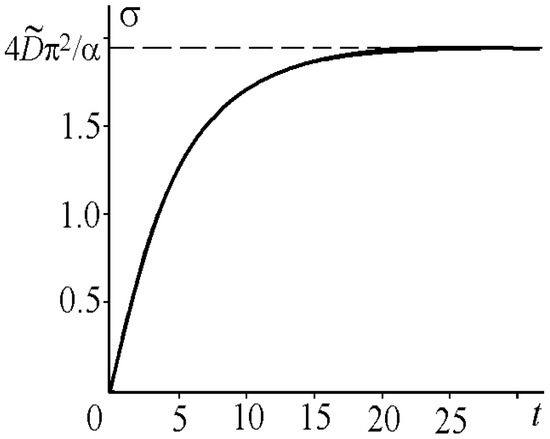
Figure 3.
Root-mean-square value of the kink momentum for , and .
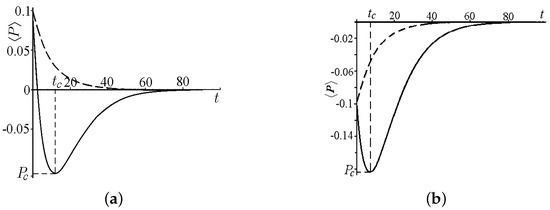
Figure 4.
Average value of the kink momentum for , , and . (a) The solid curve is for , ; the dashed curve is for , . (b) The solid curve is for , ; the dashed curve is for , .
The variance increases with time asymptotically approaching . Dependence (31) coincides with the results of numerical calculations presented in [51]. The kink root-mean-square velocity in the nonrelativistic limit ( and ) obtained from (29) for and takes the form:
that is also in agreement with the results presented in [48].
Consider now a model case of a non Markovian process in Equation (21) when the probability density function can be described by a nonlinear Fokker–Planck equation (NFPE) in accordance with [52]. Despite the discussion about the validity of Frank’s approach [52] and the NFPEs (for example, [53,54,55]), we, nevertheless, present here some features of such a stochastic process as a phenomenological model following [28].
Consider a nonlinear Fokker–Planck equation:
where is the nonlinearity parameter () and is the first moment of the function :
Let be an initial distribution, , for Equation (32), then the initial value of the first moment (33) is . From (32) and (33), we have , and consequently,
For the momentum , , the distribution function is:
The average value of the kink momentum and its variance, obtained with the help of distribution (36), have the following form:
From Formulas (37) and (38), we can obtain that the average value of the kink momentum depends both on the nonlinearity parameter and the diffusion coefficient , whereas the variance is determined by the diffusion coefficient and is independent of .
Consider the case when , which corresponds to the distribution with average value . In particular, , that is, at the initial time, the momentum has a fixed value. In this case, Expression (37) reads:
Equation (39) shows that stochasticity intensifies the dissipation. The average momentum decreases monotonically with the exponent , asymptotically vanishing.
Figure 4a,b illustrates how the nonlinearity in Equation (32) affects the evolution of the average kink momentum for (the dashed curve) and for (the solid curve). The case of is depicted in Figure 4a for and in Figure 4b for .
The evolution is determined by the first term of Equation (37) when . The average momentum decreases monotonically, asymptotically vanishing due to the dissipation () both for and for .
For , the evolution depends on both the dissipation and the random force (the second term in (37)).
The change in the momentum evolution (a rotation point) is observed at a critical time instant given by . At we have .
For , the average momentum monotonically decreases, asymptotically vanishing.
Analysis of Dependencies (37) and (38) shows that the kink dynamics under the influence of the random force with stochastic feedback has various peculiarities depending on the model parameters. This can be of interest from the viewpoint of controlling the kink dynamics by sequentially switching on and off the random force.
In addition, the above-indicated peculiarities of the kink dynamics may be important in the study of general laws of interaction between the stochasticity and nonlinearity.
2.3. Localized Energy Distributions in the Framework of The Peyrard–Bishop Model
Here, we briefly review the creation of stable localized structures in the form of localized energy distributions in the Peyrard–Bishop (PB) model [15] following [29]. We discuss the solutions of PB model equations obtained in the form of planar waves whose amplitudes are described by the nonlinear Schrodinger equation.
The processes of DNA melting and the formation of bubbles and localized structures play an important role in the functioning of DNA. Among the processes that have been described using bubbles and solitary waves are the binding of specific enzymes to DNA (e.g., DNA polymerases, recombinases, RNA polymerases), the thermal evolution of enzyme-created bubbles, and others. The concept of localized bubble-like structures that is used in explaining these phenomena sets the problem of the formation and stability of such structures. A detailed review of this problem can be found in [29]. We discuss here the problem of the creation process of soliton-like structures from localized initial conditions.
In the framework of the PB model and the helicoidal model proposed by Barbi et al. [56], it is possible to obtain the analytical expression for approximate solutions in the form of modulated plane waves called breathers, the amplitude of which is determined by the NLSE. When an initial amplitude corresponds to the one-soliton solution of NLSE, a planar wave with localized amplitude arises. This solitary wave has been proposed to be related to the transcription process of DNA. Then, the issue of whether or not solitons can arise spontaneously becomes relevant. This question was discussed in [29] in the framework of the PB model with the use of the inverse scattering transform method [37,38] for NLSE. Here, we consider how soliton-like states may arise in the BP model with the use of the IST method, which is a cornerstone in nonlinear mathematical physics. In particular, this method allows us to study and control the conditions of formation, the number and properties of localized structures that can arise from an initial condition significantly different from the solitary wave discussed above.
To introduce the equations of DNA dynamics, we note that the movement of the DNA bases can be divided into torsional, longitudinal and transversal displacements. These movements are not independent of each other; however, the time scale of the transversal movements is smaller than the others. Therefore, in an appropriate approximation, the transversal dynamics can be separated from others and studied by means of the PB model [15]. It is a one-dimensional model that describes the relative distance between each pair of complementary bases. The Hamiltonian function of this model can be written as:
Here, denotes the relative distance between bases divided by , T is the time variable, m is the base mass, is the rigidity of the harmonic potential of interaction between two bases of the same chain and is the potential of interaction between opposite bases representing the hydrogen bonds. For the PB model, is chosen as follows with parameters D and d. The evolution equations for the Hamiltonian (40) are:
where , V is a dimensionless parameter. After changing of variables:
the evolution Equations (41) become:
Equations (42) form a system of nonlinear ODEs, which cannot be solved exactly; thus, we will look for approximate localized solutions around the minimum of the potential . These solutions take the form of a modulated amplitude carrier wave:
where , a is the distance between bases. The frequency and the wave vector are related by:
From (42)–(44), we obtain the NLSE for the modulated amplitude of Equation (43) (see [29]):
where ; ; ; ; ; Q is a parameter (for details, see [29]).
To study the localization of energy in the PB model, we should analyze the NLSE and look for solutions, for which at least a part of the initial energy is stored in permanent localized structures. Thus, we will look for modulated waves with localized amplitudes.
According to the IST method [37], the solution of Equation (47) can be presented as a sum of localized and quite robust solitary waves and radiation in a class of functions that decrease at infinity.
The eigenvalue problem:
for an initial function and auxiliary functions , says that the number of eigenvalues of the discrete spectrum, , is equal to the number of solitary waves that will be created from the initial condition in the course of evolution according to (45).
The velocity of the n-th soliton is proportional to the real part of the corresponding eigenvalue, , and its amplitude and width are related to the imaginary part, . If the initial condition makes the reflection coefficient of the eigenvalue problem (48) be null, then the solution of (47) is formed only by solitons without any radiation. This means that there are solutions of Equation (45) in which the modulated amplitude of Equation (43) is localized. Then, all the models described by the Hamiltonian (40), that meet (46), can support wave solutions with a localized modulated amplitude. It allows localized concentrations of energy.
From the IST point of view, the robustness of the energy localization in the PB model means that if is not a reflectionless potential in the eigenvalue problem (48), the solutions are not, strictly speaking, solitons because the radiation is present in the system, but they possesses soliton-like features. Then, the next question arises: whether or not permanent localized structures will emerge in these cases. Rigorous results [37] show that all solutions can be decomposed into soliton-like solutions and radiation. In other words, given a non-soliton initial condition, the system can group some of the energy in soliton-like structures, while the rest of the energy is spread in the form of radiation. Then, after a transient time, we will again have a localization of energy in the system.
Consider an example of an initial condition, , that enables us to solve analytically the eigenvalue problem (48) and, therefore, control the localized structures that emerge during the system evolution. As an illustration, we take one of such functions, namely the square initial condition. For more details, refer to [29].
As an illustration, we consider an example of an initial condition, , in the form of a square function, that enables us to solve the eigenvalue problem analytically (48) and, therefore, control the localized structures that emerge during the system evolution. Following [29], we take the initial condition, , as:
with the parameters , , c, g, and substitute it in (48), which now can be written, for , in the following way:
The solution of (50) is:
For and , we obtain:
Imposing the continuity in and , we find the following quantization condition for the eigenvalues:
To satisfy this equation, it is necessary that:
Then, the eigenvalues are pure imaginary numbers and are given by the roots of the transcendental equation:
where:
The number of eigenvalues can be obtained from (52):
We note that S must be greater than its threshold value to obtain localized solutions. For the values smaller than , all the initial energy will be spread in the form of radiation without any localization of energy [37]. The example considered shows that S plays the role of a control parameter, which is related to the area of the modulus of the initial amplitude, that rules the existence of soliton-like structures.
The initial conditions different from (49) were also considered in [29]. The direct numerical solutions to Equation (47) has been obtained in [29] to verify the above analytical results. The numerical data were found to agree well with the analytical results in the cases of the square and exponential initial conditions.
2.4. Summary
Summarizing, we emphasize that the models and their consequences discussed in this section can serve rather as reference points or suggestive considerations in the study of real complex systems in biology.
Although revealing the control parameter S in localized structure formation in the PB model is an important theoretical output, its role should be estimated while taking into account the influence of the external environment on the DNA dynamics. Indeed, the stability and lifetime of localized states are sensitive to the thermal fluctuations like viscosity and temperature.
As the DNA is in contact with a thermal bath in the cell, the dissipation and thermal forces may be substantial in its internal dynamics. The essential effect of a noise on the dynamics of soliton excitations in DNA can be seen from the results of Section 2.2 by example of the SG model. Thereby, the introduction of a thermal noise in the PB model may be of interest for studying the effect of thermal perturbations on the formation and dynamics of localized structures in the DNA molecule in the cellular environment.
In the PB model describing localized excitations in polynucleotide chains of DNA and RNA, the denaturation process of these molecules is considered where the transverse base motions (Section 2.3) are taken into account. The study of such processes is important for understanding of the functioning of living systems. The process of DNA denaturation changes its structure and functions; the bonds between nitrogenous bases are destroyed, which leads to disruption of cell metabolism and, as a consequence, to structural and functional changes in tissues.
In real conditions, a noticeable change of external environment, for example, an increase in temperature, the effect of strong acids, alkalis, etc., can lead to such processes.
Along with these factors, DNA denaturation is also possible under weak external influences; for example, it can be caused by a small increase in the pH of the medium.
We also note that under “smooth” denaturation scenarios, reversible processes of renaturation or reactivation are also possible. In this case, the denatured protein, after removing the damaging substances, again self-organizes into the original structure with the restoration of its biological activity. Such transformations affect the functions of the biosystem as a whole.
It can be assumed that effects of this kind arise due to selective effects of small concentrations of active substances on a DNA molecule. Some experimental studies indicate an effect of released activity (RA), implying that highly diluted active substances are capable of exerting modifying activity on their targets [57,58,59,60,61]. The physical mechanisms of RA are poorly studied, since small physical effects in highly diluted solutions are difficult to detect by physical and chemical methods, but lead to pronounced biological effects. In this connection, it is possible to propose a hypothesis that the physical basis of RA can be associated with changes in processes at all levels of self-organization, which can be described with the use of the proposed theory.
3. Pattern Formation in Cell Populations
At the cell level, self-organization phenomena in a biological system can manifest themselves in the form of collective behavior of individual cells due to their interactions that lead to the formation of coherent structures of multicellular ensembles in the course of cells’ growth.
When small effects on a biosystem can lead to its significant response at the cellular level, pattern formation processes in cell populations can act as possible mechanisms of such a response.
The theoretical description of pattern formation in biosystems involves the concept of reaction-diffusion (RD) systems (see, e.g., a recent review [62], as well as [63,64,65,66] and the references therein).
RD model equations and systems incorporating nonlocal interaction terms are of interest of the study. This often leads to situations when competition between individuals both within a single species and between individuals of different species (i.e., intra- and inter-species interactions) cannot realistically be treated as local. For example, individuals in a population may compete with each other for a resource that can redistribute itself, or they may communicate with each other by chemical means [67].
In studying the evolution of the cell population and its spatiotemporal features, the processes of reproduction, competition for resources and diffusion are significant, and others can be neglected, such as mutation.
The characteristic features of spatio-temporal structures formed in cellular populations with nonlocal interactions can be adequately modeled on the basis of generalizations of the well-known Fisher–Kolmogorov–Petrovskii–Piskunov equation. The Fisher–KPP equation has been introduced in [68,69]. For its nonlocal generalizations, see, e.g., [67,70,71,72,73].
It has been shown that the nonlocality of interaction in a population causes the formation of structures even in a one-species population that takes place in cell populations including cancer development processes, evolution of infectious diseases, etc. (see, e.g., the review papers and other issues [70,72,74,75,76] and the references therein).
In this section, we briefly review a theoretical approach developed in [73] for the nonlocal Fisher–KPP equation:
that allows one to construct approximate solutions to Equation (54) in analytical form. Here, is a population density, and it is a smooth scalar function in the spatial variable of n-dimensional space at each instant of time t. A constant parameter D in Equation (54) denotes the diffusion coefficient. Population grows as described by a rate function , and the nonlocal competition between individuals is controlled by the influence function with a range parameter .
The evolution of a one-species population governed by the (local) Fisher–KPP equation [68,69] does not lead to the formation of patterns, i.e., space ordered inhomogeneous structures. Nonlocal Fisher–KPP models like (54) take into account that competition for the resource can be long range. Compared to the (local) Fisher–KPP equation, in nonlocal models, pattern formation can arise due to nonlocal competitive losses and diffusion (e.g., [70,71,72,73] under a certain choice of parameters. This is quite different from the well-known Turing morphogenesis where the mechanism of pattern formation relies on the competition between the activator and the inhibitor [77,78].
The approach developed in [73] considers special patterns described by Equation (54). These patterns are concentrated on k-dimensional manifolds in the space of independent variables in Equation (54), . For simplicity, we will consider the manifolds defined as:
Here, s are the real variables, , parametrizing the manifold . The real vector depends on time t and on the parameters s and describes the evolution of the concentration manifold . It should be noted that the manifold contains significant information about the evolution of the pattern geometry. Therefore, we can essentially facilitate the study of these patterns focusing on their characteristics on the concentration manifolds.
For a relevant theory, we may state that the solution of Equation (54) generates a distribution on the manifold , which is defined in [73] as a semiclassically limited distribution (SLD), as , on the space . The SLD is governed by more simple evolution equations compared to the original Equation (54).
To deduce the corresponding evolution equations for the SLD, following [73], we introduce a class of functions depending on a parameter D and concentrated on a manifold . We also assume that functions are rapidly decreasing at infinity, as . For a smooth function , we define:
where is the zero moment of the function :
Assume that there exists a limit:
and denote:
Note that as has the meaning of population density, the functions and are non-negative.
Let us describe a connection between functions and . To do this, we introduce a coordinate system in the space of independent variables in Equation (54) such that , , and with the Jacobian . The variables are complement the variables s to form a coordinate system in . Choose the variables so that their coordinate lines are orthogonal to the manifold with respect to the Euclidean inner product in a tangent space. Under these conditions, we can find the relation connecting and in the form [73]:
Then, following [73], the equations describing the evolution of the SLD and of the vector characterizing the localization manifold of the form (55) can be obtained from definitions (56)–(60) and the nonlocal Fisher–KPP Equation (54) by a limiting process (as ):
and:
We note that the model Equation (54), for the purpose of simplicity, does not contain terms responsible for convection in the system. A more general case, which takes convection into account, was considered in [73], where Equation (62) is obtained to be more complex and describes the evolution of the vector under the influence of convection. From (55) and (62), it follows that the manifold does not change in time, , and (61) describes the SLD . To each solution of Equation (54) with an initial condition:
the corresponding initial conditions for (61) are:
In the general case, we refer to Equations (61), (62) as the Einstein–Ehrenfest (EE) dynamical system of type for where k means the dimension of the manifold and M is the highest order of the moments in the system [73].
Therefore, the study of the patterns described by Equation (54) in terms of the SLD on the manifold ( for Equation (54) without convection terms) is reduced to solving the EE system (61), (62) with the initial condition (63).
Consider a method for solving the Cauchy problem for Equation (61). Equation (62) yields:
and then, (61) gives:
The initial condition is:
Here,
Following [73], to solve the problem, we consider an auxiliary linear problem of finding the eigenfunctions and eigenvalues of a Fredholm equation with kernel (see, e.g., [79]):
where is a multi-index (). We assume that (68) is a Fredholm equation with symmetric kernel and its solutions form an orthogonal system:
where is the complex conjugate of .
Then, according to [73], the solution of Equation (65) with the initial condition (66) is obtained as:
Here, we use the notation:
To make our consideration of the pattern formation easier, we restrict ourselves to a one-dimensional manifold in two-dimensional coordinate space , and we look for solutions of Equation (54) in a class of functions concentrated in a neighborhood of a 1D curve in a space . As an illustration of the above theory, we consider an exact solution of Equation (65) whose coefficients (67) are:
and the concentration manifold of the form (55) is a circumference:
The eigenfunctions and eigenvalues of the Fredholm Equation (68) with the kernel (73) have the form: [73]
Here, ; is a modified Bessel function of the first kind. The functions constitute an orthogonal system of the form (69). Then, the kernel given by (73) and Equation (72) can be written as [73]:
where,
The functions satisfy the system:
In this case, (70) takes the form:
From (77), we directly obtain that satisfy the logistic equation:
where is a given constant. Therefore, the functions:
are solutions of System (75) with initial conditions:
and expanding by , we obtain:
where is found from (74). The solution of the Cauchy problems (79) has the form:
The solution given by (80) is spatially homogeneous and does not describe any pattern. Figure 5 displays the graph of the functions (solid line).
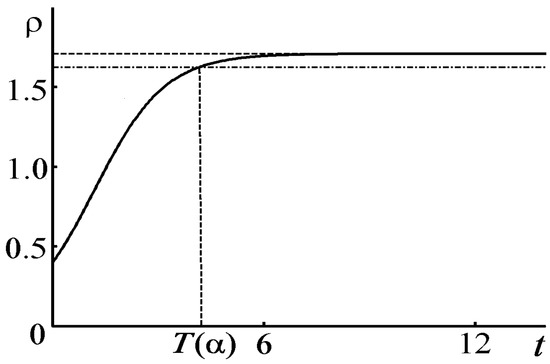
Figure 5.
Graph of the function for , .
The given example of the solution construction only illustrates the technique of finding analytical solutions within the framework of the developed approach. More complex approximate analytical solutions of the EE system (61), (62), which describes the evolution of nontrivial patterns localized on a circumference, can be found in [73]. A pattern is displayed in Figure 6.
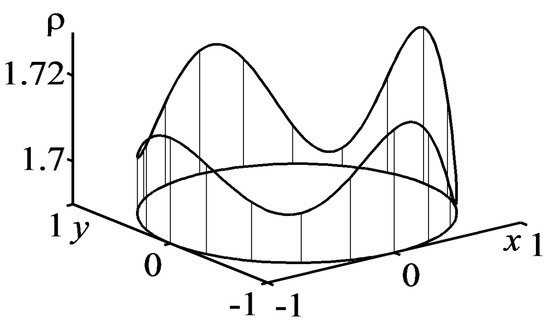
Figure 6.
Graph of the function on the manifold .
Summarizing, we note that the phenomenon of pattern formation in one-species populations was studied using a model, based on the generalized Fisher–KPP equation, taking into account nonlocal interaction effects caused by long-range interactions in the system.
We have considered a theory that describes the specific pattern formation when the patterns concentrated on a lower dimensional manifold in the space of independent variables in the nonlocal Fisher–KPP equation. To develop the theoretical approach, we adopt the ideas and technique of the semiclassical approximation method for the nonlocal Fisher–KPP equation. In this approach, we characterize the dynamics of pattern formation in terms of the SLD governed by the Einstein–Ehrenfest system, which is simpler compared to the original nonlocal Fisher–KPP Equation (54).
Despite the simplifications adopted in this approach, it enables us to obtain essential information about the characteristic features of the patterns by applying the methods developed for one-dimensional problems to multidimensional problems.
The considered nonlinear model of the cellular population dynamics with nonlocal interaction admits stationary states. In more complex and realistic nonlinear models, several similar steady-states are possible. For nonlinear systems with self-organization, a transition to one or another state under the influence of weak perturbations is characteristic, which can be caused by weak external influences.
As noted in Section 2.4 on the RA effect, the mechanisms behind the effect are little-studied. If we accept the hypothesis about the RA effect on the cell population dynamics, then one can explore the dependence between the change in the character of the population growth and the peculiarities of the corresponding small influences related to RA.
4. Conclusions
In this review, we have discussed some examples of collective effects known in nonlinear physics that manifest themselves in biosystems such as localized excitations in the DNA molecule and cell populations at different scale levels in the context of possible ways of propagation of weak random or regular effects on the entire system. This topic covers various phenomena at different levels of structural organization and functioning of the systems under study. We have only touched upon a problem that encompasses many different phenomena at different levels of structural organization and functioning of the systems.
Quantum aspects of the phenomena in biosystems are associated with decoherence and dephasing that are regarded to be a way of binding quantum and classical levels. Nontrivial quantum phenomena may occur in the presence of long-ranged, long-lived quantum states [1,2].
Although from the physical point of view it is natural to divide phenomena in the biosystem into the quantum, molecular and cellular levels, in a real complex system, collective interactions can bind different levels of their manifestations. In this connection, a number of phenomena discovered experimentally can be of interest as a means of construction of mathematical models. An example is the investigation of the RA, annotated in [57,58,59,60,61]. The physical basis of this phenomenon is currently not clear, and the specificity of the phenomenon needs further research both at the structural and functional levels.
The complexity of biosystems is studied from a number of perspectives. Systems can be embedded into other functional entities as components. Identifying a hierarchy of systems requires a certain level of abstraction, simplification and, as a result, modeling.
Large conformational changes in a biosystem can occur in the form of the motility of macromolecular domains or supramolecular clusters relative to each other facilitating catalysis or other forms of functionality in which the role of protein molecules may be quite significant.
The lack of structure in the solution may facilitate a function in which interactions must occur promiscuously with several other molecules. The dynamic structure of macromolecules enables rapid changes that impact the homeostasis of biochemical and molecular biological processes.
Acknowledgments
This work was supported by project Physical Aspects of Release Activity, Tomsk State Pedagogical University; by Tomsk State University under the International Competitiveness Improvement Program and by Tomsk Polytechnic University under the International Competitiveness Improvement Program.
Author Contributions
These authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arndt, M.; Juffmann, T.H.; Vedral, V. Quantum physics meets biology. HFSP J. 2009, 3, 386–400. [Google Scholar] [CrossRef] [PubMed]
- Fleming, G.R.; Scholes, G.D.; Cheng, Y.-C. Quantum effects in biology. Procedia Chem. 2011, 3, 38–57. [Google Scholar] [CrossRef]
- Milton, K.A.; Høye, J.S.; Brevik, I. The Reality of Casimir Friction. Symmetry 2016, 8, 29. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Romeo, A.; Bytsenko, A.A.; Zerbini, S. Zeta Regularization Techniques with Applications; World Scientific: Singapore, 1994; p. 319. [Google Scholar]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Fermionic condensate and Casimir densities in the presence of compact dimensions with applications to nanotubes. Phys. Rev. D 2011, 83, 105023. [Google Scholar] [CrossRef]
- Coveney, P.V.; Fowler, P.W. Modelling biological complexity: A physical scientist’s perspective. J. R. Soc. Interface 2005, 2, 267–280. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Opportunities in Biology; National Academy Press: Washington, DC, USA, 1989; p. 464. Available online: https://www.nap.edu/catalog/742/opportunities-in-biology (accessed on 9 February 2018).
- Davydov, A.S. Solitons in Molecular Systems; Naukova Dumka: Kiev, Ukraine, 1984; (Reprinted by Springer: Berlin/Heidelberg, Germany, 1985). [Google Scholar]
- Christiansen, P.L.; Scott, A.C. (Eds.) Davydov’s Soliton Revisited Self-Trapping of Vibrational Energy in Protein; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Yakushevich, L.V. Nonlinear Physics of DNA, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2004; p. 190. [Google Scholar]
- Davydov, A.S. The theory of contraction of proteins under their excitation. J. Theor. Biol. 1973, 38, 559–569. [Google Scholar] [CrossRef]
- Davydov, A.S. The lifetime of molecular (Davydov) solitons. J. Biol. Phys. 1991, 18, 111–125. [Google Scholar] [CrossRef]
- Brizhik, L.; Eremko, A.; Piette, B.; Zakrzewski, W. Solitons in alppha-helical proteins. Phys. Rev. E 2004, 70, 031914. [Google Scholar] [CrossRef] [PubMed]
- Brizhik, L. Nonlinear mechanism for weak photon emission from biosystems. Indian J. Exp. Biol. 2008, 46, 353–357. [Google Scholar] [PubMed]
- Peyrard, M.; Bishop, A.R. Statistical mechanics of a nonlinear model for DNA denatnration. Phys. Rev. Lett. 1989, 62, 2755–2758. [Google Scholar] [CrossRef] [PubMed]
- Scott, A. Davydov’s soliton. Phys. Rep. Rev. Sect. Phys. Lett. 1992, 217, 1–67. [Google Scholar] [CrossRef]
- Englander, S.W.; Kallenbach, N.R.; Heeger, A.J.; Krumhansl, J.A.; Litwin, S. Nature of the open state in long polynucleotide double helices: possibility of soliton excitations. Proc. Natl. Acad. Sci. USA 1980, 77, 7222–7226. [Google Scholar] [CrossRef] [PubMed]
- Takeno, S.; Homma, S. Topological solitons and modulated structure of bases in DNA double helices. Prog. Theor. Phys. 1983, 70, 308–311. [Google Scholar] [CrossRef]
- Takeno, S.; Homma, S. Self-localized anharmonic rotational modes of bases in DNA. J. Phys. Soc. 1990, 59, 1890–1901. [Google Scholar] [CrossRef]
- Yakushevich, L. Is DNA a nonlinear dynamical system where solitary conformational waves are possible? J. Biosci. 2001, 26, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Grinevich, A.A.; Yakushevich, L.V. On the modeling of the motion of a transcription bubble under constant torque. Biophysics 2016, 61, 539–546. [Google Scholar] [CrossRef]
- Musumeci, F.; Brizhik, L.S.; Ho, M. Energy and information transfer in biological systems: How physics could enrich biological understanding. In Proceedings of the International Workshop, Acireale, Catania, Italy, 18–22 September 2002; World Scientific: Singapore, 2003; p. 359. [Google Scholar]
- Brizhik, L. Influence of electromagnetic field on soliton-mediated charge transport in biological systems. Electromagn. Biol. Med. 2015, 34, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Brizhik, L.; Foletti, A. Nonlinear quantum phenomena and biophysical aspects of complexity related to health and disease. J. Biol. Regul. Homeost. Agents 2014, 28, 357–366. [Google Scholar] [PubMed]
- Foletti, A.; Brizhik, L. Nonlinearity, coherence and complexity: Biophysical aspects related to health and disease. Electromagn. Biol. Med. 2017, 36, 315–324. [Google Scholar] [CrossRef] [PubMed]
- Yakushevich, L.V.; Krasnobaeva, L.A.; Shapovalov, A.V.; Quintero, N.R. One- and two-soliton solutions of the sine-Gordon equation as applied to DNA. Biophysics 2005, 50, 404–409. [Google Scholar]
- Krasnobaeva, L.A.; Shapovalov, A.V. Kink velocity in nonstationary external fields for the sine-Gordon model with allowance for dissipation effects. Russ. Phys. J. 2008, 51, 89–98. [Google Scholar] [CrossRef]
- Krasnobaeva, L.A.; Shapovalov, A.V. Kink dynamics in the medium with a random force and dissipation in the sine-Gordon model. Russ. Phys. J. 2008, 51, 1–10. [Google Scholar] [CrossRef]
- Zamora-Sillero, E.; Shapovalov, A.V.; Esteban, F.J. Formation, control, and dynamics of N localized structures in the Peyrard–Bishop model. Phys. Rev. E 2007, 76, 066603. [Google Scholar] [CrossRef] [PubMed]
- Yomosa, S. Soliton excitations in deoxyribonucleic acid (DNA) double helices. Phys.Rev. A 1983, 27, 2120–2125. [Google Scholar] [CrossRef]
- Yomosa, S. Solitary excitations in deoxyribonuclei acid (DNA) double helices. Phys. Rev. A 1984, 30, 474–480. [Google Scholar] [CrossRef]
- Krumhansl, J.A.; Alexander, D.M. Nonlinear dynamics and conformational excitations in biomolecular materials. In Structure and Dynamics: Nucleic Acids and Proteins; Clementi, E., Sarma, R.H., Eds.; Adenine Press: New York, NY, USA, 1983; pp. 61–80. [Google Scholar]
- Krumhansl, J.A.; Wysin, G.M.; Alexander, D.M.; Garcia, A.; Lomdahl, P.S.; Layne, S.P. Further theoretical studies of nonlinear conformational motions in double-helix DNA. In Structure and Motion: Membranes, Nucleic Acids and Proteins; Clementi, E., Corongiu, G., Sarma, M.H., Sarma, R.H., Eds.; Adenine Press: New York, NY, USA, 1985; pp. 407–415. [Google Scholar]
- Fedyanin, V.K.; Yakushevich, L.V. Scattering of neutrons and light by DNA solitons. Stud. Biophys. 1984, 103, 171–178. [Google Scholar]
- Zhang, C.-T. Soliton excitations in deoxyribonucleic acid (DNA) double helices’. Phys. Rev. A 1987, 35, 886–891. [Google Scholar] [CrossRef]
- Prohofsky, E.W. Solitons hiding in DNA and their possible significance in RNA transcription. Phys. Rev. A 1988, 38, 1538–1541. [Google Scholar] [CrossRef]
- Novikov, S.; Manakov, S.V.; Pitaevskij, L.P.; Zakharov, V.E. Theory of Solitons. The Inverse Scattering Methods; Plenum Publishing Corporation: New York, NY, USA/London, UK, 1984; p. 276. [Google Scholar]
- Faddeev, L.D.; Takhtajan, L.A. Hamiltonian Methods in the Theory of Solitons; Springer Series in Soviet Mathematics; Springer: Berlin, Germay, 1987; p. 592. [Google Scholar]
- Kivshar, Y.S.; Malomed, B.A. Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 1989, 61, 763–915. [Google Scholar] [CrossRef]
- Sanchez, A.S.; Bishop, A.R. Collective coordinates and length-scale competition in spatially inhomogeneous soliton-bearing equations. SIAM Rev. 1998, 40, 579–615. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. Similarity Methods for Differential Equations; Series Title: Applied Mathematical Sciences, V. 13; Springer: New York, NY, USA, 1974; p. 333. [Google Scholar]
- Ovsyannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982; p. 432. [Google Scholar]
- Ibragimov, N.H. Transformation Groups Applied to Mathematical Physics; Soviet Series; Mathematics and its Applications; D. Reidel Publishing: Dordrecht, The Netherlands, 1985; p. 394. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Series Title: Graduate Texts in Mathematics, V. 107; Springer: New York, NY, USA, 1993; p. 513. [Google Scholar]
- Tverdislov, V.A. Chirality as an Instrument of Stratification of Hierarchical Systems in Animate and Inanimate Nature. arXiv, 2012; arXiv:1212.1677. [Google Scholar]
- McLaughlin, D.W.; Scott, A.C. Perturbation analysis of fluxon dynamics. Phys. Rev. A 1978, 18, 1652–1680. [Google Scholar] [CrossRef]
- Fogel, M.B.; Trullinger, S.E.; Bishop, A.R.; Krumhansl, J.A. Classical particlelike behavior of sine-Gordon solitons in scattering potentials and applied fields. Phys. Rev. Lett. 1976, 36, 1411–1414. [Google Scholar] [CrossRef]
- Fogel, M.B.; Trullinger, S.E.; Bishop, A.R.; Krumhansl, J.A. Dynamics of sine-Gordon solitons in the presence of perturbations. Phys. Rev. B 1976, 15, 1578–1592. [Google Scholar] [CrossRef]
- Stratonovich, R.L. Topics in the Theory of Random Noise; Gordon and Breach: New York, NY, USA, 1963. [Google Scholar]
- Gardiner, C. Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th ed.; Springer Series in Synergetics, Vol. 13; Springer: Berlin/Heidelberg, Germany, 2009; p. 447. [Google Scholar]
- Pascual, P.J.; Vazquez, L. Sine-Gordon solitons under weak stochastic perturbations. Phys. Rev. 1985, 322, 8305–8311. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker–Planck Equations. Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2005; p. 408. [Google Scholar]
- McCauley, J.L. A comment on the paper “Stochastic feedback, nonlinear families of Markov processes, and nonlinear Fokker–Planck equations” by T.D. Frank. Phys. A Stat. Mech. Appl. 2007, 382, 445–452. [Google Scholar] [CrossRef][Green Version]
- Frank, T.D. Stochastic systems with delay: Perturbation theory for second order statistics. Phys. Lett. A 2016, 380, 1341–1351. [Google Scholar] [CrossRef]
- Wedemann, R.S.; Plastino, A.R.; Tsallis, C. Curl forces and the nonlinear Fokker–Planck equation. Phys. Rev. E 2016, 94, 062105. [Google Scholar] [CrossRef] [PubMed]
- Barbi, M.; Cocco, S.; Peyrard, M. Helicoidal modelfor DNA openong. Phys. Lett. A 1999, 253, 358–369. [Google Scholar] [CrossRef]
- Epstein, O.I. The phenomenon of release activity and the hypothesis of “spatial” homeostasis. Usp. Fiziol. Nauk 2013, 44, 54–76. [Google Scholar] [PubMed]
- Epstein, O.I. Release-activity: A long way from phenomenon to new drugs. Bull. Exp. Biol. Med. 2012, 154, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Gavrilova, E.S.; Bobrovnik, S.A.; Sherriff, G.; Myslivets, A.A.; Tarasov, S.A.; Epstein, O.I. Novel Approach to Activity Evaluation for Release-Active Forms of Anti-Interferon-Gamma Antibodies Based on Enzyme-Linked Immunoassay. PLoS ONE 2014, 9, e97017. [Google Scholar] [CrossRef] [PubMed]
- Nicoll, J.; Gorbunov, E.A.; Tarasov, S.A.; Epstein, O.I. Subetta treatment increases adiponectin secretion by mature human adipocytes in vitro. Int. J. Endocrinol. 2013, 2013, 925874. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, S.A.; Zarubaev, V.V.; Gorbunov, E.A.; Sergeeva, S.A.; Epstein, O.I. Activity of ultra-low doses of antibodies to gamma-interferon against lethal influenza A (H1N1) 2009 virus infection in mice. Antivir. Res. 2012, 93, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Kondo, S.H.; Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science. 2010, 329, 1616–1620. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, S.H.; Kageyama, R.; Watanabe, D. Systems Biology: The Challenge of Complexity; Springer Science and Business Media: Berlin, Germany, 2009; p. 246. [Google Scholar]
- Othmer, H.G.; Maini, P.K.; Murray, J.D.; North Atlantic Treaty Organization. Experimental and Theoretical Advances in Biological Pattern Formation; Nato Science Series A: (Vol.259); Othmer, H.G., Maini, P.K., Murray, J.D., Eds.; Springer Science and Business Media: Berlin, Germany, 2012; p. 388. [Google Scholar]
- Vanag, V.K.; Epstein, I.R. Pattern formation mechanisms in reaction-diffusion systems. Int. J. Dev. Biol. 2009, 53, 673–681. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.J.; Meinhardt, H. Biological pattern formation: From basic mechanisms to complex structures. Rev. Mod. Phys. 1994, 66, 1481–1507. [Google Scholar] [CrossRef]
- Gourley, S.A.; Chaplain, M.A.J.; Davidson, F.A. Spatio-temporal pattern formation in a nonlocal reaction-diffusion equation. Dyn. Syst. 2001, 16, 173–192. [Google Scholar] [CrossRef]
- Fisher, R.A. The wave of advance of advantageous genes. Ann. Eugen. 1937, 7, 255–369. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Petrovskii, I.; Piskunov, N. A study of the diffusion equation with increase in the amount of substance and its application to a biology problem. Mosc. Univ. Math. Bull. 1937, 1, 1–16, (Reprinted in Selected Works of A.N. Kolmogorov; Tikhomirov, V.M., Ed.; Kluwer Academic Publishers: London, UK, 1991; Volume I, p. 242). [Google Scholar]
- Lee, C.T.; Hoopes, M.F.; Diehl, J.; Gilliland, W.; Huxel, G.; Leaver, E.V.; McCann, K.; Umbanhowar, J.; Mogilner, A. Non-local concepts and models in biology. J. Theor. Biol. 2001, 210, 201–219. [Google Scholar] [CrossRef] [PubMed]
- Mogilner, A.; Edelstein-Keshet, L. A non-local model for a swarm. J. Math. Biol. 1999, 38, 534–570. [Google Scholar] [CrossRef]
- Fuentes, M.A.; Kuperman, M.N.; Kenkre, V.M. Nonlocal interaction effects on pattern formation in population dynamics. Phys. Rev. Lett. 2003, 91, 158104. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, E.A.; Shapovalov, A.V.; Trifonov, A.Y. Pattern formation in terms of semiclassically limited distribution on lower dimensional manifolds for the nonlocal Fisher–Kolmogorov–Petrovskii–Piskunov equation. J. Phys. A Math. Theor. 2014, 47, 025209. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Iwasa, Y.; Sato, K. Mathematics for Life Science and Medicine; Biological and Medical Physics, Biomedical Engineering Vol. 10; Takeuchi, Y., Iwasa, Y., Sato, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- D’Onofrio, A.; Gandolfi, A. (Eds.) Modeling and Simulation in Science, Engineering and Technology; Springer: Berlin/Heidelberg, Germany, 2014; p. 334. [Google Scholar]
- Marciniak-Czochra, A.; Karch, G.; Suzuki, K. Unstable patterns in reaction–diffusion model of early carcinogenesis. J. Math. Pures Appl. 2013, 99, 509–543. [Google Scholar] [CrossRef]
- Maruvka, Y.E.; Shnerb, N.M. Nonlocal competition and logistic growth: Patterns, defects, and fronts. Phys. Rev. E 2006, 73, 011903. [Google Scholar] [CrossRef] [PubMed]
- Maruvka, Y.E.; Shnerb, N.M. Nonlocal competition and front propagation in branching-coalescence systems. Phys. Rev. E 2007, 75, 042901. [Google Scholar] [CrossRef] [PubMed]
- Vladimirov, V.S. Equations of Mathematical Physics; Dekker: New York, NY, USA, 1971. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).