Sufficient Conditions for Triangular Norms Preserving ⊗-Convexity

Abstract

The convexity in triangular norm (for short, ⊗−convexity) is a generalization of Zadeh’s quasiconvexity. The aggregation of two ⊗−convex sets is under the aggregation operator ⊗ is also ⊗−convex, but the aggregation operator ⊗ is not unique. To solve it in complexity, in the present paper, we give some sufficient conditions for aggregation operators preserve ⊗−convexity. In particular, when aggregation operators are triangular norms, we have that several results such as arbitrary triangular norm preserve ${\otimes }_D-$convexity and ${\otimes }_a-$convexity on bounded lattices, ${\otimes }_M$ preserves ${\otimes }_H-$convexity in the real unite interval $[0,1]$.

1. Introduction

Fuzzy set theory introduced by Zadeh in 1965, as an mathematical tool to deal with uncertainty in information system and knowledge base, has been widely used in various fields of science and technology. By applying fuzzy set theory, Zadeh in [1] proposed the concept of quasiconvex fuzzy set, and has attracted wide attention of researchers and practitioners from many different areas such as fuzzy mathematics, optimization and engineering. Subsequently, Zadeh’s quasiconvex fuzzy set was generalized with a lattice L instead of the interval $[0,1]$. A fuzzy set $\mu :{\mathbb{R}}^n\to L$ is quasiconvex if for any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$ the inequality

$$\begin{array}{c}\hfill \mu (\lambda x+(1-\lambda \left)y\right)\ge \mu \left(x\right)\wedge \mu \left(y\right)\end{array}$$

(1)

holds.

A quasiconvex fuzzy set has an important property: intersection of quasiconvex fuzzy sets is a quasiconvex fuzzy set, i.e., let $X\subseteq {\mathbb{R}}^n$, for any fuzzy sets $\mu$ and $\nu$,

$$\begin{array}{c}\hfill \mu and\nu arequasiconvex\Rightarrow \min \{\mu ,\nu \}isquasiconvex.\end{array}$$

(2)

The above condition is called intersection preserving quasiconvexity. This property is also true for lattice valued fuzzy sets.

The theory of aggregation operators [2], has been successfully used in mathematics, complex networks and decision making etc (e.g., see [3,4,5,6]). The arithmetic mean, the ordered weighted averaging operator and the probabilistic aggregation are widely used examples. In reference [7] Janiš, Král and Renčová pointed that the intersection of fuzzy sets is not the only operator preserving quasiconvexity in general, and they gave someconditions in order that an aggregation operator preserves quasiconvexity.

Triangular norms are kinds of binary aggregation operations that become an essential tool in fuzzy logic, information science and computer sciences. By using triangular norms, properties of fuzzy convexity and various generalizations of fuzzy convexity were considered by many authors (for example, see [8,9,10,11]). Suppose $\otimes :{[0,1]}^2\to [0,1]$ is a triangular norm, Nourouzi [10] given the concept of $\otimes -$convex set which generalized Zadeh’s quasiconvex fuzzy set. A $\otimes -$convex set as defined in [10] can also be generalized as being lattice-valued in the following sense. Let L be a lattice and let $\otimes :L^2\to L$ be a triangular norm. A fuzzy set $\mu :{\mathbb{R}}^n\to L$ is called $\otimes -$convex if for any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$ the inequality

$$\begin{array}{c}\hfill \mu (\lambda x+(1-\lambda \left)y\right)\ge \mu \left(x\right)\otimes \mu \left(y\right)\end{array}$$

(3)

holds.

Following [7,10], in the present paper, we continue to study sufficient conditions for aggregation operators and triangular norms that preserve $\otimes -$convexity on a bounded lattice. In Section 3, we give some sufficient conditions for aggregation operator preserving $\otimes -$convexity, those results are generalizations of Propositions 2 and 3 (in [7]). Triangular norm is a kind of important aggregation operator, we give some sufficient conditions for triangular norm preserving $\otimes -$convexity in Section 4. And Section 5 is conclusion.

2. Preliminaries

We first give the basic definitions and results from the existing literature. In following, we use L denote a bounded lattice $(L\le ,0_L,1_L)$.

Definition 1.

[2] An aggregation operation is a function $A:L^n\to L$ which satisfies

(i) 

$A(a_1,a_2,\dots ,a_n)\le A(a_1^{\prime },a_2^{\prime },\dots ,a_n^{\prime })$ whenever $a_i\le a_i^{\prime }$ for $1\le i\le n$.

(ii) 

$A(0_L,0_L,\dots ,0_L)=0_L$ and $A(1_L,1_L,\dots ,1_L)=1_L$.

A binary aggregation operation is said to be symmetric if for any $a_1,a_2\in L$, $A(a_1,a_2)=A(a_2,a_1)$. A special aggregation function is a triangular norm defined as following.

Definition 2.

[12] A map $\otimes :L^2\to L$ is called a triangular norm if

(T1) 

$a\otimes b=b\otimes a$.

(T2) 

$a_1\otimes b\le a_2\otimes b$ if $a_1\le a_2$.

(T3) 

$a\otimes (b\otimes c)=(a\otimes b)\otimes c$.

(T4) 

$a\otimes 1_L=a$.

Example 1.

The two basic triangular norms ${\otimes }_M$ and ${\otimes }_D$ defined as the following are the strongest and the weakest triangular norms on L, respectively.

$$\begin{array}{c}\hfill a{\otimes }_{M}b=a\wedge b,\end{array}$$

$$\begin{array}{c}\hfill a{\otimes }_{D}b=\left\{\begin{array}{cc}a\wedge b,\hfill & a,b\in \left\{1_L\right\},\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Example 2.

Suppose $H=(0,\lambda )\subseteq [0,1)$ and let $\ast :H^2\to H$ be an operation on H which satisfies (T1)–(T3) and

$$\begin{array}{c}\hfill a\ast b\le \min \{a,b\},\end{array}$$

$$\begin{array}{c}\hfill a{\otimes }_{H}b=\left\{\begin{array}{cc}a\ast b,\hfill & (a,b)\in H^2;\hfill \\ \min \{a,b\}\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Then ${\otimes }_H$ is a kind of triangular norms on $[0,1]$ follows from Proposition 3.60 in [13].

3. Sufficient Conditions for an Aggregation Operator Preserving $\otimes -$Convexity

In this Section, we generalize Propositions 2 and 3 (in [7]), and give some sufficient conditions for an aggregation operator which preserves $\otimes -$convexity.

Theorem 1.

Let $A:L^2\to L$ be an aggregation operator on L, let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrarily $\otimes -$convex fuzzy sets. If $A(a\otimes b,c\otimes d)=A(a,c)\otimes A(b,d)$ for each $a,b,c,d\in L$, then $A(\mu ,\nu )$ is $\otimes -$convex.

Proof. 

Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrarily $\otimes -$convex fuzzy sets, and $x,y\in {\mathbb{R}}^n$. Then we see

$$\begin{array}{cc}& A(\mu ,\nu )(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& A\left(\mu \right(\lambda x+(1-\lambda )y),\nu (\lambda x+(1-\lambda )y\left)\right)\hfill \\ \ge & A\left(\mu \right(x)\otimes \mu (y),\nu (x)\otimes \nu (y\left)\right)\hfill \\ =& A\left(\mu \right(x),\nu (x\left)\right)\otimes A\left(\mu \right(y),\nu (y\left)\right)\hfill \\ =& A(\mu ,\nu )\left(x\right)\otimes A(\mu ,\nu )\left(y\right).\hfill \end{array}$$

Thus, $A(\mu ,\nu )$ is $\otimes -$convex. □

The converse of Theorem 1, however, is in general not true. For example,

Example 3.

Consider a lattice $L=(0_L,a,b,1_L)$, where $0_L\le a\le 1_L$, $0_L\le b\le 1_L$, and $a,b$ are incomparable elements and the aggregation operator defined in Table 1. Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrarily ${\otimes }_D-$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$

$$\begin{array}{cc}& A(\mu ,\nu )(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& A\left(\mu \right(\lambda x+(1-\lambda )y),\nu (\lambda x+(1-\lambda )y\left)\right)\hfill \\ \ge & A(\mu \left(x\right){\otimes }_D\mu \left(y\right),\nu \left(x\right){\otimes }_D\nu \left(y\right))\hfill \\ =& \left\{\begin{array}{cc}A\left(\mu \right(y),\nu (y\left)\right),\hfill & \mu \left(x\right)=\nu \left(x\right)=1_L,\hfill \\ A\left(\mu \right(y),\nu (x\left)\right),\hfill & \mu \left(x\right)=\nu \left(y\right)=1_L,\hfill \\ A\left(\mu \right(x),\nu (x\left)\right),\hfill & \mu \left(y\right)=\nu \left(y\right)=1_L,\hfill \\ A\left(\mu \right(x),\nu (y\left)\right),\hfill & \mu \left(y\right)=\nu \left(x\right)=1_L,\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\hfill \end{array}$$

we have

$$\begin{array}{cc}& A(\mu ,\nu )\left(x\right){\otimes }_{D}A(\mu ,\nu )\left(y\right)\hfill \\ =& \left\{\begin{array}{cc}A\left(\mu \right(y),\nu (y\left)\right),\hfill & A(\mu ,\nu )\left(x\right)=1_L,\hfill \\ A\left(\mu \right(x),\nu (x\left)\right),\hfill & A(\mu ,\nu )\left(y\right)=1_L,\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\hfill \\ =& \left\{\begin{array}{cc}A\left(\mu \right(y),\nu (y\left)\right),\hfill & \mu \left(x\right)=\nu \left(x\right)=1_L,\hfill \\ A\left(\mu \right(x),\nu (x\left)\right),\hfill & \mu \left(y\right)=\nu \left(y\right)=1_L,\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right..\hfill \end{array}$$

Table 1. Aggregation operator A.

A	$0_{\mathit{L}}$	a	b	$1_{\mathit{L}}$
$0_L$	$0_L$	$0_L$	$0_L$	$0_L$
a	$0_L$	0	b	b
b	$0_L$	a	b	b
$1_L$	$0_L$	a	b	$1_L$

Hence, $A(\mu ,\nu )$ is ${\otimes }_D-$convex. And $A(1_L{\otimes }_{D}b,a{\otimes }_D{1}_L)=A(b,a)=a$, $A(1_L,a){\otimes }_{D}A(b,1_L)=a{\otimes }_{D}b=0_L.$

Theorem 2.

Let $A:L^2\to L$ be an aggregation operator on L, let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary $\otimes -$convex fuzzy sets. If $A(\mu ,\nu )$ is $\otimes -$convex, then $A(a\otimes b,c\otimes d)\ge A(a,c)\otimes A(b,d)$ for each $a,b,c,d\in L$. Moreover if the triangular norm ⊗ is idempotent, then $A(a\otimes b,c\otimes d)=A(a,c)\otimes A(b,d)$ for each $a,b,c,d\in L$.

Proof. 

Suppose that $A(\mu ,\nu )$ is $\otimes -$convex. Let $a,b,c,d$ be arbitrary elements of L. For $x,y\in {\mathbb{R}}^n$ and $z=\lambda x+(1-\lambda )y$, define

$$\mu \left(t\right)=\left\{\begin{array}{cc}a,\hfill & t=z+\theta (y-z),\theta <0;\hfill \\ a\otimes b,\hfill & t=z;\hfill \\ b,\hfill & t=z+\theta (y-z),\theta >0;\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\nu \left(t\right)=\left\{\begin{array}{cc}c,\hfill & t=z+\theta (y-z),\theta <0;\hfill \\ c\otimes d,\hfill & t=z;\hfill \\ d,\hfill & t=z+\theta (y-z),\theta >0;\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.$$

Clearly $\mu ,\nu$ are $\otimes -$convex. And

$$A(\mu ,\nu )\left(t\right)=\left\{\begin{array}{cc}A(a,c),\hfill & t=z+\theta (y-z),\theta <0;\hfill \\ A(a\otimes b,c\otimes d),\hfill & t=z;\hfill \\ A(b,d),\hfill & t=z+\theta (y-z),\theta >0;\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.$$

As $A(\mu ,\nu )$ has to be a $\otimes -$convex fuzzy set, we have

$$\begin{array}{c}\hfill A(a\otimes b,c\otimes d)\ge A(a,c)\otimes A(b,d).\end{array}$$

From the monotonicity of A it follows that $A(a\otimes b,c\otimes d)\le A(a,c)$ and $A(a\otimes b,c\otimes d)\le A(b,d)$. Hence

$$\begin{array}{c}\hfill A(a\otimes b,c\otimes d)\otimes A(a\otimes b,c\otimes d)\le A(a,c)\otimes A(b,d).\end{array}$$

Therefore, since the operator ⊗ is idempotent it follows that

$$\begin{array}{c}\hfill A(a\otimes b,c\otimes d)\le A(a,c)\otimes A(b,d).\end{array}$$

□

Since the triangular norm $a{\otimes }_{M}b=a\wedge b$ is idempotent, Proposition 2 (in [7]) follows from Theorems 1 and 2.

Theorem 3.

Let $A:L^2\to L$ be an aggregation operator on L, and let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary $\otimes -$convex fuzzy sets. If $A(a,b)=A(a,a)\otimes A(b,b)=A(a\otimes b,a\otimes b)$ for each $a,b\in L$, then $A(\mu ,\nu )$ is $\otimes -$convex.

Proof. 

Let $\mu ,\nu :R^n\to L$ be arbitrary $\otimes -$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$

$$\begin{array}{cc}& A(\mu ,\nu )(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& A\left(\mu \right(\lambda x+(1-\lambda )y),\nu (\lambda x+(1-\lambda )y\left)\right)\hfill \\ =& A\left(\mu \right(\lambda x+(1-\lambda )y),\mu (\lambda x+(1-\lambda )y\left)\right)\otimes A\left(\nu \right(\lambda x+(1-\lambda )y),\nu (\lambda x+(1-\lambda )y\left)\right)\hfill \\ \ge & A\left(\mu \right(x)\otimes \mu (y),\mu (x)\otimes \mu (y\left)\right)\otimes A\left(\nu \right(x)\otimes \nu (y),\nu (x)\otimes \nu (y\left)\right)\hfill \\ =& A\left(\mu \right(x),\mu (y\left)\right)\otimes A\left(\nu \right(x),\nu (y\left)\right)\hfill \\ =& \left(A\right(\mu \left(x\right),\mu \left(x\right))\otimes A(\mu \left(y\right),\mu \left(y\right)\left)\right)\otimes \left(A\right(\nu \left(x\right),\nu \left(x\right))\otimes A(\nu \left(y\right),\nu \left(y\right)\left)\right)\hfill \\ =& \left(A\right(\mu \left(x\right),\mu \left(x\right))\otimes A(\nu \left(x\right),\nu \left(x\right)\left)\right)\otimes \left(A\right(\mu \left(y\right),\mu \left(y\right))\otimes A(\nu \left(y\right),\nu \left(y\right)\left)\right)\hfill \\ =& A(\mu ,\nu )\left(x\right)\otimes A(\mu ,\nu )\left(y\right).\hfill \end{array}$$

Thus, $A(\mu ,\nu )$ is $\otimes -$convex. □

The following shows that the converse of Theorem 3 is in general not true.

Example 4.

Consider a lattice $L=(0_L,a,b,1_L)$, where $0_L\le a\le 1_L$, $0_L\le b\le 1_L$, and $a,b$ are incomparable elements and the binary symmetric aggregation operator A defined in Table 2. Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary ${\otimes }_D-$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$, can prove that $A(\mu ,\nu )$ is ${\otimes }_D-$convex. And $A(b,a)=a$, $A(b,b){\otimes }_{D}A(a,a)=a{\otimes }_{D}a=0_L$, and $A(b{\otimes }_{D}b,a{\otimes }_{D}a)=A(0_L,0_L)=0_L$.

Table 2. Aggregation operator A.

A	$0_{\mathit{L}}$	a	b	$1_{\mathit{L}}$
$0_L$	$0_L$	$0_L$	$0_L$	$0_L$
a	$0_L$	a	a	a
b	$0_L$	a	a	b
$1_L$	$0_L$	a	b	$1_L$

Theorem 4.

Let $A:L^2\to L$ be an symmetric aggregation operator on L, let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary $\otimes -$convex fuzzy sets. If $A(\mu ,\nu )$ is $\otimes -$convex, then $A(a,b)\ge A(a,a)\otimes A(b,b)$ for each $a,b\in L$. Moreover if the triangular norm ⊗ is idempotent, then $A(a,b)=A(a,a)\otimes A(b,b)=A(a\otimes b,a\otimes b)$ for each $a,b\in L$.

Proof. 

Suppose that $A(\mu ,\nu )$ is $\otimes -$convex. Let $a,b$ be arbitrary elements of L, and put, for $x,y\in {\mathbb{R}}^n$ and $0<\lambda <1$, $z=\lambda x+(1-\lambda )y$. We define

$$\mu \left(t\right)=\left\{\begin{array}{cc}a,\hfill & t=z+\theta (y-z),\theta \le 0;\hfill \\ b,\hfill & t=z+\theta (y-z),\theta >0;\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\nu \left(t\right)=\left\{\begin{array}{cc}a,\hfill & t=z+\theta (y-z),\theta <0;\hfill \\ b,\hfill & t=z+\theta (y-z),\theta \ge 0;\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.$$

Clearly $\mu ,\nu$ are $\otimes -$convex and as A preserves $\otimes -$convexity, then we have

$$\begin{array}{c}\hfill A(a,b)\ge A(a,a)\otimes A(b,b).\end{array}$$

Suppose that the triangular norm ⊗ is idempotent. Let $x,y\in {\mathbb{R}}^n$ and $z=\lambda x+(1-\lambda )y$, define

$$\mu \left(t\right)=\left\{\begin{array}{cc}a,\hfill & t=z+\theta (y-z),\theta \le 0;\hfill \\ 1_L,\hfill & t=z+\theta (y-z),\theta >0;\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\nu \left(t\right)=\left\{\begin{array}{cc}a,\hfill & t=z+\theta (y-z),\theta <0;\hfill \\ 1_L,\hfill & t=z+\theta (y-z),\theta \ge 0;\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.$$

Clearly $\mu ,\nu$ are $\otimes -$convex. Since, in addition, A preserves $\otimes -$convexity this can be combined with the fact that the triangular norm ⊗ is idempotent, we deduce

$$\begin{array}{c}\hfill A(a,a)\ge A(a,1_L)\otimes A(1_L,a)=A(1_L,a)\otimes A(1_L,a)=A(1_L,a).\end{array}$$

From the monotony of A it follows that $A(a,a)\le A(1_L,a)$. Hence

$$\begin{array}{c}\hfill A(a,a)=A(1_L,a).\end{array}$$

Therefore

$$\begin{array}{c}\hfill A(a,b)\le A(1_L,b)=A(b,b),A(a,b)\le A(1_L,a)=A(a,a).\end{array}$$

Hence

$$\begin{array}{c}\hfill A(a,b)=A(a,b)\otimes A(a,b)\le A(a,a)\otimes A(b,b).\end{array}$$

Thus

$$\begin{array}{c}\hfill A(a,b)=A(a,a)\otimes A(b,b).\end{array}$$

Let $c=a,d=b$, from Theorem 2 we have

$$\begin{array}{c}\hfill A(a,b)=A(a\otimes b,a\otimes b).\end{array}$$

□

Then Proposition 3 (in [7]) follows from Theorems 3 and 4 due to $a{\otimes }_{M}b=a\wedge b$ is idempotent.

Since the triangular norm $a{\otimes }_{M}b=\min \{a,b\}$ is the strongest triangular norm on $[0,1]$, from the definition of $\otimes -$convexity we can prove the following theorem.

Theorem 5.

If $f_1,f_2:[0,1]\to [0,1]$ are both nondecreasing, $\min \{f_1\left(0\right),f_2\left(0\right)\}=0,f_1\left(1\right)=f_2\left(1\right)=1$. Let $A:{[0,1]}^2\to [0,1]$ defined by $A(a,b)=\min \{f_1\left(a\right),f_2\left(b\right)\}$, then $A(\mu ,\nu )$ preserves $\otimes -$convexity for any triangular norm on $[0,1]$. But the converse statement is in general not true.

Example 5.

Suppose $L=[0,1]$, $A(a,b)=\frac{1}{2}(a+b).$ Then $A(\mu ,\nu )(\lambda x+(1-\lambda )y)\ge A(\mu ,\nu )\left(x\right){\otimes }_{D}A(\mu ,\nu )\left(y\right)$. i.e., $A(\mu ,\nu )$ is ${\otimes }_D-$convex. And $A(a,b)=\frac{1}{2}(a+b)\ne \min \{f_1\left(a\right),f_2\left(b\right)\}$.

4. Sufficient Conditions for Triangular Norm Preserving $\otimes -$Convexity

In this section we give some sufficient conditions which guarantee that a triangular norm preserves $\otimes -$convexity. The following theorem is obvious.

Theorem 6.

Let $\otimes :L^2\to L$ be a triangular norm on L. If $\mu ,\nu :{\mathbb{R}}^n\to L$ are arbitrary $\otimes -$convex fuzzy sets, then $\mu \otimes \nu$ is $\otimes -$convex.

Theorem 7.

Let $\otimes :L^2\to L$ be a triangular norm on L. If $\mu ,\nu :{\mathbb{R}}^n\to L$ are arbitrary ${\otimes }_D-$convex fuzzy sets, then $\mu \otimes \nu$ is ${\otimes }_D-$convex.

Proof. 

Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary ${\otimes }_D-$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$

$$\begin{array}{cc}& (\mu \otimes \nu )(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& \mu (\lambda x+(1-\lambda \left)y\right)\otimes \nu (\lambda x+(1-\lambda \left)y\right)\hfill \\ \ge & \left(\mu \left(x\right){\otimes }_D\mu \left(y\right)\right)\otimes \left(\nu \left(x\right){\otimes }_D\nu \left(y\right)\right)\hfill \\ =& \left\{\begin{array}{cc}\mu \left(x\right)\otimes \nu \left(x\right),\hfill & \mu \left(y\right)=\nu \left(y\right)=1_L,\hfill \\ \mu \left(y\right)\otimes \nu \left(y\right),\hfill & \mu \left(x\right)=\nu \left(x\right)=1_L,\hfill \\ \mu \left(x\right)\otimes \nu \left(y\right),\hfill & \mu \left(y\right)=\nu \left(x\right)=1_L,\hfill \\ \mu \left(y\right)\otimes \nu \left(x\right),\hfill & \mu \left(x\right)=\nu \left(y\right)=1_L,\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Then we see

$$\begin{array}{cc}& (\mu \otimes \nu )\left(x\right){\otimes }_D(\mu \otimes \nu )\left(y\right)\hfill \\ =& (\mu \left(x\right)\otimes \nu \left(x\right)){\otimes }_D(\mu \left(y\right)\otimes \nu \left(y\right))\hfill \\ =& \left\{\begin{array}{cc}\mu \left(x\right)\otimes \nu \left(x\right),\hfill & \mu \left(y\right)\otimes \nu \left(y\right)=1_L,\hfill \\ \mu \left(y\right)\otimes \nu \left(y\right),\hfill & \mu \left(x\right)\otimes \nu \left(x\right)=1_L,\hfill \\ 0_L,\hfill & otherwise,\hfill \end{array}\right.\hfill \\ =& \left\{\begin{array}{cc}\mu \left(x\right)\otimes \nu \left(x\right),\hfill & \mu \left(y\right)=\nu \left(y\right)=1_L,\hfill \\ \mu \left(y\right)\otimes \nu \left(y\right),\hfill & \mu \left(x\right)=\nu \left(x\right)=1_L,\hfill \\ 0_L,\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Hence

$$\begin{array}{c}\hfill (\mu \otimes \nu )(\lambda x+(1-\lambda )y)\ge (\mu \otimes \nu )\left(x\right){\otimes }_D(\mu \otimes \nu )\left(y\right).\end{array}$$

Thus, $\mu \otimes \nu$ is ${\otimes }_D-$convex. □

Let ⊗ be a triangular norm on L. Li in [14] given a family triangular norms ${\left({\otimes }_a\right)}_{a\in L}$ as follows

$$\begin{array}{c}\hfill x{\otimes }_{a}y=\left\{\begin{array}{cc}{0}_L,\hfill & x\otimes y\le aandx,y\ne 1_L;\hfill \\ x\otimes y,\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Theorem 8.

Let $\otimes :L^2\to L$ be a triangular norm on L, and $a\in L$. If $\mu ,\nu :{\mathbb{R}}^n\to L$ are arbitrary ${\otimes }_a-$convex fuzzy sets, then $\mu \otimes \nu$ is ${\otimes }_a-$convex.

Proof. 

Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary ${\otimes }_a-$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$

$$\begin{array}{cc}& (\mu \otimes \nu )(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& \mu (\lambda x+(1-\lambda \left)y\right)\otimes \nu (\lambda x+(1-\lambda \left)y\right)\hfill \\ \ge & \left(\mu \left(x\right){\otimes }_a\mu \left(y\right)\right)\otimes \left(\nu \left(x\right){\otimes }_a\nu \left(y\right)\right)\hfill \\ =& \left\{\begin{array}{cc}{0}_L,\hfill & \mu \left(x\right)\otimes \mu \left(y\right)\le aor\nu \left(x\right)\otimes \nu \left(y\right)\le a,\hfill \\ \mu \left(x\right)\otimes \mu \left(y\right)\otimes \nu \left(x\right)\otimes \nu \left(y\right),\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Then we have

$$\begin{array}{cc}& (\mu \otimes \nu )\left(x\right){\otimes }_a(\mu \otimes \nu )\left(y\right)\hfill \\ =& (\mu \left(x\right)\otimes \nu \left(x\right)){\otimes }_a(\mu \left(y\right)\otimes \nu \left(y\right))\hfill \\ =& \left\{\begin{array}{cc}{0}_L,\hfill & \mu \left(x\right)\otimes \nu \left(x\right)\otimes \mu \left(y\right)\otimes \nu \left(y\right)\le a,\hfill \\ \mu \left(x\right)\otimes \mu \left(y\right)\otimes \nu \left(x\right)\otimes \nu \left(y\right),\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Since $\mu \left(x\right)\otimes \mu \left(y\right)\le a$ or $\nu \left(x\right)\otimes \nu \left(y\right)\le a$ implies $\mu \left(x\right)\otimes \nu \left(x\right)\otimes \mu \left(y\right)\otimes \nu \left(y\right)\le a$, we have

$$\begin{array}{c}\hfill (\mu \otimes \nu )(\lambda x+(1-\lambda )y)\ge (\mu \otimes \nu )\left(x\right){\otimes }_a(\mu \otimes \nu )\left(y\right).\end{array}$$

Thus, $\mu \otimes \nu$ is ${\otimes }_a-$convex. □

Example 6.

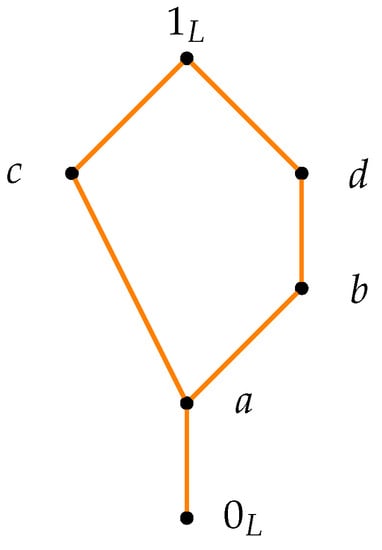
Consider the lattice $(L=\{0_L,a,b,c,d,1_L\},\le ,0,1)$ given in Figure 1. Consider the function ${\otimes }_b$ on L defined by

$$\begin{array}{c}\hfill \alpha {\otimes }_b\beta =\left\{\begin{array}{cc}{0}_L,\hfill & \alpha \wedge \beta \le band\alpha ,\beta \ne 1_L;\hfill \\ \alpha \wedge \beta ,\hfill & otherwise,\hfill \end{array}\right.\end{array}$$

then ${\otimes }_b$ is a triangular norm and ${\otimes }_b$ is described in Table 3.

Figure 1. The order ≤ on L.

Table 3. Triangular norm ${\otimes }_b$.

${\mathit{T}}_{\mathit{b}}$	$0_{\mathit{L}}$	a	b	c	d	$1_{\mathit{L}}$
$0_L$	$0_L$	$0_L$	$0_L$	$0_L$	$0_L$	$0_L$
a	$0_L$	$0_L$	$0_L$	$0_L$	$0_L$	a
b	$0_L$	$0_L$	$0_L$	$0_L$	$0_L$	b
c	$0_L$	$0_L$	$0_L$	c	$0_L$	c
d	$0_L$	$0_L$	$0_L$	$0_L$	d	d
$1_L$	$0_L$	a	b	c	d	$1_L$

Hence, for any ${\otimes }_b$-convex sets $\mu ,\nu :{\mathbb{R}}^n\to L$, $\mu {\otimes }_M\nu =\mu \wedge \nu$ is also a ${\otimes }_b$-convex set.

Theorem 9.

Let $\mu ,\nu :{\mathbb{R}}^n\to [0,1]$ be arbitrary ${\otimes }_H-$convex fuzzy sets. Then $\min \{\mu ,\nu \}$ is a ${\otimes }_H-$convex fuzzy set.

Proof. 

Let $\mu ,\nu :{\mathbb{R}}^n\to L$ be arbitrary ${\otimes }_H-$convex fuzzy sets. For any $x,y\in {\mathbb{R}}^n$ and all $\lambda \in [0,1]$

$$\begin{array}{cc}& \min \{\mu ,\nu \}(\lambda x+(1-\lambda \left)y\right)\hfill \\ =& \min \left\{\mu \right(\lambda x+(1-\lambda )y),\nu (\lambda x+(1-\lambda )y\left)\right\}\hfill \\ \ge & \min \{\mu \left(x\right){\otimes }_H\mu \left(y\right),\nu \left(x\right){\otimes }_H\nu \left(y\right)\}\hfill \\ =& \left\{\begin{array}{cc}\min \left\{\mu \right(x)\ast \mu (y),\nu (x)\ast \nu (y\left)\right\},\hfill & (\mu \left(x\right),\mu \left(y\right))\in H^{2}and(\nu \left(x\right),\nu \left(y\right))\in H^2,\hfill \\ \min \left\{\mu \right(x)\ast \mu (y),\nu (x),\nu (y\left)\right\},\hfill & (\mu \left(x\right),\mu \left(y\right))\in H^{2}and(\nu \left(x\right),\nu \left(y\right))\notin H^2,\hfill \\ \min \left\{\mu \right(x),\mu (y),\nu (x)\ast \nu (y\left)\right\},\hfill & (\mu \left(x\right),\mu \left(y\right))\notin H^{2}and(\nu \left(x\right),\nu \left(y\right))\in H^2,\hfill \\ \min \left\{\mu \right(x),\mu (y),\nu (x),\nu (y\left)\right\},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Then we deduce

$$\begin{array}{cc}& \min \{\mu ,\nu \}\left(x\right){\otimes }_H\min \{\mu ,\nu \}\left(y\right)\hfill \\ =& \min \{\mu \left(x\right),\nu \left(x\right)\}{\otimes }_H\min \{\mu \left(y\right),\nu \left(y\right)\}\hfill \\ =& \left\{\begin{array}{cc}\min \left\{\mu \right(x),\nu (x\left)\right\}\ast \min \left\{\mu \right(y),\nu (y\left)\right\},\hfill & (\min \{\mu \left(x\right),\nu \left(x\right)\},\min \{\mu \left(y\right),\nu \left(y\right)\})\in H^2,\hfill \\ \min \left\{\mu \right(x),\mu (y),\nu (x),\nu (y\left)\right\},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Since $\min \left\{\mu \right(x),\mu (y\left)\right\}\ge \mu \left(x\right)\ast \mu \left(y\right)\ge \min \left\{\mu \right(x),\nu (x\left)\right\}\ast \min \left\{\mu \right(y),\nu (y\left)\right\},\min \left\{\nu \right(x),\nu (y\left)\right\}\ge \nu \left(x\right)\ast \nu \left(y\right)\ge \min \left\{\mu \right(x),\nu (x\left)\right\}\ast \min \left\{\mu \right(y)$ we have

$$\begin{array}{c}\hfill \min \{\mu ,\nu \}(\lambda x+(1-\lambda )y)\ge \min \{\mu ,\nu \}\left(x\right){\otimes }_H\min \{\mu ,\nu \}\left(y\right).\end{array}$$

Thus, $\min \{\mu ,\nu \}$ is a ${\otimes }_H-$convex fuzzy set. □

Example 7.

Suppose $H=(0,\frac{1}{2})$ and the triangular norm ${\otimes }_H$ is

$$\begin{array}{c}\hfill a{\otimes }_{H}b=\left\{\begin{array}{cc}\frac{ab}{2},\hfill & (a,b)\in {(0,\frac{1}{2})}^2;\hfill \\ \min \{a,b\}\hfill & otherwise,\hfill \end{array}\right.\end{array}$$

then, $\min \{\mu ,\nu \}$ is a ${\otimes }_H-$convex fuzzy set.

5. Conclusions

The authors of the paper [7] discuss properties which are preserved under aggregation for arbitrary lattices and arbitrary pairs of mappings Results in this paper are also discussed under aggregation for an arbitrary lattice and an arbitrary pair of mappings. However, this does not mean that even without these conditions the aggregation of SOME quasiconvex ($\otimes -$convex) mappings to SOME lattices need not be quasiconvex ($\otimes -$convex). Which are the properties of a lattice L and an aggregation A (weaker than those from the paper by Janis, Kral and Rencova in [7]), such that A preserves quasiconvexity ($\otimes -$convex) for mappings into L? We hope to solve this problem in future work.