1. Introduction
Fuzzy set theory introduced by Zadeh in 1965, as an mathematical tool to deal with uncertainty in information system and knowledge base, has been widely used in various fields of science and technology. By applying fuzzy set theory, Zadeh in [
1] proposed the concept of quasiconvex fuzzy set, and has attracted wide attention of researchers and practitioners from many different areas such as fuzzy mathematics, optimization and engineering. Subsequently, Zadeh’s quasiconvex fuzzy set was generalized with a lattice
L instead of the interval
. A fuzzy set
is quasiconvex if for any
and all
the inequality
holds.
A quasiconvex fuzzy set has an important property: intersection of quasiconvex fuzzy sets is a quasiconvex fuzzy set, i.e., let
, for any fuzzy sets
and
,
The above condition is called intersection preserving quasiconvexity. This property is also true for lattice valued fuzzy sets.
The theory of aggregation operators [
2], has been successfully used in mathematics, complex networks and decision making etc (e.g., see [
3,
4,
5,
6]). The arithmetic mean, the ordered weighted averaging operator and the probabilistic aggregation are widely used examples. In reference [
7] Janiš, Král and Renčová pointed that the intersection of fuzzy sets is not the only operator preserving quasiconvexity in general, and they gave someconditions in order that an aggregation operator preserves quasiconvexity.
Triangular norms are kinds of binary aggregation operations that become an essential tool in fuzzy logic, information science and computer sciences. By using triangular norms, properties of fuzzy convexity and various generalizations of fuzzy convexity were considered by many authors (for example, see [
8,
9,
10,
11]). Suppose
is a triangular norm, Nourouzi [
10] given the concept of
convex set which generalized Zadeh’s quasiconvex fuzzy set. A
convex set as defined in [
10] can also be generalized as being lattice-valued in the following sense. Let
L be a lattice and let
be a triangular norm. A fuzzy set
is called
convex if for any
and all
the inequality
holds.
Following [
7,
10], in the present paper, we continue to study sufficient conditions for aggregation operators and triangular norms that preserve
convexity on a bounded lattice. In
Section 3, we give some sufficient conditions for aggregation operator preserving
convexity, those results are generalizations of Propositions 2 and 3 (in [
7]). Triangular norm is a kind of important aggregation operator, we give some sufficient conditions for triangular norm preserving
convexity in
Section 4. And
Section 5 is conclusion.
3. Sufficient Conditions for an Aggregation Operator Preserving Convexity
In this Section, we generalize Propositions 2 and 3 (in [
7]), and give some sufficient conditions for an aggregation operator which preserves
convexity.
Theorem 1. Let be an aggregation operator on L, let be arbitrarily convex fuzzy sets. If for each , then is convex.
Proof. Let
be arbitrarily
convex fuzzy sets, and
. Then we see
Thus, is convex. □
The converse of Theorem 1, however, is in general not true. For example,
Example 3. Consider a lattice , where , , and are incomparable elements and the aggregation operator defined in Table 1. Let be arbitrarily convex fuzzy sets. For any and all we have Hence, is convex. And ,
Theorem 2. Let be an aggregation operator on L, let be arbitrary convex fuzzy sets. If is convex, then for each . Moreover if the triangular norm ⊗ is idempotent, then for each .
Proof. Suppose that
is
convex. Let
be arbitrary elements of
L. For
and
, define
Clearly
are
convex. And
As
has to be a
convex fuzzy set, we have
From the monotonicity of
A it follows that
and
. Hence
Therefore, since the operator ⊗ is idempotent it follows that
□
Since the triangular norm
is idempotent, Proposition 2 (in [
7]) follows from Theorems 1 and 2.
Theorem 3. Let be an aggregation operator on L, and let be arbitrary convex fuzzy sets. If for each , then is convex.
Proof. Let
be arbitrary
convex fuzzy sets. For any
and all
Thus, is convex. □
The following shows that the converse of Theorem 3 is in general not true.
Example 4. Consider a lattice , where , , and are incomparable elements and the binary symmetric aggregation operator A defined in Table 2. Let be arbitrary convex fuzzy sets. For any and all , can prove that is convex. And , , and . Theorem 4. Let be an symmetric aggregation operator on L, let be arbitrary convex fuzzy sets. If is convex, then for each . Moreover if the triangular norm ⊗ is idempotent, then for each .
Proof. Suppose that
is
convex. Let
be arbitrary elements of
L, and put, for
and
,
. We define
Clearly
are
convex and as
A preserves
convexity, then we have
Suppose that the triangular norm ⊗ is idempotent. Let
and
, define
Clearly
are
convex. Since, in addition,
A preserves
convexity this can be combined with the fact that the triangular norm ⊗ is idempotent, we deduce
From the monotony of
A it follows that
. Hence
Let
, from Theorem 2 we have
□
Then Proposition 3 (in [
7]) follows from Theorems 3 and 4 due to
is idempotent.
Since the triangular norm is the strongest triangular norm on , from the definition of convexity we can prove the following theorem.
Theorem 5. If are both nondecreasing, . Let defined by , then preserves convexity for any triangular norm on . But the converse statement is in general not true.
Example 5. Suppose , Then . i.e., is convex. And .
4. Sufficient Conditions for Triangular Norm Preserving Convexity
In this section we give some sufficient conditions which guarantee that a triangular norm preserves convexity. The following theorem is obvious.
Theorem 6. Let be a triangular norm on L. If are arbitrary convex fuzzy sets, then is convex.
Theorem 7. Let be a triangular norm on L. If are arbitrary convex fuzzy sets, then is convex.
Proof. Let
be arbitrary
convex fuzzy sets. For any
and all
Thus, is convex. □
Let ⊗ be a triangular norm on
L. Li in [
14] given a family triangular norms
as follows
Theorem 8. Let be a triangular norm on L, and . If are arbitrary convex fuzzy sets, then is convex.
Proof. Let
be arbitrary
convex fuzzy sets. For any
and all
Since
or
implies
, we have
Thus, is convex. □
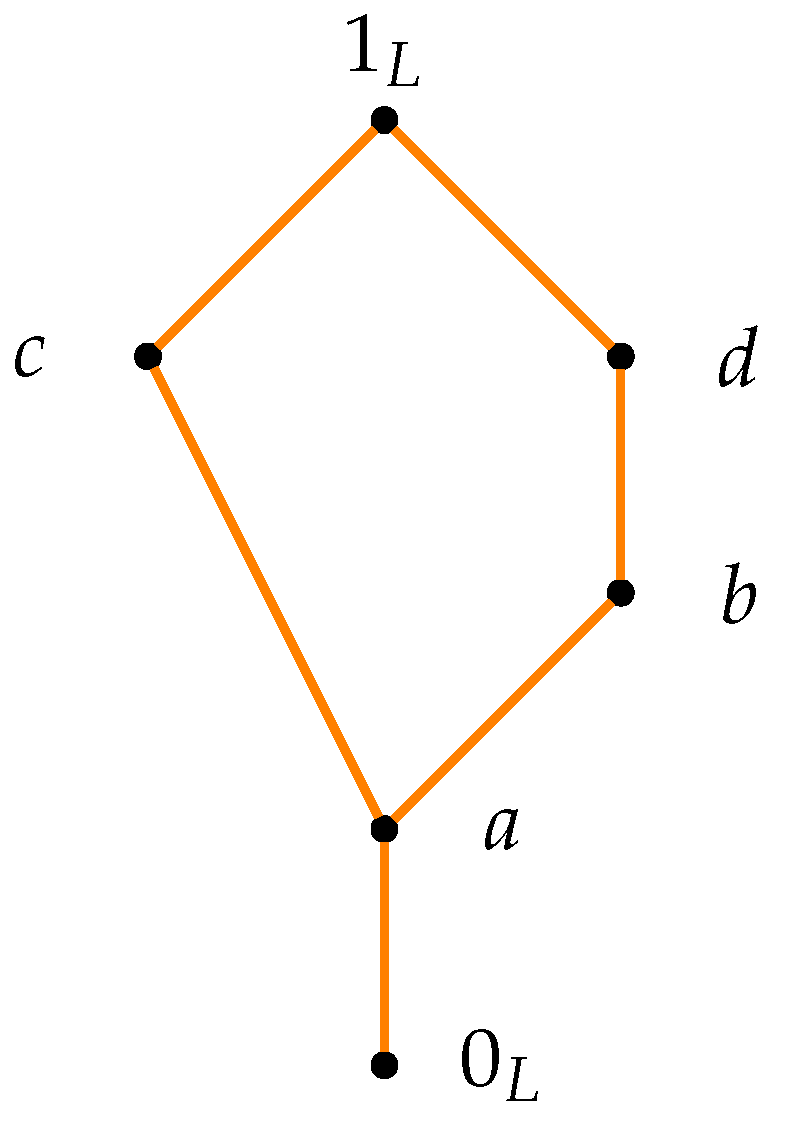
Example 6. Consider the lattice given in Figure 1. Consider the function on L defined bythen is a triangular norm and is described in Table 3. Hence, for any -convex sets , is also a -convex set.
Theorem 9. Let be arbitrary convex fuzzy sets. Then is a convex fuzzy set.
Proof. Let
be arbitrary
convex fuzzy sets. For any
and all
Since
we have
Thus, is a convex fuzzy set. □
Example 7. Suppose and the triangular norm isthen, is a convex fuzzy set.