Abstract
In this paper, we extended the idea of a neutrosophic triplet set to non-associative semihypergroups and define neutrosophic triplet -semihypergroup. We discuss some basic results and properties. At the end, we provide an application of the proposed structure in Football.
1. Introduction
The study of origin and features of neutralities lies in the scope of a new branch of philosophy known as Neutrosophy. In 1995, Smarandache (for the first time) used the idea of Neutrosophy and developed neutrosophic logic which is a more practical and realistic approach, to handle imprecise and vague information. He introduced the concept of (T-truth, I-indeterminacy, F-falsity) memberships. According to Smarandache Neutrosophic, logics generalizes the all previous logics such as fuzzy logic [1], intuitionistic fuzzy logic [2] and interval valued fuzzy logic [3]. Kandasamy and Smarandache [4] developed many neutrosophic algebraic structures, neutrosophic bigroup, neutrosophic vector space, neutrosophic groups and so on, based on neutrosophic logic. For practical applications, we refer the readers to [5,6,7,8,9]. For neutrosophic triplet sets, we refer the readers [10,11,12,13]. In 2016, Smarandache and Ali [14] gave the concept of Neutrosophic triplet groups which is a very useful addition in the theory of groups.
Hyperstucture theory was brought-out by Marty [15] in 1934, when he defined hypergroup, set about analyzing their properties and exerted them to a group. Several papers and books have been compiled in this direction, see references [16,17,18]. In 1990, in Greece, a congress was organized by Thomas Vougiouklis on hyperstructure, which was first named algebraic hyper structures and its applications algebraic hyper structures(AHA); however actually was the fourth, because there had been three more congresses in Italy by Corsini, on the same topic but random names. During this congress, Vougiouklis [19] presented the concept of weak structure, presently known as Hv-structure. A number of writers have gone through various aspects of Hv-structure. For instance, references [20,21,22,23,24,25,26,27]. Another book by Davvaz and Fotea in 2007 has been devoted especially to the study of hyperring theory [28].
Kazim and Naseeruddin [29] in 1970, presented the concept of left almost semigroups (LA-semigroups) and shifted the discussion toward non-associative structures. According to them, a groupoid S is called -semigroups, if it is satisfies the left invertive law: for all . After that, researchers started working in this direction such as, references [30,31,32] and Yusuf gave the idea of left almost rings [33]. Hila and Dine [34] in 2011, shifted the non-associative structures to non-associative hyperstructures and furnished the idea of -semihypergroup, which is generalization of semigroup, semihypergroup, -semigroup by using left invertive law with the help of Marty’s hyperoperation.Yaqoob et al. [35] expanded the work of Hila and Dine. Yousafzai et al. in [36] and Amjad et al. [37] tried to generalize different aspects of left almost semihypergroups. The concept of Hv--semigroup was laid by Gulistan et al. [38] in 2015. The idea of partially ordered left almost semihypergroups was developed by Naveed et al. [39] in 2015. Rehman et al. [40], initiated the study of -hyperrings and discussed its hyperideals and hypersystems in 2017. Nawaz et al. introduced the concept of left almost semihyperrings [41]. Yaqoob et al. [42] gave the idea of left almost polygroups in 2018.
In this paper, we extended the idea of neutrosophic triplet set to non-associative semihypergroups. We define neutrosophic triplet -semihypergroup. In neutrosophic triplet -semihypergroup every element “w” has left neut(w) and left anti(w). In neutrosophic triplet -semihypergroup left neut(w) of an element “w” may or may not be equal to left identity. We also defined the neutro-homomorphism on -semihypergroups. At the end, we present an application of the proposed structure in football.
2. Preliminaries
This section of paper consists of some basic definitions, which are directly used in our work.
Definition 1
([34]). Let be a non void set and be a hyperoperation, where is the family non-void subset of . The pair is called hypergroupoid.
For any two non-void subsets and of , then
Definition 2
([34]). An -semihypergroup is the hypergroupoid with
for all, . The equation (1) is called left invertive law.
Definition 3
([35]). An element e of an LA-semihypergroup is called left identity (resp., pure left identity) if for all (resp., ). An element e of an LA-semihypergroup is called right identity (resp., pure right identity) if for all (resp., ). An element e of an LA-semihypergroup is called identity (resp., pure right identity) if for all (resp., ).
Definition 4
([35]). An -smihypergroup with pure left identity satisfies the following property
Definition 5
([14]). Let N be a non-void set with a binary operation ∗ and . Then is said to be neutrosophic triplet if there exist an element such that
where is different from unity element. Also there exist such that
If there are more for a given , one takes that that in its turn forms a neutrosophic triplet, i.e., there exists and . We denote the neutrosophic triplet by . By , we means neutral of .
Example 1
([14]). Consider under multiplication modulo Then 2 is a neutrosophic triplet, because , as . Similarly because . Thus 2 is a neutrosophic triplet, which is denoted by . Similarly 4 is a neutrosophic triplet because . So 4 is represented by as . 3 is not a neutrosophic triplet as but does not exist in and 0 is a trivial neutrosophic triplet as . This is denoted by
3. Neutrosophic Triplet -Semihypergroups
In this section, we defined the neutrosophic triplet -semihypergroup and some results on neutrosophic triplet -semihypergroup are provided.
Definition 6.
Let be a non void set with a binary hyperoperation ∗ and . Then is called
- left neutrosophic triplet set if for every , there exist and such that
- right neutrosophic triplet set if for every , there exist and such that
- neutrosophic triplet set if for every , there exist and such that
Definition 7.
Let be a set with a binary hyperoperation ∗ and . Then is called
- pure left neutrosophic triplet set if for every , there exist and such that
- pure right neutrosophic triplet set if for every , there exist and such that
- pure neutrosophic triplet set if for every , there exist and such that
Example 2. 
Let be a se with hyperoperation defined as follows:

A Cayley table 1
Here and are neutrosophic triplets.
Definition 8.
Let be a left (resp., right, left pure, right pure) neutrosophic triplet set. Then is called left (resp., right, left pure, right pure) neutrosophic triplet -semihypergroup, if the following conditions are satisfied:
- is well defined.
- satisfies the left invertive law.
Example 3. 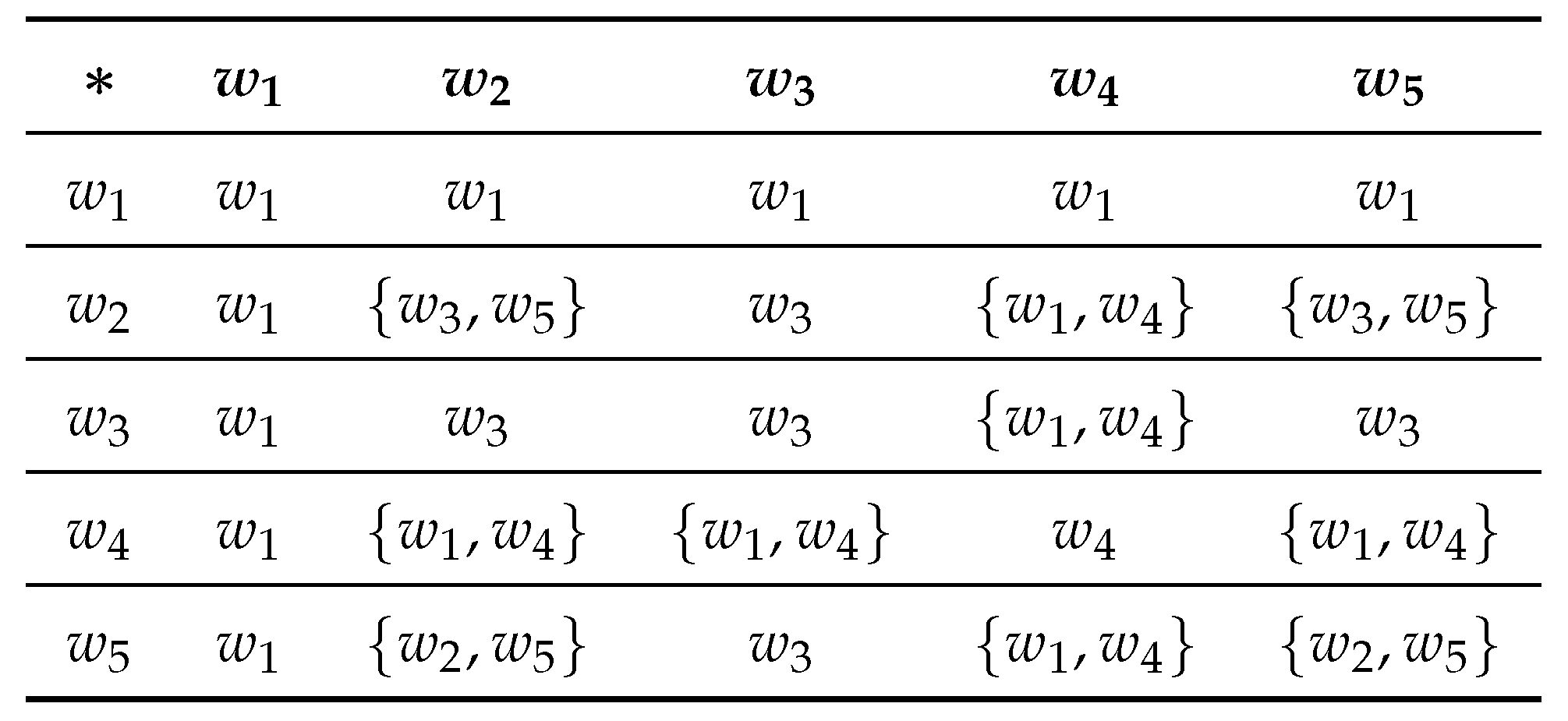
Let be a set with the hyperoperation defined as follows:
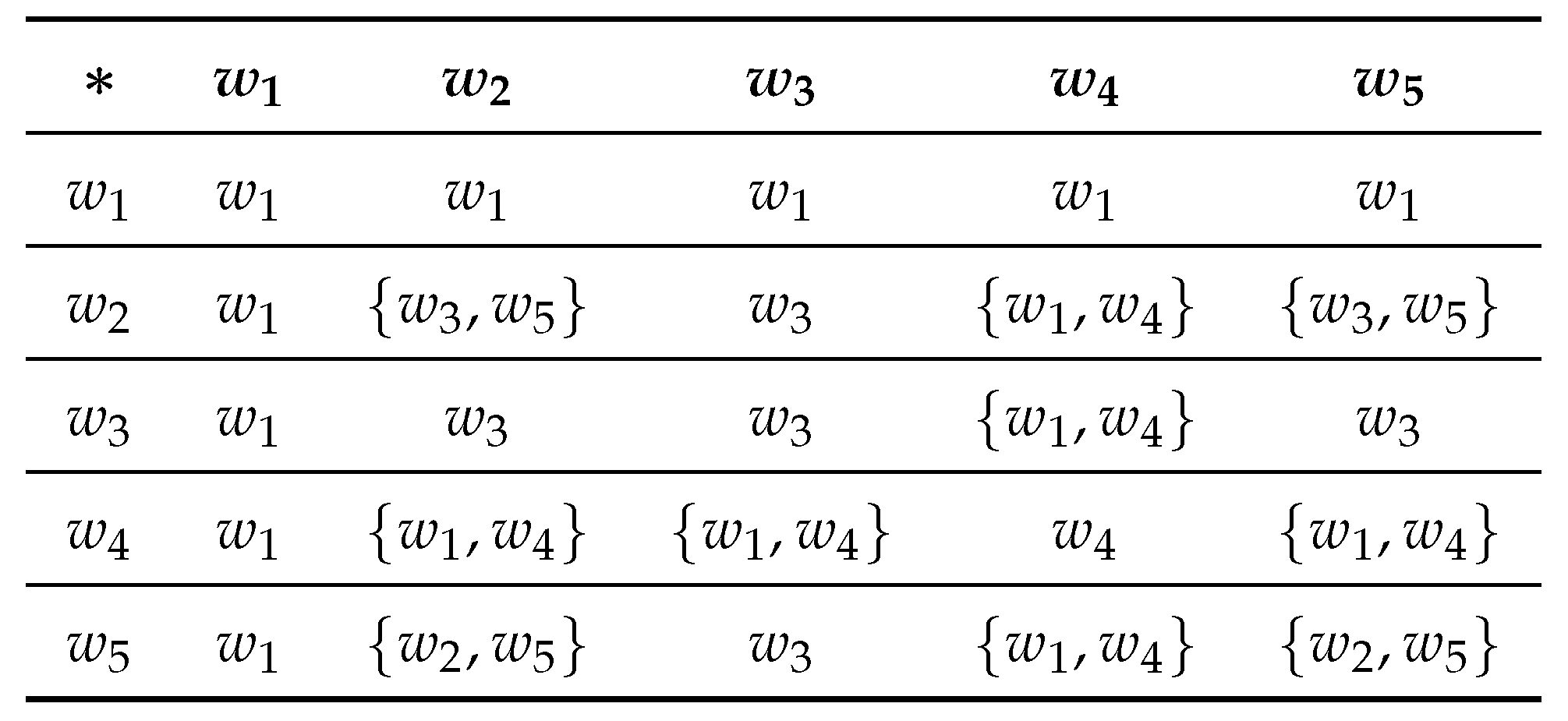
A Cayley table 2
Here is an -semihypergroup, as the element of satisfies the left invertive law. Here and are left neutrosophic triplets. Hence is a left neutrosophic triplet -semihypergroup.
Definition 9.
Let be neutrosophic (resp., pure neutrosophic) triplet set. Then is said to be neutrosophic (resp., pure neutrosophic) triplet -semihypergroup, if the following condition are satisfied:
- is a well defined.
- satisfies the left invertive law.
Example 4. 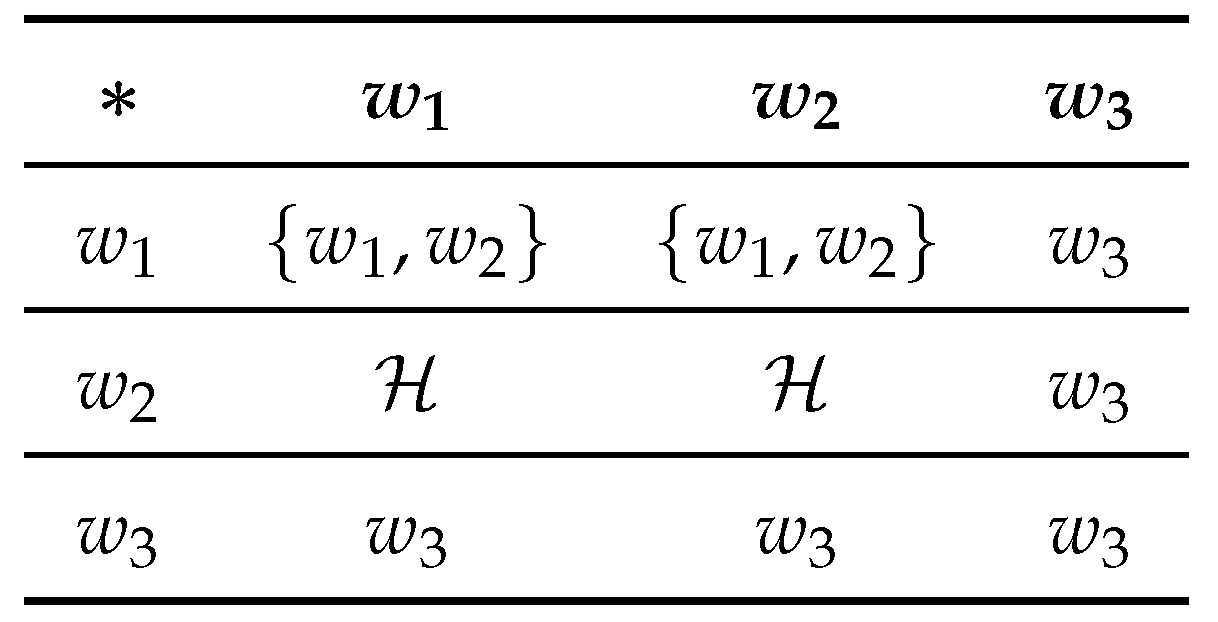
Let and the hyperoperation defined in the table as follows:
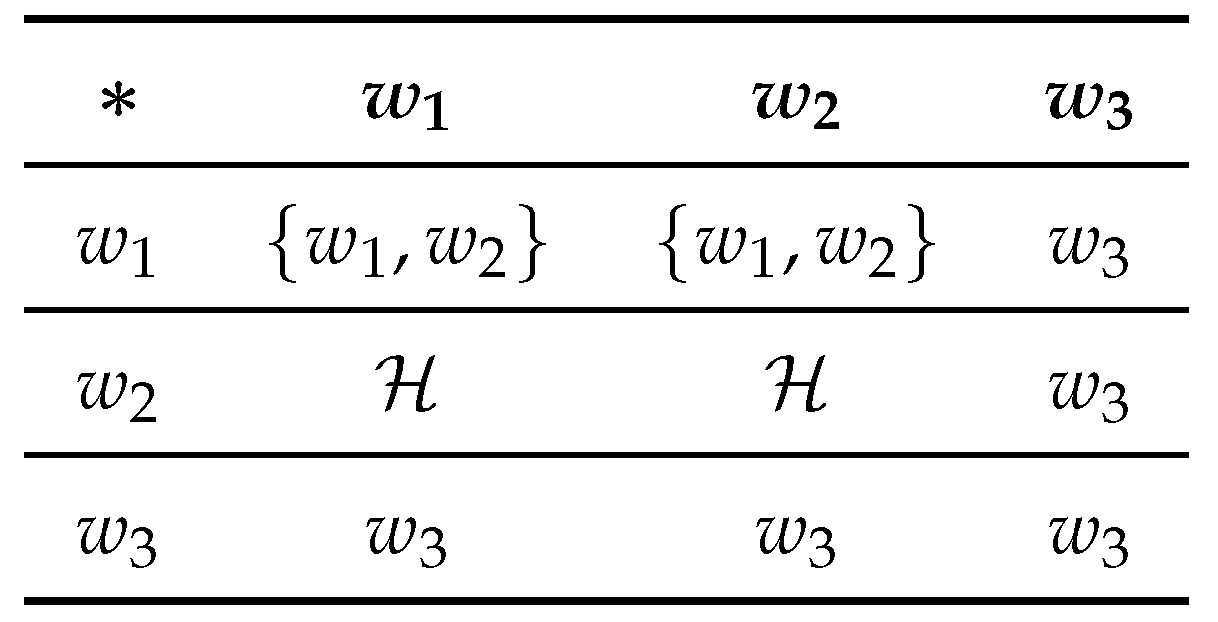
A Cayley table 3
Here is an -semihypergroup, as the element of satisfies the left invertive law. Here and are neutrosophic triplets. Hence is a neutrosophic triplet -semihypergroup.
Remark 1.
Neut() of an element “” is not unique under the hyperoperation ∗ in and depend on elements and hyperoperation. By the Example 4 neut Similarly of an element “” is not unique and depends on the element and the hyperoperation ∗.
Remark 2.
Left neut of an element is could be different from left identity.
Definition 10.
Let be a neutrosophic -semihypergroup. An element then there exist pure left such that and pure left such that
Proposition 1.
Let be a pure left neutrosophic triplet -semihypergroup with pure left identity. Then if and only if
Proof.
Suppose that for Since is a pure left neutrosophic semihypergroup, so Multiply to the right side of
Conversely, let Multiply to both right sides by
This completes the proof. ☐
Proposition 2.
Let be a pure right neutrosophic triplet -semihypergroup with pure left identity. Then if for all
Proof.
Suppose is a pure right neutrosophic triplet -semihypergroup with pure left identity and for Multiply to the left side of
Therefore,
☐
Proposition 3.
Let be a pure right neutrosophic triplet -semihypergroup. Then if for all
Proof.
Suppose is a pure right neutrosophic triplet -semihypergroup and for Multiply to the right side of
Therefore,
☐
Theorem 1.
Let be a pure right neutrosophic triplet idempotent -semihypergroup. Then .
Proof.
Consider Multiply first with to the right and then again multiply with to the right, i.e.,
This shows that
☐
Theorem 2.
Let be a pure right neutrosophic triplet idempotent -semihypergroup with pure left identity. Then
Proof.
Let be a pure right neutrosophic triplet -semihypergroup with pure left identity. Multiply to the left of both side i.e.,
This shows that
☐
Theorem 3.
Let be a pure right neutrosophic triplet -semihypergroup. Then
- for all
- for all
Proof.
1. Consider the left hand side . Multiply first with to the right and then again multiply with to the right, i.e.,
So
Now consider the right side Multiply first with to the right and then again multiply with to the right, i.e.,
So
From the Equations (2) and (3) it is clear that
2. Consider the left hand side . Multiply first with to the right and then again multiply with to the right, i.e.,
So
Now consider the right side Multiply first with to the right and then again multiply with to the right, i.e.,
So
From the Equations (4) and (5) it is clear that
☐
In the following example, we show that in a left neutrosophic triplet -semihypergroup
Example 5. 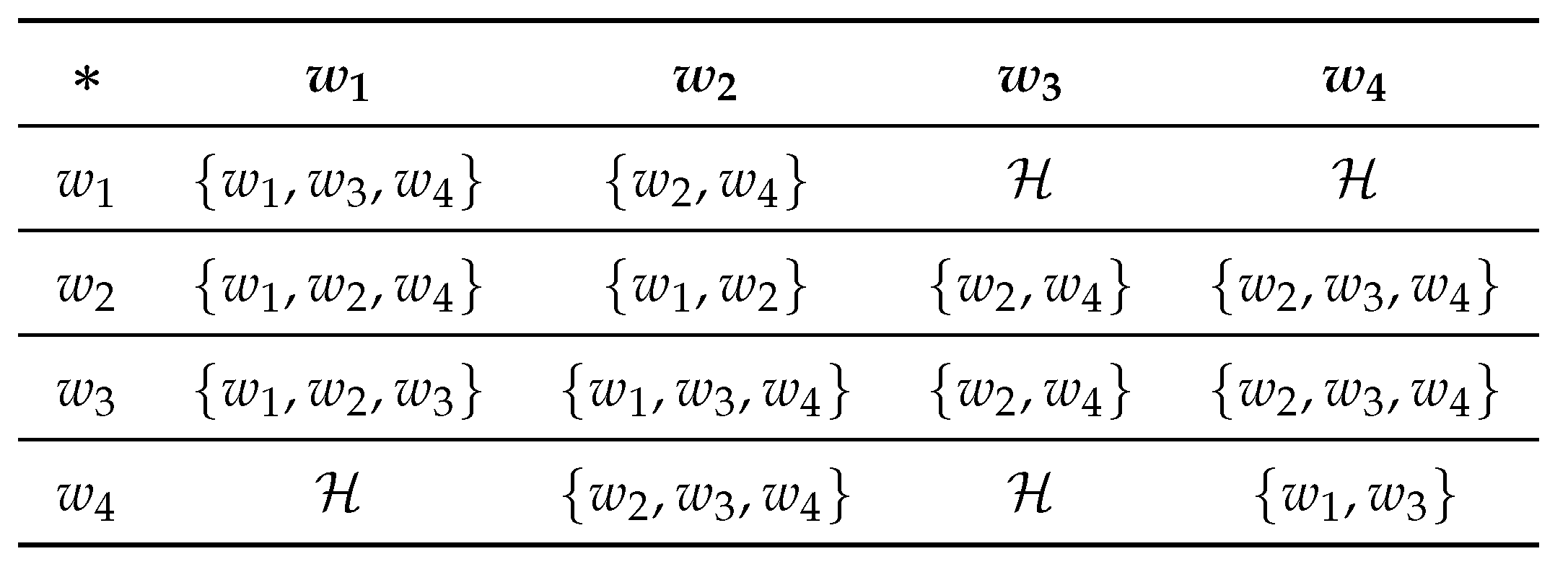 All the elements of satisfies the left invertive law. Here and are left neutrosophic triplets. Hence is a left neutrosophic triplet -semihypergroup. Now
All the elements of satisfies the left invertive law. Here and are left neutrosophic triplets. Hence is a left neutrosophic triplet -semihypergroup. Now
Let be a set with the hyperoperation defined as follow
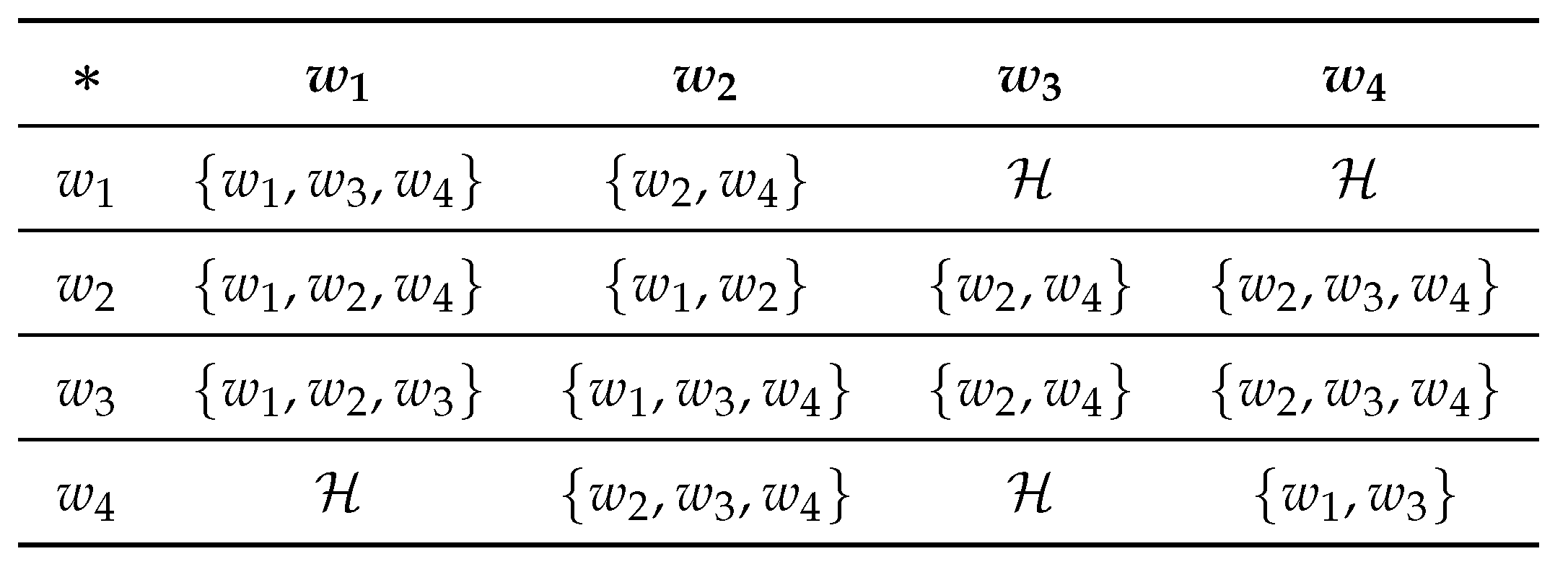
A Cayley table 4
Also
Hence this shows that and
Theorem 4.
Let be a pure left neutrosophic -semihypergroup. Then
Proof.
Let If we put then
Hence ☐
Theorem 5.
Let be a pure left neutrosophic -semihypergroup. Then
Proof.
Consider . Post multiplying both sides
Hence ☐
Definition 11.
Let be a neutrosophic -semihypergroup and let K be a subset of Then, K is called neutrosophic triplet -subsemihypergroup, if K itself is a neutrosophic triplet -semihypergroup.
Example 6. 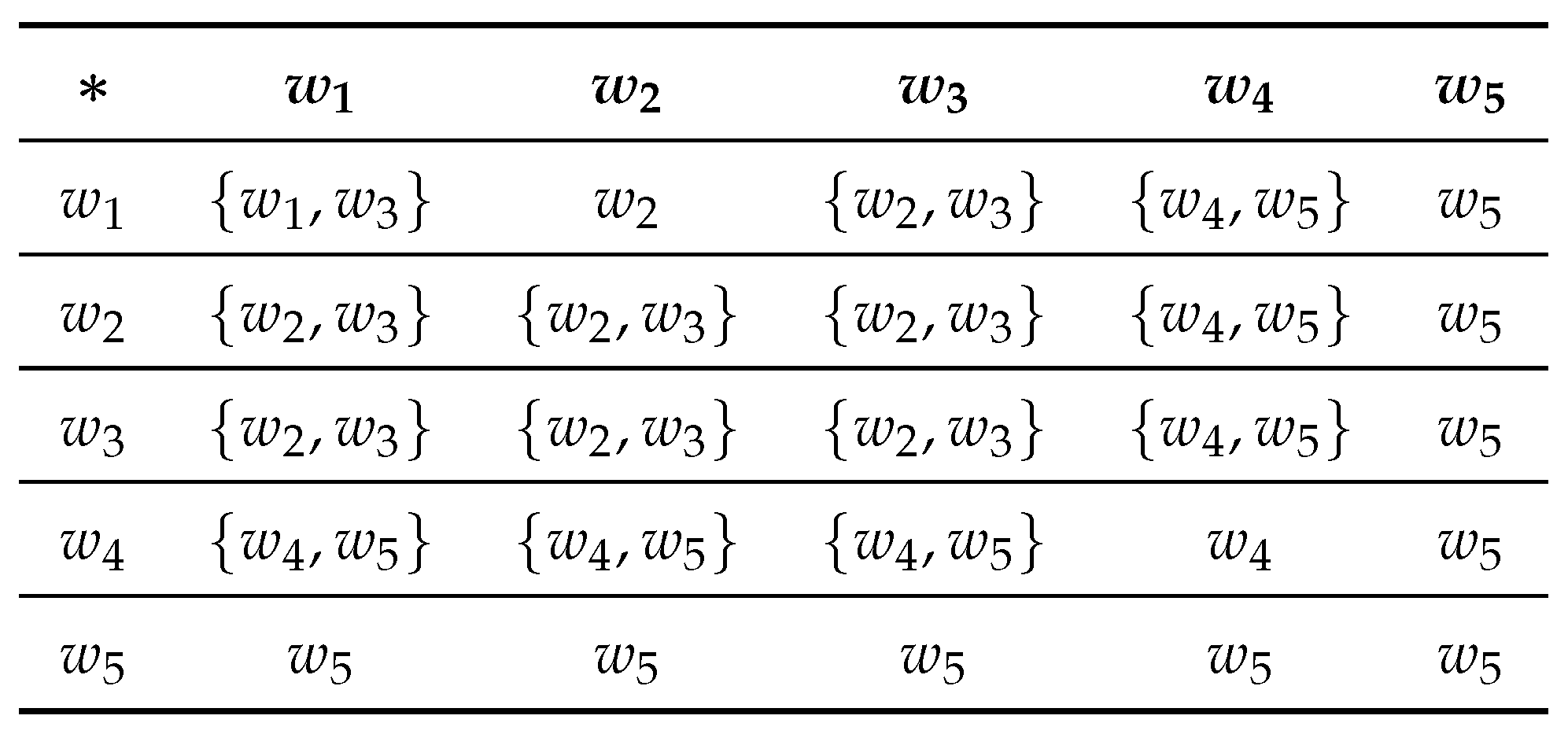 Here is an -semihypergroup, because the element of satisfies the left invertive law. Here and are neutrosophic triplet. Hence is a neutrosophic triplet -semihypergroup. Let be subset of . As K is a neutrosophic -semihypergroup under the Then K is called neutrosophic triplet -subsemihypergroup of .
Here is an -semihypergroup, because the element of satisfies the left invertive law. Here and are neutrosophic triplet. Hence is a neutrosophic triplet -semihypergroup. Let be subset of . As K is a neutrosophic -semihypergroup under the Then K is called neutrosophic triplet -subsemihypergroup of .
Let be a set with the hyperoperation defined in the table as follow

A Cayley table 5
Lemma 1.
Let K be a non-empty subset of a neutrosophic triplet -semihypergroup . The following are equivalent.
- K is a neutrosophic triplet -semihypergroup.
- For all
Proof.
The proof is straightforward. ☐
Definition 12.
Let and are two neutrosophic triplet -semihypergroups. Let be a mapping. Then f is called neutro-homomorphism if for all we have
Theorem 6.
Let be a neutro-homomorphism. Where and are two neutrosophic triplet -semihypergroup. Let
- The image of f is a neutrosophic triplet -subsemihypergroup of
- The inverse image of f is a neutrosophic -subsemihypergroup of .
Proof.
The proof is straightforward. ☐
Remark 3.
We have the following key points;
- Every neutrosophic triplet -semihypergroup is an -semihypergroup, but the reverse may or may not true.
- In neutrosophic triplet -semihypergroup, every element must have a left but in an -semihypergroup the left of an element may or may not exist.
- In neutrosophic -semihypergroup, every element must have left but in an -semihypergroup the element may or may not have semihypergroup.
- In neutrosophic -semihypergroup pure left is not equal to pure left Identity.
4. Application
Neutrosophic triplet -semihypergroups has many applications in different areas. Here, we present an application of neutrosophic triplet -semihypergroup in football. We can use different versions of neut and anti elements like left, right, pure left and pure right that we may see in different situations. The interesting prospect of this newly defined structure is that it is not comutative, so any change from the left and same types of change from the rigth of a certain element may affect the final results with respect to neut and anti.
Consider a Football team; the centre midfield player “” having a degree of performance The players “” and “” are the midfield player having degree of performance . Thus using Definition 6, the The players “” and “” are having better degree of performance , thus using Definition 6, the Neutrosophic triplet -semihypergroup can help the coach to select the players for filling the position in the playground, when a player gets injured. The major advantage of neutrosophic triplet -semihypergroup is that if we have a centre mid player and this player has the other players having the same performance on the right side as neut of it and it has one player on the left having better performance than it as shown in the following Figure 1.
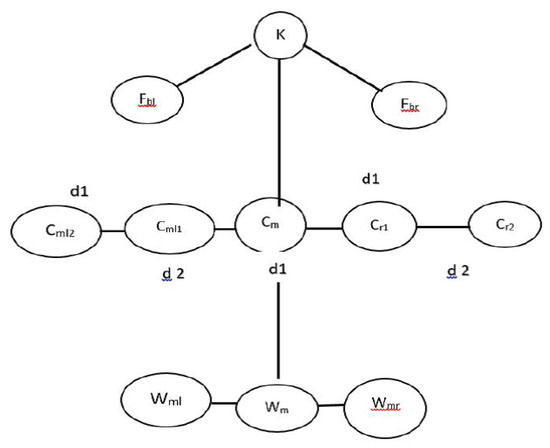
Figure 1.
A view of football match.
If the performance of a player playing on the left side and right side of a centre mid player is equal to performance of a centre mid player then the structure reduces to a duplet structure. Similarly, we can find many applications in different directions.
5. Conclusions
In this paper, we apply the idea of neutrosophic triplet sets at the very useful non-associative hyperstructures, namely -semihypergroups. We define neutrosophic triplet set (left, right, pure left, pure right). We discuss some basic results and an application of the proposed structure at the end. In future, we are aiming to extend this idea and give more interesting results.
Author Contributions
All authors contributed equally.
Funding
Universiti Kebangsaan Malaysia- Grant No. GUP-2017-105.
Acknowledgments
We are indebted to Universiti Kebangsaan Malaysia for providing financial support under the grant GUP-2017-105, and authors are highly grateful to referees for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smarandache, F. A Unifying Field in Logics. Neutrosophy, Neutrosophic Probability, Set and Logic; Rehoboth American Research Press: Rehoboth, NM, USA, 1999. [Google Scholar]
- Kandasamy, W.B.V.; Smarandache, F. Some Neutrosophic Algebraic Structures and Neutrosophic N-Algebraic Structures; Hexis: Phoenix, AZ, USA, 2006; p. 219. [Google Scholar]
- Kandasamy, W.B.V.; Smarandache, F. N-Algebraic Structures And S-N-Algebraic Structures; Hexis: Phoenix, AZ, USA, 2006; p. 209. [Google Scholar]
- Kandasamy, W.B.V.; Smarandache, F. Basic Neutrosophic Algebraic Structures and Their Applications to Fuzzy and Neutrosophic Models; Hexis: Phoenix, AZ, USA, 2004; p. 149. [Google Scholar]
- Al-Quran, A.; Hassan, N. The complex neutrosophic soft expert set and its application in decision making. J. Intell. Fuzzy Syst. 2018, 34, 569–582. [Google Scholar] [CrossRef]
- Al-Quran, A.; Hassan, N. The complex neutrosophic soft expert relation and its multiple attribute decision-making method. Entropy 2018, 20, 101. [Google Scholar] [CrossRef]
- Abu Qamar, M.; Hassan, N. Q-neutrosophic soft relation and its application in decision making. Entropy 2018, 20, 172. [Google Scholar]
- Abu Qamar, M.; Hassan, N. Entropy, measures of distance and similarity of Q-neutrosophic soft sets and some applications. Entropy 2018, 20, 672. [Google Scholar]
- Uluçay, V.; Sahin, M.; Hassan, N. Generalized neutrosophic soft expert set for multiple-criteria decision-making. Symmetry 2018, 10, 437. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras. And Applications; Pons Publishing House: Brussels, Belgium, 2017. [Google Scholar]
- Zhang, X.H.; Smarandache, F.; Liang, X.L. Neutrosophic duplet semi-group and cancellable neutrosophic triplet groups. Symmetry 2017, 9, 275. [Google Scholar] [CrossRef]
- Bal, M.; Shalla, M.M.; Olgun, N. Neutrosophic triplet cosets and quotient groups. Symmetry 2018, 10, 126. [Google Scholar] [CrossRef]
- Jaiyeola, T.G.; Smarandache, F. Some results on neutrosophic triplet group and their applications. Symmetry 2018, 10, 202. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2018, 29, 595–601. [Google Scholar] [CrossRef]
- Marty, F. Sur une generalization de la notion de groupe. In Proceedings of the 8th Congres des Mathematicians Scandinaves, Stockholm, Sweden; 1934; pp. 45–49. [Google Scholar]
- Corsini, P. Prolegomena of Hypergroup Theory; Aviani Editore: Udine, Italy, 1993. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press: Palm Harbor, FL, USA, 1994. [Google Scholar]
- Corsini, P.; Leoreanu, V. Applications of Hyperstructure Theory; Kluwer Academic: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Vougiouklis, T. A new class of hyperstructures. J. Comb. Inf. Syst. Sci. 1995, 20, 229–235. [Google Scholar]
- Vougiouklis, T. ∂-operations and Hv-fields. Acta Math. Sin. (Engl. Ser.) 2008, 24, 1067–1078. [Google Scholar] [CrossRef]
- Vougiouklis, T. The h/v-Structures, Algebraic Hyperstructures and Applications; Taru Publications: New Delhi, India, 2004; pp. 115–123. [Google Scholar]
- Spartalis, S. On Hv-semigroups. Ital. J. Pure Appl. Math. 2002, 11, 165–174. [Google Scholar]
- Spartalis, S. On reversible Hv-group. In Proceedings of the 5th International Congress on Algebraic Hyperstructures and Applications, Jasi, Romania, 4–10 July 1993; pp. 163–170. [Google Scholar]
- Vougiouklis, T. The fundamental relation in hyperrings: The general hyperfield. In Proceedings of the Algebraic Hyperstructures and Applications, Xanthi, Greece, April 1991; pp. 203–211. [Google Scholar]
- Spartalis, S. Quoitients of P-Hv-rings. In New Frontiers in Hyperstructures; Hadronic Press: Palm Harbor, FL, USA, 1996; pp. 167–176. [Google Scholar]
- Spartalis, S.; Vougiouklis, T. The fundamental relations on Hv-rings. Riv. Mat. Pura Appl. 1994, 7, 7–20. [Google Scholar]
- Spartalis, S. On the number of Hv-rings with P-hyperoperations. Discret. Math. 1996, 155, 225–231. [Google Scholar] [CrossRef]
- Davvaz, B.; Fotea, V.L. Hyperring Theory and Applications; International Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Kazim, M.A.; Naseerudin, N. On almost semigroups. Aligarh Bull. Math. 1972, 2, 41–47. [Google Scholar]
- Kamran, M.S. Conditions for LA-Semigroups to Resemble Associative Structures. Ph.D. Thesis, Quaid-i-Azam University, Islamabad, Pakistan, 1993. [Google Scholar]
- Protic, P.V.; Stevanovic, N. AG-test and some general properties of Abel-Grassmann’s groupoids. Pure Math. Appl. 1995, 6, 371–383. [Google Scholar]
- Protic, P.V.; Stevanovic, N. The structural theorem for AG*-groupoids. Ser. Math. Inform. 1995, 10, 25–33. [Google Scholar]
- Yusuf, S.M. On Left Almost Ring. In Proceedings of the 7th International Pure Mathematics Conference, Islamabad, Pakistan, 5–7 August 2006. [Google Scholar]
- Hila, K.; Dine, J. On hyperideals in left almost semihypergroups. ISRN Algebra 2011, 2011, 953124. [Google Scholar] [CrossRef]
- Yaqoob, N.; Corsini, P.; Yousafzai, F. On intra-regular left almost semihypergroups with pure left identity. J. Math. 2013, 2013, 510790. [Google Scholar] [CrossRef]
- Yousafzai, F.; Hila, K.; Corsini, P.; Zeb, A. Existence of non-associative algebraic hyperstructures and related problems. Afr. Mat. 2015, 26, 981–995. [Google Scholar] [CrossRef]
- Amjad, V.; Hila, K.; Yousafzai, F. Generalized hyperideals in locally associative left almost semihypergroups. N. Y. J. Math. 2014, 20, 1063–1076. [Google Scholar]
- Gulistan, M.; Yaqoob, N.; Shahzad, M. A Note On Hv-LA-semigroup. UPB Sci. Bull. Ser. A 2015, 77, 93–106. [Google Scholar]
- Yaqoob, N.; Gulistan, M. Partially ordered left almost semihypergroups. J. Egypt. Math. Soc. 2015, 23, 231–235. [Google Scholar] [CrossRef]
- Rehman, I.; Yaqoob, N.; Nawaz, S. Hyperideals and hypersystems in LA-hyperrings. Songklanakarin J. Sci. Technol. 2017, 39, 651–657. [Google Scholar]
- Nawaz, S.; Rehman, I.; Gulistan, M. On left almost semihyperrings. Int. J. Anal. Appl. 2018, 16, 528–541. [Google Scholar]
- Yaqoob, N.; Cristea, I.; Gulistan, M.; Nawaz, S. Left almost polygroups. Ital. J. Pure Appl. Math. 2018, 39, 465–474. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).