Applications of Cubic Structures to Subsystems of Finite State Machines

Abstract

This paper concerns three relationship between the recently proposed cubic sets and finite state machines. The notions of cubic finite state machine (cubic FSM), a subsystem of cubic FSM and cartesian composition (direct product, P-(R-) union, and P-(R-) intersection) of two subsystems of cubic FSMs are introduced. We study the cartesian composition, direct product and union of two subsystems of cubic FSMs is a subsystem of a cubic FSM. We provide many examples on each case. We consider conditions for subsystem of cubic FSM to be both an internal cubic subsystem of cubic FSM and an external cubic subsystem of cubic FSM.

1. Introduction

Zadeh presented the idea of fuzzy subset of a set [1]. Fuzzy sets have been applied in disciplines including social sciences, automata theory, medical sciences, pattern recognition, engineering, robotics, statistics, artificial intelligence and decision making.

The authors introduced cubic fsm, cubic successor, cubic transformation semigroups and cubic subsystems in their work [2]. Dörfler [3] introduced new type of product which is called the “Cartesian composition” in his work. The concept of soft finite state machine is introduced in [4], in which the authors applied soft set theory to fsms. Recently, Jun introduced “intuitionistic ffsms” and “intuitionistic ftss”, as well as produced some interesting results (see [5,6,7,8]).

Jun, Kim and Yang introduced P-union and the P-intersection of internal cubic sets [9] and prove that the “P-union and the P-intersection of external cubic sets need not be external cubic sets, and the R-union and the R-intersection of internal (resp. external) cubic sets need not be internal (resp. external) cubic sets”. Jun, Lee and Kang studied Relations between cubic p-ideals (respectively, a-ideals and q-ideals) [10].

Hwang presented the concepts of fuzzy submachine, which are the generalized form of crisp submachine of a fuzzy finite state machine [11]. Finite state machines are also studied in terms of some generalized fuzzy sets, for instance bipolar fuzzy sets [12], N-fuzzy sets [13] and interval neutrosophic sets [14]. Kumbhojkar and Chaudhari [15] gave different ways of the construction of products of ffsms. The authors in [16] studied the concept of the “Cartesian composition of fuzzy finite state machines” and showed that fuzzyfinite state machines and their Cartesian composition share many structural properties. Algebraic techniques are very significant in the study of ffsms. Malik et al. [17,18,19] applied algebraic techniques to fuzzy automata based on Wee’s concept.

Liu, Mo, Qiu and Wang introduced seven ways of construction of products for “Mealy-type fuzzy finite state machines” [20]. The authors proved that the covering relationship is held in the product of factor machines.

In Section 2, we discuss basic definitions and results. In Section 3, we provide proofs of some results on cubic subsystem of finite state machines. In Section 4, we define some operations on subsystems of cubic finite state machines and some related results are provided. Finally, in Section 5, we discuss some results related with external cubic subsystems of cubic finite state machines.

2. Preliminaries

Definition 1.

[1] “A map A map $\lambda :X\to [0,1]$ is called a fuzzy set of X.”

An interval number is $\tilde{u}=[u^{-},u^{+}]$, where $0\le u^{-}\le u^{+}\le 1$. Let $D[0,1]$ denote the family of all closed subintervals of $[0,1]$, i.e.,

$$D[0,1]=\{\tilde{u}=[u^{-},u^{+}]:u^{-}\le u^{+}, \mathrm{for} u^{-},u^{+}\in I\}.$$

We define the operations $″⪰″,$ $″⪯″,$ $″=″,$ $″rmin″$ and $″rmax″$ in case of two elements in $D[0,1].$ We consider two elements $\tilde{u}=[u^{-},u^{+}]$ and $\tilde{v}=[v^{-},v^{+}]$ in $D[0,1].$ Then,

(i)

$\tilde{u}⪰\tilde{v}$ if and only if $u^{-}\ge v^{-}$ and $u^{+}\ge v^{+}$,

(ii)

$\tilde{u}⪯\tilde{v}$ if and only if $u^{-}\le v^{-}$ and $u^{+}\le v^{+}$,

(iii)

$\tilde{u}=\tilde{v}$ if and only if $u^{-}=v^{-}$ and $u^{+}=v^{+}$,

(iv)

$rmin\{\tilde{u},\tilde{v}\}=\left[min\{u^{-},v^{-}\},min\{u^{+},v^{+}\}\right]$,

(v)

$rmax\{\tilde{u},\tilde{v}\}=\left[max\{u^{-},v^{-}\},max\{u^{+},v^{+}\}\right].$

It is obvious that ($D[0,1],⪯,\vee ,\wedge$) is a complete lattice with $\tilde{0}=[0,0]$ as its least element and $\tilde{1}=[1,1]$ as its greatest element. Let $\widetilde{u_i}\in D[0,1]$ where $i\in \mathsf{\Lambda }.$ We define

$${\displaystyle \underset{i\in \mathsf{\Lambda }}{\mathrm{rinf}}}{\tilde{u}}_i=\left[{\displaystyle \underset{i\in \mathsf{\Lambda }}{inf}}{u}_i^{-},{\displaystyle \underset{i\in \mathsf{\Lambda }}{inf}}{u}_i^{+}\right]\mathrm{and}{\displaystyle \underset{i\in \mathsf{\Lambda }}{\mathrm{rsup}}}{\tilde{u}}_i=\left[{\displaystyle \underset{i\in \mathsf{\Lambda }}{sup}}{u}_i^{-},{\displaystyle \underset{i\in \mathsf{\Lambda }}{sup}}{u}_i^{+}\right].″$$

Definition 2.

[1] “An interval valued fuzzy set (briefly, IVF-set) ${\tilde{\delta }}_A$ on X is defined as

$${\tilde{\delta }}_A=\left\{⟨x,[{\delta }_A^{-}(x),{\delta }_A^{+}(x)]⟩:x\in X\right\},$$

where ${\delta }_A^{-}(x)\le {\delta }_A^{+}(x)$, for all $x\in X$. Then, the ordinary fuzzy sets ${\delta }_A^{-}:X\to [0,1]$ and ${\delta }_A^{+}:X\to [0,1]$ are called a lower fuzzy set and an upper fuzzy set of $\tilde{\delta }$, respectively. Let ${\tilde{\delta }}_A(x)=[{\delta }_A^{-}(x),{\delta }_A^{+}(x)].$ Then,

$$A=\left\{⟨x,{\tilde{\delta }}_A(x)⟩:x\in X\right\},$$

where ${\tilde{\delta }}_A:X⟶D[0,1].$ ”

Definition 3.

[12] “Let X be a non-empty set. By a cubic set in X we mean a structure

$$\mathcal{A}=\left\{⟨x,{\tilde{\delta }}_{\mathcal{A}}(x),{\omega }_{\mathcal{A}}(x)⟩|x\in X\right\}$$

in which ${\tilde{\delta }}_{\mathcal{A}}$ is an IVF set in X and ${\omega }_{\mathcal{A}}$ is a fuzzy set in X.”

Definition 4.

[12] “Let X be a non-empty set. A cubic set $\mathcal{A}=⟨{\tilde{\delta }}_{\mathcal{A}},{\omega }_{\mathcal{A}}⟩$ in X is said to be an internal cubic set (briefly, ICS) if

$${\delta }_{\mathcal{A}}^{-}(x)\le {\omega }_{\mathcal{A}}(x)\le {\delta }_{\mathcal{A}}^{+}(x)$$

for all $x\in X.$”

Definition 5.

[12] “Let X be a non-empty set. A cubic set $\mathcal{A}=⟨{\tilde{\delta }}_{\mathcal{A}},{\omega }_{\mathcal{A}}⟩$ in X is said to be an external cubic set (briefly, ECS) if

$${\omega }_{\mathcal{A}}(x)\notin ({\delta }_{\mathcal{A}}^{-}(x),{\delta }_{\mathcal{A}}^{+}(x))$$

for all $x\in X.$”

Definition 6.

[12] “For any $A_i=\left\{⟨x,{\tilde{\delta }}_{A_i}(x),{\omega }_{A_i}(x)⟩|x\in X\right\}$ where $i\in \mathsf{\Lambda },$ we define

(a)

${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcup }_R}}{A}_i=\left\{⟨x,\left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}{\tilde{\delta }}_{A_i}\right)(x),\left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigwedge }}{\omega }_{A_i}\right)(x)⟩|x\in X\right\}$ (R-union)

(b)

${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcup }_p}}{A}_i=\left\{⟨x,\left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}{\tilde{\delta }}_{A_i}\right)(x),\left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigvee }}{\omega }_{A_i}\right)(x)⟩|x\in X\right\}$ (P-union)

(c)

${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcap }_R}}{A}_i=\left\{⟨x,\left({\displaystyle \bigcap _{i\in \mathsf{\Lambda }}}{\tilde{\delta }}_{A_i}\right)(x),\left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigvee }}{\omega }_{A_i}\right)(x)⟩|x\in X\right\}$ (R-intersection)

(d)

${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcap }_p}}{A}_i=\left\{⟨x,\left({\displaystyle \bigcap _{i\in \mathsf{\Lambda }}}{\tilde{\delta }}_{A_i}\right)(x),\left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigwedge }}{\omega }_{A_i}\right)(x)⟩|x\in X\right\}$ (P-intersection)”

Definition 7.

[2] “A cubic finite state machine (cubic FSM, shortly) is a triple $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$, where $\mathcal{S}$ and X are finite non-empty sets, called the set of states and the set of input symbols, respectively, and $\mathcal{A}=⟨{\tilde{\delta }}_{\mathcal{A}},{\omega }_{\mathcal{A}}⟩$ is a cubic set in $\mathcal{S}\times X\times \mathcal{S}.$”

“Let $X^{*}$ denote the set of all words of elements of X of finite length. Let $\lambda$ denote the empty word in $X^{*}$ and $\left|x\right|$ denote the length of x for every $x\in X^{*}.$”

Definition 8.

[2] “Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Define a cubic set ${\mathcal{A}}^{*}=⟨{\tilde{\delta }}_{\mathcal{A}}^{*},{\omega }_{\mathcal{A}}^{*}⟩$ in $\mathcal{S}\times X^{*}\times \mathcal{S}$ by

$${\tilde{\delta }}_{\mathcal{A}}^{*}(p,\lambda ,q)=\left\{\begin{array}{cc}\hfill [1,1]& if p=q\\ \hfill [0,0]& if p\ne q\end{array}\right.,{\omega }_A^{*}(p,\lambda ,q)=\left\{\begin{array}{cc}\hfill 0& if p=q\\ \hfill 1& if p\ne q\end{array}\right.$$

and

$${\tilde{\delta }}_{\mathcal{A}}^{*}(p,xa,q)={\displaystyle \underset{r\in \mathcal{S}}{\bigvee }}\left[{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,r)\wedge {\tilde{\delta }}_{\mathcal{A}}(r,a,q)\right]$$

$${\omega }_A^{*}(p,xa,q)={\displaystyle \underset{r\in \mathcal{S}}{\bigwedge }}\left[{\omega }_A^{*}(p,x,r)\vee {\omega }_A(r,a,q)\right]$$

for all $p,q\in \mathcal{S},$ $x\in X^{*}$ and $a\in X.$”

Lemma 1.

[2] “Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Then,

$${\tilde{\delta }}_{\mathcal{A}}^{*}(p,xy,q)={\displaystyle \underset{r\in \mathcal{S}}{\bigvee }}\left[{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,r)\wedge {\tilde{\delta }}_{\mathcal{A}}^{*}(r,y,q)\right]$$

$${\omega }_A^{*}(p,xy,q)={\displaystyle \underset{r\in \mathcal{S}}{\bigwedge }}\left[{\omega }_A^{*}(p,x,r)\vee {\omega }_A(r,y,q)\right]$$

for all $p,q\in \mathcal{S}$ and $x,y\in X^{*}.$”

3. Subsystems of Cubic Finite State Machines

Definition 9.

[2] “Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $\widehat{\mathcal{A}}=⟨{\tilde{\delta }}_{\widehat{\mathcal{A}}},{\omega }_{\widehat{\mathcal{A}}}⟩$ be a cubic subset in $\mathcal{S}.$ Then, $⟨\mathcal{S},\widehat{\mathcal{A}},X,\mathcal{A}⟩$ is called a cubic subsystem of $\mathcal{F}$ if and only if

$${\tilde{\delta }}_{\widehat{\mathcal{A}}}(q_2)⪰rmin\{{\tilde{\delta }}_{\widehat{\mathcal{A}}}(q_1),{\tilde{\delta }}_{\mathcal{A}}(q_1,a,q_2)\},$$

$${\omega }_{\widehat{\mathcal{A}}}(q_2)\le max\{{\omega }_{\widehat{\mathcal{A}}}(q_1),{\omega }_{\mathcal{A}}(q_1,a,q_2)\}.$$

for all $q_1,q_2\in \mathcal{S}$ and $a\in X.$”

If the cubic subsystem of $\mathcal{F}$ is $⟨\mathcal{S},\widehat{\mathcal{A}},X,\mathcal{A}⟩,$ then we simply write $\widehat{\mathcal{A}}$ for $⟨\mathcal{S},\widehat{\mathcal{A}},X,\mathcal{A}⟩.$

Example 1.

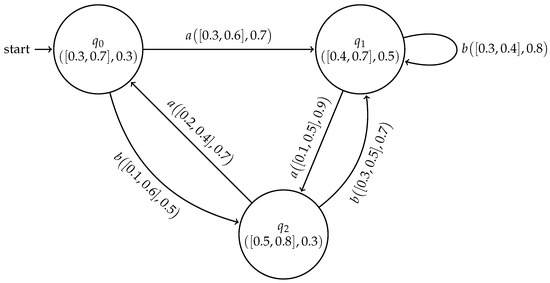
Let $\mathcal{S}=\{q_0,q_1,q_2\}$ and $X=\{a,b\}.$ Let $\mathcal{A}=⟨{\tilde{\delta }}_{\mathcal{A}},{\omega }_{\mathcal{A}}⟩$ be a cubic subset in $\mathcal{S}\times X\times \mathcal{S}$ defined by the table

$\mathcal{S}\times X\times \mathcal{S}$	${\tilde{\mathbf{\delta }}}_{\mathcal{A}}$	${\mathbf{\omega }}_{\mathcal{A}}$
$(q_0,a,q_1)$	$[0.3,0.6]$	$0.7$
$(q_1,a,q_2)$	$[0.1,0.5]$	$0.9$
$(q_2,a,q_0)$	$[0.2,0.4]$	$0.7$
$(q_0,b,q_2)$	$[0.1,0.6]$	$0.5$
$(q_2,b,q_1)$	$[0.3,0.5]$	$0.7$
$(q_1,b,q_1)$	$[0.3,0.4]$	$0.8$

Thus, $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ is a cubic FSM. Let $\widehat{\mathcal{A}}=⟨{\tilde{\delta }}_{\widehat{\mathcal{A}}},{\omega }_{\widehat{\mathcal{A}}}⟩$ be a cubic subset in $\mathcal{S}$ defined by the table

$\mathcal{S}$	${\tilde{\mathbf{\delta }}}_{\widehat{\mathcal{A}}}$	${\mathbf{\omega }}_{\widehat{\mathcal{A}}}$
$q_0$	$[0.3,0.7]$	$0.3$
$q_1$	$[0.4,0.7]$	$0.5$
$q_2$	$[0.5,0.8]$	$0.3$

Then, the transition diagram is shown in Figure 1 as follows:

Figure 1. Cubic subsystem $\widehat{\mathcal{A}}$.

Theorem 1.

[2] “Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $\widehat{\mathcal{A}}=⟨{\tilde{\delta }}_{\widehat{\mathcal{A}}},{\omega }_{\widehat{\mathcal{A}}}⟩$ be a cubic subset in $\mathcal{S}.$ Then, $⟨\mathcal{S},\widehat{\mathcal{A}},X,\mathcal{A}⟩$ is a cubic subsystem of $\mathcal{F}$ if and only if

$${\tilde{\delta }}_{\widehat{\mathcal{A}}}(q_2)⪰rmin\{{\tilde{\delta }}_{\widehat{\mathcal{A}}}(q_1),{\tilde{\delta }}_{\mathcal{A}}^{*}(q_1,x,q_2)\},$$

$${\omega }_{\widehat{\mathcal{A}}}(q_2)\le max\{{\omega }_{\widehat{\mathcal{A}}}(q_1),{\omega }_{\mathcal{A}}^{*}(q_1,x,q_2)\}.$$

for all $q_1,q_2\in \mathcal{S}$ and $x\in X^{*}.$”

Definition 10.

“Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $p,q\in \mathcal{S}.$ Then, the immediate successor p of q is defined as, if $\exists a\in X$ such that ${\tilde{\delta }}_{\mathcal{A}}(q,a,p)\succ [0,0]$ and ${\omega }_{\mathcal{A}}(q,a,p)<1.$ p is called a successor of q if $\exists x\in X^{*}$ such that ${\tilde{\delta }}_{\mathcal{A}}^{*}(q,x,p)\succ [0,0]$ and ${\omega }_{\mathcal{A}}^{*}(q,x,p)<1.$”

Let $q\in \mathcal{S}.$ Then, the set of successors of q is denoted by $S(q).$ If T is contained in $\mathcal{S},$ then we define $S(T)=\cup \{S(q)|q\in T\}.$

Definition 11.

“Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM and let $\widehat{\eta }=⟨{\tilde{\delta }}_{\widehat{\eta }},{\omega }_{\widehat{\eta }}⟩$ be a cubic subset of $\mathcal{S}.$ For all $x\in X^{*},$ define the cubic subset $\widehat{\eta }x$ of $\mathcal{S}$ by

$$({\tilde{\delta }}_{\widehat{\eta }}x)(q)={\displaystyle \underset{p\in \mathcal{S}}{rsup}}\{rmin\{{\tilde{\delta }}_{\widehat{\eta }}(p),{\tilde{\delta }}_{\mathcal{A}}(p,x,q)\}\},$$

and

$$({\omega }_{\widehat{\eta }}x)(q)={\displaystyle \underset{p\in \mathcal{S}}{inf}}\{max\{{\omega }_{\widehat{\eta }}(p),{\omega }_{\mathcal{A}}(p,x,q)\}\}.{}^{\prime \prime }$$

Proposition 1.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Then, for all cubic subsets $\widehat{\eta }=⟨{\tilde{\delta }}_{\widehat{\eta }},{\omega }_{\widehat{\eta }}⟩$ of $\mathcal{S}$ and for all $x,y\in X^{*}$,

$$({\tilde{\delta }}_{\widehat{\eta }}x)y={\tilde{\delta }}_{\widehat{\eta }}(xy)and({\omega }_{\widehat{\eta }}x)y={\omega }_{\widehat{\eta }}(xy).$$

Proof. 

Consider a cubic subset $\widehat{\eta }=⟨{\tilde{\delta }}_{\widehat{\eta }},{\omega }_{\widehat{\eta }}⟩$ of $\mathcal{S}$. Let $x,y\in X^{*}.$ If $n=0,$ then $y=\lambda .$ Let $q\in \mathcal{S}.$ Now,

$$\begin{array}{ccc}\hfill (({\tilde{\delta }}_{\widehat{\eta }}x)\lambda )(q)& =& {\displaystyle \underset{p\in \mathcal{S}}{rsup}}\{rmin\{({\tilde{\delta }}_{\widehat{\eta }}x)(p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,\lambda ,q)\}\}\hfill \\ & =& ({\tilde{\delta }}_{\widehat{\eta }}x)(q),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill (({\omega }_{\widehat{\eta }}x)\lambda )(q)& =& {\displaystyle \underset{p\in \mathcal{S}}{inf}}\{max\{({\omega }_{\widehat{\eta }}x)(p),{\omega }_{\mathcal{A}}^{*}(p,\lambda ,q)\}\}\hfill \\ & =& ({\omega }_{\widehat{\eta }}x)(q).\hfill \end{array}$$

Hence, $({\tilde{\delta }}_{\widehat{\eta }}x)\lambda ={\tilde{\delta }}_{\widehat{\eta }}x={\tilde{\delta }}_{\widehat{\eta }}(x\lambda )$ and $({\omega }_{\widehat{\eta }}x)\lambda ={\omega }_{\widehat{\eta }}x={\omega }_{\widehat{\eta }}(x\lambda )$. Assume that the result is true ∀$u\in X^{*}$ such that $\left|u\right|=n-1,$ $n>0$ and for all $\widehat{\eta }$. Let $y=ua,$ where $a\in X$, $u\in X^{*}$ and $\left|u\right|=n-1$. Let $q\in \mathcal{S}.$ Then,

$$\begin{array}{ccc}\hfill ({\tilde{\delta }}_{\widehat{\eta }}(xy))(q)& =& ({\tilde{\delta }}_{\widehat{\eta }}(xua))(q)=({\tilde{\delta }}_{\widehat{\eta }}((xu)a))(q)\hfill \\ & =& {\displaystyle \underset{r\in \mathcal{S}}{rsup}}\left\{rmin\left\{({\tilde{\delta }}_{\widehat{\eta }}(xu))(r),{\tilde{\delta }}_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{r\in \mathcal{S}}{rsup}}\left\{rmin\left\{{\displaystyle \underset{s\in \mathcal{S}}{rsup}}\left\{rmin\left\{({\tilde{\delta }}_{\widehat{\eta }}(x))(s),{\tilde{\delta }}_{\mathcal{A}}^{*}(s,u,r)\right\}\right\},{\tilde{\delta }}_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{s\in \mathcal{S}}{rsup}}\left\{rmin\left\{({\tilde{\delta }}_{\widehat{\eta }}(x))(s),{\displaystyle \underset{r\in \mathcal{S}}{rsup}}\left\{rmin\left\{{\tilde{\delta }}_{\mathcal{A}}^{*}(s,u,r),{\tilde{\delta }}_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\right\}\right\}\hfill \\ & =& {\displaystyle \underset{s\in \mathcal{S}}{rsup}}\left\{rmin\left\{({\tilde{\delta }}_{\widehat{\eta }}(x))(s),{\tilde{\delta }}_{\mathcal{A}}^{*}(s,ua,q)\right\}\right\}\hfill \\ & =& (({\tilde{\delta }}_{\widehat{\eta }}x)ua)(q)\hfill \\ & =& (({\tilde{\delta }}_{\widehat{\eta }}x)y)(q),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill ({\omega }_{\widehat{\eta }}(xy))(q)& =& ({\omega }_{\widehat{\eta }}(xua))(q)=({\omega }_{\widehat{\eta }}((xu)a))(q)\hfill \\ & =& {\displaystyle \underset{r\in \mathcal{S}}{inf}}\left\{max\left\{({\omega }_{\widehat{\eta }}(xu))(r),{\omega }_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{r\in \mathcal{S}}{inf}}\left\{max\left\{{\displaystyle \underset{s\in \mathcal{S}}{inf}}\left\{max\left\{({\omega }_{\widehat{\eta }}(x))(s),{\omega }_{\mathcal{A}}^{*}(s,u,r)\right\}\right\},{\omega }_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{s\in \mathcal{S}}{inf}}\left\{max\left\{({\omega }_{\widehat{\eta }}(x))(s),{\displaystyle \underset{r\in \mathcal{S}}{inf}}\left\{max\left\{{\omega }_{\mathcal{A}}^{*}(s,u,r),{\omega }_{\mathcal{A}}^{*}(r,a,q)\right\}\right\}\right\}\right\}\hfill \\ & =& {\displaystyle \underset{s\in \mathcal{S}}{inf}}\left\{max\left\{({\omega }_{\widehat{\eta }}(x))(s),{\omega }_{\mathcal{A}}^{*}(s,ua,q)\right\}\right\}\hfill \\ & =& (({\omega }_{\widehat{\eta }}x)ua)(q)\hfill \\ & =& (({\omega }_{\widehat{\eta }}x)y)(q).\hfill \end{array}$$

Hence, $({\tilde{\delta }}_{\widehat{\eta }}x)y={\tilde{\delta }}_{\widehat{\eta }}(xy)$ and $({\omega }_{\widehat{\eta }}x)y={\omega }_{\widehat{\eta }}(xy).$ ☐

Theorem 2.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM and let $\widehat{\eta }=⟨{\tilde{\delta }}_{\widehat{\eta }},{\omega }_{\widehat{\eta }}⟩$ be a cubic subset of $\mathcal{S}.$ Then, $\widehat{\eta }$ is subsystem of $\mathcal{F}$ if and only ${\tilde{\delta }}_{\widehat{\eta }}x\subseteq {\tilde{\delta }}_{\widehat{\eta }}$ and ${\omega }_{\widehat{\eta }}x\supseteq {\omega }_{\widehat{\eta }}$ for all $x\in X^{*}.$

Proof. 

Let $\widehat{\eta }$ be a subsystem of $\mathcal{F}$. Let $x\in X^{*}$ and $q\in \mathcal{S}.$ Then,

$$\begin{array}{ccc}\hfill ({\tilde{\delta }}_{\widehat{\eta }}x)(q)& =& {\displaystyle \underset{p\in \mathcal{S}}{rsup}}\{rmin\{{\tilde{\delta }}_{\widehat{\eta }}(p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,q)\}\}\hfill \\ & ⪯& {\tilde{\delta }}_{\widehat{\eta }}(q),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill ({\omega }_{\widehat{\eta }}x)(q)& =& {\displaystyle \underset{p\in \mathcal{S}}{inf}}\{max\{{\omega }_{\widehat{\eta }}(p),{\omega }_{\mathcal{A}}^{*}(p,x,q)\}\}\hfill \\ & ⪯& {\omega }_{\widehat{\eta }}(q).\hfill \end{array}$$

Hence, ${\tilde{\delta }}_{\widehat{\eta }}x\subseteq {\tilde{\delta }}_{\widehat{\eta }}$ and ${\omega }_{\widehat{\eta }}x\supseteq {\omega }_{\widehat{\eta }}.$ Conversely, suppose ${\tilde{\delta }}_{\widehat{\eta }}x\subseteq {\tilde{\delta }}_{\widehat{\eta }}$ and ${\omega }_{\widehat{\eta }}x\supseteq {\omega }_{\widehat{\eta }}$ for all $x\in X^{*}.$ Let $q\in \mathcal{S}$ and $x\in X^{*}.$ Now,

$$\begin{array}{ccc}\hfill {\tilde{\delta }}_{\widehat{\eta }}(q)& ⪰& ({\tilde{\delta }}_{\widehat{\eta }}x)(q)={\displaystyle \underset{p\in \mathcal{S}}{rsup}}\{rmin\{{\tilde{\delta }}_{\widehat{\eta }}(p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,q)\}\}\hfill \\ & ⪰& rmin\{{\tilde{\delta }}_{\widehat{\eta }}(p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,q)\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\omega }_{\widehat{\eta }}(q)& \le & ({\omega }_{\widehat{\eta }}x)(q)={\displaystyle \underset{p\in \mathcal{S}}{inf}}\{max\{{\omega }_{\widehat{\eta }}(p),{\omega }_{\mathcal{A}}^{*}(p,x,q)\}\}\hfill \\ & \le & max\{{\omega }_{\widehat{\eta }}(p),{\omega }_{\mathcal{A}}^{*}(p,x,q)\}.\hfill \end{array}$$

Hence, $\widehat{\eta }$ is a subsystem of $\mathcal{F}$. ☐

Definition 12.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $m=([s,t],w)\in D(0,1]\times (0,1]$ and $q\in \mathcal{S}$. Define the cubic subset $q_{m}X=⟨q_{[s,t]}X,q_{w}X⟩$ of $\mathcal{S}$ by

$$(q_{[s,t]}X)(p)={\displaystyle \underset{a\in X}{rsup}}\{rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}(q,a,p)\}\},$$

and

$$(q_{w}X)(p)={\displaystyle \underset{a\in X}{inf}}\{max\{w,{\omega }_{\mathcal{A}}(q,a,p)\}\},$$

for all $p\in \mathcal{S}.$

Definition 13.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $m=([s,t],w)\in D(0,1]\times (0,1]$ and $q\in \mathcal{S}$. Define the cubic subset $q_m{X}^{*}=⟨q_{[s,t]}{X}^{*},q_w{X}^{*}⟩$ of $\mathcal{S}$ by

$$(q_{[s,t]}{X}^{*})(p)={\displaystyle \underset{a\in X^{*}}{rsup}}\{rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,a,p)\}\},$$

and

$$(q_w{X}^{*})(p)={\displaystyle \underset{a\in X^{*}}{inf}}\{max\{w,{\omega }_{\mathcal{A}}^{*}(q,a,p)\}\},$$

for all $p\in \mathcal{S}.$

Theorem 3.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Let $m=([s,t],w)\in D(0,1]\times (0,1]$ and $q\in \mathcal{S}.$ The following assertions hold.

(i)

$q_m{X}^{*}=⟨q_{[s,t]}{X}^{*},q_w{X}^{*}⟩$ is a subsystem of $\mathcal{F}.$

(ii)

$Supp(q_m{X}^{*})=S(q).$

Proof. 

$(i)$ Let $h\in \mathcal{S}$ and $x\in X^{*}.$ Now,

$$\begin{array}{ccc}\hfill ((q_{[s,t]}{X}^{*})x)(h)& =& {\displaystyle \underset{p\in \mathcal{S}}{rsup}}\left\{rmin\left\{(q_{[s,t]}{X}^{*})(p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{p\in \mathcal{S}}{rsup}}\left\{rmin\left\{{\displaystyle \underset{y\in X^{*}}{rsup}}\{rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,y,p)\}\},{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{p\in \mathcal{S},y\in X^{*}}{rsup}}\left\{rmin\left\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,y,p),{\tilde{\delta }}_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{y\in X^{*}}{rsup}}\left\{rmin\left\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,yx,h)\right\}\right\}\hfill \\ & ⪯& {\displaystyle \underset{u\in X^{*}}{rsup}}\left\{rmin\left\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,u,h)\right\}\right\}\hfill \\ & =& (q_{[s,t]}{X}^{*})(h),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill ((q_w{X}^{*})x)(h)& =& {\displaystyle \underset{p\in \mathcal{S}}{inf}}\left\{max\left\{(q_w{X}^{*})(p),{\omega }_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{p\in \mathcal{S}}{inf}}\left\{max\left\{{\displaystyle \underset{y\in X^{*}}{inf}}\{max\{w,{\omega }_{\mathcal{A}}^{*}(q,y,p)\}\},{\omega }_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{p\in \mathcal{S},y\in X^{*}}{inf}}\left\{max\left\{w,{\omega }_{\mathcal{A}}^{*}(q,y,p),{\omega }_{\mathcal{A}}^{*}(p,x,h)\right\}\right\}\hfill \\ & =& {\displaystyle \underset{y\in X^{*}}{inf}}\left\{max\left\{w,{\omega }_{\mathcal{A}}^{*}(q,yx,h)\right\}\right\}\hfill \\ & ⪰& {\displaystyle \underset{u\in X^{*}}{inf}}\left\{max\left\{w,{\omega }_{\mathcal{A}}^{*}(q,u,h)\right\}\right\}\hfill \\ & =& (q_w{X}^{*})(h).\hfill \end{array}$$

Hence, $(q_{[s,t]}{X}^{*})x\subseteq q_{[s,t]}{X}^{*}$ and $(q_w{X}^{*})x\supseteq q_w{X}^{*}.$ Thus, $q_m{X}^{*}=⟨q_{[s,t]}{X}^{*},q_w{X}^{*}⟩$ is a subsystem of $\mathcal{F}$ by Theorem 2.

$(ii)$$p\in S(q)\iff \exists x\in X^{*}$ such that

$$\begin{array}{cc}& {\tilde{\delta }}_{\mathcal{A}}^{*}(q,x,p)⪰[0,0]\hfill \\ \iff \hfill & {\displaystyle \underset{x\in X^{*}}{rsup}}\{rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,x,p)\}\}⪰[0,0]\hfill \\ \iff \hfill & (q_{[s,t]}{X}^{*})(p)⪰[0,0]\hfill \\ \iff \hfill & p\in Supp(q_{[s,t]}{X}^{*}),\hfill \end{array}$$

and

$$\begin{array}{cc}& {\omega }_{\mathcal{A}}^{*}(q,x,p)<1\hfill \\ \iff \hfill & {\displaystyle \underset{x\in X^{*}}{inf}}\{max\{w,{\omega }_{\mathcal{A}}^{*}(q,x,p)\}\}\le 1\hfill \\ \iff \hfill & (q_w{X}^{*})(p)\le 1\hfill \\ \iff \hfill & p\in Supp(q_w{X}^{*}).\hfill \end{array}$$

Thus, $Supp(q_m{X}^{*})=S(q).$ ☐

Theorem 4.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM and let $\widehat{\eta }=⟨{\tilde{\delta }}_{\widehat{\eta }},{\omega }_{\widehat{\eta }}⟩$ be a cubic subset of $\mathcal{S}.$ The following assertions are equivalent.

(i)

$\widehat{\eta }$ is a subsystem of $\mathcal{F}$.

(ii)

$q_m{X}^{*}\subseteq \widehat{\eta },$ for all $q_m\subseteq \widehat{\eta },$ $q\in \mathcal{S},$ $m=([s,t],w)\in D(0,1]\times (0,1].$

(iii)

$q_{m}X\subseteq \widehat{\eta },$ for all $q_m\subseteq \widehat{\eta },$ $q\in \mathcal{S},$ $m=([s,t],w)\in D(0,1]\times (0,1].$

Proof. 

$(i)\Rightarrow (ii):$ Let $q_m\subseteq \widehat{\eta },$ $q\in \mathcal{S},$ $m=([s,t],w)\in D(0,1]\times (0,1]$. Let $p\in \mathcal{S}$ and $y\in X^{*}.$ Then,

$$\begin{array}{ccc}\hfill rmin\left\{[s,t],{\tilde{\delta }}_{\mathcal{A}}^{*}(q,y,p)\right\}& =& rmin\left\{q_{[s,t]}(q),{\tilde{\delta }}_{\mathcal{A}}^{*}(q,y,p)\right\}\hfill \\ & ⪯& rmin\left\{{\tilde{\delta }}_{\widehat{\eta }}(q),{\tilde{\delta }}_{\mathcal{A}}^{*}(q,y,p)\right\}\hfill \\ & ⪯& {\tilde{\delta }}_{\widehat{\eta }}(p),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill max\left\{w,{\omega }_{\mathcal{A}}^{*}(q,y,p)\right\}& =& max\left\{q_w(q),{\omega }_{\mathcal{A}}^{*}(q,y,p)\right\}\hfill \\ & \ge & max\left\{{\omega }_{\widehat{\eta }}(q),{\omega }_{\mathcal{A}}^{*}(q,y,p)\right\}\hfill \\ & \ge & {\omega }_{\widehat{\eta }}(p).\hfill \end{array}$$

Since $\widehat{\eta }$ is a subsystem. Hence, $q_m{X}^{*}\subseteq \widehat{\eta }.$

$(ii)\Rightarrow (iii):$ This is Obvious.

$(iii)\Rightarrow (i):$ Let $p,q\in \mathcal{S}$ and $a\in X.$ If ${\tilde{\delta }}_{\widehat{\eta }}(q)=[0,0]$ and ${\omega }_{\widehat{\eta }}(q)=1$ or ${\tilde{\delta }}_{\mathcal{A}}(q,a,p)=[0,0]$ and ${\omega }_{\mathcal{A}}(q,a,p)=1$ then

$${\tilde{\delta }}_{\widehat{\eta }}(p)⪰[0,0]=rmin\left\{{\tilde{\delta }}_{\widehat{\eta }}(q),{\tilde{\delta }}_{\mathcal{A}}(q,a,p)\right\},$$

and

$${\omega }_{\widehat{\eta }}(p)\le 1=max\left\{{\omega }_{\widehat{\eta }}(q),{\omega }_{\mathcal{A}}(q,a,p)\right\}.$$

Suppose ${\tilde{\delta }}_{\widehat{\eta }}(q)\ne [0,0]$ and ${\omega }_{\widehat{\eta }}(q)\ne 1$ and ${\tilde{\delta }}_{\mathcal{A}}(q,a,p)\ne [0,0]$ and ${\omega }_{\mathcal{A}}(q,a,p)\ne 1.$ Let ${\tilde{\delta }}_{\widehat{\eta }}(q)=[s,t]$ and ${\omega }_{\widehat{\eta }}(q)=w.$ Then, $q_m\subseteq \widehat{\eta }.$ Thus, by the hypothesis, $q_{m}X\subseteq \widehat{\eta }$. Thus,

$$\begin{array}{ccc}\hfill {\tilde{\delta }}_{\widehat{\eta }}(p)& ⪰& (q_{[s,t]}X)(p)={\displaystyle \underset{y\in X}{rsup}}\{rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}(q,y,p)\}\}\hfill \\ & ⪰& rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}(q,a,p)\}\hfill \\ & =& rmin\{[s,t],{\tilde{\delta }}_{\mathcal{A}}(q,a,p)\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\omega }_{\widehat{\eta }}(p)& ⪰& (q_{w}X)(p)={\displaystyle \underset{y\in X}{inf}}\{max\{w,{\omega }_{\mathcal{A}}(q,y,p)\}\}\hfill \\ & ⪰& max\{w,{\omega }_{\mathcal{A}}(q,a,p)\}\hfill \\ & =& max\{w,{\omega }_{\mathcal{A}}(q,a,p)\}.\hfill \end{array}$$

Hence, $\widehat{\eta }$ is a subsystem of $\mathcal{F}$. ☐

4. Operations on Subsystems of Cubic FSMs

In this section, we define some operations on subsystems of cubic FSMs and some related results are provided.

Definition 14.

Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, and let $X_1\cap X_2=\varnothing .$ The Cartesian composition of ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$ is denoted by

$${\widehat{\mathcal{A}}}_1\circ {\widehat{\mathcal{A}}}_2=⟨{\mathcal{S}}_1\times {\mathcal{S}}_2,{\widehat{\mathcal{A}}}_1\circ {\widehat{\mathcal{A}}}_2,X_1\cup X_2,{\mathcal{A}}_1\circ {\mathcal{A}}_2⟩$$

and is defined as follows:

(i)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}\circ {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(q_2)\}\\ ({\omega }_{{\widehat{\mathcal{A}}}_1}\circ {\omega }_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),{\omega }_{{\widehat{\mathcal{A}}}_2}(q_2)\}\end{array}\right.$ for all $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2.$

(ii)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\circ {\tilde{\delta }}_{{\mathcal{A}}_2})((p_1,r),a,(q_1,r))={\tilde{\delta }}_{{\mathcal{A}}_1}(p_1,a,q_1)\\ ({\omega }_{{\mathcal{A}}_1}\circ {\omega }_{{\mathcal{A}}_2})((p_1,r),a,(q_1,r))={\omega }_{{\mathcal{A}}_1}(p_1,a,q_1)\end{array}\right.$ for all $p_1,q_1\in {\mathcal{S}}_1,$ $r\in {\mathcal{S}}_2$ and $a\in X_1\cup X_2.$

(iii)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\circ {\tilde{\delta }}_{{\mathcal{A}}_2})((r,p_2),a,(r,q_2))={\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,a,q_2)\\ ({\omega }_{{\mathcal{A}}_1}\circ {\omega }_{{\mathcal{A}}_2})((r,p_2),a,(r,q_2))={\omega }_{{\mathcal{A}}_2}(p_2,a,q_2)\end{array}\right.$ for all $p_2,q_2\in {\mathcal{S}}_2,$ $r\in {\mathcal{S}}_1$ and $a\in X_1\cup X_2.$

Example 2.

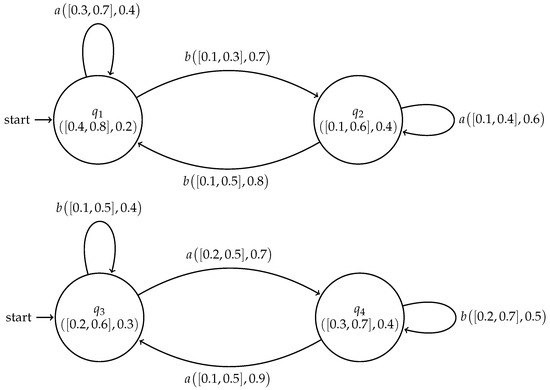
Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, as shown in Figure 2:

Figure 2. Cubic subsystems ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$.

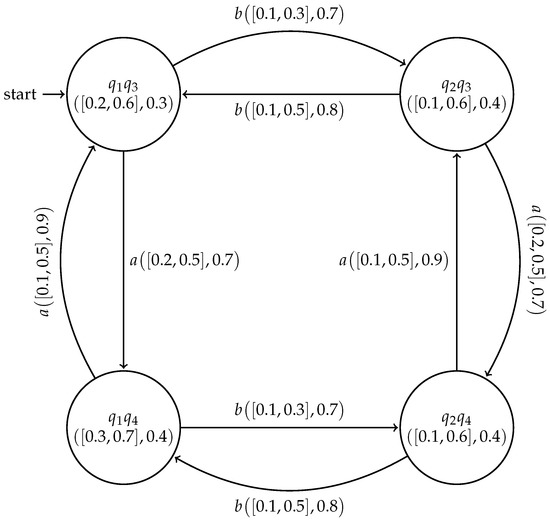
Then, their corresponding Cartesian composition ${\widehat{\mathcal{A}}}_1\circ {\widehat{\mathcal{A}}}_2$ is shown in Figure 3

Figure 3. Cartesian composition ${\widehat{\mathcal{A}}}_1\circ {\widehat{\mathcal{A}}}_2$ for Example 2.

Clearly, ${\widehat{\mathcal{A}}}_1\circ {\widehat{\mathcal{A}}}_2$ is a cubic subsystem of ${\mathcal{F}}_1\circ {\mathcal{F}}_2.$

Proposition 2.

The Cartesian composition of two cubic subsystems is a cubic subsystem.

Proof. 

Condition (i) of Definition 14 is obvious, therefore, we verify only Conditions (ii) and (iii). Let $q_1\in {\mathcal{S}}_1$ and $p_2,q_2\in {\mathcal{S}}_2$. Then,

$$\begin{array}{cc}& rmin\{({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}\circ {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q_1,p_2),({\tilde{\delta }}_{{\mathcal{A}}_1}\circ {\tilde{\delta }}_{{\mathcal{A}}_2})((q_1,p_2),a,(q_1,q_2))\}\hfill \\ =& rmin\{rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p_2)\},{\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,a,q_2)\}\hfill \\ =& rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p_2),{\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,a,q_2)\}\}\hfill \\ ⪯& rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(q_2)\}\hfill \\ =& ({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}\circ {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q_1,q_2),\hfill \end{array}$$

and

$$\begin{array}{cc}& max\{({\omega }_{{\widehat{\mathcal{A}}}_1}\circ {\omega }_{{\widehat{\mathcal{A}}}_2})(q_1,p_2),({\omega }_{{\mathcal{A}}_1}\circ {\omega }_{{\mathcal{A}}_2})((q_1,p_2),a,(q_1,q_2))\}\hfill \\ =& max\{max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),{\omega }_{{\widehat{\mathcal{A}}}_2}(p_2)\},{\omega }_{{\mathcal{A}}_2}(p_2,a,q_2)\}\hfill \\ =& max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),max\{{\omega }_{{\widehat{\mathcal{A}}}_2}(p_2),{\omega }_{{\mathcal{A}}_2}(p_2,a,q_2)\}\}\hfill \\ \ge & max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),{\omega }_{{\widehat{\mathcal{A}}}_2}(q_2)\}\hfill \\ =& ({\omega }_{{\widehat{\mathcal{A}}}_1}\circ {\omega }_{{\widehat{\mathcal{A}}}_2})(q_1,q_2).\hfill \end{array}$$

Similarly, we can prove Condition (iii) for $p_1,q_1\in {\mathcal{S}}_1$, and $p_2\in {\mathcal{S}}_2$. ☐

Definition 15.

Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, and let $X_1\cap X_2=\varnothing .$ The direct product of ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$ is denoted by

$${\widehat{\mathcal{A}}}_1\times {\widehat{\mathcal{A}}}_2=⟨{\mathcal{S}}_1\times {\mathcal{S}}_2,{\widehat{\mathcal{A}}}_1\times {\widehat{\mathcal{A}}}_2,X_1\times X_2,{\mathcal{A}}_1\times {\mathcal{A}}_2⟩$$

and is defined as follows:

(i)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}\times {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(q_2)\}\\ ({\omega }_{{\widehat{\mathcal{A}}}_1}\times {\omega }_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),{\omega }_{{\widehat{\mathcal{A}}}_2}(q_2)\}\end{array}\right.$ for all $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2.$

(ii)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\times {\tilde{\delta }}_{{\mathcal{A}}_2})((p_1,p_2),x_1,(q_1,q_2))={\tilde{\delta }}_{{\mathcal{A}}_1}(p_1,x_1,q_1)\\ ({\omega }_{{\mathcal{A}}_1}\times {\omega }_{{\mathcal{A}}_2})((p_1,p_2),x_1,(q_1,q_2))={\omega }_{{\mathcal{A}}_1}(p_1,x_1,q_1)\end{array}\right.$ for all $(p_1,p_2)$ and $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2$ and $x_1\in X_1.$

(iii)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\times {\tilde{\delta }}_{{\mathcal{A}}_2})((p_1,p_2),x_2,(q_1,q_2))={\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,x_2,q_2)\\ ({\omega }_{{\mathcal{A}}_1}\times {\omega }_{{\mathcal{A}}_2})((p_1,p_2),x_2,(q_1,q_2))={\omega }_{{\mathcal{A}}_2}(p_2,x_2,q_2)\end{array}\right.$ for all $(p_1,p_2)$ and $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2$ and $x_2\in X_2.$

(iv)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\times {\tilde{\delta }}_{{\mathcal{A}}_2})((p_1,p_2),(x_1,x_2),(q_1,q_2))=rmin\{{\tilde{\delta }}_{{\mathcal{A}}_1}(p_1,x_1,q_1),{\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,x_2,q_2)\}\\ ({\omega }_{{\mathcal{A}}_1}\times {\omega }_{{\mathcal{A}}_2})((p_1,p_2),(x_1,x_2),(q_1,q_2))=max\{{\omega }_{{\mathcal{A}}_1}(p_1,x_1,q_1),{\omega }_{{\mathcal{A}}_2}(p_2,x_2,q_2)\}\end{array}\right.$ for all $(p_1,p_2)$ and $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2$ and $(x_1,x_2)\in X_1\times X_2.$

Example 3.

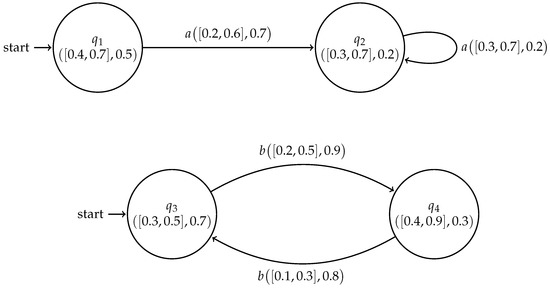
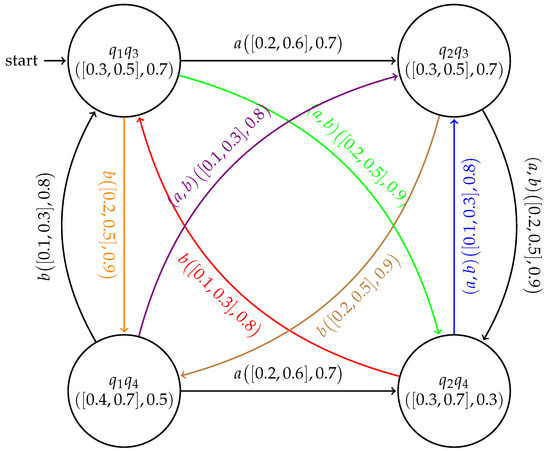
Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, as shown in Figure 4

Figure 4. Cubic subsystems ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$.

Then, their corresponding direct product ${\widehat{\mathcal{A}}}_1\times {\widehat{\mathcal{A}}}_2$ is shown in Figure 5

Figure 5. Direct product ${\widehat{\mathcal{A}}}_1\times {\widehat{\mathcal{A}}}_2$ for Example 3.

Clearly, ${\widehat{\mathcal{A}}}_1\times {\widehat{\mathcal{A}}}_2$ is a cubic subsystem of ${\mathcal{F}}_1\times {\mathcal{F}}_2.$

Proposition 3.

The direct product of two cubic subsystems is a cubic subsystem.

Proof. 

The proof is similar to the proof of Proposition 2. ☐

Definition 16.

Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X,{\mathcal{A}}_2⟩,$ respectively. The restricted direct product of ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$ is denoted by

$${\widehat{\mathcal{A}}}_1\wedge {\widehat{\mathcal{A}}}_2=⟨{\mathcal{S}}_1\times {\mathcal{S}}_2,{\widehat{\mathcal{A}}}_1\wedge {\widehat{\mathcal{A}}}_2,X,{\mathcal{A}}_1\wedge {\mathcal{A}}_2⟩$$

and is defined as follows:

(i)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}\wedge {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q_1),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(q_2)\}\\ ({\omega }_{{\widehat{\mathcal{A}}}_1}\wedge {\omega }_{{\widehat{\mathcal{A}}}_2})(q_1,q_2)=max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q_1),{\omega }_{{\widehat{\mathcal{A}}}_2}(q_2)\}\end{array}\right.$ for all $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2.$

(ii)

$\left\{\begin{array}{c}({\tilde{\delta }}_{{\mathcal{A}}_1}\wedge {\tilde{\delta }}_{{\mathcal{A}}_2})((p_1,p_2),x,(q_1,q_2))=rmin\{{\tilde{\delta }}_{{\mathcal{A}}_1}(p_1,x,q_1),{\tilde{\delta }}_{{\mathcal{A}}_2}(p_2,x,q_2)\}\\ ({\omega }_{{\mathcal{A}}_1}\wedge {\omega }_{{\mathcal{A}}_2})((p_1,p_2),x,(q_1,q_2))=max\{{\omega }_{{\mathcal{A}}_1}(p_1,x,q_1),{\omega }_{{\mathcal{A}}_2}(p_2,x,q_2)\}\end{array}\right.$ for all $(p_1,p_2)$ and $(q_1,q_2)\in {\mathcal{S}}_1\times {\mathcal{S}}_2$ and $x\in X.$

Proposition 4.

The restricted direct product of two cubic subsystems is a cubic subsystem.

Proof. 

The proof is similar to the proof of the Proposition 2. ☐

Definition 17.

Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X,{\mathcal{A}}_2⟩,$ respectively. The R-union of ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$ is denoted by

$${\widehat{\mathcal{A}}}_1{\cup }_R{\widehat{\mathcal{A}}}_2=⟨{\mathcal{S}}_1\cup {\mathcal{S}}_2,{\widehat{\mathcal{A}}}_1{\cup }_R{\widehat{\mathcal{A}}}_2,X,{\mathcal{A}}_1{\cup }_R{\mathcal{A}}_2⟩$$

and is defined as follows:

(i)

$({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(p)=\left\{\begin{array}{cc}{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(p)\hfill & if p\in {\mathcal{S}}_1-{\mathcal{S}}_2\\ {\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p)\hfill & if p\in {\mathcal{S}}_2-{\mathcal{S}}_1\\ rmax\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(p),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p)\}\hfill & if p\in {\mathcal{S}}_1\cap {\mathcal{S}}_2\end{array}\right.$

(ii)

$({\omega }_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\omega }_{{\widehat{\mathcal{A}}}_2})(p)=\left\{\begin{array}{cc}{\omega }_{{\widehat{\mathcal{A}}}_1}(p)\hfill & if p\in {\mathcal{S}}_1-{\mathcal{S}}_2\\ {\omega }_{{\widehat{\mathcal{A}}}_2}(p)\hfill & if p\in {\mathcal{S}}_2-{\mathcal{S}}_1\\ min\{{\omega }_{{\widehat{\mathcal{A}}}_1}(p),{\omega }_{{\widehat{\mathcal{A}}}_2}(p)\}\hfill & if p\in {\mathcal{S}}_1\cap {\mathcal{S}}_2\end{array}\right.$

(iii)

$({\tilde{\delta }}_{{\mathcal{A}}_1}{\cup }_R{\tilde{\delta }}_{{\mathcal{A}}_2})(p,x,q)=\left\{\begin{array}{cc}{\tilde{\delta }}_{{\mathcal{A}}_1}(p,x,q)\hfill & if p,q\in {\mathcal{S}}_1-{\mathcal{S}}_2\\ {\tilde{\delta }}_{{\mathcal{A}}_2}(p,x,q)\hfill & if p,q\in {\mathcal{S}}_2-{\mathcal{S}}_1\\ rmax\{({\tilde{\delta }}_{{\mathcal{A}}_1}(p,x,q),{\tilde{\delta }}_{{\mathcal{A}}_2}(p,x,q)\}\hfill & if p,q\in {\mathcal{S}}_1\cap {\mathcal{S}}_2\end{array}\right.$ for all $x\in X,$

(iv)

$({\omega }_{{\mathcal{A}}_1}{\cup }_R{\omega }_{{\mathcal{A}}_2})(p,x,q)=\left\{\begin{array}{cc}{\omega }_{{\mathcal{A}}_1}(p,x,q)\hfill & if p,q\in {\mathcal{S}}_1-{\mathcal{S}}_2\\ {\omega }_{{\mathcal{A}}_2}(p,x,q)\hfill & if p,q\in {\mathcal{S}}_2-{\mathcal{S}}_1\\ min\{({\omega }_{{\mathcal{A}}_1}(p,x,q),{\omega }_{{\mathcal{A}}_2}(p,x,q)\}\hfill & if p,q\in {\mathcal{S}}_1\cap {\mathcal{S}}_2\end{array}\right.$ for all $x\in X.$

P-union, R-intersection and P-intersection can be defined in a similar way.

Example 4.

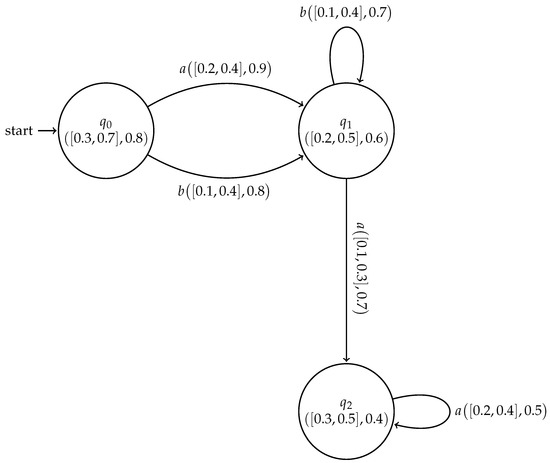
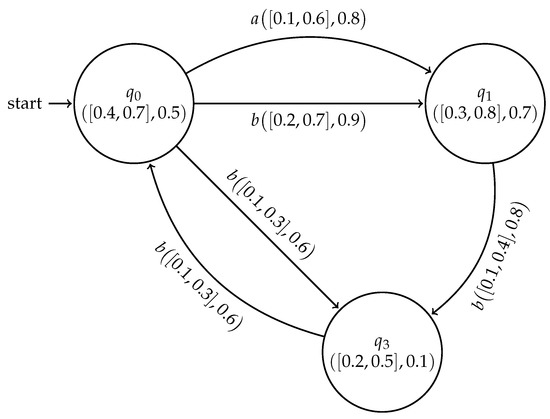
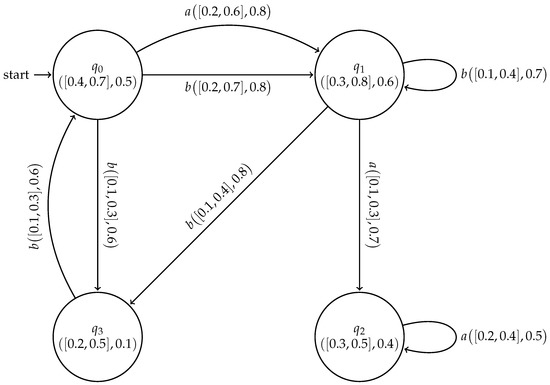
Let ${\widehat{\mathcal{A}}}_1=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1},{\omega }_{{\widehat{\mathcal{A}}}_1}⟩$ and ${\widehat{\mathcal{A}}}_2=⟨{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2},{\omega }_{{\widehat{\mathcal{A}}}_2}⟩$ be two cubic subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, as shown in Figure 6

Figure 6. Cubic subsystems ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$.

Then, their corresponding R-union ${\widehat{\mathcal{A}}}_1{\cup }_R{\widehat{\mathcal{A}}}_2$ is shown in Figure 7

Figure 7. Union of two subsystems ${\widehat{\mathcal{A}}}_1$ and ${\widehat{\mathcal{A}}}_2$ for Example 4.

Clearly, ${\widehat{\mathcal{A}}}_1{\cup }_R{\widehat{\mathcal{A}}}_2$ is a cubic subsystem of ${\mathcal{F}}_1{\cup }_R{\mathcal{F}}_2.$

Proposition 5.

The R-union (respectively, P-union, R-intersection and P-intersection) of two cubic subsystems is a cubic subsystem.

Proof. 

Conditions (i) and (ii) of Definition 17 are obvious, therefore, we verify only Conditions (iii) and (iv). Let $p,q\in {\mathcal{S}}_1\cap {\mathcal{S}}_2$ and $x\in X$. Then,

$$\begin{array}{cc}& rmin\{({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(p),({\tilde{\delta }}_{{\mathcal{A}}_1}{\cup }_R{\tilde{\delta }}_{{\mathcal{A}}_2})(p,a,q)\}\hfill \\ =& rmin\{rmax\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(p),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p)\},rmax\{{\tilde{\delta }}_{{\mathcal{A}}_1}(p,a,q),{\tilde{\delta }}_{{\mathcal{A}}_2}(p,a,q)\}\}\hfill \\ =& rmax\{rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(p),{\tilde{\delta }}_{{\mathcal{A}}_1}(p,a,q)\},rmin\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(p),{\tilde{\delta }}_{{\mathcal{A}}_2}(p,a,q)\}\}\hfill \\ ⪯& rmax\{{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}(q),{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2}(q)\}\hfill \\ =& ({\tilde{\delta }}_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\tilde{\delta }}_{{\widehat{\mathcal{A}}}_2})(q),\hfill \end{array}$$

and

$$\begin{array}{cc}& max\{({\omega }_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\omega }_{{\widehat{\mathcal{A}}}_2})(p),({\omega }_{{\mathcal{A}}_1}{\cup }_R{\omega }_{{\mathcal{A}}_2})(p,a,q)\}\hfill \\ =& max\{min\{{\omega }_{{\widehat{\mathcal{A}}}_1}(p),{\omega }_{{\widehat{\mathcal{A}}}_2}(p)\},min\{{\omega }_{{\mathcal{A}}_1}(p,a,q),{\omega }_{{\mathcal{A}}_2}(p,a,q)\}\}\hfill \\ =& min\{max\{{\omega }_{{\widehat{\mathcal{A}}}_1}(p),{\omega }_{{\mathcal{A}}_1}(p,a,q)\},max\{{\omega }_{{\widehat{\mathcal{A}}}_2}(p),{\omega }_{{\mathcal{A}}_2}(p,a,q)\}\}\hfill \\ ⪯& min\{{\omega }_{{\widehat{\mathcal{A}}}_1}(q),{\omega }_{{\widehat{\mathcal{A}}}_2}(q)\}\hfill \\ =& ({\omega }_{{\widehat{\mathcal{A}}}_1}{\cup }_R{\omega }_{{\widehat{\mathcal{A}}}_2})(q),\hfill \end{array}$$

Thus, R-union of two cubic subsystems is a cubic subsystem. Similarly, we can prove that the P-union, R-intersection and P-intersection of two cubic subsystems are cubic subsystems. ☐

5. Internal and External Cubic Subsystems

In this section, we discuss some results related with internal and external cubic subsystems of cubic FSMs.

Definition 18.

A subsystem $\widehat{{\mathcal{A}}^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^I}},{\omega }_{\widehat{{\mathcal{A}}^I}}⟩$ of a cubic FSM $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ is said to be an internal cubic subsystem (IC-subsystem) if

(i)

${\delta }_{\widehat{{\mathcal{A}}^I}}^{-}(q)\le {\omega }_{\widehat{{\mathcal{A}}^I}}(q)\le {\delta }_{\widehat{{\mathcal{A}}^I}}^{+}(q),$

(ii)

${\delta }_{\mathcal{A}}^{-}(q,a,p)\le {\omega }_{\mathcal{A}}(q,a,p)\le {\delta }_{\mathcal{A}}^{+}(q,a,p),$ for all $q,p\in \mathcal{S}$ and $a\in X.$

Definition 19.

A subsystem $\widehat{{\mathcal{A}}^E}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^E}},{\omega }_{\widehat{{\mathcal{A}}^E}}⟩$ of a cubic FSM $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ is said to be an external cubic subsystem (EC-subsystem) if

(i)

${\omega }_{\widehat{{\mathcal{A}}^E}}(q)\notin \left({\delta }_{\widehat{{\mathcal{A}}^E}}^{-}(q),{\delta }_{\widehat{{\mathcal{A}}^E}}^{+}(q)\right),$

(ii)

${\omega }_{\mathcal{A}}(q,a,p)\notin \left({\delta }_{\mathcal{A}}^{-}(q,a,p),{\delta }_{\mathcal{A}}^{+}(q,a,p)\right),$ for all $q,p\in \mathcal{S}$ and $a\in X.$

Example 5.

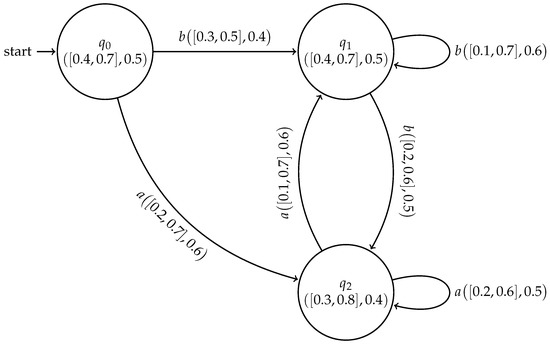
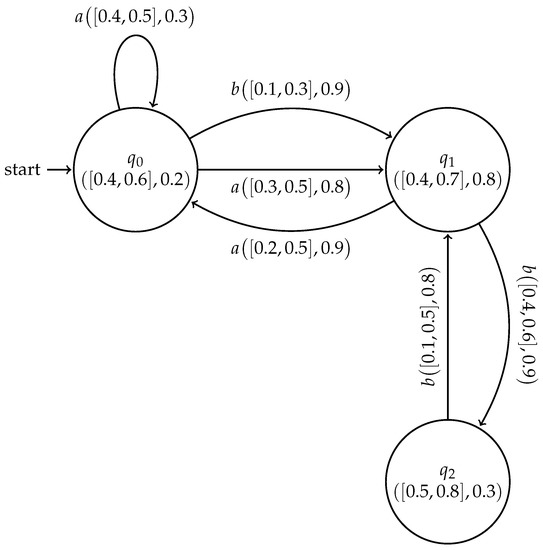
The cubic FSMs ${\mathcal{F}}^I=⟨\mathcal{S},\widehat{{\mathcal{A}}^I},X,\mathcal{A}⟩$ and ${\mathcal{F}}^E=⟨\mathcal{S},\widehat{{\mathcal{A}}^E},X,\mathcal{A}⟩$ are internal and external cubic subsystems, respectively, as shown in Figure 8 and Figure 9

Figure 8. IC-Subsystem for Example 5.

Figure 9. EC-Subsystem for Example 5.

Theorem 5.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Then, $\widehat{{\mathcal{A}}^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^I}},{\omega }_{\widehat{{\mathcal{A}}^I}}⟩$ is an internal cubic subsystem of $\mathcal{F}$ if

$${\delta }_{\widehat{{\mathcal{A}}^I}}^{-}(q)\le {\omega }_{\widehat{{\mathcal{A}}^I}}(q)\le {\delta }_{\widehat{{\mathcal{A}}^I}}^{+}(q)and{\delta }_{\mathcal{A}}^{*-}(q,x,p)\le {\omega }_{\mathcal{A}}^{*}(q,x,p)\le {\delta }_{\mathcal{A}}^{*+}(q,x,p)$$

for all $q,p\in \mathcal{S}$ and $x\in X^{*}.$

Proof. 

As it is given that ${\delta }_{\widehat{{\mathcal{A}}^I}}^{-}(q)\le {\omega }_{\widehat{{\mathcal{A}}^I}}(q)\le {\delta }_{\widehat{{\mathcal{A}}^I}}^{+}(q)$ and ${\delta }_{\mathcal{A}}^{*-}(q,x,p)\le {\omega }_{\mathcal{A}}^{*}(q,x,p)\le {\delta }_{\mathcal{A}}^{*+}(q,x,p).$ This implies that $\mathcal{A}$ and $\widehat{{\mathcal{A}}^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^I}},{\omega }_{\widehat{{\mathcal{A}}^I}}⟩$ are internal cubic subsets of $\mathcal{S}\times X\times \mathcal{S}$ and $\mathcal{S},$ respectively. Thus, by Theorem 1, $\widehat{{\mathcal{A}}^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^I}},{\omega }_{\widehat{{\mathcal{A}}^I}}⟩$ is cubic subsystem of $\mathcal{F}$. Thus, $\widehat{{\mathcal{A}}^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^I}},{\omega }_{\widehat{{\mathcal{A}}^I}}⟩$ is an internal cubic subsystem of $\mathcal{F}$. This completes the proof. ☐

Theorem 6.

Let $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩$ be a cubic FSM. Then, $\widehat{{\mathcal{A}}^E}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}^E}},{\omega }_{\widehat{{\mathcal{A}}^E}}⟩$ is an external cubic subsystem of $\mathcal{F}$ if

$${\omega }_{\widehat{{\mathcal{A}}^E}}(q)\notin \left({\delta }_{\widehat{{\mathcal{A}}^E}}^{-}(q),{\delta }_{\widehat{{\mathcal{A}}^E}}^{+}(q)\right)and{\omega }_{\mathcal{A}}^{*}(q,a,p)\notin \left({\delta }_{\mathcal{A}}^{*-}(q,a,p),{\delta }_{\mathcal{A}}^{*+}(q,a,p)\right)$$

for all $q,p\in \mathcal{S}$ and $x\in X^{*}.$

Proof. 

The proof is similar to the proof of Theorem 5. ☐

Theorem 7.

Let $\left\{\widehat{{\mathcal{A}}_i^I}=⟨{\tilde{\delta }}_{\widehat{{\mathcal{A}}_i^I}},{\omega }_{\widehat{{\mathcal{A}}_i^I}}⟩|i\in \mathsf{\Lambda }\right\}$ be a family of IC-subsystems of cubic FSMs ${\mathcal{F}}_i=⟨{\mathcal{S}}_i,X_i,{\mathcal{A}}_i⟩$. Then, ${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcup }_P}}\widehat{{\mathcal{A}}_i^I}$ is an IC-subsystem of $\mathcal{F}$.

Proof. 

Since $\widehat{{\mathcal{A}}_i^I}$ is an IC-subsystem, we have ${\delta }_{\widehat{{\mathcal{A}}^I}}^{-}(q)\le {\omega }_{\widehat{{\mathcal{A}}^I}}(q)\le {\delta }_{\widehat{{\mathcal{A}}^I}}^{+}(q)$ and ${\delta }_{\mathcal{A}}^{-}(q,a,p)\le {\omega }_{\mathcal{A}}(q,a,p)\le {\delta }_{\mathcal{A}}^{+}(q,a,p)$ for $i\in \mathsf{\Lambda }.$ This implies that

$$\left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}\delta {\delta }_{\widehat{{\mathcal{A}}^I}}^{-}\right)(q)\le \left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigvee }}{\omega }_{\widehat{{\mathcal{A}}^I}}\right)(q)\le \left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}{\delta }_{\widehat{{\mathcal{A}}^I}}^{+}\right)(q),$$

and

$$\left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}{\delta }_{\mathcal{A}}^{-}\right)(q,a,p)\le \left({\displaystyle \underset{i\in \mathsf{\Lambda }}{\bigvee }}{\omega }_{\mathcal{A}}\right)(q,a,p)\le \left({\displaystyle \bigcup _{i\in \mathsf{\Lambda }}}{\delta }_{\mathcal{A}}^{+}\right)(q,a,p).$$

Hence, ${\displaystyle \underset{i\in \mathsf{\Lambda }}{{\bigcup }_P}}\widehat{{\mathcal{A}}_i^I}$ is an IC-subsystem of $\mathcal{F}$. ☐

The following Example shows that the R-union of IC-subsystems need not be an IC-subsystem (EC-subsystem).

Example 6.

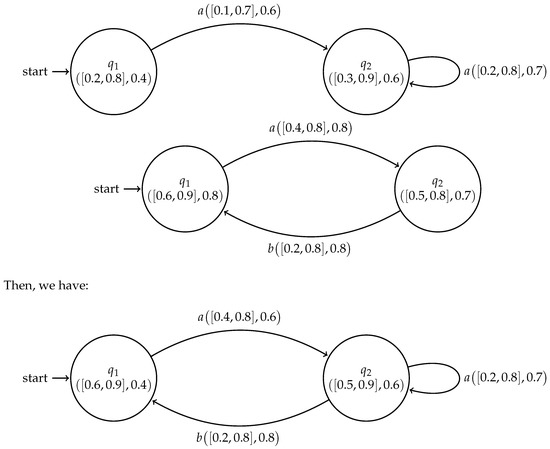
We have the following two IC-Subsystems in Figure 10:

Figure 10. Union of two IC-Subsystems for Example 6.

We provide a condition for the R-union of two IC-subsystems to be an IC-subsystem.

Theorem 8.

Let $\widehat{{\mathcal{A}}_1^I}$ and $\widehat{{\mathcal{A}}_2^I}$ be IC-subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, such that

$$max\{{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{-}(q_2)\}\le min\{{\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_2)\}$$

and

$$max\{{\delta }_{{\mathcal{A}}_1}^{-}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\le min\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}$$

for all $q_1,p_1\in {\mathcal{S}}_1,$ $q_2,p_2\in {\mathcal{S}}_2,$ $a_1\in X_1$ and $a_2\in X_2.$ Then, the R-union of two IC-subsystems is an IC-subsystem.

Proof. 

$\widehat{{\mathcal{A}}_1^I}$ and $\widehat{{\mathcal{A}}_2^I}$ be IC-subsystems which satisfy the conditions

$$max\{{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{-}(q_2)\}\le min\{{\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_2^I}}(q_2)\}$$

and

$$max\{{\delta }_{{\mathcal{A}}_1}^{-}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\le min\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}$$

for all $q_1,p_1\in {\mathcal{S}}_1,$ $q_2,p_2\in {\mathcal{S}}_2,$ $a_1\in X_1$ and $a_2\in X_2.$ Since ${\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_1)\in [{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{+}(q_1)]$, ${\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1)\in [{\delta }_{{\mathcal{A}}_1}^{-}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1)]$ and ${\omega }_{\widehat{{\mathcal{A}}_2^I}}(q_2)\in [{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{-}(q_2),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{+}(q_2)]$, ${\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\in [{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2),{\delta }_{{\mathcal{A}}_2}^{+}(q_2,a_2,p_2)].$

This implies that

$$\begin{array}{ccc}\hfill min\{{\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_2^I}}(q_2)\}& \le & max\{{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{+}(q_2)\}\hfill \\ \hfill \mathrm{and}min\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}& \le & max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{+}(q_2,a_2,p_2)\}\hfill \end{array}$$

Thus, from the given condition we get

$$\begin{array}{ccc}\hfill max\{{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{-}(q_2)\}& \le & min\{{\omega }_{\widehat{{\mathcal{A}}_1^I}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_2^I}}(q_2)\}\hfill \\ & \le & max\{{\delta }_{\widehat{{\mathcal{A}}_1^I}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^I}}^{+}(q_2)\}\hfill \end{array}$$

$$\begin{array}{ccc}\hfill max\{{\delta }_{{\mathcal{A}}_1}^{-}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}& \le & min\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}\hfill \\ & \le & max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{+}(q_2,a_2,p_2)\}\hfill \end{array}$$

This shows that $\widehat{{\mathcal{A}}_1^I}{\cup }_R\widehat{{\mathcal{A}}_2^I}$ is an IC-subsystem. ☐

With the help of an example, it is easy to show that the P-union and R-union of EC-subsystems need not be an EC-subsystem (IC-subsystem). We provide a condition for the P-union and R-union of two EC-subsystems to be an EC-subsystem.

Theorem 9.

Let $\widehat{{\mathcal{A}}_1^E}$ and $\widehat{{\mathcal{A}}_2^E}$ be EC-subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, such that

$$\begin{array}{ccc}\hfill min\left\{\begin{array}{c}max\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{-}(q_2)\},\\ max\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{+}(q_2)\}\end{array}\right\}& >& max\{{\omega }_{\widehat{{\mathcal{A}}_1^E}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_2^E}}(q_2)\}\hfill \\ & \ge & max\left\{\begin{array}{c}min\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{-}(q_2)\},\\ min\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{+}(q_2)\}\end{array}\right\}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill min\left\{\begin{array}{c}max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\},\\ max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\end{array}\right\}& >& max\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}\hfill \\ & \ge & max\left\{\begin{array}{c}min\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\},\\ min\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\end{array}\right\}\hfill \end{array}$$

for all $q_1,p_1\in {\mathcal{S}}_1,$ $q_2,p_2\in {\mathcal{S}}_2,$ $a_1\in X_1$ and $a_2\in X_2.$ Then, the P-union of two EC-subsystems is an EC-subsystem.

Theorem 10.

Let $\widehat{{\mathcal{A}}_1^E}$ and $\widehat{{\mathcal{A}}_2^E}$ be EC-subsystems of cubic FSMs ${\mathcal{F}}_1=⟨{\mathcal{S}}_1,X_1,{\mathcal{A}}_1⟩$ and ${\mathcal{F}}_2=⟨{\mathcal{S}}_2,X_2,{\mathcal{A}}_2⟩,$ respectively, such that

$$\begin{array}{ccc}\hfill min\left\{\begin{array}{c}max\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{-}(q_2)\},\\ max\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{+}(q_2)\}\end{array}\right\}& >& min\{{\omega }_{\widehat{{\mathcal{A}}_1^E}}(q_1),{\omega }_{\widehat{{\mathcal{A}}_2^E}}(q_2)\}\hfill \\ & \ge & max\left\{\begin{array}{c}min\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{+}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{-}(q_2)\},\\ min\{{\delta }_{\widehat{{\mathcal{A}}_1^E}}^{-}(q_1),{\delta }_{\widehat{{\mathcal{A}}_2^E}}^{+}(q_2)\}\end{array}\right\}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill min\left\{\begin{array}{c}max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\},\\ max\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\end{array}\right\}& >& min\{{\omega }_{{\mathcal{A}}_1}(q_1,a_1,p_1),{\omega }_{{\mathcal{A}}_2}(q_2,a_2,p_2)\}\hfill \\ & \ge & max\left\{\begin{array}{c}min\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\},\\ min\{{\delta }_{{\mathcal{A}}_1}^{+}(q_1,a_1,p_1),{\delta }_{{\mathcal{A}}_2}^{-}(q_2,a_2,p_2)\}\end{array}\right\}\hfill \end{array}$$

for all $q_1,p_1\in {\mathcal{S}}_1,$ $q_2,p_2\in {\mathcal{S}}_2,$ $a_1\in X_1$ and $a_2\in X_2.$ Then, the R-union of two EC-subsystems is an EC-subsystem.

Theorem 11.

Let $\widehat{\mathcal{A}}=⟨{\tilde{\delta }}_{\widehat{\mathcal{A}}},{\omega }_{\widehat{\mathcal{A}}}⟩$ be a subsystem of cubic FSM $\mathcal{F}=⟨\mathcal{S},X,\mathcal{A}⟩.$ If $\widehat{\mathcal{A}}$ is both an IC-subsystem and an EC-subsystem, then

$${\omega }_{\widehat{\mathcal{A}}}(p_i)\in U({\tilde{\delta }}_{\widehat{\mathcal{A}}})\cup L({\tilde{\delta }}_{\widehat{\mathcal{A}}})and{\omega }_{\mathcal{A}}(q_i,x_i,p_i)\in U({\tilde{\delta }}_{\mathcal{A}})\cup L({\tilde{\delta }}_{\mathcal{A}})$$

for all $p_i,q_i\in \mathcal{S}$ and $x_i\in X.$ Where

$$U({\tilde{\delta }}_{\widehat{\mathcal{A}}})=\{{\delta }_{\widehat{\mathcal{A}}}^{+}(p_i)|p_i\in \mathcal{S}\},L({\tilde{\delta }}_{\widehat{\mathcal{A}}})=\{{\delta }_{\widehat{\mathcal{A}}}^{-}(p_i)|p_i\in \mathcal{S}\}$$

and

$$U({\tilde{\delta }}_{\mathcal{A}})=\{{\delta }_{\mathcal{A}}^{+}(q_i,x_i,p_i)|(q_i,x_i,p_i)\in \mathcal{S}\times X\times \mathcal{S}\}, L({\tilde{\delta }}_{\mathcal{A}})=\{{\delta }_{\mathcal{A}}^{-}(q_i,x_i,p_i)|(q_i,x_i,p_i)\in \mathcal{S}\times X\times \mathcal{S}\}.$$

Proof. 

Assume that $\widehat{\mathcal{A}}=⟨{\tilde{\delta }}_{\widehat{\mathcal{A}}},{\omega }_{\widehat{\mathcal{A}}}⟩$ is both an IC-subsystem and an EC-subsystem. Then, by definition, we have

$${\omega }_{\widehat{\mathcal{A}}}(p_i)\in [{\delta }_{\widehat{\mathcal{A}}}^{-}(p_i),{\delta }_{\widehat{\mathcal{A}}}^{+}(p_i)],{\omega }_{\mathcal{A}}(q_i,x_i,p_i)\in [{\delta }_{\mathcal{A}}^{-}(q_i,x_i,p_i),{\delta }_{\mathcal{A}}^{+}(q_i,x_i,p_i)]$$

and

$${\omega }_{\widehat{\mathcal{A}}}(p_i)\notin ({\delta }_{\widehat{\mathcal{A}}}^{-}(p_i),{\delta }_{\widehat{\mathcal{A}}}^{+}(p_i)),{\omega }_{\mathcal{A}}(q_i,x_i,p_i)\notin ({\delta }_{\mathcal{A}}^{-}(q_i,x_i,p_i),{\delta }_{\mathcal{A}}^{+}(q_i,x_i,p_i)).$$

Thus, ${\omega }_{\widehat{\mathcal{A}}}(p_i)={\delta }_{\widehat{\mathcal{A}}}^{-}(p_i)$ or ${\omega }_{\widehat{\mathcal{A}}}(p_i)={\delta }_{\widehat{\mathcal{A}}}^{+}(p_i)$ and ${\omega }_{\mathcal{A}}(q_i,x_i,p_i)={\delta }_{\mathcal{A}}^{-}(q_i,x_i,p_i)$ or ${\omega }_{\mathcal{A}}(q_i,x_i,p_i)={\delta }_{\mathcal{A}}^{+}(q_i,x_i,p_i).$ Hence,

$${\omega }_{\widehat{\mathcal{A}}}(p_i)\in U({\tilde{\delta }}_{\widehat{\mathcal{A}}})\cup L({\tilde{\delta }}_{\widehat{\mathcal{A}}}) \mathrm{and} {\omega }_{\mathcal{A}}(q_i,x_i,p_i)\in U({\tilde{\delta }}_{\mathcal{A}})\cup L({\tilde{\delta }}_{\mathcal{A}})$$

for all $p_i,q_i\in \mathcal{S}$ and $x_i\in X.$ ☐

6. Conclusions

There are some generalizations in the concept of fuzzy sets, for example: vague sets, i.v fuzzy sets, bipolar fuzzy set, intuitionistic fuzzy sets, etc. Fuzzy sets deal with the positive characteristics of a problem while intuitionistic fuzzy sets deal with both the positive and negative characteristics of a problem. In addition, it is not possible in many problems to give a certain fix membership grade to a certain thing on the basis of its positive characteristics so we use cubic sets, which generalize the fuzzy sets and intutionistic fuzzy sets. Cubic sets are used for handling uncertainty if fuzzy sets, intuitionistic fuzzy sets and i.v fuzzy sets fails in dealing with uncertainty. The main advantage of the cubic set is that it contains more knowledge than the fuzzy set and the i.v fuzzy set. By using this idea, we can deal with different problems occur in several areas and can take the finest choice by means of cubic sets in different decision making problems.

A relationship between cubic sets and finite state machines was considered. We showed that the cartesian composition, direct product and union of two subsystems of cubic FSMs is a subsystem of a cubic FSM. Many Examples have been provided on each case. We considered conditions for subsystem of cubic FSM to be both an internal cubic subsystem of cubic FSM and an external cubic subsystem of cubic FSM.

Questions on the construction of “P-union, P-intersection, R-union, and R-intersection of cubic subsystems of cubic FSMs” is still open. In addition, applying the concept of cubic set theory to the switchboard state machines, which is a restricted and interesting class of FSMs, is still open.