A Comparison of Tree Segmentation Methods for Savanna Tree Extraction from TLS Point Clouds
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. 3D Vegetation Point Cloud
2.3. Pre-Processing of the TLS Point Cloud Data
2.4. Tree Segmentation- Comparative Shortest Path Algorithm
2.5. Tree Segmentation—A Shortest Path-Based Tree Isolation Method
2.6. Accuracy Assessment
2.7. Tree Reconstruction with Quantitative Structure Models
2.8. Tree-to-Tree Matching
2.9. Statistical Analysis
3. Results
3.1. Segmentation Summary & Accuracy Assessment
3.2. Voxel Volume Covering the Over and Under-Segmented Trees
3.3. Comparison of Tree Recovery by Segmentation Methods
3.4. Comparison of Plot Level Metrics Between the Segmentation Methods
3.5. Quantifying the Other Segments in the Plot
4. Discussion
4.1. Accuracy Between Segmentation Methods for Savanna Tree Extraction
4.2. Segmentation Errors Shared by Both Segmentation Methods
4.3. Uncertainty and Limitations of the Approach
4.4. Future Outlook
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| CSP (n = 124) | SPBTIM (n = 125) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | Mean | Max | Min | 95th Percentile | SEM | SD | Mean | Max | Min | 95th Percentile | SEM | SD | p Value |
| ToV (L) | 3182 | 9414 | 139 | 7379 | 189 | 2110 | 3157 | 9985 | 113 | 7317 | 188 | 2099 | 0.93 |
| TrV (L) | 812 | 2163 | 35 | 1731 | 43 | 482 | 815 | 2171 | 27 | 1711 | 43 | 478 | 0.96 |
| BrV (L) | 2370 | 7781 | 104 | 5992 | 153 | 1704 | 2342 | 8098 | 87 | 5783 | 153 | 1706 | 0.90 |
| TH (m) | 10.8 | 15.2 | 5.3 | 13.7 | 0.2 | 1.9 | 10.9 | 15.0 | 5.3 | 13.6 | 0.2 | 1.9 | 0.71 |
| BrL (m) | 701.0 | 2747.0 | 44.6 | 1688.5 | 45.5 | 506.5 | 665.6 | 2547.0 | 52.2 | 1573.2 | 43.3 | 484.4 | 0.57 |
| DBH (cm) | 43 | 73 | 11 | 63 | 1 | 14 | 43 | 75 | 10 | 64 | 1 | 14 | 0.98 |
| CA (m2) | 80.2 | 219.6 | 2.9 | 171.0 | 4.3 | 48.3 | 80.7 | 216.4 | 2.8 | 165.5 | 4.3 | 48.0 | 0.85 |
References
- Sankaran, M.; Ratnam, J.; Hanan, N. Woody cover in African savannas: The role of resources, fire and herbivory. Glob. Ecol. Biogeogr. 2008, 17, 236–245. [Google Scholar] [CrossRef]
- Smit, I.P.; Asner, G.P.; Govender, N.; Kennedy-Bowdoin, T.; Knapp, D.E.; Jacobson, J. Effects of fire on woody vegetation structure in African savanna. Ecol. Appl. 2010, 20, 1865–1875. [Google Scholar] [CrossRef]
- Grace, J.; José, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and carbon fluxes of tropical savannas. J. Biogeogr. 2006, 33, 387–400. [Google Scholar] [CrossRef]
- Stevens, N.; Lehmann, C.E.R.; Murphy, B.P.; Durigan, G. Savanna woody encroachment is widespread across three continents. Glob. Chang. Biol. 2017, 23, 235–244. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Levick, S.R. Landscape-scale effects of herbivores on treefall in African savannas. Ecol. Lett. 2012, 15, 1211–1217. [Google Scholar] [CrossRef]
- Helm, C.V.; Witkowski, E.T.F.; Kruger, L.; Hofmeyr, M.; Owen-Smith, N. Mortality and utilisation of Sclerocarya birrea subsp. Caffra between 2001 and 2008 in the Kruger National Park, South Africa. S. Afr. J. Bot. 2009, 75, 475–484. [Google Scholar] [CrossRef]
- Vanak, A.T.; Shannon, G.; Thaker, M.; Page, B.; Grant, R.; Slotow, R. Biocomplexity in large tree mortality: Interactions between elephant, fire and landscape in an African savanna. Ecography 2012, 35, 315–321. [Google Scholar] [CrossRef]
- Levick, S.R.; Asner, G.P. The rate and spatial pattern of treefall in a savanna landscape. Biol. Conserv. 2013, 157, 121–127. [Google Scholar] [CrossRef]
- Cho, M.A.; Mathieu, R.; Asner, G.P.; Naidoo, L.; van Aardt, J.; Ramoelo, A.; Debba, P.; Wessels, K.; Main, R.; Smit, I.P.J.; et al. Mapping tree species composition in South African savannas using an integrated airborne spectral and LiDAR system. Remote Sens. Environ. 2012, 125, 214–226. [Google Scholar] [CrossRef]
- Pavelka, K.; Matoušková, E.; Pavelka, K. Remarks on Geomatics Measurement Methods Focused on Forestry Inventory. Sensors 2023, 23, 7376. [Google Scholar] [CrossRef]
- Hill, R.A.; Broughton, R.K. Mapping the understorey of deciduous woodland from leaf-on and leaf-off airborne LiDAR data: A case study in lowland Britain. ISPRS J. Photogramm. Remote Sens. 2009, 64, 223–233. [Google Scholar] [CrossRef]
- Boukoberine, M.N.; Zhou, Z.; Benbouzid, M. A critical review on unmanned aerial vehicles power supply and energy management: Solutions, strategies, and prospects. Appl. Energy 2019, 255, 113823. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. ISPRS J. Photogramm. Remote Sens. 2012, 69, 167–179. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.L.; Fournier, R.A.; Côté, J.F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial LiDAR measurements. Agric. For. Meteorolo. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote. Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Tansey, K.; Selmes, N.; Anstee, A.; Tate, N.J.; Denniss, A. Estimating tree and stand variables in a Corsican Pine woodland from terrestrial laser scanner data. Int. J. Remote Sens. 2009, 30, 5195–5209. [Google Scholar] [CrossRef]
- Bogdanovich, E.; Perez-Priego, O.; El-Madany, T.S.; Guderle, M.; Pacheco-Labrador, J.; Levick, S.R.; Moreno, G.; Carrara, A.; Martín, M.P.; Migliavacca, M. Using terrestrial laser scanning for characterizing tree structural parameters and their changes under different management in a Mediterranean open woodland. For. Ecol. Manag. 2021, 486, 118945. [Google Scholar] [CrossRef]
- Tao, S.; Wu, F.; Guo, Q.; Wang, Y.; Li, W.; Xue, B.; Hu, X.; Li, P.; Tian, D.; Li, C.; et al. Segmenting tree crowns from terrestrial and mobile LiDAR data by exploring ecological theories. ISPRS J. Photogramm. Remote. Sens. 2015, 110, 66–76. [Google Scholar] [CrossRef]
- Pirotti, F.; Kobal, M.; Roussel, J.R. A COMPARISON OF TREE SEGMENTATION METHODS USING VERY HIGH DENSITY AIRBORNE LASER SCANNER DATA. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci.-ISPRS Arch. 2017, 42, 285–290. [Google Scholar] [CrossRef]
- Xu, X.; Iuricich, F.; Calders, K.; Armston, J.; De Floriani, L. Topology-based individual tree segmentation for automated processing of terrestrial laser scanning point clouds. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103145. [Google Scholar] [CrossRef]
- Zhan, Q.; Liang, Y.; Xiao, Y. Color-Based Segmentation of Point Clouds. In Laser Scanning; IAPRS: Hannover, Germany, 2009; Volume XXXVIII, pp. 248–252. [Google Scholar]
- Fisher, J.T.; Erasmus, B.F.N.; Witkowski, E.T.F.; van Aardt, J.; Wessels, K.J.; Asner, G.P. Savanna woody vegetation classification-now in 3-D. Appl. Veg. Sci. 2014, 17, 172–184. [Google Scholar] [CrossRef]
- Xin, H.L.; Malhi, Y.; Coomes, D.A.; Lin, Y.; Liu, B.L.; Yang, Q.L.; Shenkin, A. Individual tree detection and crown segmentation based on metabolic theory from airborne laser scanning data. J. Appl. Remote Sens. 2021, 15, 034504. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, W.; Zhang, J.; Liu, Y.; Xu, D.; Wang, J. Point-cloud segmentation of individual trees in complex natural forest scenes based on a trunk-growth method. J. For. Res. 2021, 32, 2403–2414. [Google Scholar] [CrossRef]
- Williams, J.; Schonlieb, C.B.; Swinfield, T.; Lee, J.; Cai, X.; Qie, L. 3D Segmentation of Trees through a Flexible Multiclass Graph Cut Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 58, 754–776. [Google Scholar] [CrossRef]
- Swetnam, T.L.; Falk, D.A. Application of Metabolic Scaling Theory to reduce error in local maxima tree segmentation from aerial LiDAR. For. Ecol. Manage. 2014, 323, 158–167. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, X.; Zheng, Y.; Xu, L.; Huang, Q. Improved Tree Segmentation Algorithm Based on Backpack-LiDAR Point Cloud. Forests 2024, 15, 136. [Google Scholar] [CrossRef]
- Raumonen, P.; Brede, B.; Lau, A.; Bartholomeus, H. A Shortest Path Based Tree Isolation Method for UAV LiDAR Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 724–727. [Google Scholar] [CrossRef]
- Scholes, R.J.; Gureja, N.; Giannecchinni, M.; Dovie, D.; Wilson, B.; Davidson, N.; Piggott, C.; McLoughlin, K.; van der Velde, A.; Freeman, S.; et al. The environment and vegetation of the flux measurement site near Skukuza, Kruger National Park. Koedoe 2001, 44, 73–84. [Google Scholar] [CrossRef]
- Dyer, C. New names for the African Acacia species in Vachellia and Senegalia. South. Forests. 2014, 76, iii. [Google Scholar] [CrossRef][Green Version]
- Muumbe, T.P.; Baade, J.; Raumonen, P.; Coetsee, C.; Singh, J.; Schmullius, C. Quantifying Tree Structural Change in an African Savanna by Utilizing Multi-Temporal TLS Data. Remote Sens. 2025, 17, 757. [Google Scholar] [CrossRef]
- MacFadyen, S.; Zambatis, N.; Van Teeffelen, A.J.A.; Hui, C. Long-term rainfall regression surfaces for the Kruger National Park, South Africa: A spatio-temporal review of patterns from 1981 to 2015. Int. J. Climatol. 2018, 38, 2506–2519. [Google Scholar] [CrossRef]
- RIEGL Laser Measurements Systems, “RIEGL VZ-1000 High-Resolution and Accurate 3D Measurements”, Data Sheet 2017, pp. 1–4. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/DataSheet_VZ-1000_2017-06-14.pdf (accessed on 15 January 2025).
- Riegl LMS GmbH, “RiSCAN PRO.” 2013, pp. 1–21. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/RiSCAN-PRO_DataSheet_2022-10-07.pdf (accessed on 15 January 2025).
- Burt, A.; Disney, M.; Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 2019, 10, 438–445. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. “CloudCompare”. Paris, France. 2022. Available online: https://github.com/CloudCompare (accessed on 15 January 2025).
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Wielgosz, M.; Puliti, S.; Xiang, B.; Schindler, K.; Astrup, R. SegmentAnyTree: A sensor and platform agnostic deep learning model for tree segmentation using laser scanning data. Remote. Sens. Environ. 2024, 313, 114367. [Google Scholar] [CrossRef]
- Singh, M.; Evans, D.; Tan, B.S.; Nin, C.S. Mapping and Characterizing Selected Canopy Tree Species at the Angkor World Heritage Site in Cambodia Using Aerial Data. PLoS ONE 2015, 10, e0121558. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lei, L.; Li, Z. Individual Tree Segmentation Based on Seed Points Detected by an Adaptive Crown Shaped Algorithm Using UAV-LiDAR Data. Remote Sens. 2024, 16, 825. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerbloma, M.; Kaasalainen, M. Massive-Scale Tree Modelling From Tls Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 189–196. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Fekry, R.; Yao, W.; Cao, L.; Shen, X. Ground-based/UAV-LiDAR data fusion for quantitative structure modeling and tree parameter retrieval in subtropical planted forest. For. Ecosyst. 2022, 9, 100065. [Google Scholar] [CrossRef]
- Wilkes, P.; Shenkin, A.; Disney, M.; Malhi, Y.; Bentley, L.P.; Vicari, M.B. Terrestrial laser scanning to reconstruct branch architecture from harvested branches. Methods Ecol. Evol. 2021, 12, 2487–2500. [Google Scholar] [CrossRef]
- Abegg, M.; Bösch, R.; Kükenbrink, D.; Morsdorf, F. Tree volume estimation with terrestrial laser scanning — Testing for bias in a 3D virtual environment. Agric. For. Meteorol. 2023, 331, 109348. [Google Scholar] [CrossRef]
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 4 December 2024).
- Wang, D. Unsupervised semantic and instance segmentation of forest point clouds. ISPRS J. Photogramm. Remote Sens. 2020, 165, 86–97. [Google Scholar] [CrossRef]
- Luck, L.; Hutley, L.B.; Calders, K.; Levick, S.R. Exploring the variability of tropical savanna tree structural allometry with terrestrial laser scanning. Remote Sens. 2020, 12, 3893. [Google Scholar] [CrossRef]
- Martin-Ducup, O.; Mofack, G.; Wang, D.; Raumonen, P.; Ploton, P.; Sonké, B.; Barbier, N.; Couteron, P.; Pélissier, R. Evaluation of automated pipelines for tree and plot metric estimation from TLS data in tropical forest areas. Ann. Bot. 2021, 128, 753–766. [Google Scholar] [CrossRef]
- Lisiewicz, M.; Kamińska, A.; Kraszewski, B.; Stereńczak, K. Correcting the Results of CHM-Based Individual Tree Detection Algorithms to Improve Their Accuracy and Reliability. Remote Sens. 2022, 14, 1822. [Google Scholar] [CrossRef]
- Wilkes, P.; Disney, M.; Armston, J.; Bartholomeus, H.; Bentley, L.; Brede, B.; Burt, A.; Calders, K.; Chavana-Bryant, C.; Clewley, D.; et al. TLS2trees: A scalable tree segmentation pipeline for TLS data. Methods Ecol. Evol. 2023, 14, 3083–3099. [Google Scholar] [CrossRef]
- Steier, J.; Goebel, M.; Iwaszczuk, D. Is Your Training Data Really Ground Truth? A Quality Assessment of Manual Annotation for Individual Tree Crown Delineation. Remote Sens. 2024, 16, 2786. [Google Scholar] [CrossRef]
- Zhang, Q.; Cai, S.; Liang, X. Individual tree segmentation in occluded complex forest stands through ellipsoid directional searching and point compensation. For. Ecosyst. 2024, 11, 100238. [Google Scholar] [CrossRef]
- Wang, D.; Liang, X.; Mofack, G.I.; Martin-Ducup, O. Individual tree extraction from terrestrial laser scanning data via graph pathing. For. Ecosyst. 2021, 8, 67. [Google Scholar] [CrossRef]
- Wardius, Y.; Hein, S. Terrestrial laser scanning vs. manual methods for assessing complex forest stand structure: A comparative analysis on plenter forests. Eur. J. For. Res. 2024, 143, 635–649. [Google Scholar] [CrossRef]
- Allen, M.J.; Owen, H.J.F.; Grieve, S.W.D.; Lines, E.R. Manual Labelling Artificially Inflates Deep Learning-Based Segmentation Performance on Closed Canopy: Validation Using TLS. arXiv 2025, arXiv:2503.14273. [Google Scholar]
- Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.M.; Bartolo, R.; Calders, K.; Derroire, G.; Moorthy, S.M.K.; Lau, A.; Levick, S.R.; et al. Non-destructive estimation of individual tree biomass: Allometric models, terrestrial and UAV laser scanning. Remote Sens Environ. 2022, 280, 113180. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Fu, H.; Li, H.; Dong, Y.; Xu, F.; Chen, F. Segmenting Individual Tree from TLS Point Clouds Using Improved DBSCAN. Forests 2022, 13, 566. [Google Scholar] [CrossRef]
- Ye, N.; van Leeuwen, L.; Nyktas, P. Analysing the potential of UAV point cloud as input in quantitative structure modelling for assessment of woody biomass of single trees. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 47–57. [Google Scholar] [CrossRef]
- Morales, A.; Macfarlane, D.W. Reducing tree volume overestimation in quantitative structure models using modeled branch topology and direct twig measurements. For. An. Int. J. For. Res. 2024, 98, 394–409. [Google Scholar] [CrossRef]
- Li, Y.; Xie, D.; Wang, Y.; Jin, S.; Zhou, K.; Zhang, Z.; Li, W.; Zhang, W.; Mu, X.; Yan, G. Individual tree segmentation of airborne and UAV LiDAR point clouds based on the watershed and optimized connection center evolution clustering. Ecol. Evol. 2023, 13, e10297. [Google Scholar] [CrossRef]
- Yang, Q.; Su, Y.; Jin, S.; Kelly, M.; Hu, T.; Ma, Q.; Li, Y.; Song, S.; Zhang, J.; Xu, G.; et al. The influence of vegetation characteristics on individual tree segmentation methods with airborne LiDAR data. Remote Sens. 2019, 11, 2880. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef]
- Chen, X.; Wang, R.; Shi, W.; Li, X.; Zhu, X.; Wang, X. An Individual Tree Segmentation Method That Combines LiDAR Data and Spectral Imagery. Forests 2023, 14, 1009. [Google Scholar] [CrossRef]
- Richardson, J.J.; Monika Moskal, L.; Bakker, J.D. Terrestrial laser scanning for vegetation sampling. Sensors 2014, 14, 20304–20319. [Google Scholar] [CrossRef]
- Goebel, M.; Iwaszczuk, D. Backpack System for Capturing 3D Point Clouds of Forests. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 10, 695–702. [Google Scholar] [CrossRef]



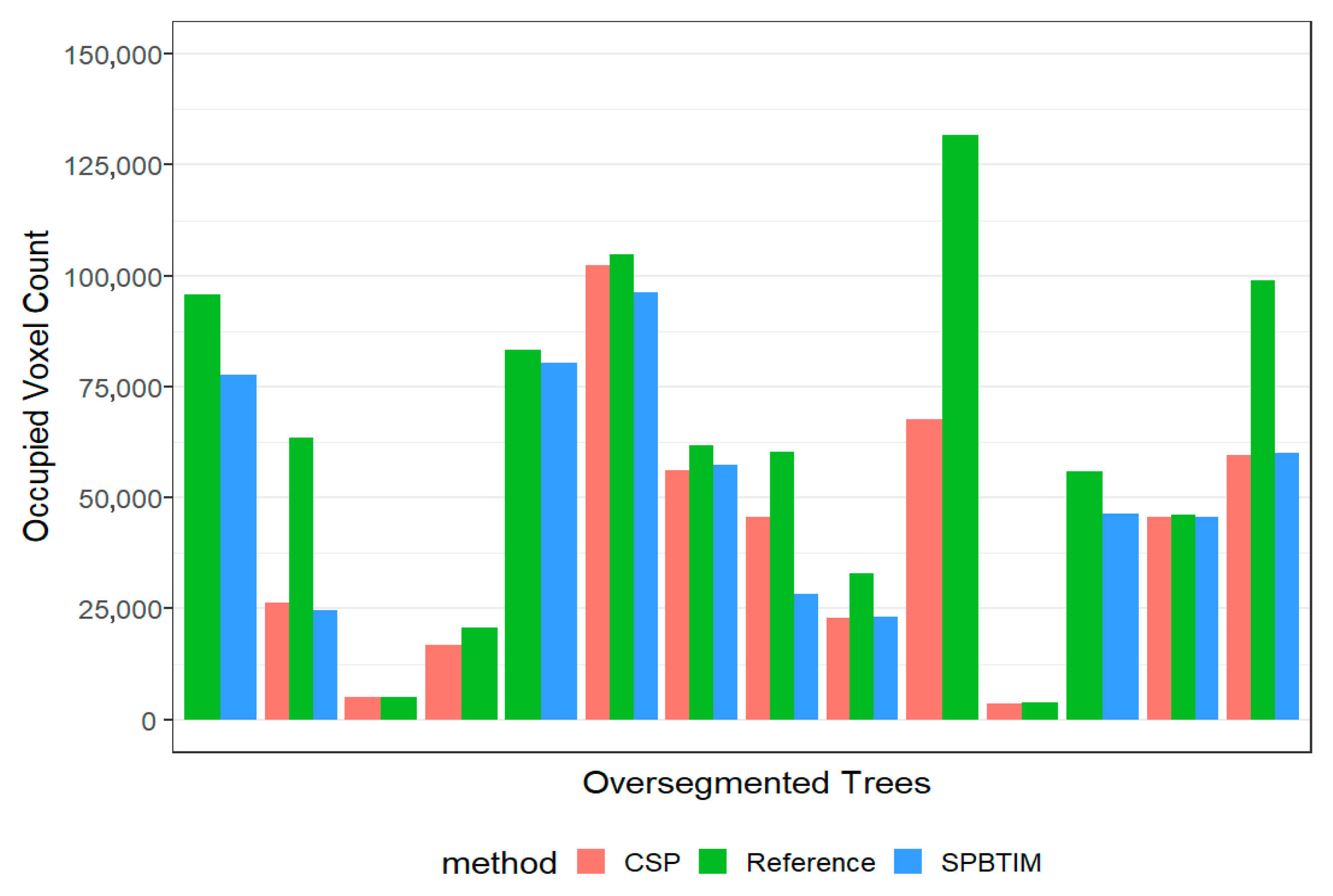
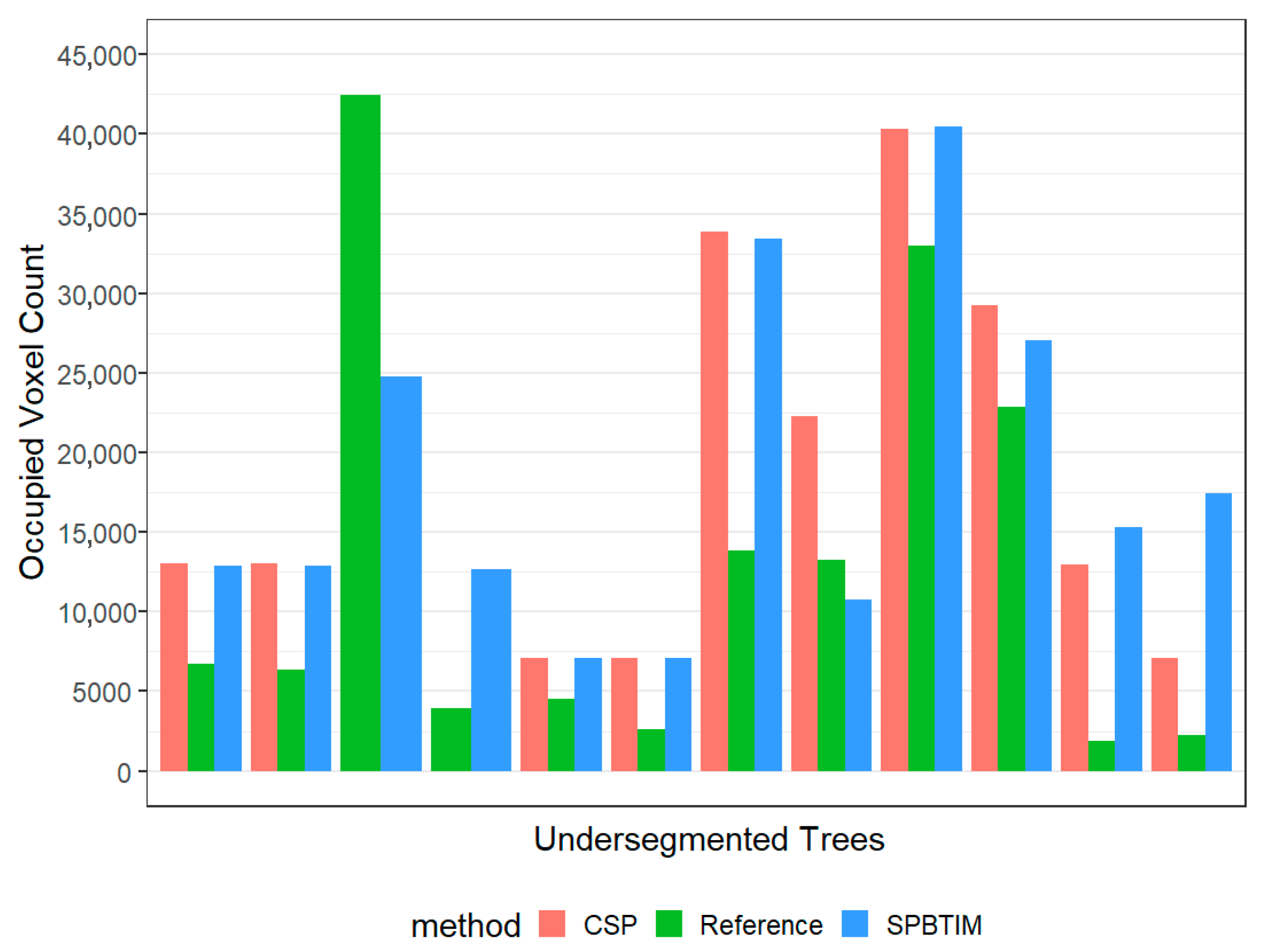






| ADVANTAGES | DISADVANTAGES |
|---|---|
|
|
| ADVANTAGES | DISADVANTAGES |
|---|---|
|
|
| Type of Segment | CSP | SPBTIM |
|---|---|---|
| True positives (perfect segmentation) | 103 | 103 |
| False positive (over-segmented) | 11 | 10 |
| False negatives (under-segmented) | 11 | 12 |
| Recall (r) | 0.90 | 0.90 |
| Precision (p) | 0.90 | 0.91 |
| F-score | 0.90 | 0.90 |
| Type of Segment (n) | CSP Mean ± SE | Reference Trees Mean ± SE | p Value |
|---|---|---|---|
| False Negatives (10) | 18,604 ± 3834 | 10,725 ± 3248 | 0.13 |
| False Positives (11) | 41,057 ± 9003 | 57,264 ± 12,524 | 0.31 |
| SPBTIM Mean ± SE | Reference trees Mean ± SE | p value | |
| False Negatives (12) | 18,486 ± 3074 | 12,804 ± 3845 | 0.26 |
| False Positives (10) | 53,982 ± 7951 | 70,352 ± 7636 | 0.15 |
| Common Trees in Both Segmentation Methods | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | False Positives—CSP | False Positives—SPBTIM | |||||||||||||||
| ID | 479 | 517 | 687 | 906 | 915 | 1044 | 1344 | Average common trees CSP | 34 | 92 | 15 | 38 | 57 | 86 | 95 | Average common trees SPBTIM | p value |
| Tov | 58.5 | 55.3 | 96.9 | 101.8 | 95.8 | 78.1 | 71.8 | 79.7 | 64.1 | 55.4 | 91.0 | 102.2 | 96.1 | 88.7 | 66.0 | 80.5 | 0.94 |
| TrV | 121.4 | 100.1 | 101.4 | 99.6 | 95.8 | 126.6 | 90.6 | 105.1 | 194.6 | 100.4 | 97.2 | 100.6 | 100.1 | 96.3 | 88.3 | 111.1 | 0.70 |
| BrV | 50.9 | 43.7 | 95.2 | 102.5 | 95.8 | 67.9 | 69.6 | 75.1 | 48.4 | 43.7 | 88.6 | 102.7 | 94.3 | 87.1 | 63.4 | 75.5 | 0.98 |
| TH | 109.9 | 97.4 | 100.9 | 100.0 | 100.5 | 73.6 | 100.3 | 97.5 | 110.2 | 97.3 | 98.6 | 100.4 | 100.5 | 66.2 | 99.8 | 96.1 | 0.84 |
| BrL | 37.1 | 36.1 | 84.9 | 80.4 | 103.0 | 64.1 | 53.6 | 65.6 | 36.5 | 34.3 | 68.7 | 79.1 | 101.2 | 34.3 | 49.4 | 57.6 | 0.57 |
| DBH | 54.2 | 99.9 | 105.1 | 98.8 | 99.3 | 103.2 | 90.8 | 93.0 | 78.3 | 102.6 | 97.4 | 99.0 | 103.5 | 89.8 | 90.3 | 94.4 | 0.86 |
| CA | 66.7 | 69.9 | 94.4 | 91.4 | 98.2 | 67.0 | 75.0 | 80.4 | 70.5 | 68.2 | 92.4 | 93.7 | 98.4 | 47.8 | 83.6 | 79.2 | 0.90 |
| Different trees | |||||||||||||||||
| Metric | False positive—CSP | False Positives—SPBTIM | |||||||||||||||
| ID | 1595 | 671 | 805 | 1513 | Average all trees CSP | 16 | 19 | 59 | Average all trees SPBTIM | p value | |||||||
| Tov | 82.5 | 98.9 | 94.7 | 50.3 | 80.4 | 100.7 | 122.2 | 89.0 | 87.5 | 0.42 | |||||||
| TrV | 118.3 | 100.2 | 100.7 | 92.5 | 104.3 | 101.6 | 83.5 | 103.8 | 106.6 | 0.83 | |||||||
| BrV | 75.4 | 96.1 | 92.2 | 41.3 | 75.5 | 100.5 | 139.9 | 82.0 | 85.1 | 0.40 | |||||||
| TH | 99.0 | 100.5 | 100.2 | 99.8 | 98.4 | 100.4 | 95.1 | 99.9 | 96.8 | 0.73 | |||||||
| BrL | 57.9 | 97.4 | 75.4 | 35.2 | 65.9 | 73.3 | 67.7 | 71.6 | 61.6 | 0.68 | |||||||
| DBH | 101.4 | 99.5 | 97.3 | 97.7 | 95.2 | 98.5 | 102.5 | 101.5 | 96.3 | 0.82 | |||||||
| CA | 66.1 | 98.6 | 88.6 | 47.5 | 78.5 | 95.9 | 72.1 | 84.3 | 80.7 | 0.76 | |||||||
| Common Trees | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metric | False Negatives—CSP | False Negatives—SPBTIM | |||||||||||||||||||||
| ID | 977 | 977 | 1723 | 1723 | 478 | 570 | 698 | 835 | 1105 | 1085 | Average common trees CSP | 114 | 114 | 133 | 133 | 76 | 122 | 64 | 83 | 115 | 111 | Average common trees SPBTIM | p value |
| Tov | 185.7 | 201.6 | 170.6 | 195.8 | 269.8 | 148.3 | 112.0 | 104.9 | 1000.9 | 451.8 | 284.1 | 192.4 | 208.8 | 175.0 | 200.9 | 240.5 | 79.3 | 106.6 | 102.9 | 1029.7 | 836.1 | 317.2 | 0.81 |
| TrV | 102.1 | 103.8 | 150.4 | 131.4 | 199.9 | 127.5 | 94.6 | 72.8 | 965.6 | 222.7 | 217.1 | 98.3 | 99.9 | 151.2 | 132.1 | 136.0 | 84.5 | 95.1 | 70.9 | 1647.0 | 452.9 | 296.8 | 0.66 |
| BrV | 224.2 | 251.2 | 179.0 | 236.2 | 292.3 | 152.9 | 119.7 | 110.9 | 1005.3 | 516.3 | 308.8 | 235.6 | 264.0 | 184.9 | 244.1 | 274.3 | 78.2 | 111.6 | 109.0 | 952.4 | 944.2 | 339.8 | 0.82 |
| TH | 97.2 | 110.2 | 100.2 | 103.6 | 218.4 | 172.7 | 116.4 | 137.7 | 213.0 | 231.2 | 150.1 | 100.1 | 113.4 | 99.2 | 102.5 | 205.7 | 170.0 | 116.0 | 142.7 | 205.0 | 251.8 | 150.6 | 0.98 |
| BrL | 169.1 | 160.2 | 147.3 | 208.0 | 212.1 | 132.6 | 113.1 | 83.7 | 501.8 | 382.5 | 211.0 | 186.2 | 176.5 | 122.5 | 173.0 | 223.8 | 72.4 | 105.8 | 79.3 | 436.6 | 834.3 | 241.0 | 0.73 |
| DBH | 108.1 | 98.3 | 134.7 | 116.1 | 143.8 | 102.3 | 101.4 | 69.2 | 343.8 | 171.2 | 138.9 | 106.2 | 96.6 | 128.9 | 111.1 | 102.7 | 102.6 | 105.0 | 63.4 | 357.9 | 186.1 | 136.1 | 0.94 |
| CA | 198.4 | 194.0 | 136.2 | 218.1 | 197.6 | 213.2 | 103.7 | 110.6 | 425.5 | 167.9 | 196.5 | 225.3 | 220.3 | 131.8 | 211.1 | 251.7 | 165.7 | 105.9 | 105.9 | 475.6 | 333.6 | 222.7 | 0.58 |
| Different trees | |||||||||||||||||||||||
| Metric | xxx | False negatives—SPBTIM | |||||||||||||||||||||
| ID | 89 | 116 | Average all trees | p value | |||||||||||||||||||
| Tov | 70.1 | 247.6 | 290.8 | 0.96 | |||||||||||||||||||
| TrV | 118.0 | 278.6 | 280.4 | 0.70 | |||||||||||||||||||
| BrV | 64.5 | 241.5 | 308.7 | 0.99 | |||||||||||||||||||
| TH | 107.0 | 180.4 | 149.5 | 0.98 | |||||||||||||||||||
| BrL | 49.0 | 219.3 | 223.2 | 0.88 | |||||||||||||||||||
| DBH | 96.8 | 107.1 | 130.4 | 0.80 | |||||||||||||||||||
| CA | 70.7 | 269.6 | 214.0 | 0.70 | |||||||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muumbe, T.P.; Raumonen, P.; Baade, J.; Coetsee, C.; Singh, J.; Schmullius, C. A Comparison of Tree Segmentation Methods for Savanna Tree Extraction from TLS Point Clouds. Land 2025, 14, 1761. https://doi.org/10.3390/land14091761
Muumbe TP, Raumonen P, Baade J, Coetsee C, Singh J, Schmullius C. A Comparison of Tree Segmentation Methods for Savanna Tree Extraction from TLS Point Clouds. Land. 2025; 14(9):1761. https://doi.org/10.3390/land14091761
Chicago/Turabian StyleMuumbe, Tasiyiwa Priscilla, Pasi Raumonen, Jussi Baade, Corli Coetsee, Jenia Singh, and Christiane Schmullius. 2025. "A Comparison of Tree Segmentation Methods for Savanna Tree Extraction from TLS Point Clouds" Land 14, no. 9: 1761. https://doi.org/10.3390/land14091761
APA StyleMuumbe, T. P., Raumonen, P., Baade, J., Coetsee, C., Singh, J., & Schmullius, C. (2025). A Comparison of Tree Segmentation Methods for Savanna Tree Extraction from TLS Point Clouds. Land, 14(9), 1761. https://doi.org/10.3390/land14091761






